随着飞行技术的发展,高速突防已成为飞行器反拦截的重要手段.目标飞行速度高于拦截器,为拦截任务带来极大的困难^{[1, 2]}.针对此问题,以往的制导律大多基于比例制导(Proportional Navigation,PN),并且可以按照拦截模式划分为逆轨拦截和顺轨拦截2种类型.采用经典比例制导律及其改进形式拦截运动速度大于拦截弹本身的目标时,通常采用逆轨拦截方式,其优势在于拦截时间短,控制力小.Kuroda和Imado等^{[3, 4]}设计了2种改进的比例制导律并推导了碰撞区域.Lin^[5]和Tyan^[6]等设计了三维纯比例制导律并推导了捕获区域.Taur^[7]推导了改进的扩展增广比例制导(Augmented Proportional Navigation,APN),在末段拦截高超声速目标.顺轨拦截的优势在于弹目接近速度低、所需过载小,但相应的研究成果较少.Golan^[8]提出的顺轨拦截制导律,通过时变的框架角引导拦截弹提前到达目标的预测位置;Shima^{[9, 10]}提出了使用滑模制导的方法,能够按照指定碰撞角顺轨拦截机动目标;Prasanna^[11]提出了负比例(Retro Proportional Navigation,RPN)制导律,加速度方向与比例制导律相反,在顺轨模式下以小碰撞角拦截目标.在逆轨拦截模式下,制导律通常会导引拦截弹按照捷径对目标进行拦截,其捕获区域(拦截弹初始路径倾角)主要集中在与视线角呈锐角的区域.虽然顺轨拦截模式的拦截时间和拦截路径较长,但是相对逆轨拦截具有更大的捕获区域.在一定范围内,目标速度越大,捕获区域的优势越明显,其捕获区域主要集中在与视线角呈钝角的区域.如果能将顺/逆轨拦截模式结合,不但拦截弹对目标的适应性增强,而且捕获区域可以大幅增加.因此,本文提出一种制导律,称作联合比例制导律(United Proportional Navigation,UPN).针对目标加速度,推导了视线角速率的解析式,为结合顺逆轨拦截的优势,设计了时变导航比,使制导律在三维条件下,可根据情况按照顺顺轨、逆逆轨和顺逆轨结合模式拦截目标,极大地提升了捕获区域.1 UPN制导律设计1.1 制导方程本文主要研究拦截弹与目标的二维平面运动,为了便于分析,做出如下假设:将拦截弹与目标看作平面上运动的质点,且速度大小恒定不变;目标加速度的大小是恒定的,且始终垂直于目标速度方向;忽略重力对拦截弹和目标的影响.UPN制导律的指令加速度表达式为
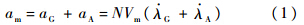
式中：a_G为常规比例制导加速度;a_A为目标加速度修正补偿部分;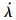_G和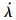_A为对应的视线角速率;N为导航比;V_m为拦截弹速度.拦截弹与目标的平面相对运动关系如图 1所示.

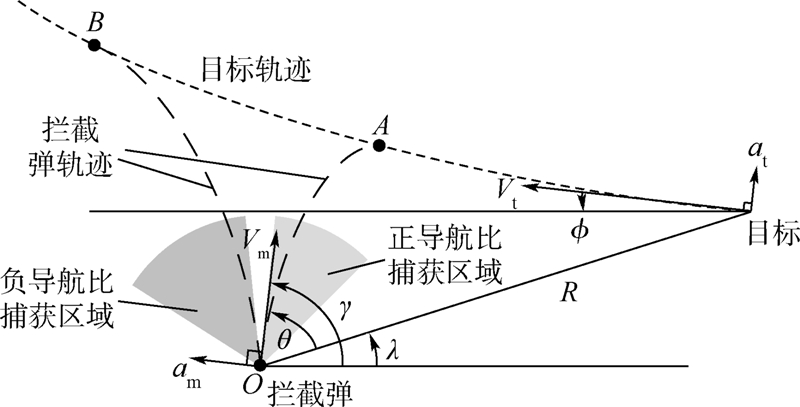R—弹目距离;λ—视线角(LOS);θ—拦截弹框架角; γ —拦截弹的路径倾角; φ —目标的路径倾角;Vt—目标速度;am—拦截弹加速度;at—目标加速度.图 1 平面相对运动几何关系Fig. 1 Planar geometry of relative engagement

图选项

垂直于视线的速度分量为
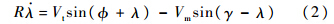
沿视线的速度分量为
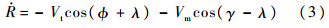
拦截弹的路径倾角变化率为
为便于分析,定义目标与拦截弹的速度比为
对式(2)求导得
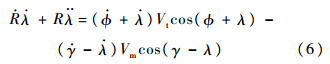
将式(3)与式(4)代入式(6)中得
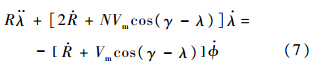
定义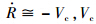为拦截弹接近速度且V_c>0,则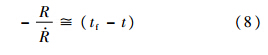
式中：t_f为总拦截时间;t为拦截弹飞行时间.通过式(7)与式(8)可推导出:
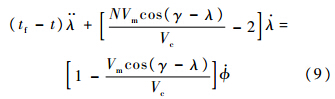
将式(9)化简为
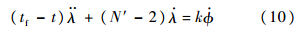
式中：
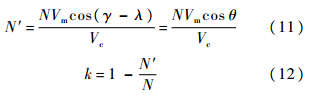
式中：N′通常被称作有效导航比^[12];k为瞬时常量.将式(10)从t₀到t进行积分并整理得
式中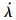：_G为常规比例制导的视线角速率;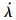_A为视线角速率针对目标加速度的补偿项,其表达式分别为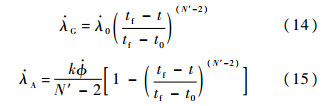
由式(14)与式(15)可知,为保证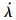收敛,N′的取值应大于2.将式(14)与式(15)代入式(1)得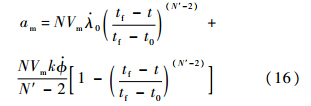
当式(16)中目标加速度a_t=0,即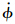=0,结合式(1),制导律为常规比例制导律: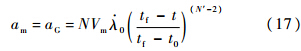
当a_t≠0时,制导指令加速度存在修正项:
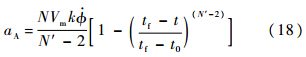
由式(14)得
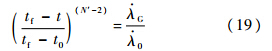
将式(19)代入式(16)可得
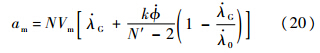
式(20)即为制导方程,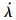_G为导引头测得的视线角速率.拦截弹运用该制导律在自主制导模式下工作时,可采用具有大视场的导引头;在指令制导模式下,接收态势感知系统测得的目标信息即可^[11].因本文所研究的拦截对象为高速目标,则有必要给出拦截弹与目标的速度比范围.引理1 为确保拦截成功,必须保证拦截弹与目标的速度比：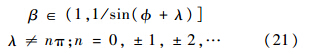
证明 由于目标速度高于拦截弹速度,所以β>1.当R→0时,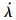=0,通过式(2)可推得: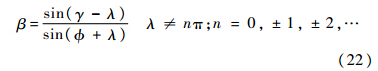
由式(22)可知，当γ－λ=90°时,速度比取到最大值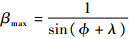.因此,对于任意拦截的制导律,要求β∈(1,1/sin(φ+λ)](λ≠nπ；n=0,±1,±2,…).1.2 导 航 比1.2.1 导航比讨论在比例制导中,通常认为导航比N的取值只能为正.在实际当中,比例制导的导航比N可以为负值,且拦截高速目标时具有更好效果.引理2如果拦截弹采用比例制导律,其导航比N可以为正也可以为负,但必须满足式(23):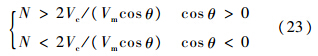
证明 通过式(15)可知,N′>2,代入式(11)得
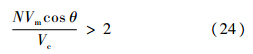
当cos θ>0时,
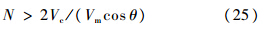
当cos θ<0时,
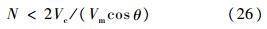
当导航比N为正值时,需满足式(25),拦截模式为逆轨拦截,路径如图 1中OA所示,其拦截时间较短,捕获区域集中在与视线角呈锐角的区域;当导航比N取值为负时,需满足式(26),拦截模式为顺轨拦截,路径如图 1中OB所示,其控制力小,捕获区域主要集中在与视线角呈钝角的区域.如果能将这2种制导律的特性相结合,不但拦截弹对目标的适应性增强,而且捕获区域可以大幅增加.1.2.2 时变导航比由式(11)可得
式中:有效导航比N′为常值,导航比N的取值主要取决于框架角θ的大小.在式(27)中,当cos θ=0时,导航比N无穷大,称为奇点.在奇点附近,导航比过大会导致制导律失效.为避免该情况,制导律中设定框架角的余弦值变化曲线如图 2所示.

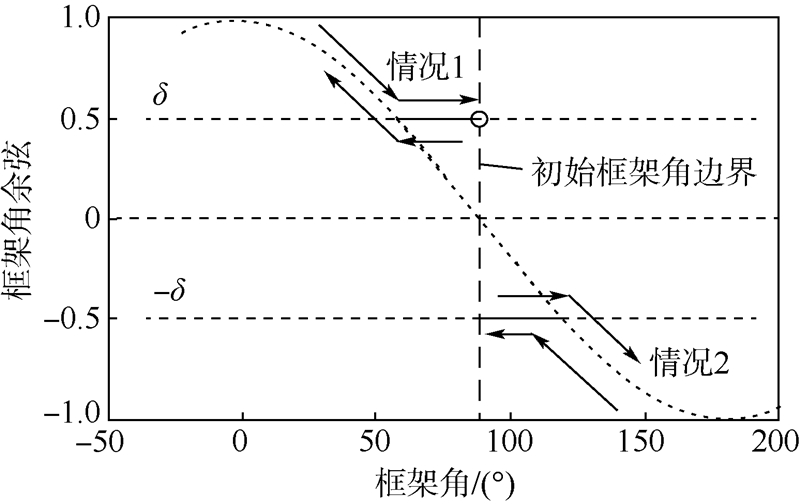图 2时变导航比原理图Fig. 2 Schematic diagram of time varying navigation ratio

图选项

导航比的取值分以下2种情况(θ_i为拦截弹框架角初始值):1) θ_i<90°.整个拦截过程中,θ值始终在θ_i附近但小于90°,对应N的取值定义如下:
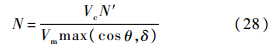
式中:δ为导航比阈值,是为了避免θ→90°时导致N过大而设定的.这种情况下导航比恒为正值,制导律拦截方式与PN制导律相似,拦截路径如图 1中OB所示.2) θ_i≥90°.整个拦截过程中,θ值始终在θ_i附近但不小于90°,对应N的取值定义如下:
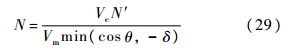
这种情况下导航比恒为负值,制导律拦截方式与RPN制导律相似,拦截路径如图 1中OA所示.由式(28)与式(29)得
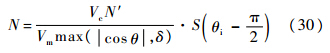
式中:
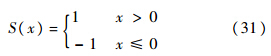
1.2.3 导航比阈值的确定导航比阈值δ是为了避免导航比奇点而设定的.由于阈值的大小能够直接限制拦截弹过载上限,因此阈值须通过所需过载来确定.将式(30)与式(13)代入式(1)得
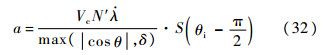
为便于对比分析δ对过载的限制,将式(32)中过载a表示为
式中:δ恒为正值;视线角速率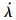取绝对值是为保证过载a为正.对于不同的阈值δ,初始加速度随初始路径倾角从0~π变化的曲线如图 3所示(其他实验参数与二维仿真实验相同).

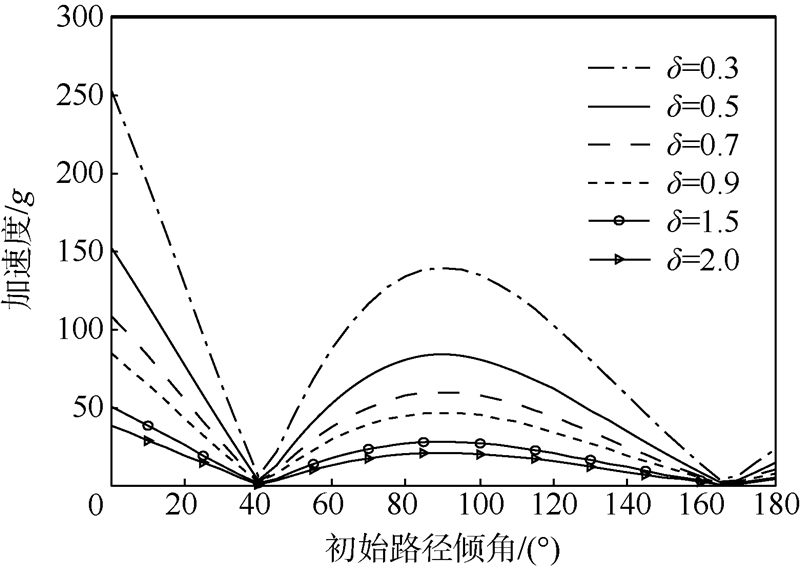图 3不同初始路径倾角下初始加速度变化范围Fig. 3 Initial acceleration variations at different initial path angle

图选项

从图 3中可以看出,当初始路径倾角在0°和90°附近时,初始加速度较大;在相同路径倾角下,当阈值δ变大时,加速度减小.因此,阈值δ可通过所需过载和初始路径倾角确定.需要注意的是:虽然在整个拦截过程中,初始路径倾角处于0°和90°附近的所需过载较大,但基于拦截高速目标的出发点,初始路径倾角不应在0°附近选取,否则所需过载会更大.例如,当需求过载为50g时,δ应该在0.4~0.7之间取值.此外,如果需求过载很小,δ的取值可以大于1,此时导航比的变化取决于V_c.1.3 三维制导律1.3.1 拦截弹模型在二维制导律的基础上实现三维制导律,是将三维制导问题分解到偏航平面(yaw plane)和俯仰平面(pitch plane).拦截弹在2个平面内分别依照前文所设计的制导律实施目标拦截,其几何关系与方程如文献^[13]所述,三维几何关系如图 4所示.

xOy—偏航平面;坐标原点O—拦截弹所在点;σyaw—偏航平面的视线角;γm_yaw—偏航平面拦截弹路径倾角;γm_pitch—俯仰平面拦截弹路径倾角;γm—拦截弹实际路径倾角;Vm_yaw—偏航平面拦截弹速度;Vm_pitch—俯仰平面拦截弹速度.图 4三维相对运动几何关系Fig. 4 3D geometry of relative engagement

图选项

在文献^{[13, 14, 15]}中,俯仰平面拦截弹路径倾角与俯仰平面拦截弹速度的计算公式分别为
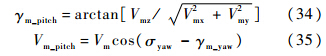
式中:V_mx、V_my和V_mz分别为V_m的三轴分量.然而式(34)与式(35)中,当cos(σ_yaw－γ_{m_yaw})→±1时,制导律误差较小;当cos(σ_yaw－γ_{m_yaw})→0时,会引起较大误差乃至制导律完全失效.因此必须重新推算γ_{m_pitch}与V_{m_pitch}的解析方程.式(34)中所计算的俯仰平面拦截弹路径倾角实为拦截弹实际路径倾角,即
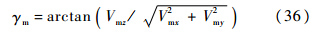
俯仰平面拦截弹速度与拦截弹速度的z轴分量相同,即
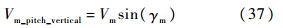
俯仰平面拦截弹速度的水平分量为
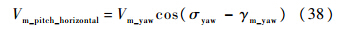
式中: V_{m_yaw}=Vmcos(γm) 俯仰平面拦截弹路径倾角为
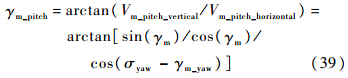
俯仰平面拦截弹速度为
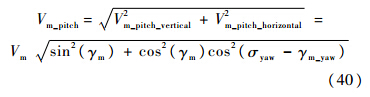
1.3.2 目标机动模型为了更好的在三维模式下验证制导律的有效性,目标的机动方向应实时选取背离拦截弹的方向.由于所建立模型中目标加速度的大小恒定,则求取加速度方向的向量即可.目标加速度方向如图 5所示.其中,坐标原点O为拦截弹所在位置,T为目标所在位置,T′为目标在水平面投影.

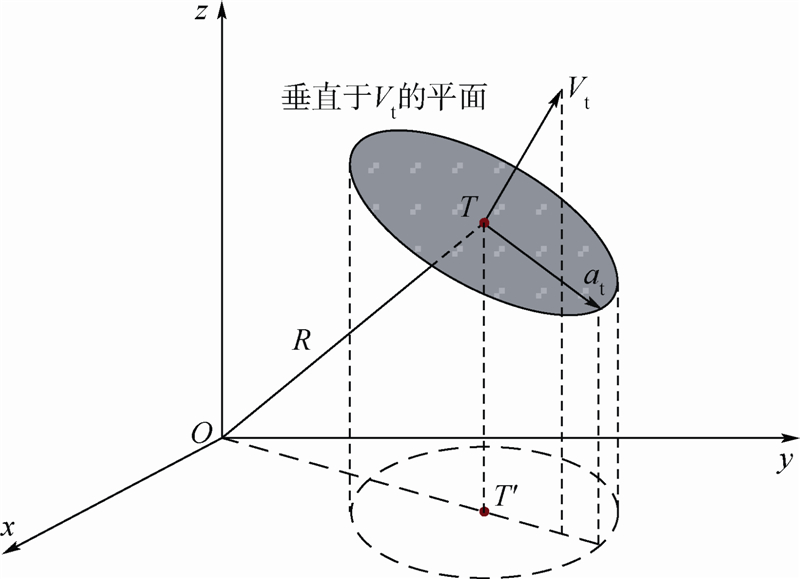图 5目标加速度示意图Fig. 5 Sketch map of target acceleration

图选项

设目标速度向量为V_t=[V₁ V₂ V₃],拦截弹指向目标向量为R=[R₁ R₂ R₃],目标加速度向量为a_t=[a₁ a₂ a₃].为满足目标加速度方向最大限度背离拦截弹,则a_t、V_t和R在同一平面:
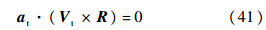
由于a_t与V_t垂直,则
通过式(41)与式(42)可得
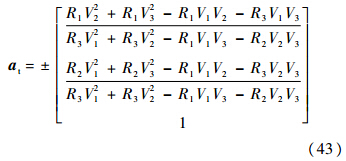
a_t的符号通过cos(a_t,R)<0进行选择,其大小值按照设定参数计算.2 仿真验证2.1 二维仿真验证仿真验证是在MATLAB环境中进行的,当V_c<0 时程序终止.定义距离R在最后时刻的取值为脱靶量;导引头模型中不含噪声且视觉范围足够大,其模型^[13]为
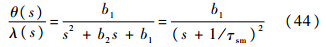
式中:导引头时间常数τ_sm=0.1 s;b₁=100;b₂=20.拦截弹自动驾驶仪模型为
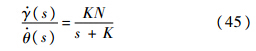
式中:常数K=1.所有仿真都在二维平面内进行,其仿真参数如表 1所示.表 1 二维仿真参数Table 1 2D simulation parameters

参数名称	取值
目标速度/(m·s-1)	1 500
拦截弹速度/(m·s-1)	600
目标加速度/g	4
初始弹目距离/km	10
拦截弹失效距离/m	30
初始视线角/(°)	8
目标初始路径倾角/(°)	0
有效导航比	3
拦截弹加速度上限/g	50
导航比阈值	0.5
更新步长/ms	0.2

表选项


拦截弹进入失效距离后,重复执行失效前最后的制导指令^[16].当采用UPN制导律拦截高速目标,导航比为正和负时,其性能分别与PN和RPN相似.因此,本文通过对比PN与RPN来验证UPN的特性.此外,文中还通过对比APN来验证UPN的命中精度特性.由于UPN中的导航比是时变的,取其导航比均值作为PN与RPN的导航比进行仿真.表 2的前2行分别给出了不同方案的序号和所使用的制导律,后3行给出了初始路径倾角、脱靶量和控制力等变量的参数,其中控制力表达式为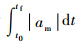.仿真结果如图 6所示,各不同方案序号通过图例给出或直接标在曲线上.图 6(d)中,相同初始发射倾角的制导律导航比值取UPN导航比的平均值.表 2 不同方案仿真结果(二维)Table 2 Results of different scenarios (2D)

方案	制导律	初始路径 倾角/(°)	脱靶量/m	控制力/ (m·s-1)
1	APN(N=4.151 6)	-20	0.204 8	882.537 0
2	PN(N=4.151 6)	-20	0.976 6	979.514 6
3	UPN	-20	0.401 9	876.947 3
4	APN(N=4.062 3)	75	0.479 2	2 160.2
5	UPN	75	0.453 1	1 615.3
6	RPN(N=-3.764 2)	135	0.881 2	1 423.2
7	UPN	135	0.328 0	1 421.8

表选项

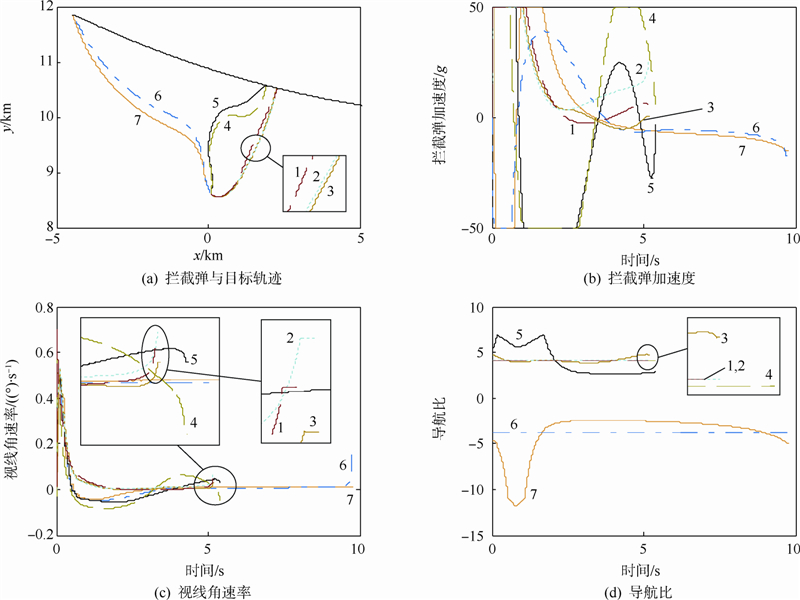图 6 二维仿真结果Fig. 6 2D simulation results

图选项

表 2第5列给出了不同方案拦截目标所需的控制力.由于UPN制导律采用时变导航比,如图 6(d)所示,在前期导航比取值较大,导致机动过载增大,利于拦截弹更早飞行至适合拦截目标的位置和角度,后期所需过载减小.因此,在相同路径倾角条件下,UPN制导律的控制力最小.表 2第4列给出了不同方案拦截目标的脱靶量.由于UPN制导律计算视线角速率时加入了目标加速度补偿项(如式(15)).因此,UPN较PN和RPN脱靶量更小.但是,由于UPN的目标加速度补偿项中对剩余拦截时间t_f－t的估计精度不足,方案3的命中精度不及方案1.由图 6(a)可知,方案4在接近碰撞点时,碰撞角接近π/2,拦截弹加速度方向与目标加速度方向接近垂直,APN的目标加速度补偿项对目标加速度不敏感,导致方案4的脱靶量大于方案5的脱靶量.2.2 三维仿真验证合成三维UPN制导律的2个平面分别计算各自的导航比.当任意平面上的接近速度V_c<0时,程序终止,此时弹目距离为脱靶量.仿真参数如表 3所示.表 3 三维仿真参数Table 3 3D simulation parameters

参数名称	取值
目标初始位置/m	(0,0,0)
拦截弹初始位置/m	(509.3,8 666.2,2 847.2)
目标初始速度/(m·s-1)	(-1 437.6,0.003 8,431.28)
目标加速度/g	4 >
第1组拦截弹初始速度/ >(m·s-1)	(367.511 5,367.511 5,-299.810 4)
第2组拦截弹初始速度/ >(m·s-1)	(369.548 9,-369.548 9,-294.703 6)
第3组拦截弹初始速度/ >(m·s-1)	(-226.286 8,391.940 2,393.928 1)
拦截弹加速度上限/g	50 >
导航比阈值	0.5
有效导航比	4
失效距离/m	30
更新步长/ms	0.2 >

表选项


仿真结果如表 4和图 7所示.表 4 不同方案仿真结果(三维)Table 4 Results of different scenarios (3D)

方案		制导律	偏航平面 导航比	俯仰平面 导航比	脱靶量/ m	控制力/ (m·s-1)
第1组	1	PN	4.368	5.109	0.874 5	668.17
	2	UPN	-	-	0.404 8	646.87
第2组	3	APN	4.750	5.114	0.401 9	1 010.30
	4	UPN	-	-	0.479 2	898.58
第3组	5	RPN	-4.569	-4.732	0.653 1	915.09
	6	UPN	-	-	0.381 2	912.64

表选项


表 4的前2列分别给出了不同方案的序号和所使用的制导律,之后的4列给出了各参数变量,包括:偏航与俯仰平面的导航比、脱靶量和控制力.仿真结果如图 7所示,各不同方案序号通过图例给出或直接标在曲线上.图 7(c)中加速度为两平面的合加速度,图 7(e)和图 7(g)中,UPN以外的制导律导航比取同组UPN导航比的平均值.

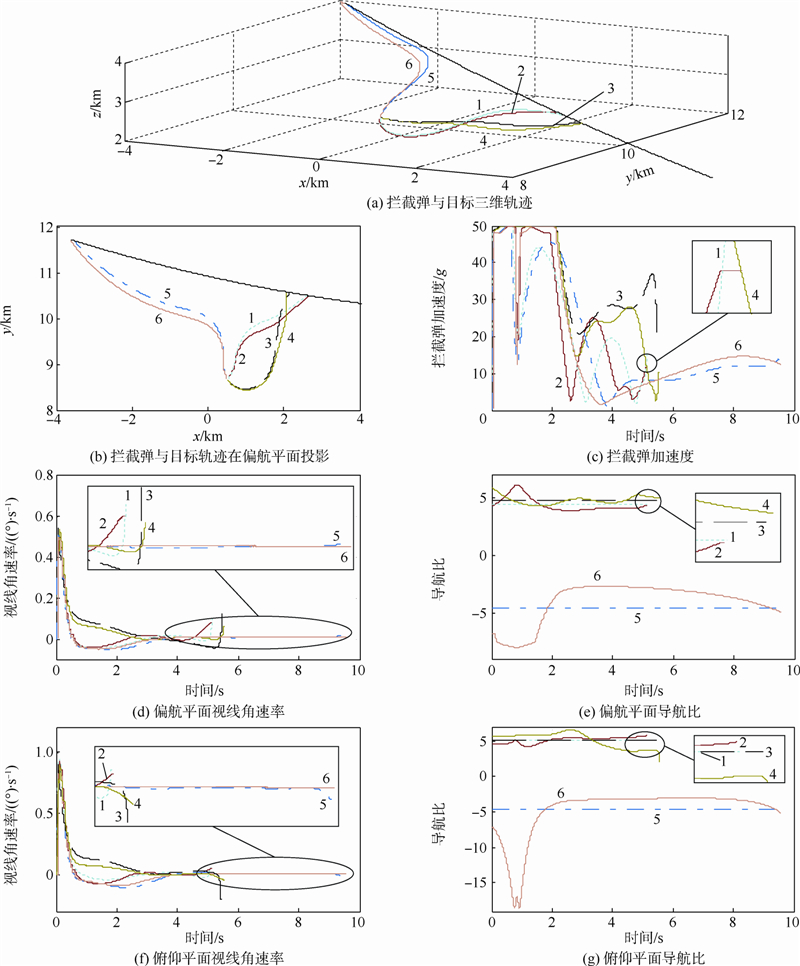图 7 三维仿真结果Fig. 7 3D simulation results

图选项

通过图 7(c)、图 7(d)和图 7(f)可知,UPN末加速度和视线角速率较同组其他制导律收敛性更强.由于UPN中对目标加速度补偿项是基于剩余拦截时间的估计(如式(8)).拦截弹越接近碰撞点,弹目距离 R 越逼近剩余拦截轨迹长度,剩余拦截时间估计精度越高,目标加速度补偿项也越有效,从而末加速度和末视线角速率较小.APN末速度和视线角速率较为发散的原因是,拦截弹在命中目标前,偏航与俯仰平面的速度方向与目标的速度方向近乎垂直,而引起APN加速度补偿项失效.另外,APN在拦截末段,偏航与俯仰平面的加速度夹角呈钝角,致使两平面加速度都大的情况下合加速度较小.图 6(d)中的曲线5与图 7(g)中的曲线6在初始阶段出现的回凹部分是由导航比处理奇点问题引起的.图 6(b)与图 7(c)中,各制导律曲线在初段上下满偏,而且之后均有多次波动的情况,是由系统中引入具有惯性环节的导引头模型(如式(44))导致.其他方面均与二维仿真类似.2.3 捕获区域仿真验证仿真中目标采用1.3.2 节中的机动模型,对UPN、APN、RPN和PN制导律的捕获区域进行对比,仿真参数如表 5、结果如图 8所示.表 5捕获区域仿真参数Table 5 Capture region simulation parameters

参数名称	取值
初始弹目距离/km	10
偏航平面初始视线角/(°)	60
俯仰平面初始视线角/(°)	15
拦截弹速度/(m·s-1)	600
目标速度/(m·s-1)	1 500
拦截弹加速度上限/g	50
允许脱靶量范围/m	1.0
导航比阈值	0.5
有效导航比	4
失效距离/m	30
更新步长/s	0.01

表选项


图 8中各符号表示拦截弹在相应初始路径倾角条件下进行拦截,脱靶量在允许范围之内.

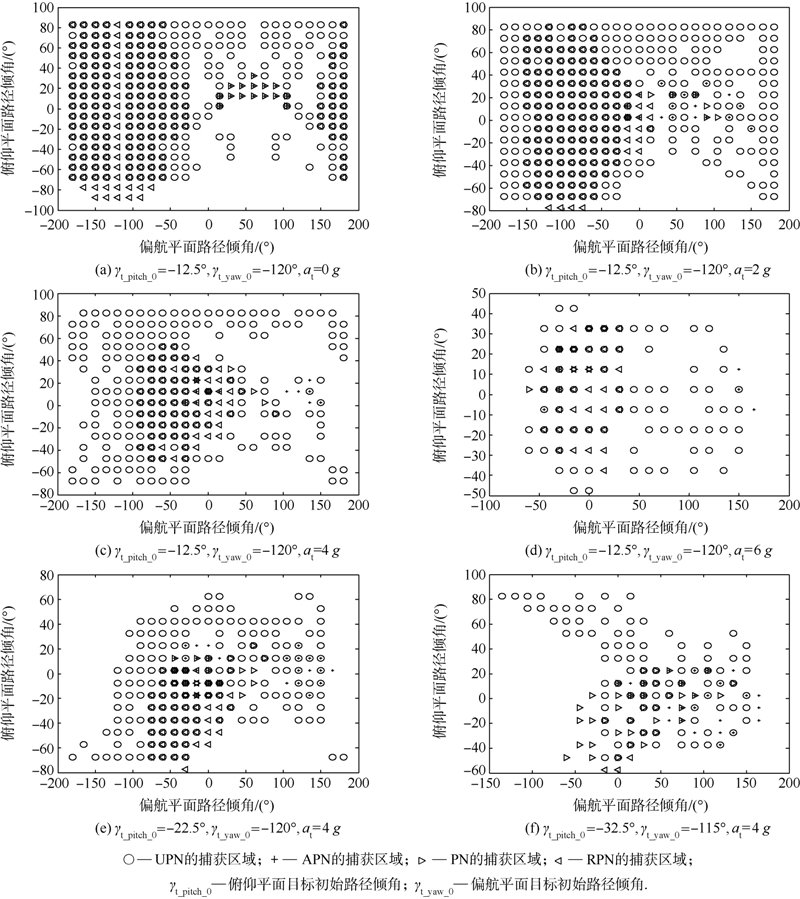图 8 捕获区域仿真结果Fig. 8 Capture region simulation results

图选项

图 8(a)~图 8(d)所示为相同目标初始路径倾角条件下,当目标加速度不同时各制导律的捕获区域.随着加速度的增大,各制导律的捕获区域逐渐减小,但UPN的捕获区域始终最大.图 8(c)、图 8(e)和图 8(f)所示为相同目标加速度条件下,当目标初始路径倾角不同时各制导律的捕获区域.各制导律的捕获区域随着目标初始路径倾角的变化而变化,但UPN的捕获区域始终最大.UPN在各情况下捕获区域均最大,主要原因是UPN中偏航和俯仰平面内,导航比N的正负由各自初始框架角θ_i决定(如式(30)),针对不同条件可能选择正负(顺逆轨)结合、同为正(逆逆轨)或同为负(顺顺轨)的3种方案,扩大了捕获区域.对于PN和APN,两平面内导航比N恒定且为正,则在拦截时全部为逆逆轨模式;而RPN两平面内导航比N为恒定负值,在拦截时全部为顺顺轨模式.在图 8中,UPN与其他3种制导律重合的捕获区域中,主要采用了逆逆轨和顺顺轨模式;而在其他3种制导律无法捕获的区域内主要采用顺逆轨结合的拦截模式(包括偏航平面逆轨、俯仰平面顺轨和偏航平面顺轨、俯仰平面逆轨2种情况).另外,导航比N的时变特性促使拦截弹在飞行初段进行大机动,将拦截弹的飞行角度和位置及早调整至更利于拦截的状态.UNP中自定义的视线角速率加入了目标加速度信息,对机动目标具有更高拦截精度,也是捕获区域更广的原因之一.虽然APN的视线角速度中包含加速度补偿项,但主要用于降低脱靶量.由于导航比相同,图 8中APN与PN捕获区域相似,并无明显优势.实验为贴近实际情况,仿真步长设定为0.01 s,而目标与拦截弹的最大相对速度为2 100 m/s,得出的步长误差最大可达21 m,远超过允许脱靶量范围.由于步长误差导致图 8中存在部分区域UPN无法拦截,而其他3种制导律可以拦截.如果步长足够小,则UPN可全覆盖PN和RPN的捕获区域.3 结 论设计了针对高速机动目标的三维UPN制导律.该制导律使用改进的视线角速率和时变的导航比.UPN制导律同时具备顺轨和逆轨2种拦截能力,且三维UPN制导律可实现顺顺轨、逆逆轨和顺逆轨结合3种拦截模式,有效扩大了捕获区域.在UPN制导律设计的过程中,完成了:1) UPN二维制导的设计,推导出了针对机动目标的视线角速率解析式;给出了时变导航比及其奇点的解决方法.2) 采用偏航平面与俯仰平面结合的方法将二维制导律扩展到三维制导律,进一步修正了前人算法中存在的问题;给出了目标加速度背离拦截弹的机动模型.3) 考虑了导引头的响应时间及失盲距离,与PN、RPN、APN制导律对比,仿真研究了UPN制导律分别拦截二维、三维高速机动目标实施过程,控制力明显小于APN,脱靶量明显小于PN和RPN,捕获区域明显大于其他三者.UPN制导律在解算过程中采用经典剩余飞行时间估计方法,误差较大,对脱靶量有一定影响.下一步需采用具有针对性的剩余飞行时间估计方法,以提高命中精度.此外,由于高速机动目标运动状态的估计和预测难度较大,还需重点研究此问题对制导律的影响.
参考文献

[1]	陈峰,肖叶伦,陈万春.基于需用速度增益曲面的大气层外超远程拦截导引方法[J].航空学报,2010,31(2):342-349. Chen F,Xiao Y L,Chen W C.Guidance based on velocity-to-be-gained surface for super-range exoatomospheric intercept[J].Acta Aeronautica et Astronautica Sinica,2010,31(2):342-349(in Chinese).
	Cited By in Cnki
[2]	宋愿贇,陈万春. 高精度快速趋近滑膜变结构末端导引方法[J].北京航空航天大学学报,2012,38(3):319-323. Song Y Y,Chen W C.High-accuracy quick-reaching sliding mode variable structure terminal guidance law[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(3): 319-323(in Chinese).
	Cited By in Cnki (4)
[3]	Kuroda T,Imado F.Advanced missile guidance system against a very high speed maneuvering target[C]//AIAA Guidance,Navigation and Control Conference.Reston:AIAA,1989:176-180.
	Click to display the text
[4]	Kuroda T,Imado F.Advanced missile guidance system against very high speed target[C]//AIAA Guidance,Navigation and Control Conference.Reston:AIAA,1988:320-324.
	Click to display the text
[5]	Lin Y P,Lin C L,Li Y H.Development of 3-D modified proportional navigation guidance law against high-speed targets[J].IEEE Transactions on Aerospace and Electronic Systems,2013,49(1):677-687.
	Click to display the text
[6]	TyanF,Jeng F S.Capture region of three dimensional PPN guidance law against a high speed-nonmaneuvering target[C]//Proceedings of the American Control Conference.Piscataway,NJ:Institute of Electrical and Electronics Engineers Inc,2008:3488-3493.
	Click to display the text
[7]	Taur D R. Composite Guidance and Navigation Strategy for a SAM Against High-Speed Target[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.Reston:AIAA,2003:1-10.
	Click to display the text
[8]	Golan O M,Shima T.Headpursuit guidance for hypervelocity interception[C]//AIAA Guidance,Navigation and Control Conference.Reston:AIAA,2004:1437-1444.
	Click to display the text
[9]	Shima T,Golan O M.Head pursuit guidance[J].Journal of Guidance,Control,and Dynamics,2007,30(5):1437-1444.
	Click to display the text
[10]	Shima T. Intercept-angle guidance[J].Journal of Guidance,Control,and Dynamics,2011,34(2):484-492.
	Click to display the text
[11]	Prasanna H M,Ghose D.Retro-proportional-navigation:a new guidance law for interception of high-speed targets[J].Journal of Guidance,Control,and Dynamics,2012,35(2):377-386.
	Click to display the text
[12]	Siouris G M. Missile guidance and control systems[M].New York:Springer Group,2004:142-173.
	Click to display the text
[13]	Francis C,Lukenbill.A target/missile engagement scenario using classical proportional navigation[D].California:Naval Postgraduate School,1990.
	Click to display the text
[14]	Peppas D I. A computer analysis of proportional navigation and command to line of sight of a command guided missile for a point defence system[D].California:Naval Postgraduate School,1992.
	Click to display the text
[15]	Costello P. Simulink simulation of proportional navigation and command to line of sight missile guidance[D].California:Naval Postgraduate School,1995.
	Click to display the text
[16]	Kim B S,Lee J G,Han H S.Biased PNG law for impact with angular constraint[J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(1):277-288.
	Click to display the text