保证零脱靶量,并带有末端约束碰撞角的轨迹成型制导律(Trajectory Shaping Guidance,TSG)设计是一项富有挑战性的任务.TSG可主动改变拦截弹的航迹角以达到期望的末端碰撞角,有效增大弹头的碰撞效能.近年来,许多****热衷于此,并提出了基于比例导引(Proportional Navigation，PN)^[1]的多种制导律.按照拦截模式可将这些算法划分为顺轨拦截和逆轨拦截2种类型.对于逆轨拦截模式,已有较多的研究成果.Kim等^[2]提出了基于偏置比例导引的制导算法,该算法采用时变的偏置角速率,改变拦截弹的航迹角以达到约束碰撞角.Zarchan^[3]基于最优理论解算出了带约束碰撞角的轨迹成型制导律的非线性、线性形式.Ratnoo和Ghose^[4]使用两阶段PN制导律,在2个阶段分别进行比例系数的调整以达到期望的约束碰撞角.Erer和Merttopcuoglu^[5]提出的制导律同样基于分段制导的思想,但与Ratnoo不同的是,前后段分别使用BPN与PN制导,以达到期望的末端约束碰撞角.Jeon等^[6]提出的AITC(Angle-Impact-Time-Control)制导律则同时使用PN和BPN制导,将控制末端约束角的制导指令作为PN的反馈指令,以调整拦截弹达到期望的末端约束碰撞角.以上研究成果的共性可概括为:制导指令包括两部分,一是用于保证脱靶量最小的标称导引部分;二是满足碰撞角约束的修正部分.文献^{[2, 3, 6]}都是在拦截全过程添加碰撞角约束的附加修正,调整拦截弹的航迹角以达到期望碰撞角.文献^{[4, 5]}在拦截局部过程附加修正部分,同时包含时变的比例系数的调整.对于顺轨拦截模式,尚未发现有****基于经典制导律设计带有约束碰撞角的制导律.Prasanna和Ghose^[7]提出了负比例制导律(Retro-Proportional-Navigation,RPN),未考虑末端碰撞角约束限制.相较于PN制导律,RPN使用负比例系数,顺轨模式拦截目标,其捕获区域主要集中在与视线角呈钝角的区域;PN使用正比例系数,逆轨模式拦截目标,其捕获区域主要集中在与视线角呈锐角的区域.顺轨模式较逆轨模式具有相对速度小、需求过载小的优点,尤其对于高速目标,有更大捕获区域^[8].综上所述,带约束碰撞角制导律的主要发展方向为:①在理想状态下,设计性能更优的制导律.即在保证较小的脱靶量、碰撞角误差的前提下,设计耗费控制力小、遭遇点过载小的制导律,如TSG^[3];②突破传统的拦截模式——逆轨拦截,设计顺轨拦截模式下的制导律,如RPN制导律^[7];③考虑制导系统的动态特性、外界扰动等条件,使其更为贴近工程实践.本文的主要研究内容集中在①和②两部分.针对顺/逆轨拦截模式,设计带约束碰撞角的闭环制导律.然后,仿真分析制导律的脱靶量、碰撞角误差、控制力等制导特性;仿真分析制导律的捕获区域.1 制导律设计1.1 逆轨拦截模式下的ACPN制导律设计ACPN(Angle Control PN)制导律的设计基于以下假设:拦截器与目标被考虑为质点;且速度恒定^[9];目标为非机动目标,为弹道导弹中段拦截的一般情况^[5];忽略重力影响.拦截弹与目标逆轨拦截模式的平面几何关系如图 1(a)所示.DP_ACPN为ACPN的轨迹；γ为拦截弹的航迹角(path angle),即拦截速度矢量的倾角;λ为视线角,即弹目连线与水平线的夹角.因目标水平飞行,为清楚地表示碰撞角,定义拦截时的航迹角γ_f为碰撞角∂_A;V_m为拦截弹的速度;R为弹目距离;y为拦截弹与目标的铅垂距离;V_t为目标的速度.将制导指令分为两部分:一部分是PN制导指令,用于保证零脱靶量；另一部分为反馈制导指令,用于调整期望碰撞角.
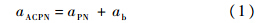
根据PN的定义^[10]:
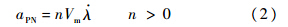
若视线角λ较小,根据图 1中的三角关系将视线角近似为^[11]
式(3)对t微分,得到视线角速率：
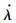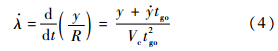
式中:t_go为剩余拦截时间;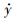为y方向的相对速度.若拦截弹的航迹角γ、视线角λ较小,拦截弹的接近速度V_c近似为
由式(2)、式(4)得到线性条件下的PN制导方程为
式中:n为比例系数.

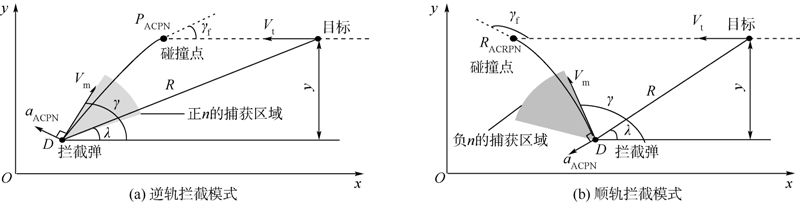图 1 平面几何关系Fig. 1 Planar engagement geometry

图选项

y方向的相对加速度为
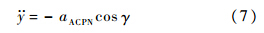
若γ较小,则式(7)为
由式(8)和式(1),可得
令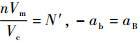,则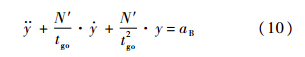
求解微分方程,得到
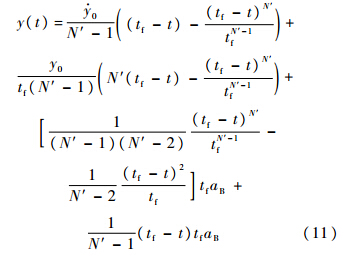
式(11)对t微分,得
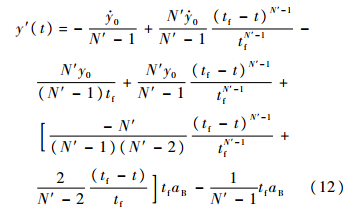
当t=tf时,得到t₀时刻ACPN的y方向的末相对速度:
式中: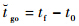,初始时刻t₀=0.对当前时刻t有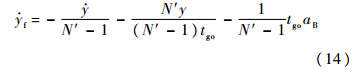
由式(3),R≈Vctgo,λ较小,可得
将式(15)代入式(14),可得
将式(6)和式(16)代入式(1),a_b=－a_B,得
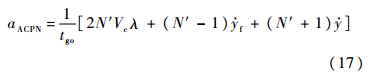
式中：
若γ较小,则式(18)为
将式(19)代入式(17),可得制导指令为
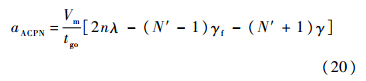
1) 与文献^[5]对比验证.由式(16)、式(19)、a_b=－a_B,可得
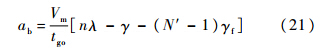
当拦截对象为静止目标时,N′=n,式(21)为
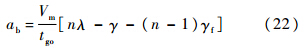
文献^[5]提出的制导律(式(22))为ACPN拦截对象为静止目标时的特例.2) 与文献^[3]对比验证.由式(3)、式(4)可得
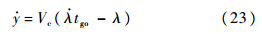
当t=t_f时,得
将式(23)和式(24)代入式(16),a_b=－a_B,得
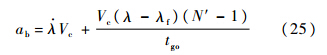
由式(1)、式(2)和式(25)可得
文献^[3]的轨迹成型制导律是式(26)N′=3时的特例.该制导律是基于最优理论推导得出,特点是保证控制力最小化.1.2 顺轨拦截模式下的ACRPN制导律设计顺轨拦截的轨迹如图 1(b)中DR_ACRPN所示.同样,将制导指令分为两部分:一部分是RPN制导指令,用于保证零脱靶量;另一部分为反馈制导指令,用于调整期望碰撞角.顺轨拦截模式下的ACRPN(Angle Control RPN)制导律:
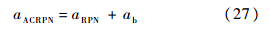
根据RPN的定义^[7]:
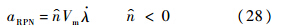
将式(4)代入式(28),可得RPN的制导方程为
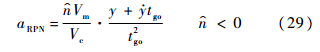
顺轨拦截,拦截弹的接近速度V_c近似为
y方向的相对加速度为
类比1.1节推导过程,式(10)则变为
式中: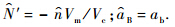同理,可得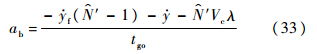
对于顺轨拦截,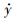近似为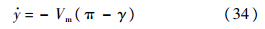
联合式(27)、式(29)、式(33)和式(34),可得
特别指出的是:虽然本文的制导律是基于三角函数的“小角度”近似得到的,与文献^{[3, 4, 5]}的制导律的特性相似,可适用于“大角度”的情况.2 仿真验证仿真目的:①逆轨拦截低速目标(目标速度低于拦截弹速度)验证ACPN制导律.选取期望碰撞角∂_A=90°,与文献^[2]提出的TV-BPN制导律、文献^[4]提出的TSPN制导律进行对比研究,比较脱靶量、控制力、碰撞角误差等制导性能.②顺轨拦截高速目标(目标速度高于拦截弹速度)验证ACRPN制导律,与TV-BPN^[2]逆轨拦截高速目标对比脱靶量、控制力、碰撞角误差等制导性能(因TSPN制导律拦截高速目标,制导性能较差,故只与TV-BPN对比).剩余拦截时间t_go=R/V_c.③与TV-BPN、PN、RPN制导律对比,研究ACPN、ACRPN拦截高速目标的捕获区域.仿真环境及参数设置:假设导引头视场足够大,但是在距离目标30 m以内失盲^[2],制导指令保持其最后的数值.飞控系统的动态特性^[12]表示为
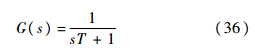
式中:时间常数T=0.3 s.初始条件:初始弹目距离R_i=10 000 m;逆轨拦截时,初始视线角λ_i=18°;顺轨拦截时初始视线角λ_i=14°.目标位置为(x_t,y_t)=(10 000,10 000)m;拦截弹的位置可由R_i、λ_i、(x_t,y_t)的几何关系求出;拦截弹速度为600 m/s;TV-BPN、PN、RPN与本文提出的制导律的比例系数绝对值为3;TSPN的比例系数恒值为3;仿真步长为0.002 s.2.1 拦截低速目标仿真目标速度V_t=400 m/s,拦截弹初始航迹角γ_i=0°.表 1为方案参数,表中各列分别表示方案序号、使用的制导律、碰撞角误差、脱靶量、控制力、末加速度.控制力定义为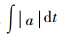^[5].图 2给出了仿真结果,其中的图例表示方案序号.由表 1与图 2可知:表 1 拦截低速目标方案参数Table 1 Scenario parameters of intercepting low speed targets

方案	制导律	碰撞角/ (°)	脱靶量/ m	控制力/ (m·s-1)	末加速度/ g
1	ACPN	0.060 6	0.052 6	897.224 3	-0.46
2	TSPN[7]	0.052 6	5.051 5	939.637 2	1.39
3	TV-BPN[5]	0.064 7	0.094 5	940.384 9	10.63

表选项


1) ACPN与TV-BPN和TSPN的碰撞角误差基本一样.ACPN、TV-BPN脱靶量小于TSPN.主要因为:ACPN、TV-BPN制导指令在拦截全过程中使用反馈制导指令调整约束碰撞角,而TSPN仅在末段调整,导致加速突降(图 2(a)).在包含惯性环节的系统中,末加速的突变将直接导致脱靶量增大.ACPN的末加速度接近于0,拦截弹的过载裕度较大,实际拦截时,存在各种在拦截弹设计时未考虑的扰动,遭遇点小的需用过载将有助于提高制导精度^[13].

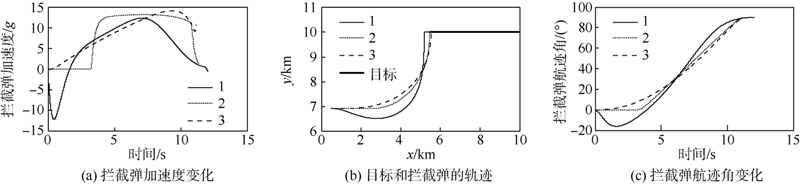图 2 拦截低速目标仿真结果Fig. 2 Simulation results for interception of low-speed targets

图选项

2) 控制力TV-BPN、TSPN较为接近,ACPN小于二者.这是因为当比例系数为3时,ACPN与最优理论推导出的制导指令相同,故控制力小于TV-BPN、TSPN. 综上,ACPN的碰撞角误差、控制力都优于TV-BPN、TSPN.2.2 拦截高速目标仿真定义分界角χ:目的是根据设定的分界角χ,可分别计算出逆/顺轨拦截模式下的拦截弹初始航迹角γ_i,HO,γ_i,HP.若目标如图 1所示的方向水平飞行,拦截弹以γ_i,HO,γ_i,HP发射拦截目标,仿真对比逆/顺轨制导律的制导性能才不失公平性.拦截弹的初始航迹角γ_i、初始视线角λ_i、分界角χ三者的关系为γ_i=π/2+λ_i±χ,χ∈[0,π].逆轨拦截取负号;顺轨拦截取正号.若χ=1°,初始视线角λ_i=14°.则逆轨拦截模式下的拦截弹初始航迹角γ_i,HO=103°,顺轨拦截模式下的拦截弹初始航迹角γ_i,HP=105°.目标速度V_t=1 600 m/s.其他仿真参数不变.逆/顺轨的碰撞角互为补角.由表 2与图 3可知:表 2 拦截高速目标方案参数Table 2 Scenario parameters of intercepting high speed targets

方案	制导律	航迹角/(°)	期望碰撞角/(°)	碰撞角/(°)	脱靶量/m	控制力/(m·s-1)
1	ACRPN	105	180	0.078 7	0.096 9	523.593 2
2	TV-BPN[5]	103	0	0.269 2	0.167 8	1 075.8
3	ACRPN	105	150	0.160 3	0.201 4	604.352 7
4	TV-BPN[5]	103	30	0.048 5	0.123 0	764.962 6

表选项


1) TV-BPN逆轨拦截高速目标,碰撞角误差、脱靶量比拦截低速目标时稍增大,ACRPN基本不变,但是拦截时间增大了近1倍.因为拦截弹牺牲拦截时间获得较小的脱靶量、碰撞角误差及控制力.2) ACRPN控制力比TV-BPN显著减小.由于顺轨拦截时间长,拦截弹的调整航迹角所用的加速度较小(图 3(a)),而末段加速度接近于0 m/s²(图 3(a)),故对时间的积分数值较小,即控制力较小(控制力的定义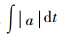^[5]).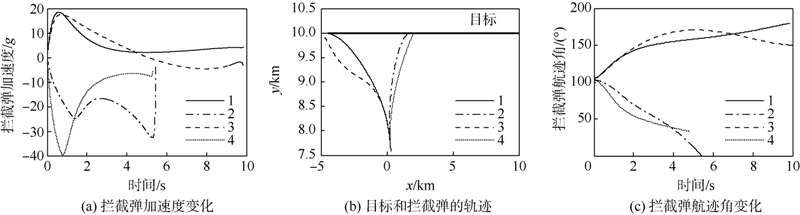

图 3 拦截高速目标仿真结果Fig. 3 Simulation results for interception of high-speed targets

图选项

2.3 拦截高速目标捕获区域分析捕获区域是制导律的主要评判指标,其定义^[14]为:在有效打击目标并满足一定的约束条件的拦截弹初始航迹角的集合,且带约束碰撞角的制导律的捕获区域只能由仿真给出^[2].本文设定:当脱靶量小于0.5 m即为能有效打击目标,约束碰撞角误差小于0.5°即为满足碰撞角的约束条件.以高速目标为例,与TV-BPN、PN、RPN制导律对比,分析在初始视线角λ=5°,10°,15°,20°的ACPN、ACRPN的捕获区域,加速度限制为40g,其他仿真参数同2.2节.仿真结果如图 4所示.

△—构成的直线之间的纵坐标范围为PN、RPN制导律的捕获区域，同时满足期望碰撞角、拦截弹初始航迹角(γd,γi )的区域即为ACPN、ACRPN的捕获区域；○—本文提出的顺/逆轨制导律的捕获区域；+—TV-BPN的捕获区域； —同时满足ACPN、TV-BPN的捕获区域. 图 4 拦截高速目标的捕获区域Fig. 4 Capture region for interception of high-speed targets

图选项

由图 4可知:1) 在视线角λ<15°时,ACPN的捕获区域比TV-BPN大,主要集中在碰撞角∂_A∈[70°,90°],这是因为:在该区域,TV-BPN的需用过载大于加速度限制,导致脱靶量、碰撞角误差突破设定范围.在视线角λ=20°,两者基本一致.此外,带约束碰撞角的制导律的捕获区域均小于未带约束的PN、RPN的捕获区域,这与文献^[15]的结论一致.2) 若令γ_i=π/2+λ_i±χ中的χ=0°,得到的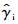=π/2+λ_i为顺/逆轨拦截的分界,即当拦截弹的初始航迹角大于等于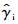,宜采用顺轨拦截模式;当拦截弹的初始航迹角小于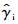,宜采用逆轨拦截模式.如图 2(b)所示,当初始视线角λ_i=10°时,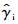=100°,捕获区域内:逆轨拦截的拦截弹航迹角最大为95°.顺轨拦截的拦截弹航迹角最小为100°(因初始航迹角是每隔5°仿真得出,故逆轨拦截的初始航迹角的最大值为95°).因此,在初始航迹角γ_i∈[0°,180°],初始视线角λ_i∈[5°,20°],随着视线角的增大,逆轨拦截时制导律的捕获区域增大,顺轨拦截制导律的捕获区域随着视线角的增大而减小.3 结 论设计了逆轨拦截模式下的ACPN制导律,顺轨拦截模式下的ACRPN制导律.完成了:1) ACPN制导律相比同类制导律所耗费的控制力小;当比例系数为3时其制导律与最优制导律一致.2) ACRPN制导律在拦截高速目标时优势较为明显,能以较大的拦截时间获取较好的脱靶量、约束碰撞角误差、控制力等制导性能.3) 拦截弹的初始航迹角π/2+λ_i为顺/逆拦截模式的分界,当初始航迹角小于π/2+λ_i时,宜用逆轨拦截模式,当初始航迹角大于等于π/2+λ_i时,宜用顺轨拦截模式.4) 从捕获区域的结论可知,存在一种结合顺/逆轨拦截模式的制导律,进一步扩大制导律的捕获区域.
参考文献

[1]	Adler F P. Missile guidance by three-dimensional proportional navigation[J].Journal of Applied Physics,1956,27(5):500-507.
	Click to display the text
[2]	Kim B S,Lee J G,Han H S.Biased PNG law for impact with angular constraint[J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(1):277-288.
	Click to display the text
[3]	Zarchan P. Tactical and strategic missile guidance[M].3rd ed.Reston:AIAA,2002:15.
	Click to display the text
[4]	Ratnoo A,Ghose D.Impact angle constrained guidance against nonstationary nonmaneuvering targets[J].Journal of Guidance,Control,and Dynamics,2010,33(1):269-275.
	Click to display the text
[5]	Erer K S,Merttopcuoglu O.Indirect impact-angle-control against stationary targets using biased pure proportional navigation[J].Journal of Guidance,Control,and Dynamics,2012,35(2):700-703.
	Click to display the text
[6]	Jeon I,Lee J,Tahk M.Impact-time-control guidance law for anti-ship missiles[J].IEEE Transactions on Control Systems Technology,2006,14(2):260-266.
	Click to display the text
[7]	Prasanna H M,Ghose D.Retro-proportional-navigation:a new guidance law for interception of high-speed targets[J].Journal of Guidance,Control,and Dynamics,2012,35(2):377-386.
	Click to display the text
[8]	Shima T. Intercept-angle guidance[J].Journal of Guidance,Control,and Dynamics,2011,34(2):484-492.
	Click to display the text
[9]	闫梁,李辕,赵继广,等.基于变节点虚拟域动态逆的轨迹实时优化[J].航空学报,2013,34(12):2794-2803. Yan L,Li Y,Zhao J G,et al.Trajectory real-time optimization based on variable node inverse dynamics in the virtual domain[J].Acta Aeronautica et Astronautica Sinica,2013,34(12):2794-2803(in Chinese).
	Cited By in Cnki (2)
[10]	Mott D L. Proportional navigation[J].American Journal of Physics,1980,48(6):486-487.
	Click to display the text
[11]	Ben-Asher J Z,Farber N,Levinson S.New proportional navigation law for ground-to-air systems[J].Journal of Guidance,Control,and Dynamics,2003,26(5):822-825.
	Click to display the text
[12]	Zarchan P. Proportional navigation and weaving targets[J].Journal of Guidance,Control,and Dynamics,1995,18(5):969-974.
	Click to display the text
[13]	闫梁,赵继广,沈怀荣,等.带末端约束碰撞角的三维联合偏置比例制导律设计[J].航空学报,2014,35(7):1999-2010. Yan L,Zhao J G,Shen H R,et al.Three-dimensional united biased proportional navigation guidance law for interception of targets with angular constraints[J].Acta Aeronautica et Astronautica Sinica,2014,35(7):1999-2010(in Chinese).
	Cited By in Cnki
[14]	Dhar A,Ghose D.Capture region for a realistic TPN guidance law[J].IEEE Transactions on Aerospace and Electronic Systems,1993,29(3):995-1003.
	Click to display the text
[15]	Yuan P J,Chern J S.Analytic study of biased proportional navigation[J].Journal of Guidance,Control,and Dynamics,1992,15(1): 185-190.
	Click to display the text