基于证据融合的雷达反隐身性能评估方法

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2021-12-25

随着外形、材料、等离子体等现代隐身技术在飞机、导弹等武器装备上的广泛应用,基于空域、频域、极化域的雷达反隐身技术作为新的探测手段应运而生^[1].如何有效、正确地评估雷达反隐身设备的各种技、战术指标及综合性能,直接影响到雷达的系统优化、装备布局及作战应用.但由于雷达的系统性、战场的复杂性及指标参数的模糊性,其客观评估困难重重.目前,针对武器装备性能评估的方法有很多,如层次分析法、分层赋权、神经网络算法、聚类分析法、模糊物元分析法、灰色关联算法等^{[2, 3, 4, 5, 6]}.但上述方法或者是由于主观性强、算法不完善等,无法分析指标间的强相关性带来的计算冗余^{[2, 3, 4]};或者是计算条件苛刻,难以实现评估结果的确定性和不确定性度量^{[5, 6]}.证据理论具有较强的理论基础,能有效处理随机不确定性信息,且不需要知道各影响因素的先验概率和条件概率密度.为此,本文提出了一种新的利用证据融合理论的雷达反隐身性能评估方法.结合雷达反隐身常用技术和作战实际给出了分层次性能指标评估体系,将熵理论、欧式距离、投影算法和证据理论相结合,实现了对雷达反隐身性能的综合评估.通过算例证明了该方法能有效解决复杂信息条件下的雷达反隐身性能评估问题.1 雷达反隐身性能评估指标1.1 建立评估指标体系的构建评估指标体系的构建是开展雷达反隐身性能评估的基础.为合理、有效地体现雷达的反隐身性能,必须依据系统性、完备性、科学性和可行性等原则选取评估指标.根据雷达反隐身的基本原理及常用技术可知,影响雷达反隐身性能的内在因素有雷达的固有参数特性及雷达的频域、空域、极化域特性.雷达反隐身的根本目的就是在克服敌方干扰的情况下为防空系统及时提供隐身目标的位置、方位和速度信息,以保卫重要军事目标,影响雷达反隐身能力的外在因素有雷达防空能力.为确定和分析指标体系,根据“指标分层法”建立雷达反隐身性能评估指标体系,构建分层次评估结构,具体见图 1.根据雷达反隐身性能指标结合“指标分解法”可将其分为距离指标、技术指标、防空能力指标,单项性能指标具体包括雷达的平均功率、天线增益、工作波段和探测概率等.

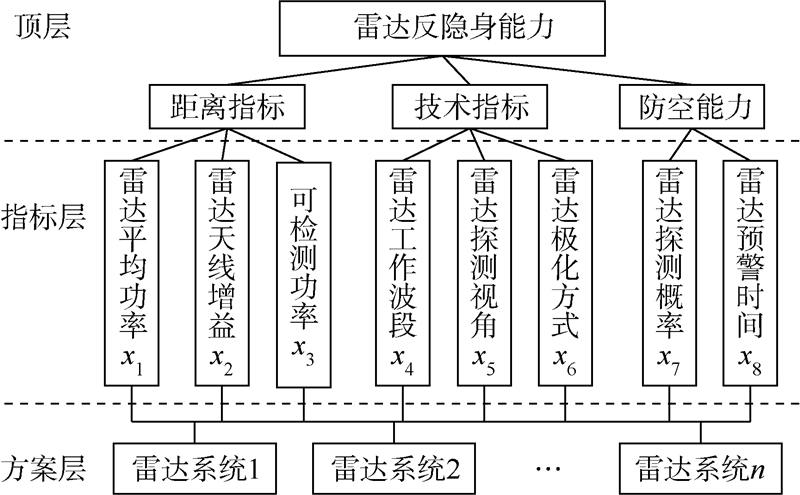
图 1 雷达反隐身性能评估指标体系Fig. 1 Indexes of radar anti-stealth performance

图选项

1.2 指标的分析与计算1) 距离指标.该指标是基于改进现有雷达技术设计的.根据雷达方程及雷达反隐身基本原理可知,为克服隐身目标雷达散射截面积(Radar Cross Section，RCS)减缩引起的探测距离减小现象,可通过增大平均功率、提高天线增益、降低最小可检测信号功率等方法实现.平均功率、天线增益、最小可检测信号功率均可通过查询雷达具体参数获得.2) 技术指标.该指标是基于现有的雷达反隐身技术手段设计的.其中,工作波段是对频域反隐身的体现,探测视角是对空域反隐身的体现,极化方式则是对极化域反隐身的体现.各指标具体计算方法如下:
① 隐身目标主要针对厘米波段雷达,频段相对单一,不能实现全频段上的隐身.研究表明,采用米波段及VHF、UHF、HF等高频段的雷达具有很强的反隐身性能.因此,雷达工作波段是雷达反隐身性能的重要评估指标,其计算公式为^[7]

式中:σ为目标在L、S等厘米波段下的RCS;f为脉冲频率.
② 目前隐身目标还不能做到全空域隐身,雷达只要避开隐身目标RCS明显减缩的方向,从其他角度对其进行照射,就能保持原有距离上对隐身目标的探测能力.因此不同的雷达探测角度使雷达具有不同的反隐身性能,如空基雷达、机载雷达、双(多)基地雷达等通过俯视、侧视、后视等角度就能大大提高探测能力.定义指标计算式为^[8]

③ 隐身飞行器RCS值的大小与雷达波的极化方向有密切的关系,通过改变极化方向、强度等方法,能使隐身目标的RCS达到其最大值,进而抑制目标RCS值的缩小^[9].定义该指标的度量值为

3) 防空能力.任何雷达系统都是防空系统的一部分,能为防空武器系统提供目标的位置、方位等信息^[10].因此,系统本身防空性能的好坏直接关系到雷达的反隐身作战性能.而探测概率、预警时间是雷达防空能力的重要体现,其中,探测概率可查询相关数据获得,预警时间计算方法如下.预警时间分析示意图如图 2所示,假设某雷达的探测范围为O₁,被保护目标的位置为O,隐身目标O₂朝向O的水平航迹投影为OO₂,隐身目标速度为v,则可根据航迹投影与探测范围交点F至被保护目标的距离l定义预警时间为

图 2 预警时间分析示意图Fig. 2 Schematic of warning time analysis

图选项

2 雷达反隐身性能评估模型证据理论是用数学方法处理不完全、不精确、不肯定信息的融合算法.其中,识别框架是整个判断的标准,基本概率分布是融合的基础,合成规则是判断过程,信任函数和似然函数是支持力度区间的上下限^[11].因此,引入证据理论对各指标原始数据进行合成运算,以效用区间为比较对象,在克服专家评估不确定性、证据冲突等因素影响下,能有效实现雷达反隐身性能的客观评估.2.1 证据融合理论分析定义1 识别框架Θ上的基本可信度分配函数:m,2^Θ→[0-1],满足m(?)=0,

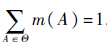
.对于Θ上的n个证据源导出的可信度分配函数m₁,m₂,…,m_n.其融合规则为

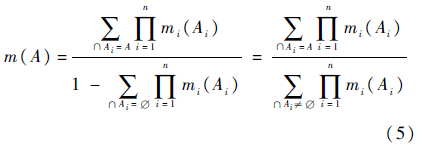
对于定义1,当各组证据源的重要性或置信度不同时,组合规则提供的结果可能与客观情况不符,即出现证据冲突现象.而通过对重要性较弱因素的规范化处理能减少证据之间的冲突.文献^{[12, 13]}根据经验或距离算法对证据源的权重进行重新赋值,得出了较为合理的融合结果,但这种方法依赖主观经验且分析不全面,缺乏对原始数据的客观、整体分析.为改善证据源信度,给出改进算法:1) 确定初始可信度分配函数m_i(A₁),m_i(A₂),…,m_i(A_j)，m_i(A_j)为第i个证据对于命题A_j的基本可信度分配.为便于评估,取i=1,2,…，M,j=1,2,…，N,M为第1层指标总数,N为方案层样本总数.2) 利用熵权法求取指标客观权重λ_i.熵权是体现证据内部相对激烈程度的系数,是对证据源重要性的客观度量.根据熵的定义,第i个证据源的熵为

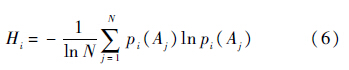
式中：

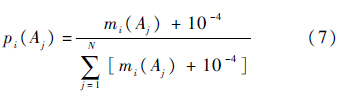
其中：p_i(A_j)为m_i(A_j)的概率;10^-4是对m_i(A_j)的修正,反映了证据源经过标准化处理后的精确位数,既能保证lnp_i(A_j)具有数学意义,又使m_i(A_j)对熵值H_i的影响被控制在合理范围之内.定义熵权公式为

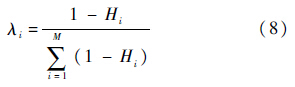
3) 利用欧式距离确定证据源受支持系数ξ_i.根据欧式距离定义,证据m_i与m_k的距离为

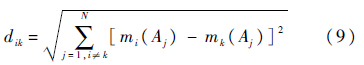
定义2 证据m_i与其他证据的平均距离为

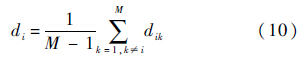
由定义2可知,证据源的平均距离越大,证据源相对于其他证据的重要性越弱,即受支持度越低;反之,证据源相对于其他证据的重要性越强,即受支持度越高.因此,可定义证据源的受支持系数为

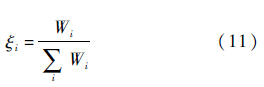
式中：W_i=1/d_i.4) 确定可信度因子ω_i.可信度因子是改善证据源信度的基础,是证据源内部相对稳定程度和某证据相对于其余证据重要程度的综合反映,即证据源熵权和受支持系数的综合反映.不妨设ω_i=f(λ_i,ξ_i),则函数满足:① 证据不能被否定,即0<f(λ_i,ξ_i)≤1.② 当λ_i(或ξ_i)不变时,f(λ_i,ξ_i)是ξ_i(或λ_i)的单调递增函数,且ξ_i(或λ_i)较大时,f(λ_i,ξ_i)变化缓慢,反之,变化较快.因此,函数f(λ_i,ξ_i)应为二元对数变化函数,根据归一化原理和对数函数基本定义可设

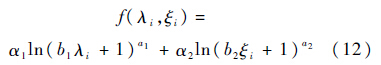
式中：α₁、α₂为比例系数;a₁、a₂、b₁、b₂为常数,且函数满足:

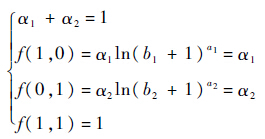
分析函数可知:α₁、α₂反映了λ_i、ξ_i的相对重要程度；a₁、b₁、a₂、b₂反映了λ_i、ξ_i的收敛速度.图 3给出了可信度因子变化趋势,其中α₁=0.4,α₂=0.6,a₁=1/ln5,b₁=4,a₂=1/ln6,b₂=5.5) 修正可信度分配函数.设修正后的可信度分配函数为m′_i(A_j).利用可信度因子w_i对m_i(A_j)进行修正,同时增加其不确定度m′_i(Θ):

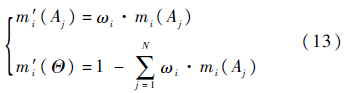
6) 用式(5)对修正后的证据进行合成运算.

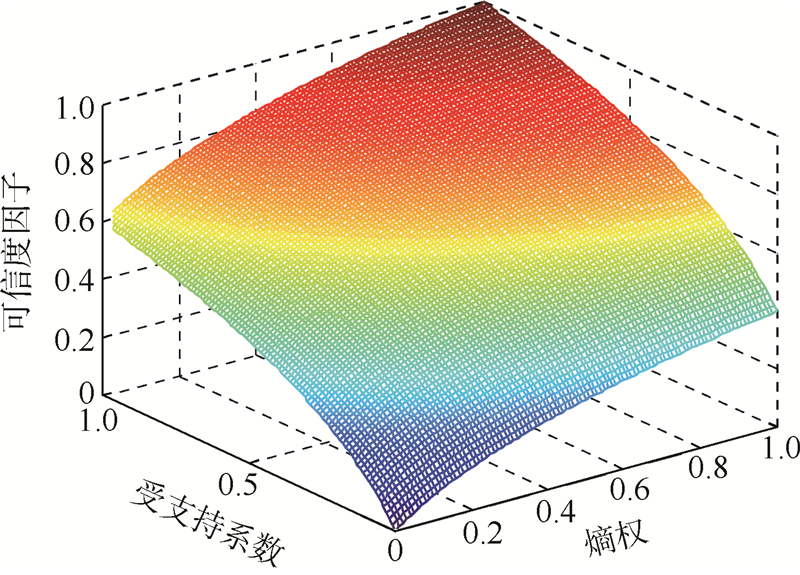图 3 可信度因子变化趋势Fig. 3 Trend of credibility factor

图选项

2.2 雷达反隐身性能评估步骤基于证据融合的雷达反隐身性能评估流程如图 4所示.

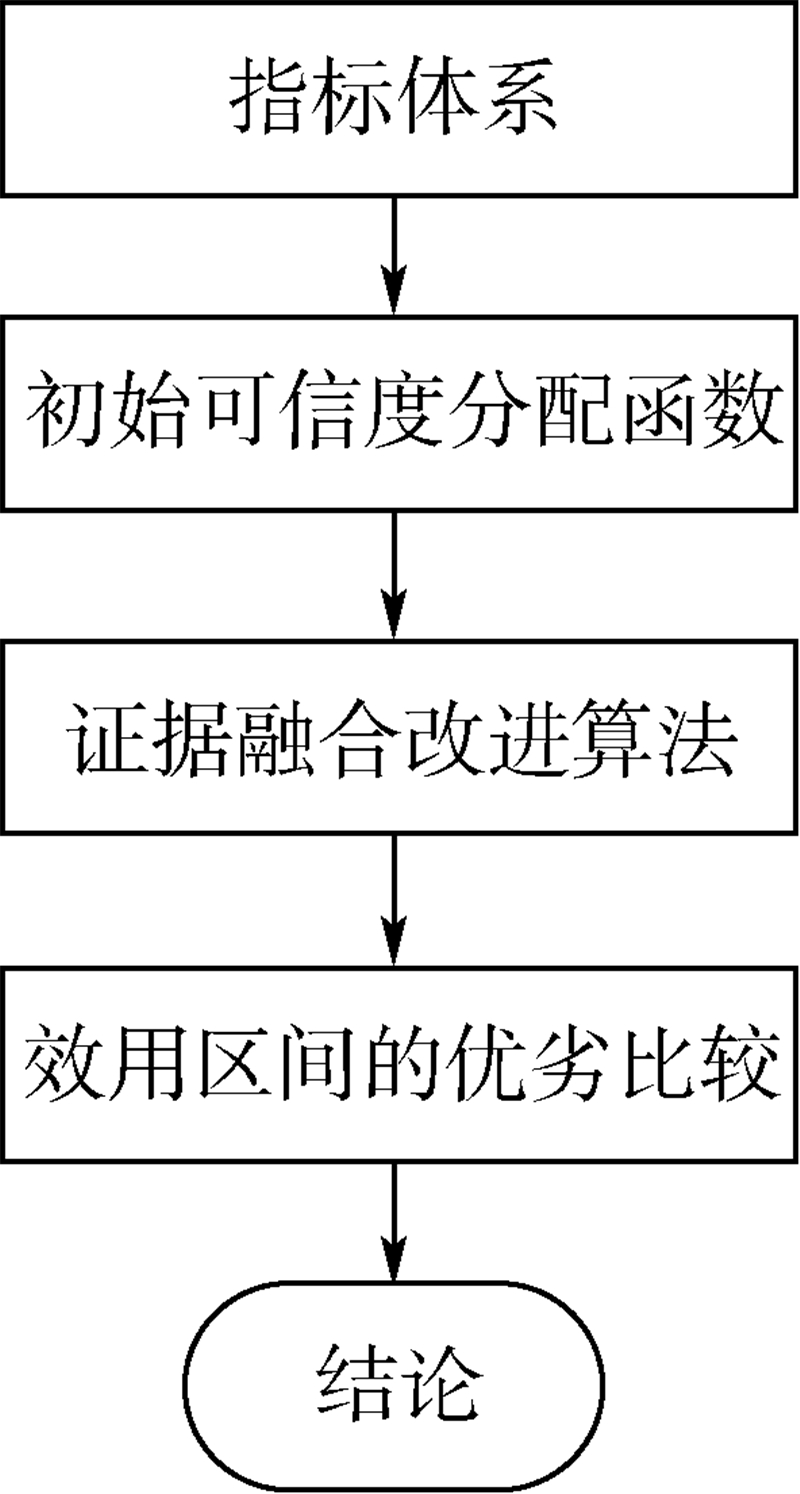图 4 雷达反隐身性能评估流程Fig. 4 Flow chart of radar anti-stealth performance evaluation

图选项

步骤1 求解初始可信度分配函数.设样本序列为X_i(j)={x_i(j)},x_i(j)为雷达反隐身性能评估的第j部雷达的第i个指标的实际统计值.以各指标的最优值和最劣值构成样本的正、负参考向量,定义为

取参考向量为ΔX(j)=X⁺(j)-X^-(j),决策向量为ΔX_i(j)=X_i(j)-X^-(j).决策向量投影图如图 5所示,根据投影原理,计算各决策向量相对于参考向量的投影角为

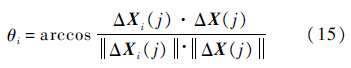
将各指标进行归一化可得可信度分配函数为

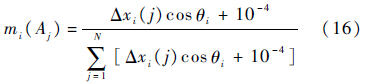
式中：10^-4是对Δx_i(j)cosθ_i的修正,反映了归一化处理后的精确位数,避免了部分证据源初始可信度分配函数为0的现象.

图 5 决策向量投影图Fig. 5 Projection drawing of decision vector

图选项

步骤2 证据合成.利用证据融合改进算法求解各证据联合作用下的可信度分配函数m′(A_j)和不确定性描述m′(Θ).步骤3 效用区间比较.由证据理论可知,信度函数(belief functions)B(A_j)反映了证据支持方案A_j的信度总和,似真函数(plausibility functions)P(A_j)反映了证据不可否定方案A_j的信度总和^[14].两者共同构成方案A_j的效用区间[B(A_j),P(A_j)].其中:

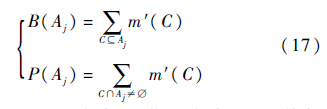
根据效用理论,方案A_j优于方案A_k的偏好度为

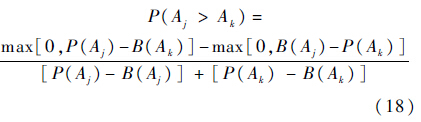
根据式(18),若P(A_j>A_k)>0.5,方案A_j优于方案A_k,即A_j>A_k;若P(A_j>A_k)=0.5,方案A_j与A_k重要程度没有差别,即A_j=A_k;若P(A_j>A_k) < 0.5,则方案A_k优于方案A_j,即A_j < A_k.步骤4 分析检验评估结果,得出评估结论.3 算例分析根据雷达反隐身能力评估指标体系,给出不同类型体制雷达的具体参数,如表 1所示^[15].根据式(1)~式(4)、式(6)~式(16)求取相应的可信度因子ω_i、不确定度m′_i(Θ)及改进可信度分配函数m′_i(A_j),可信度因子与改进的可信度分配函数如表 2所示.根据式(5)、式(17)、式(18)求取各雷达可信度函数m′(A_j)及效用区间,如表 3所示.其中,参数取值与图 3分析假定一致.为验证改进算法性能,分别采用传统证据融合理论、文献^[12]融合算法以及本文改进的证据理论进行证据融合,结果如表 4所示.表 1 雷达具体参数^[15] Table 1 Radar parameters^[15]

雷达	平均功率/kW	天线增益/dB	灵敏度/dBm	工作波段	探测模式	极化方式	探测概率	最大作用距离/km
1	6	40	-150	S	机载	多极化	0.60	45
2	5	35	-130	S	非空基	单极化	0.80	40
3	10	38	-128	L	多基地	强极化	0.65	50
4	0.05	24	-125	VHF	机载	多极化	0.56	53

表选项

注:设预警距离为雷达的最大作用距离,目标速度为1000km/h,脉冲频率为1000Hz,目标在L、S波段下的RCS为0.1m².表 2 可信度因子与改进的可信度分配函数 Table 2 Credibility factor and improved BPA

指标	雷达1	雷达2	雷达3	雷达4	不确定度	可信度因子
x₁	0.0284	0.1728	0.0598	0	0.7390	0.2610
x₂	0.0788	0	0.1477	0.0098	0.7638	0.2362
x₃	0.0733	0.0669	0.1030	0	0.7569	0.2431
x₄	0.1845	0.1012	0	0	0.7143	0.2857
x₅	0.0963	0.0977	0.0752	0	0.7309	0.2691
x₆	0.1179	0.1110	0.0473	0	0.7238	0.2762
x₇	0.0377	0.1529	0.0706	0	0.7388	0.2612
x₈	0.1129	0.1146	0	0.0280	0.7446	0.2554

表选项

注:表2中x1~x8分别对应图1中雷达反隐身性能评估指标x1~x8.
表 3 可信度函数及效用区间 Table 3 BPA and utility interval

雷达	可信度分配函数值	效用区间	融合算法总不确定度
1	0.2893	[0.2893,0.4802]	0.1909
2	0.3415	[0.3415,0.5324]
3	0.1688	[0.1688,0.3597]
4	0.0095	[0.0095,0.2004]

表选项

表 4 不同融合算法融合结论 Table 4 Conclusions of different fusion algorithms

方法	可信度分配函数值				不确定度
方法	雷达1	雷达2	雷达3	雷达4	不确定度
传统方法	0.9716	0.0284	0	0	0
文献[12]方法	0.5917	0.4080	0.0002	8.82×10 ¹⁴	1.56×10 ^-15
本文方法	0.2893	0.3415	0.1688	0.0095	0.1909

表选项

分析表 1~表 4可得出如下结论:1) 可信度因子是对指标重要程度的综合反映,是熵权和受支持系数的函数,其大小与指标数相关.由于指标数较多,各指标熵权和受支持系数相对较小,而采用可信度因子能很好地实现参数放大,且能确定某一指标对于总评估结果的贡献程度和不确定程度,进而客观地解决了指标统计过程中的数据模糊问题.如表 2中,雷达各指标的可信度因子均大于熵权值和受支持系数,且相差不大,均在0.25左右,说明了各指标重要程度相当,这也从侧面反映了指标的选择及其计算方法较为合理.2) 根据表 3和式(18)可综合排出各雷达反隐身能力优劣顺序为:雷达2>雷达1>雷达3>雷达4.分析实际统计数据可知,该结论与实际情况相符.3) 如表 4所示,在存在证据冲突的情况下,采用传统证据融合算法所得结果为m′(A₁)=0.9716,m′(A₂)=0.0284,其余约为0,这既与实际情况不符,也不能反映各雷达的反隐身性能,说明了证据冲突情况下传统证据融合算法具有很大的局限性.文献^[12]融合方法所得结果与传统算法类似,雷达1、2融合结果较大,雷达3、4融合结果和不确定度较小,无法说明各雷达的反隐身性能.这是由于该方法只是建立了可信度因子与欧式距离的函数关系,当指标较多时,所得归一化欧式距离相对较小,其可信度因子值势必较大(0.98左右),在重新计算可信度分配函数时,就会加剧证据的冲突,无法实现对证据源可信度和不确定度的综合衡量.因此该融合算法仅适用于证据源较少的证据融合.运用本文方法所得结果清晰可靠,雷达1、2可信度分配函数值差距不大(0.05左右),雷达3适中,雷达4较小(0.0095),不确定度为0.1909,相对较低,可客观衡量雷达的反隐身性能.综上所述,本文所提出的证据融合算法综合性好、准确性高、可靠性强.4) 单一指标的不确定度反映的是该指标对于综合评估的局限性,其值一般较大.融合后所得不确定度是对指标完备性、综合性的反映,其值一般较小.由表 2、表 4可知,单一指标的不确定度一般在0.75左右,而融合后的不确定度为0.19.由此说明了本文改进算法的可行性和准确性.4 结束语定量评估雷达反隐身性能对雷达的论证设计、定型验收、实践应用等方面具有极其重要的意义.结合雷达反隐身性能评估指标体系建立了基于证据理论的性能评估模型,从而实现了多因素、多方案、多层次的综合评估;通过改进证据融合算法,克服了证据冲突、主观性强等现象,有效提高了证据的可信度.且该方法计算简单,能客观地对不同类型的指标进行综合评估,仿真结果说明了该方法的可行性和有效性.但在应用中还需注意以下两个问题:一是评估指标的选择应结合实际的电磁环境决定,确保指标的实效性;二是评估问题必须同典型战场环境相结合,确保评估的应用性.
参考文献

[1]	曹丽梅, 王瑛.雷达隐身与反隐身技术发展综述[J].现代导航, 2012, 6(3):215-218. Cao L M, Wang Y.Overview on development of radar stealth and anti-stealth technologies of radar[J].Modern Navigation, 2012, 6(3):215-218(in Chinese).
	Cited By in Cnki (4)
[2]	唐政, 孙超, 刘宗伟, 等.基于灰色层次分析法的水声对抗系统性能评估[J].兵工学报, 2012, 33(4):432-436. Tang Z, Sun C, Liu Z W, et al.Research on efficiency evaluation for underwater acoustic countermeasure system based on grey hierarchy analysis[J].Aata Armamentarii, 2012, 33(4):432-436(in Chinese).
	Cited By in Cnki (10) \| Click to display the text
[3]	齐照辉, 刘雪梅, 梁伟, 等.基于分层赋权的导弹防御性能模糊评估方法[J].系统工程理论与实践, 2011, 31(9):1811-1815. Qi Z H, Liu X M, Liang W, et al.Fuzzy evaluation approach to missile defense effectiveness based on layered weight coefficients[J].Systems Engineering-Theory & Practice, 2011, 31(9):1811-1815(in Chinese).
	Cited By in Cnki (1) \| Click to display the text
[4]	Gong S F, Long W J, Huang H, et al.Polyphase orthogonal sequences design for opportunistic array radar via HGA[J].Journal of Systems Engineering and Electronics, 2013, 24(1):60-67.
	Click to display the text
[5]	吴瑕, 周焰, 杨龙坡, 等.基于聚类分析与几何的目标特征敏感性评估算法[J].控制与决策, 2012, 27(6):914-917. Wu X, Zhou Y, Yang L P, et al.Target feature sensitivity evaluation method based on clustering analysis and geometry[J].Control and Decision, 2012, 27(6):914-917(in Chinese).
	Cited By in Cnki (1) \| Click to display the text
[6]	Lei Y G, He Z J, Zi Y Y.A new approach to intelligent fault diagnosis of rotating machinery[J].Expert Systems with Applications, 2008, 35(4):1593-1600.
	Click to display the text
[7]	姜志敏, 刘婕.基于探测范围的雷达网反隐身能力评估方法[J].空军雷达学院学报, 2010, 24(2):115-118. Jiang Z M, Liu J.Method for anti-stealth capability evaluation of radar net based on detection range[J].Journal of Air Force Radar Academy, 2010, 24(2):115-118(in Chinese).
	Cited By in Cnki (3)
[8]	陈永光, 李修和, 沈阳.组网雷达作战能力分析与评估[M].北京:国防工业出版社, 2006:53-56. Chen Y G, Li X H, Shen Y.Radar network analysis and evaluation of operational capability[M].Beijing:National Defense Industry Press, 2006:53-56(in Chinese).

[9]	李金梁, 李永祯, 王雪松.米波极化雷达的反隐身研究[J].雷达科学与技术, 2005, 3(6):321-326. Li J L, Li Y Z, Wang X S.Study on anti-stealth with meter-band polari metric radar[J].Radar Science and Technology, 2005, 3(6):321-326(in Chinese).
	Cited By in Cnki (25)
[10]	美林 I·斯科尼克.雷达系统导论[M].北京:电子工业出版社, 2010:42-55. Merrill I S.Introduction to radar systems[M].Beijing:Publishing House of Electronics Industry, 2010:42-55(in Chinese).

[11]	孙锐.基于D-S证据理论的信息融合及在可靠性数据处理中的应用研究[D].成都:电子科技大学, 2011. Sun R.Research on D-S evidence theory based information fusion and its application in reliability data processing[D].Chengdu:University of Electronic Science and Technology of China, 2011(in Chinese).
	Cited By in Cnki
[12]	李巍华, 张盛刚.基于改进证据理论及多神经网络融合的故障分类[J].机械工程学报, 2010, 46(9):93-99. Li W H, Zhang S G.Fault classification based on improved evidence theory and multiple neural network fusion[J].Journal of Mechanical Engineering, 2010, 46(9):93-99(in Chinese).
	Cited By in Cnki (27) \| Click to display the text
[13]	孟光磊, 龚光红.证据源权重的计算及其在证据融合中的应用[J].北京航空航天大学学报, 2010, 36(11):1365-1368. Meng G L, Gong G H.Weight coefficients calculation for evidence sources and its application in evidences fusion[J].Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(11):1365-1368(in Chinese).
	Cited By in Cnki (3)
[14]	曹一家, 姚欢, 黄小庆, 等.基于D-S证据理论的变电站通信系统信息安全评估[J].电力自动化设备, 2011, 31(6):1-5. Cao Y J, Yao H, Huang X Q, et al.Security evaluation of substation communication system based on D-S theory[J].Electric Power Automation Equipment, 2011, 31(6):1-5(in Chinese).
	Cited By in Cnki \| Click to display the text
[15]	潘超.雷达抗干扰性能评估准则与方法研究[D].成都:电子科技大学, 2006. Pan C.Principles and method of radar ECCM effectiveness evaluation[D].Chengdu:University of Electronic Science and Technology of China, 2006(in Chinese).
	Cited By in Cnki (24)