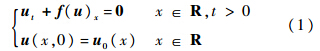
式中：f(u)为守恒型流动通量,非线性函数;u(x,t)为流动矢量;u0(x)为初始条件.如果对偏微分方程式(1)进行隐式离散,将会得到非线性隐式差分格式,这种格式仍需要进一步线化(Beam-Warming线性化[2])后,才易于求解.将这种线化方法体现为引入虚拟时间及线化项改写原方程(都是无穷小量,所以方程不变,只是离散形式变了),得:
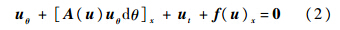
式中：A(u)=fu(u)，为Jacobi矩阵;θ为虚拟时间.收敛时uθ=0,所以式(2)添加项对于偏微分方程来说都等于0.将通量按特征值正负分裂(即Steger-Warming分裂[9]),得
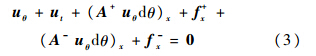
通量分裂形式为
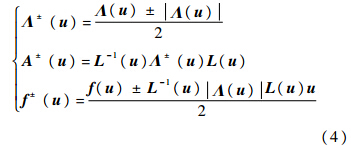
式中：Λ(u)为特征值矩阵;L(u)为左特征矩阵.进一步,式(3)需要按算子分裂(或称算子分解)的思想,在时间上将此方程分解成几个方程,因为有2种时间,故此处有2种分裂方式. 1.1 按物理时间分裂式(3)分解为
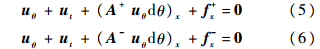
以式(5)为例推导格式,记Δukj=uk+1j－ukj,收敛时uk+1j=ukj=un+1j,上标k和n分别表示虚拟迭代次数和物理迭代次数,对式(5)做迎风离散,利用Crank-Nicolson方法,得
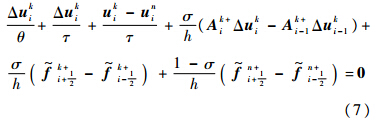
式中:σ为参数(0≤σ≤1);
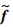为数值通量;下标i为节点序号;τ为物理时间步长;h为空间步长.整理后得到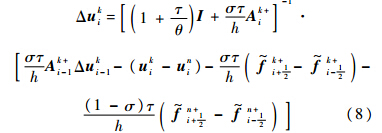
根据特征关系式(4),式(8)改写为
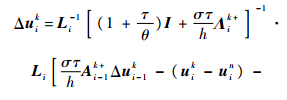
式中：I为单位阵.式(9)中需要求逆的矩阵是一个对角阵,因此避免了复杂矩阵的求逆运算,相对于常规的隐式方法减小了计算量和存储量.同理可得
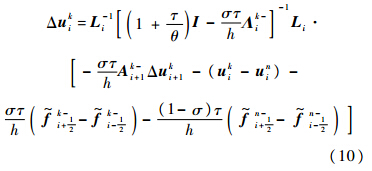
式(9)和式(10)为按物理时间分裂的最终差分格式求解公式.差分格式一个物理时间步的数值解的合成有如下2种方式:1) 2个方向分别进行虚拟时间合成,然后再做一次物理时间合成:
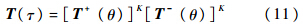
2) 2个方向混合进行虚拟时间合成:
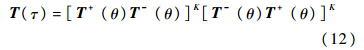
式中:T(τ)、T+(θ)、T－(θ)分别为一次物理时间的解算子、正方向一次虚拟时间的解算子、负方向一次虚拟时间的解算子;K为迭代收敛的总次数. 1.2 按虚拟时间分裂式(3)分裂为
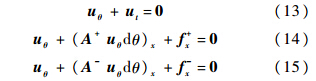
推导思路同1.1节,推导过程省略,得到按虚拟时间分裂的最终差分格式求解公式:
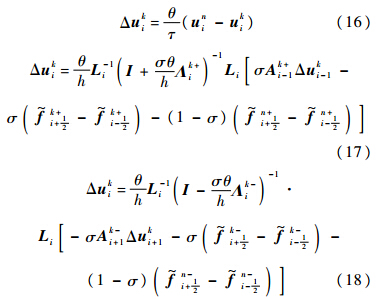
差分格式一个物理时间步的数值解的合成:
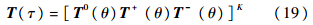
式中：T0(θ)为物理时间项的一次虚拟时间解算子.1.3 二阶时间精度 1.3.1 按虚拟时间分裂方法1物理时间离散采用二阶形式,即
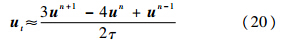
此时时间方向的公式为
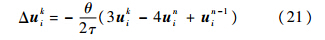
正通量方向和负通量方向的最终差分格式求解公式仍为式(17)、式(18),但取σ=1.这种方法为多步方法,需要2个时间层un、un－1的值,令un和un－1迭代初值都等于u0.方法2 令式(17)、式(18)中的σ=0.5,即为二阶时间精度[10],实际计算中为保证稳定性,内迭代最后一步取σ=0.5,其余步数σ=1.1.3.2 按物理时间分裂物理时间分裂二阶时间精度的方法与虚拟时间分裂的方法相同,这里直接给出公式.方法1
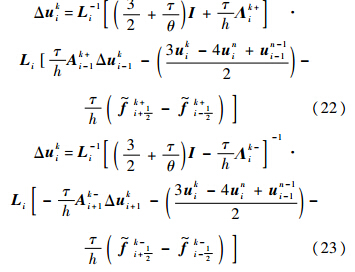
方法2式(9)、式(10)内迭代最后1步取σ=0.5,其余步数取σ=1.1.4 数值通量选择 实际计算时,f~+i+12和f~－i－12可使用各种成熟格式的通量,主要使用NND格式和MUSCL格式.NND格式通量为[11, 12]
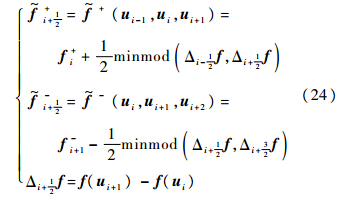
MUSCL格式通量为[13, 14]
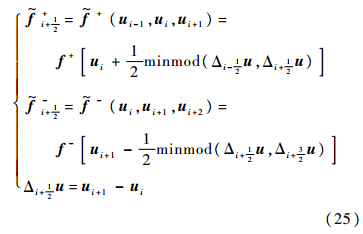
式中:minmod为最小模限制器,即
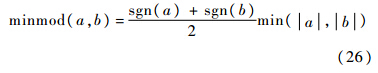
式中:sgn为符号函数.物理时间步长和虚拟时间步长选取方式为[8]
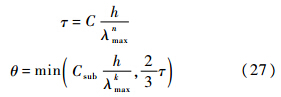
式中:C为外迭代CFL数,它是流体力学判断计算的收敛条件;Csub为内迭代CFL数；λmax为Jacobi矩阵特征值的最大值.子迭代初值:uk=0=un.子迭代收敛判据:残差定义同文献[15],为Δρkmax/θ,收敛条件为残差小于0.0001,子迭代步数限定为50. 1.5 定常问题隐式虚拟时间隐式中,取消物理时间项,即式(16),则可以得到定常Euler方程的隐式方法,定常Euler方程的最终差分格式计算公式为式(17)、式(18),取σ=1. 1.6 其他问题关于多维问题,一维问题算法可以通过维数分裂法直接推广到多维问题,因公式类似而不再重述.大量计算实践表明,在相同CFL数条件下(隐式虽然CFL数不受限制,但CFL数对解的品质有直接影响,进行效率对比必须在相同精度下进行),对于非均匀网格,分裂法比不分裂法计算速度要快,并且与不均匀度成正比.关于收敛性或稳定性问题,这里沿用Lax等价性定理(线性格式的定理,本文的隐式部分属于局部线性格式,故此定理可做参考)的结论,稳定性与收敛性是一致的,所以这个词用任何一个都意味着另一个也成立(由于虚拟时间隐式是个迭代过程,所以使用收敛性这个词).注意,分裂隐式的线化矩阵选择并不唯一,根据隐式格式的绝对稳定性要求,当线化矩阵特征值的模大于原通量相应特征值模的一半以上时,隐式迭代过程收敛.而当线化矩阵的特征值等于原通量的相应特征值时,收敛最快.并且,当虚拟时间步长与物理时间步长取一致且通量为线性退化情形时,可一步收敛.2 算例验证 2.1 Sod激波管 初始条件为
式中：ρ为气体密度；p为气体压强.采用300个等距网格,C=1.0,Csub=2.0,数值通量使用NND格式,t=0.15s时密度分布计算结果如图 1所示.
 |
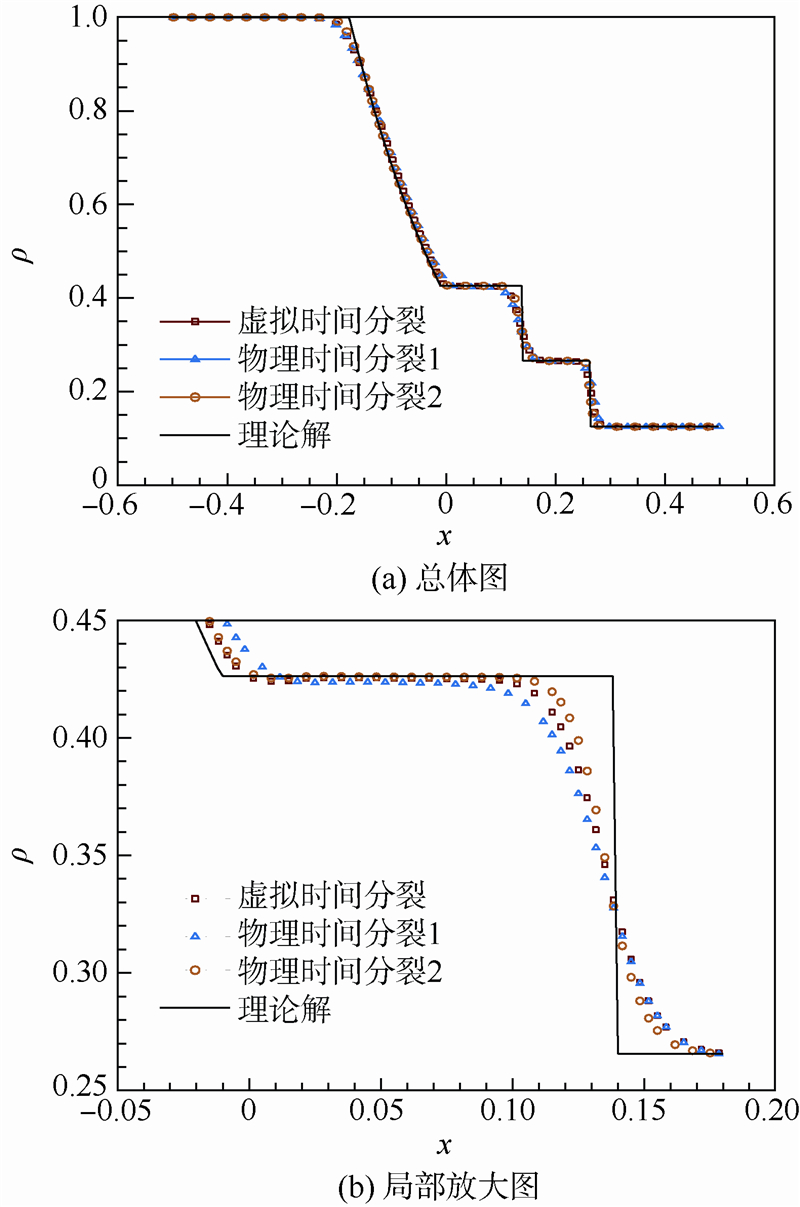| 图 1 t=0.15s时密度分布计算结果Fig. 1 Results of density distribution when t=0.15s |
| 图选项 |
由图 1可以看出,2种分裂方法都有较好的时间精度,其中物理时间分裂2格式的时间精度最高.采用物理时间分裂2格式,二阶时间精度计算结果如图 2所示.
 |
| 图 2 二阶时间精度计算结果Fig. 2 Results of second order time accuracy |
| 图选项 |
图 2表明这些二阶时间精度的方法具有提高时间精度的效果. 2.2 Lax激波管初始条件为
数值通量使用MUSCL格式,采用虚拟时间分裂格式.对于均匀网格情况,要保证相同计算量,网格数N与CFL数可取如下关系：N=300C,C分别取1.0、4.0、9.0,计算结果如图 3所示.
 |
| 图 3 均匀网格情况、相同计算量下不同CFL数的计算结果Fig. 3 Results with the same computations and different CFL numbers for uniform grid |
| 图选项 |
由图 3可看出,在相同计算量情况下,CFL数对计算结果影响不大,说明本文方法在大CFL数下也能保证一定的精度要求.2.3 改进的Lax激波管 初始条件为
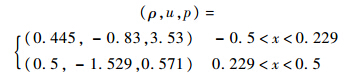
该算例是Lax激波管的修改,接触间断位置固定.此算例可考察隐式方法对定场流场的计算效果,因为接触间断位置固定,可以排除时间精度对解的影响.实际问题多采用非均匀网格,局部网格加密而时间步长不变等价于增大CFL数,为保证同等计算量,网格数与CFL数取如下关系:N=100C,C分别取1.0、6.0,数值通量使用MUSCL格式,采用虚拟时间分裂格式,计算结果如图 4所示.
 |
| 图 4 非均匀网格情况、相同计算量下,不同CFL数的计算结果Fig. 4 Results with the same computations and different CFL numbers for non-uniform grid |
| 图选项 |
由图 4可看出,当考虑非均匀网格情况时,在相同计算量下,增加CFL数可以提高计算精度,表明本文方法对于实际问题更有价值.2.4 超声速流绕前台阶流动 流动初始参数ρ1=1.0,u1=3.0,流动速度v1=0,p1=0.71429,计算模型示意图如图 5所示.
 |
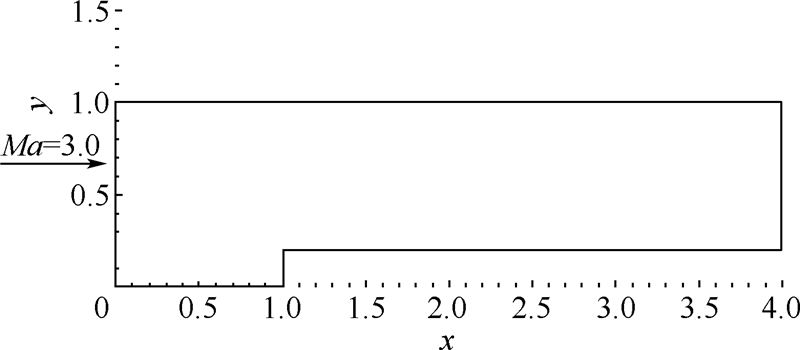| 图 5 计算模型示意图Fig. 5 Schematic diagram of calculation model |
| 图选项 |
初始条件:当t=0时,全流场内充满了马赫数为3.0的超声速气流.边界条件:左边界(x=0,0≤y≤1.0)处为马赫数为3.0的均匀来流.右边界(x=4,0.2≤y≤1.0)为自由输出条件.上边界、下边界和前台阶物面均为刚性边界,满足滑移反射边界条件.这是一个非定常问题,采用虚拟时间分裂格式,为比较相同计算量下不同CFL数对计算结果的影响,故采用两套网格进行计算.2.4.1 计算条件1采用50×10和200×40两块网格,C=1.0.前台阶网格1如图 6所示.
 |
| 图 6 前台阶网格1Fig. 6 Grid 1 of forward-facing step |
| 图选项 |
网格1前台阶绕流等密度线分布(C=1.0)随时间变化情况如图 7所示.
 |
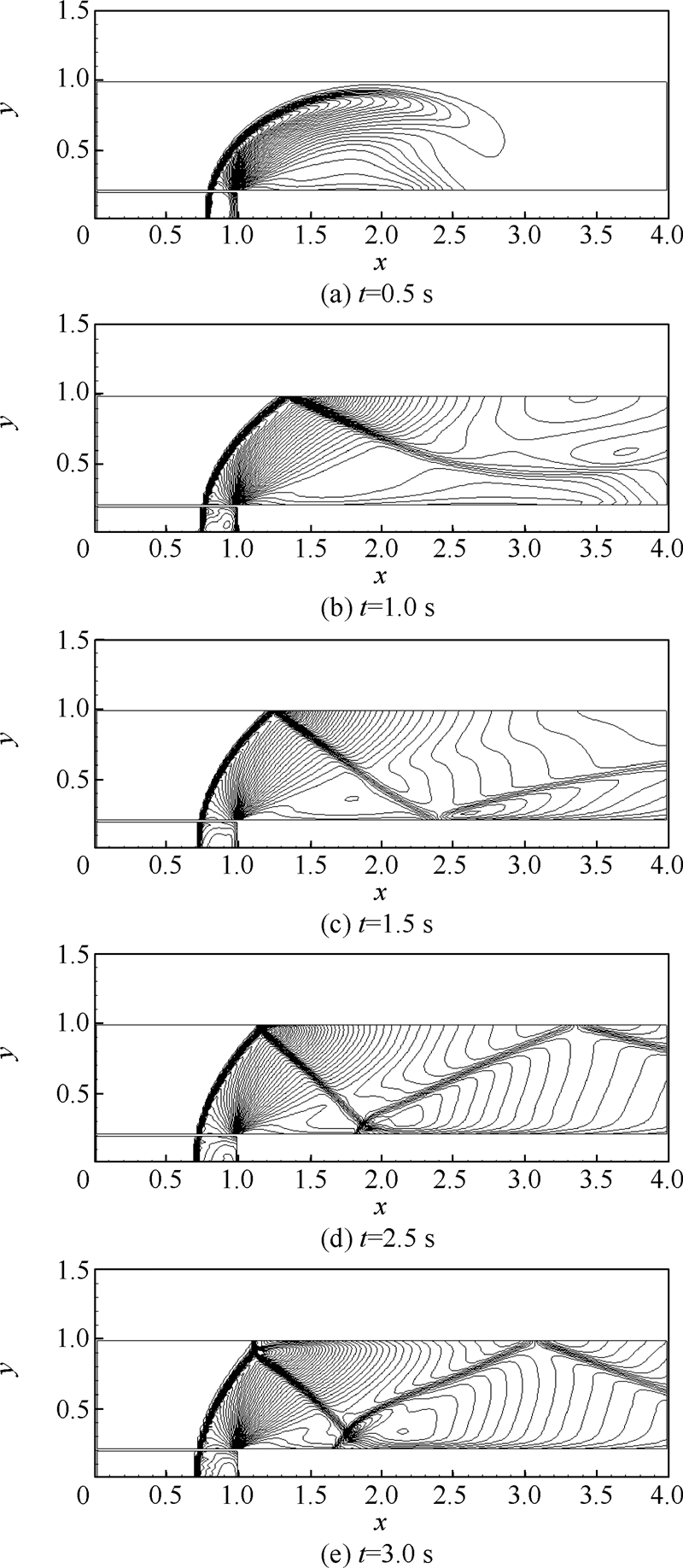| 图 7 网格1前台阶绕流等密度线分布(C=1.0)Fig. 7 Density contours of forward-facing step flow for Grid 1 (C=1.0) |
| 图选项 |
2.4.2 计算条件2采用100×20和400×80两块网格,C=8.0.前台阶网格2如图 8所示.
 |
| 图 8 前台阶网格2Fig. 8 Grid 2 of forward-facing step |
| 图选项 |
网格2前台阶绕流等密度线分布(C=8.0)随时间变化情况如图 9所示.
 |
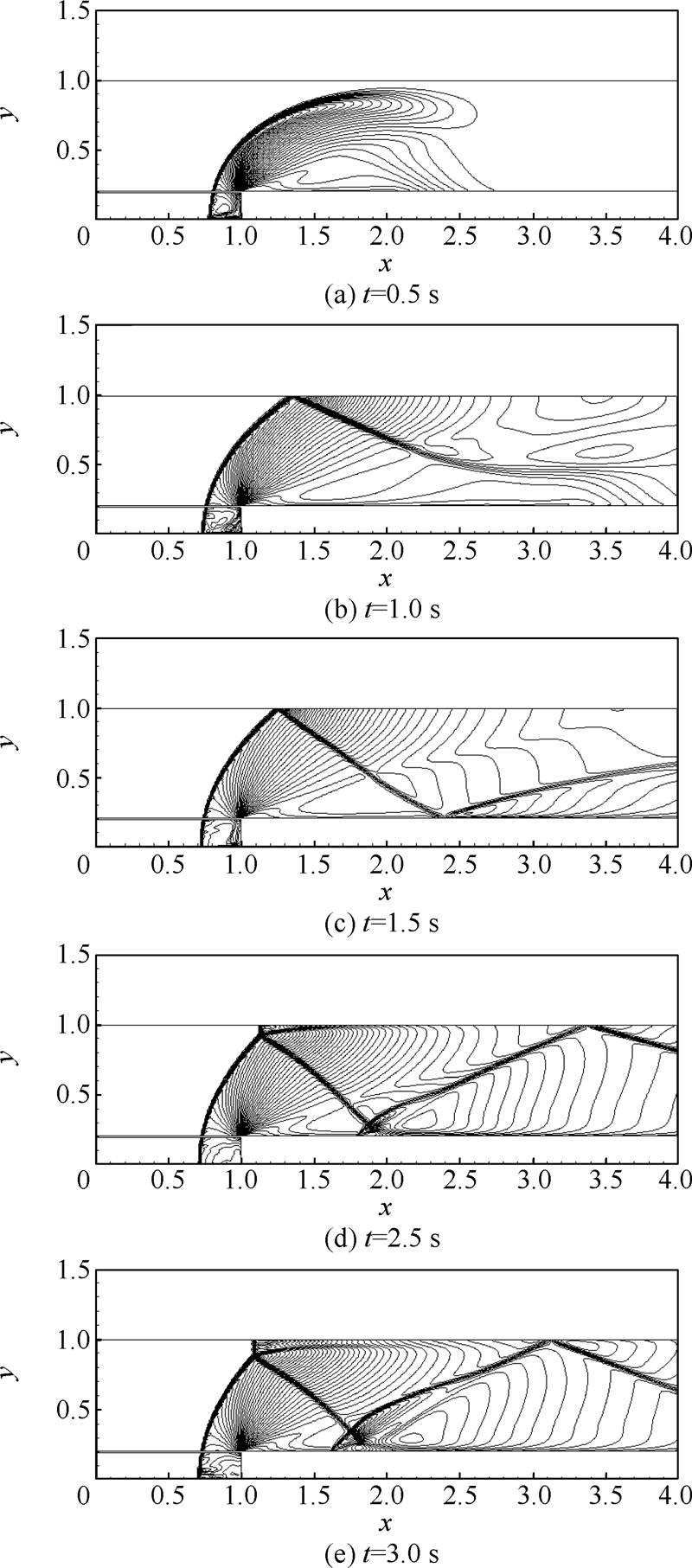| 图 9 网格2前台阶绕流等密度线分布(C=8.0)Fig. 9 Density contours of forward-facing step flow for Grid 2 (C=8.0) |
| 图选项 |
以上计算可得到与2.2节相同的结论.2.5 NACA0012翼型绕流 NACA0012翼型网格如图 10所示,网格数为239×59.
 |
| 图 10 NACA0012翼型网格Fig. 10 Grid of NACA0012 airfoil |
| 图选项 |
1) 来流马赫数为0.8,攻角为1.25°.在来流马赫数为0.8,攻角α为1.25°来流条件下,绕翼型的流场属超临界状态,在翼面上将形成附体激波.上翼面激波较强,下翼面会形成一道很弱的激波.流场压强等值线和翼型表面压强系数Cp分布如图 11(a)~图 11(d)所示.
 |
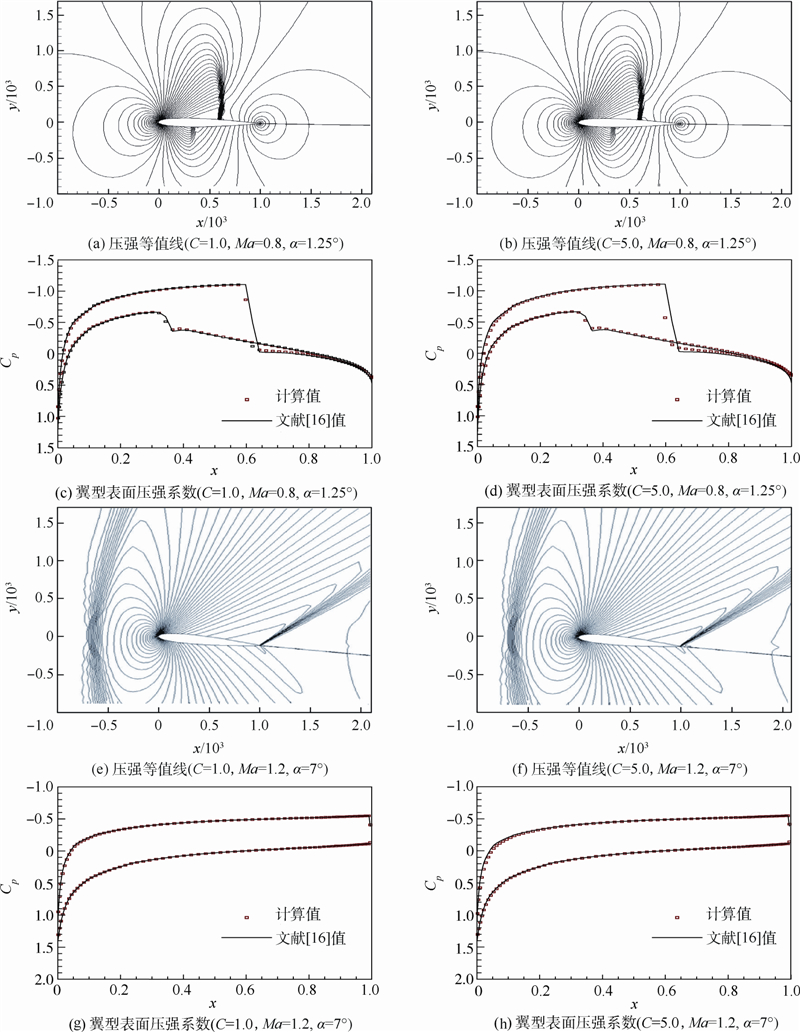| 图 11 流场压强等值线和翼型表面压强系数分布Fig. 11 Pressure contours and pressure coefficients on airfoil surface |
| 图选项 |
计算结果表明,在不同的CFL数下,本文方法均能捕捉到翼型上表面的强激波和下表面的弱激波,且与文献[16]吻合度良好.2) 来流马赫数为1.2,攻角为7°.在来流马赫数为1.2,攻角为7°来流条件下,其绕流场将在翼型头部形成脱体的弓形激波,在后缘形成鱼尾激波.流场压强等值线和翼型表面压强系数分布如图 11(e)~图 11(h)所示.计算结果表明,在不同的CFL数下,本文方法均能捕捉到头部的弓形激波和后缘的鱼尾激波,且与文献[16]吻合度良好. 2.6 双椭球无粘绕流计算网格如图 12所示,网格数为51×39×19.计算条件:来流马赫数Ma=8.0,攻角α=0°,侧滑角β=0°.实验激波纹理照片如图 13所示[17].
 |
| 图 12 计算网格Fig. 12 Grid for calculation |
| 图选项 |
 |
| 图 13 实验激波纹理照片Fig. 13 Photo of experimental texture[17] |
| 图选项 |
实验表明:在此马赫数下,椭球头部会形成脱体弓形激波,两椭球镶嵌处附近会出现二次激波.流场压强等值线和对称面上下物面压强系数如图 14所示.
 |
| 图 14 流场压强等值线和对称面上下物面压强系数Fig. 14 Pressure contours and pressure coefficients on top and low surfaces |
| 图选项 |
计算结果表明,在不同的CFL数下,本文方法均可捕捉到两道激波,且和实验吻合良好.通过2.5节和2.6节算例可以得出以下结论:本文方法可以增大CFL数，提高计算效率,并能够保持精度.3 与LU-SGS方法的比较 3.1 Sod激波管 计算条件与2.1节相同,由于计算结果相近,故不再给出,图 15为Sod激波管2种方法的比较.图 15说明了2个问题:①使用高阶时间精度的方法可以提高内迭代次数,从而提高计算效率.②在相同时间精度的情况下,本文方法物理时间推进一步所需的虚拟时间迭代次数少于LU-SGS方法的,即收敛速度更快.
 |
| 图 15 Sod激波管2种方法的比较Fig. 15 Comparison of two schemes in Sod shock tube |
| 图选项 |
3.2 超音速流绕前台阶流动 计算条件同2.4节,图 16为前台阶绕流2种方法的比较.
 |
| 图 16 前台阶绕流2种方法的比较Fig. 16 Comparison of two schemes in forward-facing step flow |
| 图选项 |
图 16的结果同样说明本文方法在收敛速度上更有优势.LU-SGS方法为了提高计算效率,避免矩阵求逆,采用了简化的A±、B±、C±分解求法,故对求解的收敛性有了一定的影响,本文方法使用了严格的A±、B±、C±分解,所以收敛性能较好,也起到了减小计算量的作用. 发展了一种新的分裂型隐式方法,并利用典型的空气动力学问题测试其性能,可以得到以下结论:1) 方法具有隐式格式的普遍优点,即稳定性好,CFL数可以放大;此外,方法格式简单,易于编程,单步时间推进不涉及方程组常规求解和矩阵求逆,计算量小,与LU-SGS方法相比,收敛更快.2) 对于定常问题,方法可以在增大CFL数、提高计算效率的情况下保证精度.3) 对于非定常问题,方法的计算精度主要由计算量决定,同等计算量下,不会随CFL数的增大而丧失精度.
参考文献
| [1] | Pulliam T H. Development of implicit method in CFD NASA Ames Research Center 1970s-1980s[J].Computers & Fluids,2011,41(1):65-71. |
| Click to display the text | |
| [2] | Beam R M,Warming R F.An implicit finite-difference algorithm for hyperbolic system in conservation law form[J].Journal of Computational Physics,1976,22(1):87-109. |
| Click to display the text | |
| [3] | Beam R W,Warming R F.An implicit factored scheme for the compressible Navier-Stokes equations[J].AIAA Journal,1978,16(4):393-402. |
| Click to display the text | |
| [4] | Biringer M,McMillan O J.Calculation of two dimensional inlet fields by an implicit method including viscous effect:program documentation and test case,NASA-CR-81-3414[R].Washington,D.C.:NASA,1981. |
| [5] | Pulliam T H,Chaussee D S.A diagonal form of an implicit approximate factorization algorithm[J].Journal of Computational Physics,1981,39(2):347-363. |
| Click to display the text | |
| [6] | Chaussee D S,Pulliam T H.Two dimensional inlet simulation using a diagonal implicit algorithm[J].AIAA Journal,1981,19(2): 153-159. |
| Click to display the text | |
| [7] | Yoon S,Jameson A.Lower-upper symmetric Gauss-Sediel method for the Euler and Navier-Stoker equations[J].AIAA Journal,1988,26(9):1025-1026. |
| Click to display the text | |
| [8] | Jameson A. Time dependent calculations using multigrid with application to unsteady flows past airfoils and wings[C]//AIAA 10th Computational Fluid Dynamics Conference.Reston:AIAA,1991:1-4. |
| Click to display the text | |
| [9] | Steger J L,Warming R F.Flux vector splitting of the inviscid gasdynamic equations with application to finite-difference methods[J].Journal of Computational Physics,1981,40(2):263-293. |
| Click to display the text | |
| [10] | 张小蜂,张红武.Crank-Nicolson格式精度的改进[J].水科学进展,2001,12(1):33-38. Zhang X F,Zhang H W.Efficient improvement of Crank-Nicolson scheme[J].Advances in Water Science,2001,12(1):33-38(in Chinese). |
| Cited By in Cnki (20) | |
| [11] | 陈培基,陆夕云,庄礼贤.一种修正的隐式NND格式[J].计算物理,1996,13(3):379-384. Chen P J,Lu X Y,Zhuang L X.A modified implicit NND difference scheme[J].Chinese Journal of Computational Physics,1996,13(3):379-384(in Chinese). |
| Cited By in Cnki | |
| [12] | 张德良. 计算流体力学教程[M].北京:高等教育出版社,2010:331-332. Zhang D L.A course in computational fluid dynamics[M].Beijing:High Education Press,2010:331-332(in Chinese). |
| [13] | Collela P. A direct Eulerian MUSCL scheme for gas dynamics[J].SIAM Journal on Scientific and Statistical Compuing,1985,6(1):104-117. |
| Click to display the text | |
| [14] | 水鸿寿. 一维流体力学差分方法[M].北京:国防工业出版社,1998:509-512. Shui H S.Difference methods of one-dimensional fluid dynamics[M].Beijing:Defense Industry Press,1998:509-512(in Chinese). |
| [15] | 赵慧勇,乐嘉陵. 双时间步方法的应用分析[J].计算物理,2008,25(3):253-258. Zhao H Y,Le J L.Application analysis on dual-time stepping[J].Chinese Journal of Computational Physics,2008,25(3):253-258(in Chinese). |
| Cited By in Cnki (5) | |
| [16] | 钱战森. 大时间步长、高分辨率差分格式研究及其应用[D].北京:北京航空航天大学,2011. Qian Z S.On large time step,high resolution finite difference schemes for hyperbolic conservation laws and applications[D].Beijing:Beijing University of Aeronautics and Astronautics,2011(in Chinese). |
| [17] | 李素循. 典型外形高超声速流动特性[M].北京:国防工业出版社,2006:18-39. Li S X.Hypersonic flow characteristics of typical shapes[M].Beijing:National Defense Industry Press,2006:18-39(in Chinese). |
