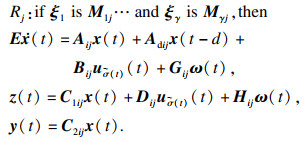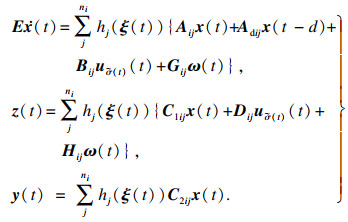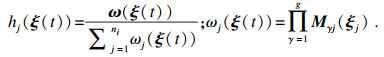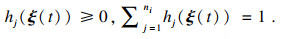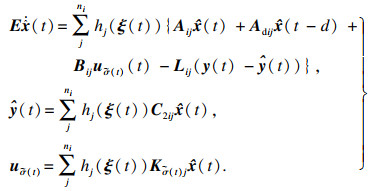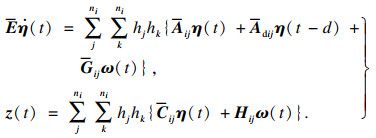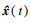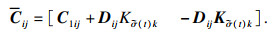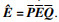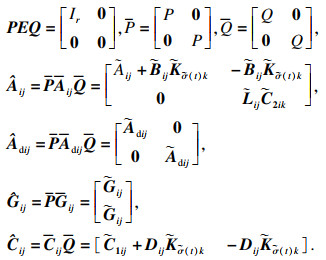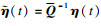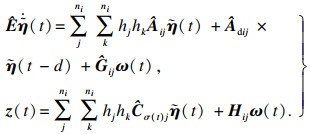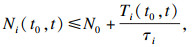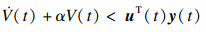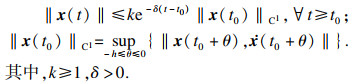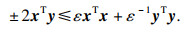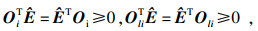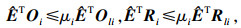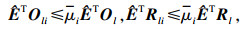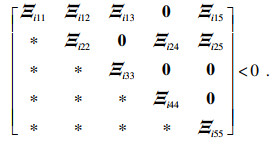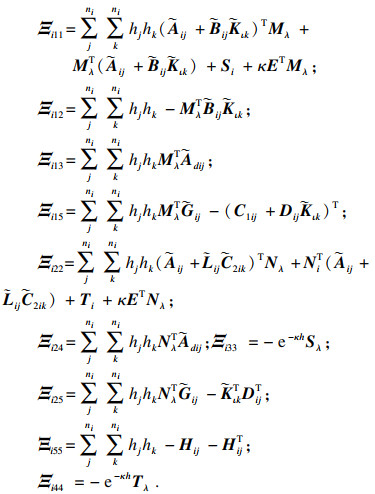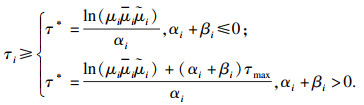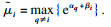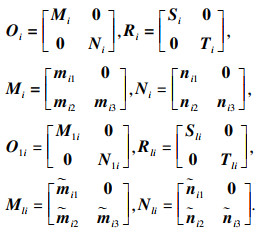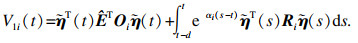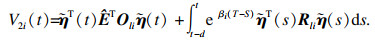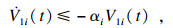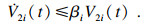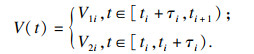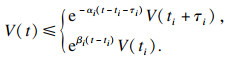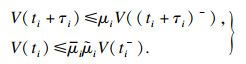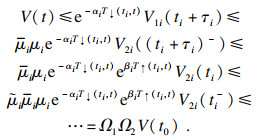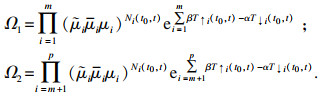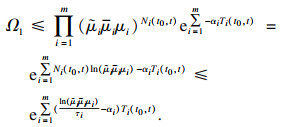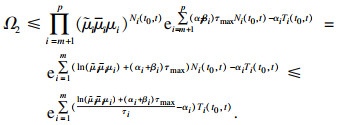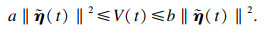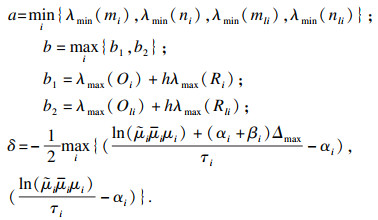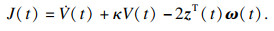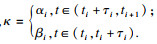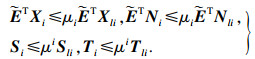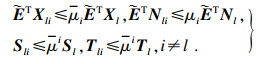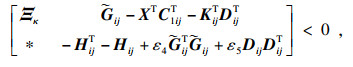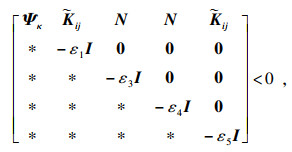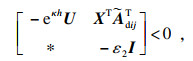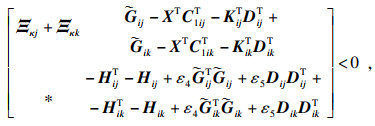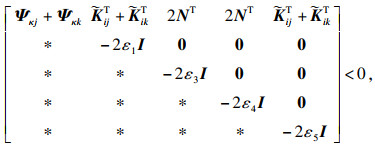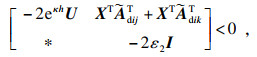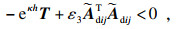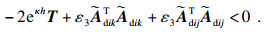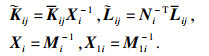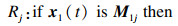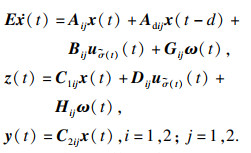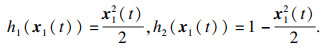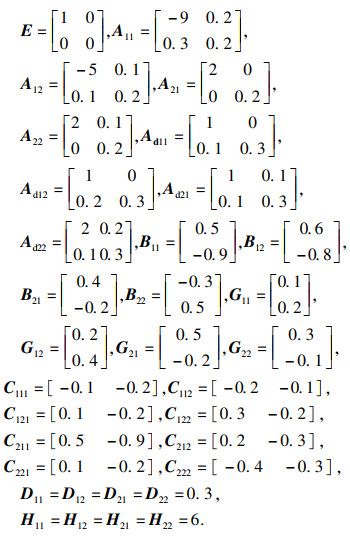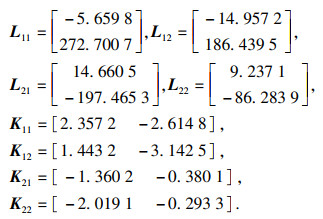杨东梅, 王傲
东北大学 理学院, 辽宁 沈阳 110819
收稿日期：2021-02-02
基金项目：国家自然科学基金资助项目(61673100)。
作者简介：杨冬梅(1966-)，女，辽宁沈阳人，东北大学教授。

摘要：引入了一种新的无源不等式到T-S模糊广义切换系统中进而研究了一类子系统切换与基于观测器的控制器切换存在不同步情况的系统无源性问题.首先, 运用分段李雅普诺夫函数和模型依赖平均驻留时间的方法, 通过无源性过剩的子系统来弥补无源性不足的子系统, 从而确保切换系统的整体无源性; 然后, 利用线性矩阵不等式的方法得到时滞T-S模糊广义切换系统的全局一致指数稳定和严格指数无源的充分条件, 并据此设计出相应的观测器和控制器, 最后给出数值算例证明该方法的有效性.
关键词：观测器时滞异步控制器无源性广义切换系统
Observer-Based Asynchronous Passive Control for T-S Fuzzy Generalized Switched Systems with Time Delay
YANG Dong-mei, WANG Ao
School of Sciences, Northeastern University, Shenyang 110819, China
Corresponding author: YANG Dong-mei, E-mail: yangdongmei@mail.neu.edu.cn.

Abstract: The concept of passivity is extended to T-S fuzzy generalized switched systems, and then the passivity problem for asynchronous situation between a class of subsystem switching and observer-based controller switching is studied. Firstly, by using piecewise Lyapunov function and model dependent average dwell time, the sub-systems with excess passivity can compensate for the sub-system with insufficient passivity, so as to ensure the overall passivity of the switched system. Afterwards, the sufficient conditions for globally uniformly exponential stability and strictly exponential passivity of T-S fuzzy generalized switched systems with time delay are obtained by using the linear matrix inequality method, and the corresponding observers and controllers are designed. Finally, numerical examples are provided to validate the effectiveness of the method.
Key words: observertime delayasynchronous controllerpassivitygeneralized switched systems
切换系统作为一种重要的混合系统, 是一个融合了诸如信息处理、微分方程和工业生产等学科的全新研究课题.随着现代控制理论的发展, 以及同其他学科的深度融合, 一种更加普遍更加贴近现实的系统得到了越来越多的关注, 被称为“广义切换系统”.如今, 控制理论大多是根据数学模型来研究的.然而在实际建模时, 大多数系统无法用线性模型表示, 且系统参数很可能随时间变化而改变, 甚至系统结构也发生改变, 而系统又因为不能完全与外部隔离, 或多或少会受到外部干扰, 以及工业水准受限使精度出现细微的偏差而导致的不确定性等因素, 都导致难以建立精确的数学模型.即使对一些复杂系统成功建立了数学模型, 模型也常常太过复杂不利于研究, 无法实现有效控制, 因此, 对于模糊控制理论的研究就变得尤为重要^[1].在实际控制问题中, 由于系统的切换需要时间识别, 因此控制器的切换不可避免地落后于系统的切换, 导致子系统与控制器之间出现短暂的不同步.无源性作为一种特殊的耗散性, 是以系统的输入和输出的叉乘作为系统的供给率, 在有些情形下储存函数可以作为系统的能量函数, 因此对于广义切换系统的无源性和异步控制问题的研究同样尤为重要.文献[2]针对具有结构不确定性的非线性切换系统, 提出了鲁棒半无源性和实用稳定性分析.文献[3]针对一类广义Lurie切换系统采用类李雅普诺夫函数的方法研究了系统的鲁棒无源性.文献[4]针对具有多个存储函数和多个供给率的离散非线性切换系统的几何拟无源性、反馈拟通性及其相关性质进行了研究.文献[5]针对一类严格反馈非线性系统在适当的状态依赖切换律下研究了基于无源性的镇定问题.文献[6]分析了非线性切换系统，提出增量式无源性、增量式无源化和增量式镇定问题.然而对于T-S模糊广义切换系统的无源性问题的研究成果鲜有人发表.
本文对一类时滞T-S模糊广义切换系统引入一种新的无源不等式, 探讨了在控制器切换不同步情况下系统的指数稳定性和无源性问题, 并利用分段李雅普诺夫函数和线性矩阵不等式的方法, 得到了使时滞T-S模糊广义切换系统全局一致指数稳定且严格指数无源的充分条件.由于系统的状态不易得到, 本文得出了一种基于观测器的控制器设计方法，并通过仿真证明了该方法的有效性.
1 问题描述本文主要探讨时滞T-S模糊广义切换系统的无源性问题, 其子系统模型由如下形式的模糊规则构成：
其中: M _rj(r=1, 2, …, γ)为模糊集; x(t)为状态向量; u(t)为控制输入; y(t)为量测输出; z(t)为受控输出; ω(t)为干扰变量; A_ij, B_ij, C_1ij, C_2ij, D_ij, G_ij, H_ij为具有合适阶数的实常数矩阵; A_dij为滞后常数矩阵；d为时间滞后量，满足0 < d < h; ?(t)是控制器切换信号且满足?(t)=σ(t-Δ_i), σ(t)是切换信号; ξ(t)=[ξ₁(τ), ξ₂(τ), …, ξ_γ(τ)]^T为前件变量，是状态变量的函数; E为奇异矩阵.通过单点模糊化^[7]、乘积推理^[8-9]和加权平均化^[10-12]的推理方法, T-S模糊广义切换系统的子系统的全局模型可以写为

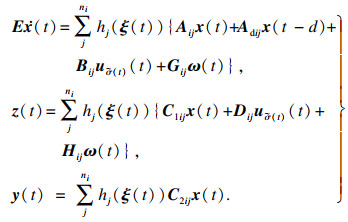(1)

其中：n_i为模糊规则数;
M_γj(ξ_j)表示ξ_γ在模糊集M_γj上的隶属度.且h_j(ξ(t))满足
假设系统(1)是能检测的, 设计状态观测器和控制器, 其系统描述为

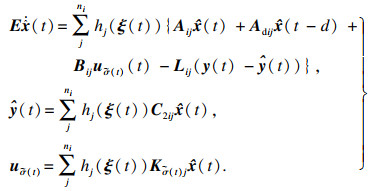(2)

得到增广闭环系统为

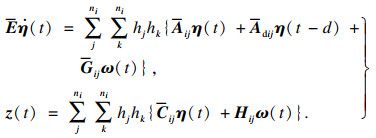(3)

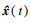
令η(t)=[x^T(t) e^T(t)]^T, e(t)=x(t)－ 以及
存在可逆矩阵P, Q, 使得=.
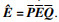
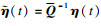
因则系统(3)与系统(4)等价：

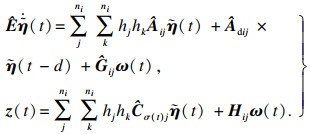(4)

定义1 ^[13]??对于切换信号σ(t)和?t≥t₀≥0, N_i(t₀, t), T_i(t₀, t)分别表示子系统在时间间隔(t₀, t)上的切换次数和运行时间, 如果满足：
且τ_i>0, 称τ_i为子系统i的平均驻留时间.
定义2^[14] ??对于给定的α>0, 系统的输入u(t)和输出y(t), 如果：
成立, 其中V(t)是一个非负函数, 那么系统是严格指数无源的.
定义3 ^[15]??系统平衡点x=0在切换信号σ(t)作用下是全局一致指数稳定的, 系统的解x(t)在给定初始值x(t₀), 以及ω(t)=0时满足：
引理1 ^[16]??对于任意的n维向量x, y和任意常量ε>0, 有
2 主要结果为证明过程方便, 令T_↓i(t₀, t), T_↑i(t₀, t)分别表示子系统i在时间间隔(t₀, t)上的控制器匹配和不配的运行时间, T_↓(t₀, t), T_↑(t₀, t)分别表示系统在时间间隔(t₀, t)上的控制器匹配和不配的运行时间.
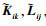
定理1 ??考虑系统(4)，若给定实数α_i>0, β_i < 0, 存在实数μ_i≥1，μ_i≥1，可逆矩阵Q_i, Q_li, 对称正定矩阵R_i>0, R_li>0, 和矩阵, i=1, 2, …, p, i≠l满足:

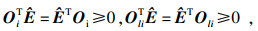(5)

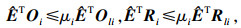(6)

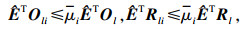(7)

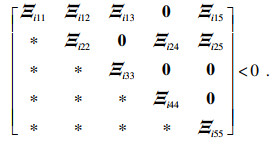(8)

式中:
其中, κ∈{α_i, －β_i}.当κ=α_i时, λ=ι=i; 当κ=－β_i时, λ=li, ι=l, 则系统(4)对于满足平均驻留时间：
的切换信号是全局一致指数稳定且严格指数无源的, 其中
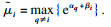
证明 ??将系统按照α_i+β_i的取值分为两类, 当α_i+β_i≤0时, 子系统属于θ₁={1, 2, …, m}, 当α_i+β_i>0时, 属于θ₂={m+1, m+2, …, p}.令:
当t∈(t_i+τ_i, t_i+1)时, 构造如下李雅普诺夫函数:
当t∈(t_i, t_i+τ_i)时, 构造如下李雅普诺夫函数:
对V_1i(t)和V_2i(t)求导, 并且由式(8)可知

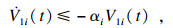(9)

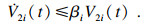(10)

在t∈[t₀, t)上令:
由式(9), 式(10)可得

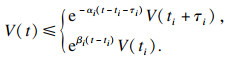(11)

再由式(6), 式(7)可得

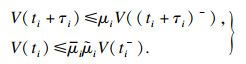(12)

令Δ_max=maxΔ_i, N₀=0，则由式(13), 式(14)可得

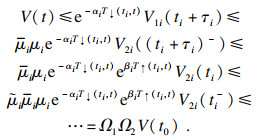(13)

其中:
对于Ω₁, 有α_i+β_i≤0, 则
对于Ω₂, 有T_↑i(t₀, t)≤Δ_maxN_i(t₀, t), 则
由V(t)易得

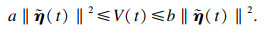(14)

其中:
再由式(13), 式(14)可得
考虑:
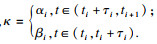
其中, 由式(8)显然有J(t) < 0, 由定义2、定义3可知定理得证.
由于定理1中的不等式条件不是线性的, 不容易求解, 下面基于引理1适当地缩放不等式的条件, 使之成为线性矩阵不等式.
定理2 ??若存在可逆矩阵x_i, N_i, x_li, N_li, 实数ε₁>0, ε₂>0, ε₃>0, ε₄>0, ε₅>0, α_i>0, β_i < 0, μ_i≥1, μ _i≥1, 对称正定矩阵U_i>0, T_i>0, U_li>0, T_li>0和矩阵K _ij, L_ij, i=1, 2, …, p, 使得

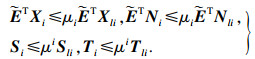(15)

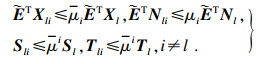(16)

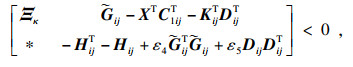(17)

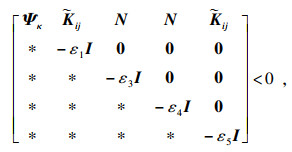(18)

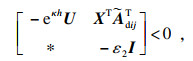(19)

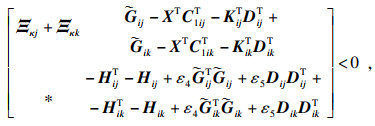(20)

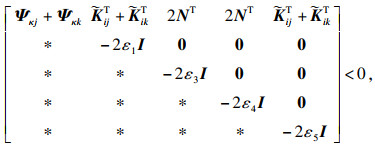(21)

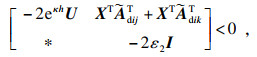(22)

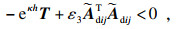(23)

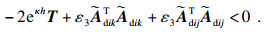(24)

其中:
定理1中的控制器和观测器的增益矩阵:
证明 ??利用引理1对式(8)进行变换, 可得到式(8)可由式(17)~式(24)推出, 定理得证.
3 算例考虑如下有两个子系统的例子.
规范化隶属函数分别为
各子系统的局部子系统的参数为
选取α₁=1.33, α₂=1.2, β₁=－1.3, β₂=－0.7, 按照上述定理得到控制器和观测器增益矩阵为
以及各个参数: μ₁=2, μ₂=8.7, μ ₁=6.5, μ₂=8.5, ?₁=1.0725, ?₂=2.0138, 经计算可得τ₁^*=0.7817, τ₂^*=0.6033.
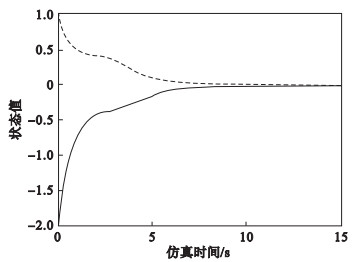
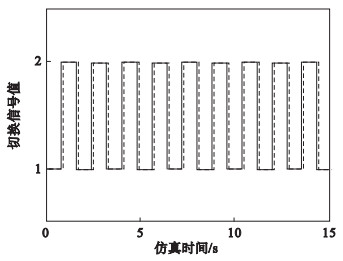
选取平均驻留时间τ₁=0.8>τ₁^*, τ₂=0.8>τ₂^*，令控制器相对子系统切换滞后量最大值Δτ_max=0.2, 初值为x (t₀)=[1, -2]^T, 由图 1，图 2可知系统是稳定的.这证明了方法的有效性.
图 1(Fig. 1)

图 1 状态轨迹Fig.1 The curves of state

图 2(Fig. 2)

图 2 切换信号Fig.2 The curves of switch signal

4 结语本文引入了一种新的无源不等式, 给出了时滞T-S模糊广义切换系统在控制器存在切换滞后的情况下保证系统是全局指数稳定且严格指数无源的充分条件, 通过数值仿真验证了该结果的有效性.
参考文献

[1]	张庆灵, 朱宝彦. T-S模糊广义系统的分析与控制[M]. 北京: 国防工业出版社, 2011. (Zhang Qing-ling, Zhu Bao-yan. Analysis and control of T-S fuzzy singular systems[M]. Beijing: National Defense Industry Press, 2011.)
[2]	Liu S, Pang H. Robust semi-passivity and practical stability for uncertain switched nonlinear systems[J]. IEEE Access, 2020, 8: 12096-12104. DOI:10.1109/ACCESS.2020.2964725
[3]	秦燕飞, 包俊东. 不确定多状态变时滞广义Lurie切换系统的鲁棒无源控制[J]. 动力系统与控制, 2020, 9(1): 50-61. (Qin Yan-fei, Bao Jun-dong. Robust passive control of uncertain singular Lurie switched systems with multiple time-varying delays[J]. Dynamical Systems and Control, 2020, 9(1): 50-61.)
[4]	Liu S, Pang H. Geometrical quasi-passivity and practical stability property for switched discrete-time nonlinear systems[J]. IEEE Access, 2020, 8: 59862-59869. DOI:10.1109/ACCESS.2020.2983093
[5]	Sun Y, Zhao J. Passivity-based stabilization for a strict-feedback nonlinear system under a proper state-dependent switching[C]// 2017 36th Chinese Control Conference(CCC). Dalian, 2017: 2361-2366.
[6]	Pang H, Li C. Incremental passivity and stabilization for switched nonlinear systems[J]. Transactions the Institute of Measurement and Control, 2020, 42(4): 014233122090538.
[7]	Zhai D, Lu A Y, Li J H, et al. Robust H∞ control for switched singular linear systems with uncertainties in the derivative matrices: an improved average dwell time approach[J]. Optimal Control Applications & Methods, 2016, 37(2): 441-460.
[8]	Zhang L, Gao H. Asynchronously switched control of switched linear systems with average dwell time[J]. Automatica, 2010, 46(5): 953-958. DOI:10.1016/j.automatica.2010.02.021
[9]	Wang R, Wu Z G, Shi P. Dynamic output feedback control for a class of switched delay systems under asynchronous switching[J]. Information Sciences, 2013, 225: 72-80. DOI:10.1016/j.ins.2012.10.040
[10]	Liu X. Passivity and passification of T-S fuzzy-model-based switched uncertain systems[C]// International Conference on Fuzzy Systems & Knowledge Discovery. Haikou, 2007: 30-34.
[11]	Zhu S, Shen Y, Chen G. Exponential passivity of neural networks with time-varying delay and uncertainty[J]. Physics Letters A, 2010, 375(2): 136-142. DOI:10.1016/j.physleta.2010.10.045
[12]	陈跃鹏, 张庆灵, 翟丁, 等. 基于观测器的广义系统H∞可靠性控制器[J]. 东北大学学报(自然科学版), 2003, 24(7): 631-634. (Chen Yue-peng, Zhang Qing-ling, Zhai Ding, et al. Observer based H∞ reliability controller for singular systems[J]. Journal of Northeastern University(Natural Science), 2003, 24(7): 631-634. DOI:10.3321/j.issn:1005-3026.2003.07.006)
[13]	Zhao X, Zhang L, Shi P, et al. Stability and stabilization of switched linear systems with mode-dependent average dwell time[J]. IEEE Transactions on Automatic Control, 2012, 57(7): 1809-1815. DOI:10.1109/TAC.2011.2178629
[14]	Wu Z G, Park J H, Su H, et al. New results on exponential passivity of neural networks with time-varying delays[J]. Nonlinear Analysis Real World Applications, 2012, 13(4): 1593-1599. DOI:10.1016/j.nonrwa.2011.11.017
[15]	Sun X M, Zhao J, Hill D J. Stability and L2-gain analysis for switched delay systems: a delay-dependent method[J]. Automatica, 2006, 42(10): 1769-1774. DOI:10.1016/j.automatica.2006.05.007
[16]	朱宝彦, 刘爱斌, 赵恩良. 基于观测器的时滞T-S模糊广义系统无源控制[J]. 沈阳建筑大学学报(自然科学版), 2015(2): 377-384. (Zhu Bao-yan, Liu Ai-bin, Zhao En-liang. Observer based passive control for T-S fuzzy descriptor systems with time delay[J]. Journal of Shenyang Jianzhu University(Natural Science), 2015(2): 377-384.)