, 张超, 王鹏宇 东北大学 资源与土木工程学院, 辽宁 沈阳 110819
收稿日期：2020-08-03
基金项目：国家自然科学基金资助项目(U1602232)；辽宁省科学技术计划项目(2019JH2/10100035)；中央高校基本科研业务费专项资金资助项目(N170108029)。
作者简介：王述红(1969-), 男, 江苏泰州人, 东北大学教授, 博士生导师。
摘要：基于稳定函数, 给出了求解支撑结构系统临界力的计算方法, 推导了不同荷载作用位置的3种双层支撑结构系统临界力的计算公式.结果表明: 基于稳定函数的理论推导公式求出的解析解与二阶弹性分析数值解计算结果相近, 误差均在3 % 以内; 双层1~3跨带摇摆柱支撑结构系统总承载力理论值与试验值的结果验证了本文求解支撑结构系统临界力计算方法的准确性.基于稳定函数的支撑结构系统临界力计算方法具有普遍的适用性、较高的计算精度, 为工程应用提供理论基础.
关键词：支撑结构稳定分析临界力有效长度系数摇摆柱
Calculation Method of the Critical Force of Support Structure System Based on Stability Function
WANG Shu-hong, YAO Qian
, ZHANG Chao, WANG Peng-yu School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: YAO Qian, E-mail: yaoqianneu@163.com.
Abstract: Based on the stability function, a calculation method for solving the critical force of the support structure system was given, and the calculation formula for the critical force of three double-layer support structure systems at different load positions was derived. The results show that the analytical solution derived from formula based on the stability function theory is similar to the numerical solution of the second-order elastic analysis with an error less than 3 %. The accuracy of the calculation method for the critical force of the support structure system was verified by the the theoretical and experimental values of the total bearing capacity of the double-layer 1~3-span rocking column support structure system. The critical force calculation method of the support structure system provides a theoretical basis for engineering applications due to its universal applicability and high calculation accuracy.
Key words: support structurestability analysiscritical forceeffective length factorsway column
施工阶段, 工地常使用木支撑、可调钢管支柱、钢管脚手架及型钢架等, 通过各种组搭方式来配置模板支撑.由于模板支撑属于施工阶段的临时性结构, 工程结束后即被拆除, 其重要性常被忽视.目前国内对于此类结构的安全问题还不够重视, 因此工地常发生模板支撑倒塌事故.
摇摆柱常出现在工地模板支撑结构系统中, 摇摆柱的存在会使支撑结构系统的临界力降低.对于受压结构系统, 两端为铰接的承压构件，称为摇摆柱.当支撑结构系统中的柱受压致使边界产生侧向位移时, 该柱可视为摇摆柱.摇摆柱不但无法为结构系统提供承载力, 还会产生额外的水平侧向力, 这将导致结构系统的临界力大幅下降.
国内外****[1-6]对各种类型的支撑结构系统做了大量的试验, 认为施工单位对于支撑结构的临界力计算多以单根柱的力学行为作为指标, 设计单位多注重在结构永久使用阶段的问题, 很少直接计算整个结构系统的承载力, 忽略了支撑结构系统整体的破坏行为, 这种计算方法所得结果与试验结果有一定差距.《GB 50017—2017钢结构设计规范》[7]和《JGJ300—2013建筑施工临时支撑结构技术规范》[8]给出了框架柱和支撑结构的计算长度系数表格, 但计算长度系数法无法反应支撑结构系统整体的真实临界力, 与精确解相比有较大误差.文献[9-11]基于挠度法研究了框架结构的临界力计算方法.田炜烽等[12]推导了考虑柱间相互作用的阶形柱计算长度系数的计算公式.郝际平等[13]提出了多层有侧移框架整体稳定的计算方法.国内关于支撑结构系统稳定承载力的研究[14-16]多以单一类型的支撑结构为主, 且没有形成系统的计算方法.
支撑结构在竖向荷载下的失稳为二阶问题, 本文从结构稳定分析角度出发, 在文献[17]的基础上将稳定函数扩展运用到求解支撑结构系统的临界力上, 可将求解压杆临界力转化为计算压杆挠度和结构侧移, 运用转角位移法推导出各类支撑结构系统的临界力计算公式, 再通过一般非线性方程的数值解法求出整个结构系统的临界力.
1 稳定函数基本理论支撑结构系统中的主要受力构件为梁柱, 梁柱是既受弯曲又受压缩的结构构件.由于支撑结构的弯曲和轴向效应都是显著的, 分析时既涉及梁的挠度问题, 也涉及柱的稳定性问题.支撑结构的构件发生屈服时, 弯矩-曲率关系将变为非线性, 在这种情况下必须借助数值方法来获得解析解[18].
支撑结构主要受端部力矩和轴力, 如图 1所示, 构件左右两端受端弯矩MA, MB及轴向力P作用, 从左端取长度为x的梁柱段的隔离体图.
图 1(Fig. 1)
 | 图 1 受端弯矩和轴力作用的梁柱构件Fig.1 Beam-column members loaded by end bending moments and axial forces (a)—受端弯矩和轴力作用；(b)—隔离体图. |
作用在截面上的外部力矩为
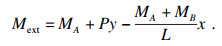 | (1) |
将内力矩Mext改写为－EIy″, 引入k2=P/EI, 可得:
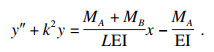 | (2) |
代入边界条件可得该梁柱的挠度函数:
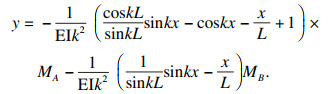 | (3) |
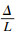
图 2(Fig. 2)
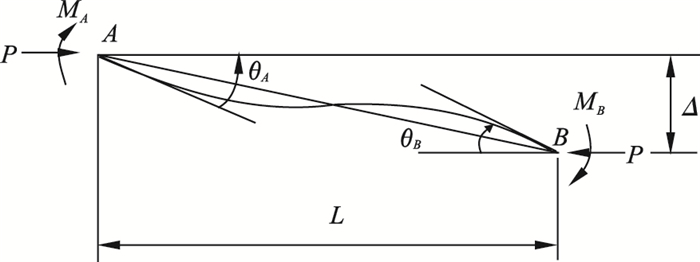 | 图 2 受端弯矩的梁柱(有相对位移)Fig.2 Beam-column loaded by end bending moment(with relative displacement) |
图 2所示有侧移的梁柱结构的挠度函数同式(3), 易知θA=y′(0), θB=y′(L), y(L)=Δ, 代入式(3)可得端力矩和转角位移之间的关系为
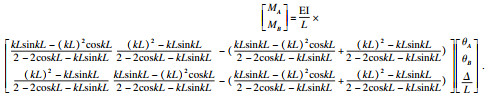 | (4) |
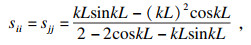 | (5) |
 | (6) |
 | (7) |
2 支撑结构力学模型及计算公式在桥梁工程中, 由于钢筋混凝土构造物的内部挑空较大, 施工单位为了降低成本, 常采用双层组搭模板支撑, 如双层单一可调钢管支柱组搭、脚手架和可调钢管支柱混合组搭、脚手架和木支撑混合组搭、型钢架和可调钢管支柱混合组搭等.
模板支撑在组搭时, 下端通常直接放置于地面或楼板面, 上端置于水平顶撑下, 由于两端未作任何抗弯补强, 分析时两端可简化视为铰接.模板支撑倒塌时主要考虑新浇灌混凝土的垂直荷载, 如果模板支撑设置在海边或强风环境中, 则需要考虑侧向力的影响, 本文主要考虑受垂直荷载的支撑结构系统整体失稳屈曲的临界承载力.因此, 模板支撑的荷载主要作用于上层支撑架顶部和水平杆上, 模板支撑很少导致水平杆的破坏发生倒塌, 需重点考虑立柱的破坏行为, 可将水平杆上的荷载简化为节点处的集中力.为了模拟图 3所示工地现场各种支撑结构系统实际的配置情形, 采用简化的双层支撑模式为力学模型, 根据荷载作用位置的不同分为3个模型：模型Ⅰ荷载P主要作用在水平杆上, 模型Ⅱ荷载P作用于上层支撑顶部, 模型Ⅲ是上层支撑架顶部和水平杆上分别作用的荷载βP和P.支撑结构的下层立柱长度为L, 刚度为EI; 上层立柱长度为αL, 刚度为γEI; 水平杆的长度为aL, 刚度为ηEI, 力学模型如图 3所示.
图 3(Fig. 3)
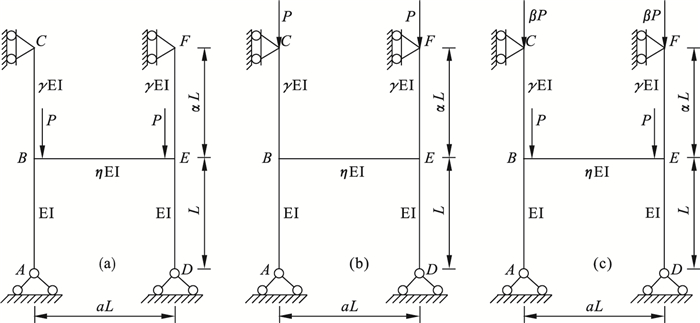 | 图 3 三种简化的支撑结构力学模型Fig.3 Three simplified mechanical models of support structures (a)—模型Ⅰ；(b)—模型Ⅱ；(c)—模型Ⅲ. |
以模型Ⅱ为例, 基于稳定函数推导该支撑结构系统的临界力计算公式.双层支撑结构系统变形示意图如图 4所示.
图 4(Fig. 4)
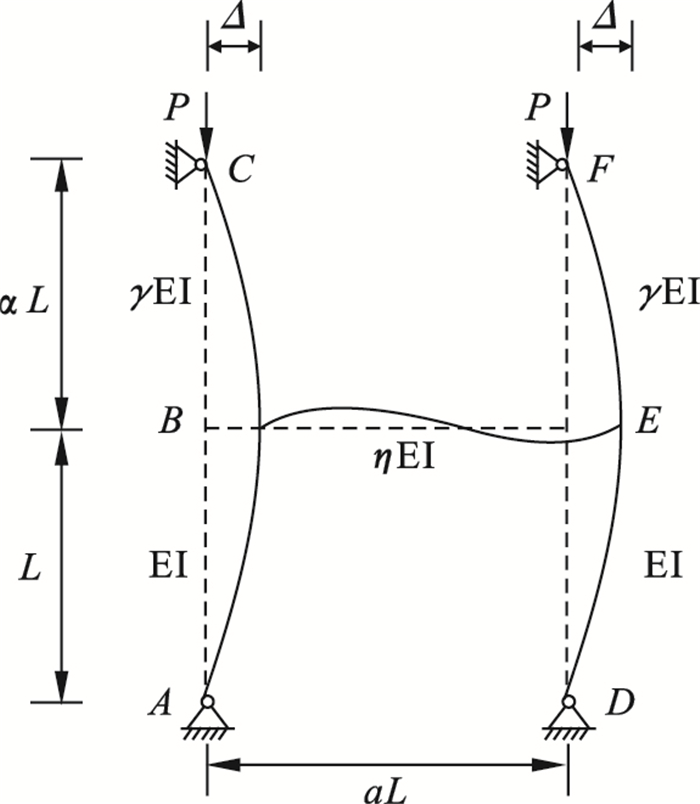 | 图 4 双层支撑结构系统变形示意图(模型Ⅱ)Fig.4 Schematic diagram of the deformation of the double-layer support structure system (Model Ⅱ) Δ为支撑结构系统失稳时水平杆产生的侧移. |
基于稳定函数式(4)及式(5), 可得到支撑结构系统各杆件的端弯矩与转角位移之间的关系.为区分不同杆件, AB杆的稳定函数用Sii1, Sij1表示, BE杆的稳定函数用Sii2, Sij2表示, BC杆的稳定函数用Sii3, Sij3表示.其中DE杆同AB杆, EF杆同BC杆.各杆件端的弯矩为
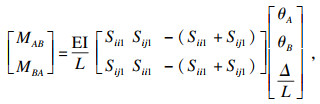 | (8) |
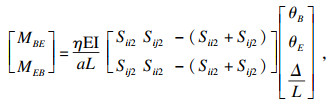 | (9) |
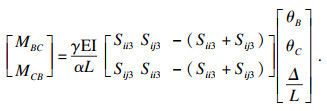 | (10) |
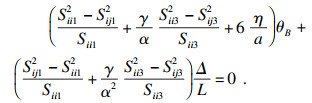 | (11) |
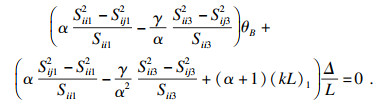 | (12) |
将式(11)与式(12)联立可得该支撑结构系统临界力计算公式.为直观表示, 该公式的矩阵形式为
 | (13) |
 | (14) |
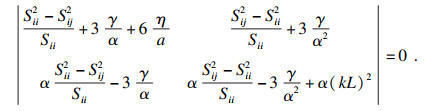 | (15) |
 | (16) |
3 算例分析3.1 求解带摇摆柱的支撑结构为方便比较, 本文单跨支撑分析模式主要参考彭瑞麟等[17]的研究, 采用简化的双层支撑模式为力学模型, 根据荷载作用位置的不同将支撑模式分为3个模型.图 5为模型Ⅱ带摇摆柱的双层支撑结构力学模型.根据摇摆柱数量和位置的不同共分为6种配置, 为方便描述, 无摇摆柱用NL表示, 1根摇摆柱在上方用1LT表示, 1根摇摆柱在下方用1LB表示, 2根摇摆柱在上方用2LT表示, 2根摇摆柱在同一侧用2LS表示, 3根摇摆柱用3L表示.
图 5(Fig. 5)
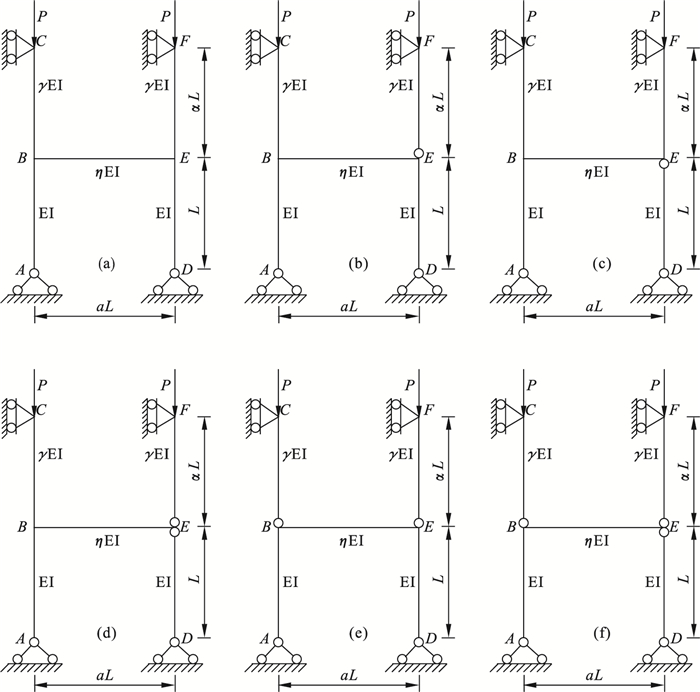 | 图 5 带摇摆柱的支撑结构力学模型Fig.5 Mechanical models of the support structure with swing column (a)—NL; (b)—1LB; (c)—1LT; (d)—2LS; (e)—2LT; (f)—3L. |
用基于稳定函数的支撑结构系统临界力计算方法可求得图 5中各支撑结构临界力的计算公式, 再通过一般非线性方程的数值解法求得kL的最小非零解.再根据公式:
 | (17) |
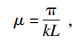 | (18) |
表 1(Table 1)
 表 1 带摇摆柱支撑结构的临界力及计算长度系数Table 1 Critical force and calculation length coefficient of the support structure with rocking column
| 表 1 带摇摆柱支撑结构的临界力及计算长度系数 Table 1 Critical force and calculation length coefficient of the support structure with rocking column | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
由表 1可知: 基于稳定函数的理论推导公式求出的解析解与二阶弹性分析数值解计算结果相近, 误差均在3 % 以内, 表明此方法具有高度准确性.而规范解计算结果偏差相对较大, 其中NL, 1LT, 1LB, 2LS类支撑结构系统临界力的计算结果偏于保守; 而2LT, 3L类支撑结构系统临界力的计算结果偏不安全, 这是受摇摆柱效应的影响, 即摇摆柱不但无法为整体结构提供承载力, 还会引发系统产生额外的水平侧向力, 导致整个支撑结构系统的极限承载力大幅下降.当支撑结构系统内摇摆柱较多时, 这种影响将不可忽略, 这也是工地大多数支撑结构在浇筑混凝土时倒塌的原因.
3.2 试验对比以文献[20]中的靠杆试验为对比, 试验的支撑材料以钢管为主, 材质属于中碳钢(S45C), 截面尺寸为35.70 mm, 通过材料试验测得钢管的弹性模量E=1.96 N/mm2.
试验模式[20]采用上下两层组搭配置, 中间使用型钢H100 mm×100 mm×6 mm×8 mm作为双层组搭的中间平台, 设置上下层高度比为1∶ 1, 即α=1, 上下边界无侧移, 仅允许层与层之间的水平侧向位移.
为了模拟工地实际组搭时的初始缺陷, 中间水平型钢初始侧向位移设置为5 mm, 且工地实际配置情形中常出现摇摆柱结构, 试验时将可抵抗侧向弯矩的强柱(图 5中的AB杆)配置在下层, 其余杆件皆为摇摆柱.
图 6为带摇摆柱的单跨、双跨、三跨支撑结构试验图.试验中上下层钢管材质完全相同, 因此参数α, γ取值均为1;同层的钢管跨距为40 cm, 钢管的长度L=112.5 cm, 因此参数a取值为0.356(40/112.5);中间使用的型钢刚度远大于钢管柱的刚度, 因此参数η近似于无穷大.
图 6(Fig. 6)
 | 图 6 双层支撑结构试验图Fig.6 Test diagrams of double layer support structure (a)—单跨；(b)—双跨；(c)—三跨. |
基于稳定函数求解此类支撑结构临界力的计算公式为
 | (19) |
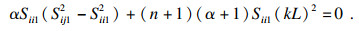 | (20) |
将测得的试验值(图 6中各支撑结构系统通过试验测得的总临界力∑Pcr2)与计算公式推导出的理论值(通过公式(20)求得的总临界力∑Pcr1) 对比, 结果如表 2所示.
表 2(Table 2)
表 2 总承载力及计算长度系数理论值与试验值对比Table 2 Comparison between thetheoretical and experimental values of the total bearing capacity and the calculation length coefficient
| 表 2 总承载力及计算长度系数理论值与试验值对比 Table 2 Comparison between thetheoretical and experimental values of the total bearing capacity and the calculation length coefficient | |||||||||||||||||||||||||||
由表 2可知, 计算误差均在7 % 以内, 说明本文基于稳定函数求解支撑结构系统临界力的计算方法具有较高精度.
由上述结果可知, 当支撑结构增加的杆件均为摇摆柱时, 整个支撑结构系统的总承载力Pcr并无明显变化.国内工地经常以增加支撑数量的方式来提高支撑结构的承载力, 但应特别注意, 当增加的支撑杆件类似于摇摆柱结构时, 对整个支撑结构系统的总承载力贡献不大.
4 结论1) 以稳定函数为基础, 给出支撑结构系统临界力的计算方法, 并推导了荷载作用位置不同的3种支撑结构系统临界力的计算公式.
2) 求解带摇摆柱支撑结构系统的计算长度系数和临界力, 理论解与数值解的误差在3 % 以内, 验证了本文求解支撑结构系统临界力的计算方法具有高度的准确性.
3) 建议在施工和设计中, 工程技术人员应该更加注重支撑结构系统整体的破坏行为, 并在增加支撑杆件时, 防止出现大量的摇摆柱结构.摇摆柱不但无法为结构系统提供承载力, 还会产生额外的水平侧向力, 这将导致结构系统的临界力大幅下降, 使其有不可预测的倒塌危险.
致谢 本文部分成果为东北大学-云林科技大学学术合作内容, 特此感谢云林科技大学彭瑞麟教授及其团队吴忠卫、陈明铮、张育尘、吴冠霖等给予的帮助和支持.
参考文献
| [1] | Peng J L, Wang C S, Wang S H, et al. Study on stability and design guidelines for the combined system of scaffolds and shores[J]. Steel and Composite Structures, 2020, 35(3): 385-404. |
| [2] | Chan J L Y, Lo S H. Direct analysis of steel frames with asymmetrical semi-rigid joints[J]. Steel and Composite Structures, 2019, 31(1): 99-112. |
| [3] | Cimellaro G P, Domaneschi M. Stability analysis of different types of steel scaffolds[J]. Engineering Structures, 2017, 152(12): 535-548. |
| [4] | Peng J L. Experiment and stability analysis on heavy-duty scaffold systems with top shores[J]. Advanced Steel Construction, 2017, 13: 293-317. |
| [5] | Mitch G. Experimental investigation on the load capacity of a scaffolding frame[J]. International Journal of Engineering Education, 2016, 8(6): 2460-2467. |
| [6] | Peng J L, Ho C M, Lin C C, et al. Load-carrying capacity of single-row steel scaffolds with various setups[J]. Advanced Steel Construction, 2015, 11(2): 185-210. |
| [7] | 中华人民共和国住房和城乡建设部. 钢结构设计规范: GB 50017—2017[S]. 北京: 中国建筑工业出版社, 2018. (Ministry of Housing and Urban-Rural Development of the People's Republic of China. Code for design of steel structures: GB 50017—2017[S]. Beijing: China Construction Industry Press, 2018. ) |
| [8] | 中华人民共和国住房和城乡建设部. 建筑施工临时支撑结构技术规范: JGJ 300—2013[S]. 北京: 中国建筑工业出版社, 2013. (Ministry of Housing and Urban-Rural Development of the People's Republic of China. Technical specification for temporary support structures for building construction: JGJ 300—2013[S]. Beijing: China Building Industry Press, 2013. ) |
| [9] | 兰树伟, 周东华, 双超. 基于挠度法的有侧移框架临界力计算方法[J]. 华中科技大学学报, 2019, 47(5): 122-127. (Lan Shu-wei, Zhou Dong-hua, Shuang Chao. Calculation method of critical force of frame with lateral displacement based on deflection method[J]. Journal of Huazhong University of Science and Technology, 2019, 47(5): 122-127.) |
| [10] | 兰树伟, 周东华, 双超, 等. 有侧移框架临界承载力的实用计算方法[J]. 振动与冲击, 2019, 38(11): 180-186. (Lan Shu-wei, Zhou Dong-hua, Shuang Chao, et al. Practical calculation method for critical bearing capacity of side-shift frame[J]. Vibration and Shock, 2019, 38(11): 180-186.) |
| [11] | 双超, 周东华, 兰树伟, 等. 有侧移框架临界力的简便计算方法[J]. 华中科技大学学报, 2019, 47(8): 55-59. (Shuang Chao, Zhou Dong-hua, Lan Shu-wei, et al. A simple method for calculating the critical force of a side-shift frame[J]. Journal of Huazhong University of Science and Technology, 2019, 47(8): 55-59.) |
| [12] | 田炜烽, 孙嘉亮, 郝际平. 考虑柱间相互作用的阶形柱计算长度系数[J]. 建筑结构学报, 2020, 41(1): 1-13. (Tian Wei-feng, Sun Jia-liang, Hao Ji-ping. Calculated length coefficient of stepped column considering the interaction between columns[J]. Journal of Building Structures, 2020, 41(1): 1-13.) |
| [13] | 郝际平, 田炜烽, 王先铁. 多层有侧移框架整体稳定的简便计算方法[J]. 建筑结构学报, 2011, 32(11): 183-188. (Hao Ji-ping, Tian Wei-feng, Wang Xian-tie. A simple and convenient method for calculating the overall stability of a multi-story frame with lateral shifting[J]. Journal of Building Structures, 2011, 32(11): 183-188.) |
| [14] | 庄明智, 方圣恩. 半刚性钢框架稳定理论的扣件式钢管满堂支撑体系极限承载力分析[J]. 福州大学学报(自然科学版), 2016, 44(4): 557-562. (Zhuang Ming-zhi, Fang Sheng-en. Analysis of ultimate bearing capacity of fastener-style steel tube full-floor bracing system based on the stability theory of semi-rigid steel frame[J]. Journal of Fuzhou University (Natural Science Edition), 2016, 44(4): 557-562.) |
| [15] | 兰培培. 扣件式钢管高大模板支撑架整体力学性能分析[D]. 合肥: 合肥工业大学, 2010. (Lan Pei-pei. Analysis of the overall mechanical performance of the fastener-type steel tube tall formwork support frame[D]. Hefei: Hefei University of Technology, 2010. ) |
| [16] | 陈红英. 双层单跨支撑框架弹性稳定分析的有限元方法[J]. 青海大学学报(自然科学版), 2001(2): 6-10. (Chen Hong-ying. Finite element method for the elastic stability analysis of double-layer single-span braced frames[J]. Journal of Qinghai University (Natural Science Edition), 2001(2): 6-10.) |
| [17] | 彭瑞麟, 陈明铮, 陈冠宏, 等. 靠杆效应对支撑结构系统极限承载力影响之探讨[C]// 台湾第七届结构工程研讨会. 斗六市, 2004: 1-8. (Peng Rui-lin, Chen Ming-zheng, Chen Guan-hong, et al. Discussion on the influence of the lever effect on the ultimate bearing capacity of the supporting structure system[C]// The 7th Taiwan Structural Engineering Symposium. Douliu City, 2004: 1-8. ) |
| [18] | Chen W F, Lui E M. Structural stability: theory and implementation[M]. Washington D C: Elsevier Science Publishing Co Inc, 1988. |
| [19] | 彭瑞麟, 吕良正, 陈惠发, 等. 从模板支撑破坏机制谈国道六号北山交流道工程模板支撑倒塌问题[J]. 台湾结构工程学报, 2013, 28(3): 61-93. (Peng Rui-lin, Lyu Liang-zheng, Chen Hui-fa, et al. Discussion on the collapse of formwork support in the Beishan Interchange Project of National Highway No.6 from the failure mechanism of formwork support[J]. Taiwan Journal of Structural Engineering, 2013, 28(3): 61-93.) |
| [20] | 吴忠卫. 系统鹰架承载力、支撑结构受靠杆效应影响与支撑构件接头劲度之试验研究[D]. 台湾: 台湾云林科技大学, 2014. (Wu Zhong-wei. Experimental study on the bearing capacity of the system scaffolding, the supporting structure affected by the effect of the supporting member and the joint stiffness of the supporting member[D]. Taiwan: Yunlin University of Science and Technology, 2014. ) |
