
 , 郭思伟1,2, 于长帅1,2, 何凤霞1,2
, 郭思伟1,2, 于长帅1,2, 何凤霞1,2 1. 东北大学 机械工程与自动化学院, 辽宁 沈阳 110819;
2. 东北大学 航空动力装备振动及控制教育部重点实验室, 辽宁 沈阳 110819
收稿日期:2020-07-03
基金项目:国家自然科学基金资助项目(11872148,U1908217);中央高校基本科研业务费专项资金资助项目(N2003012,N2003013,N180703018)。
作者简介:罗忠(1978-), 男, 内蒙古集宁人, 东北大学教授, 博士生导师。
摘要:为了提高黏弹性约束阻尼结构模型仿真精度, 提出一种考虑频变特性的约束阻尼结构建模方法, 并开展了试验验证.首先, 对ZN-3黏弹性材料进行动态试验测试, 基于最小二乘法获取黏弹性材料模量和损耗因子表达式; 其次, 根据ZN-3黏弹性材料损耗因子关系表达式, 基于考虑频变特性的修正模态应变能法, 求解了约束阻尼结构的固有频率和模态损耗因子; 最后, 以贴敷黏弹性阻尼材料的悬臂约束阻尼薄板为例, 从理论与试验两方面校验, 结果表明, 考虑频变特性的约束阻尼结构有限元模型具有较高精度, 与试验测试结果比较误差在5%以内, 验证了建模方法的准确性.
关键词:黏弹性材料频变特性约束阻尼结构最小二乘法有限元模型
Modeling and Experimental Research of Constrained Damping Structure Considering Frequency-Dependent Characteristics
LUO Zhong1,2

 , GUO Si-wei1,2, YU Chang-shuai1,2, HE Feng-xia1,2
, GUO Si-wei1,2, YU Chang-shuai1,2, HE Feng-xia1,2 1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China;
2. Key Laboratory of Vibration and Control of Aero-Propulsion Systems, Ministry of Education, Northeastern University, Shenyang 110819, China
Corresponding author: LUO Zhong, E-mail: zhluo@mail.neu.edu.cn.
Abstract: In order to improve the simulation accuracy of viscoelastic constrained damping structure model, a modeling method of constrained damping structure considering frequency-dependent characteristics was proposed and then a test was performed for verification. Firstly, the dynamic test of ZN-3 viscoelastic material was carried out, and the expressions of modulus and loss factor of viscoelastic material were obtained using the least squares method. Secondly, according to the expression of loss factor of ZN-3 viscoelastic material, the natural frequency and modal loss factor of constrained damping structure were solved using the modified modal strain energy method considering frequency-dependent characteristics. Finally, the cantilever constrained damping structure attaching the viscoelastic damping material was chosen and verified from both theory and test, whose results showed that the finite element model considering frequency-dependent characteristics has higher accuracy and the error of model to test is within 5%, which verifies the accuracy of the modeling method.
Key words: viscoelastic materialfrequency-dependent characteristicsconstrained damping structureleast squares methodfinite element model
黏弹性阻尼具有高耗能特性, 广泛应用于航空航天薄壁结构的振动抑制中.振动过程中激励频率在较宽的频带范围内变化, 黏弹性材料的力学特性参数, 例如模量、损耗因子等会随激励频率变化而变化, 即表现为频变特性[1].为了对黏弹性约束阻尼结构的减振性能进行准确性地评估, 如何考虑在黏弹性阻尼材料的频变特性情况下准确进行建模是约束阻尼结构中振动分析的关键.
黏弹性材料的频变特性导致在建立黏弹性约束阻尼结构有限元模型时遇到许多困难.起初, Ravi等[2]和Park等[3]采用有限元法建立了弹性-黏弹性复合梁整体动力学模型, 但仅仅将黏弹性材料的力学性能参数(模量和损耗因子)考虑成定值, 没有考虑频变特性.Torres等[4]提出了近似求解考虑频变特性的黏弹性约束阻尼结构固有特性的方法.杨云昭等[5]基于Layerwise离散层理论, 建立黏弹性约束阻尼结构, 发展一种考虑黏弹性材料频变特性的频率响应计算方法.后来, 一些****考虑频变特性, 通过黏弹性材料的静态试验, 诸如蠕变、应力松弛等, 通过本构模型表征黏弹性材料的力学特性参数.刘天雄等[6]和Felippe等[7]分别采用GHM和Biot模型来描述黏弹性材料力学特性, 并建立了约束阻尼结构有限元模型.孙伟等[8-11]对包含黏弹性阻尼的复合结构进行深入研究, 分别就板、壳等贴敷阻尼的复合结构进行动力学特性分析, 通过黏弹性材料动态试验拟合参数方程表征黏弹性材料力学特性, 并探究了黏弹性材料频变特性对自由阻尼结构的固有特性及振动响应影响, 结果表明, 求解模态损耗因子和共振响应时, 需要引入黏弹性材料的频变特性.总而言之, 目前建立约束阻尼结构有限元模型时, 大多通过黏弹性材料蠕变、应力松弛等静态试验获得其力学特性参数, 从而实现黏弹性材料约束阻尼结构有限元建模.由于黏弹性材料静态试验测试时间长、测试设备复杂, 而动态试验测试操作简单,能更直观地描述材料的复模量随频率的变化关系, 动态试验测试已成为主流.目前基于动态试验测试获得黏弹性材料力学性能参数,从而建立黏弹性约束阻尼结构有限元模型并未得到深入研究.另外, 求解约束阻尼结构使用传统的模态应变能无法考虑阻尼材料的频变特性.
针对上述问题, 本文基于黏弹性材料的动态试验测试, 建立考虑黏弹性材料频变特性的约束阻尼结构有限元模型,并求解结构的固有特性.该模型方法建立考虑频变特性的修正模态应变能法, 能够进行模态损耗因子的准确计算; 并搭建了悬臂约束阻尼结构固有特性试验测试系统, 从而能够进行模态试验验证.同时通过算例分析和模态试验验证了该建模方法的准确性.
1 黏弹性材料的频变特性参数拟合基于频变特性的黏弹性约束阻尼结构有限元建模前提是获得黏弹性材料的频变关系.为了准确描述其频变关系, 开展了动态试验测试, 基于最小二乘对ZN-3型黏弹性材料建立了力学特性参数公式, 为接下来约束阻尼结构有限元建模打下基础.
1.1 黏弹性材料动态试验测试工程应用中, 黏弹性材料承受的载荷往往是交替载荷, 其动态力学行为在交变应力下应力-应变曲线与弹性材料不同.弹性材料施加交变应力时材料内部应力和应变是正相关, 二者没有相位差, 即应力-应变曲线呈线性增长或减小, 如图 1a所示.相反, 黏弹性材料的应变则会按一定相位差滞后于内应力, 它的应力-应变曲线是一条椭圆迟滞回线, 如图 1b所示.
图 1(Fig. 1)
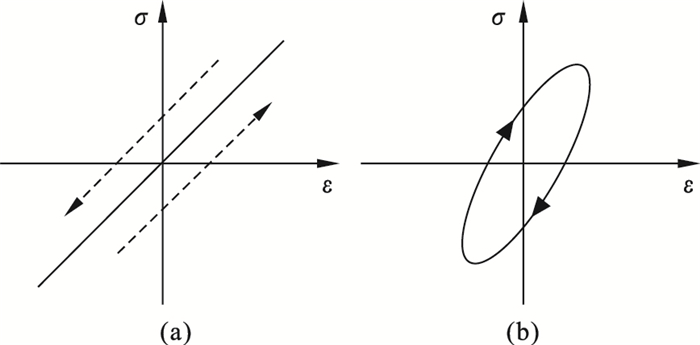 | 图 1 材料应力-应变曲线Fig.1 Stress-strain curve for material (a)—弹性材料应力-应变曲线;(b)—黏弹性材料应力-应变曲线. |
为了准确获取黏弹性材料动态力学行为, 开展了动态黏弹性测试, 其原理是橡胶材料在交变应力或交变应变作用下, 观察其应变或应力随频率或振幅的变化[12-13].测试中最主要使用方法是动态力学分析仪(dynamic mechanical analysis, DMA), 在不同的温度下对试样在一定频率范围内进行扫描, 通过应力振幅与应变的位置比较, 得到应力与应变的相位差, 经过仪器的自处理得到材料的储能模量、损耗模量随频率的变化关系.
橡胶材料主要具有温频特性与频变特性[14], 为了准确获得黏弹性材料的频变特性, 即需保证黏弹性材料的温度恒定.动态测试过程中需要保证测试系统的温控箱保持在25 ℃, 本文对丁基橡胶ZN-3进行定温扫频试验, 橡胶材料由航天材料及工艺研究所制备.试验测试仪器为TA Q800黏弹谱仪, 由美国公司生产, 如图 2所示.扫频范围为0.1~200 Hz, 扫频步长为1 Hz, 预设动态位移为20 μm, 重复试验为5次, 保证测量数据点的正确性与有效性.测试结果如表 1所示.
图 2(Fig. 2)
 | 图 2 TA Q800黏弹谱仪Fig.2 TA Q800 viscoelasticity spectrometer |
表 1(Table 1)
| 表 1 橡胶材料的储能模量、损耗模量测试数据 Table 1 Storage modulus, loss modulus test data of rubber material |
1.2 基于最小二乘法的黏弹性材料力学参数拟合黏弹性阻尼材料性能介于黏性材料和弹性材料之间, 在交变应力作用下产生结构变形, 一部分能量储存起来, 同时也会耗散部分能量.在交变应力作用下, 应变则会按一定相位差滞后于内应力, 其力学行为常采用复模量模型表征其本构关系:
 | (1) |
 | (2) |
 | (3) |
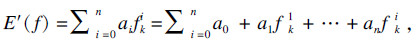 | (4) |
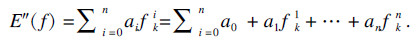 | (5) |
根据最小二乘法, 构造矩阵形式为
 | (6) |
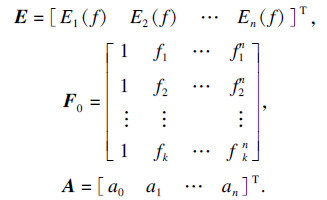 |
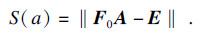 | (7) |

 | (8) |

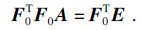 | (9) |
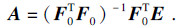 | (10) |
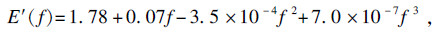 | (11) |
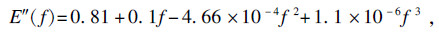 | (12) |
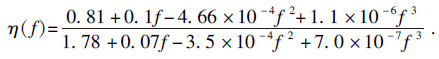 | (13) |
图 3(Fig. 3)
 | 图 3 储能模量、损耗模量拟合曲线Fig.3 Fitting curves of storage modulus and loss modulus |
2 基于频变特性的有限元建模黏弹性约束阻尼结构如图 4所示, 由约束层、黏弹性阻尼层和基层组成.其中黏弹性阻尼层材料具有频变特性, 为了准确进行约束阻尼结构的有限元建模, 依据文献[15]的假定条件, 采用能量法, 推导约束阻尼结构能量方程, 基于上述最小二乘拟合得到阻尼材料的模量随着频率变化关系表达式, 采用迭代算法对约束阻尼结构的固有特性和模态损耗因子进行求解.
图 4(Fig. 4)
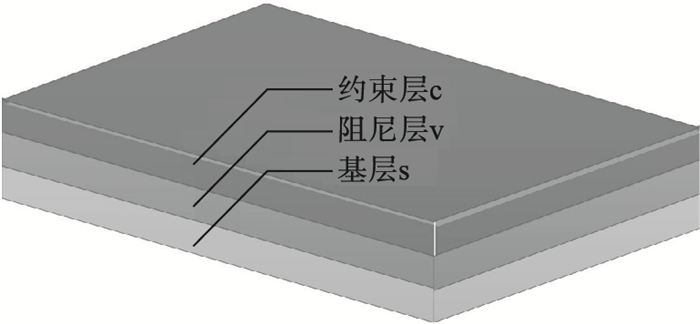 | 图 4 约束阻尼结构模型Fig.4 Constrained damping structure model |
约束阻尼结构的动力学方程表示为
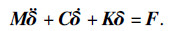 | (14) |
约束阻尼结构的质量矩阵M和刚度矩阵K为
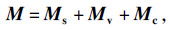 | (15) |
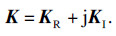 | (16) |
 | (17) |
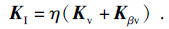 | (18) |
式(14)对应的无阻尼自由振动方程结构动力学方程为
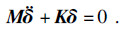 | (19) |
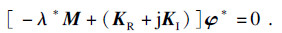 | (20) |
阻尼结构的模态损耗因子对于高精度结构设计以及预测动力学特性非常必要, 模态应变能法是从能量的角度考虑, 以耗散能量与总的变形能的比值来确定阻尼复合结构的损耗因子, 即阻尼材料的应变势能与结构的应变势能的比值[16].
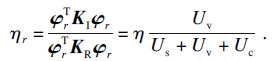 | (21) |
根据模态应变能法, 不考虑虚部的特征矢量方程为
 | (22) |
 | (23) |
图 5(Fig. 5)
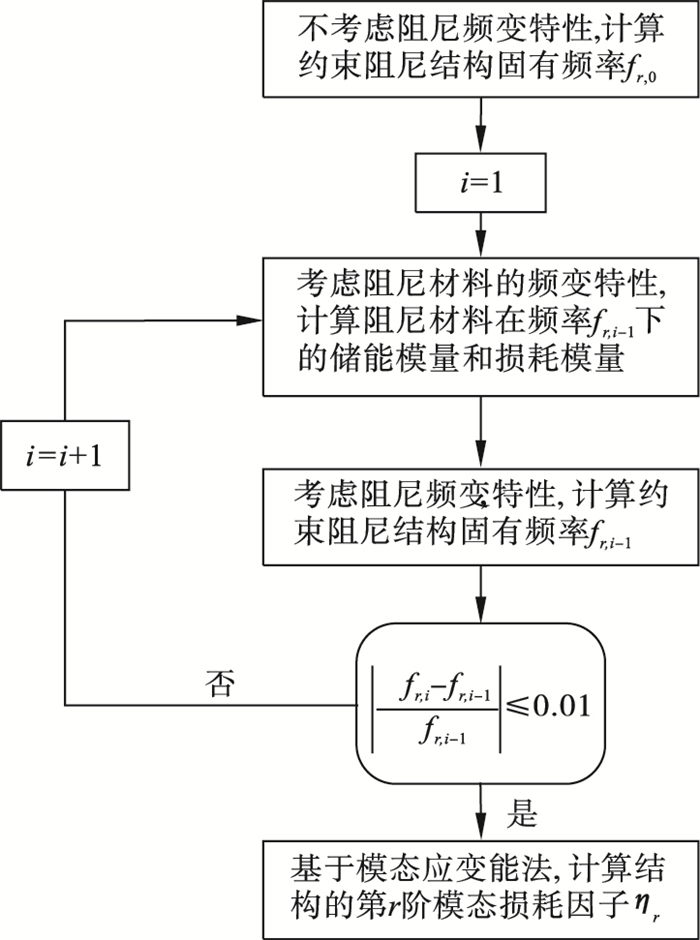 | 图 5 计算流程图Fig.5 Calculation flow chart |
步骤1??首先, 根据传统模态应变能法, 计算不考虑黏弹性材料频变特性的各阶固有频率.
步骤2??选取所关注的频率范围内黏弹性材料的储能模量和损耗模量, 计算出模态损耗因子, 将其代入到结构的模态分析中, 求解出第r阶的固有频率和模态损耗因子.
步骤3??利用误差公式|(fr, i-fr, i-1)/fr, i-1|≤0.01对步骤2和步骤1计算出的固有频率进行判定, 若满足条件, 则输出r阶的固有频率和模态损耗因子; 若不满足条件, 则重复步骤1和步骤2, 再次进行模态分析, 直到满足条件, 停止迭代计算.
3 算例分析及试验验证为了验证文中提出考虑频变特性的约束阻尼结构有限元建模的准确性和可靠性, 以悬臂边界条件下的约束阻尼薄板结构为研究对象, 并计算其固有特性和模态损耗因子.采用的约束阻尼薄板结构如图 6所示.其中阻尼层采用前文试验测试材料丁基橡胶ZN-3, 模量参数由上述试验测得, 如表 1所示.基层和约束层采用铝, 其模量均为70 GPa, 约束阻尼结构各层材料参数和几何尺寸如表 2所示.
图 6(Fig. 6)
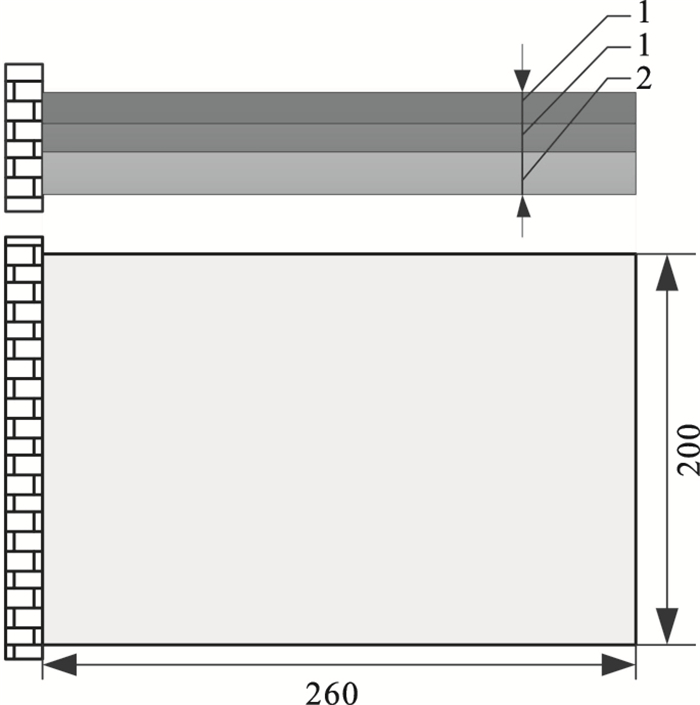 | 图 6 约束阻尼薄板模型(单位: mm)Fig.6 Model of constrained damping thin plate(unit: mm) |
表 2(Table 2)
| 表 2 材料参数和几何尺寸 Table 2 Material parameters and geometric dimensions |
本文搭建了约束阻尼薄板固有特性和模态损耗因子的测试系统, 以保证试验测试的准确性.试验测试系统的组成如图 7所示.测试系统组成分别包括: ①力锤PCB 8206-002模态力锤; ②便携式采集前端BK 3050-A-060;③三相加速度传感器BK 4524B-xyz; ④工作站与MTC hammer测试软件.在测试过程中, 力锤用于激起约束阻尼薄板的频率, 在敲击过程中, 应保持垂直方向敲击, 力量适度, 保证每次激励力纯粹无杂波和二次回弹信号.加速度传感器将响应信号传递给便携式采集前端BK, 其用于记录每次响应信号.计算机中MTC hammer测试软件用于控制测试系统,得到阻尼比和固有频率测试结果并将数据保存下来.
图 7(Fig. 7)
 | 图 7 约束阻尼薄板结构测试系统Fig.7 Test system of constrained damping thin plate structure |
如图 8所示, 对于试验试样约束阻尼薄板结构, 留有28 mm距离的夹持端, 并在夹持端处有4个直径13.5 mm的孔并配4个M12的螺栓.除此之外, 采用力矩扳手拧紧螺栓, 拧紧力为34 N.其目的是为了真实地模拟悬臂约束条件, 减小试验带来的误差, 确保试验准确性.
图 8(Fig. 8)
 | 图 8 约束阻尼薄板结构Fig.8 Constrained damping thin plate structure |
根据上述所提出考虑频变特性的约束阻尼结构建模方法, 计算得到结构的前三阶固有频率和模态损耗因子, 并将不考虑频变特性约束阻尼结构的固有频率和模态损耗因子和上述试验测试系统测得试验数据进行对比分析, 如表 3所示.
表 3(Table 3)
| 表 3 数据对比分析结果 Table 3 Results of data comparative analysis | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
从表 3可知, 本文所建立的约束阻尼结构模型的有限元计算结果更接近试验结果, 约束阻尼结构前三阶预测固有频率的误差均在5%以内.频变特性的影响对于第一阶模态固有频率较弱, 然而, 随着模态阶数的升高, 频变特性的影响逐渐增大.这是由于约束阻尼结构变形时, 黏弹性阻尼材料产生剪切应变, 从而耗散能量.因此, 随着频率的升高, 黏弹性阻尼材料的损耗模量(剪切模量)增大, 耗能能力增强, 频变特性更加显著, 但模态损耗因子有所差异.其原因:一是黏弹性材料还具有温频特性, 在对约束阻尼结构进行模态测试的过程中, 由于室内温度没有达到理想温度25 ℃, 造成黏弹性阻尼材料的模态损耗因子偏小, 从而使得结构模态损耗因子测试结果偏小; 二是本文基于有限元法进行建模, 建模过程中划分网格的精细程度会影响计算精度, 在一定程度上, 随着网格划分越密, 即网格越小, 计算结果越大, 当网格数量增加到一定程度时, 将不再改变计算结果.
4 结论1) 本文进行黏弹性ZN-3阻尼材料动态试验测试, 并基于最小二乘拟合得到了该材料储能模量、损耗模量随频率的变化关系, 发现黏弹性阻尼材料力学特性受频率影响显著.
2) 所提出的考虑黏弹性材料频变特性的约束阻尼结构有限元建模, 通过迭代思想计算了阻尼材料的频变特性的表达式, 保证结构固有特性和模态损耗因子的计算准确性.同时以悬臂约束阻尼薄板模型为例进行分析和模态试验验证, 前三阶预测固有频率的误差均在5%以内, 验证了建模方法的准确性.
3) 对比不考虑黏弹性材料频变特性的有限元模型, 验证了考虑阻尼材料频变特性在计算约束阻尼结构的固有特性和模态损耗因子方面尤其重要, 具有一定理论价值.
参考文献
| [1] | Cortés F, Jesús M. Structural vibration of flexural beams with thick unconstrained layer damping[J]. International Journal of Solids and Structures, 2008, 45(22): 5805-5813. |
| [2] | Ravi S, Kundra T K, Nakra B C. A response re-analysis of damped beams using eigenparameter perturbation[J]. Journal of Sound and Vibration, 1995, 179(3): 399-412. DOI:10.1006/jsvi.1995.0026 |
| [3] | Park C H, Baz A. Comparison between finite element formulations of active constrained layer damping using classical and layer-wise laminate theory[J]. Finite Elements in Analysis and Design, 2001, 37(1): 35-56. DOI:10.1016/S0168-874X(00)00017-2 |
| [4] | Torres D A F, Mendon?a P T R. Analysis of piezoelectric laminates by generalized finite element method and mixed layerwise-HSDT models[J]. Smart Materials & Structures, 2010, 19(3): 35-40. |
| [5] | 杨云昭, 徐超, 吴妙章. 考虑黏弹性材料频变特性的复合结构频率响应分析[J]. 固体力学学报, 2015, 36(1): 112-117. (Yang Yun-zhao, Xu Chao, Wu Miao-zhang. Frequency response analysis of composite structure considering frequency-dependent characteristics of viscoelastic materials[J]. Journal of Solid Mechanics, 2015, 36(1): 112-117.) |
| [6] | 刘天雄, 华宏星, 陈兆能, 等. 约束层阻尼板的有限元建模研究[J]. 机械工程学报, 2002, 38(4): 108-114. (Liu Tian-xiong, Hua Hong-xing, Chen Zhao-neng, et al. Research on finite element modeling of constrained layer damping plate[J]. Journal of Mechanical Engineering, 2002, 38(4): 108-114. DOI:10.3321/j.issn:0577-6686.2002.04.024) |
| [7] | Felippe W N, Barbosa F S. A nondeterministic GHM based model applied to sandwich beams[J]. Procedia Engineering, 2017, 199: 1098-1103. DOI:10.1016/j.proeng.2017.09.200 |
| [8] | 孙伟, 刘小舟, 王茁. 硬涂层悬臂层合板固有特性的解析分析[J]. 东北大学学报(自然科学版), 2017, 38(8): 1123-1127. (Sun Wei, Liu Xiao-zhou, Wang Zhuo. Analytical analysis of inherent characteristics of hard-coated cantilever laminates[J]. Journal of Northeastern University (Natural Science), 2017, 38(8): 1123-1127.) |
| [9] | 高峰, 孙伟, 高俊男. 基于有限元法的硬涂层-整体叶盘振动特性[J]. 东北大学学报(自然科学版), 2019, 40(5): 688-693. (Gao Feng, Sun Wei, Gao Jun-nan. Vibration characteristics study for the hard coating blisk using finite element method[J]. Journal of Northeastern University(Natural Science), 2019, 40(5): 688-693.) |
| [10] | Zhang Y, Sun W, Yang J, et al. Analytical analysis of forced vibration of the hard-coating cylindrical shell with material nonlinearity and elastic constraint[J]. Composite Structures, 2018, 187: 281-293. DOI:10.1016/j.compstruct.2017.12.045 |
| [11] | Sun W, Liu Y. Vibration analysis of hard-coated composite beam considering the strain dependent characteristic of coating material[J]. Acta Mechanica Sinica, 2016, 32(4): 731-742. DOI:10.1007/s10409-016-0564-4 |
| [12] | Yaya K, Bechir H. A new hyperelasticity model for predicting multi-axial behavior of rubber-like material: formulation and computational aspects[J]. Mechanics of Time-Dependent Materials, 2017, 22: 1-20. DOI:10.1007/s11043-017-9355-y |
| [13] | Jung H, Song H, Lee M, et al. Determination of viscoelastic properties of thin pressure sensitive adhesive using dynamic mechanical analysis[J]. Mechanics of Time-Dependent Materials, 2019(1): 138-149. DOI:10.1007/s11043-019-09412-5 |
| [14] | Xu C, Xu Z, Ge T, et al. Experimental and numerical study on dynamic properties of viscoelastic microvibration damper considering temperature and frequency effects[J]. Journal of Computational & Nonlinear Dynamics, 2016, 11(6): 1-17. |
| [15] | Huang Z, Wang X, Wu N. A finite element model for the vibration analysis of sandwich beam with frequency-dependent viscoelastic material core[J]. Materials, 2019, 12: 2-15. |
| [16] | 刘岚, 刘雨侬, 刘超, 等. 考虑阻尼材料频变特性的结构响应计算方法[J]. 振动与冲击, 2019, 38(24): 56-62. (Liu Lan, Liu Yu-nong, Liu Chao, et al. A calculation method of structural response considering dynamics characteristics of damping materials[J]. Journal of Vibration and Shock, 2019, 38(24): 56-62.) |
