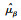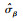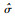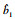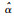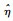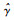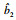, 申强, 韩凯忠, 王超 东北大学 机械工程与自动化学院, 辽宁 沈阳 110819
收稿日期：2020-11-23
基金项目：中央高校基本科研业务费专项资金资助项目(N2023023); 北京卫星环境工程研究所CAST-BISEE项目(CAST-BISEE2019-019); 河北省自然科学基金资助项目(E2020501013)。
作者简介：王新刚(1979-), 男, 黑龙江齐齐哈尔人, 东北大学教授, 博士生导师。
摘要：为了解决航空发动机的竞争失效下多元退化系统可靠性评估问题, 提出一种多元退化失效和突发失效之间相关竞争失效的可靠性评估方法.以具有随机效应的非线性Wiener过程与Gamma过程描述退化失效过程, 选择合适的Copula函数对多元退化失效相关性进行建模, 通过马尔科夫链蒙特卡洛方法进行多元退化系统相关失效模型参数估计；引入Weibull分布描述突发失效时间, 采用比例危险模型构建关于性能退化量的突发失效率函数, 利用两步极大似然估计法识别模型参数.结合航空发动机的性能退化数据实现了竞争失效下多元退化系统可靠性评估, 通过分析结果验证了模型的有效性与准确性.
关键词：竞争失效多元退化随机过程Copula函数比例危险模型
Reliability Analysis of Aero-engines Based on Multivariate Degradation Modeling Under Competitive Failure
WANG Xin-gang
, SHEN Qiang, HAN Kai-zhong, WANG Chao School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China
Corresponding author: WANG Xin-gang, E-mail: xgwang@neuq.edu.cn.
Abstract: In order to solve the problem of aero-engines' reliability evaluation of multi-degraded systems under competitive failure, a reliability evaluation method of related competitive failure between multi-degraded failure and sudden failure is proposed. The non-linear Wiener process and Gamma process with random effects are used to describe the degenerate failure process of the system, the appropriate Copula function is chosen to model the failure correlation of the multivariate degenerate system, and parameter of multivariate degradation-related failure model is estimated by Markov chain Monte Carlo method. The Weibull distribution is introduced to describe the sudden failure time, the proportional hazard model is used to construct the sudden failure rate function about the performance degradation, and the two-step maximum likelihood estimation method is used to identify the model parameters. Combined with the performance degradation data of aero-engines, the reliability evaluation of the multivariate degradation system under competitive failure is realized, and the validity and accuracy of the model are verified through the analysis results.
Key words: competitive failuremultivariate degradationstochastic processCopula functionproportional hazard model
航空发动机作为飞机的核心动力源, 其可靠性水平直接关系到飞机运行安全, 也是制定维修决策的基础.在航空发动机运行中, 由于系统工作性能会逐渐退化, 常出现燃油消耗量偏差过高、排气温度裕度过低等现象, 导致发动机系统发生退化失效；同时可能出现发动机系统连杆或涡轮叶片的疲劳断裂等机械故障, 使其完全丧失运行功能, 即发生突发失效.通常情况下, 作为典型复杂系统的航空发动机多种失效模式共存, 在运行期间发生的失效是多元退化失效和突发失效之间竞争失效.目前对竞争失效下多元退化系统可靠性建模主要从多元退化建模和竞争失效建模两方面进行研究[1].
对多元性能参数系统进行退化建模, 常见的处理方法为多元性能参数数据融合[2-3]和建立多元性能参数的联合寿命分布函数[4-5].在多元性能参数的数据融合方面, 文献[2]通过贝叶斯线性模型建立多个测试参数与系统退化量之间的内在联系，但难以适用于多个参数与退化量之间存在非线性关系的情形；文献[3]利用状态空间模型将多个特征参数转化为一个特征量，描述系统整体退化程度.在建立多元性能参数的联合寿命分布模型方面, 文献[4]采用多元正态分布函数和协方差分析方法进行多元性能参数的相关退化过程建模, 但是其边际分布模型需为正态分布函数且具有线性相关性.文献[5]通过使用Copula函数对多元退化相关失效系统进行可靠性分析, 其边际分布可以为任何最适合数据的函数模型.
对退化失效与突发失效两种失效模式共存的竞争失效过程建模[6-8]：文献[6]假设两种失效模式相互独立, 利用串联模型进行系统可靠性评估, 降低了评估的准确性；文献[7]假设突发失效与系统的性能退化量存在内在联系, 采用比例危险模型, 定量分析系统性能退化过程对突发失效过程产生的影响；文献[8]采用退化阈值冲击(DTS)模型, 考虑系统运行环境因素的影响, 能够提高评估精度, 但建模过程较为复杂.
在进行系统可靠性评估时, 上述文献只运用随机过程进行系统退化建模, 没有考虑到退化过程的非线性以及不同个体之间存在差异性.同时, 对于失效相关性问题, 较少进行多元退化失效和突发失效的相关竞争失效研究.因此, 本文依据航空发动机性能退化数据分析其存在的失效模式；基于具有随机效应非线性随机过程建立各性能参数退化失效模型；使用Copula函数定量描述多元退化参数的相关性；采用比例危险模型, 建立性能退化影响下的突发失效与退化失效的竞争失效模型, 最终实现航空发动机系统的可靠性评估.
1 系统可靠性建模1.1 基本假设1) 系统失效是多元退化失效和突发失效两种失效模式相互竞争的结果, 且多元退化数据可由随机过程拟合；
2) 可以使用某种Copula函数定量描述多元退化失效系统之间存在的相关性；
3) 系统的突发失效时间服从Weibull分布且性能退化量与突发失效率存在正相关关系.
1.2 退化失效过程建模分析通常采用随机过程对系统性能退化进行描述, 基于随机过程建立退化模型能够体现出系统性能退化随时间进行不间断无序变化.随机过程中Wiener过程和Gamma过程因具有良好的适用性, 在退化建模中较为常见.考虑到性能退化数据的平均退化轨迹存在非线性特征, 以及由于加工制造误差、工作环境等因素的影响, 不同系统的退化轨迹也会表现出明显不同, 即存在个体差异性[9].因此, 利用具有随机效应的非线性Wiener过程和Gamma过程分别对具有多元性能参数的系统进行退化建模分析.
具有随机效应的非线性Wiener过程表示为
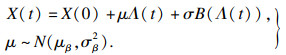 | (1) |
利用退化量X(t)~N(μΛ(t), σ2Λ(t)), 且μ~N(μβ, σβ2), 通过连续型随机变量的全概率公式, 可计算考虑非线性和个体差异性的性能退化过程的概率密度函数和分布函数分别为
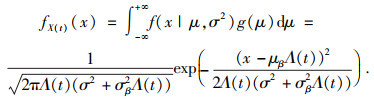 | (2) |
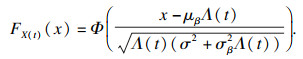 | (3) |
定义性能退化量为X1(t), 退化特征失效阈值为w1, 则其失效时所用的时间T1为
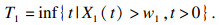 | (4) |
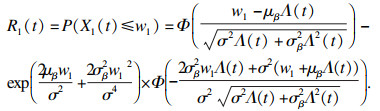 | (5) |
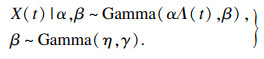 | (6) |
利用Gamma过程退化量具有的性质, 且随机变量β~Gamma(η, γ), 通过连续型随机变量的全概率公式, 可计算考虑非线性和个体差异性的性能退化过程的概率密度函数为
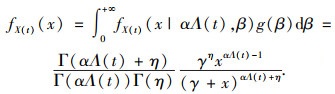 | (7) |
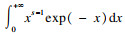
从上式可知, 对于固定的时间t, 令Z(t)=ηX(t)/αγΛ(t)，经过推导可得Z(t)服从自由度为2αΛ(t)和2η的F分布，定义Z(t)的累积分布函数为F2αΛ(t), 2η(z).
此时退化量X(t)的分布函数为
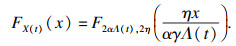 | (8) |
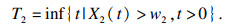 | (9) |
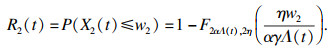 | (10) |
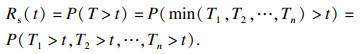 | (11) |
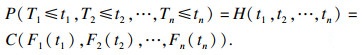 | (12) |
基于上述分析, 若假设系统中n种退化失效之间存在相关性, 结合式(11)和(12), 建立多元退化相关失效可靠性模型为
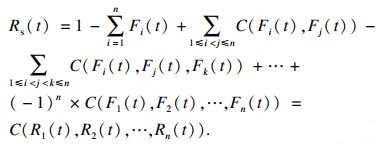 | (13) |
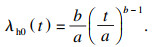 | (14) |
系统突发失效与退化失效之间的相关性体现在突发失效率随着性能退化量不断变化.若认为系统突发失效与性能退化量存在相关性, 则采用比例危险模型, 建立相应的突发失效率关于系统性能退化量的正相关函数.假设到时刻t时系统仍未失效, 此时系统突发失效率记为λh(t|X(t)), 可表示为
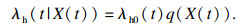 | (15) |
为保证t时刻系统不发生退化失效, 将上式改写为
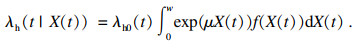 | (16) |
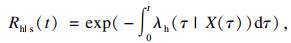 | (17) |
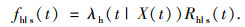 | (18) |
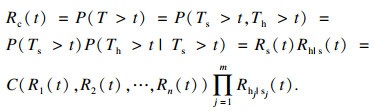 | (19) |
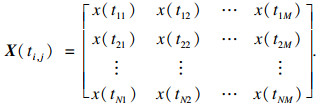 | (20) |
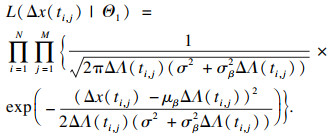 | (21) |
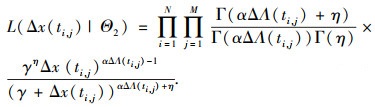 | (22) |
由于考虑非线性和个体差异性建立的退化模型参数较多, 将上述似然函数最大化得到参数估计值比较困难, 因此本文采用Bayesian MCMC方法对其进行参数估计, MCMC方法具体原理和用法可参考文献[11], 不再赘述.
系统各性能参数退化增量的边际分布函数记为Fi(Δxi)，i=1, 2, …, n，利用Copula函数表示退化增量的联合分布函数为C(F1(Δx1), F2(Δx2), …, Fn(Δxn))，对其求偏导，可以得到退化增量的联合概率密度函数为
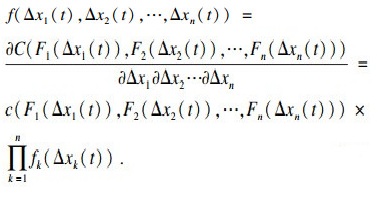 | (23) |
以二元退化系统为例建立的退化模型对数似然函数为
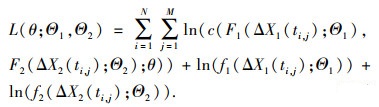 | (24) |
选择常用的Gaussian Copula和Archimedean Copula函数构造的模型基本包含所有线性与非线性相关信息.使用AIC准则选择拟合效果最好的Copula函数, AIC值越小, 则该Copula函数描述退化过程之间的相关性越优.
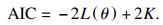 | (25) |
2.2 突发失效过程参数估计假设在进行性能退化试验时, 共有m个试验样本发生突发失效, 分别记突发失效时刻为t1, t2, …, tm, 突发失效时刻对应的性能退化量为X(t1), X(t2), …, X(tm).将突发失效率条件概率模型中的未知参数集合记为ω={a, b, μ}, 由前文分析, 突发失效模型服从双参数威布尔分布, 采用极大似然估计法对参数进行估计:
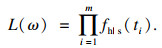 | (26) |
3 实例分析航空发动机作为典型的复杂系统, 具有多元退化失效和突发失效两种失效模式并存的特点.表 1所示为某航空公司对同时投入使用的15台航空发动机进行状态监测得到的数据, 由表征起飞阶段发动机性能的排气温度裕度(EGTM)和巡航阶段性能的燃油消耗量偏差(DWF)两个指标组成, 将得到的监测数据作为本文数据样本.随着航空发动机工作性能逐渐退化, 导致飞机全推力下降, 涡轮排气温度上升, 造成EGTM降低.当EGTM降低时导致发动机燃油消耗量增大, 进而会使DWF逐渐增大, 最终会导致发动机发生退化失效.随着发动机性能逐渐退化, 在退化失效过程中经常会伴随发动机涡轮叶片的疲劳断裂等机械故障发生, 导致发动机突发失效.由上述分析可知, 航空发动机的退化失效和突发失效相互竞争, 并且存在一定相关性.EGTM的失效阈值w1=26, DWF的失效阈值w2=2.3.表 1中的退化数据来源于航空发动机运行中实际采集和依据航空发动机的退化速率使用插值法和蒙特卡罗仿真方法获得.
表 1(Table 1)
 表 1 航空发动机的EGTM与DWF性能退化数据Table 1 EGTM and DWF performance degradation data of aero-engines
| 表 1 航空发动机的EGTM与DWF性能退化数据 Table 1 EGTM and DWF performance degradation data of aero-engines | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.1 退化失效过程将本文建立的退化模型运用到航空发动机两参数性能退化建模中, 依据退化数据特点, 选用Wiener过程和Gamma过程分别对EGTM数据和DWF数据进行拟合.使用分位数图示法(Q-Q图)和K-S假设检验法进行数据验证分析, 表明了对于不同的退化过程采取相应随机过程的合理性.
基于航空发动机退化模型和MCMC参数估计方法, 估计退化模型中的未知参数.使用Openbugs软件进行Gibbs抽样迭代, 对稳态后验分布的抽样点进行统计推断, 可得边缘分布函数中各参数Θ1, Θ2的估计结果如表 2所示.
表 2(Table 2)
表 2 多元相关退化模型参数估计结果Table 2 Parameter estimation results of the multivariate correlated degradation model
| 表 2 多元相关退化模型参数估计结果 Table 2 Parameter estimation results of the multivariate correlated degradation model |
利用极大似然法对Copula函数中的参数进行估计, 将MCMC方法得到的退化模型参数估计值代入式(24)中, 使用4种常见Copula函数模型, 参数的估计值、对数似然值(log-LF)以及AIC准则计算结果如表 3所示.
表 3(Table 3)
表 3 Copula函数相关估计值Table 3 Copula function correlation estimation value
| 表 3 Copula函数相关估计值 Table 3 Copula function correlation estimation value |
从表 3可知, Clayton Copula模型对应的AIC结果最小, 因此本文利用Clayton Copula函数描述航空发动机性能退化过程两个性能退化特征之间的相关关系是最佳选择.
多元退化失效过程可靠度曲线如图 1所示, 表明使用Clayton Copula函数可以有效进行多元退化失效相关性建模, 消除多元退化相关性对多元退化系统可靠性评估结果潜在的影响, 从而改善系统可靠性评估结果.
图 1(Fig. 1)
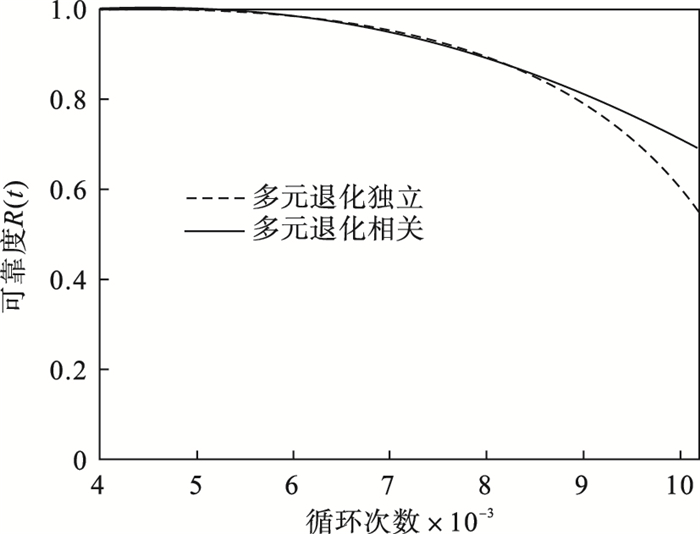 | 图 1 多元退化失效可靠度曲线Fig.1 Reliability curves of multivariate degradation failure |
3.2 突发失效过程根据失效判据可知, 对于航空发动机的EGTM退化指标, 在测试期内有4个发动机产品发生突发失效, 编号为4, 6, 11, 13, 突发失效时间T={9 800, 10 000, 9 800, 9 600}, 对应的性能退化程度为X={29, 46, 26, 20}, 从表 1中的退化数据可以看出, 突发失效是随着系统性能逐渐退化而发生的, 并非发生在初始退化阶段, 因此认为性能退化和突发失效之间具有相关性.设定参数μ的初值为0.025, 利用MATLAB中的fminsearch函数, 对式(26)进行遍历搜索, 最终得到参数估计值为
 |
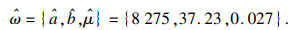因此, 得到如图 2所示的航空发动机竞争失效可靠度函数曲线, 可以看出, 建立关于退化量的突发失效率模型很好描述了退化失效与突发失效之间的相关性问题, 如忽略二者之间的相关性, 系统可靠度会被高估, 将会大大降低可靠性评估精度.
图 2(Fig. 2)
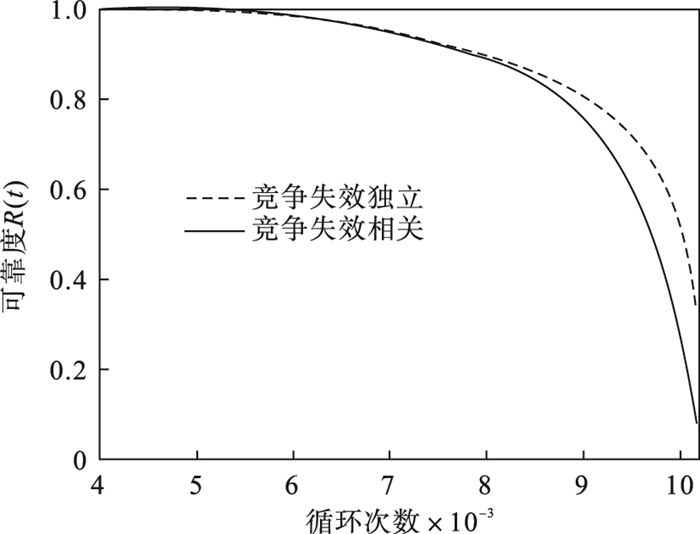 | 图 2 竞争失效可靠度曲线Fig.2 Reliability curves of competitive failure |
通过图 3可以看出, 随着飞行循环次数的增加, 航空发动机突发失效对于系统可靠性评估结果产生较大的影响, 多元退化相关失效可靠度曲线与相关竞争失效可靠度曲线之间的偏差逐渐增大.这是因为航空发动机是高可靠性、长寿命的系统, 在系统退化过程的前中期, 发动机具有相对稳定的性能和较低失效率, 可靠度变化相对缓慢；随着时间推移, 在系统退化过程的后期, 系统内部许多关键部件出现突发性故障, 将会导致系统发生突发失效, 失效率大幅增加, 可靠度迅速降低.因此, 考虑突发失效对航空发动机可靠性，评估的影响是必要的, 能够提高系统可靠性评估准确性.
图 3(Fig. 3)
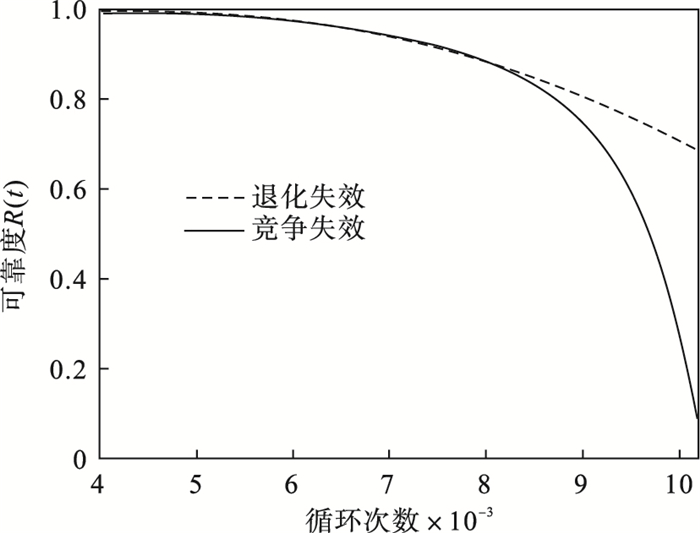 | 图 3 退化失效与竞争失效可靠度曲线Fig.3 Reliability curves of degradation failure and competitive failure |
将本文利用随机过程和Copula函数建立的可靠度模型记为M1, 使用多元正态分布与协方差分析方法记为M2, 通过图 4可靠度曲线对比, 两种方法得到可靠度曲线大体一致, 仅有略微差别.当飞行循环次数为0~7.9×103时, 可靠度评估结果M1>M2, 此阶段系统性能相对稳定, M2可靠度估计结果过于保守, 这可能会加大发动机的运营和维护成本, 降低发动机使用和维修的经济性；当飞行循环次数为7.9×103~10.2×103时, 可靠度评估结果为M1 < M2, 此阶段为系统运行后期, 易发生突发失效, 对可靠性评估准确性要求较高, M1可靠度估计结果优于M2.
图 4(Fig. 4)
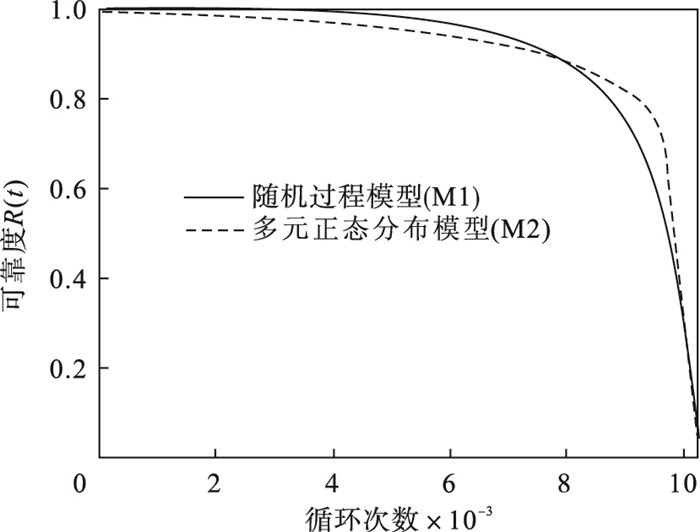 | 图 4 不同方法下的相关竞争失效可靠度曲线Fig.4 Relevant competitive failure reliability curves under different methods |
综上所述, 由于本文可靠性模型综合考虑退化过程非线性和不同样本之间具有的差异性, 使退化模型更加贴近退化数据, 因此本文模型的可靠度评估结果更加符合航空发动机可靠度实际变化情况, 更能反映出其真实的运行状态.
对于航空发动机来说, 考虑多元性能退化及不同退化失效过程之间相互影响, 可减少或避免航空发动机多元退化的相关性对可靠性评估结果的影响.若忽视航空发动机在运行过程中的突发失效以及退化失效对于突发失效的影响, 系统可靠性会被高估.合理的相关竞争失效可靠性评估模型得到的可靠度分析结果, 可为飞机维修保障计划的制定提供依据, 能够降低飞行过程中所面临的风险, 保证系统运行的安全可靠性，又能实现最大的经济效益.
4 结论1) 充分考虑试验样本平均退化轨迹的非线性以及个体差异性, 使用具有随机效应的非线性随机过程对系统退化过程进行建模, 能较好地拟合各参数的退化特征.
2) 多元退化过程之间的相关性可以通过Copula函数来定量分析, 利用AIC准则选取最优Copula函数, 避免多个退化数据之间的相关性对可靠性评估产生影响.
3) 考虑突发失效率与性能退化量之间的相关性, 采用比例危险模型, 建立客观描述性能退化对突发失效影响的突发失效可靠度模型, 使可靠度评估结果更加准确.
4) 将本文提出的基于随机过程建立竞争失效模型与基于多元正态分布建立的竞争失效模型进行对比, 分析结果表明本文模型具有较好的评估精度, 更加符合工程实际.
参考文献
| [1] | Wang X L, Balakrishnan N, Guo B, et al. Residual life estimation based on bivariate non-stationary gamma degradation process[J]. Journal of Statistical Computation and Simulation, 2015, 85(2): 405-421. DOI:10.1080/00949655.2013.824448 |
| [2] | 王华伟, 高军, 吴海桥. 基于竞争失效的航空发动机剩余寿命预测[J]. 机械工程学报, 2014, 50(6): 197-205. (Wang Hua-wei, Gao Jun, Wu Hai-qiao. Remaining life prediction of aero-engine based on competitive failure[J]. Journal of Mechanical Engineering, 2014, 50(6): 197-205.) |
| [3] | 蔡忠义, 项华春, 王攀, 等. 竞争失效下多元退化建模的导弹贮存寿命评估[J]. 系统工程与电子技术, 2018, 40(5): 1183-1188. (Cai Zhong-yi, Xiang Hua-chun, Wang Pan, et al. Missile storage life assessment based on multiple degradation modeling under competitive failure[J]. Journal of Systems Engineering and Electronics, 2018, 40(5): 1183-1188.) |
| [4] | Olatubosun S A, Zhang Z J. Multivariate analysis of critical parameters influencing the reliability of thermal-hydraulic passive safety system[J]. Nuclear Engineering and Technology, 2018, 51(1): 45-53. |
| [5] | Fang G Q, Pan R, Hong Y L. Copula-based reliability analysis of degrading systems with dependent failures[J]. Reliability Engineering and System Safety, 2020, 193: 106618. DOI:10.1016/j.ress.2019.106618 |
| [6] | Su C, Qu Z, Hao H. Reliability assessment considering dependent competing failure process and shifting-threshold[J]. Journal of Southeast University(English Edition), 2013, 29(1): 52-56. |
| [7] | Su C, Zhang Y, Zhang H. Product reliability assessment based on proportional hazard degradation model[J]. Journal of Southeast University(English Edition), 2010, 26(3): 480-483. |
| [8] | Hao S H, Yang J, Ma X B, et al. Reliability modeling for mutually dependent competing failure processes due to degradation and random shocks[J]. Applied Mathematical Modelling, 2017, 51: 232-249. DOI:10.1016/j.apm.2017.06.014 |
| [9] | Wang X F, Wang B X, Jiang P H. Accurate reliability inference based on Wiener process with random effects for degradation data[J]. Reliability Engineering and System Safety, 2020, 193: 106631. DOI:10.1016/j.ress.2019.106631 |
| [10] | Jin C X, Ran Y, Wang Z C, et al. Reliability analysis of gear rotation meta-action unit based on Weibull and inverse Gaussian competing failure process[J]. Engineering Failure Analysis, 2020, 117: 104953. DOI:10.1016/j.engfailanal.2020.104953 |
| [11] | 刘金山, 夏强. 基于MCMC算法的贝叶斯统计方法[M]. 北京: 科学出版社, 2015: 4-24. (Liu Jin-shan, Xia Qiang. Bayesian statistical method based on MCMC algorithm[M]. Beijing: Science Press, 2015: 4-24.) |
| [12] | Cai Z Y, Chen Y X, Zhang Q, et al. Residual lifetime prediction model of nonlinear accelerated degradation data with measurement error[J]. Journal of Systems Engineering and Electronics, 2017, 28(5): 1028-1038. DOI:10.21629/JSEE.2017.05.21 |
