刘士琦¹, 宋锦春¹, 杨滨²
1. 东北大学 机械工程与自动化学院, 辽宁 沈阳 110819;
2. 上海宝钢节能环保技术有限公司, 上海 201206
收稿日期：2020-08-01
基金项目：上海市科学技术委员会科技攻关计划项目(13dz1201700)。
作者简介：刘士琦(1993-), 男, 辽宁锦州人, 东北大学博士研究生;
宋锦春(1957-), 男, 辽宁沈阳人, 东北大学教授, 博士生导师。

摘要：根据换热网络分级超结构模型, 提出了针对冷却水换热网络的3种改进换热模型.与传统的分级结构不同之处在于水网络不需要公用工程的设计, 冷流只包括冷却水.并且3种设计方法均考虑了水的分流和汇流, 实现了水的非等温混合.结构二和结构三可以实现换热器中水的分阶段混合.通过权衡公用工程费用和投资费用的关系来确定最小年度总成本.使用粒子群算法优化了换热水网络中的热负荷和水的质量流量.通过两个案例可知, 提出的3种改进结构费用低于前人的研究结果, 案例1中结构3的费用最低, 案例2中结构1的经济性最优.
关键词：冷却水网络分级超结构非等温混合粒子群算法年度总成本
Comparison of Three Stage-Wise Superstructures of Water Network Based on Particle Swarm Optimization
LIU Shi-qi¹, SONG Jin-chun¹, YANG Bin²
1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China;
2. Shanghai Baosteel Energy Saving and Environmental Protection Technology Co., Ltd., China
Corresponding author: SONG Jin-chun, E-mail: jchsong@mail.neu.edu.cn.

Abstract: Based on the stage-wise superstructure model of the heat exchanger network, three improved cooling water exchange networks are proposed. The hot and cold utilities are dispensable and the cold stream only contains cooling water, which is different from the traditional heat exchanger synthesis. The three design approaches all consider the water splitting and mixing to achieve the non-isothermal mixing of water. The second and third configuration can achieve phased water mixing. The minimum total annual cost is determined by the trade-off utility cost and capital cost. Particle swarm optimization (PSO) is demonstrated to optimize the heat load and the water mass flow rate in the water network. Two cases show that the total annual cost of the three improved structures proposed is better than the previous research results and in Case 1, configuration 3 has the lowest cost, and in Case 2, configuration 1 has the best economic performance.
Key words: cooling water networkstage-wise superstructurenon-isothermal mixingparticle swarm optimization (PSO)total annual cost
换热器是工业过程中最主要的热交换途径.换热网络合成(heat exchanger network synthesis)是化工设计中一个系统优化设计的问题, 经过了近50年的发展, 其理论模型和数学方法的研究已经较为成熟^[1].其主要分析方法可分为夹点分析法^[2-3]和数学规划法^[4-5]两种.分级超结构^[5]是一种广泛应用的换热网络合成与建模方法.
冷却水网络合成归属于换热网络中冷公用工程部分的优化设计.换热网络中的热量经冷流冷却后剩余部分由公用工程进行冷却, 冷却水是最主要的冷却途径.传统的工业冷却水设计采用并联式结构, 广泛应用于工业.由于设计中水流量较大, 会产生高额的操作费用^[6].夹点技术^[7]应用于水网络设计, 水流量得到了明显的降低.Feng等^[8]提出了两级式水网络设计方法, 可以使部分换热器使用热交换后的回用水, 因此水流量明显降低.然而基于水流量的优化方式无法实现操作费用和投资费用的权衡, 因此总费用较高.Ponce-Ortega等^[9]首次将换热网络中的分级超结构应用于水网络设计, 建立了水网络的混合整数非线性规划模型(MINLP), 采用优化软件GAMS中的DICOPT求解器进行求解, 获得了较低的年度经济费用.随着冷却水换热问题的深入研究, 数学模型更加复杂多变, 采用启发式算法求解水网络的优化问题是未来研究的趋势.换热水网络模型结构和计算方法仍有很大的研究空间.
本文对换热水网络的模型结构和优化方法进行研究.首先, 针对换热网络超结构建立3种改进的分级结构模型.其次, 优化方法采用粒子群算法进行求解, 包括换热量和水的质量流量, 以及二进制逻辑变量的优化.最后, 通过两个案例对比3种分级结构年度费用, 并与前人的研究模型对比, 验证本文提出的模型和优化方法对降低年度总费用的有效性.
1 问题描述在冷却水网络合成中, 热工艺流的入口和出口温度、热容量和热负荷为已知, 水流的入口温度通常设置为环境温度.热流出口温度与入口温度的固定差值为ΔT_min.对于冷却网络中的换热器, 通常水的热容量大于热流体的热容量, 考虑到温差和结垢的影响, 出口温度低于设定值.为了降低流量, 通常出口温度尽可能高, 入口温度尽可能低.Kim等^[7]的方法是组合不同的热交换器以减少流量.冷却水系统的设计通常先假定温差, 然后计算水侧的流量和温度.这可以降低冷公用工程的成本, 但冷却水系统的设计忽略了投资成本的影响.固定的温差可能导致较高的传热面积.
冷却水网络设计.对于一个热流, 只包含一个换热器.如果同时有两个换热器对一个热流进行冷却, 换热器的总面积肯定会比单个换热器的要大.但由于水的复用, 流量会有所降低.所以增加换热器后总费用的增减未可知.因此, 在现有的单热流体单换热器研究基础上, 建立单热流体的多换热器模型具有其实际的意义.
为了解释上面讨论的问题, 3种分级式超结构分别如图 1~图 3所示.其结构与换热网络合成的区别有如下几点：
图 1(Fig. 1)

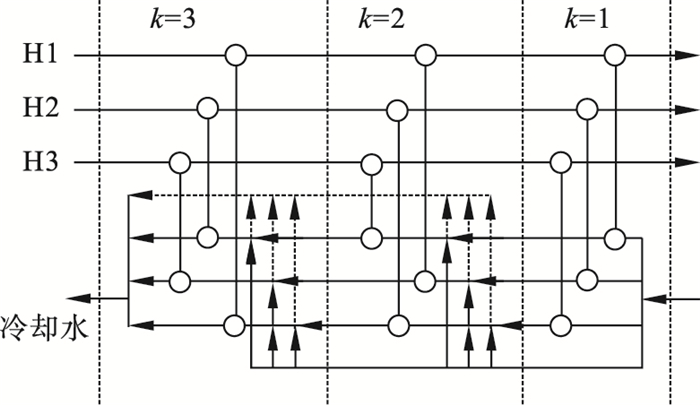图 1 分级式水网络结构(结构1)Fig.1 Stage-wise structure of water network (configuration 1)

图 2(Fig. 2)

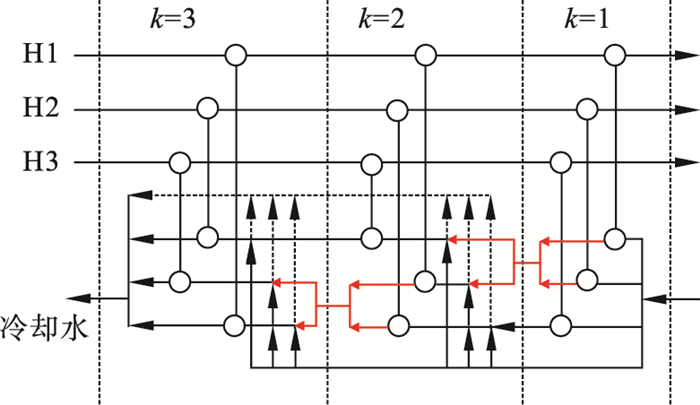图 2 分级式水网络结构(结构2)Fig.2 Stage-wise structure of water network (configuration 2)

图 3(Fig. 3)

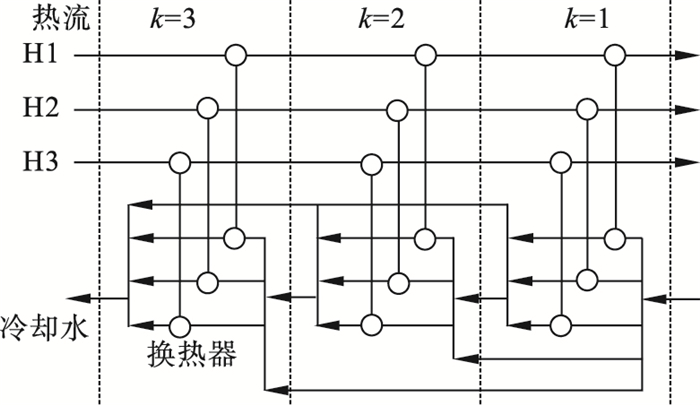图 3 分级式水网络结构(结构3)Fig.3 Stage-wise structure of water network (configuration 3)

1) 本文提出的分级结构等效为一个只有一条冷流的换热网络, 不考虑热流的分流, 而对应于冷却水的冷流考虑了分流的影响.
2) 冷流对应的冷却水流量是未知的, 入口温度设定为已知, 考虑冷却塔效率和结垢的影响, 出口温度应尽可能低.换热网络的设计均为已知参数.
3) 冷却水管网的优化相当于换热网中冷却设施的设计, 因此在整个冷却水管网的设计中不需要增加冷热公用设施.
在结构1中, 在每级换热之后, 没有水流的混合, 而是直接进入下一个阶段, 同时模型允许新鲜水的流入和混合水直接流出(虚线所示).在结构2中, 每一级的最后允许冷水流的随机非等温混合, 混合后的水流入下一级或者流出网络.在结构3中, 每一级最后的冷却水全部进行非等温混合.每个阶段的每个水支路分别与对应热流进行热交换.其中结构1和结构2中的换热器采用不重复随机排列布置.在不同阶段, 热流与冷流对应的支路均不相同, 这样可以避免由于热流冷流匹配相同而导致的换热器合并.3种方法均可实现阶段内的冷却水补充和混合水的流出.
2 3种分级结构的数学模型热流的热负荷和温度在结构中是已知的.换热器的位置、热负荷和水流量是需要通过计算求解的变量.冷流的数量为1, 因此关于热交换的二维矩阵中, i表示为热流的顺序, k表示为级数.整体热平衡确保每个热/冷流都能获得足够的冷量或热量, 以达到其所需的温度.对于热流i第k级的换热器, 其热平衡可由式(1)表示.

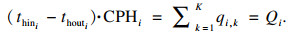(1)

其中：t_hin为热流的入口温度; t_hout为热流的出口温度; CPH为热流的热容流量; q为换热器的换热量, Q为热流的总换热量.
对于每个换热器, 其热流入口温度和出口温度由式(2)和式(3)计算.

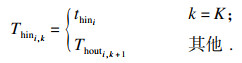(2)

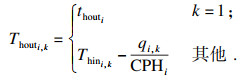(3)

其中：T_hin为换热器的入口温度；T_hout为换热器的出口温度.
对于冷流, 即冷却水流, 换热量与流量的关系可表示为

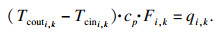(4)

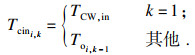其中: T_cout为冷却水流的出口温度; T_cin为水流的入口温度; c_p为水的比热容; F为水的质量流量.水的入口温度可由式(5)计算.

(5)

其中：T_{CW, in}为水的入口温度; T_o为每一级混合或者非混合后的温度.
由于3种模型的非等温混合条件不同, 因此分级的出口温度和水流量计算方法并不相同.对于结构1, 其值为冷流换热器的出口温度与入口冷水的温度的混合.对于结构2, 其值为非等温混合换热器与入口冷水的出口温度的混合.对于结构3, 为所有支路混合后的水温.由式(6)~(8)进行计算.

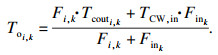(6)

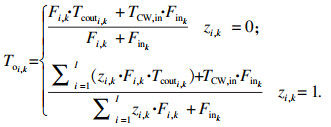(7)

(8)

其中F_in为每一级加入冷却水的质量流量.在结构2中加入二进制变量z, 用于确定出口是否进行非等温混合.如果z_{i, k}=1则在出口处和其他冷流进行混合, 如果z_{i, k}=0, 则不进行混合.如果在本级的所有支路中, 只有一个支路的二进制变量不为0, 也不进行非等温混合.
冷流的总流量为流入各级的冷却水流量之和.

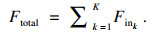(9)

对于第一级的结构, 其入口流量为第一级所有换热器水量之和, 表示为

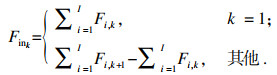(10)

对于结构1和结构2, 每一级直接流入出口的冷却水流量可以计算为

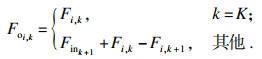(11)

其中, F_o为每一级出口的水量.对于结构3, 出口流量为

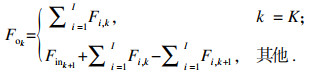(12)

对于结构2, 本文假设流过混合节点前后各支路的水量不变.根据图 1及图 2, 可以计算出结构1和结构2水网络最终的出口流量和温度分别为

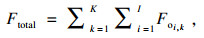(13)

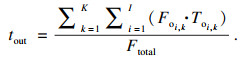(14)

对于结构3, 其出口流量和温度为

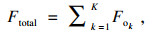(15)

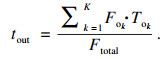(16)

考虑结垢对换热器的影响, 设计的网络的出口温度需在设定的范围内, 即

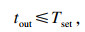(17)

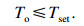(18)

流过换热器的冷却水, 其流量被限制在一定的范围内, 即

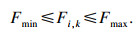(19)

系统优化的目标为年度经济总费用, 包括投资费用C_capital和公用工程费用C_utility两部分, 即

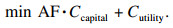(20)

其中AF为年度费用系数.
水的公用工程费用为

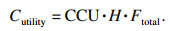(21)

其中：CCU为单位冷公用工程费用; H为操作时间.
投资费用主要为换热器的投资费用, 即

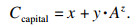(22)

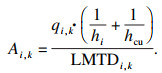其中：A为换热器的换热面积；x, y, z为常数.换热面积可由式(23)计算.

(23)

其中：h_i, h_cu分别为热流和水的传热系数; LMTD_{i, k}为对数平均温差：

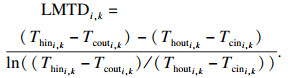(24)

换热器设计时, 两端温度应大于最小温差, 即

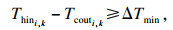(25)

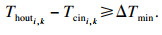(26)

3 优化模型的求解粒子群优化(particle swarm optimization, PSO)算法最早由Kennedy等^[10]在1995年提出, 用于求解非线性函数.PSO算法没有遗传算法的选择、交叉和变异等操作, 使用简单结构进行迭代计算, 参数易调整、计算速度快, 在最优化领域被广泛地应用.
本文假设粒子的种群总数n为30, 对于结构1和结构3, 搜索变量为换热量和水的质量流量, 搜索空间的总维数为D=2·K·I, 对于结构2, 搜索包含逻辑变量, 总维数为D=3·K·I.则第m个粒子所在位置表示为X_m=(x_m1, x_m2, …, x_mD), m=1, 2, …, n, 其位置分量在约束范围内取值.对于结构2, 逻辑变量的位置范围在0与1之间, 当位置值大于等于0.5, 其值为1, 当小于0.5时, 其值为0.根据X_m所对应的目标函数适应值大小, 判断粒子的优劣.第m个粒子飞行速度为V_m=(v_m1, v_m2, …, v_mD)(m=1, 2, …, n), 速度表示粒子在问题空间搜索的“步伐”.则对于每个粒子, 其第d维(1≤d≤D)的位置和速度将分别根据式(27)和式(28)迭代.

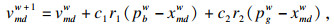(27)

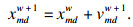(28)

式中: v_md^w为经过w次迭代后粒子m在d维方向上的速度分量；x_md^w为经过w次迭代后粒子m的d维方向上的位置分量；粒子m经历w次搜索后达到的最优位置(p_best)为p_b^w, 所有粒子的w次搜索中达到的全局历史最优适应值位置(g_best)为p_g^w；c₁和c₂为学习因子(或称加速系数)；r₁和r₂为介于0到1的随机数.
本文中适应值函数为式(20), 如果随机生成的换热量和流量不满足式(17), (18), (25), (26), 则需对目标函数的适应值函数加以惩罚, 使其年度总费用变为较大的数值.粒子群算法的具体实现步骤如下：
步骤1??设定种群基本参数, 包括学习因子、种群维数、个体数目、最大迭代次数(300), 以及粒子各维度变化范围(c₁=c₂=1.49).
步骤2??随机初始化种群粒子的初始位置和速度, 即随机产生换热量和流量, 计算各粒子初始适应值, 各个粒子初始适应值即为个体粒子历史最优p_best, 其中最佳的p_best即为全体粒子历史最优g_best.
步骤3??按照式(27), (28)更新粒子的位置和速度, 如果换热器的换热量小于设定值, 则取消该位置的换热器, 其对应的流量也为0.
步骤4??计算各粒子更新后的适应值, 对不满足约束的粒子加以惩罚.
步骤5??对比更新后的每个粒子和其p_best的适应值, 若更新后的粒子的适应值更佳, 则用该粒子更新后的信息更新p_best的位置和适应值, 否则保留p_best信息；对比每个p_best和迭代至今的全体历史最优g_best的适应值, 若存在比g_best的适应值更佳的p_best, 则以p_best信息更新g_best位置和适应值, 否则保留g_best信息.
步骤6??判断是否达到最大迭代次数, 若达到最大迭代次数则优化过程结束, 否则返回步骤3.
4 案例分析本文通过两个算例来分析对比换热水网络的经济性.案例的数据来自文献[9], 水的比热容为4.193 kJ/(kg·℃), 冷公用工程的传热系数为2.5 kW/(m²·℃), 换热器的费用系数分别为1 000, 700, 1, 操作时间为2.88×10⁷ s/a, 费用系数为0.298 3.换热器最小温差为10 ℃, 热流的相关数据如表 1所示.
表 1(Table 1)

表 1 热流参数Table 1 Hot stream parameters 案例 编号 入口温度/℃ 出口温度/℃ 换热量 传热系数 kW kW·m-2·℃-1 H1 76.6 40 3 660 1.089 案例1 H2 82 60 1 320 0.845 H3 108.85 45 400 0.903 H1 120 20 2 500 2.102 H2 80 30 7 500 2.325 案例2 H3 135 50 12 325 2.004 H4 220 20 2 000 2.345 H5 135 25 14 300 2.185

表 1 热流参数 Table 1 Hot stream parameters

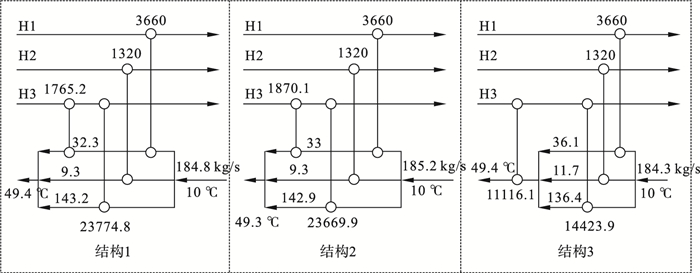
4.1 案例1已知热流的个数为3, 水网络的入口温度为10 ℃, 出口温度上限为70 ℃, 公用工程费用为＄ 1.594 9×10^-5/kg, 优化后的网络结构如图 4所示.其费用对比如表 2所示.
图 4(Fig. 4)

图 4 案例1的3种结构对比Fig.4 Comparison of three structures in Case 1

表 2(Table 2)

表 2 案例1费用对比Table 2 Cost comparison of Case 1 类型 投资费用 工程费用 总费用 ＄·a-1 ＄·a-1 ＄·a-1 并联 290 538 56 124 346 662 串联 287 598 55 723 343 321 文献[9] 218 690 85 559 304 249 结构1 218 472 84 917 303 389 结构2 218 315 85 072 303 387 结构3 218 234 84 700 302 934

表 2 案例1费用对比 Table 2 Cost comparison of Case 1

串联与并联虽然公用工程费用较低, 但由于换热器温差较大, 导致换热器的投资费用较高.文献[9]采用MINLP模型对水网络进行优化, 本文提出的3种结构的年度总费用均低于其结果.结构1与结构2的布置接近, 由于混合整数非线性模型的非凸性, 很难计算得到全局最小值, 因此结构1和结构2获得局部极小值点.结构3的费用和水流量最低, 更多支路的非等温混合可以得到更好的经济性.
4.2 案例2热流共包含5条, 入口温度为10 ℃, 出口温度上限为65 ℃, 公用工程费用为＄ 9.9×10^-6/kg, 优化后的结构分别如图 5~图 7所示.费用对比见表 3.
图 5(Fig. 5)

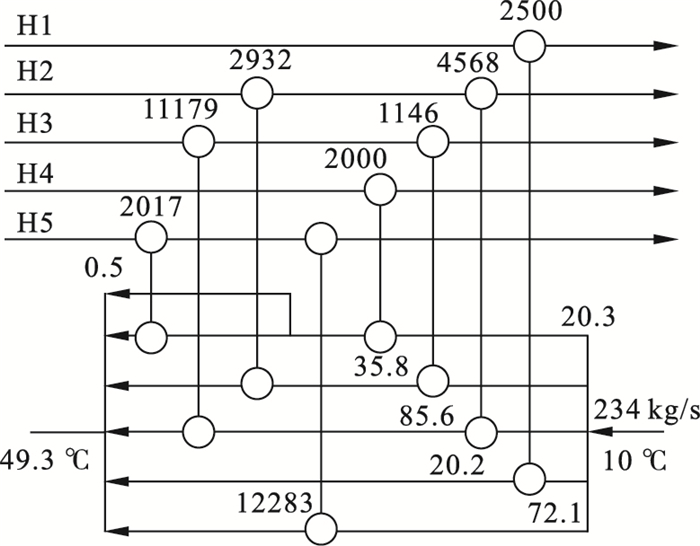图 5 案例2结构1网络Fig.5 Water network of configuration 1 in Case 2

图 6(Fig. 6)

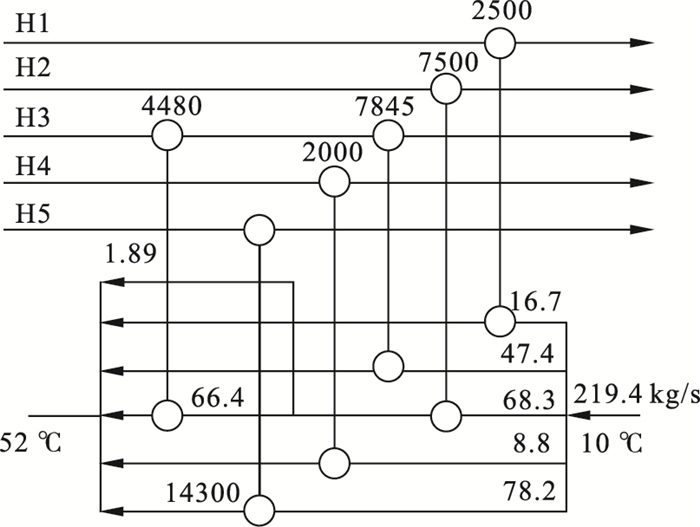图 6 案例2结构2网络Fig.6 Water network of configuration 2 in Case 2

图 7(Fig. 7)

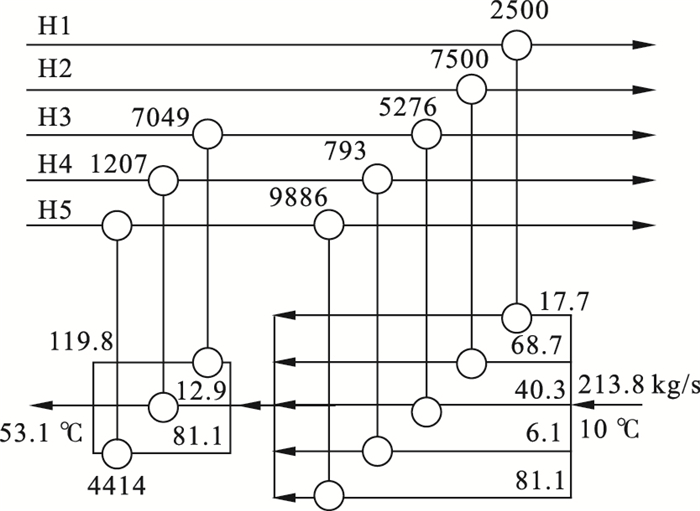图 7 案例2结构3网络Fig.7 Water network of configuration 3 in Case 2

表 3(Table 3)

表 3 案例2费用对比Table 3 Cost comparison of Case 2 类型 投资费用 工程费用 总费用 ＄·a-1 ＄·a-1 ＄·a-1 文献[9] 174 901 61 607 236 509 结构1 168 085 66 761 234 846 结构2 173 160 62 574 235 734 结构3 174 855 60 970 235 825

表 3 案例2费用对比 Table 3 Cost comparison of Case 2

3种结构的年度总费用均低于文献[9]得出的结果, 结构1的费用最低, 为234 846 ＄/a.结构2的换热器个数最少, 共6个.结构1和结构3均为8个.结构1和结构2存在支路, 将中间过程的冷却水直接引至出口.结构3中, 前一级的水非等温直接混合后流入下一级.
5 结论本文建立了3种改进结构，优化换热水网络的年度总费用.结构1不考虑阶段内的非等温混合, 结构2随机非等温混合, 结构3所有支路均非等温混合.采用粒子群优化算法求解优化模型.优化结果表明, 3种结构经济性均好于前人的优化结果.并且在不同热流条件下经济表现可能不同.案例1中结构3的经济性最佳.案例2中结构1的经济性最佳, 结构2使用的换热器最少.本文研究对冷却水网络的优化设计具有指导意义.
参考文献

[1]	Furman K C, Sahinidis N V. A critical review and annotated bibliography for heat exchanger network synthesis in the 20th century[J]. Industrial & Engineering Chemistry Research, 2002, 41(10): 2335-2370.
[2]	Linnhoff B, Flower J R. Synthesis of heat exchanger networks: I.Systematic generation of energy optimal networks[J]. AIChE Journal, 1978, 24(4): 633-642. DOI:10.1002/aic.690240411
[3]	Linnhoff B, Flower J R. Synthesis of heat exchanger networks: Ⅱ.Evolutionary generation of networks with various criteria of optimality[J]. AIChE Journal, 1978, 24(4): 642-654. DOI:10.1002/aic.690240412
[4]	Floudas C A, Ciric A R, Grossmann I E. Automatic synthesis of optimum heat exchanger network configurations[J]. AIChE Journal, 1986, 32(2): 276-290.
[5]	Yee T F, Grossmann I E. Simultaneous optimization models for heat integration-Ⅱ.Heat exchanger network synthesis[J]. Computers & Chemical Engineering, 1990, 14(10): 1165-1184.
[6]	Liu S, Song J, Shi J, et al. An improved series-parallel optimization approach for cooling water system[J]. Applied Thermal Engineering, 2019, 154: 368-379.
[7]	Kim J K, Smith R. Cooling water system design[J]. Chemical Engineering Science, 2001, 56(12): 3641-3658.
[8]	Feng X, Shen R J, Wang B. Recirculating cooling-water network with an intermediate cooling-water main[J]. Energy & Fuels, 2005, 19(4): 1723-1728.
[9]	Ponce-Ortega J M, Serna-Gonzalez M, Jiménez-Gutiérrez A. MINLP synthesis of optimal cooling networks[J]. Chemical Engineering Science, 2007, 62(21): 5728-5735.
[10]	Kennedy J, Eberhart R. Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks. Piscataway: IEEE, 1995: 1942-1948.