, 芦甜1,2, 郭文欣1, 王旭1 1. 东北大学 信息科学与工程学院, 辽宁 沈阳 110819;
2. 东北大学 辽宁省红外光电材料及微纳器件重点实验室, 辽宁 沈阳 110819;
3. 东北大学 智能工业数据解析与优化教育部重点实验室, 辽宁 沈阳 110819
收稿日期：2020-09-11
基金项目：国家自然科学基金资助项目(51607029, 61836011)；中央高校基本科研业务费专项资金资助项目(2020GFZD008, 2020GFYD011)。
作者简介：杨丹(1979-), 女, 辽宁营口人, 东北大学副教授。
摘要：为了改善逆问题病态性又能提高图像重建质量, 提出了一种基于模拟退火粒子群算法的MIT图像重建方法.根据Hessian矩阵的维度, 构建了一种Tikhonov和NOSER型混合多参数正则化算法.将模拟退火算法和粒子群算法进行组合, 以广义交叉准则构建目标函数, 进行正则化多参数寻优.结果表明, 所提方法不仅有效克服了MIT重建图像数值解的不稳定性, 增强了抗噪性能, 而且所获得的重建图像的质量优于Tikhonov正则化和混合正则化算法, 为MIT技术应用提供了理论参考.
关键词：逆问题病态性图像重建Hessian矩阵模拟退火粒子群算法
MIT Image Reconstruction Method Based on Simulated Annealing Particle Swarm Algorithm
YANG Dan1,2,3
, LU Tian1,2, GUO Wen-xin1, WANG Xu1 1. School of Information Science & Engineering, Northeastern University, Shenyang 110819, China;
2. Key Laboratory of Infrared Optoelectric Materials and Micro-Nano Devices, Northeastern University, Shenyang 110819, China;
3. Key Laboratory of Ministry of Education on Data Analytics and Optimization for Smart Industry, Northeastern University, Shenyang 110819, China
Corresponding author: YANG Dan, E-mail: yandan@mail.neu.edu.cn.
Abstract: In order to improve the ill-posed inverse problem and improve the quality of image reconstruction, a MIT image reconstruction method based on simulated annealing and particle swarm optimization was proposed. According to the dimensions of the Hessian matrix, a Tikhonov and NOSER hybrid multi-parameter regularization algorithm was constructed. The simulated annealing algorithm and particle swarm algorithm were combined, the objective function was constructed by the generalized cross criterion, and the regularized multi-parameter optimization was performed.The results show that not only the proposed method effectively overcomes the instability of the numerical solution of the MIT reconstructed image and enhances the anti-noise performance, but also the quality of the obtained reconstructed image is better than that of Tikhonov regularization and hybrid regularization algorithms, which provides a theoretical reference for the application of MIT technology.
Key words: ill-posed inverse problemimage reconstructionHessian matrixsimulated annealingparticle swarm optimization
磁感应断层成像(magnetic induction tomography, MIT)是一种新兴的电磁特性成像技术, 该技术是在外加交流激励磁场的作用下, 目标导体会因电磁感应作用而产生涡流, 当目标导体发生变化时, 涡流的强度和分布也会随之发生相应的变化, 通过测量检测线圈的信号, 再利用合适的算法重建出目标导体内部结构的分布图.MIT技术具有无辐射、非侵入、非接触、实时图像监护等优点, 在生物医学[1-4]、工业过程控制[5-6]、异物监测及地质勘探[7]等领域有着广泛的应用前景.
MIT研究分为正问题和逆问题: 其中正问题指已知目标导体电导率的分布信息来求解目标体内的涡流分布和边界感应信号; 逆问题是根据检测线圈上测得的感应电压或相位等信号, 用合适的算法重建出目标体内的电参数分布图.获取有效的电导率图像分布是MIT研究的终极目标, 由于测量数据少、组织间电导率差异不明显, 使得MIT图像重建问题是一个非线性的病态问题, 其解存在严重的不适定性.关于MIT的图像重建研究主要集中在采用正则化算法来改善其病态性, 使其解适定.国内外的研究****对正则化方法开展了大量的研究工作, Sun等[8]将提取患者肺组织的电导率分布作为先验信息纳入成像过程中, 提出了一种用于肺癌监测的改进Tikhonov正则化算法, 提高了重建图像的空间分辨率.Yan等[9]用伪逆矩阵代替灵敏度矩阵作为图像重建的初值, 采用Landweber-Tikhonov算法的交替迭代过程进行图像重建, 解决了由于“软场”和病态问题而导致的重建图像质量较差的问题.Gong等[10]将全广义变分正则化应用到图像重建的有限元模型框架中, 重建图像更加真实.Song等[11]根据空间特征优化正则化项和正则化因子, 提出了自适应全变差正则化算法, 提高了重建图像的分辨率.Liu等[12]在分析Tikhonov正则化算法和全变分(total variation, TV)正则化算法优缺点的基础上, 提出了混合正则化算法, 与传统算法相比, 有更好的重建效果.He等[13]提出基于Tikhonov和NOSER型正则化的混合正则化算法来解决三维电阻抗成像逆问题的病态性问题, 有效地改善了图像质量.邓娟等[14]采用Tikhonov-NOSER组合正则化算法研究在各种激励模式下不同位置目标的成像效果.
虽然国内****针对MIT图像重建开展大量工作, 但MIT逆问题病态性尚未得到有效解决, 现有的图像重建算法中正则化算法具有一定的优势.然而, 正则化参数的选取直接影响到算法性能, 适当的正则化参数很难确定, 较大或较小的正则化参数都将对重构图像质量产生不良影响.为了解决此问题, 本文基于Hessian矩阵维度, 提出了一种多参数混合正则化算法; 并通过粒子群算法(particle swarm optimization, PSO)和模拟退火算法(simulated annealing, SA) 组合进行多正则化参数的选择, 详细介绍了所提方法的基本原理及执行步骤.最后, 通过实验研究, 证明本文方法的重建图像质量有明显改善, 是一种有效的MIT图像重建方法.
1 基于SAPSO的图像重建方法1.1 考虑Hessian矩阵的混合正则化算法为了改善MIT图像分辨率及边缘平滑度, 多采用混合正则化算法.基于最小二乘法[15], 将Tikhonov和NOSER型正则化方法(Tik-NOSER) 相结合的MIT逆问题求解方法为
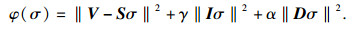 | (1) |
对式(1)采用牛顿-拉夫逊算法进行求解, 迭代形式为
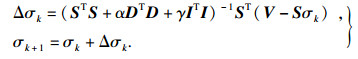 | (2) |
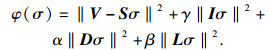 | (3) |
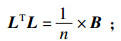 | (4) |
在考虑目标函数式(3)的最小化时, 通常采用牛顿-拉夫逊法.
计算目标函数式(3)的一阶梯度:
 | (5) |
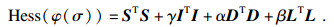 | (6) |
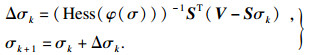 | (7) |
 |
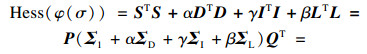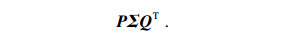 | (8) |
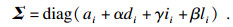 | (9) |
1.2 基于SAPSO的正则化参数选择传统的正则化参数选择方法不适用于多正则化参数选择, 且正则化参数选择耗时, 为了解决上述问题, 本文利用粒子群和模拟退火组合算法来选择正则化参数.
1.2.1 粒子群算法粒子群算法是一种全局优化算法, 由Kennedy和Eberhart共同提出.它的基本思想是通过对鸟类的群体行为建模与仿真研究结果而得到启发[16].为了加快算法的收敛速度, 本文采用了收缩因子粒子群算法[17].在该算法中, 每个潜在的解称为粒子, 每个粒子在迭代过程中, 通过追踪个体极值和种群极值来更新自己的速度和位置, 粒子速度和位置更新表达式如下:
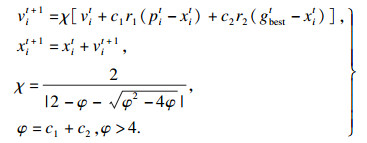 | (10) |
1.2.2 模拟退火粒子群算法模拟退火粒子群算法是在保证继承PSO算法计算速度快、机制简单特性的基础上, 引入模拟退火机制[18], 在每个粒子的速度和位置迭代更新过程中利用Metropolis准则, 计算更新前后粒子适应度值的差值, 根据Metropolis准则接受最优解的同时以一定概率接受恶化解, 使PSO算法呈现跳跃性, 从局部最优解区域中跳出, 然后降低温度, 粒子便逐渐形成低能量基态, 收敛至全局最优解.温度更新函数为
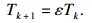 | (11) |
1.2.3 参数选取步骤本文运用SAPSO算法选择最优正则化参数.正则化参数α, γ, β为一个三维粒子, 即xi=(αi, γi, βi), 应用广义交叉原则构建适应度函数, 求解正则化参数的最优解.
根据正则化参数的经验范围生成三维搜索空间, 随机产生该空间的三维坐标点作为初始粒子, 适应度函数为
 | (12) |
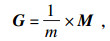 | (13) |
通过粒子的不断搜索, 找到使适应度函数取最小值x*, 即最优解, 这个最优解就是最优正则化参数(α*, γ*, β*).参数优化流程如下:
步骤1 ?设定种群大小Q, 每个粒子的维度为3维, 最大迭代次数为R.正则化参数可取xmin和xmax, 并按照下式初始化每个粒子的速度和位置:
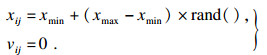 | (14) |
步骤3 ?设置足够高的初始温度T0, 一般设为T0=f(gbest0)/ln5, 其中f(gbest0)为初始化种群得到的全局最优位置所对应的适应度值.
步骤4 ?根据式(10)更新每个粒子的速度和位置.
步骤5 ?根据式(12)计算每个粒子的适应度值, 采用Metropolis准则优化生成个体最优位置pi和全局最优位置gbest.
步骤6 ?退火操作: Tk+1=εTk, 判断是否达到最大迭代次数R, 若达到, 则输出的全局最优位置gbest为最优正则化参数, 并进行图像重建, 否则跳到步骤4.
基于SAPSO优化正则化参数的具体流程如图 1所示.
图 1(Fig. 1)
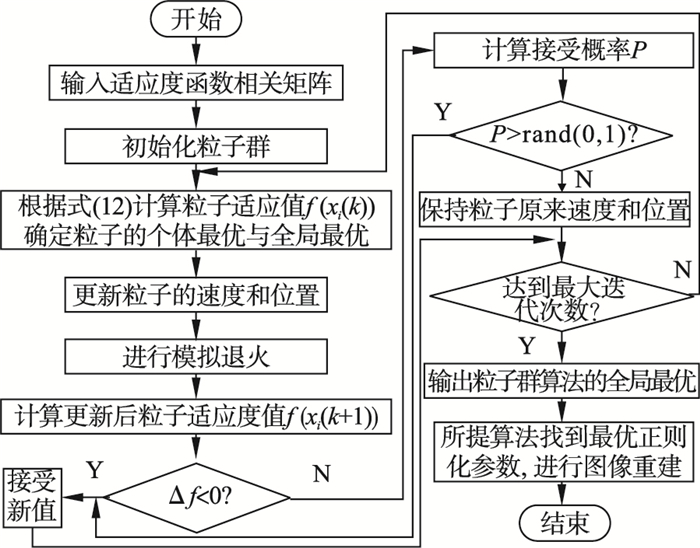 | 图 1 SAPSO优化多正则化参数流程图Fig.1 Flowchart of optimizing multiple regularization parameters by SAPSO |
2 仿真实验及结果2.1 仿真实验本文选择了6种具有代表性的电导率分布模型进行仿真, 如图 2所示.以半径为10 cm的圆形区域为研究对象, 蓝色区域表示背景, 红色为扰动目标.测量数据通过COMSOL软件建模得到, 采用8激励-接收线圈模式, 研究对象的背景和目标区域的电导率分别为0.001 S/m和2 S/m.线圈材料设置为铜, 它的直径和横截面积分别为50 mm和4e-6 m2.在激励线圈中, 通以电流密度为1 A/m2、激励频率为10 MHz正弦交变电流.
图 2(Fig. 2)
 | 图 2 4种算法的6种成像结果Fig.2 6 imaging results of 4 algorithms (a)—单圆扰动; (b)—双圆扰动; (c)—“θ”形扰动; (d)—“十”形扰动; (e)—铜币形扰动; (f)—“NEU”形扰动. |
2.2 算法稳定性分析图 3给出了原始Hessian矩阵及分别经Tikhonov正则化、Tik-NOSER正则化和本文方法正则化后的奇异值分布.原始Hessian矩阵的奇异值基本接近于0.Tik-NOSER正则化算法得到的Hessian矩阵的奇异值略高于Tikhonov正则化算法, 但其高奇异值趋势在一开始衰减迅速.而本文方法的奇异值衰减速度相对缓慢, 产生的奇异值更高.
图 3(Fig. 3)
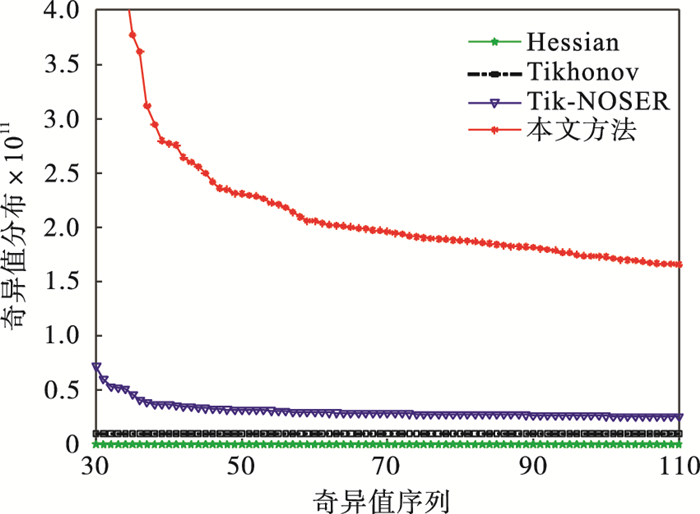 | 图 3 原始Hessian矩阵及正则化后的奇异值分布Fig.3 Singular value distribution of the original and regularized Hessian matrix |
为了更好地评价图像重建算法稳定性, 采用Hessian矩阵的条件数作为评价指标:
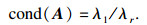 | (16) |
表 1给出了Hessian矩阵及分别经Tikhonov正则化、Tik-NOSER正则化和本文正则化后的条件数.从表中可以看出, 原始Hessian矩阵的条件数达到1.46e+24, 经过Tikhonov和Tik-NOSER正则化后, 条件数分别降到2.68e+21和9.38e+17, 在一定程度上改善了逆问题的病态性, 而本文方法将条件数降至9.21e+16, 优于另外2种正则化算法, 以上结果表明, 本文方法的稳定性良好.
表 1(Table 1)
 表 1 原始Hessian矩阵及正则化后的条件数Table 1 Condition number of original and regularized Hessian matrix
| 表 1 原始Hessian矩阵及正则化后的条件数 Table 1 Condition number of original and regularized Hessian matrix |
2.3 图像重建效果分析图 2中第2, 3, 4列分别是是传统Tikhonov正则化、Tik-NOSER正则化和本文算法的图像重建结果.可以看出, 本文算法无论是简单模型还是复杂模型都能够较好地确定目标的位置、形状, 且目标导体与背景区域的边界较清晰, 伪影较少, 重建图像质量好于其他2种算法.
为了更客观地评价算法性能, 本文引入相关系数(CC)和相对误差(RE) 2个评价指标.RE表示计算结果与真实值之间的误差大小, CC描述原始图像与重建图像之间的相关程度.RE值越小, CC值越大, 重建效果较好.CC和RE的定义如下:
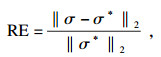 | (15) |
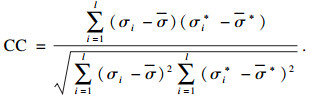 | (16) |
传统Tikhonov正则化、Tik-NOSER正则化和本文算法重建6种电导率分布模型的RE值和CC值如表 2所示.本文算法重建的电导率分布更接近原始电导率分布, 重建图像与原始图像的相关程度较大.
表 2(Table 2)
表 2 三种正则化图像重建算法性能的评价指标Table 2 Evaluation index of the performance of three regularized image reconstruction algorithms
| 表 2 三种正则化图像重建算法性能的评价指标 Table 2 Evaluation index of the performance of three regularized image reconstruction algorithms | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
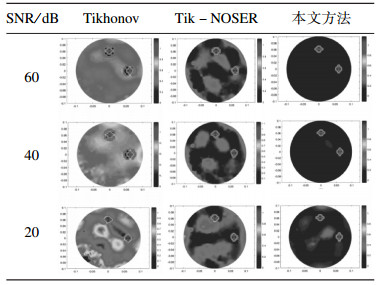
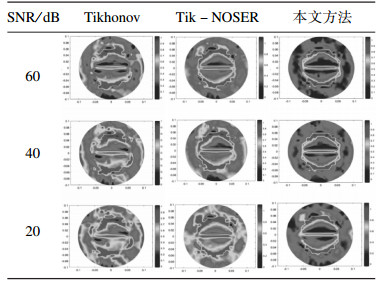
为了验证所提出算法的抗噪性能, 选择图 2a和图 2c为仿真实例.在原始电压数据中, 加入信噪比(SNR)分别为60, 40和20 dB的高斯噪声, 测试不同方法在最优情况下的仿真结果.表 3和表 4分别为基于上述3种方法的图 2a和图 2c的重建结果.从结果可以看出, 随着噪声水平的增加, Tikhonov正则化算法得到的重建图像中伪影较多, 增加了目标真实特征的模糊性.Tik-NOSER正则化的重建图像在目标周围区域存在较强的伪影, 对目标形状的重建存在一定程度的变形.与前2种算法相比, 本文方法仍能清晰地区分目标与背景之间的边界, 且能重建目标的真实形状, 有很好的抗噪性能.
表 3(Table 3)
表 3 图 2b在不同信噪比下的成像结果Table 3 The results of fig. 2b with different SNR
| 表 3 图 2b在不同信噪比下的成像结果 Table 3 The results of fig. 2b with different SNR |
表 4(Table 4)
表 4 图 2c在不同信噪比下的成像结果Table 4 The results of fig. 2c with different SNR
| 表 4 图 2c在不同信噪比下的成像结果 Table 4 The results of fig. 2c with different SNR |
在不同SNR下, 表 5和表 6分别给出了用传统Tikhonov正则化、Tik-NOSER正则化和本文算法重建图 2b和2c的RE值和CC值.从表 5可以看出, 在相同仿真条件下, 当SNR从60 dB下降到20 dB时, Tikhonov正则化、Tik-NOSER正则化和本文方法的CC值分别下降了0.113 3, 0.110 8和0.076 7, 同时RE值增加了0.128 6, 0.103 8和0.082.从表 6可以看出, 当SNR从60 dB下降到20 dB时, Tikhonov正则化、Tik-NOSER正则化和本文方法的CC值分别下降了0.182 4, 0.170 3和0.147 9, 同时RE值增加了0.187 4, 0.172 2和0.140 1.与Tikhonov正则化和Tik-NOSER正则化相比, 本文方法对噪声变化的敏感性较低, 且在不同的噪声下可以得到最大CC值和最小RE值, 进一步说明所提算法成像质量好, 具有较强的抗噪性能.
表 5(Table 5)
表 5 三种算法在不同SNR下对图 2b的重建结果Table 5 Reconstruction results of three algorithms with different SNR in fig. 2b
| 表 5 三种算法在不同SNR下对图 2b的重建结果 Table 5 Reconstruction results of three algorithms with different SNR in fig. 2b | |||||||||||||||||||||||||||||||||||||||||||
表 6(Table 6)
表 6 三种算法在不同SNR下对图 2c的重建结果Table 6 Reconstruction results of three algorithms with different SNR in fig. 2c
| 表 6 三种算法在不同SNR下对图 2c的重建结果 Table 6 Reconstruction results of three algorithms with different SNR in fig. 2c | |||||||||||||||||||||||||||||||||||||||||||
3 结论多参数正则化算法多用于解决MIT不适定逆问题, 而参数选择直接影响重建图像的质量.为了获得更好的重建效果, 本文提出了一种基于SAPSO的图像重建方法.该方法基于Hessian矩阵维度构建了一种混合正则化算法, 并用SAPSO寻优正则化参数.以RE, CC和Hessian矩阵的条件数作为评价指标, 实验验证了本文方法在MIT图像重建方面的稳定性、准确性和抗噪性.
参考文献
| [1] | Wang L. Screening and biosensor-based approaches for lung cancer detection[J]. Sensors, 2017, 17(10): 2420-2442. DOI:10.3390/s17102420 |
| [2] | Marmugi L, Renzoni F. Optical magnetic induction tomography of the heart[J]. Scientific Reports, 2016, 6(1): 23962-23970. DOI:10.1038/srep23962 |
| [3] | Zolgharni M, Ledger P D, Armitage D W, et al. Imaging cerebral haemorrhage with magnetic induction tomography: numerical modelling[J]. Physiological Measurement, 2009, 30(6): S187-S200. DOI:10.1088/0967-3334/30/6/S13 |
| [4] | Wei H Y, Soleimani M. Hardware and software design for a national instrument-based magnetic induction tomography system for prospective biomedical applications[J]. Physiological Measurement, 2012, 33(5): 863-879. DOI:10.1088/0967-3334/33/5/863 |
| [5] | Ma L, Spagnul S, Soleimani M. Metal solidification imaging process by magnetic induction tomography[J]. Scientific Reports, 2017, 7(1): 1-11. DOI:10.1038/s41598-016-0028-x |
| [6] | Wei H Y, Soleimani M. A magnetic induction tomography system for prospective industrial processing applications[J]. Chinese Journal of Chemical Engineering, 2012, 20(2): 406-410. DOI:10.1016/S1004-9541(12)60404-2 |
| [7] | Zhdanov S, Yoshioka M, Cross-well K. Electromagnetic imaging in three dimensions[J]. Exploration Geophysics, 2003, 34(2): 34-40. |
| [8] | Sun B, Yue S, Hao Z, et al. An improved Tikhonov regularization method for lung cancer monitoring using electrical impedance tomography[J]. IEEE Sensors Journal, 2019, 8(12): 3049-3057. |
| [9] | Yan C, Zhang D, Lu G, et al. An improved algorithm based on Landweber-Tikhonov alternating iteration for ECT image reconstruction[J]. Journal of Physics Conference Series, 2018, 1069: 012178-012184. DOI:10.1088/1742-6596/1069/1/012178 |
| [10] | Gong B, Schullcke B, Krueger-Ziolek S, et al. Higher order total variation regularization for EIT reconstruction[J]. Medical & Biological Engineering & Computing, 2018, 56(8): 1367-1378. DOI:10.1007/s11517-017-1782-z |
| [11] | Song X Z. A spatially adaptive total variation regularization method for electrical resistance tomography[J]. Measurement Science & Technology, 2015, 26(12): 125401-125415. |
| [12] | Liu X, Liu Z. A novel algorithm based on L1-Lp norm for inverse problem of electromagnetic tomography[J]. Flow Measurement and Instrumentation, 2019, 65: 318-326. DOI:10.1016/j.flowmeasinst.2019.01.010 |
| [13] | He W, Ran P, Xu Z, et al. A 3D visualization method for bladder filling examination based on EIT[J]. Computational and Mathematical Methods in Medicine, 2012, 2012: 528096-528105. |
| [14] | 邓娟, 王妍, 赵舒, 等. EIT系统分辨率和信噪比对图像重建的影响[J]. 国际生物医学工程杂志, 2015, 38(3): 143-147. (Deng Juan, Wang Yan, Zhao Shu, et al. Impact of measurement resolution and signal-to-noise of EIT system on reconstruction image[J]. International Journal of Biomedical Engineering, 2015, 38(3): 143-147. DOI:10.3760/cma.j.issn.1673-4181.2015.03.004) |
| [15] | Markovsky I, Luisa-Rastello M, Premoli A, et al. The element-wise weighted total least squares problem[J]. Computational Statistics & Data Analysis, 2006, 50(1): 181-209. |
| [16] | Kennedy J, Eberhart R. Particle swarm optimization[C]// Proceeding of the 1995 IEEE International Conference on Neural Networks. Perth, Australia, 2011: 1942-1948. |
| [17] | Naik B B, Raju C P, Rao R S. A constriction factor based particle swarm optimization for congestion management in transmission systems[J]. International Journal on Electrical Engineering and Informatics, 2018, 10(2): 232-241. DOI:10.15676/ijeei.2018.10.2.3 |
| [18] | Javidrad F, Nazari M. A new hybrid particle swarm and simulated annealing stochastic optimization method[J]. Applied Soft Computing, 2017, 60: 634-654. DOI:10.1016/j.asoc.2017.07.023 |
