, 徐世达 东北大学 深部金属矿山安全开采教育部重点实验室, 辽宁 沈阳 110819
收稿日期：2020-10-29
基金项目："十三五"国家重点研发计划项目(2016YFC0801605)；国家自然科学基金青年基金资助项目(51704056)；中央高校基本科研业务费专项资金资助项目(N160103006)；中国博士后基金资助项目(2017M621152)。
作者简介：李元辉(1968-)，男，山东莱州人，东北大学教授，博士生导师。
摘要：针对已知波速型声发射定位算法精度高度受制于初始波速测试准确性的问题, 基于粒子群优化算法(PSO)开发了一种声发射定位算法, 无需预先测试波速.以传感器接收到时差构建适应值函数, 通过该算法求解此函数, 得到声发射源位置和波速.研究不同波速赋值范围差、不同波速赋值范围上、下界与真实波速值的差值比(φ)对算法精度的影响. 在此基础上, 开展断铅试验, 对比分析PSO定位算法与单纯形定位算法的定位精度. 结果表明: 不同波速赋值范围差、不同φ值下的PSO算法定位误差小于10 %; 当波速赋值范围差为2 000 m/s, 且φ取1时, 算法精度最高; 本文算法定位精度明显优于传统单纯形定位算法.
关键词：声发射定位粒子群优化无需预测波速波速赋值范围定位精度
Influence of Wave Velocity Range on Accuracy of PSO Location Algorithm
LI Yuan-hui, CHEN Zhi-yang
, XU Shi-da Key Laboratory of Ministry of Education on Safe Mining of Deep Metal Mines, Northeastern University, Shenyang 110819, China
Corresponding author: CHEN Zhi-yang,E-mail:zhi_yang_chen@163.com.
Abstract: The accuracy of the known wave-speed acoustic emission positioning algorithm is highly restricted by the accuracy of the initial wave speed test, an acoustic emission location algorithm was developed based on the particle swarm optimization (PSO) algorithm no need to pretesting wave velocity. The fitness function was constructed based on the time difference received by the sensor, and the function was solved by the algorithm to obtain the acoustic emission source position and wave velocity. The influence of the difference of different wave speed assignment ranges and the difference ratio (φ) between the upper and lower bounds of different wave speed assignment ranges and the real wave speed value on the accuracy of the algorithm was studied. Then, a lead-off test was carried out to compare and analyze the location accuracy of the PSO algorithm and the simplex algorithm. The results show that the PSO algorithm location error is less than 10 % under different wave velocity ranges and different φ values. When the wave velocity assignment range difference is 2 000 m/s and φ is 1, the algorithm accuracy is the highest. The positioning accuracy of the algorithm in this paper is significantly better than the traditional simplex positioning algorithm.
Key words: acoustic emission locationparticle swarm optimizationno need to pre-testing wave velocitywave velocity assignment rangelocation accuracy
岩石材料在外荷载作用下, 其内部微裂隙发展、贯通导致局部能量快速释放产生弹性波的现象, 称为声发射. 采用声发射监测技术和定位算法, 可研究岩石内部微裂隙时空演化规律, 已被广泛应用于岩石材料的损伤破坏机理以及岩体稳定性研究中.声发射定位算法多基于各传感器实际接收到的时差建立方程, 通过算法求解得出声发射源位置. 常见的定位算法是将预先测试的岩石内部波速作为已知量进行输入, 如最小二乘法[1-2]、单纯形法[3-4]、Geiger法[5]等定位算法. 然而随着岩石损伤的积累, 岩石内部的波速不断变化, 将波速作为已知量的方式势必导致定位算法的精度有所降低. 因此, 对于波速未知型定位算法的研究显得尤为迫切. 为降低波速对定位算法精度的影响, 开展了无需预先测试岩石波速的定位算法研究, 取得了一定的成果. Dong等[6-7]通过构建未知波速系统的微震(声发射)震源定位的控制方程, 求解得到此系统下的震源位置坐标. Dong等[8]采用数学方法, 推导化简了未知波速的声发射定位算法, 通过优化算法对其进行求解, 得到声发射源位置和波速. 近年来, 基于计算机技术的智能优化算法得到迅速发展, 粒子群算法因其参数少、程序简单、运算速度快等特点被广泛应用于岩土工程中[9-11]. 陈炳瑞等[12]基于粒子群算法提出了微震源分层定位方法, 利用粒子群算法求解震源位置和波速, 进而反演微震发震时间, 成功应用于实际工程中. Li等[13]利用群波时间差信息构建一种无须预先测试波速的TDOA模型, 结合粒子群优化算法进行微震震源定位. 杨道学等[14]通过模拟得到粒子群定位算法中最优的惯性权重值, 并以此进行实验室断铅试验, 取得了较好的效果.
采用无需预先测试岩石波速的粒子群算法进行声发射源位置定位时, 算法的惯性权重和加速因子的赋值已普遍达成共识, 但在岩石波速的初始赋值问题上还鲜有****进行研究. 因此, 本文开展不同波速赋值范围差和不同波速赋值范围上、下界与真实波速值的差值比对粒子群定位算法影响的模拟研究. 在此研究基础上, 开展断铅试验, 与单纯形定位算法结果进行对比, 分析了本文算法的实际定位效果.
1 粒子群定位算法模型受鸟群觅食行为启发, James等[15]于1995年联合提出了粒子群优化算法(PSO). 基本思想是通过粒子间的相互影响, 不断搜索找到种群中最优粒子. 假设D维空间中包含S个粒子, 第i个粒子在空间中的位置为xi=(x1, x2, …, xD), 它的搜索速度为vi=(v1, v2, …, vD), 种群中个体最优粒子为pi=(p1, p2, …, pD), 全局最优粒子为pg=(p1, p2, …, pD). 粒子的搜索过程会受到个体最优粒子pi和全局最优粒子pg的共同影响. 第k+1次迭代时第i个粒子的搜索速度和搜索位置分别为
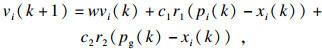 | (1) |
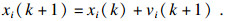 | (2) |
在粒子搜索期间, 为了保证粒子搜索的稳定性, 需对粒子的搜索速度和搜索位置加以限制, 防止粒子搜索速度过大越过最优粒子所在的位置, 粒子搜索速度过小效率过低. 因此, 当粒子的搜索速度vi>Vmax时, 令vi=Vmax; 当vi＜Vmin时, 令vi=Vmin, Vmax, Vmin分别为最大、最小搜索速度, 并满足Vmin=-Vmax, 一般Vmax=0.1×abs(Xmax-Xmin); 当粒子的搜索位置xi>Xmax时, 令xi=Xmax; 当xi＜Xmin时, 令xi=Vmin, Xmax, Xmin分别为最大、最小种群边界.
粒子群算法的计算步骤如图 1所示: ①对粒子群的参数(粒子维度、种群大小、迭代终止需满足的条件、最大迭代次数或给定适应值函数精度)、惯性因子、加速因子进行初始化; ②对粒子的搜索位置x(k)、搜索速度v(k)进行初始化, 并设置当前迭代次数k=1;③计算当前迭代种群中每个粒子的适应值, 同时选取个体最优粒子和全局最优粒子; ④根据式(1)更新粒子的搜索速度, 并进行速度控制, 根据式(2)更新粒子的搜索位置, 并进行位置控制, 随后再更新个体及全局最优粒子; ⑤判断结果是否满足迭代终止条件, 满足, 则迭代终止并输出结果; 不满足, 设k=k+1进行下一次迭代, 直到满足迭代终止条件为止.
图 1(Fig. 1)
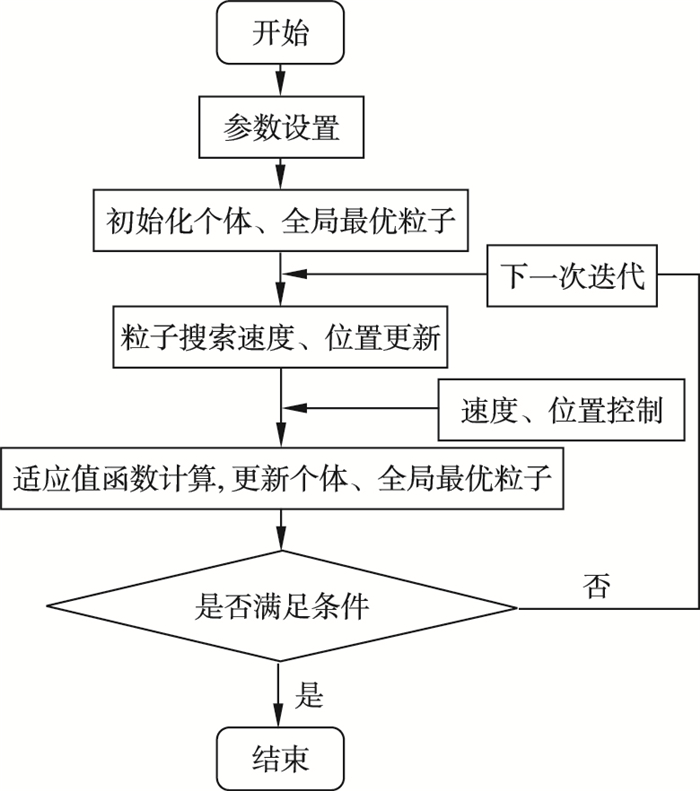 | 图 1 粒子群定位算法流程图Fig.1 Flowchart of PSO positioning algorithm |
2 无需预先测试波速的粒子群定位算法适应值函数构建对于无需预先测试岩石波速的声发射定位问题, 其适应值函数是各传感器的理论接收到时和实际监测到时之差的和.假设有n个传感器, 则第i个传感器的理论接收声波到时间为
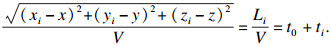 | (3) |
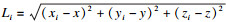
第i个与第i-1个传感器的理论接收声波到时差为
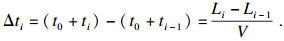 | (4) |
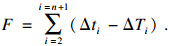 | (5) |
3 波速赋值范围对粒子群定位算法精度的影响通过粒子群定位算法的不断搜索迭代找到使适应值函数最小的粒子, 此粒子的值(声发射源坐标和岩石波速)即为最优. 算法迭代前, 需对粒子的种群大小即所求目标参数(声发射源坐标和岩石波速)的赋值范围进行初始化, 声发射源坐标(x, y, z)的赋值范围可由试验模型直接确定, 而对于岩石波速V的赋值范围还鲜有****对其进行研究. 因此本文设计一系列模拟试验, 研究波速赋值范围对算法精度的影响, 以期找到最优波速赋值范围, 减少波速对定位误差的影响.
3.1 波速的赋值范围差对粒子群定位算法精度的影响声波的传播速度与岩石的孔洞、裂隙等结构紧密相关. 岩石在受压状态下, 内部细微结构的不断改变导致声波的传播速度逐渐变化. 为了满足岩石损伤破坏过程中波速的变化幅度, 设置波速赋值范围差为1 000, 1 500, 2 000, 2 500, 3 000 m/s的5组试验进行模拟. 粒子群定位算法的惯性权重w选取Suganthan[16]的线性递减方式: w(k)=ws-((ws-we)/kmax) · k, ws最大值为0.95, we最小值为0.2, kmax最大迭代次数为50;学习因子c1=c2=2, 种群中粒子数为25. 岩石的尺寸为50 mm×50 mm×100 mm, 岩石的真实波速值设为4 000 m/s, 为了模拟数据的有效性、科学性, 每组试验模拟50次取平均值, 各传感器坐标如表 1所示, 波速赋值方案如表 2所示, 算法的定位误差和波速反演误差如图 2所示.
表 1(Table 1)
 表 1 传感器坐标Table 1 Sensor coordinates
| 表 1 传感器坐标 Table 1 Sensor coordinates |
表 2(Table 2)
表 2 波速赋值方案Table 2 The wave velocity assignment scheme
| 表 2 波速赋值方案 Table 2 The wave velocity assignment scheme |
图 2(Fig. 2)
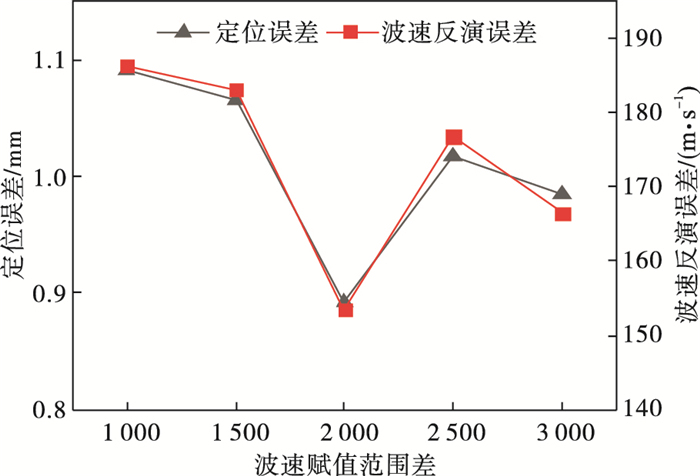 | 图 2 不同波速赋值范围差对定位算法精度的影响Fig.2 Influence of different wave velocity assignment range difference on accuracy of positioning algorithm |
由图 2可知, 波速的赋值范围差对定位算法的精度造成了一定的影响: 当波速赋值范围差为1 000 m/s时, 最大定位误差为1.09 mm; 当波速赋值范围差为2 000 m/s时, 最小定位误差为0.89 mm.当波速赋值范围差为1 000 m/s时，最大波速反演误差为186.30 m/s；当波速赋值范围差为2 000 m/s时，最小波速反演误差仅为153.47 m/s.因此, 对于综合定位误差和波速反演误差, 当波速取范围差为2 000 m/s时, 算法的精度最好. 定位误差和波速反演误差存在一定的对应关系, 当波速反演误差越小时, 算法的定位精度越高, 波速反演误差越大, 定位误差越大, 这也直观表现出岩石波速的准确性对定位算法精度的重要性.
3.2 波速赋值范围上、下界与岩石真实波速值的差值比对粒子群定位算法精度的影响上述只针对真实波速值等于波速赋值范围中值的情况进行了模拟, 为了探究真实波速值偏离波速赋值范围中值的程度对算法精度的影响, 本文引入变量φ, 表示波速赋值范围的上界与真实波速值的差值及速度赋值范围下界与真实波速值的差值之比(后文统称为上、下界差值比), φ值越大, 表明真实波速值越靠近波速赋值范围的下界; φ值越小, 则越靠近波速赋值范围的上界. 对φ取0.2, 0.4, 0.6, 0.8, 1, 1.3, 1.7, 2.5, 5共9组情况开展模拟试验, 如表 3所示. 采用3.1的模型, 每组模拟50次取平均值, 结果如图 3所示.
表 3(Table 3)
表 3 不同φ值的模拟方案Table 3 Simulation schemes under different φ values
| 表 3 不同φ值的模拟方案 Table 3 Simulation schemes under different φ values | ||||||||||||||||||||||||||||||||
图 3(Fig. 3)
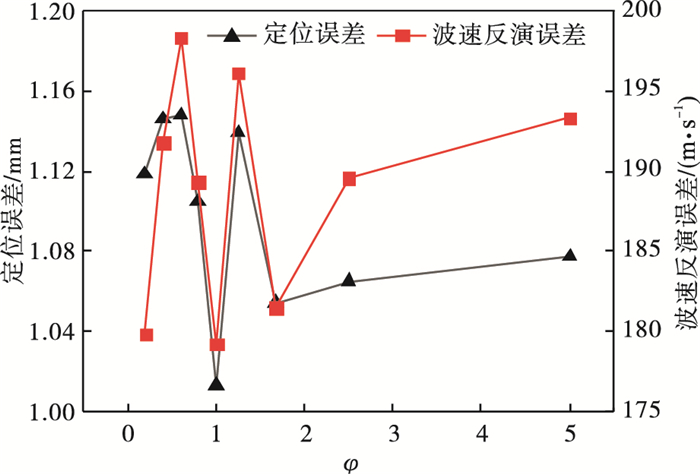 | 图 3 不同上、下界差值比的算法误差Fig.3 Algorithmic error under difference ratios of different upper and lower bounds |
由图 3可知, φ值变化时, 算法的精度有一定差异, 定位误差在1~1.2 mm之间波动时, 算法的波速反演误差在179~197 m/s之间进行变化. 当φ取1时, 即真实波速等于波速赋值范围中值时, 算法的定位误差最小为1.01 mm, 波速反演误差也最小为179.25 m/s.
4 定位算法验证试验在模拟结果基础上, 开展实验室断铅试验, 对算法的实际定位效果进行检验. 为了减少其他因素对算法精度的影响, 采取PAC型高精度声发射监测系统, 配置Nano 30探头, 并在探头和试样接触面涂抹凡士林进行耦合. 试样为50 mm×50 mm×100 mm的花岗岩, 传感器布置如图 4所示. 断铅点位于(19, 35, 100 mm), 试验前利用超声波探测仪测得岩石的平均波速为3 516.26 m/s. 设置波速赋值范围为2 516~4 516 m/s, 即岩石波速赋值范围差为2 000 m/s, 上、下界差值比φ取1. 经数次断铅, 将声发射系统监测到的数据利用本文算法和传统单纯形算法进行定位计算, 随机选取两种算法结果中的5组数据进行对比分析, 结果如表 4所示, 两种方法的定位误差如图 5所示.
图 4(Fig. 4)
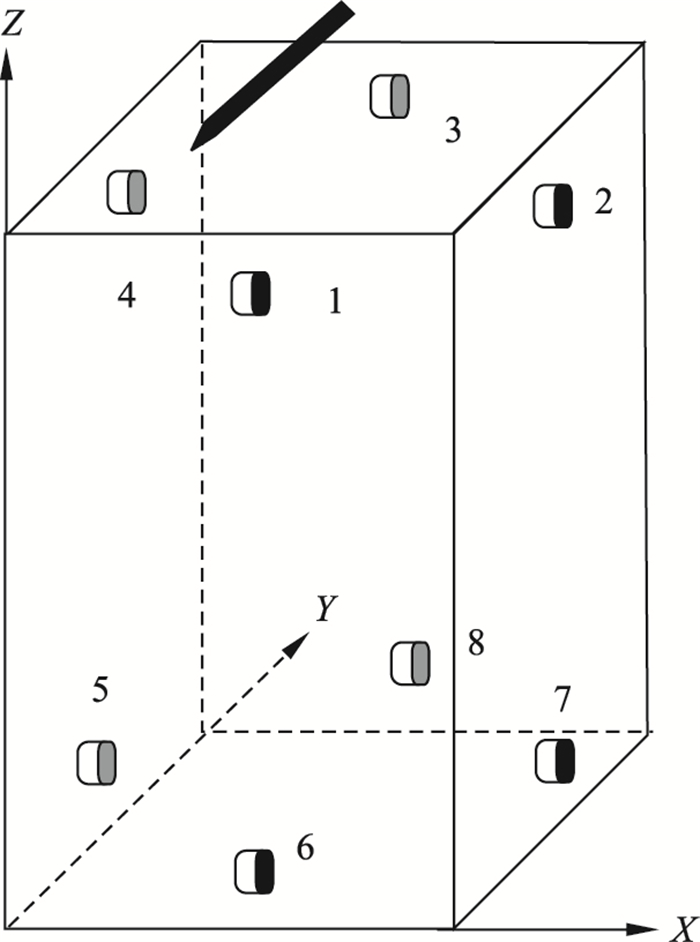 | 图 4 传感器布置及断铅点示意图Fig.4 The schematic diagram of sensors layout and the lead breaking points |
表 4(Table 4)
表 4 粒子群算法和单纯形算法定位结果比较Table 4 Comparison of location results of PSO and simplex algorithm
| 表 4 粒子群算法和单纯形算法定位结果比较 Table 4 Comparison of location results of PSO and simplex algorithm |
图 5(Fig. 5)
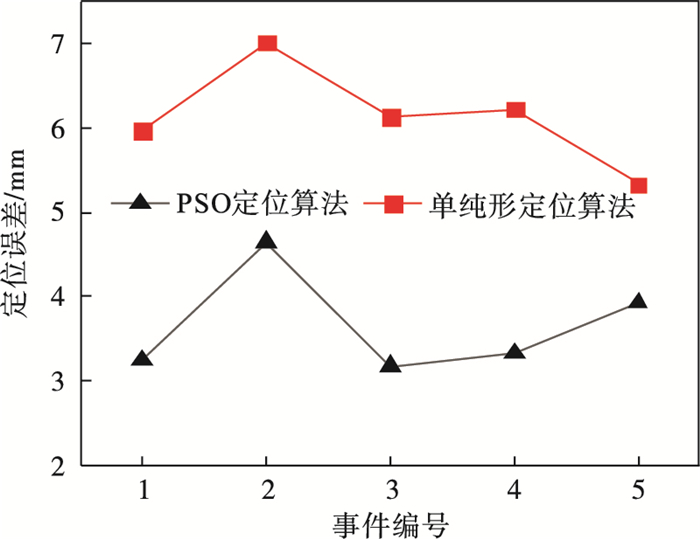 | 图 5 粒子群算法和单纯形算法定位结果比较Fig.5 Comparison of location results of PSO and simplex algorithm |
本文算法平均定位误差为3.66 mm, 而单纯形算法的平均定位误差为6.14 mm, 可知, 本文算法的定位精度明显优于传统单纯形定位算法.本文算法将波速作为未知量, 根据传感器接收到的时差构建适应值函数, 通过粒子群定位算法迭代求得此时的波速值, 减少了波速对定位算法精度的影响, 更大程度地提高了声发射源定位的精度, 为试验研究提供了更有效的数据支撑. 因此, 本文算法更适合于实际工程中的应用.
对比模拟和断铅试验的定位算法结果可以发现, 试验的精度要低于模拟的精度, 是因为模拟时为了提高算法的可行性, 将传感器接收到时的误差控制在一个较小范围之内, 从而导致模拟的定位精度相对较高. 而在实验室试验时, 由于探头与岩石之间的耦合度、断铅操作等不可控因素导致算法定位误差有所增大, 其误差控制在10 % 以内, 并不影响本文算法结果的可靠性.
5 结论1) 不同波速赋值范围差对算法的定位精度产生了一定的影响, 当波速赋值范围差为2 000 m/s时, 算法的定位误差最小为0.89 mm; 当波速赋值范围差为1 000 m/s时, 定位误差最大为1.09 mm.
2) 当真实波速值偏离波速赋值范围中值时, 定位算法的精度有一定的差异. 真实波速值等于波速赋值范围中值时(φ取1), 算法的定位误差最小为1.01 mm.
3) 断铅试验的结果表明, 本文无需预先测试波速的粒子群声发射定位算法, 其精度明显优于传统已知波速型的单纯形定位算法. 本文算法克服了传统定位算法中波速难以确定的困难, 减少了传感器接收到时的误差, 提高了算法定位精度.
参考文献
| [1] | Fedorow V V. Regression problems with controllable variables subject to error[J]. Biometrika, 1974(61): 49-55. |
| [2] | 康玉梅, 刘建坡, 李海滨, 等. 一类基于最小二乘法的声发射源组合定位算法[J]. 东北大学学报(自然科学版), 2010, 31(11): 1648-1651. (kang Yu-mei, Liu Jian-po, Li Hai-bin, et al. An AE source location combination algorithm based on least square method[J]. Journal of Northeastern University(Natural Science), 2010, 31(11): 1648-1651.) |
| [3] | Nelder J, Mead R. A simple method for function minimization[J]. Computer Journals, 1965, 7: 308-312. |
| [4] | 刘建坡, 王洪勇, 杨宇江, 等. 不同岩石声发射定位算法及其实验研究[J]. 东北大学学报(自然科学版), 2009, 30(8): 1193-1196. (Liu Jian-po, Wang Hong-yong, Yang Yu-jiang, et al. Experimental study on different rock locating algorithms with acoustic emission[J]. Journal of Northeastern University(Natural Science), 2009, 30(8): 1193-1196.) |
| [5] | Geiger L. Probability method for the determination of earthquake epicenters from the arrival time only[J]. Bulletin of Saint Louis University, 1912(8): 60-71. |
| [6] | Dong L, Li X, Xie G. An analytical solution for acoustic emission source location for known P wave velocity system[J]. Mathematical Problems in Engineering, 2014, 4(5): 1-6. |
| [7] | Dong L, Li X. A microseismic/acoustic emission source location method using arrival times of PS waves for unknown velocity system[J]. International Journal of Distributed Sensor Networks, 2013, 9(10): 1843-1854. |
| [8] | Dong L, Sun D, Li X, et al. Theoretical and experimental studies of localization methodology for AE and microseismicsources without pre-measured wave velocity in mines[J]. IEEE Access, 2017, 5: 16818-16828. DOI:10.1109/ACCESS.2017.2743115 |
| [9] | Zhang S, Liu H, Gao D T, et al. Determining the input dimension of a neural network for nonlinear time series prediction[J]. Chinese Journal of Chemical Physics, 2003, 12(6): 594-598. |
| [10] | Parsopoulos K E, Vrahatis M N. Recent approaches to global optimization problems through particle swarm optimization[J]. Natural Computing, 2002, 1(2/3): 235-306. DOI:10.1023/A:1016568309421 |
| [11] | Eberhart R C, Kennedy J. A new optimizer using particle swarm theory[C] // Proceedings of Sixth International Symposium on Micro Machine and Human Science. Nagoya, Japan, 1995: 66-73. |
| [12] | 陈炳瑞, 冯夏庭, 李庶林, 等. 基于粒子群算法的岩体微震源分层定位方法[J]. 岩石力学与工程学报, 2009, 28(4): 740-749. (Chen Bing-rui, Feng Xia-ting, Li Shu-lin, et al. Microseism source location with hierarchical strategy based on particle swarm optimization[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(4): 740-749. DOI:10.3321/j.issn:1000-6915.2009.04.012) |
| [13] | Li J, Wu D, Han Y. A PSO microseismic localization method based on group waves' time difference information[J]. Journal of Measurement Science and Instrumentation, 2016, 7(3): 241-246. |
| [14] | 杨道学, 赵奎, 曾鹏, 等. 基于粒子群优化算法的未知波速声发射定位数值模拟[J]. 岩土力学, 2019, 40(sup1): 494-502. (Yang Dao-xue, Zhao Kui, Zeng Peng, et al. Numerical simulation of unknown wave velocity acoustic emission localization based on particle swarm optimization algorithm[J]. Rock and Soil Mechanics, 2019, 40(sup1): 494-502.) |
| [15] | James K, Russell E. Particle swarm optimization[C] //Proceeding of Neural Networks. Perth, 1995: 1942-1948. |
| [16] | Suganthan P N. Particle swarm optimiser with neighbourhood operator[C]// Congress on Evolutionary Computation. Washington D C, 1999: 1958-1962. |
