曾小华, 陈虹旭, 崔臣, 宋大凤
吉林大学 汽车仿真与控制国家重点实验室，吉林 长春 130025
收稿日期：2020-04-13
基金项目：国家重点研发计划项目(2018YFB0105900)。
作者简介：曾小华(1977-), 男, 江西吉安人, 吉林大学教授, 博士生导师;
宋大凤(1977-), 女, 山东东营人, 吉林大学教授, 博士生导师。

摘要：为开发有效可靠的永磁同步电机无位置传感器控制算法，针对考虑铁损电阻的电机等效电路模型，分别在d-q旋转坐标系和α-β静止坐标系下推导得到了扭矩电流状态微分表达式，在此基础上设计滑模观测器观测电机转速和转子位置信号.为验证观测效果，对两种坐标系下的无位置传感器算法进行了仿真和对比分析.根据d-q轴系下转子位置信号准确度低、α-β轴系下观测信号存在高频抖振但准确性高的特点，提出一种基于扩展卡尔曼滤波的融合观测算法.仿真结果表明，该融合观测算法的观测结果误差更小，且具有良好的动态特性，并通过实验验证了融合观测算法的有效性.
关键词：永磁同步电机铁损电阻无位置传感器控制扩展卡尔曼滤波融合观测算法
Sensorless Control Algorithm for Permanent Magnet Synchronous Motors Considering Iron Loss
ZENG Xiao-hua, CHEN Hong-xu, CUI Chen, SONG Da-feng
State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130025, China
Corresponding author: SONG Da-feng, E-mail: songdf@jlu.edu.cn.

Abstract: Aiming at developing an effective and reliable sensorless control algorithm for permanent magnet synchronous motors, for the equivalent circuit model considering iron loss resistance, the differential expression of the torque current state was derived under the d-q rotating axis system and the α-β stationary axis system. On this basis, a sliding mode observer was designed to estimate the speed and rotor position signals. In order to verify the observation effect, the sensorless algorithm was simulated and compared under the two axis systems. A fusion observation algorithm based on the extended Kalman filtering was proposed according to the characteristics of the low accuracy of the rotor position signal under the d-q axis system and the high frequency chattering of the signals under the α-β axis system. Simulation results showed that the fusion observation algorithm has less error and good dynamic characteristics. Besides, the effectiveness of the fusion observation algorithm was verified by experiments.
Key words: permanent magnet synchronous motor(PMSM)iron loss resistancesensorless controlextended Kalman filterfusion observation algorithm
面对日益严峻的能源危机和环境问题，汽车行业正经历着从传统内燃机汽车向新能源汽车的转变，永磁同步电机(permanent magnet synchronous motor，PMSM)因其效率高、调速范围宽等优点，广泛应用于车用驱动电机领域^[1].为实现对永磁同步电机的精确控制，常在电机中安装高精度位置传感器，如霍尔传感器、光电编码器等，但是位置传感器的使用会提高电机系统成本，还易受振动、噪声等因素影响降低系统的可靠性^[2].因此，在电机控制系统的软件层面开发无位置传感器算法可以有效地降低成本、提高系统可靠性.
无位置传感器算法可分为两类：高频注入法和观测器法.高频注入法主要适用于零速和低速工况，通过外加高频激励实现对转子位置的估计，该方法需设计多个滤波器，控制复杂且运算量大^[3-4].
滑模观测器(sliding mode obsever，SMO)算法通过设计合理的趋近律使观测量估计值与测量值的差值趋近于零，根据观测出的反电动势值计算转子位置和转速^[5].该方法具有鲁棒性强、对模型参数变化的敏感性低等优点，许多****对基于SMO的无位置传感器算法展开了研究.Peng等^[6]在SMO算法的基础上设计锁相环从反电动势中解算转子位置和速度信号，以降低信号中的高频抖振；Kim等^[7]为克服传统SMO算法中由于低通滤波器引入而产生的时间延迟问题，采用Sigmoid饱和函数代替开关函数获得了良好的观测效果；陈炜等^[8]提出一种自适应滑模观测器算法对反电动势进行估计，改善了低速下转子位置和转速的估计效果；刘震等^[9]采用二阶滑模理论设计反电动势观测器，减轻了观测系统的抖振并提高了响应速度.但上述这些无位置传感器算法的研究均是基于简化的PMSM等效电路模型，该模型以定子铜损作为电机运行中的唯一损耗而忽略铁芯损耗，基于简化模型开发的无位置传感器算法易造成转子位置定位不准、定子电压易饱和等问题^[10]，苑婷等^[11]重构PMSM铁损模型，在此模型的基础上应用SMO算法观测扩展反电动势实现无位置传感器控制.目前考虑PMSM铁损的无位置传感器算法的研究还比较少.
基于以上的研究现状，本文根据考虑铁损的PMSM等效电路模型，得到扭矩电流的状态微分表达式；分别在d-q轴系和α-β轴系下设计滑模观测器，估计转子转速和位置，在稳态条件和动态条件下进行了仿真分析；对不同轴系下得到的观测结果进行对比，提出了基于扩展卡尔曼滤波的融合算法，通过仿真与实验验证了算法的观测效果.
1 永磁同步电机铁损模型1.1 铁损产生机理电机在运行过程中，转子铁芯和定子铁芯中产生的损耗即为铁芯损耗，简称铁损.由Bertotti铁损分离模型可知，铁损按产生机理分为：涡流损耗、磁滞损耗和异常损耗^[12]，只考虑铁芯中磁感应强度在大小上的变化，得到单位体积上的铁芯损耗功率为

(1)

式中:P_h为磁滞损耗，W/m³；P_c为涡流损耗，W/m³；P_a为异常损耗，W/m³；k_h为铁芯的磁滞损耗系数，与材料和加工工艺相关；f为外加磁场的变化频率，Hz；B_m为磁感应强度幅值，T；k_c为涡流损耗系数，与硅钢片的电导率、厚度和密度有关；k_a为异常损耗系数.
由式(1)可见，铁芯损耗随外加磁场频率的增大而增大，即随电机转速的升高，铁芯损耗增大.且当电机转速逐渐升高时，铁芯损耗占电机总损耗的比重会越来越大^[11]，这也是对调速性能要求更严格、电机控制系统不能忽略铁损的原因.
1.2 考虑铁损的PMSM等效电路模型将铁芯损耗等效成在一铁芯内阻上产生的损耗，这个等效内阻即为铁损电阻.得到考虑铁损电阻的永磁同步电机在d-q轴上的等效电路模型如图 1所示.图中d-q轴电流分量i_d/i_q一部分流经铁损电阻R_f产生铁芯损耗，称为铁损电流i_df/i_qf；另一部分产生电磁转矩，称为扭矩电流i_dt/i_qt.
图 1(Fig. 1)

图 1 考虑铁损电阻的PMSM等效电路图Fig.1 PMSM equivalent circuit considering iron loss resistance (a)—d轴等效电路图；(b)—q轴等效电路图.

根据图 1分别写出d，q轴下的电压方程和电流方程为

(2)

(3)

式中：R_c为铜损电阻；L为d，q轴上的电感，表贴式转子结构的d，q轴电感相同；ω_e为电机电角速度；ψ_f为永磁体磁链.
由式(2)和式(3)得到扭矩电流的微分方程为

(4)

该状态微分方程是考虑铁损的永磁同步电机无位置传感器控制算法研究的基础.
2 d-q轴系下的无位置传感器算法滑模观测器算法的基本思路是以电流误差作为滑模面函数的输入，以反电动势E作为观测值，根据反电动势的观测值计算得到转速和转子位置信息.由于考虑铁损的PMSM模型建立在两相旋转坐标系(d-q轴系)下，本节在该轴系下设计滑模观测器进行无位置传感器算法研究.
2.1 滑模观测器设计根据式(4)，将电流状态微分方程改写为

(5)

式中，
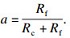
将式(5)中包含电机电转速ω_e的反电动势ω_eψ_f作为观测变量，记为E_q，d轴上的反电动势E_d=0.记d，q轴上的反电动势观测值分别为ê_d，ê_q，则得到电流状态观测方程为

(6)

式中，?_dt，?_qt分别为d-q轴扭矩电流的估计值.
选取电流估计误差作为滑模面函数，如式(7)所示：

(7)

式中，?_dt，?_qt表示扭矩电流的估计误差.
传统的滑模观测器选取开关函数构造反电动势观测值，但由于开关函数是一个不连续的函数，会造成反电动势观测结果的高频抖振，常增加低通滤波器以获得光滑的观测信号，但低通滤波器的引入会造成观测结果延迟，因此本文采用连续饱和的Sigmoid函数代替开关函数，该函数的表达式为

(8)

式中，α为一正实数.
反电动势观测值的表达式为

(9)

对式(6)和式(5)作差，得到电流误差的微分方程为

(10)

根据滑模面函数的收敛准则，须满足s^T?≤0，因此，将式(7)与式(10)相乘可得

(11)

若想满足收敛条件，只需满足式(11)第二项恒小于等于0即可.将式(9)代入，式(11)的第二项可表示为

(12)

由于式(12)中的f(?_dt)·?_dt≥0始终成立，为便于调试取k_d=0，即_d=E_d=0，令d轴上反电动势的观测值始终等于真实值，因此当k_q≥ω_eψ_f时式(12)恒成立，则转子的电角速度和位置的观测值为

(13)

2.2 仿真结果分析本文仿真所用电机为一台31 W的表贴式永磁同步电机，电机的部分参数：定子电阻为2.1 Ω，电感为1.4 mH，极对数为4，额定直流电压为24 V，额定电流为1.8 A，铁损电阻为(0.06ω_e+50)(由试验测得)，应用Matlab/Simulink搭建的PMSM无位置传感器控制系统进行仿真.
其中，由电流传感器得到定子三相电流i_a，i_b，i_c，经坐标变换得到i_d，i_q，根据式(14)得到扭矩电流的测量值i_dt和i_qt.

(14)

首先给定目标转速3 000 r/min，得到电机转速和转子位置的观测结果如图 2所示.
图 2(Fig. 2)

图 2 3 000 r/min目标转速下观测结果及误差Fig.2 Observation results and error at 3 000 r/min (a)—转速；(b)—位置；(c)—转速观测误差；(d)—位置观测误差.

由图 2可以看出，转速观测值能够很好地跟随实际值，最大误差只有1 r/min，转子位置观测值由转速观测值积分得到，存在-0.12°的微小误差.
设定目标转速为500 r/min，验证电机控制系统在低速时的转速跟随情况，得到电机转速和转子位置的观测结果和误差如图 3所示.对比图 3与图 2，在保证参数k_q和α不变的前提下，目标转速较低时收敛相对缓慢，转速的观测误差在0.5 r/min以内，且转子位置的观测误差在-0.22°左右，精度足够，算法的鲁棒性较好.
图 3(Fig. 3)

图 3 目标转速为500 r/min下观测结果及误差Fig.3 Observation results and error at 500 r/min (a)—转速；(b)—位置；(c)—转速观测误差；(d)—位置观测误差.

为了进一步验证滑模观测器的动态特性，分别在目标转速为0~3 000 r/min斜坡变化和3 000~500 r/min阶跃变化下进行仿真，得到无位置传感器算法的转速和转子位置观测结果如图 4，图 5所示.
图 4(Fig. 4)

图 4 目标转速为0~3 000 r/min斜坡变化下观测结果及误差Fig.4 Observation results and error at 0~3 000 r/min slope speed (a)—转速；(b)—位置；(c)—转速观测误差；(d)—位置观测误差.

图 5(Fig. 5)

图 5 目标转速为3 000~500 r/min阶跃变化下观测结果及误差Fig.5 Observation results and error at 3 000~500 r/min step speed (a)—转速；(b)—位置；(c)—转速观测误差；(d)—位置观测误差.

由图 4可看出，斜坡输入下转速观测值能持续跟随目标转速，转速误差最大为-0.5 r/min，转子位置误差最大为-0.15°.图 5中在转速突然变化后，转速的估计值也能很好地跟随实际值，最大误差为-1 r/min，转子位置误差在-0.2°左右，不会影响到电机控制系统的稳定性，说明d-q轴系下设计的无位置传感器算法具有良好的动态特性.
3 α-β轴系下的无位置传感器算法为简化PMSM的数学模型，采用坐标变换将自然坐标系变换到α-β两相静止坐标系(Clark变换)和d-q同步旋转坐标系(Park变换)^[13].变换后的d-q轴系是以同步电角速度ω_e旋转，从而将三相交流量变换为d-q轴上的直流量，在d-q轴系上建立的电压、电流等方程不包含转子位置θ_e，而自然坐标系和α-β轴系下均包含.由式(5)可以看出，d-q轴上的反电动势只含有转速信号，转子位置信号通过转速估计值积分得到，因此，上节中所述的d-q轴上的滑模观测器算法在电机长时间运行时转子位置信号易造成累积误差，影响观测结果的准确性.针对这一问题，本节在α-β轴系下设计滑模观测器，进行无位置传感器算法的研究.
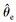
3.1 α-β轴系下的电机模型首先推导α-β轴系下的扭矩电流状态微分表达式.根据式(2)和式(3)，得到电压状态方程的矩阵形式为

(15)

对式(15)进行反Park变换，反Park变换矩阵如式(16)所示，得到α-β轴系下的电压状态方程见式(17).

(16)

(17)

对式(17)进一步整理得到α-β轴系下的扭矩电流i_αt和i_βt的状态微分表达式为

(18)

对比式(18)和式(5)，α-β轴系下的扭矩电流状态方程没有两轴间的电流耦合，两轴上的反电动势既包含转子的转速信号，也包含位置信号，因此通过观测该轴系下的反电动势计算得到的转子位置信号，可以避免由转速积分带来的累计误差.
其中，针对扭矩电流的测量值i_αt，i_βt，由传感器直接测量的i_a，i_b和i_c经过坐标变换得到i_α和i_β后推导计算得到.其表达式为

(19)

3.2 滑模观测器设计根据式(18)，两轴上的反电动势分量分别为E_α=-ω_eψ_fsinθ_e，E_β=ω_eψ_fcosθ_e.根据式(18)建立观测器模型为

(20)

选取扭矩电流估计误差作为滑模面函数s，其微分表达式为

(21)

参照2.1节的设计思路，使用Sigmoid函数f(x)表示反电动势的估计值为

(22)

根据收敛准则，得到可调参数k_α，k_β的收敛条件为k_α，k_β≥ω_eψ_f.
转子转速和位置的观测值通过式(23)计算得到：

(23)

3.3 仿真结果分析当目标转速为3 000 r/min时，转子转速和位置的观测结果如图 6所示.由图可见，α-β轴系下的观测结果中存在较大幅值的高频抖动现象.对比d-q轴系下的反电动势表达式，α-β轴系下的反电动势为一正弦(余弦)信号.由式(22)可知，由于铁损电阻的引入和电机控制系统中电流环的调节作用，难以保证扭矩电流误差信号为一标准的正弦信号，因此由电流误差信号观测得到的反电动势及由此算出的转速和转子位置信号存在高频抖振.
图 6(Fig. 6)

图 6 3 000 r/min目标转速下观测结果及误差Fig.6 Observation results and error at 3 000 r/min (a)—转速；(b)—位置；(c)—转速观测误差；(d)—位置观测误差.

图 7为α-β轴上的电流信号及误差，由图 7e, 图 7f放大图可以看出，电流信号中掺杂着不规则谐波.对比图 2所示d-q轴系下的转速观测结果，d-q轴系下反电动势为一正比于转速的稳定信号，其电流估计误差也为稳定信号，因此转速观测信号稳定，观测效果较好.虽然α-β轴系下转速观测结果较差，但由于转子位置信号的观测值通过反三角函数计算得到，不依赖于转速信号，且在设计观测器时，两轴上并无耦合关系，因此转子位置的观测结果对比图 2中d-q轴系下的观测结果，其观测误差最大值为0.06°，在0.02 s后，虽然存在高频抖振，但抖振幅值在0.005°左右，与实际信号误差很小，准确性较高.
图 7(Fig. 7)

图 7 电流信号观测结果及误差Fig.7 Observation results and error of current signals (a)—α轴电流；(b)—β轴电流；(c)—α轴电流误差；(d)—β轴电流误差；(e)—图 7c局部放大；(f)—图 7d局部放大.

3.4 基于EKF的融合观测算法根据2.2节和3.3节的仿真分析结果可知，在d-q轴系下设计的算法可以较准确地观测出转速信号，但转子位置信号的观测值易产生累计误差；而在α-β轴系下得到的观测信号中含有不规则抖振，难以直接应用在电机控制系统，但位置观测信号的准确性较高.因此设计基于扩展卡尔曼滤波(extended Kalman filter，EKF)的融合观测算法，将α-β轴系下的转子位置信号中的抖振信号视作噪声，对其进行滤波处理获得可信性更高的转子位置信号.该方法首先将电机模型离散化，然后通过预测、计算卡尔曼增益、修正等环节得到转子位置和转速信号^[14-15].
将d-q轴系下观测到的第k个步长的转速值记为，作为对转子位置的预测：

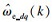
(24)

将α-β轴系下观测到的转子位置值记为，作为含噪信号，表达式为

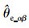
(25)

式中，V(k)为第k个步长下中的噪声.
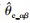
根据式(24)和式(25)，EKF算法可以表示为

(26)

(27)

(28)

(29)

(30)

其中：式(26)，式(27)为预测阶段方程；P(k|k-1)为第k步下误差协方差的预测值；Q为预测过程噪声的方差；式(28)为卡尔曼增益计算方程，R为V的方差；式(29)，式(30)为修正阶段方程.
式(29)即为卡尔曼滤波器最终输出的转子位置信号，转速信号仍采用d-q轴系下的观测值.为验证融合观测算法在电机长时间运行、工况发生改变后的观测效果，设置仿真时间为1 s的多变工况，采用d-q轴系下设计的观测算法与基于EKF的融合观测算法观测结果如图 8和图 9所示.
图 8(Fig. 8)

图 8 基于d-q轴系的无位置传感器算法观测结果Fig.8 Observation results based on sensorless algorithm under d-q axis system (a)—转速；(b)—位置；(c)—转速观测误差；(d)—位置观测误差.

图 9(Fig. 9)

图 9 基于EKF的融合观测算法观测结果Fig.9 Observation results based on EKF fusion algorithm (a)—转速；(b)—位置；(c)—转速观测误差；(d)—位置观测误差.

由观测结果可见，该仿真条件下基于d-q轴系的观测算法的转速观测误差最大值为1.2 r/min，转子位置观测误差最大值为-1.1°；采用融合观测算法得到转速观测误差最大值为0.1 r/min，位置观测误差最大值为-0.08°，误差缩小到原误差的10%以下.
4 实验分析基于图 10所示的硬件系统对基于EKF的融合观测算法进行实验验证，电机为仿真所用31 W表贴式永磁同步电机，内装有混合式光电编码器，用于验证无位置传感器观测算法的准确性.
图 10(Fig. 10)

图 10 永磁同步电机实验硬件系统Fig.10 Experimental hardware system for PMSM

首先应用Simulink软件搭建PMSM无位置传感器控制系统的各模块；然后进行数据管理与参数配置，对各模块进行编译生成代码；最后将生成的代码在CCS(code composer studio)软件环境下进行集成，编译进仿真器进行实验.
在转速控制模式下，PMSM的控制目标、传感器测量和由无位置传感器观测到的转速对比曲线及其细节放大图如图 11所示，由传感器测得的转子位置与融合观测算法得到的转子位置误差曲线如图 12所示.
图 11(Fig. 11)

图 11 转速结果对比Fig.11 Comparison of rotational speed results (a)—转速对比；(b)—图 11a局部放大.

图 12(Fig. 12)

图 12 转子位置误差Fig.12 Experimental error of rotor position

在电机的实际控制系统中，由于逆变器的死区效应、电机本体永磁体磁场的设计偏差与工艺限制等影响，都会在电机的输出转矩和转速中引入谐波，从而导致电机实际输出转速在目标转速附近存在波动，而在电机的仿真系统中这些因素的影响均被忽略，同时，传感器也会存在一定的测量误差.由传感器测得和基于EKF融合观测算法得到的转子位置误差在±3°范围内，电机转速实验结果统计如表 1所示.由表 1可见，传感器测量转速相比于目标转速的平均误差率为0.299%，基于EKF融合观测算法观测转速相比于目标转速的平均误差率为0.32%，传感器与融合观测算法的相对误差率为0.021%，对比图 9的仿真结果，转速误差率最大值为0.01%，实验结果相比仿真结果误差增大，但仍保证了较高的准确性.实验结果说明所提出的基于EKF的融合观测算法能达到与传感器相当的效果，可用于实际的电机控制系统.
表 1(Table 1)

表 1 机械转速实验结果统计Table 1 Experimental results of mechanical speed 项目 传感器测量 融合观测算法 转速波动幅值/(r·min-1) 17 21 转速误差绝对值的平均值/(r·min-1) 7 9 平均误差率/% 0.299 0.32

表 1 机械转速实验结果统计 Table 1 Experimental results of mechanical speed

5 结论1) 针对考虑铁损的PMSM等效电路模型，分别在d-q轴系和α-β轴系设计滑模观测器进行无位置传感器算法研究.在两轴系下搭建了观测器模型并进行了仿真验证.结果表明，d-q轴系下的无位置传感器算法得到的转速观测信号准确度高、鲁棒性好、动态特性良好，但转子位置信号易产生累计误差；α-β轴系下的无位置传感器算法得到的观测信号存在高频抖振，难以应用于电机控制系统，但转子位置信号的准确度更高.
2) 采用卡尔曼滤波器对两轴系下的观测信号进行融合，得到可信度更高的转子位置信号.仿真结果表明：基于EKF的融合观测算法对比d-q轴系下的SMO算法，观测结果误差小，观测信号中不存在高频抖振.融合观测算法实验表明：由传感器测量和融合观测算法得到的转速其相对转速误差率较小，验证了基于EKF的融合观测算法的有效性，具有实际应用价值.
参考文献

[1]	于雪锋.电动汽车用永磁同步电机控制方法及其实现研究[D].长沙: 湖南工业大学, 2019. (Yu Xue-feng.Research on control method and implement of permanent magnet synchronous motor for electric vehicle[D].Changsha: Hunan University of Technology, 2019. )
[2]	Bolognani S, Calligaro S, Petrella R. Sensorless control of IPM motors in the low-speed range and at stand-still by HF injection and DFT processing[J]. IEEE Transactions on Industry Applications, 2011, 47(1): 96-104. DOI:10.1109/TIA.2010.2090317
[3]	Shen H L, Zhang C W.A new efficient sensorless I/f control method for IPMSM drives[C]//IEEE International Symposium on Industrial Electronics (ISIE).Edinburgh, 2017: 209-213.
[4]	Tu W Y, Xiao G L, Suo C, et al.A design of sensorless permanent magnet synchronous motor drive based on V/f control[C]//International Conference on Electrical Machines and Systems (ICEMS).Sydney, 2017: 1-5.
[5]	Zhu W K. A position sensorless control strategy for SPMSM based on an improved sliding mode observer[J]. IPO Conference Series:Earth and Environmental Science, 2019, 252(3): 21-35.
[6]	Peng T, Wang F X, Mei X Z.PLL with piecewise judgement function for SMO based sensorless control of PMSM[C]//International Conference on Enterprise System.Beijing, 2017: 190-194.
[7]	Kim H, Son J, Lee J. A high-speed sliding-mode observer for the sensorless speed control of a PMSM[J]. IEEE Transactions on Industrial Electronics, 2011, 58(9): 4069-4077. DOI:10.1109/TIE.2010.2098357
[8]	陈炜, 张志伟. 基于自适应滑模观测器的永磁同步电机无位置传感器控制[J]. 电工电能新技术, 2016, 35(8): 8-14. (Chen Wei, Zhang Zhi-wei. A position sensorless control strategy for PMSM based on adaptive sliding mode observer[J]. Advanced Technology of Electrical Engineering and Energy, 2016, 35(8): 8-14. DOI:10.3969/j.issn.1003-3076.2016.08.002)
[9]	刘震, 苗述, 李汶浍, 等. 基于Super-Twisting滑模观测器的永磁同步电机无传感器控制[J]. 东北大学学报(自然科学版), 2020, 41(5): 741-746. (Liu Zhen, Miao Shu, Li Wen-hui, et al. Super-twisting sliding mode observer based sensorless control of PMSM[J]. Journal of Northeastern University(Natural Science), 2020, 41(5): 741-746.)
[10]	Wijenayake A H, Sehmidt P B.A more accurate permanent magnet synchronous motor model by taking parameter variations and loss components into account for sensorless control applications[C]//IEEE International Electric Machines & Drives Conference (IEMDC).Milwaukee, 1997: 1-3.
[11]	苑婷, 李志新, 李长娟, 等. 考虑铁损的超高速永磁同步电机无传感器控制[J]. 电力电子技术, 2017, 51(3): 74-77. (Yuan Ting, Li Zhi-xin, Li Chang-juan, et al. Sensorless control of ultrahigh speed permanent magnet synchronous motor by considering iron loss[J]. Power Electronics, 2017, 51(3): 74-77.)
[12]	Yang G Q, Cui Z Z, Song L W.Analysis of iron losses in induction motor with an improved iron-loss model[C]//IEEE Transportation Electrification Conference, Asia-Pacific (ITEC Asia-Pacific).Beijing, 2014: 138-142.
[13]	Urasaki N, Senjyu T, Uezato K.An accurate modeling for permanent magnet synchronous motor drives[C]//Applied Power Electronics Conference and Exposition.New Orleans, 2000: 387-392.
[14]	Hussain S, Bazaz M A. Sensorless control of PMSM drive using extended Kalman filter and fuzzy logic controller[J]. International Journal of Industrial Electronics and Drives, 2016, 3(1): 12-19. DOI:10.1504/IJIED.2016.077677
[15]	Aydogmus Z, Aydogmus O. A comparison of artificial neural network and extended Kalman filter based sensorless speed estimation[J]. Measurement, 2015, 63: 152-167. DOI:10.1016/j.measurement.2014.12.010