基于PDChirp-Golay信号的编码激励算法

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2021-12-15

鲍喜荣, 高浩森, 历正双, 张石
东北大学计算机科学与工程学院, 辽宁沈阳 110169
收稿日期：2020-04-15
基金项目：中央高校基本科研业务费专项资金资助项目(N171604011)。
作者简介：鲍喜荣(1978－), 男, 湖北当阳人, 东北大学讲师, 博士;
张石(1963－), 男, 辽宁抚顺人, 东北大学教授, 博士生导师。

摘要：线性调频信号编码激励超声成像算法旁瓣过高, 针对这个问题, 提出一种基于幅度加权的预失真线性调频信号调制Golay码(PDChirp-Golay)编码新方法.该方法将线性调频发射信号采用预失真处理, 可以补偿超声探头对发射信号的影响, 使回波信号的带宽增大, 提高轴向分辨力, 并同时消除发射信号幅频特性的菲涅耳波纹, 实现旁瓣抑制; 之后使用预失真处理的线性调频发射信号调制Golay码.Golay码理论上距离旁瓣水平为零, 可以利用Golay码这一特点进一步进行旁瓣抑制.仿真结果表明, 相较于单独的预失真线性调频信号与Golay码, 预失真Chirp信号调制的Golay码提高了轴向分辨力和对比度, 并且具有很好的抗噪性, 为实现高质量的超声成像系统提供了理论依据.
关键词：编码激励预失真线性调频信号Golay码轴向分辨力超声成像
Coding Incentive Algorithm Based on PDChirp-Golay Signal
BAO Xi-rong, GAO Hao-sen, LI Zheng-shuang, ZHANG Shi
School of Computer Science & Engineering, Northeastern University, Shenyang 110169, China
Corresponding author: GAO Hao-sen, E-mail: 1801687@stu.neu.edu.cn.

Abstract: To solve the problem of high sidelobe in ultrasonic imaging algorithms induced by LFM signal coding, a new method of PDChirp-Golay coding based on amplitude weighting is proposed. This method predistorts linear frequency modulation(LFM) signals, thus compensating the influence of ultrasonic probe on the emission signal, which makes the bandwidth of the echo signal increase, improves the axial resolution, and eliminates the Fresnel corrugation of the emission signal amplitude frequency characteristics at the same time, realizing sidelobe suppression. Then, the predistorted LFM signal is used to modulate Golay code. The range sidelobe level of Golay code is zero in theory, which makes the sidelobe further suppressed. The simulation results show that, compared with the single predistorted LFM signal and Golay code, Golay code modulated by the predistorted Chirp signal improves the axial resolution and contrast, and has a good anti-noise performance, which provides a theoretical basis for the realization of high-quality ultrasonic imaging system.
Key words: coded excitationpredistorted LFM signalGolay codeaxial resolutionultrasonic imaging
在医学超声成像系统中, 轴向分辨力和信噪比是图像质量的主要指标, 但是在传统超声成像系统中这两个参数之间需要有一个取舍^[1].而在编码激励技术中通过发送长编码脉冲来提高信噪比, 将接收到的信号压缩到很短的时间间隔来恢复轴向分辨力, 从而解决了这一问题.O’Donnell讨论了改善信噪比的可能性, 表明编码激励可以使信噪比提高15~20 dB^[2].编码激励在一些实际生产中也有应用, 如腹部超声和眼科超声生物仪^[3].近年来, 人们提出了一些新的激励信号产生方法, 并将其应用于实际情况.文献[4]提出一种延迟激励算法, 主要适用于高频超声成像.文献[5]在激励中引入接收间隔或暂停, 从而提高信噪比.然而, 最广泛研究的方法仍然是线性调频信号、伪线性调频信号、Barker码和Golay码.文献[6]介绍了这些代码的一些基础知识, 并进行了详细的比较.文献[7-11]讨论了线性调频信号和伪线性调频信号.文献[12]使用一个碱基序列调制的Golay编码来提高信噪比.文献[13]采用线性调频信号作为载波来调制Barker码.文献[3]将Golay码编码激励引入眼科超声生物计.文献[14]使用改进的Golay编码用于谐波成像.文献[15]采用Golay编码序列研究编码传输的位长对超声图像分辨力和穿透深度的影响.文献[16]为抵消探头的脉冲响应, 提出幅度加权的线性调频信号作为编码激励信号, 从而提高轴向分辨力.文献[17]通过幅度调制, 对线性调频发射信号进行改进, 使其带宽提高, 并选取适合的失配滤波, 降低旁瓣水平.文献[18]提出一种基于幅度加权的预失真线性调频编码新方法, 降低探头脉冲响应的影响, 增大回波带宽, 降低旁瓣水平, 从而提高轴向分辨力.
综上所述, 线性调频信号是目前使用最为广泛的一种编码方式, 具有很好的自相关特性和频移鲁棒性, 但存在距离旁瓣较高的问题, 而Golay码理论上可以完全消除距离旁瓣.因此, 本文采用经幅度加权预失真线性调频编码调制的Golay码, 抵消探头的脉冲响应, 并同时消除发射信号幅频特性的菲涅耳波纹, 实现旁瓣抑制, 提高轴向分辨力, 并同时确保较好的对比度和信噪比.
1 PDChirp-Golay信号的设计1.1 预失真线性调频信号的设计线性调频信号(Chirp信号)是使用较广泛的一种编码信号, 其表达式为

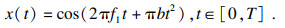(1)

式中: f₁是信号的起始频率; b为调制斜率; T是时间宽度; 信号的最大频率值f₂=f₁+bT; 带宽B=bT= f₂-f₁;中心频率f₀=f₁+B/2.
Chirp发射信号的预失真处理信号PDChirp表示为

(2)

式中: w(t)为幅度加权函数, 其设计要从两个方面考虑, 即

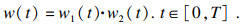(3)

其中, w₁(t)加权函数用来消除探头的脉冲响应对线性调频信号的影响, 从而消除回波信号因探头的脉冲效应而产生的局限性, 提高轴向分辨力.探头的脉冲响应是高斯包络调制的余弦波, 因此w₁(t)为高斯函数的倒数, 即

(4)

式中D是幅度加权系数, 表示幅度加权的程度.D值越小, 对线性调频发射信号低频和高频处幅度加权的程度越大, 即幅值越大.D的取值与探头的脉冲响应、发射信号的带宽和时间宽度有关系.
w₂(t)采用Lanczos窗12%的幅度削减函数, 用来消除因补偿探头响应对线性调频信号频谱产生的菲涅尔波纹, 降低旁瓣幅度水平, 提高轴向分辨力.
1.2 用预失真线性调频信号调制Golay码Golay互补序列对是由码长相等的二进制有限序列对A和B组成, A和B互补, 可以表示为

(5)

(6)

式中n是Golay码的长度.n的取值为两个非负整数的平方和, 且为偶数.
用预失真线性调频信号分别调制Golay互补序列对A和B, 可以得到PDChirp-Golay编码信号对, 如式(7)和式(8)所示:

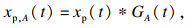(7)

(8)

式中: G_A(t)和G_B(t)是序列A和B的过采样信号; x_{p, A}和x_{p, B}为PDChirp-Golay编码信号对.
PDChirp-Golay编码信号和脉冲压缩流程如图 1所示.
图 1(Fig. 1)

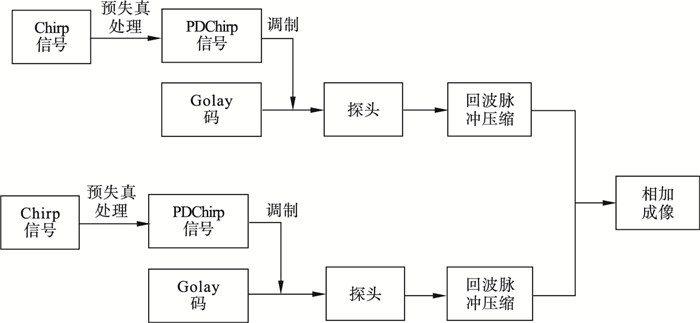图 1 PDChirp-Golay编码信号和脉冲压缩Fig.1 PDChirp-Golay code signals and pulse compression

2 仿真结果与分析本文的仿真使用Field II仿真平台.Field II是丹麦超声专家J. A. Jensen等利用声学原理设计的一个模拟超声传感器声场, 使用线性声学超声成像的MATLAB仿真程序, 它可以仿真超声探头所形成的声场和超声图像等.
本次仿真选取4种信号作为对比, 分别为8周期的正弦波、8周期的PDChirp信号、8位正弦波调制的Golay码, 以及PDChirp信号调制的8位Golay码.仿真后对结果进行分析并同时证明PDChirp-Golay信号的优越性.
2.1 点散射目标仿体图像和横向响应图本文共设定10个点目标(分为5对), 等距分布在20~60 mm深度处, 同一深度的两个目标点横向间隔为2 mm, 对应的横坐标分别为-1 mm和1 mm, 仿真采用的超声波发射方式和接收方式均为动态聚焦方式, 4种编码激励算法的成像结果如图 2所示.由图 2a可以看出, 传统正弦波激励的轴向分辨力较差；图 2b是PDChirp信号激励算法的图像, 其成像效果明显优于正弦波激励, 轴向分辨力较好；图 2c是Golay码激励算法, 轴向分辨力效果较正弦波激励有很大提升；图 2d是本文提出的PDChirp-Golay算法, 与已有的编码激励算法相比, 其轴向分辨力好于其他编码激励算法.直观上看, 4种算法在横向分辨力上没有明显差别, 都有较好的横向分辨力性能.
图 2(Fig. 2)

图 2 五对点目标仿体的仿真图像Fig.2 Simulation images of a five-point target imitations (a)—正弦波；(b)—PDChirp；(c)—Golay；(d)—PDChirp-Golay.

为了更好地研究PDChirp-Golay算法的轴向分辨力, 本文还设定了4组仿真实验, 在50 mm深度处和50 mm深度以下1 mm处设定两对点目标, 分析PDChirp-Golay算法纵向分辨力性能, 4种编码激励算法的成像结果如图 3所示.从图 3可以看出, 正弦波与PDChirp基本无法区分上下2对目标点, Golay相较而言可以区分, 而PDChirp-Golay具有最明显的边界, 具有良好的纵向分辨力.
图 3(Fig. 3)

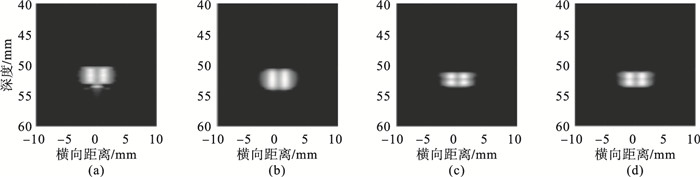图 3 两对点目标仿体的仿真图像Fig.3 A simulation image of two pairs of target imitations (a)—正弦波；(b)—PDChirp；(c)—Golay；(d)—PDChirp-Golay.

为了更加准确地比较不同算法在横向分辨力上的差异, 选取了深度为50 mm处的横向波束响应幅度图, 通过观察其主瓣宽度和峰值旁瓣水平来进行进一步的对比分析, 如图 4所示.
图 4(Fig. 4)

图 4 50 mm深度横向波束响应幅度图Fig.4 Transverse beam amplitude response diagram at 50 mm depth

由图 4可见, PDChirp-Golay信号相较于其他3种信号, 主瓣宽度最小, 峰值距离旁瓣水平最低, 轴向分辨力最好, 成像效果最佳.具体主瓣宽度与峰值距离旁瓣幅度数值如表 1所示.
表 1(Table 1)

表 1 点目标实验50 mm处主瓣宽度和峰值距离旁瓣幅度值Table 1 Width of the main lobe and the amplitude value of the peak distance from the side lobe at 50 mm in the point target experiment

激励信号	-6 dB主瓣宽度/mm	峰值距离旁瓣幅度/dB
正弦波	0.847	-56.5
PDChirp	0.784	-53.5
Golay	0.777	-59.6
PDCirp-Golay	0.731	-62.6

表 1 点目标实验50 mm处主瓣宽度和峰值距离旁瓣幅度值 Table 1 Width of the main lobe and the amplitude value of the peak distance from the side lobe at 50 mm in the point target experiment

2.2 囊肿仿体成像结果本文除点目标外还设定了一组囊肿目标仿体, 囊肿中心设置在40 mm深度处, 囊肿半径设置为4 mm, 在囊肿外部随机分布10 000个散射点, 模拟均匀的人体组织.仿真采用的发射方式为定点聚焦, 焦点定于40 mm深度, 接收方式为动态聚焦, 其他参数与2.1节中点目标成像所设参数相同, 图 5为不同编码激励算法的成像结果.
图 5(Fig. 5)

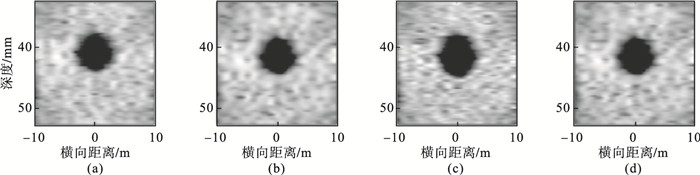图 5 囊肿目标仿体仿真图像Fig.5 Simulation images of cyst target imitation (a)—正弦波；(b)—PDChirp；(c)—Golay；(d)—PDChirp-Golay.

如图 5所示, 正弦波囊肿图像的边界存在伪影, 囊肿边缘不够圆润; PDChirp囊肿图像较正弦波有所增强, 但是仍有伪影, 边缘有毛刺; Golay码成像的边界有白色伪影存在, 囊肿呈现出椭圆形; PDChirp-Golay算法的成像效果最好, 囊肿图像边界更为清晰, 更加光滑, 成像效果最好.在此基础上, 画出了深度为40 mm处, 即囊肿中心所在位置的横向波束响应幅度图, 如图 6所示.
图 6(Fig. 6)

图 6 40 mm深度横向波束响应幅度图Fig.6 Transverse beam amplitude response diagram at 40 mm depth

2.3 结果分析综上所述, 通过对点目标和囊肿目标的仿真实验, 证明PDChirp-Golay编码激励算法缩小了回波信号主瓣宽度, 降低了峰值旁瓣水平, 横向和纵向分辨力都很好; 在确保对比度和信噪比的情况下, 有效提高了成像的轴向分辨力与成像质量.
3 结语本文介绍了一种基于幅度加权的预失真线性调频信号调制Golay码的编码激励算法, 补偿了超声探头对发射信号的影响, 使得回波信号的带宽不局限于探头, 提高了轴向分辨力, 并同时消除了发射信号幅频特性的菲涅耳波纹, 实现旁瓣抑制.利用Golay码的特性, 进一步抑制旁瓣, 提高成像质量, 并最终通过仿真证实了该方法在确保成像对比度和信噪比的同时能够有效提高轴向分辨力与成像效果, 为提高超声成像的质量提供了理论依据.
参考文献

[1]	Chiao R Y, Hao X H. Coded excitation for diagnostic ultrasound: a system developer's perspective[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2005, 52(2): 160-170. DOI:10.1109/TUFFC.2005.1406543
[2]	O'Donnell M. Coded excitation system for improving the penetration of real-time phased-array imaging systems[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 1992, 39(3): 341-351. DOI:10.1109/58.143168
[3]	Zhou S, Wang X C, Ji J J, et al.Ophthalmological ultrasound biometer using Golay-coded pulse excitation[C/OL]// 2014 7th International Conference on Biomedical Engineering and Informatics.Dalian, 2014[2020-02-15]. https://doi.org/10.1109/BMEI.2014.7002746.
[4]	Qiu W B, Xia J J, Shi Y L, et al. A delayed-excitation data acquisition method for high-frequency ultrasound imaging[J]. IEEE Transactions on Biomedical Engineering, 2018, 65(1): 15-20. DOI:10.1109/TBME.2017.2687948
[5]	Isla J, Cegla F. Coded excitation for pulse-echo systems[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2017, 64(4): 736-748. DOI:10.1109/TUFFC.2017.2661383
[6]	Lin J, Hua J D, Zeng L, et al. Excitation waveform design for Lamb wave pulse compression[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2016, 63(1): 165-177. DOI:10.1109/TUFFC.2015.2496292
[7]	Tseng H W, Qin Y X, O'Donnell M, et al.Improving sensitivity in acoustoelectric imaging with coded excitation and optimized inverse filter[C/OL]// 2017 IEEE International Ultrasonics Symposium.Washington DC, 2017[2020-02-16]. https://doi.org/10.1109/ULTSYM.2017.8092982.
[8]	Mamou J, Ketterling J A, Silverman R H. Chirp-coded excitation imaging with a high-frequency ultrasound annular array[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2008, 55(2): 508-513. DOI:10.1109/TUFFC.2008.670
[9]	Bosisio M R, Hasquenoph J M, Sandrin L, et al. Real-time chirp-coded imaging with a programmable ultrasound biomicroscope[J]. IEEE Transactions on Biomedical Engineering, 2010, 57(3): 654-664. DOI:10.1109/TBME.2009.2033036
[10]	Kang J B, Kim Y J, Lee W Y, et al. A new dynamic complex baseband pulse compression method for chirp-coded excitation in medical ultrasound imaging[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2017, 64(11): 1698-1710. DOI:10.1109/TUFFC.2017.2748165
[11]	Danial D, Porat M, Friedman Z.On chirp excitation and compression for ultrasound imaging[C/OL]// 2016 IEEE International Conference on the Science of Electrical Engineering(ICSEE).Eilat, Israel, 2016[2020-02-15]. https://doi.org/10.1109/ICSEE.2016.7806106.
[12]	Song X J, Ta D, Wang W Q. A base-sequence-modulated Golay code improves the excitation and measurement of ultrasonic guided waves in long bones[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2012, 59(11): 2580-2583.
[13]	Fu J M, Wei G, Huang Q.Barker coded excitation using LFM carrier for improving axial resolution in ultrasound imaging[C/OL].2013 ICME International Conference on Complex Medical Engineering.Beijing, 2013[2020-02-18]. https://doi.org/10.1109/ICCME.2013.6548229.
[14]	Shen C C, Chen R A.Improved ultrasound harmonic golay encoding using pulse-width-modulation transmit[C]// 2017 40th International Conference on Telecommunications and Signal Processing(TSP).Barcelona, 2017: 387-390.
[15]	Trots I, Nowicki A, Postema M. Ultrasound image improvement by code bit elongation[J]. IEEE Signal Processing Letters, 2018, 25(3): 437-441. DOI:10.1109/LSP.2017.2776040
[16]	da Costa-Felix R P B, Machado J C, Barros A L P.A frequency-compensated coded-excitation pulse to improve axial resolution of ultrasonic system[C]// Proceedings of the IEEE Ultrasonics Symposium.Vancouver, 2006: 1651-1654.
[17]	Avanji S A I, Far A M, Asl B M.Investigation of the effects of transducer parameters on adaptive MV beamformers in medical ultrasound applications[C/OL]// 2013 21st Iranian Conference on Electrical Engineering(ICEE).Mashhad, Iran, 2013[2020-02-18]. https://doi.org/10.1109/IranianCEE.2013.6599758.
[18]	傅娟, 韦岗, 黄庆华. 基于幅度加权的预失真线性调频超声编码激励[J]. 电子与信息学报, 2013, 35(2): 244-248. (Fu Juan, Wei Gang, Huang Qing-hua. Predistorted linear frequency modulation ultrasound coded excitation based on amplitude weighting[J]. Journal of Electronics & Information Technology, 2013, 35(2): 244-248.)