顾天奇, 罗祖德, 胡晨捷, 林述温
福州大学 机械工程及自动化学院, 福建 福州 350116
收稿日期：2020-08-18
基金项目：国家自然科学基金资助项目(51605094，51605091)。
作者简介：顾天奇(1983-)，男，河北邢台人，福州大学副教授;
林述温(1962-)，男，福建平潭人，福州大学教授，博士生导师。

摘要：移动最小二乘法由于其良好的逼近性能而广泛用于曲线曲面拟合, 但处理含有粗大误差的数据时, 拟合结果极不稳定.为了减少粗大误差对拟合精度的影响, 本文提出一种移动最小截平方法, 该方法在支持域内引入最小截平方法代替最小二乘法, 在所有节点当中选出剔除异常值的最优节点组合, 确定局部拟合系数.该方法不需要人为地分配权重或设定阈值, 可避免主观操作带来的影响.数值模拟和实验数据处理表明, 移动最小截平方法能有效地处理测量数据中的粗大误差, 拟合结果明显优于移动最小二乘法, 具有良好的拟合精度和鲁棒性.
关键词：曲线曲面拟合粗大误差移动最小二乘法最小截平方法局部拟合
Curve and Surface Fitting Algorithm for Measurement Data
GU Tian-qi, LUO Zu-de, HU Chen-jie, LIN Shu-wen
College of Mechanical Engineering & Automation, Fuzhou University, Fuzhou 350116, China
Corresponding author: GU Tian-qi, E-mail: tqgu2014@fzu.edu.cn.

Abstract: The moving least squares (MLS) method is widely used in curve and surface fitting due to its good approximation performance. However, the fitting accuracy is extremely unstable when processing data with gross error.In order to reduce the effect of gross error on the fitting accuracy, a moving least trimmed squares (MLTS)method was proposed. In this method, the least trimmed square (LTS) method was introduced in the influence domain to replace the least square (LS) method, and the optimal group of nodes without abnormal data was selected among all the nodes to determine the local fitting coefficient.Assigning weights or setting threshold values artificially is unnecessary, which avoids the influence of subjective operations. Numerical simulation and experimental data processing showed that the gross error of measurement data can be handled effectively, and the fitting results of the MLTS method are better than those of the MLS method, which has good fitting accuracy and robustness.
Key words: curve and surface fittinggross errormoving least squares(MLS)least trimmed square (LTS)local fitting
无网格方法由于良好的逼近性能被广泛应用于各个工程领域, 其主要算法有无单元伽辽金法(EFG)^[1]、径向基函数法(RBF)^[2]、再生核粒子法(RKPM)^[3]、移动最小二乘法(MLS)等.1981年, Lancaster等^[4]提出移动最小二乘法(moving least squares, MLS), 并将其应用于曲面拟合, 它与传统的最小二乘法(least squares, LS)通过完备多项式来建立拟合函数不同, MLS的拟合函数由基函数和系数向量构成.在移动最小二乘法的基础上, 很多****对它进行了改进, 如程玉民等^[5-6]提出对向量函数逼近的复变量移动最小二乘法用于解决力学问题; 崔小曼等^[7]通过引入正则化, 避免了病态方程组的形成; Wang等^[8]提出改进的正则化插值移动最小二乘法, 避免了奇异矩阵的形成, 解决了难以施加边界条件的问题; Wang等^[9]提出一种增广移动最小二乘法, 提高了移动最小二乘法在拟合中的近似性能.
然而, 测量数据不可避免地会出现一些粗大误差^[10], 在对这些数据进行拟合重构时, 这些粗大误差会对拟合产生较大影响, 使用传统的MLS拟合会造成粗大误差周围的拟合曲线产生较大偏离.目前剔除粗大误差的方法主要是设定阈值, 如朱广堂等^[11]提出通过计算支持域内每个节点的曲率, 设定一个曲率阈值, 比较曲率与阈值的大小去除粗大误差, 这种方法设定的阈值需要与各点的曲率大小相比较, 但很多曲线曲率变化很大, 设定一个合适的阈值较为困难; 李睿等^[12]通过计算节点的残差并且逐个与其2倍标准偏差相比较, 多次进行这样的操作达到去除粗大误差的目的, 这种方法可能剔除的点较多造成重构的曲线曲面失真; Amir等^[13]通过给定的函数进行拟合得到试函数, 在各节点处计算差值, 如果差值大于设定的阈值则剔除这个点, 但事实上大多数情况下给定函数都是未知的.此外, Fleishman等^[14]基于一种粗大误差检测的鲁棒统计方法——前向搜索范式, 对粗大误差进行处理.
最小截平方法(least trimmed squares, LTS)^[15]是一种比较稳健的估计方法, 是在最小二乘法(least square, LS)的基础上改进的, 能有效剔除粗大误差.该方法具有良好的鲁棒性^[16-17], 崩溃值^[18]超过了50%.最小截平方法已在很多领域中使用, 如数值估计^[19]、图像处理^[20]、甚至卫星导航领域^[21].然而, LTS也继承了LS的缺点, 是一种全域拟合算法, 拟合的曲线无法实现局部逼近.为了剔除数据中的粗大误差, 并使拟合曲线具有局部逼近功能, 本文提出一种移动最小截平方法(moving least trimmed square, MLTS), 它在MLS的支持域中引入最小截平方法代替最小二乘法, 在支持域的所有节点当中选出不包含异常值的最优节点组合得到局部拟合系数.该方法能有效地处理测量数据中的粗大误差, 不需要人为地分配权重或设定阈值, 可避免主观操作带来的影响.
1 MLS算法1.1 拟合原理MLS在支持域中应用加权最小二乘法对所有节点进行拟合, 在每个支持域中进行这样的操作完成全局拟合, 是加权和分段最小二乘的组合, 对于曲线曲面重构具有高精度的特点^[22].在MLS的每个支持域当中构造拟合函数f(x):

(1)

式中: p(x)=[p₁(x), p₂(x), …, p_m(x)]^T为基函数; a(x)=[a₁(x), a₂(x), …, a_m(x)] T为待求系数; p(x)为完备多项式, 一般选择
线性基: p(x)=[1, x, y]^T, m=3;
二次基: a(x)=[1, x, y, x², xy, y²]^T, m=6.
假设有n个离散点, x=[x₁, x₂, …, x_n], y=[y₁, y₂, …, y_n], 在支持域内进行加权最小二乘, 以节点加权残差平方和为目标函数对系数向量a(x)进行求解, 表示为

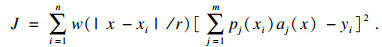(2)

写成矩阵形式为

(3)

式中: u=y^T; r为支持域的半径; w(|x－x_i|/r)=w_i(s)表示的是节点x_i的权值; x为支持域的中点, 支持域随着x的移动而移动.这样, 求取系数矩阵转化为式(2)的最小值问题, 令J对a(x)求导:

(4)

解得

(5)

其中:

(6)

(7)

(8)

(9)

将系数矩阵(5)代入拟合函数(1), 得到

(10)

1.2 权函数介绍权函数w(s)在拟合中起到非常重要的作用, w(s)的值随着s的增大而减小.如图 1所示，当离散点在支持域外时权值为0, 在区间[0, 1]上w(s)≥0并具有连续性, 这是拟合的曲线曲面具有局部逼近性质的关键.
图 1(Fig. 1)

图 1 紧支性权函数Fig.1 Weight function with compact support

权函数的选择有很多, 如样条权函数、高斯权函数、指数权函数等.本文选用指数权函数:

(11)

式中g的值可根据逼近的程度来选择, 其函数曲线如图 2所示.
图 2(Fig. 2)

图 2 指数权函数Fig.2 Exponential weight function

2 MLTS算法原理本文在MLS算法的支持域内引入LTS算法确定最优局部拟合系数, 提出新的曲线曲面拟合算法——MLTS算法, 其原理如图 3所示, 局部拟合步骤如下:
图 3(Fig. 3)

图 3 MLTS算法原理Fig.3 Principle of MLTS algorithm

1) 在某个支持域中, 离散数据的样本规模为N, 在这个样本中抽取k+1(k+1 < N)点的节点组合, 则可以抽取的不同节点组合的个数为C_N^k+1;
2) 对每个节点组合用LS进行拟合得到拟合系数X_i(i=1, 2, …, C_N^k+1);
3) 将各节点组合得到的拟合系数代入总样本中, 求取各点残差平方, 并按照升序排列: 0≤d₁²≤d₂²≤…≤d_N²;
4) 设定截取常数h=int[(N+k+1)/2], 选择升序排列的前h进行求和, 并得出局部拟合的目标值，

(12)

5) 选择X_opt作为该支持域的拟合回归系数.
选取回归系数的依据是: 通过截取前h项残差平方求和, 排除后面(N-h)可能包含粗大误差的残差较大项, 选择前h项残差平方和最小的节点组合重构得到的回归系数a(x).通过这样选出的节点组合得出的拟合系数能有效减少粗大误差对拟合的影响.
3 MLTS算法验证3.1 数值模拟评价流程通过模拟数据和实验数据验证MLTS算法的有效性, 其计算过程如图 4所示.
图 4(Fig. 4)

图 4 评价流程Fig.4 Evaluation process

采用拟合数据与函数模型生成的数据误差绝对值之和s与均方根RMS作为拟合精度的评价标准:

(13)

(14)

式中: n为离散点的个数; y_2i与y_0i分别为拟合数据和理论数据.
3.2 模拟数据验证案例1 ?曲线拟合

(15)

式中, c=1/1 038, l=－1.3, 获取均匀分布的离散点(x_0i, y_0i), 在数据上添加服从正态分布、期望值为0的随机误差和异常值(0, Δy_0i)，得到模拟数据(x_1i, y_1i)如图 5所示, Δy_0i分布在0.08~0.2之间.支持域半径r=x_t×0.4/10, 其中x_t=max(x₀)-min(x₀).MLTS和MLS算法拟合所得到的s和RMS如表 1所示, 拟合曲线如图 5所示, 拟合误差如图 6所示.
图 5(Fig. 5)

图 5 曲线拟合对比Fig.5 Comparison of curve fitting

表 1(Table 1)

表 1 曲线拟合误差对比Table 1 Comparison of curve fitting errors 标准差 s RMS x，y z MLS MLTS MLS MLTS 0.000 001 0.001 0.362 378 0.032 152 0.011 807 0.000 659 0.000 01 0.001 0.361 491 0.032 905 0.0117 54 0.000 677 0.000 1 0.001 0.359 541 0.0316 88 0.011 757 0.000 650 0.001 0.001 0.361 195 0.031 089 0.011 764 0.000 637 0.001 0.000 1 0.348 891 0.003 223 0.011 746 0.000 068 0.001 0.000 01 0.347 772 0.000 565 0.011 744 0.000 012 0.001 0.000 001 0.347 76 0.000 451 0.011 744 0.000 010

表 1 曲线拟合误差对比 Table 1 Comparison of curve fitting errors

图 6(Fig. 6)

图 6 曲线拟合误差对比Fig.6 Comparison of curve fitting errors

由表 1和图 6可知, 移动最小截平方法能够有效地削减粗大误差对曲线拟合的影响.MLS拟合的曲线在靠近粗大误差时都会产生较大偏离, 因此, 即使只存在少数几个异常值, 都会对算法的拟合精度产生较大的影响.而MLTS算法能够自动消除粗大误差的负面影响, 具有更高的拟合精度.
案例2 ?曲面拟合

(16)

如式(16)所示, 在区域Ω=[-1, 1]×[-1, 1]上选取1 089个均匀分布的离散点, 依照案例1的方式添加随机误差和粗大误差(0, 0, Δz_0i), 获得模拟数据(x_1i, y_1i, z_1i)如图 7所示, Δz_0i分布在0.13~0.16之间.支持域半径r=x_t×0.4/10, 其中x_t=max(x₀)+max(y₀).分别采用两种算法进行拟合, 得到s与RMS如表 2所示, MLTS拟合的曲面和误差见图 8和图 9, MLS拟合得到的曲面和误差见图 10和图 11.
图 7(Fig. 7)

图 7 曲面拟合仿真离散数据Fig.7 The simulated discrete data for surface fitting

表 2(Table 2)

表 2 曲面拟合误差对比Table 2 Comparison of surface fitting errors 标准差 s RMS x, y z MLS MLTS MLS MLTS 0.000 001 0.001 1.622 295 0.778 644 0.005 185 0.000 589 0.000 01 0.001 1.617 13 0.797 249 0.005 161 0.000 604 0.000 1 0.001 1.609 724 0.792 644 0.005 174 0.000 59 0.001 0.001 1.593 025 0.769 888 0.005 111 0.000 587 0.001 0.000 1 0.921 488 0.313 255 0.005 190 0.000 235 0.001 0.000 01 0.900 830 0.350 780 0.005 065 0.000 260 0.001 0.000 001 0.863 265 0.301 043 0.005 051 0.000 218

表 2 曲面拟合误差对比 Table 2 Comparison of surface fitting errors

图 8(Fig. 8)

图 8 MLTS拟合曲面Fig.8 Fitting surface of MLTS

图 9(Fig. 9)

图 9 MLTS拟合误差Fig.9 Fitting errors of MLTS

图 10(Fig. 10)

图 10 MLS拟合曲面Fig.10 The fitting surface of MLS

图 11(Fig. 11)

图 11 MLS拟合误差Fig.11 Fitting errors of MLS

由拟合结果可知, 由于移动最小二乘法具有良好的逼近功能, 因此受粗大误差影响导致周围拟合结果不稳定；而移动最小截平方法通过剔除异常值的最优节点组合确定局部拟合系数, 克服了移动最小二乘法对粗大误差敏感的缺点, 实现曲线曲面的稳健拟合.
3.3 实验数据验证为进一步验证MLTS算法的可靠性, 通过三坐标测量机测量标准圆柱获取廓线测量数据, 标准圆柱的标定半径为40.184 0 mm, 将得到的测量数据分别采用MLTS和MLS算法进行拟合, 然后对两种算法的拟合数据用最小二乘方法的圆参数回归算法进行处理, 得到回归半径R.
图 12为三坐标测量机测量标准圆柱的实验, 图 13为三坐标测量机原理简图, 使用LK-G150激光位移传感器对水平标准圆柱表面廓线进行测量, 测量点数为819.
图 12(Fig. 12)

图 12 三坐标测量机测量标准圆柱实验Fig.12 Experiment of measuring standard cylinder with CMM

图 13(Fig. 13)

图 13 三坐标测量机测量示意图Fig.13 Measuring schematic diagram of CMM

两种算法处理测量数据获得的回归半径R如表 3所示, MLTS算法拟合曲线如图 14所示.
表 3(Table 3)

表 3 回归半径对比Table 3 Comparison of regression radius 拟合方法 R/mm 移动最小二乘法 40.017 3 移动最小截平方法 40.025 9

表 3 回归半径对比 Table 3 Comparison of regression radius

图 14(Fig. 14)

图 14 MLTS拟合曲线Fig.14 Fitting curve of MLTS

由表 3可知, 移动最小截平方法获得的拟合曲线在经过回归计算后, 计算得到的回归半径更加接近标定半径, 这说明移动最小截平方法处理后的数据曲线更能真实地反映圆柱的实际廓形.验证算法3个案例的处理结果表明, 提出的移动最小截平方法结合了移动最小二乘法和最小截平方法的优点, 能有效地处理测量数据中的粗大误差, 不需要人为地分配权重或设定阈值, 可避免主观操作带来的影响.
4 结语本文在移动最小二乘法的每个支持域中引入最小截平方法代替最小二乘法, 在支持域中选择最优节点组合得到局部拟合系数, 构造移动最小截平方法.为验证算法的有效性, 在数值模拟验证中对存在有多个粗大误差的数据进行处理, 结果表明移动最小截平方法能够有效地处理数据中的粗大误差, 精度较移动最小二乘法有极大提高.从3个案例中可以看出移动最小截平方法既具有移动最小二乘法局部逼近功能, 又具有剔除粗大误差的功能, 削减了粗大误差对拟合的影响, 具有良好的稳健性.
参考文献

[1]	崔青玲, 李长生, 刘相华, 等. 模拟平板轧制的新方法——无网格伽辽金法[J]. 东北大学学报(自然科学版), 2005, 26(5): 463-466. (Cui Qing-ling, Li Chang-sheng, Liu Xiang-hua, et al. A new method to simulation of plate rolling: element-free Galerkin method (EFGM)[J]. Journal of Northeastern University(Natural Science), 2005, 26(5): 463-466.)
[2]	Mirzaei D. A greedy meshless local Petrov-Galerkin method based on radial basis functions[J]. Numerical Methods for Partial Differential Equations, 2016, 32(3): 847-861. DOI:10.1002/num.22031
[3]	Liu H S, Xing Z W, Yang Y Y. Simulation of sheet metal forming process using reproducing kernel particle method[J]. International Journal for Numerical Methods in Biomedical Engineering, 2010, 26(11): 1462-1476. DOI:10.1002/cnm.1229
[4]	Lancaster P, Salkauskas K. Surface generated by moving least square methods[J]. Mathematics of Computation, 1981, 37: 141-158. DOI:10.1090/S0025-5718-1981-0616367-1
[5]	程玉民, 李九红. 弹性力学的复变量无网格方法[J]. 物理学报, 2005, 54(10): 4463-4471. (Cheng Yu-min, Li Jiu-hong. A meshless method with complex variables for elasticity[J]. Acta Physica Sinica, 2005, 54(10): 4463-4471.)
[6]	Cheng Y M, Li J H. A complex variable meshless method for fracture problems[J]. Science China Physics, Mechanics & Astronomy, 2006, 49(1): 46-59.
[7]	崔小曼, 于凤芹. 利用Tikhonov正则化改进移动最小二乘的图像变形算法[J]. 激光与光电子学进展, 2019, 56(23): 100-106. (Cui Xiao-man, Yu Feng-qin. Moving least squares based image deformation algorithm improved with Tikhonov regularization[J]. Laser and Optoelectronics Progress, 2019, 56(23): 100-106.)
[8]	Wang Q, Zhou W, Cheng Y G, et al. Regularized moving least-square method and regularized improved interpolating moving least-square method with nonsingular moment matrices[J]. Applied Mathematics and Computation, 2018, 325: 120-145. DOI:10.1016/j.amc.2017.12.017
[9]	Wang F J, Qu W Z, Li X L. Augmented moving least squares approximation using fundamental solutions[J]. Engineering Analysis with Boundary Elements, 2020, 115: 10-20. DOI:10.1016/j.enganabound.2020.03.003
[10]	秦亚光, 罗周全, 汪伟, 等. 采空区三维激光扫描点云数据处理技术[J]. 东北大学学报(自然科学版), 2016, 37(11): 1635-1639. (Qin Ya-guang, Luo Zhou-quan, Wang Wei, et al. Cavity three-dimensional laser scanning point cloud data processing technology[J]. Journal of Northeastern University(Natural Science), 2016, 37(11): 1635-1639.)
[11]	朱广堂, 叶珉吕. 基于曲率特征的点云去噪及定量评价方法研究[J]. 测绘通报, 2019(6): 105-108. (Zhu Guang-tang, Ye Min-lyu. Research on the method of point cloud denoising based on curvature characteristics and quantitative evaluation[J]. Bulletin of Surveying and Mapping, 2019(6): 105-108.)
[12]	李睿, 林海荣, 吴小燕. 基于稳健移动最小二乘法的点云数据拟合[J]. 测绘与空间地理信息, 2017, 40(5): 122-124. (Li Rui, Lin Hai-rong, Wu Xiao-yan. Point cloud data fitting based on robust moving least square method[J]. Mapping and Spatial Geographic Information, 2017, 40(5): 122-124.)
[13]	Amir A, Levin D. Quasi-interpolation and outliers removal[J]. Numerical Algorithms, 2018, 78(3): 805-825. DOI:10.1007/s11075-017-0401-2
[14]	Fleishman S, Cohenor D, Silva C T, et al. Robust moving least-squares fitting with sharp features[J]. ACM Transactions on Graphics, 2005, 24(3): 544-552. DOI:10.1145/1073204.1073227
[15]	Mili L, Cheniae M G, Rousseeuw P J, et al. Robust state estimation of electric power systems[J]. IEEE Transactions on Circuits and Systems Irregular Papers, 1994, 41(5): 349-358. DOI:10.1109/81.296336
[16]	Torti F, Perrotta D, Atkinson A C, et al. Benchmark testing of algorithms for very robust regression: FS, LMS and LTS[J]. Computational Statistics & Data Analysis, 2012, 56(8): 2501-2512.
[17]	Beliakov G, Kelarev A V, Yearwood J, et al. Derivative-free optimization and neural networks for robust regression[J]. Optimization, 2012, 61(12): 1467-1490. DOI:10.1080/02331934.2012.674946
[18]	Mount D M, Netanyahu N S, Piatko C D, et al. A practical approximation algorithm for the LTS estimator[J]. Computational Statistics & Data Analysis, 2016, 99: 148-170.
[19]	Adedia D, Adebanji A, Labeodan M, et al. Ordinary least squares and robust estimators in linear regression: impacts of outliers, error and response contaminations[J]. British Journal of Mathematics & Computer Science, 2016, 13(4): 1-11.
[20]	Tong G W, Chen H Y, Liu S, et al. Memetic reconstruction algorithm for the ECT[J]. Iet Science Measurement & Technology, 2018, 12(7): 917-924.
[21]	Koch I E, Veronez M R, Silva R M, et al. Least trimmed squares estimator with redundancy constraint for outlier detection in GNSS networks[J]. Expert Systems with Applications, 2017, 88: 230-237. DOI:10.1016/j.eswa.2017.07.009
[22]	Zhang H Q, Guo C X, Su X F, et al. Measurement data fitting based on moving least squares method[J]. Mathematical Problems in Engineering, 2015(6): 1-10.