王新刚, 王超, 韩凯忠
东北大学 机械工程与自动化学院, 辽宁 沈阳 110819
收稿日期：2020-09-07
基金项目：中央高校基本科研业务费专项资金资助项目(N2023023)；北京卫星环境工程研究所CAST-BISEE项目(CAST-BISEE2019-019)；河北省自然科学基金资助项目(E2020501013)。
作者简介：王新刚(1979-)，男，黑龙江齐齐哈尔人，东北大学教授，博士生导师。

摘要：针对滚动轴承早期故障信号易受噪声等背景信息干扰难于提取故障特征的现象, 提出了将优化K值的变分模态分解(VMD)和粒子群优化算法(PSO)优化参数L, M的最大相关峭度解卷积(MCKD)相结合提取滚动轴承故障特征频率的方法.首先, 确定VMD中K值, 对信号进行分解后得到一系列模态分量; 然后利用EWK指标选择包含故障信息最多的有效模态分量进行后续分析, 利用优化的MCKD对其进行增强; 最后对增强信号进行包络解调提取故障特征频率, 验证所提方法的有效性.仿真和实验表明该方法可以精确地提取出轴承故障信号中的特征频率, 实现故障诊断.
关键词：VMD的K值优化EWK指标粒子群优化最大相关峭度解卷积(MCKD)故障诊断
Early Fault Diagnosis Method of Rolling Bearings Based on Optimization of VMD and MCKD
WANG Xin-gang, WANG Chao, HAN Kai-zhong
School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China
Corresponding author: WANG Xin-gang, E-mail: xgwang@neuq.edu.cn.

Abstract: Considering the phenomenon that the early fault signals of rolling bearings are easily interfered by noise and background information and it is difficult to extract fault characteristics, a method combining K value optimization of variational mode decomposition (VMD) and particle swarm optimization (PSO) optimizing the maximum correlated kurtosis deconvolution (MCKD) parameters L, M was proposed to extract the fault characteristic frequency of rolling bearings. Firstly, the K value in VMD was calculated, and the signal was decomposed to obtain a series of modal components. EWK index was used to select the effective modal components that contain the most fault information for subsequent analysis and the optimized MCKD was used to enhance it. Finally, the enhanced signal was subjected to envelope demodulation to extract the fault characteristic frequency, which verified the effectiveness of the proposed method. Simulations and experiments showed that this method can accurately extract the fault characteristic frequency of the signal and realize fault diagnosis.
Key words: K value optimization of VMDEWK indexparticle swarm optimization (PSO)maximum correlated kurtosis deconvolution (MCKD)fault diagnosis
滚动轴承广泛应用于旋转机械中, 由于恶劣的工作条件导致其失效概率较高, 为保证设备安全运行对其进行早期故障诊断尤为重要^[1].滚动轴承局部出现故障时, 会在运行过程中产生周期性脉冲冲击、噪声等背景信息对信号造成污染, 对故障特征提取产生影响, 因此如何增强信号中的有用信息是亟待解决的问题^[2].
目前基于振动信号处理的故障诊断方法广泛应用, 如模态分解、信号解卷积等.经验模态分解(empirical mode decomposition, EMD)可以将信号分解为由高频到低频的一系列本征模态函数之和, 但容易出现模态混叠现象.2014年Dragomiretskiy等^[3]提出变分模态分解(variational modal decomposition, VMD)方法, 在使用VMD之前, 需设定模态分解数K, 若K值较小会出现欠分解，即原始信号信息缺失, 如果K值较大则会发生过分解.张建财等^[4]利用观察相邻模态中心频率是否接近的方法来确定K值, Deng等^[5]利用计算两相邻模态中心频率间关系来确定带宽傅里叶分解(bandwidth Fourier decomposition, BFD)中K的取值, 避免了人为观察造成的误差, 本文将其引入VMD算法来确定K的取值.
选取有效模态分量分析, 可以减少噪声的影响, 达到降噪的目的.滚动轴承发生故障时振动信号会出现冲击成分, 峭度值能够有效地反映信号中的冲击成分.但当冲击成分周期性地出现在振动信号中时, 峭度值则不能有效地对其进行描述, 本文结合相关系数与峭度准则, 引入EWK指标形成一种全面的评价准则提取有效分量.
最小熵解卷积(minimum entropy deconvolution, MED)方法于1978年提出, 目的是提取信号中的突变成分.McDonald等^[6]发现在进行故障特征提取时MED仅能解卷积出单个脉冲和虚假脉冲信号, 因此提出最大相关峭度解卷积(maximum correlated kurtosis deconvolution, MCKD)算法, 该算法可以从故障信号中解卷积出周期性的脉冲.虽然MCKD算法能突出淹没在噪声中的冲击成分, 但对于早期、微弱故障信号效果不明显.同时, MCKD算法中参数的设置对于故障诊断结果来说具有重要影响, 多个参数之间相互协调, MCKD算法才能够得到较好的结果.为此, 国内外相关研究人员对MCKD算法进行了一系列的研究和改进.杨斌等^[7]将ELMD算法、Wang等^[8]将CEEMD算法分别与MCKD算法相结合对信号进行分解后提取主要分量进行信号增强、包络解调得到故障特征频率, 实现故障诊断.Zhang等^[9]利用蚱蜢优化算法对MCKD算法进行参数优化, 得到最优(L, M)参数组合.Lyu等^[10]利用量子遗传算法对MCKD算法进行优化, 得到最优(L, T)组合.由于T可求, 本文以最小包络熵为目标函数优化L, M两参数.
本文首先对VMD分解过程中K值选择进行研究, 利用VMD算法对轴承振动信号进行分解, 选择EWK指标最大的分量为有效分量.用粒子群算法对MCKD算法进行参数寻优并对有效分量进行增强, 最后对增强信号进行包络提取轴承故障特征, 通过仿真和实验验证本文方法的有效性.
1 故障诊断算法及流程1.1 VMD中K值选取根据VMD原理, VMD的K值对分解结果有很大影响.如果K值过小, 会造成欠分解; 如果K值过大, 会造成过分解.为避免出现过分解、欠分解现象, 按照以下方法确定K值.
步骤1??给定最小模态数K=2.
步骤2??对输入信号进行VMD处理.
步骤3??根据式(1)判断是否存在过分解.如果满足式(1), 则表明至少有两个中心频率过近, 出现过分解.然后, 令K=K-1, 结束循环; 否则, 执行步骤4.

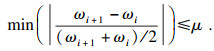(1)

式中: ω_i+1, ω_i为两相近中心频率; μ为常数.
步骤4??令K=K+1, 重复步骤2、步骤3.
可以看出, 模态数K是由中心频率的分布决定的, 常数μ来判断是否发生过分解, 根据文献[5], 本文设置μ=0.1.
1.2 EWK指标信号分解后, 峭度准则、相关性准则通常用来选取有效模态分量进行信号重构.峭度准则只考虑了冲击信号的分布密度, 而忽略了选择振幅大、分布分散的模态分量, 相关系数表达了模态分量与原信号的相关性, 但受噪声影响大.为了综合考虑, 引入有效加权峭度指标(efficient weighted kurtosis index, EWK)来评价模态分量, 如式(2)~式(3)所示^[11]:

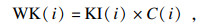(2)

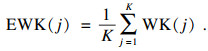(3)

式中: i, j=1~K；KI为各模态分量的峭度; C为各模态分量与原始信号的相关系数.
1.3 基于PSO的MCKD参数选择MCKD算法的根本是寻找一个FIR滤波器f(L), 使原始冲击信号的相关峭度最大, 从而恢复其所具有的特性, 达到增强信号的目的.
相关峭度的定义为

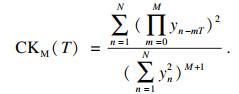(4)

为求得最大相关峭度, 即CK_M(T)最大, 令

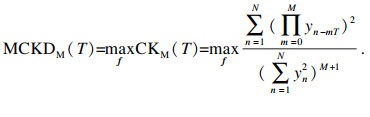(5)

式中: T为冲击信号的周期; M为位移数; f为滤波器向量, f =[f₁, f₂, …, f_L]^T，L为FIR滤波器的长度; y_n为冲击信号.
由式(5)可知算法有3个重要参数T, L, M, 并且已知其中f_s为采样频率, f_c为故障特征频率.因此, 可以通过PSO优化L, M两个参数来求解式(5).
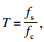
信号包络熵能够表示其稀疏性, 分解后, 模态分量中故障信息越多, 包络熵越小, 由此可以将求取包络熵最小值定为粒子群优化算法的目标函数, 包络熵计算公式^[12]见式(6):

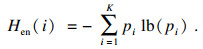(6)

式中: H_en(i)为每一个模态分量的包络熵; p_i是每个分量的归一化.
设定粒子群算法中学习因子c₁=c₂=2, 惯性权重ω=1, 种群规模N_s=30, 迭代次数N_iter=20, L的取值范围是[100, 500], M的取值范围是[1, 7].本文以求取有效分量包络熵最小值为目标函数对MCKD算法进行粒子群优化，求得最佳组合(L, M).
1.4 故障诊断流程本文方法流程图如图 1所示，具体步骤如下：
图 1(Fig. 1)

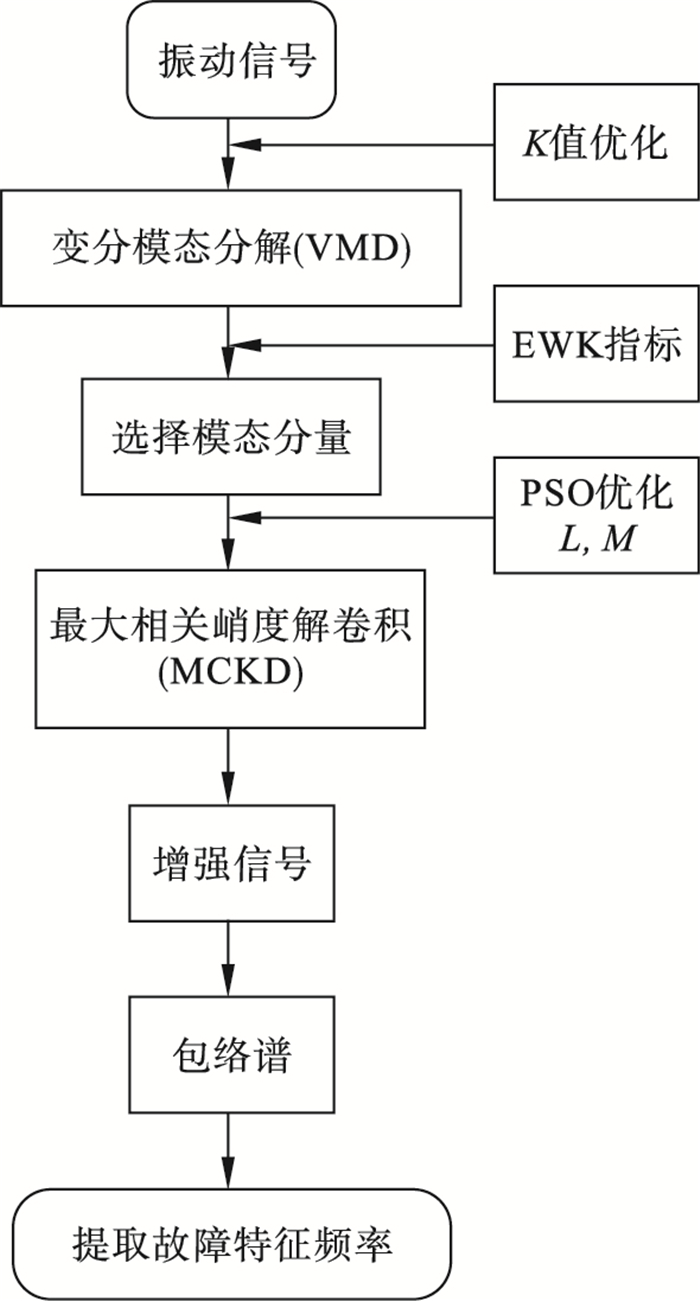图 1 滚动轴承早期故障诊断流程图Fig.1 Flow chart of early fault diagnosis of rolling bearings

1) 根据式(1)选择K, 对故障信号进行VMD分解, 得到一系列模态分量, 根据EWK指标选取有效分量.
2) 对选定模态分量进行MCKD增强, 用粒子群算法优化L, M两个参数.
3) 将增强信号进行包络解调, 观察有无故障特征频率, 达到故障诊断的目的.
2 仿真分析为验证本文方法是否有效, 利用滚动轴承故障模型模拟脉冲冲击信号, 并向其中加入白噪声模拟早期故障信号^[13], 仿真信号如式(7)所示:

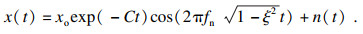(7)

式中: 位移常数x_o=5;衰减系数C=800;载波频率f_n=3 000 Hz; 阻尼系数ξ=0.1;t为采样时刻; n(t)为高斯白噪声.
设定冲击故障的周期T_s=0.01 s, 采样频率f_s=20 kHz, 采样点数N=4 096, 可以得出故障频率f_c=100 Hz.从仿真信号的时域波形图 2可以看出, 轴承发生故障时产生的冲击信号已完全被噪声淹没.表 1展示了不同K值对应的各模态中心频率.通过表 1可知, 当K=11时, 第10和第11模态中心频率接近, 且代入式(1)结果小于0.1, 由此可以推断产生过分解, 因此确定K=10.对仿真信号进行VMD分解(K=10, α=2 000).表 2中展示了各模态分量的EWK指标, 用粒子群优化的MCKD对EWK指标最大的IMF4进行信号增强, IMF4包络谱如图 3所示, 经计算T=200, 得到进化曲线如图 4所示, 在第4代求取最佳(L, M)组合, 其中L=413, M=7.进行滤波后对其进行包络得到图 5, 可以明显看出轴承故障周期冲击频率102.5 Hz(在误差允许范围内)及其倍频(200, 300, 400, 500 Hz等).仿真分析证明了本文方法适用于噪声干扰下的故障特征提取.
图 2(Fig. 2)

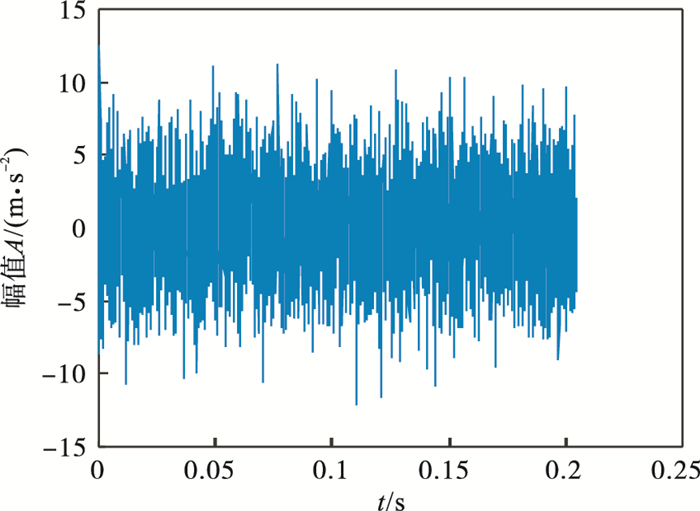图 2 仿真信号Fig.2 Simulation signal

表 1(Table 1)

表 1 不同K值对应的各模态中心频率Table 1 Center frequency of each mode corresponding to different K values K 中心频率/Hz 2 2 999.9 6 242.1 3 1 260.0 3 040.2 7 082.7 4 1 249.6 3 032.6 6 095.1 8 518.6 5 1 203.3 2 976.6 4 308.3 6 294.8 8 591.3 6 568.2 1 933.4 3 064.2 5 083.4 6 978.9 8 767.2 7 546.6 1 864.8 3 015.5 4 263.2 6 029.2 7 508.3 9 086.7 8 537.6 1 836.4 2 996.0 4 088.6 5 460.0 6 822.6 8 138.9 9 391.1 9 402.5 1 323.5 2 253.9 3 054.7 4 197.8 5 667.1 6 962.7 8 199.9 9 419.5 10 397.4 1 307.8 2 218.8 3 025.8 3 981.1 5 083.8 6 170.2 7 252.6 8 382.2 9 494.5 11 396.5 1 304.9 2 212.5 3 020.6 3 945.5 5 013.2 6 048.8 6 986.5 7 885.3 8 716.5 9 607.0

表 1 不同K值对应的各模态中心频率 Table 1 Center frequency of each mode corresponding to different K values

表 2(Table 2)

表 2 各模态分量的EWK值Table 2 EWK value of each modal component 变量 IMF1 IMF2 IMF3 IMF4 IMF5 IMF6 IMF7 IMF8 IMF9 IMF10 相关系数 0.303 3 0.328 4 0.349 5 0.427 1 0.360 5 0.349 6 0.354 3 0.353 3 0.352 1 0.318 7 峭度 3.260 1 3.009 4 3.160 4 3.421 0 3.122 5 3.224 8 2.816 7 3.085 4 2.765 0 2.900 9 EWK -0.090 7 -0.091 2 0.025 1 0.381 6 0.046 2 0.047 9 -0.065 6 0.010 6 -0.109 1 -0.155 0

表 2 各模态分量的EWK值 Table 2 EWK value of each modal component

图 3(Fig. 3)

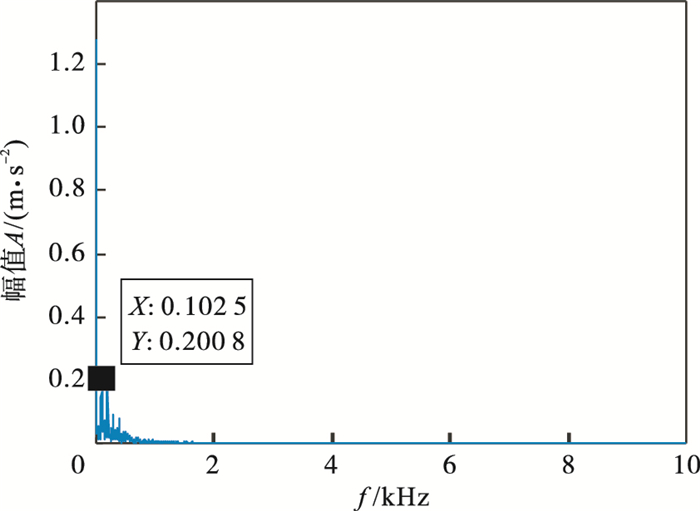图 3 IMF4包络谱Fig.3 Envelope spectrum of IMF4

图 4(Fig. 4)

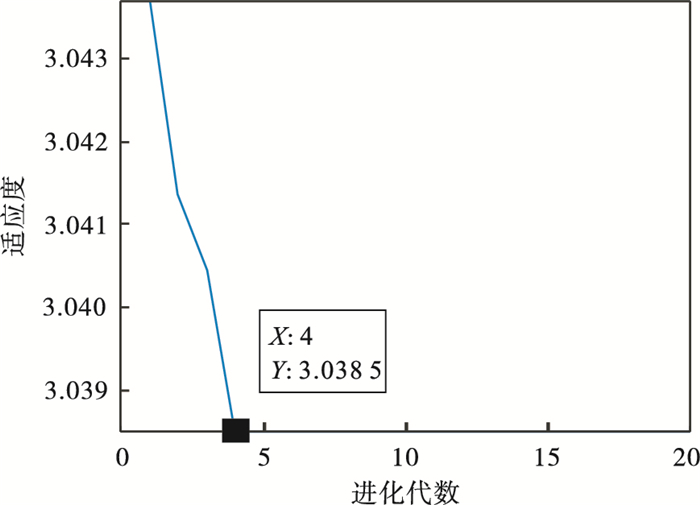图 4 粒子群优化图Fig.4 Diagram of particle swarm optimization

图 5(Fig. 5)

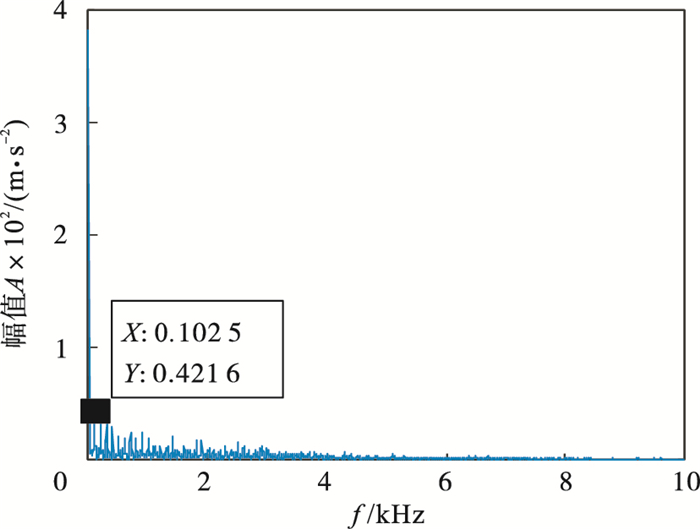图 5 增强后信号包络谱Fig.5 Envelope spectrum of enhanced signal

3 应用实例以凯斯西储大学电气工程实验室中不同故障类型的振动信号^[14]为对象, 已知实验选用了型号为6205-2RS JEM的SKF深沟球轴承, 通过人为放电操作引入故障直径0.178 mm的故障点, 滚动体数目N=9, 滚动体直径d=7.94 mm, 轴承节径D=39.04 mm, 接触角θ=0, 采样频率为12 kHz, 电机负荷为0(电机转速n=1 797 r/min).本文采用早期振动信号进行研究.已知故障频率计算如式(8)~式(11)所示:

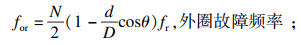(8)

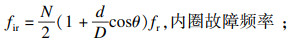(9)

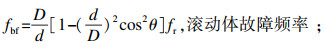(10)

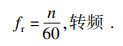(11)

经理论计算可得f_or=107.36 Hz, f_ir= 162.19 Hz, f_bf=141.88 Hz, f_r=29.95 Hz.
3.1 内圈故障诊断图 6为滚动轴承内圈故障信号, 由于噪声干扰, 冲击不明显.表 3展示了不同K值对应的各模态中心频率.通过表 3可知, 当K=8时, 第6和第7模态中心频率接近, 且式(1)计算结果小于0.1, 由此可以推断产生过分解, 因此确定K=7.对内圈故障信号进行VMD分解(K=7, α=2 000), 得到各模态分量的EWK指标见表 4, 选取EWK指标最大的模态分量IMF5进行增强, IMF5包络谱见图 7.经计算T=74, 得到的进化曲线如图 8所示, 在第3代求取最佳(L, M)组合, 其中L=427, M=5.增强后的信号包络谱如图 9所示, 可以明显看出故障特征频率164.1 Hz(在误差允许范围内)及其倍频.该方法明显提高了故障诊断的精确性.
图 6(Fig. 6)

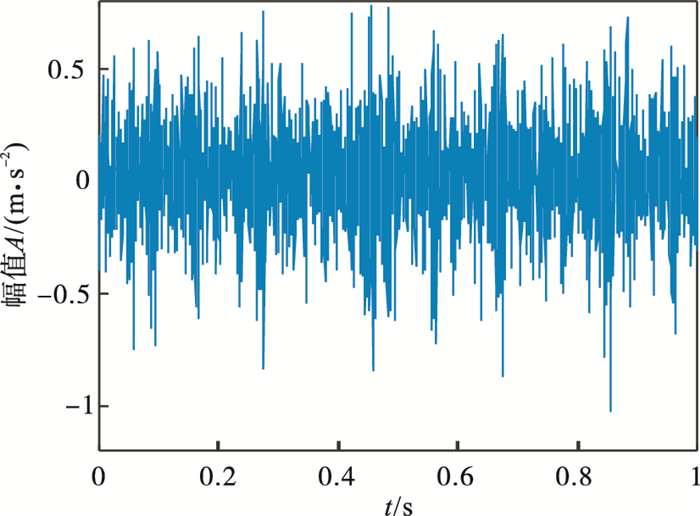图 6 内圈故障信号时域图Fig.6 Time domain diagram of inner ring fault signal

表 3(Table 3)

表 3 不同K值对应的各模态中心频率Table 3 Center frequency of each mode corresponding to different K values K 中心频率/Hz 2 1 454.2 1 956.2 3 1 454.2 1 955.5 4 140.0 4 77.1 1 474.2 2 514.3 4 141.3 5 68.1 1 456.7 1 956.0 4 136.6 5 158.3 6 65.0 1 456.3 1 951.0 2 852.4 4 140.4 5 161.0 7 38.8 1 111.5 1 474.1 1 953.9 2 856.2 4 141.7 5 161.4 8 12.6 658.8 1 462.9 1 952.5 2 854.0 4 124.5 4 413.5 5 172.1

表 3 不同K值对应的各模态中心频率 Table 3 Center frequency of each mode corresponding to different K values

表 4(Table 4)

表 4 各模态分量的EWK值Table 4 EWK value of each modal component 变量 IMF1 IMF2 IMF3 IMF4 IMF5 IMF6 IMF7 相关系数 0.266 3 0.397 2 0.594 4 0.490 2 0.323 9 0.323 7 0.168 2 峭度 3.971 6 2.454 5 2.404 5 2.610 5 5.630 1 2.275 6 2.372 8 EWK -0.042 6 -0.125 1 0.329 1 0.179 5 0.723 7 -0.363 6 -0.700 9

表 4 各模态分量的EWK值 Table 4 EWK value of each modal component

图 7(Fig. 7)

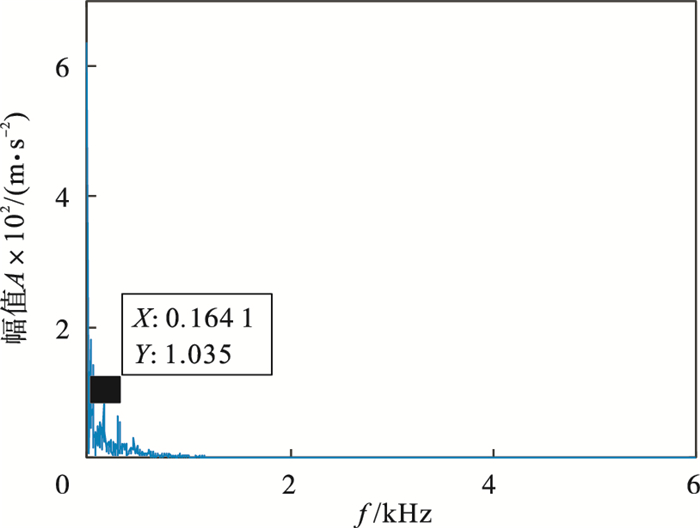图 7 IMF5包络谱Fig.7 Envelope spectrum of IMF5

图 8(Fig. 8)

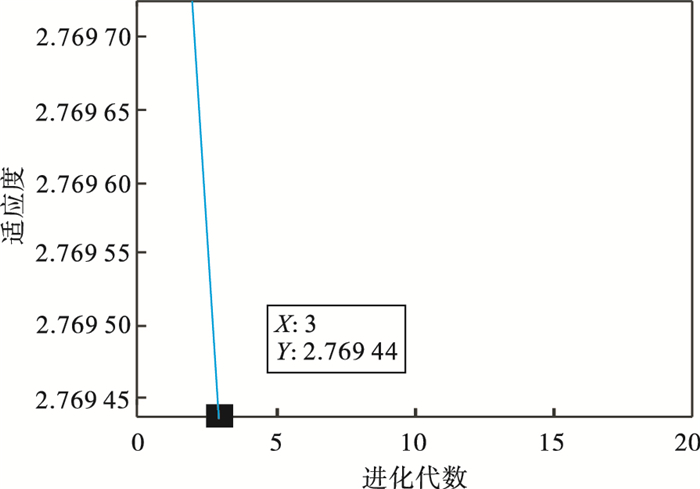图 8 粒子群优化图Fig.8 Diagram of particle swarm optimization

图 9(Fig. 9)

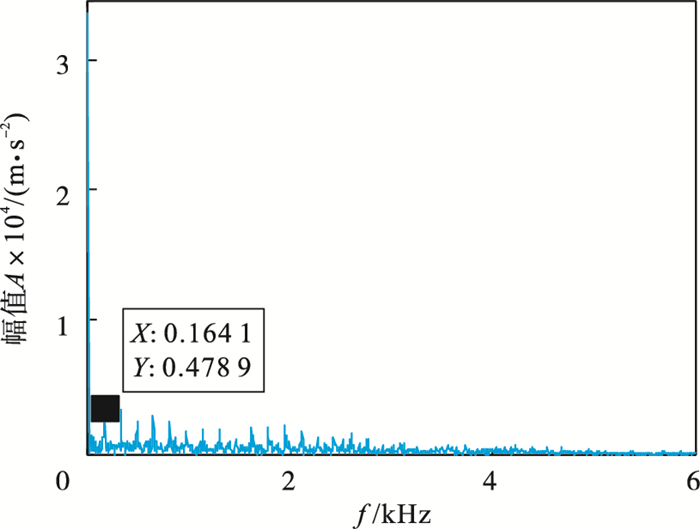图 9 增强后信号包络谱Fig.9 Envelope spectrum of enhanced signal

3.2 外圈故障诊断图 10为滚动轴承外圈故障振动信号的时域图, 由于噪声较多, 信号中冲击不明显.表 5展示了不同K值对应的各模态中心频率.通过表 5可知, 当K=8时, 第6和第7模态中心频率接近, 且式(1)计算结果小于0.1, 由此可以推断产生过分解, 因此确定K=7.对其进行VMD分解(K=7, α=2 000), 得到各模态分量的峭度值以及与原始信号的相关系数, 见表 6.选取EWK指标最大的模态分量(IMF5)进行信号增强, IMF5包络谱如图 11所示, 经计算T=112, 得到的进化曲线见图 12, 在第6代求取最佳(L, M)组合, 其中L=119, M=2.故障信号增强后包络解调得到图 13, 可以明显看出外圈故障特征频率105.5 Hz(在误差允许范围内)及其倍频成分.
图 10(Fig. 10)

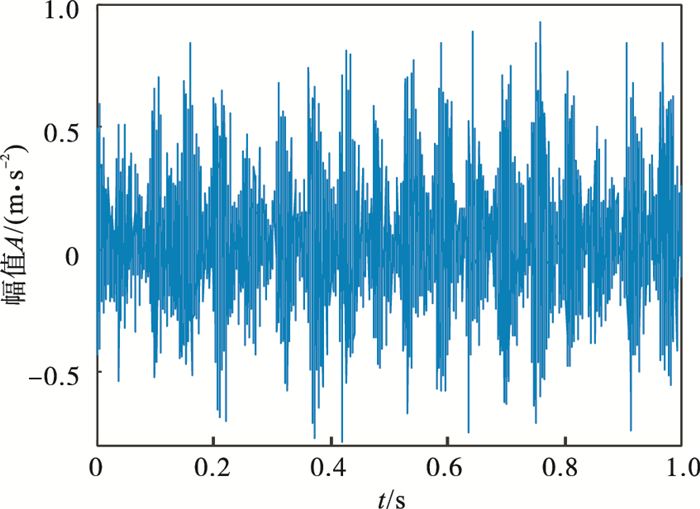图 10 外圈故障信号时域图Fig.10 Time domain diagram of outer ring fault signal

表 5(Table 5)

表 5 不同K值对应的各模态中心频率Table 5 Center frequency of each mode corresponding to different K values K 中心频率/Hz 2 37.2 3 337.2 3 34.8 1 947.6 3 338.4 4 33.6 1 941.6 3 334.8 4 129.2 5 19.2 786.0 2 860.8 3 343.2 4 129.2 6 4.09 440.4 1 942.8 3 333.6 4 108.8 5 168.4 7 3.82 439.2 1 922.4 2 865.6 3 339.6 4 111.2 5 168.4 8 3.77 438.0 1 921.2 2 864.4 3 339.6 4 077.6 4 486.8 5 174.4

表 5 不同K值对应的各模态中心频率 Table 5 Center frequency of each mode corresponding to different K values

表 6(Table 6)

表 6 各模态分量的EWK值Table 6 EWK value of each modal component 变量 IMF1 IMF2 IMF3 IMF4 IMF5 IMF6 IMF7 相关系数 0.123 5 0.178 0 0.204 6 0.315 8 0.738 6 0.385 0 0.416 1 峭度 4.315 0 2.572 7 5.148 4 3.716 6 3.664 8 2.801 1 4.080 2 EWK -0.710 1 -0.785 1 -0.189 4 -0.069 4 1.463 9 -0.164 7 0.454 8

表 6 各模态分量的EWK值 Table 6 EWK value of each modal component

图 11(Fig. 11)

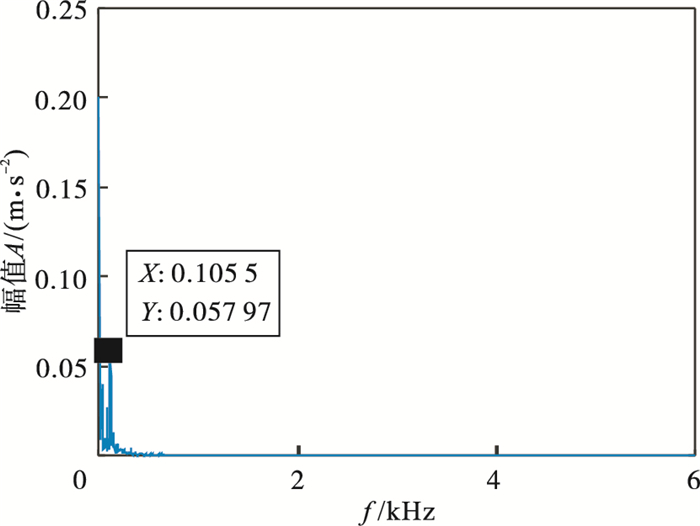图 11 IMF5包络谱Fig.11 Envelope spectrum of IMF5

图 12(Fig. 12)

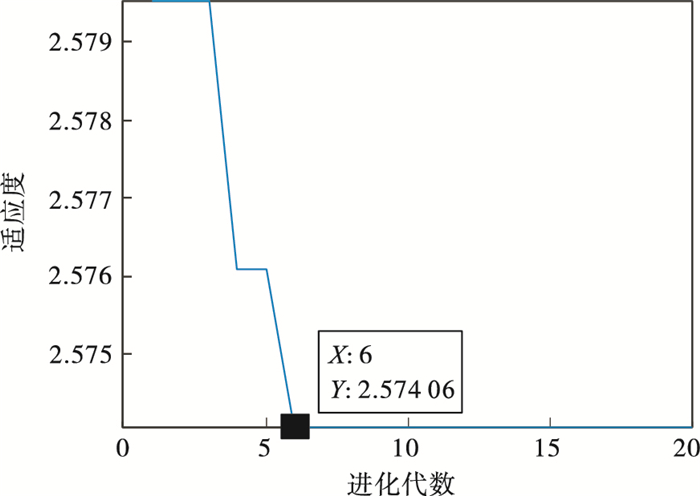图 12 粒子群优化图Fig.12 Diagram of particle swarm optimization

图 13(Fig. 13)

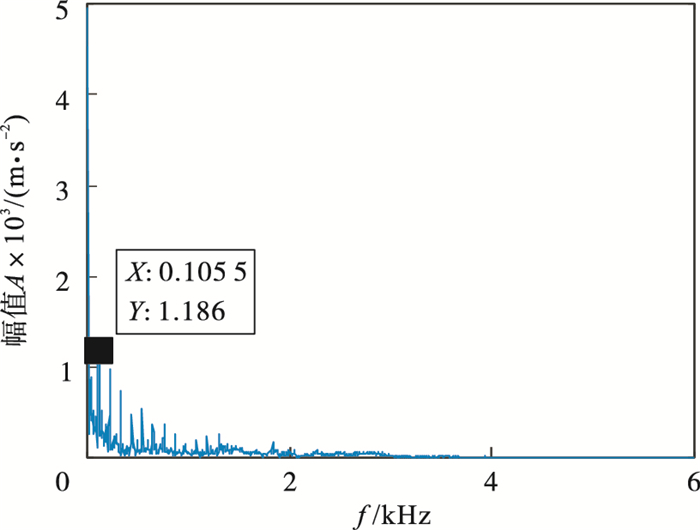图 13 增强后信号包络谱Fig.13 Envelope spectrum of enhanced signal

3.3 滚动体故障诊断图 14为轴承滚动体故障信号, 由于噪声较多，其中冲击不明显.表 7展示了不同K值对应的各模态中心频率.通过表 7可知, 当K=5时, 第4和第5模态中心频率接近, 且式(1)计算结果小于0.1, 由此可以推断产生过分解, 因此确定K=4.对其进行VMD分解(K=4, α=2 000).各模态峭度值、相关系数、EWK指标见表 8, 选取EWK指标最大的模态分量(IMF4)进行信号增强, IMF4包络谱如图 15所示.经计算T=85, 得到的进化曲线如图 16所示, 在第5代求取最佳(L, M)组合, 其中L=362, M=3.增强后的信号包络谱如图 17所示, 可以明显看出滚动体故障特征频率140.6 Hz(在误差允许范围内)及其倍频.
图 14(Fig. 14)

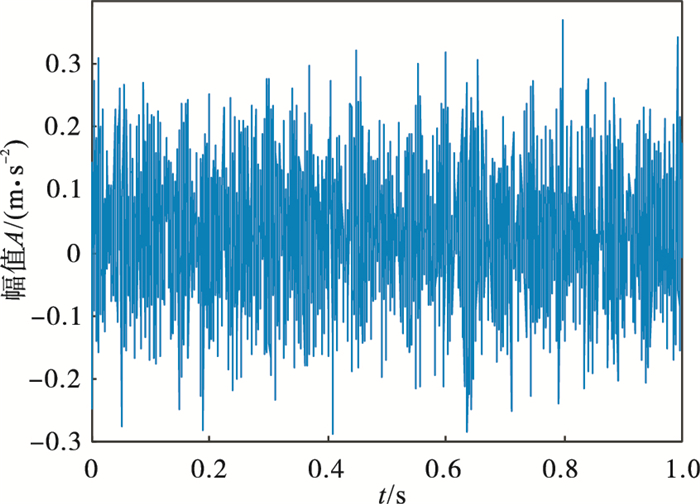图 14 滚动体故障信号时域图Fig.14 Time domain diagram of rolling element fault signal

表 7(Table 7)

表 7 不同K值对应的各模态中心频率Table 7 Center frequency of each mode corresponding to different K values K 中心频率/Hz 2 26.1 4 114.3 3 25.2 2 536.6 4 114.8 4 9.4 778.2 3 423.7 4 117.9 5 9.2 777.1 2 540.2 4 106.8 4 249.2

表 7 不同K值对应的各模态中心频率 Table 7 Center frequency of each mode corresponding to different K values

表 8(Table 8)

表 8 各模态分量的EWK值Table 8 EWK value of each modal component 变量 IMF1 IMF2 IMF3 IMF4 相关系数 0.254 2 0.454 8 0.294 0 0.761 0 峭度 2.678 5 3.434 8 2.654 7 2.093 7 EWK -0.473 2 0.407 8 -0.373 6 0.439 0

表 8 各模态分量的EWK值 Table 8 EWK value of each modal component

图 15(Fig. 15)

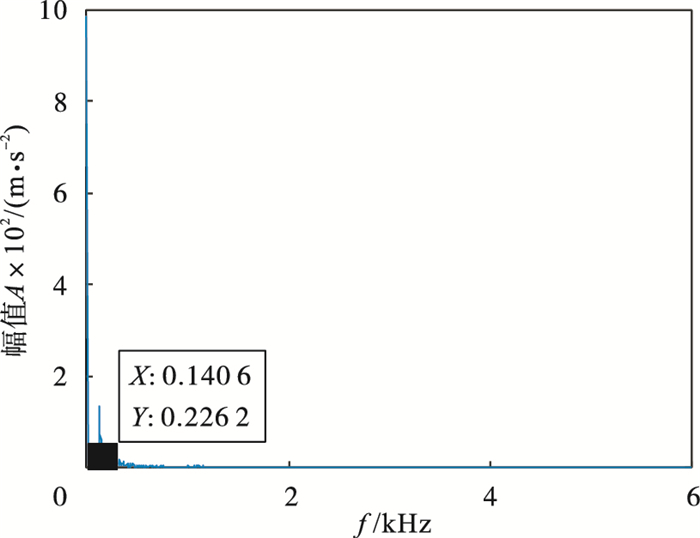图 15 IMF4包络谱Fig.15 Envelope spectrum of IMF4

图 16(Fig. 16)

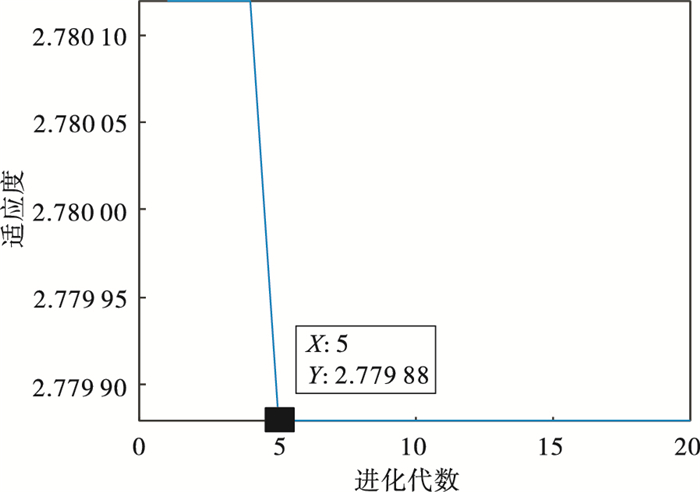图 16 粒子群优化图Fig.16 Diagram of particle swarm optimization

图 17(Fig. 17)

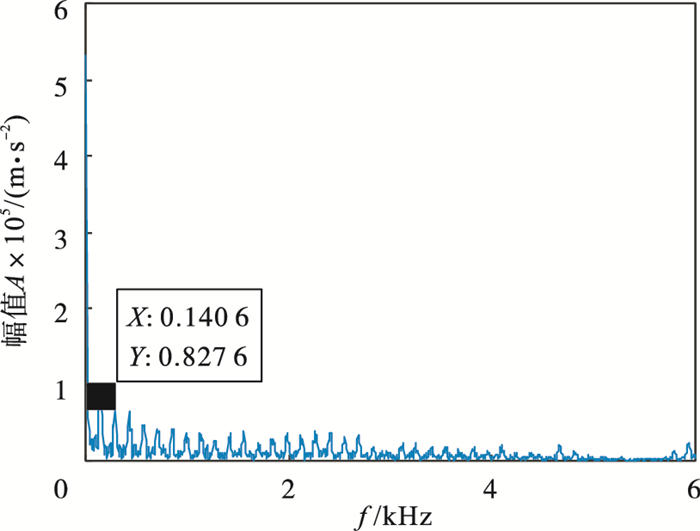图 17 增强后信号包络谱Fig.17 Envelope spectrum of enhanced signal

3.4 对比分析滚动体故障特征频率比内圈、外圈故障特征频率提取更加困难.本节对3.3节滚动体故障信号直接利用PSO优化的MCKD进行增强, 得到进化曲线如图 18所示, 可见在第3代求取最佳(L, M)组合, 其中L=181, M=1.对增强后的信号进行包络解调得到图 19, 发现信号未经过优化K值的VMD分解以及利用EWK指标选取有效模态分量增强的处理下提取的故障特征频率不明显.与3.3节对比分析验证了本文方法在强噪声背景下提取故障特征频率的有效性.
图 18(Fig. 18)

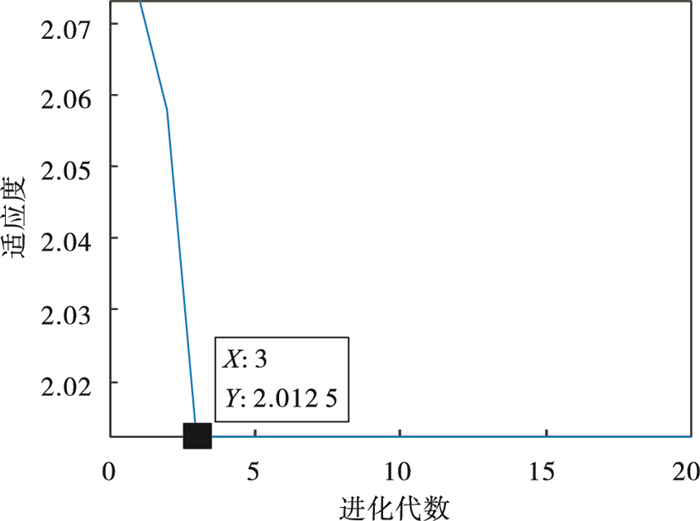图 18 粒子群优化图Fig.18 Diagram of particle swarm optimization

图 19(Fig. 19)

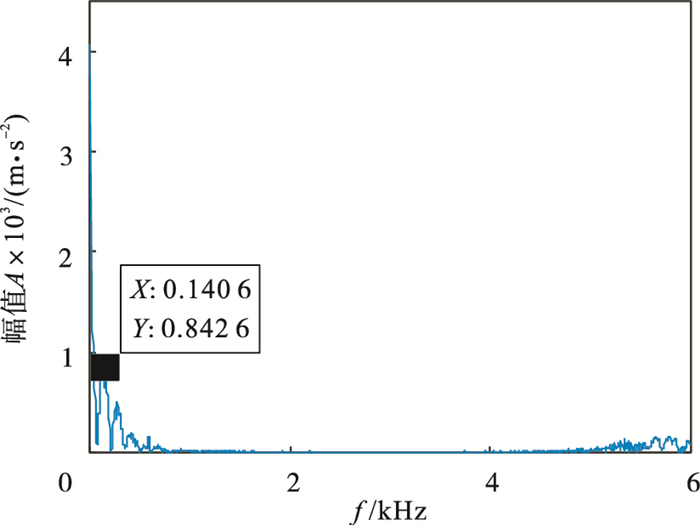图 19 增强后信号包络谱Fig.19 Envelope spectrum of enhanced signal

4 结论1) 通过优化VMD中K值, 可减少通过观察法设定K值带来的不确定性.
2) 通过EWK指标选取有效模态分量, 使其既保留了原信号的故障信息, 又能有效滤除噪声, 方便信号后续处理.
3) PSO优化MCKD中L, M两个重要参数, 提高了其参数选择的合理性.
4) 基于优化VMD和MCKD的方法能减少滚动轴承早期故障信号中噪声干扰、增强冲击成分, 对增强信号进行包络解调, 可以有效提取故障特征频率及其倍频, 增强了故障诊断的可靠性.
参考文献

[1]	Zheng K, Yang D W, Zhang B, et al. A group sparse representation method in frequency domain with adaptive parameters optimization of detecting incipient rolling bearing fault[J]. Journal of Sound and Vibration, 2019, 462: 114931. DOI:10.1016/j.jsv.2019.114931
[2]	齐咏生, 刘飞, 高学金, 等. 基于MCKD和Teager能量算子的滚动轴承复合故障诊断[J]. 大连理工大学学报, 2019, 59(1): 35-44. (Qi Yong-sheng, Liu Fei, Gao Xue-jin, et al. Composite fault diagnosis of rolling bearing based on MCKD and Teager energy operator[J]. Journal of Dalian University of Technology, 2019, 59(1): 35-44.)
[3]	Dragomiretskiy K, Zosso D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544. DOI:10.1109/TSP.2013.2288675
[4]	张建财, 高军伟. 基于变分模态分解和多尺度排列熵的滚动轴承故障诊断[J]. 噪声与振动控制, 2019, 39(6): 181-186. (Zhang Jian-cai, Gao Jun-wei. Fault diagnosis of train rolling bearings based on variational modal decomposition and multi-scale permutation entropy[J]. Noise and Vibration Control, 2019, 39(6): 181-186.)
[5]	Deng M Q, Deng A D, Zhu J, et al. Bandwidth fourier decomposition and its application in incipient fault identification of rolling bearings[J]. Measurement Science and Technology, 2020, 31(1): 015012. DOI:10.1088/1361-6501/ab4069
[6]	Mcdonald G L, Zhao Q, Zuo M J. Maximum correlated kurtosis deconvolution and application on gear tooth chip fault detection[J]. Mechanical Systems and Signal Processing, 2012, 33: 237-255. DOI:10.1016/j.ymssp.2012.06.010
[7]	杨斌, 张家玮, 樊改荣, 等. 最优参数MCKD与ELMD在轴承复合故障诊断中的应用研究[J]. 振动与冲击, 2019, 38(11): 59-67. (Yang Bin, Zhang Jia-wei, Fan Gai-rong, et al. Application of OPMCKD and ELMD in bearing compound fault diagnosis[J]. Journal of Vibration and Shock, 2019, 38(11): 59-67.)
[8]	Wang F T, Liu C X, Su W S, et al. Combined failure diagnosis of slewing bearings based on MCKD-CEEMD-ApEn[J]. Shock and Vibration, 2018, 2018: 6321785.
[9]	Zhang J, Zhang J Q, Zhong M, et al. Detection for incipient damages of wind turbine rolling bearing based on VMD-AMCKD method[J]. IEEE Access, 2019, 7: 67944-67959. DOI:10.1109/ACCESS.2019.2918343
[10]	Lyu X, Hu Z Q, Zhou H L, et al. Application of improved MCKD method based on QGA in planetary gear compound fault diagnosis[J]. Measurement, 2019, 139: 236-248. DOI:10.1016/j.measurement.2019.02.071
[11]	Gu R, Chen J, Hong R J, et al. Incipient fault diagnosis of rolling bearings based on adaptive variational mode decomposition and Teager energy operator[J]. Measurement, 2020, 149: 106941. DOI:10.1016/j.measurement.2019.106941
[12]	Wang X B, Yang Z X, Yan X A. Novel particle swarm optimization based variational mode decomposition method for the fault diagnosis of complex rotating machinery[J]. Energy, 2018, 23(1): 68-79.
[13]	夏均忠, 赵磊, 白云川, 等. 基于MCKD和VMD的滚动轴承微弱故障特征提取[J]. 振动与冲击, 2017, 36(20): 78-83. (Xia Jun-zhong, Zhao Lei, Bai Yun-chuan, et al. Feature extraction for rolling element bearing weak fault based on MCKD and VMD[J]. Journal of Vibration and Shock, 2017, 36(20): 78-83.)
[14]	Wade A S, Robert B R. Rolling element bearing diagnostics using the case western reserve university data: a benchmark study[J]. Mechanical Signal Processing, 2015, 64/65: 100-131. DOI:10.1016/j.ymssp.2015.04.021