
 , 孙晓辉3
, 孙晓辉3 1. 东北大学 信息科学与工程学院,辽宁 沈阳 110819;
2. 东北大学 流程工业综合自动化国家重点实验室,辽宁 沈阳 110819;
3. 大连天籁安全风险管理技术有限公司, 辽宁 大连 116600
收稿日期:2020-06-24
基金项目:国家自然科学基金资助项目(61973057, 61903272, 61533007);矿冶过程自动化国家重点实验室开放基金资助项目(BGRIMM-KZSKL-2018-09)。
作者简介:袁杰(1987-), 男, 山东潍坊人, 东北大学博士研究生;
王福利(1957-), 男, 辽宁沈阳人, 东北大学教授,博士生导师。
摘要:电熔镁炉熔炼过程信息包含大量的不确定性,基于大数据分析的方法难以应用.为准确识别电熔镁炉熔炼过程的异常工况,提出一种基于改进的主观贝叶斯在线规则推理方法.传统的主观贝叶斯方法参数赋值范围过大,针对这一问题,使用映射函数将参数赋值范围缩小到有限区间,以提高方法的实用性.在规则推理时,使用模糊隶属度函数对观察和证据进行模糊匹配,以提高工况识别的鲁棒性和准确率.仿真分析表明该方法可以有效描述规则中的不确定性信息,准确识别电熔镁炉熔炼过程的异常工况.
关键词:电熔镁炉异常工况识别主观贝叶斯不确定推理模糊函数
Abnormal Condition Recognition Based on Improved Subjective Bayesian Method for Fused Magnesium Furnace
YUAN Jie1, WANG Shu1,2, WANG Fu-li1,2

 , SUN Xiao-hui3
, SUN Xiao-hui3 1. School of Information Science & Engineering, Northeastern University, Shenyang 110819, China;
2. State Key Laboratory of Synthetical Automation for Process Industries, Northeastern University, Shenyang 110819, China;
3. Tianlai Security Risk Management Technology Co., Ltd., Dalian 116600, China
Corresponding author: WANG Fu-li, E-mail: wangfuli@mail.neu.edu.cn.
Abstract: It is difficult for big data analysis to be applied to the smelting process of fused magnesium furnace because of a lot of uncertain information of the process. In order to identify abnormal conditions accurately, an online rule reasoning method based on improved subjective Bayesian is proposed. In view of the problem that the parameter value range of the traditional subjective Bayesian method is too wide, the mapping function is used to limit the value range to a finite interval, which improves the practicability of the method. In order to improve the robustness and accuracy of condition recognition, the fuzzy membership function is utilized to match the observation and evidence in the reasoning. Simulation results show that the method can effectively describe the uncertain information in the rules and accurately identify the abnormal conditions in the smelting process of fused magnesium furnace.
Key words: fused magnesium furnaceabnormal condition recognitionsubjective Bayesianuncertain reasoningfuzzy function
电熔镁砂耐高温、耐腐蚀、绝缘性好,在钢铁、玻璃、水泥、有色金属冶炼等诸多行业得到非常广泛的应用.我国长期以来一直采用电熔镁炉冶炼电熔镁砂[1].大部分的电熔镁炉生产需要较多的生产经验且劳动强度大,并且经常发生异常,引起产品产量减少、单吨能耗增加等问题,严重时会对熔炼设备与操作工人的安全构成威胁.提高熔炼过程的自动化水平,实现准确的工况识别是亟需解决的问题[2].近年来,随着深度学习等方法的提出,通过声音、图像等信息对电熔镁炉的熔炼过程进行工况识别的方法得到广泛研究[3-4].文献[5]通过时序图像的深度学习实现了对电熔镁炉熔炼过程典型工况的识别.文献[6]充分利用多源信息,同时使用声音、图像和电流信息实现了电熔镁炉过程异常工况的严重程度识别.这些工况识别都是在现场各类传感器充足且过程数据准确的前提下进行的; 然而,在大部分情况下,由于现场条件恶劣,并不一定完全具备这些条件,整个熔炼过程伴随着很多不确定的信息.
不确定性推理是从不确定性的初始证据出发,通过运用不确定的知识,推导出具有一定程度不确定性结论的思维过程.不确定性推理方法主要有基于规则推理的方法[7]、确定性因子方法[8]、粗糙集理论[9]、证据理论[10]、动态因果图[11]等.基于规则的不确定性推理方法在规则表达上符合人类语言习惯,能对过程的不确定性问题进行有效描述且因果关系表达清晰,因而被广泛应用.主观贝叶斯方法[12-13]是规则推理方法的一种,以贝叶斯理论为依据,克服了实际应用时先验概率很难获得的问题.然而,主观贝叶斯方法中充分性似然因子和必要性似然因子两个主要参数存在值域范围无限大的问题,实际过程中参数大小难以确定,这在一定程度上限制了它的应用.
为有效处理过程不确定信息,实现准确的异常工况识别,本文提出一种基于改进主观贝叶斯的电熔镁炉熔炼过程异常工况识别方法.首先,针对传统主观贝叶斯方法参数赋值范围过大的问题,给出一种有限范围的参数赋值方法,提高了方法的实用性.其次,在规则推理时,使用模糊隶属度函数对观察和证据进行模糊匹配,提高了工况识别的鲁棒性和准确率.最后,将这种改进的主观贝叶斯方法应用到电熔镁炉熔炼过程的工况识别中,取得了较好的实验结果.
1 主观贝叶斯方法主观贝叶斯方法是由贝叶斯公式改进而来的.含有两个参数LS和LN,分别称为充分性似然因子和必要性似然因子.LS和LN的表达式为
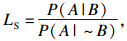 | (1) |
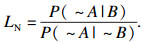 | (2) |
在实际使用中,LS和LN的值由专家主观给出.但参数的值域范围太大,限制了该方法的应用.在主观贝叶斯方法中,含有不确定性的产生式规则用以下形式表示:
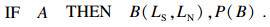 |
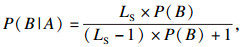 | (3) |
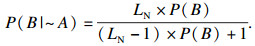 | (4) |
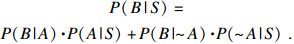 | (5) |
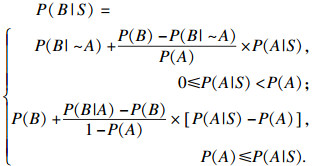 | (6) |
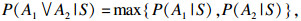 | (7) |
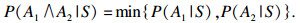 | (8) |
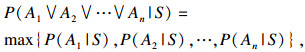 | (9) |
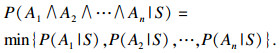 | (10) |
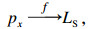 |
1) px增大,LS也增大.px的值取值范围为[0, 1],从0到1支持度越来越强,使用e指数函数有
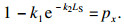 | (11) |
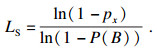 | (12) |
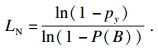 | (13) |
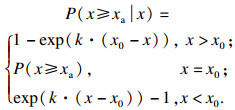 | (14) |
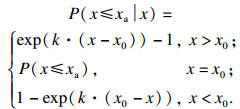 | (15) |
2.3 推理过程及异常识别步骤主观贝叶斯方法的推理过程,就是根据观察S推理得到结论B发生的后验概率的过程.主观贝叶斯方法的不确定性推理框图如图 1所示.
图 1(Fig. 1)
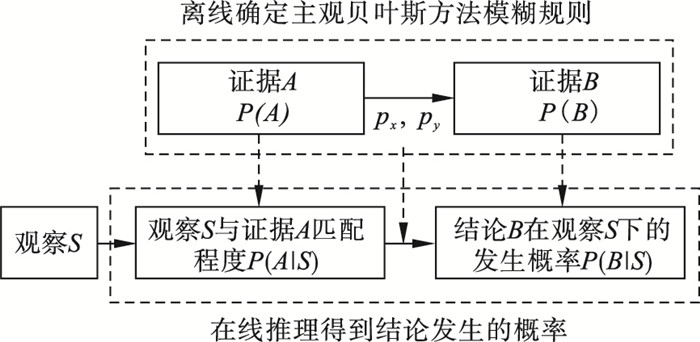 | 图 1 改进的主观贝叶斯方法推理机制Fig.1 Reasoning mechanism of the improved subjective Bayesian method |
首先,在实际应用时,获得观察S,该观察与规则中的证据A进行模糊匹配,得到相应的P(A|S).通过离线规则中确定的先验概率P(A), P(B), 并结合专家给出的px,py,得到P(B|S).如果规则的证据中存在多个子证据,则通过上述方法单独计算每个子证据下结论B发生的后验概率, 然后通过式(7)~式(10)计算最终B发生的后验概率.
假设一个过程的异常工况识别规则库由N条专家规则构成,这些规则都是由特征变量和限定值构成的产生式规则.将上述改进的主观贝叶斯方法应用于异常工况识别的步骤如下:
1) n=1.
2) 判断规则证据是否由多个子证据构成:如果不是,通过主观贝叶斯方法推理得到该规则对应的异常发生的后验概率; 如果是,则通过主观贝叶斯推理得到每个子证据得到对应的异常发生的后验概率,并通过式(7)~式(10)计算该异常发生的最终的后验概率.
3) 遍历所有规则,直到n=N,得到所有N条规则的结论.判断是否存在同一工况的识别由多条规则产生:如果不是,工况发生的后验概率由对应规则的结论确定; 如果是,则通过式(7)~式(10)融合得到最终的异常工况后验概率.
4) 如果某异常发生的概率大于设定的阈值(阈值设为0.5),则认为异常工况发生.
3 仿真验证3.1 电熔镁炉熔炼过程介绍电熔镁炉的熔炼设备主要包括供电系统、信号检测系统、电极位置调节系统、炉体旋转系统、加料系统,以及炉体本身[6],系统结构如图 2所示.
图 2(Fig. 2)
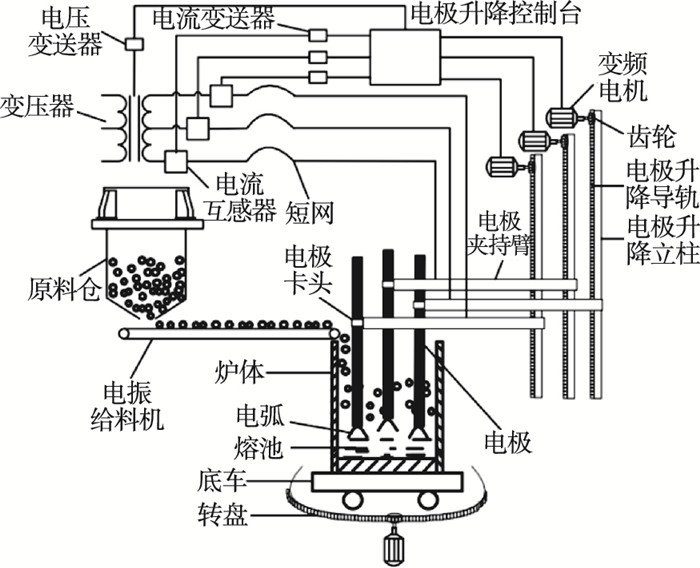 | 图 2 电熔镁炉熔炼设备示意图Fig.2 Schematic diagram of smelting equipment for fused magnesium furnace |
电极位置调节系统是电熔镁炉生产过程的重要设备.在电熔镁炉工作过程中,炉内的原料状态时刻发生变化,电弧长度也不断变化,造成熔炼电流出现大范围波动.电熔镁炉的电极一般选用石墨电极,通过电极卡头固定在电极夹持臂上,电极夹持臂另一端与电极升降立柱连接.电极夹持臂上有用于调节位置的齿条,三相电极通过带动齿条来控制电极上下移动,进而调节电极的电流值.
在电熔镁炉熔炼过程中,因为炉料状态时刻发生变化,电极的电流值也不断发生改变,如果不能及时调节电极以跟踪设定电流值,就会引起异常工况的发生.异常工况可以用电流的跟踪误差、变化率及持续的时间来表示.
电流跟踪误差E(t)表示为
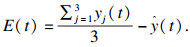 | (16) |
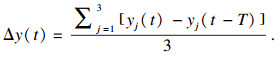 | (17) |
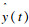
表 1(Table 1)
| 表 1 常用的电熔镁炉异常工况识别规则 Table 1 Common rules for abnormal condition recognition of fused magnesium furnace |
表 1中HE1和HE2表示电流跟踪误差E(t)的低限和高限,HE2>HE1; HΔI1,HΔI2表示电流变化率Δy(t)的低限和高限,HΔI2>HΔI1; th表示电流值以一种特征变化时所持续的时间.
由表 1可知,识别电熔镁炉异常工况的规则都是由特征变量和相应的限定值构成的.用传统的产生式规则识别异常时,如果相应变量的值处于某一范围,则认定异常一定发生或者一定没有发生; 然而,考虑到实际生产过程中,大部分变量都存在测量不准或受噪声影响的问题,因此,确定性的产生式规则并不一定可靠.特别是特征变量取值在限定值附近时,容易造成误判.因此,在工况识别规则中通过主观贝叶斯方法引入不确定性,能提高异常工况识别的准确率.
主观贝叶斯方法的产生式规则形式:
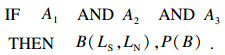 | (18) |
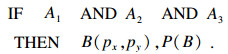 | (19) |
 | (20) |
表 2(Table 2)
| 表 2 主观贝叶斯框架的电熔镁炉熔炼工况识别规则 Table 2 Abnormal condition recognition rules for fused magnesium furnace under subjective Bayesian | |||||||||||||||||||||
3.2 仿真实验本节中通过两个仿真实验说明改进的主观贝叶斯方法在处理不确定性问题时的优势和有效性.第一个仿真实验是对现场收集的离线数据进行工况识别,相比于传统产生式规则方法和传统主观贝叶斯方法,改进的主观贝叶斯方法在数据存在大量噪声或测量不准时有优势.第二个仿真实验是对电熔镁炉熔炼过程进行在线工况识别,识别效果证明了改进主观贝叶斯方法的有效性.
首先,从现场收集的电熔镁炉异常运行数据中,选择200个异常工况样本.每个样本包含采样时的电流、采样时刻与之前时刻的电流变化率和跟踪误差.这些样本都是异常工况稳定运行时的数据,因此满足异常持续时间的要求,在仿真中不再考虑持续时间对结果的影响.这些异常工况样本主要是电流的跟踪误差和电流变化率存在差异.样本的跟踪误差都在2 000 A以上,电流变化率都控制在(1 200±50)A范围内.在这200个异常样本中,前100个是熔炼过程中出现半融化异常,后100个是熔炼过程中出现过加热异常.为了表示方便,分别使用数字1,2表示半熔化异常和过加热异常,0表示正常熔炼工况.图 3a是利用表 1中传统的产生式规则进行异常工况识别的结果,大量的样本点出现了识别错误.图 3b是利用传统的主观贝叶斯方法对异常样本进行识别,只有12个识别错误样本,可见识别错误的样本大量减少,诊断效率明显提高.在使用主观贝叶斯方法时,先验概率P(A)和P(B)如表 2所示.实验中LS=5, LN=0.1.
图 3(Fig. 3)
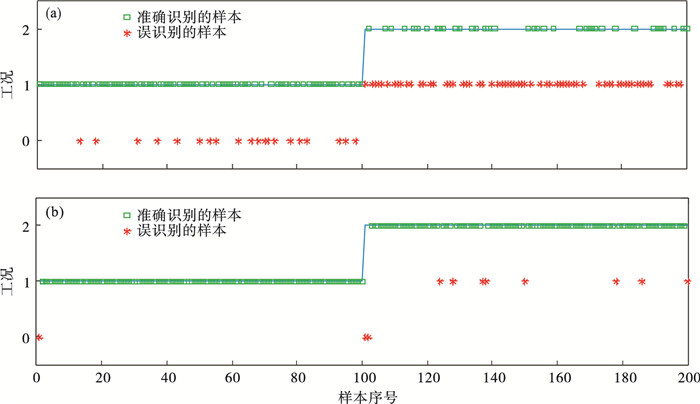 | 图 3 不同方法异常工况识别结果Fig.3 Abnormal condition recognition results of different methods (a)—传统产生式规则方法; (b)—传统主观贝叶斯方法. |
图 4将LS和px两个参数的关系直观地表示出来,可见LS=5对于结论的支持度仅为0.7左右,并不高.通过px给出支持度,确定支持度和不支持度,px1=px2=0.9,py1=py2=0.2.通过改进后的主观贝叶斯方法进行异常工况识别,结果如图 5所示.所有异常样本都被准确地识别出来.
图 4(Fig. 4)
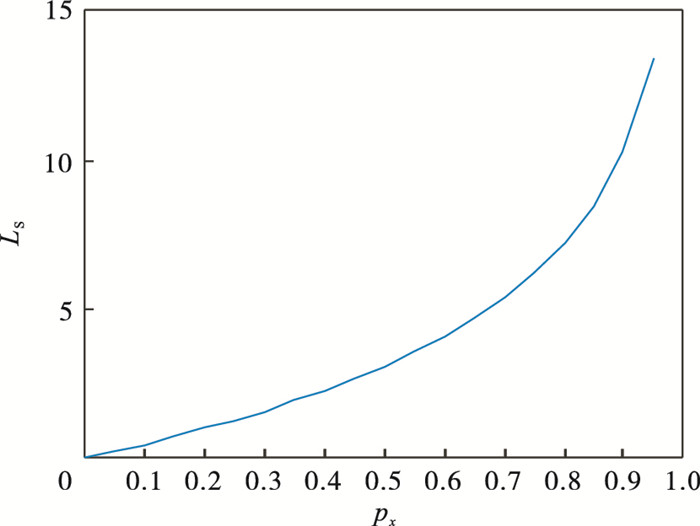 | 图 4 LS和px的关系Fig.4 Relationship between LS and px |
图 5(Fig. 5)
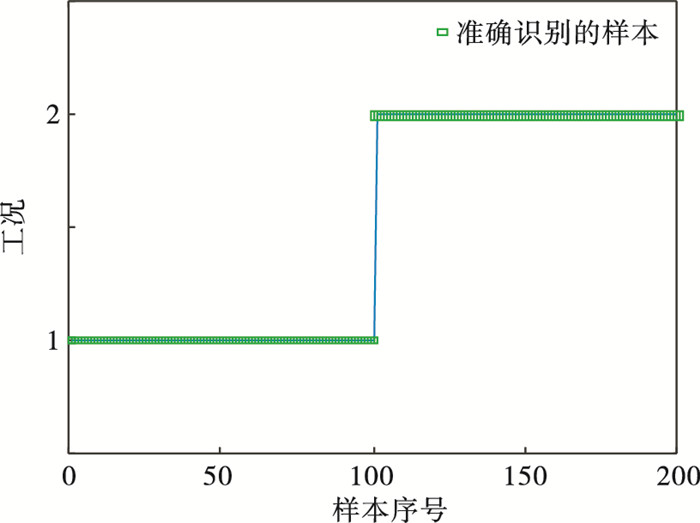 | 图 5 改进主观贝叶斯方法异常工况识别结果Fig.5 Abnormal condition recognition results of the improved subjective Bayesian method |
通过以上对比实验证明,改进参数给定方式的主观贝叶斯方法能更好地识别存在不确定性问题的异常工况.使用传统产生式规则方法、传统主观贝叶斯方法和改进主观贝叶斯方法,对现场收集的5 000组离线异常样本进行异常工况识别,总体的识别正确率如表 3所示,与传统的主观贝叶斯方法相比,改进的主观贝叶斯方法提高了工况识别正确率.
表 3(Table 3)
| 表 3 三种方法的识别正确率 Table 3 Recognition precision of three methods |
在现场收集的电熔镁炉熔炼过程持续时间300 s的数据中,由于电极操作原因,导致电熔镁炉运行工况从第50 s开始由正常工况转变为过加热异常工况.分别使用改进的主观贝叶斯方法和传统的主观贝叶斯方法对该批次的熔炼过程数据进行在线工况识别,使用的主要参数与仿真1中参数相同.在图 6a中,改进的主观贝叶斯方法工况识别有6个时刻出现了误报,将过加热状态认定为正常状态.而使用传统的主观贝叶斯方法,共有10个时刻出现了误报,如图 6b所示.在线工况识别结果说明,改进的主观贝叶斯方法能更快地识别出异常工况且诊断正确率有所提高.
图 6(Fig. 6)
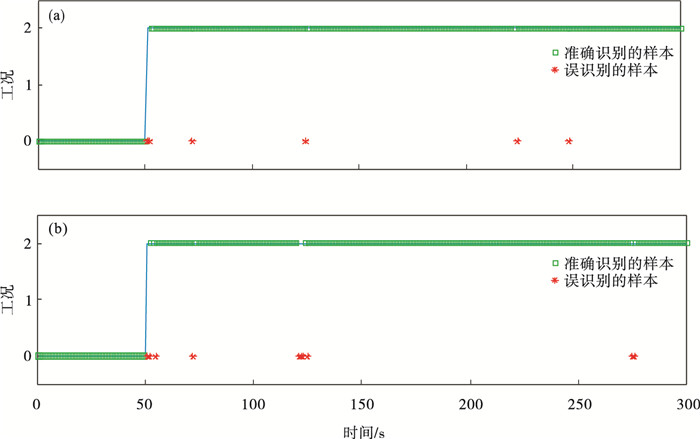 | 图 6 两种贝叶斯方法异常工况识别结果Fig.6 Abnormal condition recognition results of two Bayesian methods (a)—传统主观贝叶斯方法; (b)—改进主观贝叶斯方法. |
4 结语本文提出一种基于改进主观贝叶斯的电熔镁炉熔炼过程异常工况识别方法,克服了传统主观贝叶斯方法中参数取值范围过大、难以确定的问题,更具实用性.同时,使用模糊隶属度函数对观察和证据进行匹配,有效解决了熔炼过程中信息的不确定性问题,提高了异常工况识别的准确率.使用改进主观贝叶斯方法对电熔镁炉熔炼过程中的两种主要异常工况进行了识别,取得了较好的识别效果.
参考文献
| [1] | Wu Z W, Liu T F, Jiang Z P, et al. Nonlinear control tools for fused magnesium furnaces: design and implementation[J]. IEEE Transactions on Industrial Electronics, 2018, 65(9): 7248-7257. DOI:10.1109/TIE.2017.2767545 |
| [2] | 李荟, 王福利, 李鸿儒. 电熔镁炉熔炼过程异常工况识别及自愈控制方法[J]. 自动化学报, 2020, 46(7): 1411-1419. (Li Hui, Wang Fu-li, Li Hong-ru. Abnormal condition identification and self-healing control scheme for the electro-fused magnesia smelting process[J]. Acta Automatica Sinica, 2020, 46(7): 1411-1419.) |
| [3] | Ding S Y, Wang Z J, Kong W J, et al. Electrode regulating system modeling in electrical smelting furnace using recurrent neural network with attention mechanism[J]. Neurocomputing, 2019, 359: 32-40. DOI:10.1016/j.neucom.2019.05.060 |
| [4] | 卢绍文, 王克栋, 吴志伟, 等. 基于深度卷积网络的电熔镁炉欠烧工况在线识别[J]. 控制与决策, 2019, 34(7): 1537-1544. (Lu Shao-wen, Wang Ke-dong, Wu Zhi-wei, et al. Online detection of semi-molten of fused magnesium furnace based on deep convolutional neural network[J]. Control and Decision, 2019, 34(7): 1537-1544.) |
| [5] | 吴高昌, 刘强, 柴天佑, 等. 基于时序图像深度学习的电熔镁炉异常工况诊断[J]. 自动化学报, 2019, 45(8): 1475-1485. (Wu Gao-chang, Liu Qiang, Chai Tian-you, et al. Abnormal condition diagnosis through deep learning of image sequences for fused magnesium furnaces[J]. Acta Automatica Sinica, 2019, 45(8): 1475-1485.) |
| [6] | 李鸿儒, 王奕文, 邓靖川. 基于信息融合的电熔镁炉熔炼异常工况等级识别[J]. 东北大学学报(自然科学版), 2020, 41(2): 153-157. (Li Hong-ru, Wang Yi-wen, Deng Jing-chuan. Information fusion based abnormal condition levels recognition of smelting in fused magnesium furnace[J]. Journal of Northeastern University(Natural Science), 2020, 41(2): 153-157.) |
| [7] | Coulibaly L, Kamsu-Foguem B, Tangara F. Rule-based machine learning for knowledge discovering in weather data[J]. Future Generation Computer Systems, 2020, 108: 861-878. DOI:10.1016/j.future.2020.03.012 |
| [8] | Vera J C D, Ortiz G M N, Molina C, et al. Extending knowledge based redundancy in association rules with imprecise knowledge[J]. IEEE Latin America Transactions, 2019, 17(4): 648-653. DOI:10.1109/TLA.2019.8891930 |
| [9] | Xie T, Gong Z T. A hesitant soft fuzzy rough set and its applications[J]. IEEE Access, 2019, 7: 167766-167783. DOI:10.1109/ACCESS.2019.2954179 |
| [10] | Zhao G Z, Chen A G, Lu G X, et al. Data fusion algorithm based on fuzzy sets and D-S theory of evidence[J]. Tsinghua Science and Technology, 2020, 25(1): 12-19. DOI:10.26599/TST.2018.9010138 |
| [11] | Li L, Yue W C. Dynamic uncertain causality graph based on intuitionistic fuzzy sets and its application to root cause analysis[J]. Applied Intelligence, 2020, 50(1): 241-255. DOI:10.1007/s10489-019-01520-6 |
| [12] | G?nen M, Johnson W O, Lu Y G, et al. Comparing objective and subjective Bayes factors for the two-sample comparison: the classification theorem in action[J]. The American Statistician, 2019, 73(1): 22-31. DOI:10.1080/00031305.2017.1322142 |
| [13] | Uzuno?lu B. An adaptive Bayesian approach with subjective logic reliability networks for preventive maintenance[J]. IEEE Transactions on Reliability, 2020, 69(3): 916-924. DOI:10.1109/TR.2019.2916722 |
