
 , 耿蓉, 李伯群
, 耿蓉, 李伯群 东北大学 计算机科学与工程学院, 辽宁 沈阳 110169
收稿日期:2020-04-24
基金项目:国家自然科学基金资助项目(61671141, 61701100, 61673093)。
作者简介:季策(1969-),女,辽宁沈阳人,东北大学副教授;
李伯群(1970-),男,辽宁鞍山人,辽宁科技大学教授。
摘要:针对基于稀疏分量分析的欠定盲源分离问题, 提出一种基于优化支撑的稀疏度自适应子空间追踪(OS-SASP)算法.通过引入自适应思想, 克服传统子空间追踪(SP)算法对稀疏度的依赖; 同时在迭代开始之前通过离散余弦变换的能量集中特性确定最小支撑集的大小, 对最小支撑集求并集获得优化支撑集, 优化支撑集联合迭代过程中的候选集来定位最佳原子, 提高源信号的恢复精度.仿真结果表明, OS-SASP算法在一维稀疏信号与语音信号的欠定盲源恢复过程中表现出良好的性能.
关键词:欠定盲源分离源信号重构自适应离散余弦变换优化支撑集子空间追踪
Underdetermined Blind Source Separation Based on OS-SASP Algorithm
JI Ce, ZHANG Huan

 , GENG Rong, LI Bo-qun
, GENG Rong, LI Bo-qun School of Computer Science & Engineering, Northeastern University, Shenyang 110169, China
Corresponding author: ZHANG Huan, E-mail: 1197152922@qq.com.
Abstract: A sparse adaptive subspace pursuit based on the optimal support(OS-SASP)algorithm was proposed to deal with the problem of underdetermined blind source separation based on sparse component analysis. By introducing the idea of self-adaptation, the dependence of the traditional subspace pursuit(SP)algorithm on sparsity was overcome. At the same time, the size of the minimum support set was determined by the energy concentration characteristic of discrete cosine transform before the start of iteration. Further, the optimal support set was obtained by calculating the union of the minimum support sets. And the combination of the optimal support set and the candidate set in the joint iteration was used to locate the best atom, so as to improve the source signal′s restore accuracy. The simulation results showed that the OS-SASP algorithm can achieve promising performance in the underdetermined blind source recovery of the one-dimensional sparse signals and speech signals.
Key words: underdetermined blind source separationsource signal reconstructionself-adaptiondiscrete cosine transformoptimize support setsubspace pursuit(SP)
盲源分离(blind source separation, BSS)起源于鸡尾酒会问题, 当观测信号数目小于源信号数目时, 即为欠定盲源分离[1].目前, 针对于欠定盲源分离问题的主流研究聚焦于基于稀疏分量分析的“两步法”[2-4].第一步, 通过观测信号对混合矩阵进行估计; 第二步, 将第一步的估计结果作为已知信息对源信号进行重构.在源信号重构过程中, 方程组是欠定形式, 对混合矩阵求逆并不能有效解决源信号重构问题, 这让欠定盲源分离的发展受到了限制.
2006年, Donoho等提出压缩感知(compressive sensing, CS)理论, 这种理论一经提出就引起了学术界的广泛关注, 在众多领域都发挥了积极作用[5].文献[6-9]首次发现压缩感知模型与欠定盲源分离模型的相似性, 并且借助压缩感知理论成功实现了欠定盲源分离, 这为解决欠定盲源分离问题开辟了新的思路.目前压缩感知主要包括以下三类方法: 凸松弛类算法、组合类算法及贪婪类算法[10-11].贪婪类算法在进行欠定盲源分离源信号恢复时, 因为恢复速度快、精度高等优点备受关注.正交匹配追踪(orthogonal matching pursuit, OMP)算法在所有贪婪类算法中占据主要地位, 是其他贪婪类算法的理论基础[12], 但OMP算法较高的时间复杂度让源信号恢复效率低下.针对此问题, 2009年, Dai等提出了子空间追踪(subspace pursuit, SP)算法[13], 该算法根据残差与观测矩阵的相似度在迭代时选择K个原子扩充候选集, 利用回溯的方法剔除候选集中不可靠原子, 将剩余原子保留作为支撑集.但是它必须提前知道信号的稀疏度K, 并且初始支撑集的大小为K, 这样会造成候选集中的原子之间相互干扰, 支撑集的准确性下降, 进而导致源信号恢复精度下降.
针对SP算法中存在的缺陷, 提出了基于优化支撑的稀疏度自适应子空间追踪(sparse adaptive subspace pursuit based on optimal support, OS-SASP)算法.该算法在迭代开始之前对最小支撑集求并集,进而获得优化支撑集, 优化支撑集联合迭代过程中的候选集共同定位最佳原子.通过自适应思想逐步逼近稀疏度K, 当残差满足阈值条件时停止迭代.仿真结果表明, OS-SASP算法与传统SP及OMP算法相比, 一维稀疏信号的信噪比提高8dB左右, 均方差仅为SP和OMP算法的1/2, 3路语音信号的相似系数均高于SP和OMP算法, 可以达到0.9以上.
1 相关理论介绍1.1 欠定盲源分离盲源分离的数学模型为
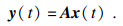 | (1) |
 | (2) |
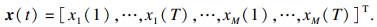 | (3) |
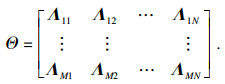 | (4) |
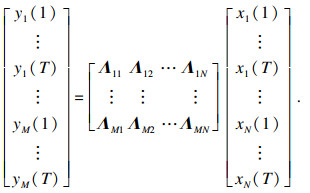 | (5) |
1.2 基于SP算法的欠定盲源分离SP算法在解决欠定盲源分离源信号恢复问题时, 根据残差相关性从原子库中选择K个原子加入候选集, 通过回溯的方式删除候选集中不可靠的原子, 剩余的K个原子构成新的支撑集.当迭代过程中的残差增大时停止迭代, 重构信号, SP算法的原理框图如图 1所示.
图 1(Fig. 1)
 | 图 1 SP算法原理框图Fig.1 Block diagram of SP algorithm |
SP算法具体流程如下:
输入: 观测矩阵Θ, 观测信号y, 稀疏度K.
初始化: 初始残差r0=y, 候选集Λ=?, 支撑集F=?, 索引集Γadd, 迭代次数t=1.
迭代:
步骤1??计算相关系数, 选择原子与残差相关性最大的K个原子, 将这些原子的索引放入集合Γadd:
 | (6) |
 | (7) |
 | (8) |

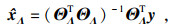 | (9) |
 | (10) |
 | (11) |
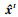
输出: 重构信号
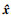
自然界中大多数信号, 例如声音、图像等信号的稀疏度都是未知的, 所以依赖稀疏度的SP算法在恢复此类信号时会受到限制; 在SP算法中, 初始支撑集与候选集的大小都是K, 因此SP算法需要在2K个原子中选择K个原子进行信号重构, 这样直接导致原子之间相互干扰, 一些错误的原子被混入最终的支撑集, 进而影响源信号的恢复精度.
2 基于OS-SASP算法的欠定盲源分离本文提出的OS-SASP算法不仅克服了传统SP算法对稀疏度的依赖, 而且对支撑集的选取方式进行相应优化, 在迭代开始之前确立了一个优化支撑集, 利用优化支撑集联合迭代过程中的候选集共同定位最佳原子.
2.1 支撑集的选择在图像处理过程中, 需要对观测信号进行离散余弦变换(discrete cosine transform, DCT), 取变换之后的局部测量值进行压缩感知重构, 通常能够以极大的概率恢复原始数据, 这是由于DCT变换具有能量集中特性[14].在OS-SASP算法中, 可以根据DCT变换的能量集中特性确定最小支撑集的大小.具体确定方式如下:
1) ?计算观测矩阵Θ与观测信号y的乘积, 获取相关性向量x(m):
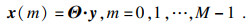 | (12) |
 | (13) |
 | (14) |
 | (15) |
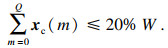 | (16) |
将两个最小支撑集SK1, SK2取并集得到优化支撑集SK, 优化支撑集SK联合迭代过程中的候选集CK共同构成初始支撑集F, OS-SASP算法优化支撑模块见图 2.其中, 两个最小支撑集SK1, SK2的选取原则为: 根据残差的相关性, 选择相关性最大的前2Q个原子构成候选集SK1, 对SK1中的原子进行正则化处理, 选取能量大于最大相关0.15倍的原子更新候选集SK1, 利用回溯对SK1中不可靠的原子进行二次剔除, 选取系数最大的Q个原子组成最小支撑集SK1, 计算残差R1; 最小支撑集SK2的选取原则与最小支撑集SK1类似, 大小为Q/2;将最小支撑集SK1与SK2求并集获得优化支撑集SK, 计算残差R2.
图 2(Fig. 2)
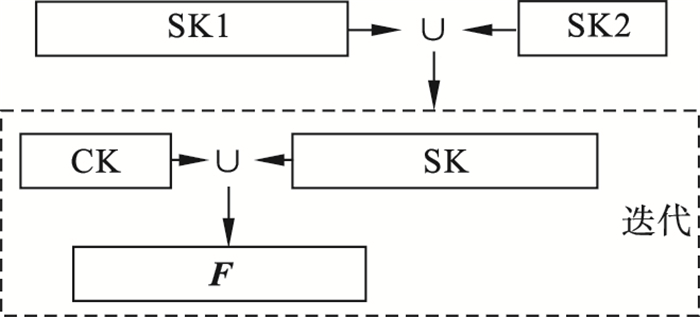 | 图 2 OS-SASP算法优化支撑模块图Fig.2 Block diagram for optimized support used in OS-SASP algorithm |
2.2 自适应确立稀疏度K将OS-SASP算法引入自适应的思想, 能够随着迭代的进行自适应地调整支撑集中原子的数目, 迭代终止时支撑集中所含原子个数就是稀疏度K的值.具体实施方法为: 利用残差的大小判断迭代所处阶段, 当处于迭代前期时, 说明支撑集中原子数目远小于稀疏度K的值, 此时利用大步长进行迭代; 当处于迭代后期时, 说明支撑集中原子数目接近于稀疏度K的值, 此时利用小步长进行迭代, 当达到终止条件时停止迭代.OS-SASP算法具体流程如下:
输入: 观测矩阵Θ, 观测信号y;
初始化:
步骤1?计算观测信号y与观测矩阵中所有原子的内积x(m), 对x(m)做DCT变换确定最小支撑集的大小Q, 选择|x(m)|中前2Q个最大相关的原子索引放入集合S0; 对集合S0中的2Q个原子进行正则化处理, 剔除集合中不可靠原子:
 | (17) |
步骤2?计算残差R1,
 | (18) |
 | (19) |
步骤4?将最小支撑集SK1与最小支撑集SK2取并集得到优化支撑集SK, 作为迭代的初始支撑集Λ.
步骤5?计算残差R2,
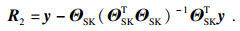 | (20) |
迭代:
步骤1?计算相关系数, 选择原子与残差相关性最大的Q个原子, 将这些原子的索引放入集合Γadd,
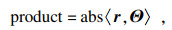 | (21) |
 | (22) |
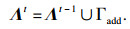 | (23) |

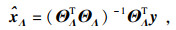 | (24) |
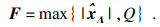 | (25) |
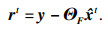 | (26) |
1) ?如果‖rt‖2≤ε1‖y‖2, 输出信号
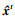
2) ?如果‖rt‖2≤‖rt-1‖2, 则令Λt=F, r=rt, Q=Q, t=t+1,继续进行迭代; 否则转入3);
3) ?如果‖rt‖2≤ε2‖y‖2, 则令Λt=F, r=rt, Q=

输出: 重构信号
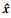
本文主要研究基于OS-SASP算法的盲源分离问题, 首先利用混合矩阵将三路源信号进行混合, 变为两路观测信号, 构建欠定盲源分离模型; 然后将欠定盲源分离模型转换为压缩感知模型, 利用本文改进的OS-SASP算法获取源信号, 实现欠定盲源分离.
3 相关参数设定3.1 原子能量大小的设定所选择原子的能量会直接决定最小支撑集的大小, 若所选择能量太大, 最小支撑集中所含原子数目也会随之增多, 很有可能会超过稀疏度K, 导致源信号恢复失败;若所选择原子的能量太小, 最小支撑集中所含原子数目也会随之减少, 迭代次数增加.综合考虑迭代次数与恢复精度的影响, 本文选择原子的能量为原子总能量的20%.
3.2 正则化过程阈值设定正则化过程中阈值选取区间为(0, 0.35), 经过多次仿真实验, 发现阈值系数设定为0.15时, 所需迭代次数最少, 并且此时的源信号恢复结果也较为理想, 故本文在确定最小支撑集时, 正则化过程的阈值系数设定为0.15.
3.3 迭代步长大小的设定迭代步长的选择应同时兼顾恢复精度与迭代次数, 故在设定时不仅应该远小于信号稀疏度K, 而且设定值不能太小.本文中最小支撑集大小的确立满足以上两条原则, 故迭代步长的大小设定为最小支撑集大小的一半, 即S=Q/2.
4 仿真实验4.1 一维稀疏信号的仿真实验本文选择三路一维稀疏源信号对OMP算法、SP算法及OS-SASP算法进行仿真实验, 选择的三路一维随机稀疏信号为
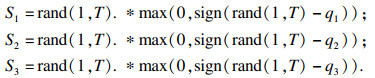 |
图 3(Fig. 3)
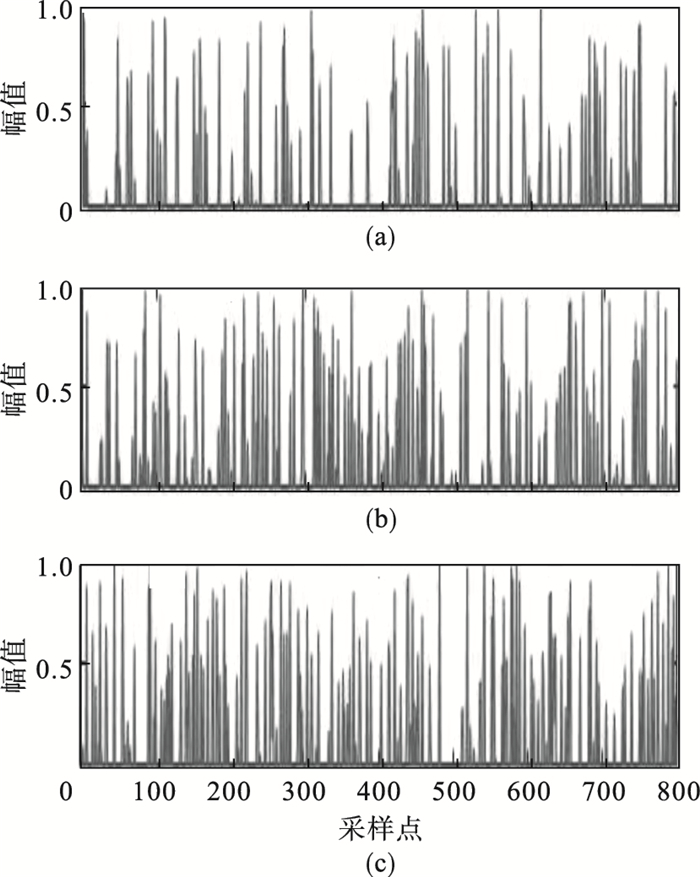 | 图 3 三路源信号Fig.3 Three source signals (a)—输入信号1;(b)—输入信号2;(c)—输入信号3. |
将三路一维稀疏源信号由2×3维的观测矩阵
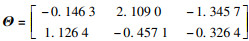
图 4(Fig. 4)
 | 图 4 混合后的两路观测信号Fig.4 Two mixed observation signals (a)—混合信号1;(b)—混合信号2. |
利用OMP算法进行盲源分离, 恢复出的源信号如图 5所示.
图 5(Fig. 5)
 | 图 5 OMP算法恢复出的源信号Fig.5 Source signal recovered by OMP algorithm (a)—OMP分解信号1;(b)—OMP分解信号2;(c)—OMP分解信号3. |
利用SP算法进行盲源分离, 恢复出的源信号如图 6所示.
图 6(Fig. 6)
 | 图 6 SP算法恢复出的源信号Fig.6 Source signal recovered by SP algorithm (a)—SP分解信号1;(b)—SP分解信号2;(c)—SP分解信号3. |
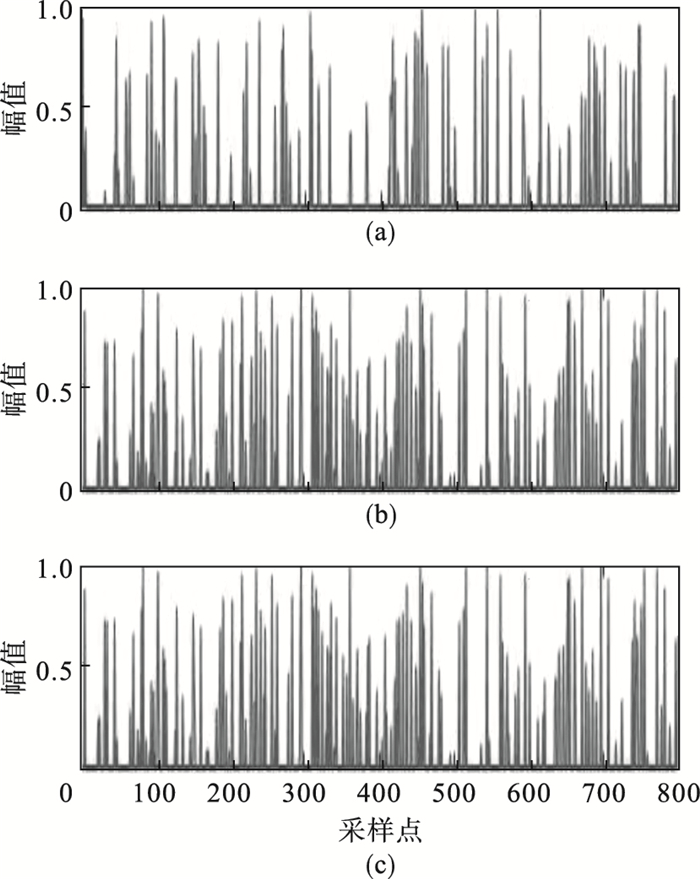
利用OS-SASP算法进行盲源分离, 选取ε1=0.01, ε2=0.05为最优阈值系数, 恢复出的源信号如图 7所示.
图 7(Fig. 7)
 | 图 7 OS-SASP算法恢复出的源信号Fig.7 Source signal recovered by OS-SASP algorithm (a)—改进SP分解信号1;(b)—改进SP分解信号2;(c)—改进SP分解信号3. |
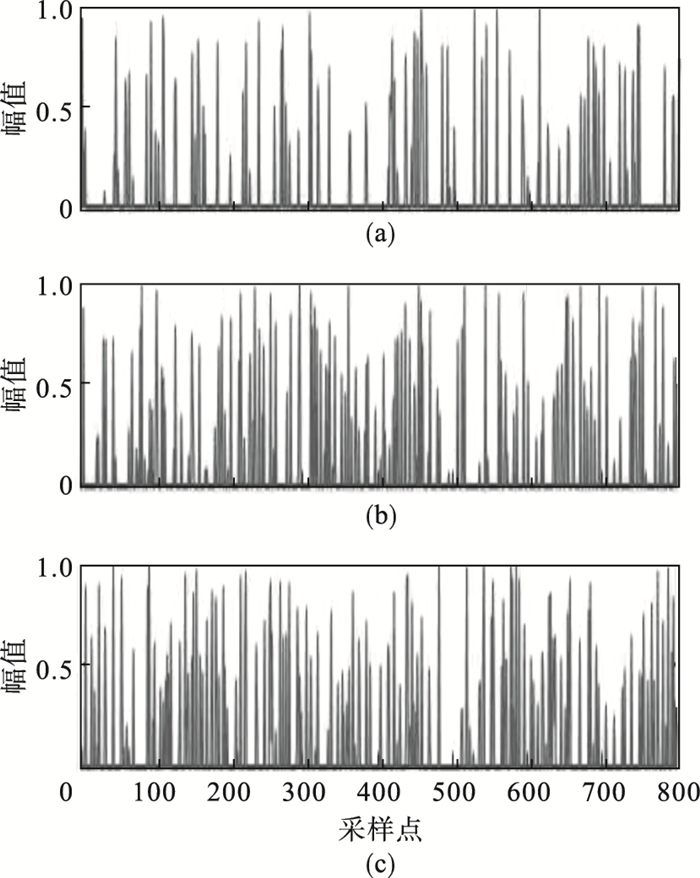
4.2 语音信号的仿真实验语音信号与一维稀疏信号相比存在很大的差异, 其波形图相对来说更加复杂, 在时域并不满足稀疏性.但贪婪类算法在进行欠定盲源分离时, 源信号的恢复精度与信号的稀疏性密切相关, 具体来说就是稀疏性越强, 恢复精度越高.首先利用2×3维的观测矩阵对三路语音信号进行混合, 对混合之后的两路观测信号进行快速傅里叶变换, 增强信号的稀疏性, 在频域完成欠定盲源分离源信号的恢复, 对恢复出的三路信号进行快速傅里叶逆变换, 得到其在时域的波形图.三路语音信号在时域的波形图如图 8所示.
图 8(Fig. 8)
 | 图 8 三路源信号Fig.8 Three source signals (a)—输入信号1;(b)—输入信号2;(c)—输入信号3. |
将三路语音源信号由2×3维的观测矩阵

图 9(Fig. 9)
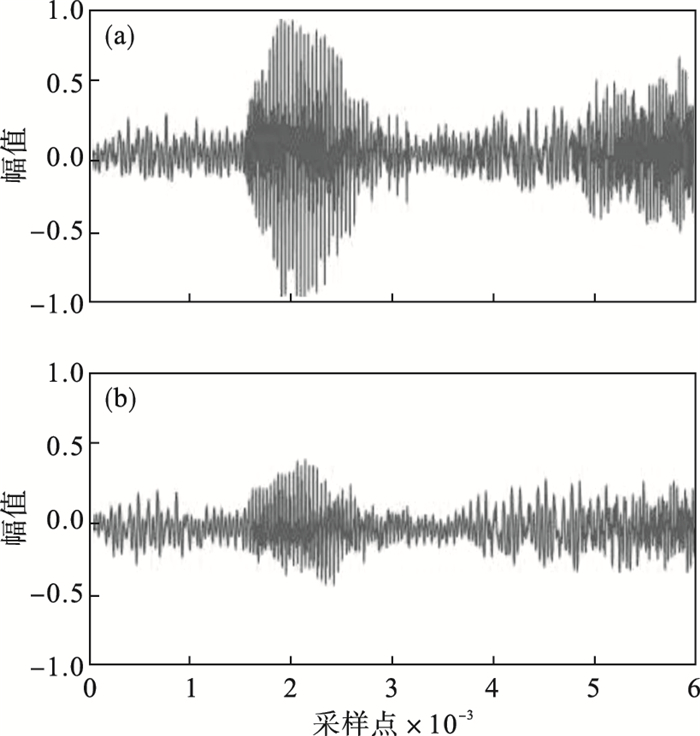 | 图 9 混合后的两路观测信号Fig.9 Two mixed observation signals (a)—混合信号1;(b)—混合信号2. |
利用OMP算法进行盲源分离, 恢复出的源信号如图 10所示. 利用SP算法进行盲源分离, 恢复出的源信号如图 11所示. 利用OS-SASP算法进行盲源分离, 恢复出的源信号如图 12所示.
图 10(Fig. 10)
 | 图 10 OMP算法恢复出的源信号Fig.10 Source signal recovered by OMP algorithm (a)—OMP分解信号1;(b)—OMP分解信号2;(c)—OMP分解信号3. |
图 11(Fig. 11)
 | 图 11 SP算法恢复出的源信号Fig.11 Source signal recovered by SP algorithm (a)—SP分解信号1;(b)—SP分解信号2;(c)—SP分解信号3. |
图 12(Fig. 12)
 | 图 12 OS-SASP算法恢复出的源信号Fig.12 Source signal recovered by OS-SASP algorithm (a)—改进SP分解信号1;(b)—改进SP分解信号2;(c)—改进SP分解信号3. |
4.3 算法性能分析对于一维稀疏信号的欠定盲源分离, 本文通过均方差与信噪比两项技术指标, 分别对OMP算法、SP算法及本文提出的OS-SASP算法进行对比分析.表 1是3种算法的均方差对比结果, 表 2是3种算法的信噪比对比结果.
表 1(Table 1)
| 表 1 3种算法的均方差 Table 1 MSE of three algorithms |
表 2(Table 2)
| 表 2 3种算法的信噪比 Table 2 SNR of three algorithms |
对于语音信号的欠定盲源分离, 本文通过相似系数, 分别对OMP算法, SP算法及本文提出的OS-SASP算法进行对比分析.表 3是3种算法的相似系数对比结果.
表 3(Table 3)
| 表 3 3种算法的相似系数 Table 3 Similarity coefficient of three algorithms |
由表 1和表 2可以看出, 本文所提出的OS-SASP算法在进行一维稀疏信号恢复时, 均方差和信噪比两项技术指标都明显优于其他两种算法, 其中均方差的大小控制在0.002的范围之内, 仅为其他两种算法的1/2;信噪比保持在40以上, 相比其他两种算法提高了8 dB左右.
由表 3可以看出, 本文所提出的OS-SASP算法在进行语音信号恢复时, 3路信号的相似系数均明显优于其他2种算法, 能够保持在0.9以上.
5 结论对欠定盲源分离中的源信号恢复展开研究, 提出了一种基于优化支撑的稀疏度自适应子空间追踪算法.与基于子空间追踪的欠定盲源分离源信号恢复算法相比, 本文算法对初始支撑集的选取进行优化, 同时利用自适应变步长的方式在逼近稀疏度K的同时恢复源信号, 不仅克服了子空间追踪算法对稀疏度的依赖, 而且还显著提升信号的恢复精度.仿真实验验证了该算法的有效性.
参考文献
| [1] | 王川川, 曾勇虎. 欠定盲源分离算法的研究现状及展望[J]. 北京邮电大学学报, 2018, 41(6): 107-113. (Wang Chuan-chuan, Zeng Yong-hu. Research status and prospects of underdetermined blind source separation algorithms[J]. Journal of Beijing University of Posts and Telecommunications, 2018, 41(6): 107-113.) |
| [2] | Bofill P, Zibulevsky M. Underdetermined blind source separation using sparse representations[J]. Signal Processing, 2001, 81(11): 2353-2362. DOI:10.1016/S0165-1684(01)00120-7 |
| [3] | Yu K, Yang K, Bai Y. Estimation of modal parameters using the sparse component analysis based underdetermined blind source separation[J]. Mechanical Systems & Signal Processing, 2014, 45(2): 302-316. |
| [4] | Ren M R, Wang P. Underdetermined blind source separation based on sparse component[C]// International Conference on Electronic Computer Technology. Macau: IEEE, 2009: 174-177. |
| [5] | Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52: 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [6] | Wang C C, Zeng Y H, Wang L D. Comparison of source signal recovery algorithms based on compressed sensing for underdetermined blind source separation[J]. High Power Laser and Particle Beams, 2018, 30(5): 89-95. |
| [7] | Zhang C, Wang Y, Jing F. Underdetermined blind source separation of synchronous orthogonal frequency-hopping signals based on tensor decomposition method[J]. IEEE Access, 2018, 6: 69407-69414. DOI:10.1109/ACCESS.2018.2880237 |
| [8] | Zhen L, Peng D, Yi Z, et al. Underdetermined blind source separation using sparse coding[J]. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(12): 3102-3108. DOI:10.1109/TNNLS.2016.2610960 |
| [9] | He X S, He F, Cai W H. Underdetermined BSS based on K-means and AP clustering[J]. Circuits Systems and Signal Processing, 2016, 35(8): 2881-2913. DOI:10.1007/s00034-015-0173-7 |
| [10] | Deka B, Datta S. Compressed sensing magnetic resonance image reconstruction algorithms[M]. Bombay: Springer, 2019: 75-98. |
| [11] | Osamy W, Salim A, Aziz A. Sparse signals reconstruction via adaptive iterative greedy algorithm[J]. International Journal of Computer Applications, 2014, 90(17): 5-11. DOI:10.5120/15810-4715 |
| [12] | Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655-4666. DOI:10.1109/TIT.2007.909108 |
| [13] | Dai W, Milenkovic O. Subspace pursuit for compressive sensing signal reconstruction[J]. IEEE Transactions on Information Theory, 2009, 55(5): 2230-2249. DOI:10.1109/TIT.2009.2016006 |
| [14] | Roy A, Tariang D B, Chakraborty R S, et al. Discrete cosine transform residual feature based filtering forgery and splicing detection in JPEG images[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops(CVPRW). Salt Lake City: IEEE, 2018: 111-119. |
| [15] | 唐朝伟, 王雪锋, 杜永光. 一种稀疏度自适应分段正交匹配追踪算法[J]. 中南大学学报(自然科学版), 2016, 259(3): 80-88. (Tang Chao-wei, Wang Xue-feng, Du Yong-guang. A sparsity adaptive segmented orthogonal matching pursuit algorithm[J]. Journal of Central South University(Naturel Science), 2016, 259(3): 80-88.) |
 )
) )
) )
)