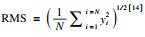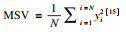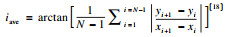, 尹宏, 张泽, 魏崴
, 尹宏, 张泽, 魏崴 东北大学 资源与土木工程学院, 辽宁 沈阳 110819
收稿日期:2020-03-03
基金项目:国家自然科学基金资助项目(U1602232);中央高校基本科研业务费专项资金资助项目(N170108029);辽宁省重点研发计划项目(2019JH2/10100035)。
作者简介:王述红(1969-),男,江苏泰州人,东北大学教授,博士生导师。
摘要:为进一步修正Grasselli结构面三维形貌参数系统, 获得一个能够反映结构面剪切机理的预测模型.深度分析视倾角和分布参数, 提出单值分布函数Aθ**, 并将其作为权重函数参与平均视倾角的计算; 定义相对分布参数C*, 揭示了分布参数对结构面抵抗剪切的控制作用; 最后, 提出一个新的峰值剪切强度预测模型, 利用国内外****发表的50组数据验证, 新模型相较于Grasselli系模型的预测精度最佳.另外, 定义了分布参数C的物理和数学边界, 从理论上解释了实验值不小于1的现象, 总结了视倾角的分布规律和初始剪胀角的构成, 将Grasselli系模型从理论上划归至统一形式.新的预测模型参数更为简洁, 物理意义和数学定义明晰, 同时能够较好地揭示结构面的剪切机理.
关键词:岩石力学结构面三维形貌峰值剪切强度分布参数
A New Prediction Model for Peak Shear Strength of Rock Joints Considering the 3D Morphology Parameters
WANG Shu-hong

 , YIN Hong, ZHANG Ze, WEI Wei
, YIN Hong, ZHANG Ze, WEI Wei School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: WANG Shu-hong, E-mail: wangshuhong@mail.neu.edu.cn.
Abstract: The apparent dip angle and the distribution parameter are camprehensively analyzed to correct Grasselli's 3D morphology parameters system as well as get a new prediction model reflecting the shear behavior of rock joints. The single-valued distribution function Aθ** is used as the weight function to calculate the average apparent dip angle. By defining the relative distribution parameters C*, revealing the control function of distribution parameters on resisting shear. A new peak shear strength prediction model is proposed. Compared with Grasselli's model, the prediction accuracy of the new model is better verified through 50 sets of published data. The physical and mathematical boundary of distribution parameter C is proposed, and the phenomenon that the value of C from experiments is not less than 1 is explained. The distribution law of apparent dip angle and the composition of initial dilatancy angle are summarized, and the Grasselli's model is classified into a unified form.The new prediction model has concise parameters, clear physical meaning and mathematical definition, and reveal the shear mechanism of rock joints.
Key words: rock mechanicrock joint3D morphologypeak shear strengthdistributed parameter
岩体中非连续结构面的物理力学性能是一个包含空间几何性状的复杂系统.事实证明, 岩体的工程性失稳和地质类灾害大部分与结构面对岩体力学性能的削弱效应[1]密切相关, 尤以剪切性能的表现最为突出.合理构建剪切强度预测模型符合一般物理学意义, 对于实际工程应用和揭示岩石力学响应机制具有重大意义.从宏观而言, 岩石节理适用于普通物理学中的库伦-阿蒙顿定律, 即理想状态下的岩体节理面法向应力和节理面粗糙程度是决定剪切强度的主要指标, 1776年库伦建立了其在岩石力学范围内的基本形式τb=σntanφb+c, 在此基础上用剪胀角模型表征粗糙度以在形式上符合莫尔库伦定律成为该领域研究的主要方向, 其关键在于:①定义粗糙度指标定量表征结构面形貌; ②确定合适的初始剪胀角和峰值剪胀角的关系函数.
结构面形貌的表征限于测量手段经历了一个从二维到三维的过程, 大体上可视为JRC-JCS经典模型的进一步展拓.一方面许多统计参数沿用了将结构面离散为剖切轮廓线的思路, 侧重起伏高、起伏角或接触度参数的不同权重的表征, 部分****基于此加密剖切轮廓线将二维参量推广至三维, 并发展一系列强度模型; 另一方面JRC作为国际岩石力学学会(ISRM)认定的统一标准[2],成为诸多****验证新参数精确度和可靠性的重要指标.但是基于二维轮廓线的形貌表征是以牺牲精度为前提的, 无法有效描述形貌的空间展布.自Mandelbrot[3]提出分形理论以来, 分形维数被广泛应用于结构面形貌表征, 但其本质依旧是对剖切轮廓线的起伏程度的表征, 无法体现形貌的三维特性[4].伴随着三维激光扫描、三维结构光测量、摄影测量技术的发展, 部分****提出了基于表征起伏程度空间分布的思路.葛云峰等[5]通过虚拟光源照射结构面表面, 在灰度阈值140的设定下基于图像处理技术提出了光亮面积百分比BAP的表征参数; 蔡毅等[6]将潜在接触部分沿垂直于剪切方向的投影与水平向的投影的比值PAP作为表征参数; 葛云峰等[7]报道了结构面的形貌特征与抵抗剪切时产生的热量具有相关性, 提出了基于能量思想的结构面形貌表征的新思路, 上述方法对测量设备和外部环境的包容性较差, 难以在工程实际条件下实现, 仅停留在理论阶段.
Grasselli等[8-10]基于剪切向视倾角分布的概念提出一套三维形貌表征系统, 得到国内外****的广泛认可.经过众多****的不断完善和发展形成了Grasselli系模型, 由此衍生出一系列峰值剪切强度预测模型.随着剪切行为过程的进一步揭示, 背剪向的形貌特征也逐渐受到重视.Xia等[11-12]的研究表明, 剪切破坏以结构面表面凸体微元的受拉破坏为主, 因此模型中, 应当使用岩石抗拉强度σt表征材料特性, 通常采用劈裂抗拉强度.
本文基于Grasselli三维形貌参数系统, 推导并讨论分布参数的数学和物理意义, 将初始剪胀角与视倾角分布规律相联系, 解释部分****报道的有关实验现象, 修正Grasselli强度模型, 提出新的预测模型并论证合理性, 以期为相关研究提供参考.
1 Grasselli三维形貌表征1.1 Grasselli三维形貌参数测算方法Grasselli等[8-10]利用数字光栅-双目成像设备(图 1)在实验室范围内对不同类型岩石标准试件的结构面表面三维形貌进行测量, 生成点云模型并进行三角网格化, 在此基础上提出了视倾角θ*的概念, 并建立凸体表面外法向量和剪切方向的数学关系(图 2).
图 1(Fig. 1)
 | 图 1 测量原理示意图Fig.1 Measurement principle |
图 2(Fig. 2)
 | 图 2 Grasselli’s结构面三维形貌表征及其计算模型Fig.2 Grasselli's morphology characterization of rock joints in 3D and its calculation model |
 | (1) |
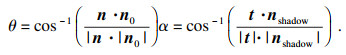 | (2) |
Grasselli模型被认为是一套真正意义上的对结构面表面形貌的三维表征理论[13].与其他统计参数(表 1)以表面剖切曲线特征(图 3)为控制参量在二维层面表征并向三维扩展的思路不同, Grasselli模型将视倾角θ*的空间分布作为表征结构面粗糙度的控制参量, 并通过大量实验和统计规律建立了视倾角空间分布的数学表达:
表 1(Table 1)
| 表 1 部分结构面形貌二维表征统计参数 Table 1 Statistical morphology parameters of rock joints in 2D |
图 3(Fig. 3)
 | 图 3 二维形貌表征示意图Fig.3 Morphology characterization in 2D |
 | (3) |
1.2 Grasselli系节理峰值剪切强度预测模型Grasselli将θmax*/C作为表征结构面形貌的粗糙度指标, 并由此导出了峰值抗剪强度的计算公式:
 | (4) |
该模型将θmax*/C的组合参量通过放大法系数的形式反映结构面形貌抵抗剪切的能力, 一方面θmax*和C的组合缺乏物理释义, 另一方面在形式上不符合莫尔-库伦的形式[11], 同时C值的量纲在视倾角的分布函数和峰值剪切强度模型中不统一.
Grasselli三维形貌参数的实质是对起伏角参数的空间面积分布做定量表征, 用C值控制(图 4).类似于颗粒集配曲线的概念, 分布函数是一个累进函数, 将式(3)左右两侧对θ*求二阶导可得
图 4(Fig. 4)
 | 图 4 视倾角分布函数Fig.4 Distribution function of apparent dip angle |
 | (5) |
 | (6) |
在此基础上, 国内外****通过建立初始剪胀角与峰值剪胀角的函数关系获得形式上符合莫尔-库伦的峰值剪切强度预测模型:
 | (7) |
表 2(Table 2)
| 表 2 Grasselli系结构面峰值剪切强度预测模型及其初始剪胀角 Table 2 Grasselli's prediction model of peak shear strength of joints and its initial dilatancy angle |
进一步分析Grasselli系峰值剪切强度预测模型, 以Grasselli三维形貌参数为支撑的粗糙度表达真正意义上反映了形貌特征对剪切强度的贡献, 模型通过描述初始剪胀角和峰值剪胀角的函数关系解释了剪切过程的强度演变.但模型在边界上缺乏数学定义, 同时多项参数的物理释义不明确, 量纲导出不统一, Yang模型[26-27]以材料抗压强度作为材料本征性质与节理在剪切时以凸体受拉破坏为主的结论相矛盾, Tian模型[25]的初始剪胀角是一个经验模型, 对于结构形貌与剪切行为的考察上, 凸体迎剪向的不同视倾角对抵抗剪切的贡献不明确.
2 初始剪胀角2.1 视倾角分布规律Grasselli三维形貌参数通过方位角α将凸体倾角转化至剪切方向, 定义为视倾角, 其实质是从空间角度反映单个凸体沿剪切方向的起伏度, 对于吻合新鲜结构面而言, 峰值剪切强度主要取决于小部分较陡的凸体微元, 陈曦等[29]将分布函数与土颗粒集配分析曲线做类比, 指明其“累积”的特性, 将分布函数做变式:
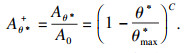 | (8) |
为进一步研究视倾角在某一数值上的分布, 定义Aθ*+反映某一视倾角的凸体面积与迎剪向凸体面积的比值, 可表达为
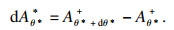 | (9) |
 | (10) |
 | (11) |
 | (12) |
 | (13) |
1) 结构面形貌受凸体微元的迎剪向视倾角控制, 在空间的位置分布上受结构面生成方式的影响具有随机性.
2) 凸体微元迎剪向视倾角的分布通过分布函数和单值分布函数共同描述, 前者反映其累积特性, 与剪切强度密切相关, 后者反映其在数值上的分布.
3) 凸体微元迎剪向视倾角的数值分布呈现平缓视倾角含量占比远高于较陡视倾角含量占比的规律.
2.2 初始剪胀角部分****的研究结果表明结构面的抗剪强度主要受少数迎剪向较陡视倾角的凸体微元控制, 大多数平缓凸体不参与抗剪过程[4].陈曦等[29]通过拟合的方式定义了临界视倾角θcr*, 即参与抵抗剪切能力的最小视倾角, 以占比含量表示, 并引入反映累计特性的分布函数变式作为权重值进一步强化了较陡视倾角的抗剪贡献, 由此计算了平均视倾角.考虑到2.1节提出的单值分布函数, 临界视倾角θcr*也可作如下定义.
将单值分布函数(式(13))作为权重函数代入计算平均视倾角.
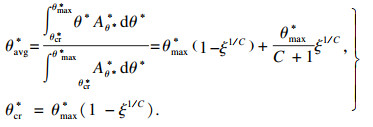 | (14) |
进一步分析式(14), 导出的平均视倾角即初始剪胀角实质上由两部分组成, 即
 | (15) |
 | (16) |
从机理上而言, i01反映的是剪胀角中需要克服较大视倾角的部分, i02反映的是剪胀角中受分布参数调配的需要克服的次大视倾角的部分.对于天然非规则的结构面而言, 需要克服的主要是接近最大视倾角的剪胀角部分.结合前述数学推导, 可将初始剪胀角进一步简化为i01.
3 视倾角空间分布参数C的讨论3.1 分布参数C的边界和取值范围分布参数C反映结构面表面凸体迎剪向视倾角的空间分布, 实质是一个拟合参数用以描述结构面形貌的粗糙特征.Tian等[25]指出C值是一个对结构面抵抗剪切强度的控制性指标, 但C值在Grasselli系模型中的量纲因兼顾粗糙度系数和关系函数导致量纲导出无法统一, 同时角度值的计算单位出现混乱.在边界处Tatone等[21]作了如下定义: C=0时, 结构面形貌呈现规则锯齿形, 迎剪向抗剪能力最大;C→∞时为光滑结构面, 迎剪向抗剪能力最小.这一观点被国内外****广泛接受, 但该推论缺乏理论支撑, 同时对于C值左边界的取值存在实验统计结果的奇异.为此, 利用分布函数的变式作如下推导:
将式(8)左右取对数:
 | (17) |
当C→∞时, (θmax*-θ*)=ο(θmax*), 即?θ*→0, θ*∈[0, θmax*), 结构面形貌趋向于平坦光滑, 此时的抗剪强度最小.
当C≤1时, 即
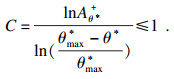 | (18) |
 | (19) |
 | (20) |
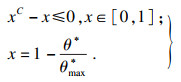 | (21) |
图 5(Fig. 5)
 | 图 5 C分布规律Fig.5 C distribution |
需要说明的是, 修正后的C值取值范围左边界存在数学边界和物理边界两个概念, 前者是依据理论推导和实验数据确定的实际取值边界, 后者从结构面形貌的角度定义了一个理想边界, 用以反映绝对光滑平坦的结构面形貌, 而在右边界的数学边界和物理边界在理论推导和形式上都得到了统一.
3.2 相对分布参数C*的提出Gressalli三维形貌参数中, A0和θmax*对结构面抗剪能力的控制作用远远不及分布参数C, 如前文所述,为了突出C值的影响, 部分****在实验数据统计的基础上将A0直接定义为0.5[22], 但是越来越多的数据表明(图 6), A0的取值范围大致分布在0.4~0.6之间, 由于A0的相对独立性, 该误差通过θmax*/A0(C+1)可以放大到10倍, 因此不能简单地将A0取值为0.5, 应当做数据拟合.另一方面, 实验研究表明θmax*的变化通过C值的调配, θmax*/A0(C+1)的取值保持稳定[25], 再一次表明了分布参数C的控制作用.
图 6(Fig. 6)
 | 图 6 A0分布规律Fig.6 A0 distribution |
为了进一步凸显C值的作用, 本文提出相对分布参数C*的概念, 其定义可由分布函数变式而来:
 | (22) |
 | (23) |
4 新峰值剪切强度预测模型4.1 新模型建立2.2节中, 利用临界视倾角和单值分布函数计算出了平均视倾角, 将根据剪切行为过程和数学计算简化的剪胀角与Grasselli系模型[11-12]中的初始剪胀角作等效, 有
 | (24) |
 | (25) |
表 3(Table 3)
| 表 3 岩石结构面三维形貌参数及实测峰值剪切强度(Yang[26-27]) Table 3 Morphology parameters of rock joints in 3D and measured peak shear strength, Yang[26-27] |
表 4(Table 4)
| 表 4 岩石结构面三维形貌参数及实测峰值剪切强度(Grasselli[7-9]) Table 4 Three-dimensional morphology parameters of rock joints and measured peak shear strength(Grasselli[7-9]) |
 | (26) |
 | (27) |
 | (28) |
 | (29) |
根据3.2节中提出的简化假设, 考虑到ξ为一个偏小值, 确定临界视倾角为近似等于对应A0值为0.15 % 时的视倾角, 即ξ=0.0015.
由此导出峰值抗剪强度模型:
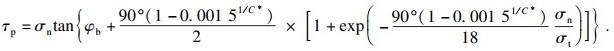 | (30) |
 | (31) |
5 结论1) 新模型与Grasselli系模型相比, 预测精度较高, 同时参数指标划归为相对分布参数C*的单一参数, 将Grasselli系模型统一为对临界视倾角数值的确定上, 解释了初始剪胀角的构成与剪切过程行为的关系.
2) 提出结构面形貌的单值分布函数, 在此基础上总结了结构面形貌凸体微元迎剪向视倾角的分布规律主要为较陡视倾角占比远大于较缓视倾角占比, 分布函数反映累进特性, 单值分布函数反映数值分布.
3) 通过数学推导确定了分布参数的边界, 定义了物理左边界和数学左边界, 推导出分布参数C的取值范围为[1, ∞).
4) 定义了相对分布参数C*, 将最大视倾角和初始接触比对抗剪能力的间接贡献通过分布参数C反映出来, 进一步揭示了形貌特征和剪切行为的过程机理.
参考文献
| [1] | Zhang X B, Jiang Q H, Chen N, et al. Laboratory investigation on shear behavior of rock joints and a new peak shear strength criterion[J]. Rock Mechanics and Rock Engineering, 2016, 49(9): 3495-3512. DOI:10.1007/s00603-016-1012-2 |
| [2] | Barton N, Choubey V. The shear strength of rock joints in theory and practice[J]. Rock Mechanics and Rock Engineering, 1977, 10(1): 1-54. |
| [3] | Mandelbrot B B. How long is the coast of Britain[J]. Science, 1967, 156(3775): 636-638. DOI:10.1126/science.156.3775.636 |
| [4] | Grasselli G. Shear strength of rock joints based on quantified surface description[D]. Switzerland: Swiss Federal Institute of Technology, 2001. |
| [5] | 葛云峰. 基于BAP的岩体节理面粗糙度与峰值抗剪强度研究[D]. 武汉: 中国地质大学(武汉), 2014. (Ge Yun-feng. Research on roughness and peak shear strength for rock discontinuties based on BAP[D]. Wuhan: China University of Geosciences(Wuhan), 2014. ) |
| [6] | 蔡毅, 唐辉明, 葛云峰, 等. 岩体结构面三维粗糙度评价的新方法[J]. 岩石力学与工程学报, 2017, 36(5): 1101-1110. (Cai Yi, Tang Min-hui, Ge Yun-feng, et al. A new method for evaluating the roughness of three-dimensional discontinuity surface of rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(5): 1101-1110.) |
| [7] | 葛云峰, 唐辉明, 程昊, 等. 基于直剪试验的岩体结构面表面温度与粗糙度关系研究[J]. 工程地质学报, 2015(4): 624-633. (Ge Yun-feng, Tang Hui-ming, Cheng Hao, et al. Direct shear tests study for relationship between surface temperature and surface roughness of rock joints[J]. Journal of Engineering Geology, 2015(4): 624-633.) |
| [8] | Grasselli G, Egger P. Constitutive law for the shear strength of rock joints based on three-dimensional surface parameters[J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(1): 25-40. DOI:10.1016/S1365-1609(02)00101-6 |
| [9] | Grasselli G, Wirth J, Egger P. Quantitative three-dimensional description of a rough surface and parameter evolution with shearing[J]. International Journal of Rock Mechanics and Mining Sciences, 2002, 39(6): 789-800. DOI:10.1016/S1365-1609(02)00070-9 |
| [10] | Grasselli G. Manuel rocha medal recipient shear strength of rock joints based on quantified surface description[J]. Rock Mechanics and Rock Engineering, 2006, 39(4): 295. DOI:10.1007/s00603-006-0100-0 |
| [11] | Xia C C, Tang Z C, Xiao W M, et al. New peak shear strength criterion of rock joints based on quantified surface description[J]. Rock Mechanics and Rock Engineering, 2014, 47(2): 387-400. DOI:10.1007/s00603-013-0395-6 |
| [12] | 唐志成, 夏才初, 宋英龙, 等. Grasselli节理峰值抗剪强度公式再探[J]. 岩石力学与工程学报, 2012, 31(2): 356-364. (Tang Zhi-cheng, Xia Cai-chu, Song Ying-long, et al. Discussion about Grasselli′s peak shear strength criterion for rock joints[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(2): 356-364. DOI:10.3969/j.issn.1000-6915.2012.02.015) |
| [13] | 夏才初, 唐志成, 宋英龙. 基于三维形貌参数的偶合节理峰值抗剪强度公式[J]. 岩石力学与工程学报, 2011, 32(sup1): 2833-2839. (Xia Cai-chu, Tang Zhi-cheng, Song Ying-long. A new peak shear strength formula for matching irregular joints based on 3D morphology parameters[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 32(sup1): 2833-2839.) |
| [14] | Tse R, Cruden D M. Estimating joint roughness coefficients[J]. Iternational Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1979, 16(5): 303-307. |
| [15] | Lee S D, Lee C I, Park Y. Characterization of joint profiles and their roughness parameters[J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(3/4): 174.e1-174.e5. |
| [16] | Zhang G C, Karakus M, Tang H M, et al. A new method estimating the 2D joint roughness coefficient for discontinuity surfaces in rock masses[J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 72: 191-198. DOI:10.1016/j.ijrmms.2014.09.009 |
| [17] | Sayles R S, Thomas T R. The spatial representation of surface roughness by means of the structure function: a practical alternative to correlation[J]. Wear, 1977, 42(2): 263-276. DOI:10.1016/0043-1648(77)90057-6 |
| [18] | Yu X B, Vayssade B. Joint profiles and their roughness parameters[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1991, 28(4): 333-336. |
| [19] | Myers N O. Characterization of surface roughness[J]. Wear,, 1962, 5(3): 182-189. DOI:10.1016/0043-1648(62)90002-9 |
| [20] | Maerz N H, Franklin J A, Bennett C P. Joint roughness measurement using shadow profilometry[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1990, 27(5): 329-343. |
| [21] | Tatone B S, Grasselli G. A method to evaluate the three dimensional roughness of fracture surfaces in brittle geomaterials[J]. Review of Scientific Instruments, 2009, 80(12): 181-106. |
| [22] | Liu Q S, Tian Y C, Liu D F, et al. Updates to JRC-JCS model for estimating the peak shear strength of rock joints based on quantified surface description[J]. Engineering Geology, 2017, 228: 282-300. DOI:10.1016/j.enggeo.2017.08.020 |
| [23] | 唐志成, 刘泉声, 刘小燕. 节理的剪切力学性质与含三维形貌参数的剪切强度准则比较研究[J]. 岩土工程学报, 2014, 36(5): 873-879. (Tang Zhi-cheng, Liu Quan-sheng, Liu Xiao-yan. Shear behavior of rock joints and comparative study on shear strength criteria with three-dimensional morphology parameters[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(5): 873-879.) |
| [24] | 唐志成, 夏才初, 宋英龙. 粗糙节理的峰值抗剪强度准则[J]. 岩土工程学报, 2013, 35(3): 571-577. (Tang Zhi-cheng, Xia Cai-chu, Song Ying-long. New peak shear strength criteria for roughness joints[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(3): 571-577.) |
| [25] | Tian Y C, Liu Q S, Liu D F, et al. Updates to Grasselli's peak shear strength model[J]. Rock Mechanics and Rock Engineering, 2018, 51(7): 2115-2133. DOI:10.1007/s00603-018-1469-2 |
| [26] | Yang J, Rong G, Hou D, et al. Experimental study on peak shear strength criterion for rock joints[J]. Rock Mechanics and Rock Engineering, 2016, 49(3): 821-835. DOI:10.1007/s00603-015-0791-1 |
| [27] | 杨洁, 荣冠, 程龙, 等. 节理峰值抗剪强度试验研究[J]. 岩石力学与工程学报, 2015, 34(5): 884-894. (Yang Jie, Rong Guan, Cheng Long, et al. Experimental study of peak shear strength of rock joints[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(5): 884-894.) |
| [28] | Tatone B S A. Quantitative characterization of natural rock discontinuity roughness in-situ and in the laboratory[D]. Toronto: University of Toronto, 2010. |
| [29] | 陈曦, 曾亚武, 孙翰卿, 等. 基于Grasselli形貌参数的岩石节理初始剪胀角新模型[J]. 岩石力学与工程学报, 2019, 38(1): 133-152. (Chen Xi, Zeng Ya-wu, Sun Han-qing, et al. A new model of the initial dilatancy angle of rock joints based on Grasselli's morphological parameters[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(1): 133-152.) |