
 , 李勃, 郭广勇
, 李勃, 郭广勇 吉林大学 机械与航空航天工程学院, 吉林 长春 130025
收稿日期:2021-01-04
基金项目:国家自然科学基金资助项目(51775225)。
作者简介:张灏岩(1996-),女,满族,河北承德人,吉林大学硕士研究生。
摘要:在进行机械结构可靠性分析时, 由于很多工程问题的性能函数较为复杂, 计算成本很高, 所以常采用代理模型拟合隐式性能函数来降低计算成本.为了能够利用较少的样本信息, 获得较高的可靠度计算精度, 将Kriging代理模型与学习函数相结合, 提出一种主动学习可靠性分析计算方法.该方法找出学习效果最好的样本点对Kriging模型进行更新, 提高了模型的拟合精度.用马尔科夫链蒙特卡洛(MCMC)方法对结构的可靠性进行了评估, 加快了样本点的收敛速度, 节约了样本空间.通过分析4个算例的结果表明与其他方法相比, 该方法能通过较少的样本点得到精度更高的计算结果, 降低了计算成本.
关键词:可靠性KrigingMCMC主动学习失效概率
Active Learning Algorithm of Structural Reliability Based on Kriging and MCMC
ZHANG Hao-yan, BI Qiu-shi

 , LI Bo, GUO Guang-yong
, LI Bo, GUO Guang-yong School of Mechanical and Aerospace Engineering, Jilin University, Changchun 130025, China
Corresponding author: BI Qiu-shi, E-mail: bqs@jlu.edu.cn.
Abstract: Because the performance functions of many engineering problems are more complicated and the calculation cost is high in the reliability analysis of mechanical structures, the agent model is often used to fit the implicit performance function to reduce the calculation cost. In order to use less sample information and obtain higher reliability calculation accuracy, the Kriging agent model is combined with the learning function, and an active learning reliability analysis and calculation method is proposed. This method finds the sample points with the best learning effect to update the Kriging model, which improves the fitting accuracy of the model. Markov chain Monte Carlo(MCMC)method is used to evaluate the reliability of the structure, which speeds up the convergence speed of sample points and saves sample space. Analyzing the results of 4 calculation examples shows that compared with the other methods, this method can obtain higher precision calculation results with fewer sample points, and reduce the calculation cost.
Key words: reliabilityKrigingMCMCactive learningfailure probability
可靠性分析是对结构或系统在给定条件下的安全性进行度量, 在实际工程问题中越来越被人们所重视, 因此可靠性分析方法也得到了广泛发展和深入研究.其中常用的分析方法可分为三类: 基于矩的方法、抽样方法和代理模型方法.在基于矩的常见方法中, 一阶和二阶可靠性方法(FORM, SORM)是一类在可靠性研究的早期阶段就被提出的传统方法, 但对于高度非线性的性能函数或具有多个最大可能失效点的性能函数, 解可能具有较大误差[1].在抽样方法中, 蒙特卡洛(MC)方法由于其易实现和高精度而被广泛使用, 但该方法需计算所有样本的功能函数值, 当功能函数为复杂的计算模型时, 其计算成本非常高.为了降低计算成本, 利用子集模拟方法、重要性采样方法和线采样方法等减少样本点, 但这些方法依然不能满足某些更复杂的可靠性问题对计算效率的要求.由于前两类分析方法在精度和计算成本上常存在问题, 近些年来通过采用代理模型计算结构可靠性的方法得到了迅速发展.通过创建代理模型来模拟高精度或复杂模拟模型既能减小计算量又能得到与原模型非常接近的计算结果.常见的代理模型包括多项式响应面方法(response surface methodology), 神经网络(neural network), 支持向量机(support vector machine), 多项式混沌展开(polynomial chaos expansion), 克里金法(Kriging)等.其中, Kriging模型是一种插值方法, 能够获得随机过程中的最优线性无偏估计.此外, 还能够获得克里金方差, 该值可量化克里金模型的局部精度或性能函数值的局部认知不确定性.因此, 很多****都基于Kriging模型对结构进行了可靠性分析[2-3].为了提高分析方法的性能, 文献[4-6]将新的抽样方法与拟合函数相结合, 文献[6-7]对Kriging模型中的参数进行了相关优化, 文献[8-9]利用自主选点函数拟合函数的样本点.在对结构可靠性进行评估时, 文献[10]采用了基于MC方法的评估模型.以上研究方法常存在以下不足之处: ①对可靠性的评估效率偏低或评估结果不够准确, 常用的MC方法需要大量的样本点才能获得较为准确的数值; MC的抽样方法产生独立随机序列, 样本之间没有关系, 而在实际工程中, 机械结构失效原因之间可能存在一定关联.②不能对样本点充分利用, 导致结果不够准确,或过多选择样本点增加计算成本, 降低了计算效率.
针对上述问题, 提出了一种基于Kriging和MCMC的结构可靠性主动学习算法.该方法将Kriging代理模型方法与拉丁超立方抽样方法相结合, 利用学习函数自适应选点, 充分使用所选样本点的信息, 实现模型自主学习的功能, 减少了所需样本点数目.将基于马尔科夫链的蒙特卡洛(MCMC)方法引入结构可靠性分析中, 克服了蒙特卡洛(MC)方法的收敛效率低、静态性、维数高的缺点.
1 Kriging模型的基本原理Kriging模型是一种高效的插值方法, 在构造响应值y(x) 与输入变量x之间的关系时, 通常认为Kriging模型由多项式和随机分布两部分组成:
 | (1) |
其协方差为
 | (2) |
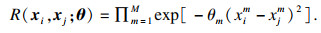 | (3) |
待测点估计和方差分别为
 | (4) |
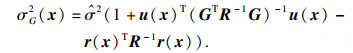 | (5) |
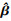
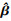
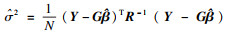
 |
2.1 马尔科夫链若序列x0, x1, x2, …, xk+1产生于{xk+1|xk} 的条件概率分布, 且条件概率满足:
 |
当k→∞时, xk与初始值无关, 即当k增大时, 马尔科夫链中随机向量将收敛于稳态分布π(x), 此时认为马尔科夫链为收敛状态.在马尔科夫链未达到收敛状态期间时, 认为各状态的概率密度分布不能达到平稳分布.因此在评估时, 应去掉未达到稳态分布状态的前M次采样值, 采用后n-M个采样值进行评估:
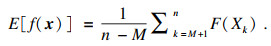 | (6) |
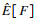
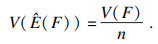 | (7) |
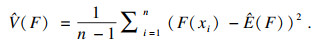 | (8) |
2.2 Mente Carlo方法设结构的功能函数为Z=g(X), 基本随机变量X的联合概率密度函数为f(x).功能函数值Z=g(X)为根据函数f(x)对X进行随机抽样后计算所得.如果Z < 0, 可认为结构失效一次.如果总模拟次数为N, 其中随机事件Z < 0的次数为nf, 则依据大数定律的相关理论可知, 随机事件Z < 0在N次独立试验中的频率nf收敛于此事件的概率pf:
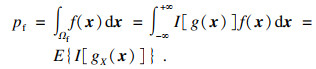 | (9) |
令随机变量X的第i个样本值为xi, 那么结构失效概率pf的估计值为
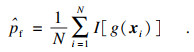 | (10) |

 | (11) |

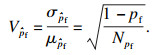 | (12) |
3.1 U函数原理根据Echard等[9]提出的理论, 主动学习函数U定义如下:
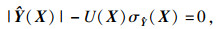 |
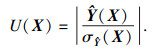 |
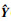
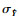
U(X) 可以作为反映一个点被错误归类的几率的可靠性指标, 令U(X)值最小的点被错误分类的几率最大, 所以要在待估计的点中找到令U(X)最小的值.在应用学习函数训练Kriging模型时, 需要一个停止准则来停止训练过程.根据相关研究可知, U=2代表在这一点上出错的概率φ(2)=0.023, 即U=2可以保证估计结果的高精度, 所以本文的停止准则定义为min(U(X)) ≥2.
3.2 基本步骤基于Kriging模型和MCMC法提出机构可靠性分析主动算法, 该方法流程如图 1所示.
图 1(Fig. 1)
 | 图 1 算法流程图Fig.1 Algorithm flow chart |
4 算例4.1 算例1本算例为一个经典二维随机变量小失效概率的例子[6].功能函数为
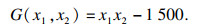 |
用AK-MCMC算法对函数进行计算, 比较选取不同数量的初始样本点对计算结果的影响, 结果如表 1所示.
表 1(Table 1)
| 表 1 算例1不同初始样本点个数的AK-MCMC计算结果 Table 1 Calculation results of AK-MCMC with different initial sample numbers in example 1 |
AK-MCMC算法表示本文提出的基于Kriging模型和MCMC法的可靠性主动学习算法, 样本点数表示所需调用真实功能函数的样本点数量, 由初始样本点和自适应学习样本点两部分共同组成; tcpu表示MATLAB软件运行算法时, 计算机CPU的计算时间; ε表示所得失效概率相比于MC法的相对误差, 其中ε=|pf-pf, MC|/pf, MC.
由表 1计算结果可知, 在初始样本数达到6个之后, 不同初始样本点个数的条件下计算结果差距不大, 所得失效概率以及相对误差均基本稳定.CPU的计算时间也较为接近.
由上述试验对算例1的计算结果可知, 当初始样本数目达到6个后, 所得失效概率基本稳定.于是选取初始样本点数目分别为8, 10, 12时, 使用本文方法对算例1连续进行15次失效概率计算.不同初始样本点数目下的失效概率趋势如图 2所示, N表示初始样本点数目.将本文方法计算结果与MC法计算结果进行比较, 当初始样本点数目为8个时, 与MC的






图 2(Fig. 2)
 | 图 2 不同计算次数下的失效概率Fig.2 Failure probability under different calculation times |
不同初始样本点下的失效概率的平均值及标准差如表 2所示.由失效概率计算的平均值及标准差可知, 本文方法所得失效概率较为均衡稳定.
表 2(Table 2)
| 表 2 均值及标准差 Table 2 Mean and standard deviation |
通过其他4种方法分别对算例1进行计算, 结果如表 3所示.其中MC表示蒙特卡洛算法, K-MC表示基于Kriging模型的蒙特卡洛算法, K-MCMC表示基于Kriging模型的马尔科夫链蒙特卡洛算法, BP表示BP神经网络算法, RSM表示响应面算法.
表 3(Table 3)
| 表 3 算例1各方法计算结果 Table 3 Calculation results of each method in example 1 |
算例1的结果表明, 相比于未添加学习函数的Kriging模型和BP神经网络模型, 本文算法的CPU计算时间稍长, 但调用的真实功能函数次数明显更少且可靠性计算精度也较高.采用MCMC方法的Kriging模型的计算可靠性与采用MC方法的Kriging模型的计算可靠性相比, CPU计算时间近似, 而采用MCMC方法的结果准确性更高.
4.2 算例2本算例选用经典6维随机变量非线性系统例子[1], 其系统结构如图 3所示.功能函数的表达式为
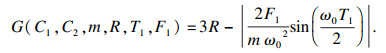 |
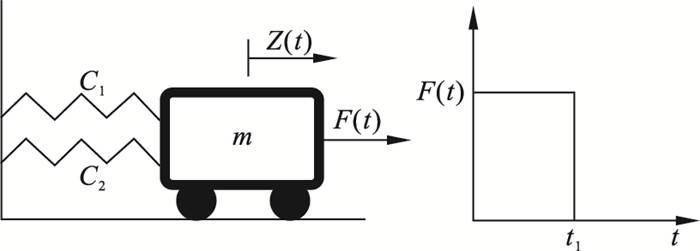 | 图 3 非线性系统Fig.3 Nonlinear system |
式中,
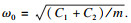
表 4(Table 4)
| 表 4 系统变量分布情况 Table 4 Distribution of system variables |
通过6种不同方法对算例2进行计算, 结果如表 5所示.
表 5(Table 5)
| 表 5 算例2各方法计算结果 Table 5 Calculation results of each method in example 2 |
算例2的结果表明, 对比响应面方法、BP神经网络模型、MC方法和传统Kriging模型, 本文方法明显较少地调用了真实功能函数, 当总样本达到99=30+69时就可得到精确的可靠度结果.相较于Kriging-MC方法, Kriging-MCMC方法在生成样本计算可靠度时, 生成1.2×105个样本即可使

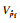

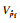
图 4(Fig. 4)
 | 图 4 样本数对变异系数的影响Fig.4 Effect of sample number on variation coefficient |
4.3 算例3算例3是一个经典的具有多个设计点的状态函数[9], 其功能函数为
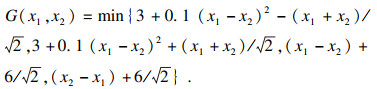 |
表 6(Table 6)
| 表 6 算例3各方法计算结果 Table 6 Calculation results of each method in example 3 |
算例3结果表明, 在总样本点数量达83=30+53时即初始样本点数量为30时, 本文方法即可得到相对误差为0.002的可靠性计算结果.与Kriging-MCMC相比, 本文算法添加了学习函数从而对被错误分类的几率最大的样本点进行了自主学习, 对Kriging模型进行了有效更新, 因此采用了学习函数的方法能够调用更少的功能函数的样本点达到更高的计算精度.分析两种方法调用不同数量的样本点时相对误差情况如图 5所示.相比于另外几种方法, 本文算法所需调用的真实功能函数次数依然最少且计算准确性在初始采样点数量仅为30时就达到了较高水平.基于MCMC方法的Kriging模型的相对误差率明显低于基于MC方法的Kriging模型.
图 5(Fig. 5)
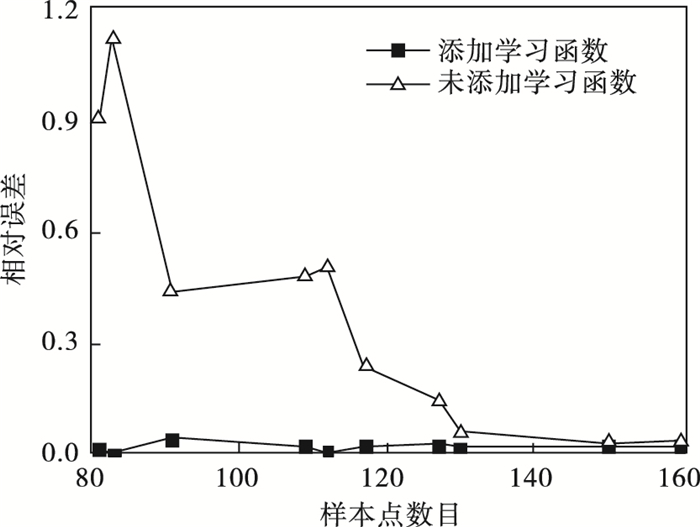 | 图 5 样本点数对相对误差的影响Fig.5 Effect of sample number on relative error |
4.4 算例4算例4中的十杆桁架结构来源于工程应用[14], 其结构如图 6所示.图中1~8为桁架各杆, (1)~(6)为桁架节点.桁架的水平杆、垂直杆及倾斜杆选用3种不同横截面积的铝合金杆件.杆件结构的弹性模量E为68 947 570 kPa, 杆件长度L为9.144 m, 材料密度ρ为2 768 kg/m3.
图 6(Fig. 6)
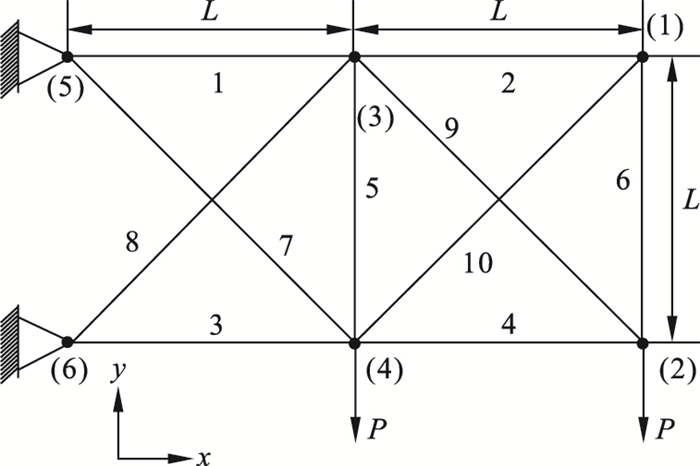 | 图 6 桁架结构Fig.6 Truss structure |
仅考虑节点(2)处的位移变化, 节点(2)处位移的极限状态函数的解析表达式为
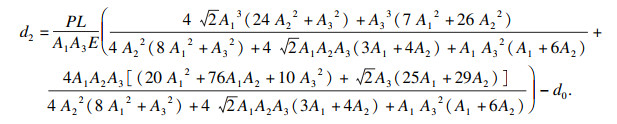 |
表 7(Table 7)
| 表 7 变量分布 Table 7 Distribution of variables |
通过5种不同方法对算例4进行计算, 结果如表 8所示.
表 8(Table 8)
| 表 8 算例4各方法的计算结果 Table 8 Calculation results of each method in example 4 |
算例4结果表明, 在初始样本点数量为18时, 即总样本点数目为23时本文方法即可得到相对误差仅为0.003 5的可靠性计算结果.相比于其他模型, 本文方法所需调用的真实功能函数次数最少.在很多工程实际问题中的功能函数常为复杂非线性函数或为隐式, 求解功能函数的响应值时常需要花费数十分钟甚至更多时间.由于本文方法大大减少了对功能函数的调用和求解, 相比之下此方法是计算效率较高的可靠性计算方法.
6 结论1) 通过与MC方法的对比, 本文采用的MCMC方法能通过较少次的抽样得到较精确的结果, 增加了收敛速度, 节约了样本空间; 样本是已满足稳态分布的马尔科夫链, 样本值与初始值无关, 所以用该方法获得的运行结果更为稳定.
2) 将拉丁超立方抽样、学习函数与Kriging模型相结合, 挑选出训练效果好的样本点, 充分利用有限的样本信息, 减少了所需样本点数目, 提高了模型的拟合精度和可靠性计算的准确性.
3) 通过算例分析, 本文方法相较于其他方法, 能通过较少次数地调用真实功能函数得到较高精度的计算结果, 说明本文方法具有更高的计算效率和计算精度.
4) 由于在实际工程中存在隐式性能函数或复杂性能函数的问题, 而本文方法能不依靠真实性能函数进行计算, 降低了计算成本, 因此本文方法有一定的工程应用价值.
参考文献
| [1] | Shi Y, Lu Z, He R, et al. A novel learning function based on Kriging for reliability analysis[J]. Reliability Engineering and System Safety, 2020, 198: 106857. DOI:10.1016/j.ress.2020.106857 |
| [2] | Morató A, Sriramula S, Krishnan N. Kriging models for aero-elastic simulations and reliability analysis of offshore wind turbine support structures[J]. Ships & Offshore Structures, 2019, 14(6): 545-558. |
| [3] | Cai Y, Xie Q, Xue S, et al. Fragility modelling framework for transmission line towers under winds[J]. Engineering Structures, 2019, 191: 686-697. DOI:10.1016/j.engstruct.2019.04.096 |
| [4] | Zhang J, Xiao M, Gao L. An active learning reliability method combining Kriging constructed with exploration and exploitation of failure region and subset simulation[J]. Reliability Engineering and System Safety, 2019, 188: 90-102. DOI:10.1016/j.ress.2019.03.002 |
| [5] | Barkhori M, Shayanfar M A, Barkhordari M A, et al. Kriging-aided cross-entropy-based adaptive importance sampling using Gaussian mixture[J]. Iranian Journal of Science and Technology, 2019, 43(1): S81-S88. DOI:10.1007/s40996-018-0143-y |
| [6] | 刘瞻, 张建国, 王灿灿, 等. 基于优化Kriging模型和重要抽样法的结构可靠度混合算法[J]. 航空学报, 2013, 34(6): 1347-1355. (Liu Zhan, Zhang Jian-guo, Wang Can-can, et al. Structural reliability hybrid algorithm based on optimized Kriging model and importance sampling method[J]. Acta Aeronautica Sinica, 2013, 34(6): 1347-1355.) |
| [7] | Soubra A H, Al-Bittar T, Thajeel J, et al. Probabilistic analysis of strip footings resting on spatially varying soils using Kriging meta modeling and importance sampling[J]. Computers and Geotechnics, 2019, 114: 103-107. |
| [8] | 佟操, 孙志礼, 杨丽, 等. 一种基于Kriging和Monte Carlo的主动学习可靠度算法[J]. 航空学报, 2015, 36(9): 2992-3001. (Tong Cao, Sun Zhi-li, Yang Li, et al. An active learning reliability algorithm based on Kriging and Monte Carlo[J]. Journal of Aeronautics, 2015, 36(9): 2992-3001.) |
| [9] | Echard B, Gayton N, Lemaire M. AK-MCS: an active learning reliability method combining Kriging and Monte Carlo simulation[J]. Structural Safety, 2011, 33(2): 145-154. DOI:10.1016/j.strusafe.2011.01.002 |
| [10] | Zhang J, Xiao M, Gao L, et al. A combined projection-outline-based active learning Kriging and adaptive importance sampling method for hybrid reliability analysis with small failure probabilities[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 344: 13-33. DOI:10.1016/j.cma.2018.10.003 |
| [11] | Kuhnt S, Steinberg D M. Design and analysis of computer experiments[J]. Asta Advances in Statistical Analysis, 1989, 4(4): 409-423. |
| [12] | Koehler J R, Owen A B. 9 Computer experiments[J]. Handbook of Statistics, 1996, 13: 261-308. |
| [13] | Andrieu C, Freitas N D, Doucet A, et al. An introduction to MCMC for machine learning[J]. Machine Learning, 2003, 50(1): 5-43. |
| [14] | Hong L, Li H, Peng K, et al. A novel Kriging based active learning method for structural reliability analysis[J]. Journal of Mechanical Science and Technology, 2020, 34(4): 1545-1556. DOI:10.1007/s12206-020-0317-y |
