
 , 张瑶, 朱亚锟, 陈晓波
, 张瑶, 朱亚锟, 陈晓波 东北大学秦皇岛分校 控制工程学院, 河北 秦皇岛 066004
收稿日期:2020-12-21
基金项目:国家自然科学基金资助项目(61703079);秦皇岛市大学生科技创新创业专项基金资助项目(2018-79, 121)。
作者简介:王海芳(1976-), 男, 山西高平人, 东北大学副教授。
摘要:针对复杂环境下移动机器人的局部最优路径规划, 提出一种基于目标偏置扩展和Cantmull-Rom样条插值的双向RRT*路径规划算法.双向RRT*算法同时创建两颗搜索树, 交替进行相向搜索, 同时以一定的概率进行随机点的目标偏置选择, 以提高算法的整体收敛效率; 再对当前节点重选父节点和重布线, 以增强算法对环境的敏感程度.为确保路径安全可行, 对环境中的障碍物进行膨胀处理, 再对初始路径进行碰撞检测; 修剪冗余节点, 缩短可行路径长度, 再利用Cantmull-Rom样条插值法平滑路径.在Matlab仿真平台和ROS机器人仿真平台分别进行2D和3D的对比实验, 验证了改进双向RRT*算法的有效性和优越性.
关键词:快速探索随机树Cantmull-Rom样条插值ROS机器人仿真平台改进双向RRT*
Mobile Robot Path Planning Based on Improved Bidirectional RRT*
WANG Hai-fang

 , ZHANG Yao, ZHU Ya-kun, CHEN Xiao-bo
, ZHANG Yao, ZHU Ya-kun, CHEN Xiao-bo School of Control Engineering, Northeastern University at Qinhuangdao, Qinhuangdao 066004, China
Corresponding author: WANG Hai-fang, E-mail: hfwang@neuq.edu.cn.
Abstract: Aiming at local optimal path planning of mobile robots in complex environments, a bidirectional rapidly exploring random tree star(Bi-RRT*)path planning algorithm based on target offset expansion and Cantmull-Rom spline interpolation is proposed. In the Bi-RRT* algorithm, two search trees are created at the same time, and opposite searches are alternately performed with the target bias of random points selected at a certain probability, in order to improve the overall convergence efficiency of the algorithm. By reselecting the parent node of the current node and rewiring the nodes, the sensitivity to the environment of path planning is enhanced. To ensure the path safe and feasible, the obstacles in environment are expanded and collision detection is performed on the initial path. Redundant nodes are trimmed so that the feasible path length is shortened. Then, the path is smoothed by the Cantmull-Rom spline interpolation. The 2D and 3D comparative experiments were conducted for the improved Bi-RRT* algorithm based on Matlab and ROS robot simulation platform, respectively, and the experiment results verified the effectiveness and superiority of the improved Bi-RRT* algorithm.
Key words: rapidly exploring random treeCantmull-Rom spline interpolationROS robot simulation platformimproved Bi-RRT*
路径规划是指在包含障碍物的给定区域内搜索到一条从起点到终点的安全无碰撞、可行的路径[1].基于随机点采样的快速探索随机树(rapidly exploring random tree, RRT)是目前广泛应用于机器人路径规划的一种算法[2], 但也存在一些明显的缺点: 对环境信息不敏感, 当可行区域狭窄且复杂, 或者存在大量不规则障碍物时, RRT算法收敛到最优解的效率会大打折扣, 甚至探索失败.针对这一问题, Wei等[3]提出一种平滑RRT(S-RRT)算法, 实现了机器人在动态路径上的自主避障; Nasir等[4]提出一种RRT*-smart算法, 通过启发式函数实现随机点的智能采样搜索, 提高最优路径收敛速度; Wang等[5]提出一种引入强化学习的多路径机器人路径规划方法LM-RRT, 以增强每棵树的局部空间探测能力, 保证了全局路径规划效率并证明了对狭窄通道单查询路径规划问题的有效性; 宋晓琳等[6]提出基于B样条插值的改进RRT算法, 采用高斯分布描述随机采样, 解决了弯道导航环境下的转向问题.
上述算法在一定程度上对传统的RRT算法进行了改进, 提高了算法稳定性, 但容易导致生成路径与最优解存在较大差异.考虑到RRT*算法的导向性以及双向RRT算法[7]的快速收敛性, 本文提出了改进双向RRT*算法, 该算法在面对复杂环境空间时可以做出迅速反应.与RRT一样, 双向RRT*也用树来搜索空间, 不同之处在于, 从起始点到目标点不是一棵树, 而是两棵树.第一棵树从起始点开始, 有方向性地向终点生长, 第二棵树从终点开始, 有方向性地向起始点生长; 当两棵树相遇时, 就表示搜索路径成功.
1 算法介绍1.1 RRT*算法与RRT算法搜索方式相似, RRT*搜索[8]从初始点(作为搜索树的根)开始, 即起点作为第一个点加入到随机搜索树中, 为了克服搜索盲目性, 以一定的概率朝着偏向于目标点的方向搜索.在每次迭代过程中, 系统随机生成的随机数如果小于算法给定的一个值, 那么算法会在配置空间中生成一个随机点P, 否则就将随机点设置为终点坐标;接着在搜索树中找到离该随机点P距离最近的点, 记作M, 以M为起点,
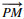
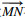
图 1(Fig. 1)
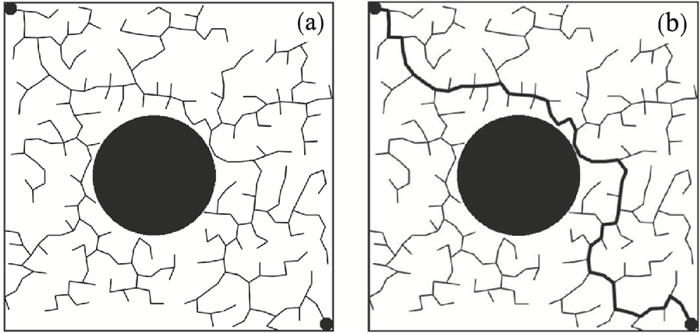 | 图 1 RRT*算法的搜索过程Fig.1 Search process of RRT* algorithm (a)—搜索过程;(b)—搜索结果. |
RRT*算法保留了RRT算法原有的优势: 概率完备性和渐近最优性[9], 即只要路径探索迭代的次数足够多, 得到的最终路径就可以是较为接近最短的可行路径; 但RRT*算法在处理较为复杂的环境时收敛速率缓慢, 搜索时间较长.
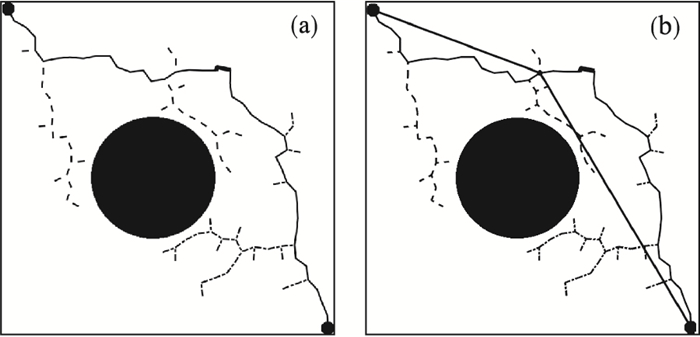
1.2 双向RRT*算法采用单一搜索策略的RRT*算法每次搜索都是从给定的初始区域点出发在整个状态空间随机搜索的树形搜索方式, 如果从初始区域点和目标区域点同时相向进行单一搜索, 整体的搜索效率会更高.为此, 在原有具有实用导向性特点的RRT*基础上, 提出基于双向扩展平衡的联结型双树RRT*算法[9-10].在这种双向搜索中, 一棵快速搜索随机树从初始区域生成(图 2左上角区域), 另一棵快速搜索随机树从目标区域生成(图 2右下角区域).这种算法的双向特性使它们天生比单一树搜索更快, RRT*的概率目标偏置策略引导两棵树相互靠近, 从而更快地收敛到最优解, 更快地生成可行路径.图 2为双向RRT*的搜索过程, 左上角为起点, 右下角为终点, 从起点和终点分别开始搜索, 直至两棵搜索树中的节点相连找到一条从起点至终点的可行路径.
图 2(Fig. 2)
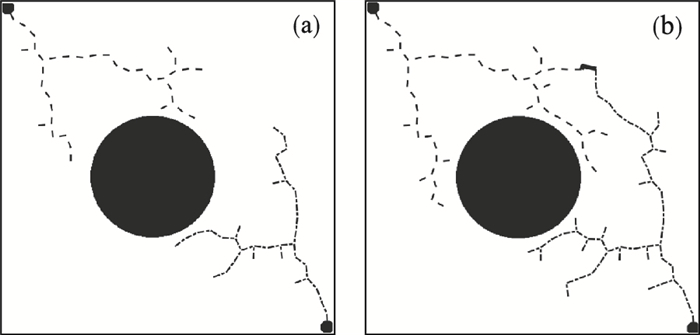 | 图 2 双向RRT*算法的搜索过程Fig.2 Search process of a bidirectional RRT* algorithm (a)—双向搜索过程;(b)—搜索到可行路径. |
在搜索速度、搜索效率方面, 这种双向的RRT技术与RRT*算法相比有了显著提高, 更具有良好的搜索特性.首先, 相较于单一步长探索, 双向RRT*算法在总的探索步长上更长, 加快了随机树的生长; 其次, 不同于随机探索生长的方式, 双向RRT*的随机树不断朝向对方交替探索生长, 特别是当起始位置和目标位置处于约束区域时, 两棵树可以通过朝向对方方向快速扩展而逃离各自的约束区域.这种带有方向性的扩展使得树的扩展更加贪婪和明确, 使得双向RRT算法较之单向RRT算法更加有效和快速.
2 算法改进策略2.1 环境模型的膨胀在移动机器人路径规划过程中, 机器人避障是路径可行性的一个重要指标.仿真实验中一般将机器人视作一个质点, 但在实际应用中, 机器人的大小是一个不容忽视的因素.为了保证机器人的安全, 使仿真实验更具有实用性, 以及将机器人视为质点更具可行性与说服力, 在仿真过程中将障碍区域进行相应程度的膨胀, 膨胀大小为实际运行中移动机器人体宽的一半.
2.2 重置父节点与重布线在确定随机点位置后, 为了优化搜索路径, 减少路径代价, 对新加入搜索树的新节点进行重选父节点和重新布线操作, 图 3中节点标号表示树中节点产生的顺序, 节点1表示初始节点, 节点8, 即newNode表示新加入的节点, nearNode表示树中已有与随机点距离最近的节点, 默认为newNode的父节点, 节点与节点之间连线上的数字表示两节点之间的路径代价.重置父节点就是找到一条从初始节点1到节点8的路径代价值最小的可行路径, 在图 3a中以newNode为中心, 给定阈值范围内的节点为待选节点, 找到各个待选节点与newNode相连接后节点代价值最低的待选节点作为父节点, 重置newNode的父节点, 待选节点分别为节点4和节点7, 原来的路径1—5—8, 路径代价为10+2=12, 备选节点与newNode组成的路径为1—2—4—8和1—5—7—8, 路径代价分别为2+5+3=10和10+3+2=15, 因此将节点8的父节点改为节点4, 完成父节点重置, 图 3b是重新生成的随机树.为进一步使随机树节点间连接的代价尽量小, 对随机树进行重新布线.重布线的过程可以表述为: 如果待选节点的父节点改为newNode可以减小路径代价, 则进行更改, 图 3c中的待选节点为节点5和节点7, 节点5的父节点是节点1, 路径是1—5, 路径代价为10, 如果将节点5的父节点重置为节点8, 那么到达节点的路径为1—2—4—8—5, 代价为2+5+3+2=12, 大于原始的路径代价, 不对节点5进行重布线操作, 同理, 将节点7的父节点由节点5更改为节点8后, 更改后的路径为1—2—4—8—7, 路径代价为2+5+3+2=12, 小于原始路径1—5—7的路径代价, 即10+3=13, 因此, 将节点7的父节点重置为节点8, 图 3d是重布线后的随机树.
图 3(Fig. 3)
 | 图 3 算法的重置过程Fig.3 Reset process of algorithm |
2.3 修剪冗余节点采用双向RRT*算法规划的原始路径是由一些离散点组成的折线段, 有可能不满足机器人转弯曲率的要求, 还会导致机器人在转弯途中增加不必要的转向时间; 此外, 得到的初始路径含有许多冗余节点, 增加了整体运行时长, 因此有必要进行路径优化处理[3], 即消除冗余节点得到最短的折线路径.首先, 采用贪心算法过滤冗余节点, 从起点(终点)开始, 寻找能够无碰撞连接终点(起点)的节点, 记录该点为p, 再将该点p作为新一轮起点, 依次寻找能够无碰撞连接的路径节点, 直到起点(终点)和终点(起点)能够无碰撞连接, 将记录的所有点p连接,得到非光滑的折线段路径.为了保证路径朝最优解逼近, 比较从起点连接终点的路径和从终点连接起点的路径, 选择较短的路径长度作为待平滑处理的折线段路径[11].图 4黑色折线段是剪枝后的非光滑路径.
图 4(Fig. 4)
 | 图 4 修剪冗余节点过程Fig.4 Process of pruning redundant nodes (a)—初始可行路径;(b)—修剪后可行路径. |
2.4 Cantmull-Rom样条插值函数Cantmull-Rom样条插值是一种分段函数[12], 它有如下特点: ①每一点的正切值与相邻两点的斜率成正比; ②能够保证样条曲线经过从第二个控制点到倒数第二个控制点之间的所有点.正是因为这样的特点, 使得该插值函数适用于作轨迹线算法.
作为一个立方插值函数, 此算法受到至少4个控制点的影响, 分别是P0(Pi-2), P1(Pi-1), P2(Pi), P3(Pi+1), 这里的点Pi, i=1, 2, 3, 4都是曲线上的点, Pi处的切线τ会影响曲线的曲率, 曲率记作τ(Pi+1-Pi-1).Cantmull-Rom样条插值函数可以用以下多项式函数抽象表示:
 | (1) |
对式(1)进行初始化, 得
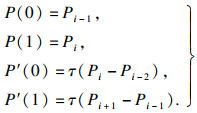 | (2) |
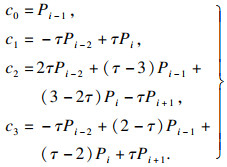 | (3) |
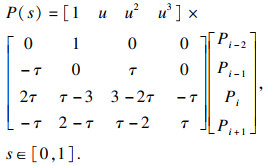 | (4) |
图 5(Fig. 5)
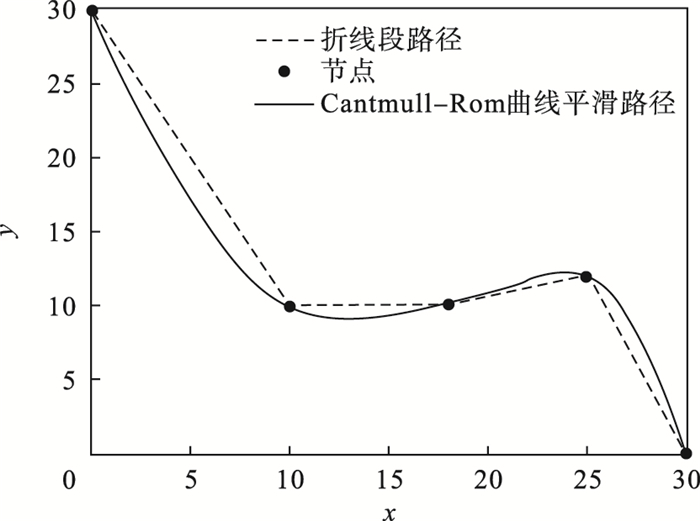 | 图 5 采用Cantmull-Rom插值法平滑节点Fig.5 Smoothing nodes by Cantmull-Rom interpolation |
3 基于Matlab实验仿真为了验证本文提出的改进双向RRT*算法的性能, 采用3种轨迹规划算法——RRT*[13],GCSE-RRT*[13]和本文算法,在Matlab仿真平台上对4种不同的环境进行100次仿真模拟.仿真时将机器人视为质点运动; 原始地图的分辨率为100×100;固定起点(左下角黑色实心点)和终点(右上角黑色实心点), 坐标分别为[5,5]和[95,95].将仿真结果与RRT*和GCSE-RRT*算法进行对比, 验证本文算法的正确性和优越性.
图 6是4个不同环境下的仿真结果.从左下角开始的虚线表示从起点开始扩展的树的分支, 从右上角开始的点画线表示从终点开始扩展的树的分支, 当从起点开始的扩展随机树与从终点开始的扩展随机树连接到一起时, 就形成初始路径, 黑色曲线表示经过Cantmull-Rom平滑处理后的最终路径.在仿真过程中, 如果一个周期规划的路径到达了终点, 表示这次规划是成功的.
图 6(Fig. 6)
 | 图 6 本文算法的搜索过程Fig.6 Search process of the proposed algorithm (a)—Map1; (b)—Map2; (c)—Map3; (d)—Map4. |
表 1记录了每个环境中采用不同算法的仿真结果, 其中统计的各个指标均是平均值, 表 1中的实验数据包括搜索树总的节点数量、有效节点数量、节点利用率、路径过程中的迭代次数、生成路径所用时间, 以及路径长度.仿真证明, 优化路径的步骤可以删除很多不必要的节点, 缩短路径, 同时减少机器人转体的次数.
表 1(Table 1)
| 表 1 4种仿真环境中的实验数据 Table 1 Experimental data in 4 simulation environments |
根据表 1数据可知: RRT*的扩展节点平均数213个, GCSE-RRT* 110个, 而本文算法有59个, 比前两种算法分别减少了72 % 和46 %; RRT*的有效节点平均数20个, GCSE-RRT*有22个, 本文算法有35个, 远大于前两个算法的平均有效节点个数; 同时本文算法的节点平均利用率在50 % 以上, 可见本文算法占用内存更小, 节点利用率更高.RRT*的平均迭代次数为432, GCSE-RRT*为307, 而本文算法为243, 比前两种算法分别减少了43 % 和21 %;同时, RRT*的平均运行时间是0.25 s, GCSE-RRT*是0.14 s, 与本文算法所用的0.13 s相比, 前两种算法分别提高了48 % 和7 %, 可见本文算法在路径迭代次数和运行时间上有较大优势, 因此路径规划效率也会更高.最后, RRT*规划路径的平均长度是163.19 m, GCSE-RRT*是160.07 m, 而本文算法是150.35 m, 比前两种算法缩短了8 % 和6 %.由图 6可见, 本文算法得到的路径更加平滑, 路径规划效果更优.
4 基于ROS平台的实验验证计算机配置为Ubuntu16.04LTS, 处理器Intel I5-6500, 主频为3.2 Hz, 运行内存为16 GB.仿真在开源机器人操作平台ROS下进行, 并在Rviz中使用SLAM技术进行机器人自主定位与地图建立工作, 在Gazebo中将最终规划的路径进行可视化显示, 选择第三代TurtleBot 3双轮差分驱动机器人为实验对象.TurtleBot 3是一款体积小、成本低、可用于编程的、基于ROS开发的移动机器人.机器人顶部安装的激光雷达可对6 m之内的位置环境进行扫面定位, 图 7a是TurtleBot 3机器人实物, 图 7b是在Gazebo中建立的TurtleBot 3机器人模型[14], 用于ROS仿真实验.
图 7(Fig. 7)
 | 图 7 TurtleBot 3移动机器人Fig.7 Mobile robot TurtleBot 3 (a)—实物; (b)—模型. |
在Gazebo中建立环境地图, 地图规模是5 m×5 m的正方形区域, 内部是一个含有内凹空间和狭窄通道的迷宫环境, 原点在右下方, 设置起点坐标为(-2.0, -1.7, 0.1)m, 终点坐标为(1.1, 1.8, 0.1)m; 其次, 为保证机器人运行安全, 采用障碍物膨胀策略, 添加地图的膨胀距离为机器人体宽的一半, 仿真设置为0.2 m.利用ROS中的amcl和google-cartographer功能包对机器人SLAM定位与建图, 通过电脑键盘控制机器人围绕环境运动一周, 在控制机器人移动建图的过程中地图会以一种渐变的形式由浅至深的出现, 图 8a是建立完成的地图, 图中的多个坐标图标表示机器人在建图过程中途经的位置, 白色部分表示可移动区域, 黑色部分表示障碍物区域, 灰色部分表示机器人未检测的未知区域.最后利用ROS中的导航功能包和C++语言实现算法功能, 发送路径信息, 在Rviz中接收相应的路径信息, 分别在Rviz和Gazebo中可视化显示最终的路径导航信息并记录实验数据.图 8b和图 8c是移动机器人根据本文算法得到的全局路径导航效果图. 在图 8b中, 机器人从初始点出发, 在逐渐靠近障碍物区域时, 由于改进算法中障碍物膨胀策略的应用, 机器人机身能够在以最大限度接近障碍物的情况下避免与障碍物碰撞, 此时机器人可以安全地沿着已发布的全局规划路径行驶.在实际的仿真过程中, 机器人安全到达目标点后需要进行原地旋转, 使机器人自身方向与目标点所指方向一致.图 8c显示了机器人最后的状态: 到达指定目标点, 原地旋转调整自身方向为箭头所指方向, 算法规划结束.最后将3种路径规划算法的导航仿真结果汇总于表 2.
图 8(Fig. 8)
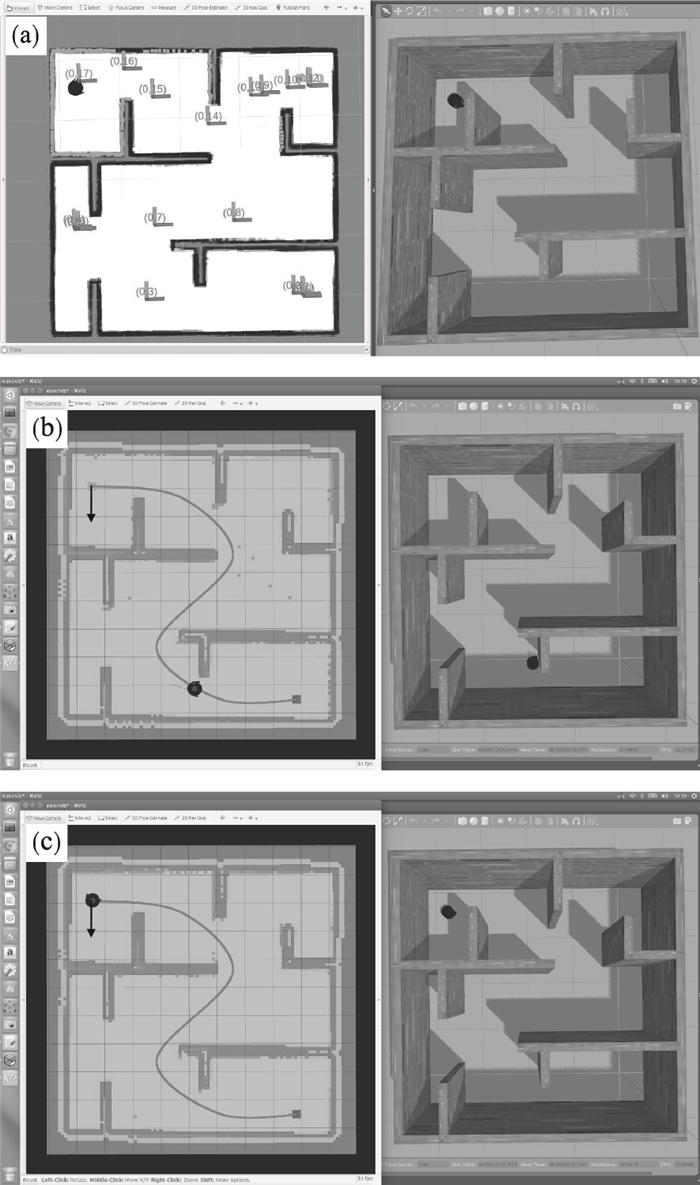 | 图 8 本文算法的导航路径Fig.8 Navigation path of the proposed algorithm (a)—SLAM建图过程; (b)—机器人避障过程中; (c)—机器人到达目标点. |
表 2(Table 2)
| 表 2 ROS仿真结果 Table 2 ROS simulation results |
由表 2数据可知, 相比RRT*和GCSE-RRT*, 本文算法的路径规划时间分别缩短了88 % 和49 %, Gazebo仿真时间分别缩短了33 % 和3.7 %, 同时本文算法的路径长度更短.因此本文算法能为TurtleBot 3机器人规划出安全可行的路径, 所获得路径也更优.
5 结语本文以RRT*算法为基础, 结合双向RRT算法在扩展策略上的优势, 提出改进双向RRT*算法.首先为了提高收敛效率, 设置一定概率进行目标偏置搜索, 同时根据节点代价值重置搜索节点的父节点, 减小路径成本; 其次, 为了降低机器人与障碍物碰撞的可能性, 设置行驶过程中的安全距离, 对障碍物进行相应的膨胀处理; 最后考虑到移动机器人在折线段节点处行驶的低效率, 对初始路径进行碰撞检测, 剪枝冗余节点, 减少路径长度, 并对折线段路径进行Cantmull-Rom插值平滑处理, 减少仿真过程中机器人的转向时间, 使机器人平稳行走.改进后的双向RRT*在内存使用、路径生成速度、路径长度、运行时间、平滑性上具有明显优势.
参考文献
| [1] | Gasparetto A, Boscariol P, Lanzutti A, et al. Path planning and trajectory planning algorithms: a general overview[J]. Motion and Operation Planning of Robotic Systems, Mechanisms and Machine Science, 2015, 29(1): 3-27. |
| [2] | Sertac K, Emilio F. Sampling-based algorithms for optimal motion planning[J]. The International Journal of Robotics Research, 2011, 30(7): 846-894. DOI:10.1177/0278364911406761 |
| [3] | Wei K, Ren B Y. A method on dynamic path planning for robotic manipulator autonomous obstacle avoidance based on an improved RRT algorithm[J]. Sensors, 2018, 18(2): 571-585. DOI:10.3390/s18020571 |
| [4] | Nasir J, Islam F, Malik U, et al. RRT* -smart: a rapid convergence implementation of RRT*[J]. International Journal of Advanced Robotic Systems, 2013[2020-10-18]. https://www.researchgate.net/deref/http%3A%2F%2Fdx.doi.org%2F10.5772%2F56718. |
| [5] | Wang W, Zuo L, Xu X. A learning-based multi-RRT approach for robot path planning in narrow passages[J]. Journal of Intelligent & Robotic Systems, 2018, 90(1/2): 81-100. |
| [6] | 宋晓琳, 周南, 黄正瑜, 等. 改进RRT在汽车避障局部路径规划中的应用[J]. 湖南大学学报(自然科学版), 2017, 44(4): 30-37. (Song Xiao-lin, Zhou Nan, Huang Zheng-yu, et al. Application of improved RRT in local path planning of vehicle obstacle avoidance[J]. Journal of Hunan University(Natural Science Edition), 2017, 44(4): 30-37.) |
| [7] | 王坤, 曾国辉, 鲁敦科, 等. 基于改进渐进最优的双向快速扩展随机树的移动机器人路径规划算法[J]. 计算机应用, 2019, 39(5): 1312-1317. (Wang Kun, Zeng Guo-hui, Lu Dun-ke, et al. Path planning algorithm for mobile robot based on improved asymptotically optimal bi-directional rapidly expanding random tree[J]. Computer Applications, 2019, 39(5): 1312-1317.) |
| [8] | Noreen I, Khan A, Habib Z. A comparison of RRT, RRT* and RRT* -smart path planning algorithms[J]. International Journal of Computer Science and Network Security, 2016, 16(10): 20-27. |
| [9] | Tahir Z, Qureshi A H, Ayaz Y, et al. Potentially guided bidirectionalized RRT* for fast optimal path planning in cluttered environments[J]. Robotics and Autonomous Systems, 2018, 108: 13-27. DOI:10.1016/j.robot.2018.06.013 |
| [10] | Qureshi A H, Ayaz Y. Intelligent bidirectional rapidly-exploring random trees for optimal motion planning in complex cluttered environments[J]. Robotics and Autonomous Systems, 2015, 68(1): 1-11. |
| [11] | Yang K, Sukkarieh S. An analytical continuous-curvature path-smoothing algorithm[J]. IEEE Transactions on Robotics, 2010, 26(3): 561-568. DOI:10.1109/TRO.2010.2042990 |
| [12] | Song X G, Fan X, Cao Z Q, et al. A TC-RRT-based path planning algorithm for the nonholonomic mobile robots[C/OL]//2017 36th Chinese Control Conference, Dalian: 2017[2020-10-20]. https://doi.org/10.23919/ChiCC.2017.8028409. |
| [13] | 张伟民, 付仕雄. 基于改进RRT*算法的移动机器人路径规划[J]. 华中科技大学学报(自然科学版), 2021, 49(1): 31-36. (Zhang Wei-min, Fu Shi-xiong. Mobile robot path planning based on improved RRT* algorithm[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2021, 49(1): 31-36.) |
| [14] | 胡春旭. ROS机器人开发实践[M]. 北京: 机械工业出版社, 2018: 114-155. (Hu Chun-xu. ROS robot development practice[M]. Beijing: China Machine Press, 2018: 114-155.) |
