鲍喜荣, 历正双, 高浩森, 张石
东北大学 计算机科学与工程学院, 辽宁 沈阳 110169
收稿日期：2020-10-10
基金项目：中央高校基本科研业务费专项资金资助项目(N171604011)。
作者简介：鲍喜荣(1978-), 男, 湖北当阳人, 东北大学讲师, 博士;
张石(1963-), 男, 辽宁抚顺人, 东北大学教授, 博士生导师。

摘要：针对超声成像中双重延时乘累加算法不适用于高噪声环境的问题, 提出一种基于均值-标准差加权因子的双重延时乘累加算法, 即RD-DMAS算法.该加权因子对解决高噪声带来的图像斑点问题具有显著效果, 而双重延时乘累加波束形成算法能大幅提高超声成像分辨率, 使所提算法能得到高分辨率和高对比度的重建图像.对该算法在点散射目标仿体、囊肿仿体和噪声环境下进行了仿真, 结果表明, RD-DMAS算法有最小旁瓣以及较窄的主瓣.DAS, DMAS, DS-DMAS, RD-DMAS算法的对比度(CR)分别为9.72, 11.72, 13.28和19.86.不管环境中是否有噪声, RD-DMAS算法的成像效果都是最好的.
关键词：波束形成算法加权因子延时乘累加超声成像重建图像
Double Delay Multiplication and Accumulation Beamforming Algorithm Based on Weighting Factor
BAO Xi-rong, LI Zheng-shuang, GAO Hao-sen, ZHANG Shi
School of Computer Science & Engineering, Northeastern University, Shenyang 110169, China
Corresponding author: LI Zheng-shuang, E-mail: 1801688@stu.neu.edu.cn.

Abstract: In order to solve the problem that the double delay multiplication and accumulation algorithm in ultrasonic imaging is not suitable for high noise environments, a double delay multiplication and accumulation algorithm based on mean-standard deviation weighting factor, namely RD-DMAS algorithm, is proposed. The weighted factor has a significant effects on solving the image speckle problem caused by strong noises, and the dual delay multiplication and accumulation beamforming algorithm can greatly improve the resolution of ultrasonic imaging, so the new method can obtain high resolution and high contrast image reconstruction. The algorithm was simulated in point scattering target replicas, cyst replicas and noise environments, and the results show that the RD-DMAS has the smallest sidelobe and narrower main lobe. The contrast ratios(CR)of DAS, DMAS, DS-DMAS and RD-DMAS were 9.72, 11.72, 13.28 and 19.86, respectively. RD-DMAS provides the best imaging performance regardless of noise in the environment.
Key words: beamforming algorithmweighting factordelay multiplication and accumulationultrasonic imagingimage reconstruction
超声成像中对回波数据的处理, 其中波束形成占据了90%以上, 所以对此算法的研究是重中之重.波束形成整体分为非自适应波束形成器和自适应波束形成器.除了自适应波束形成器之外, 加权因子也越来越成为研究的重点.本文就是从加权因子和非自适应波束形成器两个角度对算法优化.最早的自适应波束形成器是Capon提出的最小方差(MV)波束形成器^[1], 得到了广泛应用, 根据研究表明它比最经典的非自适应波束形成器——延时累加(delay and sum, DAS)的分辨率和抗干扰能力强很多^[2-6], 但对MV波束形成器对比度的提高并不是很满意^[7].因此，自适应加权因子应运而生, 显著提高了图像质量, 广泛应用于波束形成中.早期的加权因子主要为相干因子(CF), 它是相干信号的功率与阵列信号的总功率比值, 它可以减少杂波噪声等非相干分量.尽管它提升了对比度, 却在散斑图中引入了黑区伪影^[8].Li等提出了广义相干因子(GCF)^[9], 减少了声速不均引起的聚焦误差, 获得了更好的鲁棒性.Camacho等^[10]提出了相位相干因子(PCF)和符号相干因子(SCF), 分别用在测量孔径接收到的回波的相位和符号的相干性以减少散射信息.交叉相干因子(CCF)^[11]用在延时散射信号中, 用合并传输的方法减少旁瓣引起的伪影.除了有基于相干系数的加权因子, 还有可用于对超声B模式诊断法进行加权的短时空间相干(short-lag spatial coherence, SLSC), 有****得出SLSC加权因子分别与DAS^[12], MV^[13], ESBMV^[14]相结合, 可以在高复杂度情况下增强对比度, 但对于分辨率没有改善.Zheng等^[15]提出的信号特征因子(SEF)在分辨率上有较大提升.Bandaru等^[16]发明的延时和标准差(DASD)波束形成方法, 可作为提高对比度的加权因子.虽然自适应加权因子可以提高图像的分辨率或对比度，但引入的散斑偏差又会降低散斑的质量, 由于散斑中含有一定的不相干成分^[17], 利用自适应加权技术可以增大一部分散斑方差, 这可能会限制加权因子的性能, 而较大的散斑方差会导致暗斑强度和黑区伪影.本文设计的信号标准偏差因子适用于产生斑点的目标, 能提高对比度.Matrone等^[18]针对DAS中的声音幅值相叠加操作, 提出了一种新的算法——DMAS算法, 该算法大幅度提高了图像的成像质量.随后Matrone等^[19]利用合成孔径技术对DMAS算法的成像质量做了进一步提升.文献[20]提出了更适合噪声环境的双重延时乘累加(DS-DMAS)波束形成算法, 然而, 在具有低信噪比(SNR)的嘈杂环境中, 该方法仍然不好.所以本文采用加权因子与DMAS结合形成新的高对比度高分辨率的波束形成算法(RD-DMAS).
1 方法本文的算法原理来源于波束形成器和自适应波束形成因子的结合, 采用64阵元线性换能器, 64个等间距换能器组成的阵列, 每次开启32个阵元发射信号及32个接收信号.得到一系列样本, 公式表示为

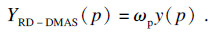(1)

其中: ω_p表示本文提出的SMSF加权因子; y(p)表示非自适应波束形成器.
1.1 加权因子在图像处理领域, 将均值-标准差比(MSR)定义为感兴趣区域(ROI)中像素均值与标准差的比值, 作为评价图像质量的指标.较大的MSR值表示ROI中较少的人为可变性.此外, MSR值会随着ROI中像素值的增大而减小.所以均值标准差可以作为评价图像质量的一个很好的度量.假设N个换能器阵元发射信号后经过时延补偿后在t时刻接收到的回波信号为Χ(t)=[x₁(t), x₂(t), …, x_N(t)]^T, 均值标准差加权因子(SMSF)公式为

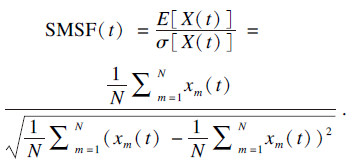(2)

其中: E[·]为平均值; σ[·]为标准差.
1.2 波束形成方法本文的双重延时乘累加算法, 源自于文献[18]提出的DMAS, 此算法用公式表示为

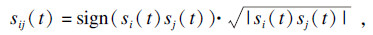(3)

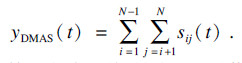(4)

其中: s_i为第i个阵元接收到的延时信号; N为接收信号的有效阵元数.式(4)也可以扩展成

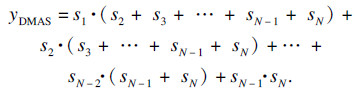(5)

其中, 为方便表示, 在这里忽略了绝对平方根操作, 式(5)中每一项都可以看作是一个DAS波束形成器, 因此, 为了提高波束形成结果, 可以在每一项的基础上再扩展一项.以此形成两阶段延时乘累加, 这就是本文采用的算法, 公式为

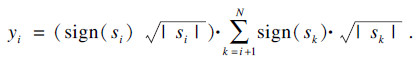(6)

得到新信号之后, 再将DMAS波束形成算法应用于这些新信号以产生第二级的输出:

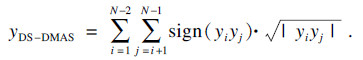(7)

该算法用伪代码表示分为两个步骤, 如下所示.
for i=1:(N-1)
???????temp: =0
???????for j=(i+1): (N)
??????????????temp=temp+sign(s_j)·
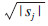
???????end
???????y_i=sign(s_i)··temp
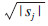
end
y: =0
for i=1:(N-2)
???????for j=i: (N-1)
??????????????y=y+sign(y_i·y_j)·sqrt(abs(y_i·y_j))
???????end
end
事实上, 本文提出的RD-DMAS, 在使用延时乘累加操作时是用DMAS扩展了每一项输出, 合成一系列新信号y_i, 然后将DMAS再应用到这些新信号以产生最终结果, RD-DMAS在此基础上采用了一种较为先进的SMSF进一步改善了成像质量.顺便提一下, 还有一种简单方法, 即式(8)和式(9)相结合用于减少DMAS中的绝对值符号和开平方根运算.

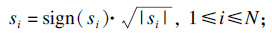(8)

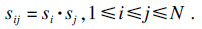(9)

经过上述操作, 将返回值存在新变量中.之后, 这些新变量直接应用于DMAS, 因此波束形成时只有乘法和加法.对于方程得到的结果, 式(7)中由于信号多次交叉相乘, 在频谱中将产生多个谐波分量.本文选择二次谐波分量作输出.首先通过正交将二次谐波分量移至零点处^[21], 然后通过低通滤波器得到最终结果.根据奈奎斯特采样定理可以推论出, 频率越高, 采样率越高, 也就意味着采集数据量越大.经过上述考虑, 本文选择二次谐波.
2 实验结果为了显示本文算法RD-DMAS的良好性能, 采用MATLAB对本文所涉及的算法进行仿真和测试, 将RD-DMAS算法与DAS, DMAS和DS-DMAS算法进行对比.仿真主要考虑点散射目标仿体、囊肿仿体和噪声环境对算法的影响.在本文的测试中, 探头采用线性阵列扫描的方式, 包括128个阵元(宽度为0.51 mm, 间距为0.026 mm, 高度为5 mm), 焦距为20 mm, 中心频率为3 MHz, 发射超声信号的方式为定点聚焦, 接收方式为动态聚焦接收信号.采用汉宁窗加权两周期正弦脉冲作为激励脉冲, 采样频率为100 MHz, 使用64阵元的孔径发射和接收.由于孔径宽度保持一致, 所有操作可使用相同的设定.同时, 为了模拟真实的噪声环境, 把高斯白噪声添加到所有的信号中, 进行对比实验.
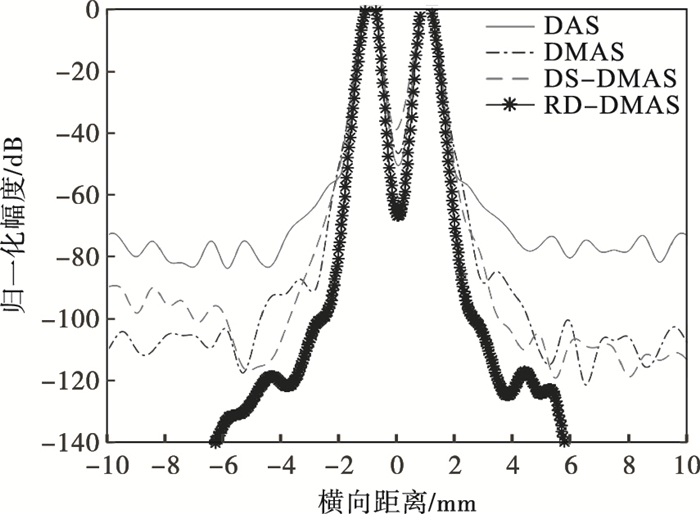
2.1 点散射目标仿体图像和横向响应图超声成像中, 分辨率是影响成像质量的关键因素, 因此采用合成点散射目标仿体仿真图像评估4种算法的分辨率, 12个点分布在10 mm至35 mm深度的仿体上, 步长为5 mm.图 1显示了点目标体的最终仿真图像, 它们由DAS, DMAS, DS-DMAS, RD-DMAS算法重建而成, 显然, 图 1a中的那些点较为模糊, 无法很好区分; 图 1b中的点可以基本区分, 但存在很多拖尾.图 1c已经基本能分清每个点, 但是个别还是有一些粘连, 而图 1d所有点清晰可见, 毫无粘连.在图 1中很明显可以看出DS-DMAS和RD-DMAS算法的效果优于DMAS算法, 更远远优于DAS算法.图 2为20 mm深度的横向响应图, 可以作为证据进一步证明得到的结论, 图 2还展示了图 1中4幅图像的旁瓣水平, DAS算法的旁瓣值约为20 dB, DMAS, DS-DMAS, RD-DMAS相应的旁瓣值为27, 36, 44 dB.从图 2可以看出RD-DMAS算法的旁瓣低于其他所有算法.可以看出旁瓣对RD-DMAS算法的影响最小, 两组峰之间的波谷也属RD-DMAS算法最低, 进一步说明它的分辨率显著.除了旁瓣水平, 半峰全宽(FWHM)也是一个重要指标, 表 1为FWHM数据, 由表 1可看出RD-DMAS算法获得的效果最好.
图 1(Fig. 1)

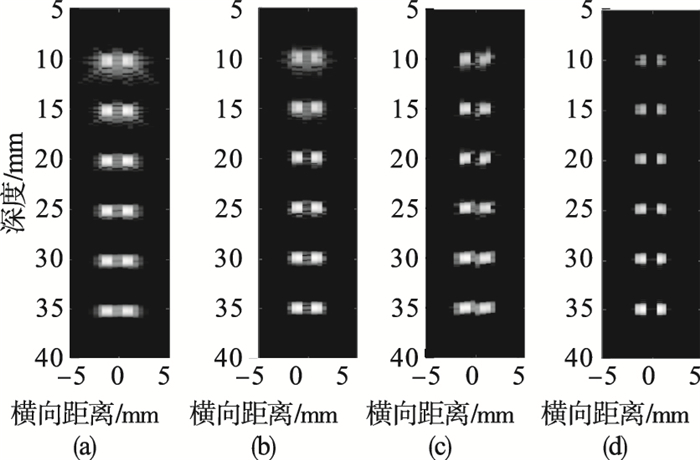图 1 点散射目标仿真图像Fig.1 Simulation image of point target (a)—DAS; (b)—DMAS; (c)—DS-DMAS; (d)—RD-DMAS.

图 2(Fig. 2)

图 2 横向响应图Fig.2 Horizontal response diagram

表 1(Table 1)

表 1 不同深度的FWHMTable 1 FWHM at different depths? mm 深度 DAS DMAS DS-DMAS RD-DMAS 10 0.456 5 0.227 4 0.165 4 0.119 7 15 0.387 4 0.217 6 0.156 1 0.115 8 20 0.266 8 0.198 1 0.148 7 0.101 8 25 0.374 8 0.210 8 0.153 4 0.113 5 30 0.415 6 0.223 6 0.162 3 0.117 8 35 0.473 8 0.237 2 0.172 5 0.120 6

表 1 不同深度的FWHM Table 1 FWHM at different depths?

2.2 囊肿仿体成像结果为了评价RD-DMAS波束形成算法, 设计了由30 000个散射点组成的囊肿仿体, 其中, 囊肿半径为5 mm, 圆心位于(x, y, z)=(0, 0, 20) mm处, 这些散射点分布在20 mm×10 mm×20 mm区域处.为了模拟真实环境, 每个解析单元设置10个散射子, 散射强度在囊肿内部为零, 外部服从高斯分布.
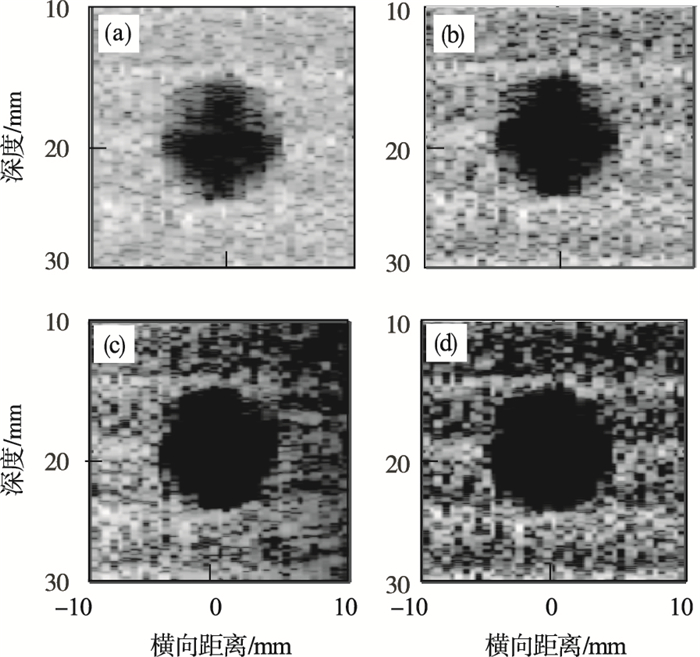
不同波束形成的囊肿仿体仿真图如图 3所示, 从图中可以看出, RD-DMAS算法得到的囊肿图最接近圆形, 图中无其他斑点带来的误差, 囊肿边界也更光滑、清晰.DAS算法得到的囊肿最模糊且对比度最差.发生这种现象主要是由于DAS算法对旁瓣的抑制能力不足, 使其旁瓣水平较高.这意味着RD-DMAS波束形成算法对信号旁瓣影响最大.从图中可以看出, RD-DMAS，DS-DMAS和DMAS算法的波束形成效果依次递减, 但都比DAS算法强.
图 3(Fig. 3)

图 3 20 mm处囊肿仿体成像结果Fig.3 Imaging results of a cyst at 20 mm (a)—DAS; (b)—DMAS; (c)—DS-DMAS; (d)—RD-DMAS.

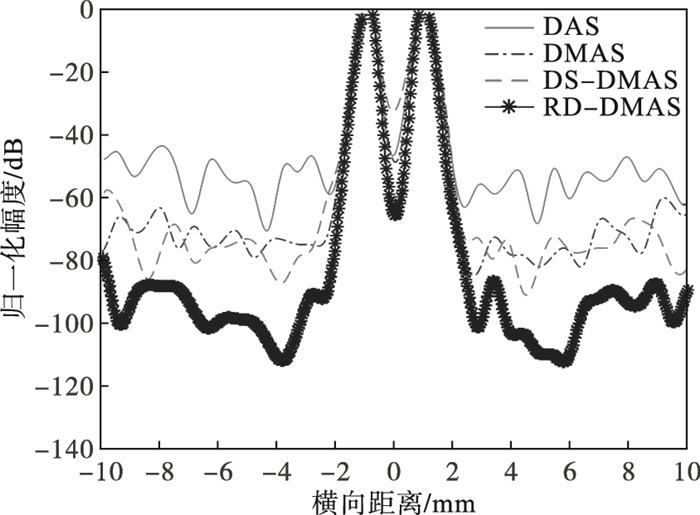
2.3 噪声影响在现实世界中, 噪声是不可忽略的重要影响因素, 因此, 噪声也应该在考虑范围内, 本文中, 把分析信道加性噪声的理想模型, 也是通信中的主要噪声源高斯白噪声添加到信号中, 并且SNR设置为-6 dB, 图 4和图 5分别为添加噪声后得到的点目标仿真图像和横向响应图.图 4a中无法清晰地看到目标点, 完全被噪声所掩盖, 同样图 4b和图 4c的点尤其处于远场中的点也是很模糊, 这也说明新算法DS-DMAS的去噪效果相比较于DMAS算法并没有多少改进, 在现实生活中, 当处在嘈杂环境中时成像效果会受到很大限制, 而图 4d中几乎所有的点都能清晰区分, 可见, 本文提出的RD-DMAS算法在实际的噪声环境中依然很出色, 从图 5中也可以看到RD-DMAS算法所获得的主瓣宽度最窄, 旁瓣宽度最低, 它的优化效果最明显.
图 4(Fig. 4)

图 4 -6 dB噪声点目标仿真图像Fig.4 Simulation image of point target with -6 dB noise (a)—DAS; (b)—DMAS; (c)—DS-DMAS; (d)—RD-DMAS.

图 5(Fig. 5)

图 5 加噪横向响应图Fig.5 Horizontal response diagram with noise

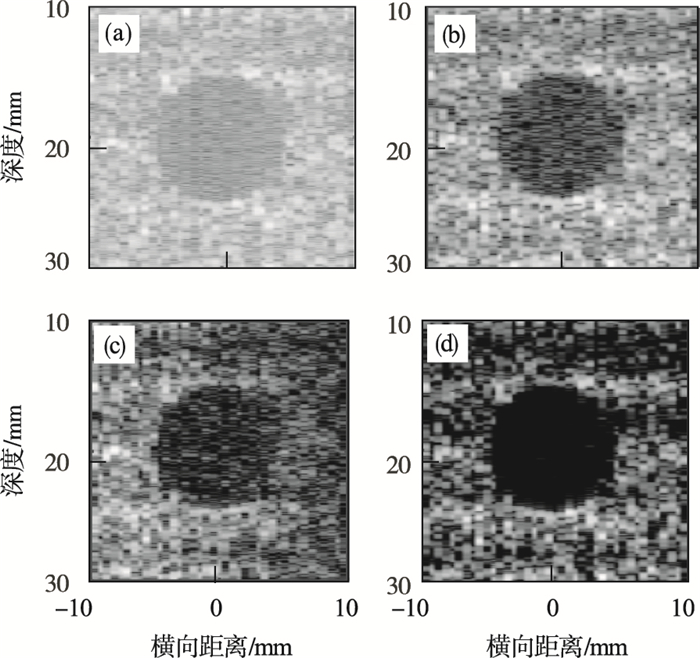
除了点目标仿真及其横向响应图, 在噪声分析中, 还在囊肿的回波信号中添加了信噪比为-6 dB的高斯白噪声, 并进行了仿真.图 6展示了不同方法得到的囊肿图像.
图 6(Fig. 6)

图 6 加噪20 mm处不同算法囊肿仿体成像结果Fig.6 Simulated imaging results of cyst with noise at 20 mm by different algorithms (a)—DAS; (b)—DMAS; (c)—DS-DMAS; (d)—RD-DMAS.

在添加噪声之后, 能看到DAS算法的囊肿图尽管仍能分清, 但已经被淹没在噪声中.DMAS算法的囊肿图看上去效果强了很多, 但它依然受噪声的影响, 尤其在囊肿的中间区域.DS-DMAS和RD-DMAS算法的囊肿图恢复效果比DAS和DMAS算法好, 但在囊肿内部及边缘区域DS-DMAS算法恢复效果略差, 较粗糙.同时, 在图 5的横向响应图中基本上是RD-DMAS算法的旁瓣最低.综上, 在囊肿含有噪声情况下, RD-DMAS算法依然有较高的对比度且效果最好.
本文用对比度(CR)和对比噪声率(CNR)来定量评价不同波束形成算法在对比度方面的性能, 公式为

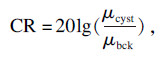(10)

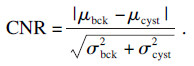(11)

其中：μ_cyst和μ_bck分别代表囊肿区域内部和囊肿背景图像的平均密度; σ_cyst²和σ_bck²代表其相应的方差.可以看出, CR与CNR的值越大, 图像的对比度越好, 图像质量在现实应用中具有更高的价值.不同波束形成算法对应的CR和CNR值如表 2所示, 从表中可以看出, RD-DMAS算法波束形成的CR值为19.86 dB, 比DAS(CR=9.72 dB)和DMAS(CR=11.72 dB)两者的波束形成算法的值大很多, 而比DS-DMAS算法(CR=13.28 dB)所对应的值稍大, RD-DMAS算法对CNR的影响与对CR的影响相同, 这意味着在几种算法中, 本文的RD-DMAS算法在实际的噪声环境中表现最为突出.
表 2(Table 2)

表 2 -6 dB高斯白噪声背景下囊肿仿体波束形成的CR和CNR值Table 2 CR and CNR values of biomimetic beamforming of cysts under the background of -6 dB Gaussian white noise 算法 内部方差 外部方差 CR/dB CNR DAS 2.87 1.07 9.72 21.34 DMAS 2.49 2.00 11.72 22.69 DS-DMAS 2.12 1.84 13.28 26.35 RD-DMAS 1.82 1.55 19.86 30.87

表 2 -6 dB高斯白噪声背景下囊肿仿体波束形成的CR和CNR值 Table 2 CR and CNR values of biomimetic beamforming of cysts under the background of -6 dB Gaussian white noise

3 讨论仿真结果表明, RD-DMAS算法的性能远远强于DAS和DMAS算法, 也优于DS-DMAS算法, 在高斯白噪声的嘈杂环境中RD-DMAS算法在分辨率和对比度方面的效果比DAS, DMAS, DS-DMAS算法好很多.RD-DMAS算法的原理与DS-DMAS算法相似, 已证明两者都优于DAS和DMAS算法, DS-DMAS算法只考虑了非自适应波束形成器, 改善了主流的算法, 而RD-DMAS算法还考虑了自适应波束形成因子, 进一步优化了算法, 提升了超声成像的分辨率.从数学角度看, DS-DMAS算法在合成新信号的过程中可以认为将DAS波束形成器应用在了原始信号中, 总的来说就是应用两步DMAS算法的思想.在2019年7月也有****提出R-DMAS算法^[22], 它的原理是在DS-DMAS算法的基础上提出来的, 就是在合成新信号的过程中将DMAS波束形成器应用在原始信号中, 虽然成像效果有一定改进, 但改进效果有限, 且造成计算量大幅增加, 得不偿失.而本文使用的加权因子与DS-DMAS算法结合而成的RD-DMAS算法能够显著提升成像质量, 加权因子计算方式能直接在DS-DMAS算法的基础上提取特征数据进行计算, 所以计算量并不大, 同时还能获得较优的效果.
4 结语本文在DS-DMAS算法的基础上, 引入了均值-标准差自适应加权因子, 提出了RD-DMAS算法, 该算法在点散射目标仿体、囊肿仿体和噪声环境下都表现出了较优的性能.与DAS, DMAS和DS-DMAS算法相比, 本文算法有最小的旁瓣, 对比度(CR)最高, 为19.86 dB, 不管环境中有无噪声, 本文算法的成像效果都是最好的.
参考文献

[1]	Capon J. High-resolution frequency-wavenumber spectrum analysis[J]. Proceedings of the IEEE, 1969, 57(8): 1408-1418. DOI:10.1109/PROC.1969.7278
[2]	Synnevag J F, Austeng A, Holm S. Adaptive beamforming applied to medical ultrasound imaging[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2007, 54(8): 1606-1613. DOI:10.1109/TUFFC.2007.431
[3]	Synnevag J, Austeng A, Holm S. Benefits of minimum-variance beamforming in medical ultrasound imaging[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2009, 56(9): 1868-1879. DOI:10.1109/TUFFC.2009.1263
[4]	Zhao J, Wang Y, Yu J, et al. Subarray coherence based postfilter for eigenspace based minimum variance beamformer in ultrasound planewave imaging[J]. Ultrasonics, 2016, 65(2): 23-33.
[5]	Diamantis K, Greenaway A, Anderson T, et al. Experimental performance assessment of the sub-band minimum variance beamformer for ultrasound imaging[J]. Ultrasonics, 2017, 79(6): 87-95.
[6]	Asl B M, Mahloojifar A. Minimum variance beamforming combined with adaptive coherence weighting applied to medical ultrasound imaging[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2009, 56(9): 1923-1931. DOI:10.1109/TUFFC.2009.1268
[7]	Asl B M, Mahloojifar A. Eigenspace-based minimum variance beamforming applied to medical ultrasound imaging[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2010, 57(11): 2381-2390. DOI:10.1109/TUFFC.2010.1706
[8]	Nilsen C C, Holm S. Wiener beamforming and the coherence factor in ultrasound imaging[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2010, 57(6): 1329-1346. DOI:10.1109/TUFFC.2010.1553
[9]	Li P C, Li M L. Adaptive imaging using the generalized coherence factor[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2003, 50(2): 128-141. DOI:10.1109/TUFFC.2003.1182117
[10]	Camacho J, Parrilla M, Fritsch C. Phase coherence imaging[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2009, 56(5): 958-974. DOI:10.1109/TUFFC.2009.1128
[11]	Zhang Y, Guo Y, Lee W. Ultrafast ultrasound imaging using combined transmissions with cross-coherence-based reconstruction[J]. IEEE Transactions on Medical Imaging, 2018, 37(2): 337-348. DOI:10.1109/TMI.2017.2736423
[12]	Alles E J, Jaeger M, Bamber J C. Photoacoustic clutter reduction using short-lag spatial coherence weighted imaging[C]//2014 IEEE International Ultrasonics Symposium. Chicago, 2014: 41-44.
[13]	Chau G, Lavarello R, Dahl J. Short-lag spatial coherence weighted minimum variance beamformer for plane-wave images[C]//2016 IEEE International Ultrasonics Symposium(IUS). Tours, 2016: 1-3.
[14]	Graham M T, Bell MAL. Theoretical application of short-lag spatial coherence to photoacoustic imaging[C]//2017 IEEE International Ultrasonics Symposium(IUS). Washington D C, 2017: 1-4.
[15]	Zheng C, Zha Q, Zhang L, et al. Signal eigenvalue factor for synthetic transmit aperture ultrasound imaging[J]. IEEE Access, 2018, 6(6): 495-503.
[16]	Bandaru R S, Sornes A R, Hermans J, et al. Delay and standard deviation beamforming to enhance specular reflections in ultrasound imaging[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2016, 63(12): 2057-2068. DOI:10.1109/TUFFC.2016.2613963
[17]	Hideyuki H, Ryo N. Singular value decomposition filter for speckle reduction in adaptive ultrasound imaging[J/OL]. Japanese Journal of Applied Physics, 2019, 58(2019-07-01)[2020-12-20]. https://iopscience.iop.org/article/10.7567/1347-4065/ab0ad6.
[18]	Matrone G, Savoia A S, Caliano G, et al. The delay multiply and sum beamforming algorithm in ultrasound B-mode medical imaging[J]. IEEE Transactions on Medical Imaging, 2015, 34(4): 940-949. DOI:10.1109/TMI.2014.2371235
[19]	Matrone G, Savoia A S, Caliano G, et al. Ultrasound synthetic aperture with the delay multiply and sum beamforming algorithm[C]// International Conference of the IEEE Engineering in Medicine and Biology Society(EMBC). Milan, 2015: 137-140.
[20]	Mardi Z, Mahloojifar A. Signal to noise ratio improvement of ultrasound harmonic images using coded excitation and adaptive line enhancer[C]//Iranian Conference onElectrical Engineering(ICEE). Mashhad, 2018: 1446-1449.
[21]	Lyons R. Quadrature signals, complex, but not complex[EB/OL]. (2018-11-15)[2020-03-05]. https://dspguru.com/files/QuadSignals.pdf.
[22]	Song K, Liu P, Liu D C. Recursively apply delay multiply and sum beamforming algorithm to enhance quality of ultrasonic image[J]. Journal of Medical Imaging and Health Informatics, 2019, 9(5): 1028-1036. DOI:10.1166/jmihi.2019.2676