
 , 郭锦华
, 郭锦华 东北大学 轧制技术及连轧自动化国家重点实验室, 辽宁 沈阳 110819
收稿日期:2020-12-21
基金项目:国家重点研发计划项目(2018YFB1308705, 2017YFB0304100)。
作者简介:丁敬国(1981-),男,吉林白山人,东北大学副教授。
摘要:为提高热连轧粗轧带钢生产过程中换钢种、换规格及换辊后的首块带钢宽度设定模型精度, 本文提出一种基于主成分分析协同随机森林(PCA-RF)算法的宽度预测模型.采用主成分分析法对数据样本合理分析, 通过计算特征值、主成分贡献度及累计贡献度进行特征选择.在PCA筛选的变量数据集上训练最佳随机森林宽度预测模型.同时, 使用支持向量机回归(SVR)、K-最近邻(KNN)模型进行对比验证.通过实际应用表明, PCA-RF各道次宽度模型R-squared值控制在99.9 % ~1, 且96 % 以上样本点预测误差在-5~5 mm, 从而证明该模型实现了换钢种、换规格及换辊后的首块钢宽度的高精度预测.
关键词:热连轧粗轧主成分分析特征选择宽度预测随机森林算法
Prediction of Rough Rolling Width Based on Principal Component Analysis Collaborated with Random Forest Algorithm
DING Jing-guo

 , GUO Jin-hua
, GUO Jin-hua State Key Laboratory of Rolling and Automation, Northeastern University, Shenyang 110819, China
Corresponding author: DING Jing-guo, E-mail: dijg@ral.neu.edu.cn.
Abstract: To improve the accuracy of the predicted width of the first piece of steel after changing the steel type, the steel specification and the roll in the process of hot continuous rough rolling strip production, a new width prediction model based on the principal component analysis collaborated with random forest (PCA-RF) algorithm is proposed in this work. The PCA method is used to analyze the reasonability of data samples and the feature selection is carried out by calculating the eigenvalue, and principal component and cumulative contribution degrees. The best RF model is trained on variant dataset selected from the PCA. At the same time, support vector machine regression(SVR)and K-nearest neighbor(KNN)models are used for comparison and verification. The practical applications show that the R-squared value from the each pass width predicted by the PCA-RF model is controlled within the range of 0.999~1, and the prediction error of more than 96 % samples is -5~5 mm, which proves that the model can predict the steel width with a high precision.
Key words: hot continuous rough rollingprincipal component analysis(PCA)feature selectionwidth predictionrandom forest(RF) algorithm
板带宽度是热连轧轧制过程中除厚度、板形等外一项极为重要的产品质量控制指标[1-2].在板带材过程控制系统中, 考核宽度模型精准度的方法通常是考核同一钢板或通卷带钢的全长上的宽度平均值与产品目标值的偏差值.宽度偏差每减小1 mm, 成材率就可提高0.1 % [3].宽度精度的高低严重地影响着带钢产品的质量与产量.良好的宽度精度不仅可以提高产品的成材率、降低板带损耗率, 更可以帮助热轧产品下游用户提供优良的生产原料, 减少质量缺陷[4].精确的宽度控制对于带钢的产品质量具有重要意义, 改进、寻求更加完善的宽度控制策略, 提高带钢宽度控制精度已经成为当前轧钢领域研究的热点.
为提高热连轧粗轧带钢宽度精度, 国内外****进行了大量的研究工作.在带钢宽度设定研究方面, 丁敬国等[5]采用粒子群算法优化神经网络连接权值和阈值的方式对板带宽度进行预测, 将偏差控制在6 mm以内; 2011年李文婷[6]采用改进粒子群算法来优化神经网络, 建立带钢宽度预测模型, 从而进一步提高预报精度;2013年Song等[3]将朴素贝叶斯算法引入神经网络进行优化, 来预测带钢宽度, 结果证明了贝叶斯神经网络比一般BP神经网络预测精度高; 在带钢头尾缺陷研究方面, Li等[7]通过仿真分析对板坯头尾在V-H热轧过程中鱼尾形状和鱼尾缺陷面积进行预测, 提出了随着影响因素变化的鱼尾缺陷面积的数学模型.实验结果表明, 该鱼尾形状预测的准确性超过95 %.Kim等[8]使用有限元方法来分析板坯首尾两端的宽度变化行为, 并开发了一种用于垂直-水平轧制过程的高级SSC模型, 提高了由于轧制率和减少板坯头端和尾端宽度造成的损失.上述文献对带钢宽度精准控制技术的发展起到了积极的推动作用, 但随着信息时代的发展以及人工智能时代的到来, 其传统控制模型已经不能满足当前生产力发展及下游企业对宽度尺寸精度的要求, 日益激烈的全球竞争和钢铁行业的产能过剩危机对热轧带钢的生产技术和产品质量提出了更高的要求.
主成分分析旨在通过降维的方法, 在损失很少信息的前提下, 将多指标转化为几个综合指标, 是一种很好的数据分析算法.随机森林是近年兴起的一种高度灵活的机器学习算法, 可以用于分类和回归问题, 具有预测精度高, 对缺失值、异常值不敏感, 模型泛化能力强, 训练速度快等优点.上述方法为热连轧宽度自动控制领域智能化提供了新思路、新方法.本文基于国内某2 250 mm热连轧生产线的实测数据, 提出了一种基于PCA-RF的宽度预测模型, 采用主成分分析法对换钢种、换规格及换辊后的首块钢宽度数据预处理, 科学合理地选择出对带钢宽度影响大的参数, 并作为输入项构建随机森林宽度预测模型, 通过仿真实验和在线测试验证其可行性; 同时, 采用MSE, MAPE和拟合决定系数来评估模型预测精度.
1 2 250 mm生产线布置及热轧数据1.1 2 250 mm热连轧生产线布置典型的热轧机主要由加热炉、定宽压力机、粗轧机、飞剪、精轧机、输送辊道和卷取机组成[9].2 250 mm热连轧机组是由德国西马克公司设计的, 采用日本TMEIC公司自动控制系统, 其产品厚度范围为1.2~25.4 mm, 宽度范围800~2 130 mm.全线配备3座加热炉、1台定宽压力机、2台带有立辊的可逆粗轧机、带有小立辊的7机架精轧机组, 1套层流冷却装置、3台地下卷取机.图 1所示为2 250 mm轧机生产线设备布置示意图.在这些组件中, 宽度控制主要在粗轧区实现, 粗轧机组由2个水平轧机和2个立辊轧机组成, 每个立辊的最大减宽量为50 mm.板坯经过粗轧机时, 每个奇数道次都可以在线测宽并对宽度设定进行修正直至最终的目标宽度设定值.
图 1(Fig. 1)
 | 图 1 2 250 mm轧机生产线设备布置示意图Fig.1 Schematic of the layout of 2 250 mm rolling mill production line |
1.2 热连轧数据来源由于生产过程的非线性、耦合性、复杂性, 影响粗轧宽度的因素有很多, 包括坯料的尺寸、组成成分, 立辊、平辊的压下量, 以及轧制工艺中的一些参数.本文采集2 250 mm热连轧生产线实际生产数据, 样本数据总量为983组, 每个样本点包括52个参数(如表 1所示), 预测目标为换钢种、换规格及换辊后的首块带钢平均宽度以及带钢第一道次、第三道次和第五道次的出口宽度.
表 1(Table 1)
| 表 1 带钢宽度影响参数及类别 Table 1 Influence parameters and types of strip width |
2 主成分分析协同随机森林算法2.1 数据标准化由于数据参数单位不一致, 在分析过程中无法进行比较, 为消除量纲影响, 则需要进行数据标准化.假设数据中含有m个样本, 每个样本有n 个指标, 且第i个样本对应的第j个指标为xij, 从而构造成一个m×n维的矩阵.
根据式(1)进行数据标准化,
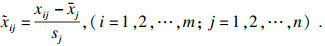 | (1) |
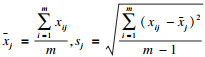
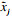
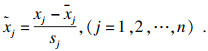 | (2) |
根据标准化后的数据集计算协方差矩阵R:
 | (3) |
 | (4) |
 | (5) |
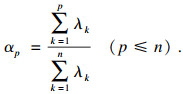 | (6) |
2.3 随机森林算法随机森林算法是由Breiman[11]在2001年提出的一种高度灵活的机器学习算法, 也是一种重要的基于Bagging的集成算法.目前, 随机森林算法已经开始应用在生物[12]、交通[13]、钢铁[14]等领域.它的基本思想是基于统计学理论, 利用Bootstrap重抽样方法从原始样本中有放回地抽取多个样本, 构建多个不同的训练集, 再基于这些分裂样本分别构建决策树, 每棵树都会输出一个预测值, 若是进行分类, 则投票决定, 若是回归预测, 则取所有决策树预测的平均值作为最终预测结果.这种算法在组合多棵决策树的基础上进行优化, 主要用于解决分类和回归问题.若从独立同分布的随机向量(X, Y)中抽取训练集, X为输入向量, Y为输出向量, 此时通过在训练集上的训练, 建立多棵决策树, 每棵决策树输出一个预测值, 通过对k棵决策树{g(θk, Xk)}取平均数, 则预测输出为g(X), 令g(X)的均方泛化误差为
 | (7) |
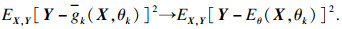 | (8) |
 | (9) |
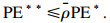 | (10) |
随机森林算法步骤可归纳为[15]: 首先采用Bootstrap方法在训练样本集S中重采样, 随机抽取s个样本, 产生t个训练集; 再使用每个训练集, 并生成相应的决策树, 在每个叶节点中选择属性之前, 从K个特征中随机提取k个特征作为该训练集的当前节点, 并在k个特征中进行最佳分裂选择最优的切分点作左右子树划分; 尽量让每棵树都得到最大限度的生长, 不进行剪枝; 对于测试集样本, 每棵决策树的预测结果为该样本点所到叶节点的均值; 最后随机森林回归模型最终的预测结果为所有回归树预测结果的均值.
2.4 基于PCA-RF宽度预测模型本文将PCA-RF模型应用到热连轧带钢宽度控制中, 对换钢种、换规格及换辊后的首块带钢平均出口宽度及第一、三、五道次出口宽度进行建模预测.图 2为PCA-RF宽度预测模型的基本流程图.
图 2(Fig. 2)
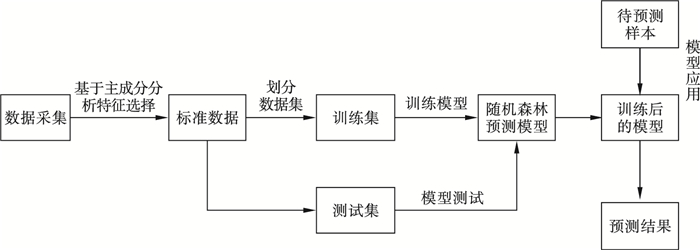 | 图 2 PCA-RF宽度预测模型流程框图Fig.2 Flow chart of PCA-RF width prediction model |
主要步骤有: 选择宽度在1 100~1 700 mm的换钢种、换规格及换辊后的首块带钢样本作为数据集, 对预处理后数据集进行主成分分析, 提取重要特征.由于热连轧粗轧过程中带钢宽度主要由立辊、平辊控制, 且受温度影响较大, 故将立辊开口度、水平轧制过程的宽展以及降温导致的收缩度直接作为模型的输入项, 不再进行基于PCA的特征选择.将特征选择后的标准数据集按照7∶3的比例划分为训练集和测试集, 在训练数据集上构建预测模型.并通过网格搜寻、交叉验证[16]调参得到最佳模型.
2.5 模型评估为评估模型预测值与实际值的偏差大小, 本文采用了均方误差(mean squared error, MSE)、平均绝对百分比误差(mean absolute percent error, MAPE)和拟合决定系数(coefficient of determination, R-squared)来衡量宽度回归预测模型的准确度.
均方误差(MSE)是反映真实值与估计值之间差异程度的一种度量, 即真实值与估计值之差的平方的期望值, 也即误差平方和的平均数.MSE值越小, 则说明预测模型可以更精确地描述实验数据.
MSE公式为
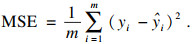 | (11) |
MAPE公式为
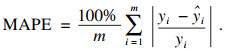 | (12) |
R-squared的公式为
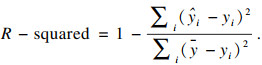 | (13) |
3 实际应用与结果分析3.1 基于主成分分析的特征选择参与主成分分析的换钢种、换规格及换辊后的首块带钢数据集参数为49个, 样本数量为983组, 将此数据集总体设为G,
 | (14) |
由于每个变量对预测目标的影响程度各不相同, 若将所有因素都作为特征输入到预测模型中, 就可能会造成维度灾难, 对宽度的预测造成负面影响.对于此问题, 本文采用主成分分析法对数据进行降维和特征选择.
采用PCA对预处理后的标准数据进行分析, 首先根据式(3)计算协方差矩阵, 得矩阵的特征值以及对应的特征向量, 由式(5)和式(6)求出各个主成分对应的贡献率及累计贡献率.
由表 2可知, KMO统计量为0.819(>0.700), Bartlett球形度检验值为0.0, 表明各个变量在一定程度上存在相互独立关系, 可以采用PCA法进行数据降维及特征选择.
表 2(Table 2)
| 表 2 KMO和Bartlett检验 Table 2 KMO and Bartlett tests | |||||||||||
根据表 3, 当主成分数为8时, 其特征值为1.548(≥1), 累计方差贡献率为85.463 % (≥85 %), 故选取前8个主成分所包含的信息代替全部数据的信息含量.根据成分矩阵选择载荷值≥0.7的指标, 提取出20个影响宽度的主要参数, 其中包括最大宽度、目标宽度、最小宽度、定宽压力机出口宽度、板坯宽度、来料热态宽度、R2-1实际轧制力、R2-2实际轧制力、R2-3实际轧制力、R2-4实际轧制力、R2-5实际轧制力、R1-1辊缝、R2-1辊缝、R2-3辊缝、定宽压力机辊缝、最大入口温度、R2-4速度、R2-5穿带速度、R2-1压下量、E2-3压下量变量, 这20项变量均被筛选为宽度模型的输入项.
表 3(Table 3)
| 表 3 主成分特征值和方差贡献率 Table 3 Principal component eigenvalues and variance contribution rates | |||||||||||||||||||||||||||||||||||||||||||||||
3.2 模型在线预测结果比较图 3所示为RF, SVR, KNN模型主成分分析前后, 换钢种、换规格及换辊后的首块带钢平均宽度预测模型精度对比图.由图可知, 各模型在六次交叉验证中, 经过主成分分析后的RF, SVR, KNN模型精度有所提升; 且图中可明显看出, RF模型比另外两种模型预测精度高很多.
图 3(Fig. 3)
 | 图 3 PCA降维前后各模型带钢平均宽度预测精度比较Fig.3 Comparison of the prediction accuracy for the average width of the strip from different models before and after PCA dimension reduction |
图 4a, 4b, 4c分别为PCA-RF, PCA-SVR, PCA-KNN模型平均宽度预测误差频率直方图.由图可知, PCA-RF模型预测误差集中在-10~10 mm, 误差较小; PCA-SVR模型预测误差主要集中在-20~20 mm, 误差较大; 而PCA-KNN模型预测误差范围很大, 主要分布在-100~100 mm内, 难以准确预测带钢宽度.
图 4(Fig. 4)
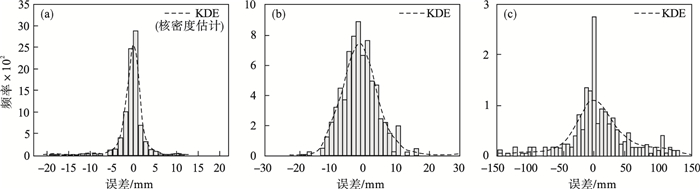 | 图 4 各个模型平均宽度预测误差频率直方图Fig.4 Prediction error frequency histogram of average width from different models (a)—PCA-RF; (b)—PCA-SVR; (c)—PCA-KNN. |
图 3, 图 4综合比较证明了PCA-RF模型预测精度更高、效果更佳, 将此模型应用到带钢各个道次出口宽度的预测中, 图 5, 图 6为实验结果.
图 5(Fig. 5)
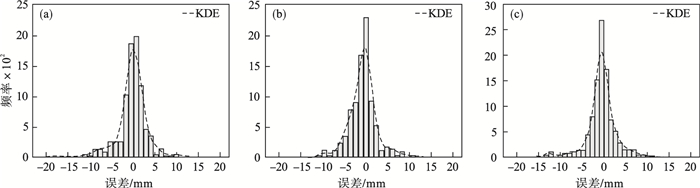 | 图 5 各道次宽度PCA-RF模型预测误差频率直方图Fig.5 Prediction error frequency histogram of each pass width from the PCA-RF model (a)—带钢第一道次; (b)—带钢第三道次; (c)—带钢第五道次. |
图 6(Fig. 6)
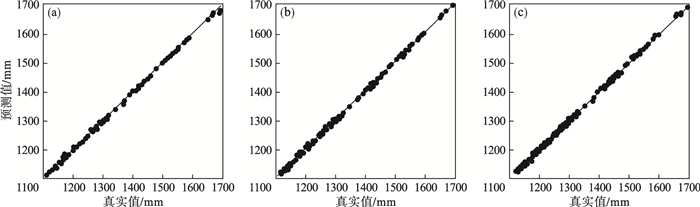 | 图 6 各道次宽度PCA-RF模型预测值与真实值比较Fig.6 Comparison of the PCA-RF predicted and real widths in each pass (a)—带钢第一道次; (b)—带钢第三道次; (c)—带钢第五道次. |
图 5为各道次出口宽度的PCA-RF模型, 误差主要集中在-10~10 mm, 且96 % 以上的样本点的预测误差在-5~5 mm.由图 6可知各道次宽度真实值-预测值的一系列离散点均匀地分布在y=x直线上, 误差较小.图 5, 图 6显示换钢种、换规格及换辊后首块带钢的宽度预测精度显著提高.
为进一步证实PCA-RF预测模型可行性, 本文采用MSE, MAPE和R-squared函数来评估模型, 表 4为分析结果.表 4中各道次样本点MSE值分布在8~11, MAPE值分布在0.1~0.2, 而R-squared值控制在了0.999~1, 进一步说明了该模型精度较高, 预测偏差较小, 可以有效改善换钢种、换规格及换辊后的首块带钢精度偏低的问题.同时, 将该模型的在线计算时间进行统计, 其运算时间均小于200 ms, 因此, PCA-RF模型可实现换钢种、换规格及换辊后的首块带钢的高精度和高实时性预测.
表 4(Table 4)
| 表 4 宽度误差对照表 Table 4 Comparison of the width errors |
4 结论1) 采用主成分分析方法对高维实验数据进行特征选择, 选取累计方差贡献率为85.463 % 的前八个主成分, 将数据维度降低到20维, 剔除一些影响不大的变量.
2) 将PCA-RF方法用于换钢种、换规格及换辊后首块带钢的在线宽度预测, 应用结果表明PCA-RF模型预测误差集中在-10~10 mm, 而PCA-SVR模型预测误差主要分布在-20~20 mm, PCA-KNN算法模型预测误差主要分布在-100~100 mm, PCA-RF方法宽度预测效果最优.
3) 基于PCA-RF对带钢各道次出口宽度进行建模, 并采用MSE,MAPE和R-squared函数评估模型.结果显示各道次模型MSE值分布在8~11, MAPE值分布在0.1~0.2, R-squared值控制在了0.999 ~1.在线应用结果表明, 换钢种、换规格及换辊后首块带钢采用PCA-RF模型预测误差集中在-10~10 mm, 其中96 % 以上样本点的预测误差在-5~5 mm.
参考文献
| [1] | Ding J G, Li Q Y, Ma G S, et al. Analytical approach for compulsory broadsiding of continuous rough rolling process[J]. Proceedings of the Institution of Mechanical Engineers.Part C: Journal of Mechanical Engineering Science, 2018, 232(20): 3685-3695. DOI:10.1177/0954406217742936 |
| [2] | Park C J, Han S H, Lee D M, et al. Direct width control systems based on width prediction models in hot strip mill[J]. ISIJ International, 2007, 47(1): 105-113. DOI:10.2355/isijinternational.47.105 |
| [3] | Song X R, Hu Z H, He X Q, et al. The prediction of the hot strip's width based on Bayesian neural network[J]. Advanced Materials Research, 2013, 823: 489-493. DOI:10.4028/www.scientific.net/AMR.823.489 |
| [4] | 吕程, 王国栋, 刘相华, 等. 利用人工神经网络预测热连轧精轧机组带钢宽度变化[J]. 上海金属, 1998, 20(4): 36-39. (Lyu Cheng, Wang Guo-dong, Liu Xiang-hua, et al. Predicting the width variation of strip in the finishing stand by artificial neural networks[J]. Shanghai Metal, 1998, 20(4): 36-39.) |
| [5] | 丁敬国, 焦景民, 昝培, 等. 基于模糊聚类的PSO-神经网络预测热连轧粗轧宽度[J]. 东北大学学报(自然科学版), 2007, 28(9): 1282-1284. (Ding Jing-guo, Jiao Jing-min, Zan Pei, et al. Hot strip width prediction during rough rolling with PSO neural network based on fuzzy clustering[J]. Journal of Northeastern University(Natural Science), 2007, 28(9): 1282-1284. DOI:10.3321/j.issn:1005-3026.2007.09.017) |
| [6] | 李文婷. 基于改进型粒子群算法的热轧带钢宽度神经网络预报模型的研究[D]. 太原: 太原理工大学, 2011. (Li Wen-ting. Research on neural network prediction model of hot strip width based on improved particle swarm algorithm[D]. Taiyuan: Taiyuan University of Technology, 2011. ) |
| [7] | Li X, Wang H Y, Ding J G, et al. Analysis and prediction of fishtail during V-H hot rolling process[J]. Journal of Central South University, 2015, 22(4): 1184-1190. DOI:10.1007/s11771-015-2632-5 |
| [8] | Kim B, Lee K, Jeon J. Short stroke control model for improving width precision at head and tail of slab in hot vertical-horizontal rolling process[J]. International Journal of Precision Engineering and Manufacturing, 2020, 21(4): 699-710. DOI:10.1007/s12541-019-00293-9 |
| [9] | Lee K, Han J, Park J, et al. Prediction and control of front-end curvature in hot finish rolling process[J]. Advances in Mechanical Engineering, 2015, 7(11): 1-10. |
| [10] | He D, Liu R. Ultra-short-term wind power prediction using ANN ensemble based on PCA[C] // IEEE 7th International Power Electronics and Motion Control Conference—ECCE Asia. Harbin, 2012: 2108-2112. |
| [11] | Breiman L. Random forests[J]. Machine Learning, 2001, 45(1): 5-32. DOI:10.1023/A:1010933404324 |
| [12] | Avdi M, Ma?eti Z, Sayed A E, et al. A novel approach in determination of biofilm forming capacity of bacteria using random forest classifier[M]. Cham: Springer-International-Publishing, 2019: 273-279. |
| [13] | Guo J, Wang J, Li Q, et al. Construction of prediction model of neural network railway bulk cargo floating price based on random forest regression algorithm[J]. Neural Computing and Applications, 2019, 31(12): 8139-8145. DOI:10.1007/s00521-018-3903-5 |
| [14] | 纪英俊, 勇晓玥, 刘英林, 等. 基于随机森林的热轧带钢质量分析与预测方法[J]. 东北大学学报(自然科学版), 2019, 40(1): 11-15. (Ji Ying-jun, Yong Xiao-yue, Liu Ying-lin, et al. Random forest based quality analysis and prediction methodfor hot-rolled Strip[J]. Journal of Northeastern University (Natural Science ), 2019, 40(1): 11-15.) |
| [15] | Zhou Y J, Guo J L, Fu L Y, et al. Research on aero-engine maintenance level decision based on improved artificial fish-swarm optimization random forest algorithm[C] // IEEE 2018 International Conference on Sensing, Diagnostics, Prognostics, and Control. Xi'an, 2018: 606-610. |
| [16] | 吕何, 孔政敏, 张成刚. 基于混合优化随机森林回归的短期电力负荷预测[J]. 武汉大学学报(工学版), 2020, 53(8): 704-711. (Lyu He, Kong Zheng-min, Zhang Cheng-gang. Short-term power load forecasting based on hybrid optimization stochastic forest regression[J]. Journal of Wuhan University(Engineering Edition), 2020, 53(8): 704-711.) |
