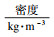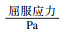, 张皓炜, 龙求喜, 刘杰
, 张皓炜, 龙求喜, 刘杰 东北大学 资源与土木工程学院, 辽宁 沈阳 110819
收稿日期:2020-11-29
基金项目:国家自然科学基金资助项目(51779045);大学生创新创业训练计划项目(S202010145176)。
作者简介:王者超(1980-),男,山东高唐人,东北大学教授。
摘要:为研究粗糙单裂隙中宾汉姆流体的渗流规律, 提出了描述岩体裂隙中宾汉姆流体黏性和黏惯性流动的渗流模型, 并采用数值模拟和室内试验结果对模型进行了验证.在粗糙裂隙中, 开展了不同流变参数的宾汉姆流体在大范围压力梯度下的渗流模拟, 结合修正的Forchheimer方程分析了宾汉姆流体在不同裂隙几何参数及流变参数下的非达西系数β、临界雷诺数Rec、非达西效应因子E等变化特性.结果表明: 由宾汉姆流体本构方程推导出的黏性模型能更好地描述黏性渗流.修正的Forchheimer方程能更好地描述宾汉姆流体在粗糙裂隙中的黏惯性渗流特征.粗糙度及流变参数会对渗流特性产生显著影响: 裂隙粗糙度越大, 浆液屈服应力越大; 浆液塑性黏度越大, 惯性作用越强.
关键词:粗糙裂隙流变参数渗流规律数值分析Forchheimer方程宾汉姆流体
Bingham Fluid Seepage Model in Rock Fractures
WANG Zhe-chao

 , ZHANG Hao-wei, LONG Qiu-xi, LIU Jie
, ZHANG Hao-wei, LONG Qiu-xi, LIU Jie School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: WANG Zhe-chao, E-mail: wang_zhechao@hotmail.com.
Abstract: In order to study the seepage law of Bingham fluid in a rough single fracture, a seepage model describing the viscous and viscous inertial flow of Bingham fluid in rock mass fractures was proposed, and the model was verified by numerical simulation and laboratory tests. The seepage simulation of Bingham fluid with different rheological parameters in rough fractures under a wide range of pressure gradients was carried out. Combined with the modified Forchheimer equation, the non-Darcy coefficient β, critical Reynolds number Rec, non-Darcy effect factor E and other variation characteristics of Bingham fluid under different geometric parameters and rheological parameters of fractures were analyzed. The results show that the viscosity model derived from the Bingham fluid constitutive equation can better describe the viscous flow. The modified Forchheimer equation can better describe the visco-inertial seepage characteristics of Bingham fluid in rough fractures. Roughness and rheological parameters have a significant impact on seepage characteristics: the larger the fracture roughness, the larger the yield stress of the slurry; the larger the plastic viscosity of the slurry, the stronger the inertia effect.
Key words: rough fracturerheological parameterseepage lawnumerical analysisForchheimer equationBingham fluid
天然岩体中存在大量节理、裂隙等结构面, 致使岩体自身强度降低、渗透性增强.为提高岩体工程性能, 对裂隙岩体注浆, 提高岩体强度, 降低岩体渗透性.在裂隙渗流中, 对单裂隙渗流的渗流特性研究十分重要, 渗流特性是指在裂隙渗流过程中, 流量随压力梯度增长的关系[1].对于牛顿流体, 常采用渗流特性中的线性段描述黏性作用主导下的流动规律, 渗流特性中的非线性段描述惯性作用主导下的流动规律.而对于浆液这一非牛顿流体, 即便在以黏性为主导作用的渗流中, 流量与压力梯度关系仍为非线性.因此, 分析浆液在黏性和惯性作用下的岩体裂隙流动规律及其渗流模型的建立具有重要意义.在牛顿流体的裂隙渗流非线性研究中, 常采用临界雷诺数Rec表示线性与非线性变化的临界位置.本研究对宾汉姆流体临界雷诺数的确定给出了一些见解.
目前, 许多****对裂隙渗流进行了大量研究, 王者超等[1]运用数值分析结合实验手段对二维裂隙中非线性水流流态的界定进行了定量研究; 许凯等[2]通过数值分析确定了非线性渗流参数的研究; 高圣元等[3]将浆液视为宾汉姆流体通过立方定律分析了等效隙宽随浆液黏度的变化关系; Shamu等[4]通过超声测速实验首次测出宾汉姆流体在平板裂隙注浆中的速度分布, 观测到流核区的存在.上述研究为分析浆液在岩体裂隙中流动规律奠定了良好基础.但现有研究尚缺乏从宾汉姆流体的本构关系角度对渗流过程影响的分析.在考虑塑性黏度和屈服应力时, 现有渗流方程对宾汉姆流体渗流的拟合结果欠佳, 而且流变参数和裂隙粗糙度对渗流特性的影响重大.
从宾汉姆流体的本构关系出发, 推导了描述宾汉姆流体黏性渗流的模型, 引入流变参数修正了Forchheimer方程, 对大范围压力梯度下的渗流模拟进行验证.利用模拟结果对不同流变参数和不同裂隙粗糙度对渗流特性的影响进行分析讨论.
1 渗流模型1.1 黏性渗流模型图 1为宾汉姆流体在间距为e的平板中作层流流动, 宾汉姆流体存在屈服应力, 当流体所受切应力τ=τ0时, 不会产生剪切流动[5].因此宾汉姆流体在平行板间做层流运动时会出现厚度为e0的流核区.
图 1(Fig. 1)
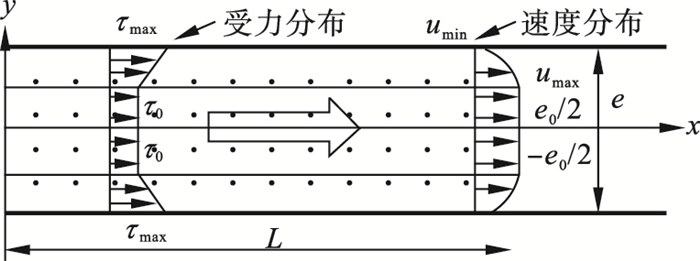 | 图 1 宾汉姆流体在光滑平行板间的渗流示意图Fig.1 Schematic diagram of Bingham fluid seepage between smooth parallel plates |
在图 1中: e为光滑裂隙平板的开度, m; e0为流核区宽度, m; umin为流体沿x方向最小速度, m/s; umax为流体沿x方向最大速度, m/s; τ0为流核区流体所受的屈服应力, Pa; τmax为速度梯度区流体所受的最大剪切应力,Pa.
浆液在流核区内存在以下速度边界条件:
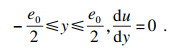 | (1) |
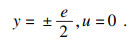 | (2) |
利用N-S方程求解流体在裂隙中的渗流方程:
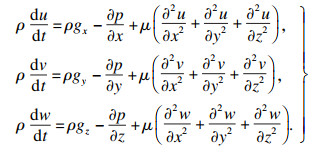 | (3) |
由假定①~④将N-S方程化简为
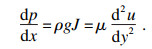 | (4) |
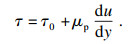 | (5) |
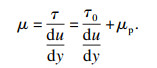 | (6) |
将式(6)代入式(4):
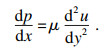 | (7) |
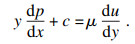 | (8) |
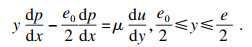 | (9) |
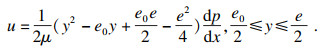 | (10) |
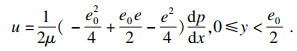 | (11) |
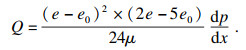 | (12) |
图 2(Fig. 2)
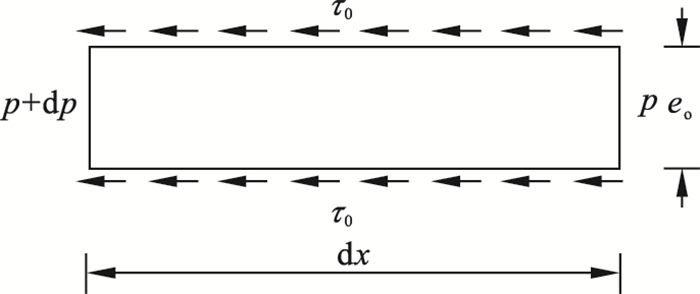 | 图 2 流核区单元体受力示意图Fig.2 Stress diagram of the flow core unit |
分析单元体受力平衡得:
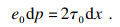 | (13) |
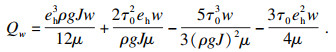 | (14) |
式(14)中第一项表示压力克服黏滞力作用产生的流量; 第二、三项分别表示压力克服流体可变屈服强度部分对流量的贡献或抑制作用; 第四项表示压力克服流体固定屈服强度部分对流量的抑制作用.该式描述流体渗流的流量为零时, 对应水力梯度J=2τ0/pgeh.
1.2 黏惯性渗流模型黏惯性模型同时考虑了黏性与惯性的作用, 能描述浆液的全压力梯度范围的渗流特性.对于牛顿流体的非线性渗流裂隙渗流, 已有****提出并验证了符合非线性关系的经验公式Forchheimer[7], 文献[8]提出的参数表达式为
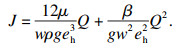 | (15) |
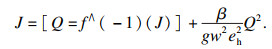 | (16) |
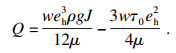 | (17) |
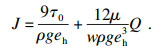 | (18) |
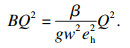 | (19) |
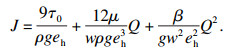 | (20) |
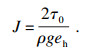 | (21) |
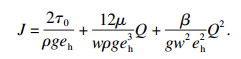 | (22) |
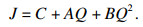 | (23) |
2 模型验证2.1 建立验证模型裂隙由标准JRC曲线导入得到.建立9个不同裂隙几何参数的三维单裂隙几何模型, 初始开度分别为0.8, 1.0, 1.2 mm, 裂隙模型的平面尺寸为200 mm×50 mm, 三维裂隙几何模型如图 3所示.
图 3(Fig. 3)
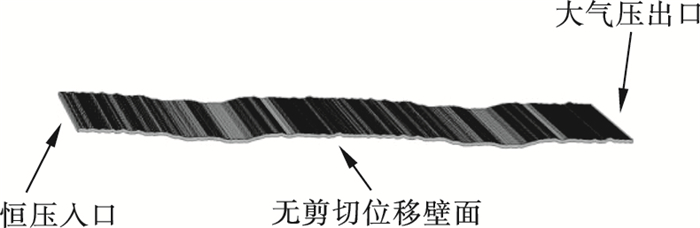 | 图 3 三维裂隙几何模型Fig.3 Three dimensional fracture geometric model |
式(24)为验证模型的物理模型:
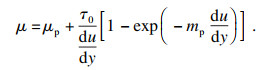 | (24) |
表 1(Table 1)
| 表 1 各浆液流变参数 Table 1 Rheological parameters of each slurry |
岩体裂隙中裂隙的渗透率远大于壁面孔隙介质的渗透率, 不考虑流体向壁面的扩散[3].为研究浆液在裂隙中的扩散性能, 忽略浆液黏度时变性, 认为渗流过程为定常流动[5], 并考虑惯性力作用.
3种水灰比浆液在不同裂隙粗糙度及不同裂隙开度所组成的27个模拟工况参数如表 2所示.
表 2(Table 2)
| 表 2 不同工况模拟参数及拟合参数 Table 2 Simulation parameters and fitting parameters under different cases |
2.2 模拟验证2.2.1 黏性模型验证在进行数值模拟验证时应注意式(14)的适用性, 本文采用的验证模型为
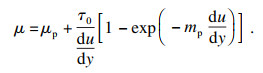 | (25) |
许多****推导了用于描述浆液的渗流模型, 其不同在于数学简化手段的不同.被广泛采用的主流模型有两种:
王晓玲模型[5]:
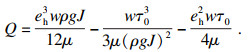 | (26) |
孙小康模型[9]:
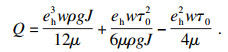 | (27) |
图 4(Fig. 4)
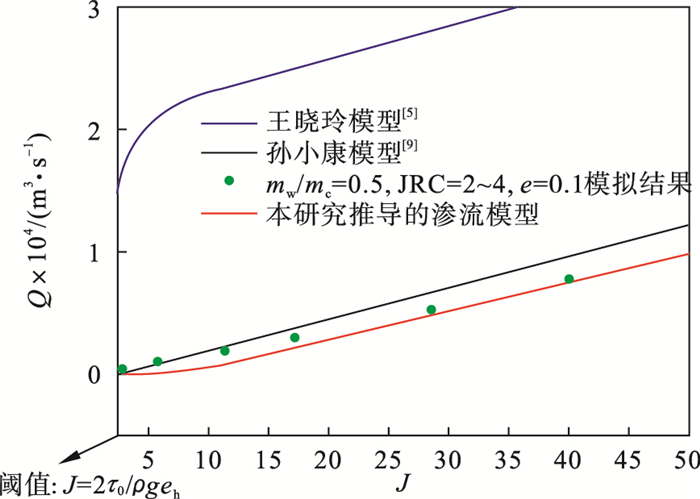 | 图 4 3个不同渗流方程的对比Fig.4 Comparison of three different seepage equations |
本文所推导的黏性模型相比于其他黏性模型有以下特点: ①在同一压力作用下, 本文所推导的黏性模型因充分考虑了宾汉姆流体的本构方程中各流变参数对渗流的影响, 而没有过大估计流体的流量.②充分考虑了边界条件的影响, 流量符合从零开始的物理意义.
2.2.2 黏惯性模型验证利用修正的Forchheimer经验方程对数值模拟结果进行拟合, 不同工况的线性项系数A、惯性项系数B、塑性项系数C和非达西系数β的拟合结果如表 2所示, 拟合曲线如图 5~图 7所示.可见修正后的Forchheimer经验方程拟合效果较好, 方差均在0.995以上.屈服强度较高的浆液更具备类似于宾汉姆流体的流变特性, 修正的经验方程有更好的拟合效果; 水灰比为1.0的浆液屈服强度较低, 具备较弱的宾汉姆流体流变特性, 系数C的值过小, 若视为牛顿流体, 修正的经验方程将C项取值为0可同样适用, 并与Forchheimer经验方程有相近的拟合效果.修正的经验方程对于其他水灰比浆液所对应的非牛顿流体有一定使用限制.
图 5(Fig. 5)
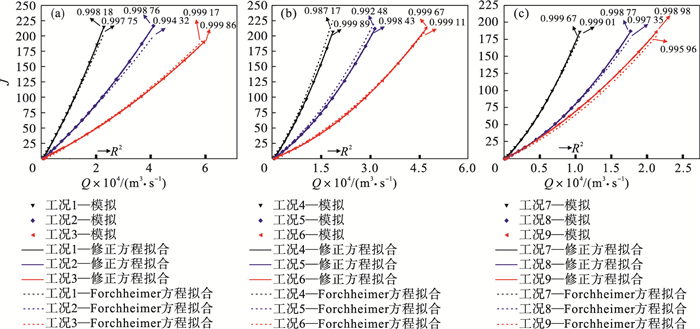 | 图 5 水灰比为0.5时模拟数据与拟合曲线对比Fig.5 Comparison between the simulation data and the fitted curves under a water-cement ratio of 0.5 (a)—JRC=2~4; (b)—JRC=8~10; (c)—JRC=18~20. |
图 6(Fig. 6)
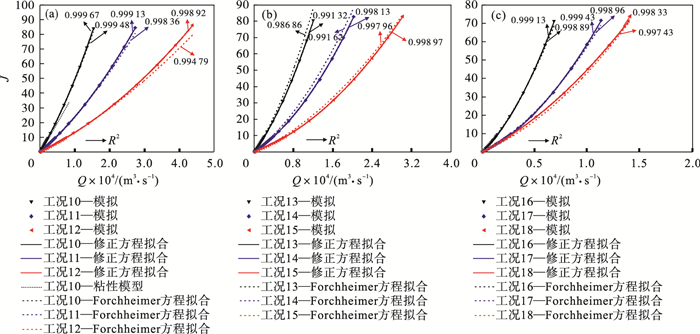 | 图 6 水灰比为0.7时模拟数据与拟合曲线对比Fig.6 Comparison between the simulation data and the fitted curves under a water-cement ratio of 0.7 (a)—JRC=2~4; (b)—JRC=8~10; (c)—JRC=18~20. |
图 7(Fig. 7)
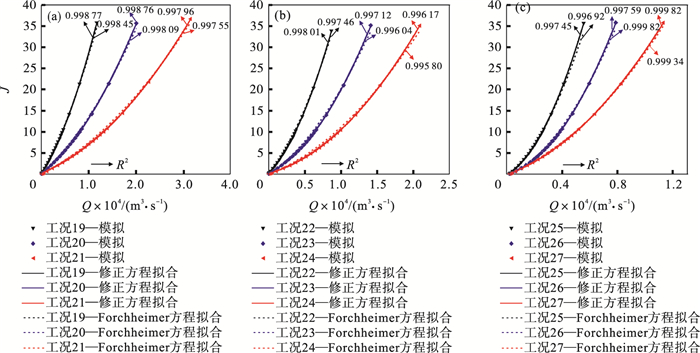 | 图 7 水灰比为1.0时模拟数据与拟合曲线对比Fig.7 Comparison between the simulation data and the fitted curves under a water-cement ratio of 1.0 (a)—JRC=2~4; (b)—JRC=8~10; (c)—JRC=18~20. |
3 讨论3.1 流变参数对渗流特性的影响将同裂隙渗流条件下水与浆液的渗流规律进行对比, 如图 8所示.两种流体的宏观渗流特性规律相近, 随压力的逐渐增大, 两种流体都逐渐偏离黏性方程的描述, 呈现出惯性渗流的特性.浆液的渗流特性受黏度影响较大, 随着塑性黏度的提高, 其黏滞力所致压力梯度损失作用越明显, 浆液需要更高的压力以达到与水同等的流量.此外, 浆液由于屈服应力的存在, 在初始压力梯度段需一定的阈值压力梯度来克服屈服强度的作用从而产生流量.图 8的拟合结果表明由于屈服强度的作用, 拟合曲线在y轴上应有截距.但模块提供的物理模型的本构关系与假定μ=μp不同, 因此宾汉姆流体渗流模型与数值模拟对于渗流过程的描述在黏性渗流段有一定误差, 数值模拟难以体现阈值压力这一特性.
图 8(Fig. 8)
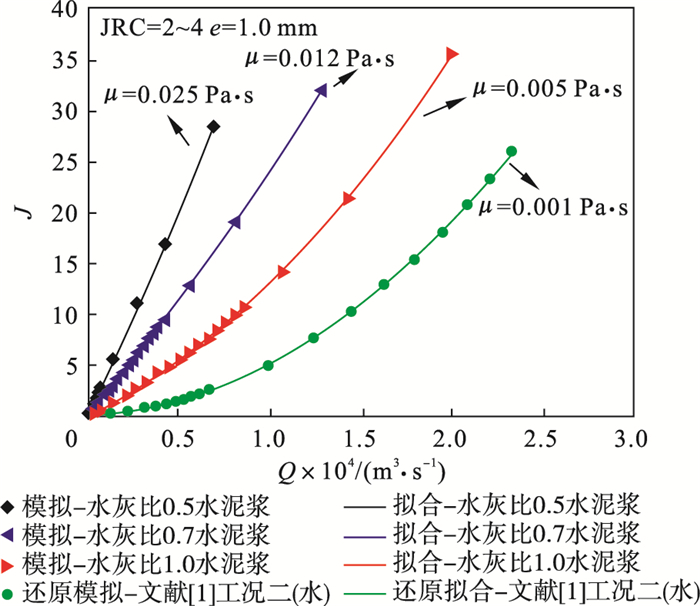 | 图 8 牛顿流体与宾汉姆流体渗流特性的对比Fig.8 Comparison of seepage characteristics between Newtonian fluid and Bingham fluid |
由式(13)可知, 流核区宽度随压力梯度的增大而减小.式(14)中第二、三项表示浆液在渗流过程中随压力增大导致流体屈服强度作用被逐渐削弱, 流核区宽度减小, 具有屈服强度的流核区部分受到破坏, 屈服应力对渗流特性的影响随压力的增大而削弱.
3.2 裂隙粗糙度对渗流特性的影响由于裂隙粗糙度对黏性渗流的影响微弱, 故只讨论裂隙粗糙度对惯性渗流的影响.利用式(22)对非达西系数β进行拟合, 并通过拟合结果分析式(22)的适用性.不同粗糙度非达西系数β随水力开度的变化如图 9所示.
图 9(Fig. 9)
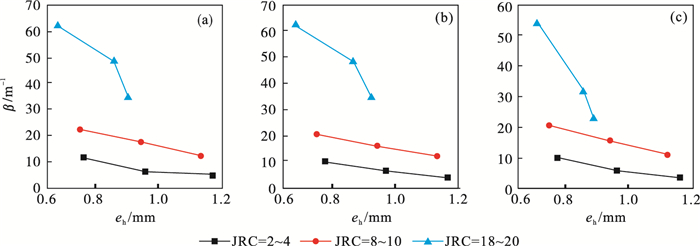 | 图 9 不同粗糙度β随水力开度的变化Fig.9 Change of β with hydraulic opening under different roughness (a)—mw/mc=0.5; (b)—mw/mc=0.7; (c)—mw/mc=1.0. |
由图 9可知, 非达西系数β随裂隙粗糙度的增加而增大, 随等效隙宽的增大而减小.β主要受裂隙粗糙度影响, 对于不同水灰比的浆液, β的变化也不大.在相同粗糙度的渗流条件下, β应具有一致性.
得到β值后, 可通过β定量流体渗流中因惯性作用所损失的压力梯度, 进而量化流体渗流中惯性作用的影响.在牛顿流体中, 常利用非达西效应因子E[7]来描述惯性作用的影响, 其表达式为
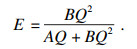 | (28) |
 | (29) |
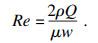 | (30) |
图 10(Fig. 10)
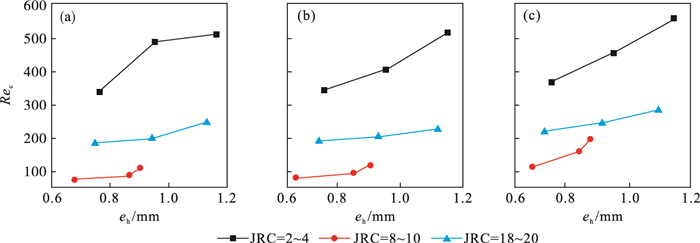 | 图 10 不同水灰比下临界雷诺数Fig.10 Critical Reynolds number at different water-cement ratio (a)—mw/mc=0.5; (b)—mw/mc=0.7; (c)—mw/mc=1.0. |
由模拟结果整理EB与Rec的关系如图 11所示.在裂隙粗糙度较大的渗流条件下, 其惯性渗流占比增长趋势明显高于裂隙粗糙度较小的渗流条件, 同等压力范围下惯性作用占比峰值也较高.
图 11(Fig. 11)
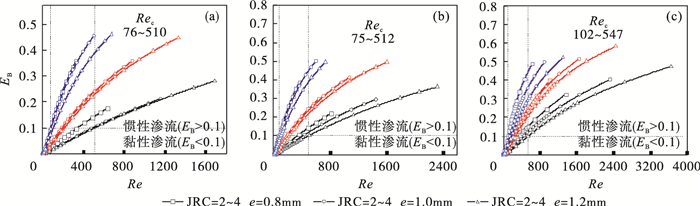 | 图 11 EB与Re的关系Fig.11 Relationship between EB and Re (a)—mw/mc=0.5; (b)—mw/mc=0.7; (c)—mw/mc=1.0. |
在相同粗糙度下, 裂隙开度较小的渗流条件中惯性渗流占比增长速度高于裂隙开度较大的渗流条件, 表明小裂隙开度条件下, 粗糙度对流体运动阻碍作用较大, 利于惯性渗流发生.随着雷诺数的增加, 由惯性力所致的压力梯度损耗在总压力梯度损耗中占比变大.相比于高塑性黏度浆液, 在相同的裂隙几何渗流条件下, 低塑性黏度浆液中的惯性渗流增长更为迅速, 最终以惯性作用为主要作用损失压力梯度, 其峰值更高, 占比50 % 以上.
4 结论1) 基于宾汉姆流体的本构关系建立了黏性渗流模型, 通过与两种渗流模型的对比, 说明了黏性渗流模型的适用性.
2) 基于Forchheimer经验方程引入了宾汉姆流体的流变参数, 推导出可描述宾汉姆流体黏惯性渗流方程, 并对方程进行黏惯性模拟验证.拟合结果表明, 浆液的渗流特性与修正的经验方程较Forchheimer经验方程有更好的拟合效果.
3) 对比了水和不同流变参数的宾汉姆流体在相同粗糙度下压力梯度损失的情况,宾汉姆流体的渗流特性受塑性黏度与屈服应力的影响.相同裂隙下塑性黏度越大, 压力梯度损失越大; 屈服应力表现为流体具备一定屈服强度的部分对压力梯度的损失作用, 随着压力梯度的增大屈服应力对渗流特性的影响削弱, 在惯性渗流特性的分析中可以一定程度上忽略屈服应力对渗流特性的影响.
4) 基于修正方程在不同粗糙度下对非达西系数β进行拟合, 结果表明β主要受粗糙度变化的影响为主导而变化.对于不同水灰比的浆液其β的变化也不大, 可认为对于宾汉姆流体而言, 在一定粗糙度条件下β具有较好的一致性.
5) 基于非达西效应因子E引入宾汉姆流体流变参数, 推出修正后的效应因子EB.结果表明: EB受流体塑性黏度参数影响, 导致同粗糙度中不同水灰比的浆液渗流Rec并不一致, EB=0.1不能综合反应其惯渗流临界情况.
参考文献
| [1] | 刘杰, 王者超, 张宇鹏, 等. 岩石粗糙裂隙大范围雷诺数条件下渗流特性[J]. 山东大学学报(工学版), 2019, 49(4): 70-77, 85. (Liu Jie, Wang Zhe-chao, Zhang Yu-peng, et al. Seepage characteristics of rock under large range of Reynolds number[J]. Journal of Shandong University(Engineering Science), 2019, 49(4): 70-77, 85.) |
| [2] | 许凯, 雷学文, 孟庆山, 等. 非达西渗流惯性系数研究[J]. 岩石力学与工程学报, 2012, 31(1): 164-170. (Xu Kai, Lei Xue-wen, Meng Qing-shan, et al. Study on inertia coefficient of non Darcy seepage[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(1): 164-170.) |
| [3] | 高圣元. 基于宾汉姆流体的微裂隙岩体注浆扩散影响机制分析[J]. 岩石力学与工程学报, 2016, 35(sup2): 3492-3500. (Gao Sheng-yuan. Analysis on the mechanism of grouting diffusion in micro fractured rock mass based on Bingham fluid[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(sup2): 3492-3500.) |
| [4] | Shamu T J, Zou L. Radial flow velocity profiles of a yield stress fluid between smooth parallel disks[J]. Rheologica Acta, 2020(3): 239-254. DOI:10.1007/s00397-020-01203-x |
| [5] | 王晓玲, 刘长欣, 李瑞金, 等. 大坝基岩单裂隙灌浆流固耦合模拟研究[J]. 天津大学学报(自然科学与工程技术版), 2017, 50(10): 1037-1046. (Wang Xiao-ling, Liu Chang-xin, Li Rui-jin, et al. Fluid solid coupling simulation of single crack grouting in dam bedrock[J]. Journal of Tianjin University(Natural Science and Engineering Technology Edition), 2017, 50(10): 1037-1046.) |
| [6] | Rosquo?t F, Alexis A. Khelidj A, et al. Experimental study of cement grout[J]. Cement and Concrete Research, 2003, 33(5): 713-722. DOI:10.1016/S0008-8846(02)01036-0 |
| [7] | Zeng Z, Grigg R. A criterion for non-farcy flow in porous media[J]. Transport in Porous Media, 2006, 63(1): 57-69. DOI:10.1007/s11242-005-2720-3 |
| [8] | Chen Y F, Zhou J Q, Hu S H, et al. Evaluation of forchheimer equation coefficients for non-Darcy flow in deformable rough-walled fractures[J]. Journal of Hydrology, 2015, 529: 993-1006. |
| [9] | 孙小康. 深部裂隙岩体注浆浆液扩散机理研究[D]. 徐州: 中国矿业大学, 2019. (Sun Xiao-kang. Study on the diffusion mechanism of grouting fluid in deep fractured rock mass[D]. Xuzhou: China University of Mining and Technology, 2019. ) |
| [10] | Yu L, Liu R, Jiang Y. A review of critical conditions for the onset of nonlinear fluid flow in rock fractures[J]. Geofluids, 2017, 2017: 1-17. |