, 王素欣1,3, 王雷震1,3 1. 东北大学 信息科学与工程学院, 辽宁 沈阳 110819;
2. 燕山大学 经济管理学院, 河北 秦皇岛 066004;
3. 东北大学秦皇岛分校 控制工程学院, 河北 秦皇岛 066004
收稿日期：2020-12-23
基金项目：国家重点研发计划项目(2020YFB1712802)；国家自然科学基金资助项目(71401027)；河北省自然科学基金资助项目(G2016501086)；河北省高等学校人文社会科学研究项目(SQ202002)。
作者简介：杜子超(1996-)，男，内蒙古呼和浩特人，东北大学硕士研究生;
王雷震(1965-)，男，河北行唐人，东北大学教授。
摘要：针对众包抢单模式和众包派单模式的配送特点, 建立众包配送车辆调度模型, 将两种配送模式有机结合, 优势互补, 并根据模型特点采用蚁群-量子粒子群混合优化算法进行求解.以深圳清湖冷链配送为例, 从配送距离和成本等角度, 分别与传统配送模式、抢单配送模型和派单配送模型进行比较, 实验充分证明了众包配送模型的有效性; 同时, 将蚁群-量子粒子群混合算法与蚁群、粒子群等算法优化结果进行比较, 证明了蚁群-量子粒子群混合算法的有效性.
关键词：众包车辆调度优化抢单模式派单模式蚁群算法量子粒子群算法
Vehicle Scheduling Model and Optimization of Crowdsourcing Logistics Distribution
DU Zi-chao1, LU Fu-qiang2
, WANG Su-xin1,3, WANG Lei-zhen1,3 1. School of Information Science & Engineering, Northeastern University, Shenyang 110819, China;
2. School of Economics and Management, Yanshan University, Qinhuangdao 066004, China;
3. School of Control Engineering, Northeastern University at Qinhuangdao, Qinhuangdao 066004, China
Corresponding author: LU Fu-qiang, E-mail: fuqiang_lu@126.com.
Abstract: Considering the distribution characteristics of crowdsourcing order grabbing/dispatching modes, a crowdsourcing distribution vehicle scheduling model is established, in which two distribution modes are combined, complementing each other. According to the characteristics of the model, a hybrid algorithm of ant colony coupled with quantum particle swarm optimization is proposed to solve the model. Taking Qinghu cold chain distribution in Shenzhen as an example, the crowdsourcing distribution model is compared with the traditional model and order grabbing/dispatching models from the perspective of distribution distance and cost. The experiment fully proves the effectiveness of the crowdsourcing distribution model. The optimization results of hybrid algorithm proposed is compared with that of the ant colony algorithm and particle swarm optimization algorithm, thus verifying the effectiveness of the proposed algorithm.
Key words: optimization of crowdsourcing vehicle schedulingorder grabbing modeorder dispatching modeant colony algorithmquantum particle swarm algorithm
随着电子商务的发展, 物流配送行业对配送员的需求持续快速增长, 传统配送模式面临着在需求高峰时人手短缺的风险.为降低物流企业的配送成本, 同时满足特定时段激增的订单量, 一种基于共享经济理念而提出的“众包”配送模式被提出并得到了应用.“众包”是指某个单位将以往内部职工需要完成的工作内容, 通过自由自愿的模式, 向非特定的社会人员外包来实现的运作模式.社会中潜藏着数量巨大的“潜在快递员”, 像一个蓄水池一样储备着丰富多样的配送资源[1].将这些社会配送资源有效地利用在物流配送方面可以极大地缓解传统的物流配送所面临的配送成本、人员等压力, 更好地配置资源, 提高配送效率, 降低物流公司风险.然而, 对众包车辆调度问题进行研究的文献较少, 且未能提出有效的众包配送车辆调度模型和优化算法.本文正是基于这一研究背景, 结合国内外众包研究成果, 进一步挖掘众包配送的内在特征, 进一步发挥其优势, 并将“众包”理念应用到物流配送车辆调度问题中, 使其得到更好的应用.
研究众包配送问题首先需要研究国内外众包配送模式的发展现状.早在2013年沃尔玛就通过沃尔玛网站(walmart.com)从沃尔玛消费者当中招募“兼职快递员”, 顺道为其他消费者配送商品, 这是初始的众包配送模式; 随后, 基于特定区域居民习惯和基础设施的众包配送模式得到了应用, 国外一些****对此也展开了研究.2013年12月, DHL公司推出独特的My ways应用程序, 通过研究居民日常出行规律, 为斯德哥尔摩地区的居民提供“顺路配送服务”, 以促进最后一英里的交付.Dupljanin等[2]通过比较不同种类配送车辆的配送效率得出, 在哥本哈根的基础设施条件下, 采用自行车配送的众包车队配送效率更高; Akeb等[3]依据法国巴黎的社区与人口收入研究分析了众包配送模式下配送范围、配送定价、人口密度等因素对众包配送的影响.到此为止, 众包配送模式的应用研究偏向于小范围、小批量、特殊化的配送情况, 配送模式难以在其他地区广泛推行, 限制了众包配送模式的大规模应用.近年来, 在打车、小件配送等领域, 国内外许多公司开始尝试在较大范围内推广众包配送模式, 如2015年, 亚马逊以5美元的报酬招募“众包出租车司机”为配送中心提供配送服务, 同年5月国内京东以“京东到家”网络平台为依托, 发布订单信息, 招募配送员在三到五公里距离范围内进行配送, 闪送、人人快递也紧随其后推出相应的众包配送服务, 国内一些文献也针对此类问题开展了基于众包配送模式的定价策略等方面的研究[4-5].其他关于众包配送的文献有关于众包配送模式特性的研究, 如2018年, Castillo等[6]深入分析了众包配送模式实际应用中所面临的挑战, 提出相比于用专业配送员的传统物流模式, 众包配送模式在面临配送需求量变动、时间窗设置较紧的情况下配送效果急剧下降; 也有结合众包背景对客户社交等行为的研究[7-8].然而, 很少有文献对众包模式在车辆调度方面建立数学模型, 尽管Wang等[1]在2016年提出的大规模众包配送模型和算法比较经典, 但其配送模型更接近抢单模式.2020年以来有****开始在传统配送模式的成果上研究更加接近于传统配送的派单配送模型, 但与实际配送差异较大, 且没有考虑配送车型不同而造成的配送价格、可使用数量的差异, 未能考虑不同配送节点对车型的限制, 也未能同时考虑“抢单”和“派单”这两种众包配送模式在众包配送问题中的应用.因此, 本文将结合国内外文献对众包的研究理论成果, 并考虑近几年在众包配送方面的应用情况, 重新建立更加贴近实际配送情况的众包配送模型.
1 众包配送车辆调度问题1.1 问题描述在最后一公里的物流配送研究中, 常常将城市划分为一个个的配送单元, 并在每个单元内设置配送中心进行配送[9-11].本文也在每一个小的配送单元内研究众包配送, 分析总结传统物流和众包配送模式差异, 建立涵盖所有众包配送模式基本特征的数学模型.
企业运作和学术研究的众包配送模式分为“抢单”和“派单”两种众包配送模式[12], 前者是靠平台直接将配送信息和相应报酬信息发出来, 由平台上面的众包司机抢单配送, 这种模式管理简单, 而且容易通过报酬奖励等方式招募到众包配送员, 但容易出现盲目抢单、以量定胜等配送现象, 造成有些订单实际无法完成, 不适合大规模复杂的配送任务; 而派单模式是有平台根据一定算法尽可能地对货物和车辆提前进行分类, 对于大规模的车辆调度而言更加可靠, 但也存在如模式复杂、调度周期较长等问题.综合考虑这两种众包模式的优势和劣势, 本文研究主要采用“派单”和“抢单”相结合的众包配送模式, 将众包配送分成两个阶段进行: 先由平台选出众包配送员, 按照众包平台提出的配送要求进行派单配送, 这是第一次配送; 当第一次配送有未完成的少量订单, 则由抢单配送完成, 用报酬激励的方式招募配送员参与配送, 作为第二次配送以满足所有客户节点的需求.
传统配送和众包配送在配送路径上差异明显.传统配送模式需要配送车辆人员统一从一个配送中心出发, 完成配送后再返回配送中心, 在配送路径上是闭环的.在传统配送模式中, 一辆车往往需要服务多个客户节点, 返回配送中心时是空载运行, 而这一部分路径也被算入配送成本, 造成了配送资源的浪费.在众包配送模式中, 配送中心将接收到的需要配送的客户信息通过网络信息平台向散布在各处的众包配送员发布, 众包配送员从配送中心取件后去往指定的配送节点, 无需再次返回配送中心.
现对问题简述如下: 在一个配送单元中, 有一个配送中心O, 已知客户节点集合N, 且已知各客户节点的需求量集合及允许停靠车型Li; 已知社会车辆型号集合P(主要是按照车辆体积划分), 各类社会车辆的起步价及单位距离行驶补贴成本Gpk; 从社会潜在的配送车辆集合S中选取可进行配送的车辆集合K, 对各个客户节点进行配送, 一辆车可以服务多个客户节点, 同时一个客户节点也可以由多辆车配送, 要满足每个客户节点的需求, 同时配送车辆不能超载.
1.2 众包配送车辆调度模型1.2.1 模型假设与符号说明1) 模型假设: ①除配送体积不同外, 所有配送货物不做特殊区分; ②假设配送报酬足够高时可以招募到足够的配送司机参与第二次配送; ③不考虑车型的交通水平等外界因素对配送造成的影响.
2) 符号定义见表 1.
表 1(Table 1)
 表 1 符号说明Table 1 Description of symbols
| 表 1 符号说明 Table 1 Description of symbols |
1.2.2 数学模型
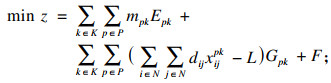 | (1) |
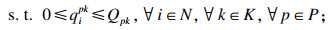 | (2) |
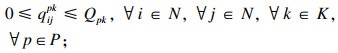 | (3) |
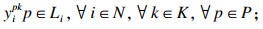 | (4) |
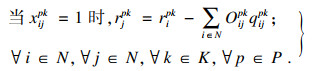 | (5) |
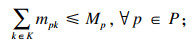 | (6) |
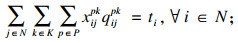 | (7) |
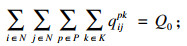 | (8) |
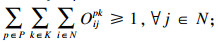 | (9) |
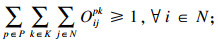 | (10) |
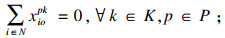 | (11) |
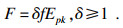 | (12) |
2 蚁群-量子粒子群混合优化算法本文在对众包配送模式和传统配送模式深入研究对比后, 将众包配送问题分成任务指派和配送路径优化两部分来解决: 对指派方案和路径进行联合优化, 以成本最低为优化目标; 每生成一组指派方案就对车辆路径进行优化, 以成本为衡量指标对生成方案进行筛选, 得到最优解.
配送方案的优化采用蚁群-量子粒子群优化(ant colony optimization-quantum particles swarm optimization, ACO-QPSO)算法.其中, QPSO算法的全局搜索能力远远优于一般PSO算法, 已经应用于各个领域的研究[13-19].
QPSO算法中的粒子以聚集态散布在解空间, 理论上比PSO算法更有可能达到全局最优, 且涉及参数较少.该算法迭代求解共有3个主要步骤:
1) 计算每一个粒子i的收敛点(即当前最优值) Pi, 以保证整个算法收敛, Pi=[Pi1, Pi2, …, Pid]:
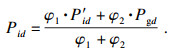 | (13) |
2) 计算用于粒子进化迭代的平均最优值P mbest:
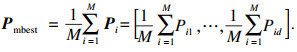 | (14) |
3) 对各个粒子迭代进化:
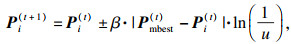 | (15) |
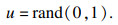 | (16) |
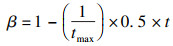 | (17) |
应用ACO-QPSO算法求解众包车辆调度模型流程如图 1所示.
图 1(Fig. 1)
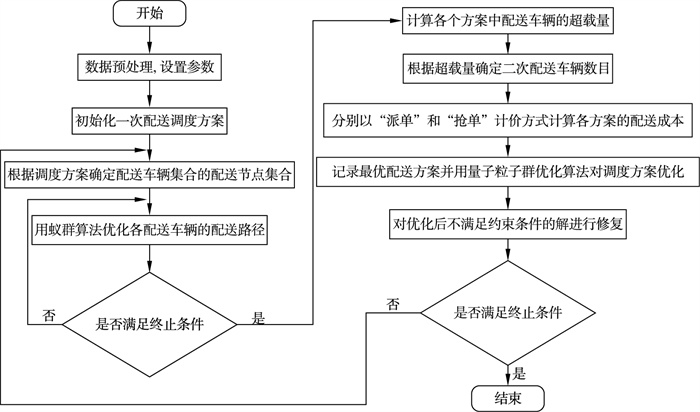 | 图 1 配送模型求解流程Fig.1 Solution flow of the distribution model |
3 算例设计本文选取深圳清湖冷链配送中心对周边客户节点配送货物的实际案例, 根据经纬坐标画出配送中心及配送客户节点的分布, 如图 2所示.
图 2(Fig. 2)
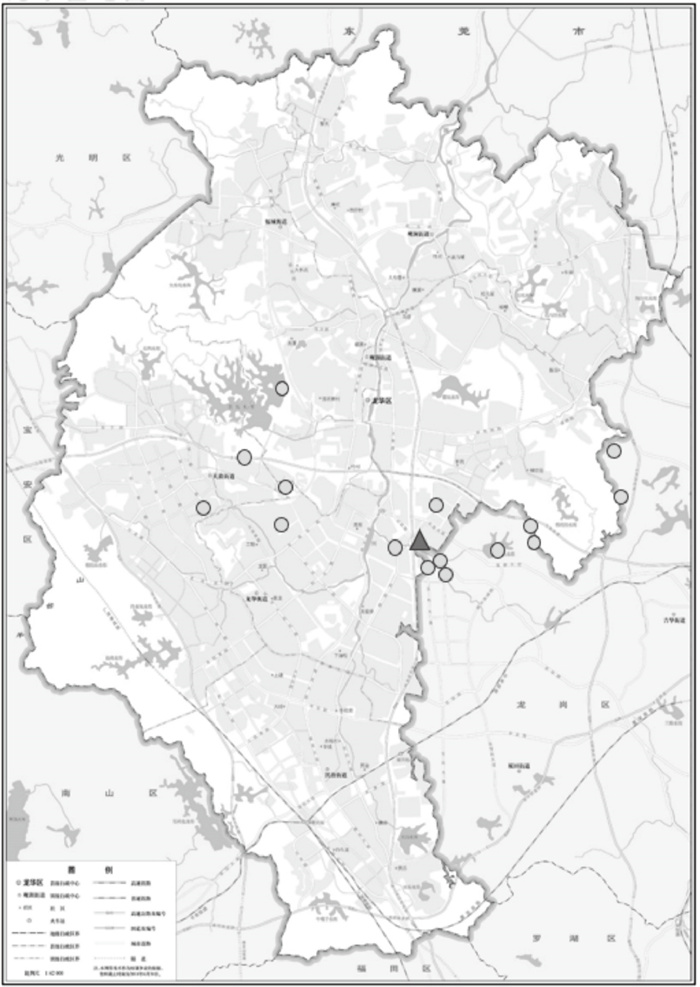 | 图 2 配送中心及配送节点的相对位置分布图Fig.2 Distribution of delivery centers and distribution nodes |
用A, B, C分别表示实际配送中使用的DXCH14FT，DXCH18FT和XTLU25FT三种不同的车型, 并给出三种车型的基本信息, 见表 2.从实际配送节点中筛选15个不同的配送节点信息, 见表 3.
表 2(Table 2)
表 2 各型车辆基本参数Table 2 Basic parameters of all types of vehicles
| 表 2 各型车辆基本参数 Table 2 Basic parameters of all types of vehicles |
表 3(Table 3)
表 3 客户节点信息Table 3 Information of customer nodes
| 表 3 客户节点信息 Table 3 Information of customer nodes |
对车型和节点信息进行预处理, 按照允许参与配送的车型将配送节点分成两类: 仅允许A型车的配送节点, 记为LA; A, B, C三种车型均允许参与配送的节点, 记为LABC.建立不同车型集合, 并将车辆按照车型顺序编号: A型车编号为A1~A50, B型车编号为B51和B52, C型车编号为C53.用QPSO算法对两类配送节点按要求进行车辆指派方案和路径的联合优化.算法中包含两次调度, 第一次调度按照“派单”计价方式随机从相应车辆集合中为配送节点派遣车辆; 如果发生超载则安排以“抢单”计价方式安排数量最充足的A型车补充配送, 并将报酬激励因子δ设置为3.整个算法迭代300次, 并对每次迭代后产生的不满足约束条件的解进行修复, 保证每次迭代生成的解可行.
4 实验与结果分析4.1 实验设置与实验结果根据第3节设计的算例分别设置模型对比实验和算法对比实验来验证本文提出的模型和算法的有效性.
在模型对比实验中, 用ACO-QPSO算法分别对传统配送模式和众包配送模式下的“抢单”众包配送模型、“派单”众包配送模型和本文提出的综合考虑“抢单”和“派单”的“抢/派单”众包配送模型共四种模型进行求解, 并从三个方面来比较配送效果, 即配送成本、配送距离和最长配送时间.“抢/派单”众包配送各车辆的车辆序号、配送路径等信息见表 4, 各种配送模型的配送效果见表 5, 配送路径见图 3.实验中不同配送模型下的配送车型、数量等条件保持一致以确保实验公平.
表 4(Table 4)
表 4 众包配送模式车辆调度结果Table 4 Results of vehicle scheduling in the crowdsourcing distribution mode
| 表 4 众包配送模式车辆调度结果 Table 4 Results of vehicle scheduling in the crowdsourcing distribution mode |
表 5(Table 5)
表 5 不同配送模式下效果对比Table 5 Comparison of the distribution effects under different modes
| 表 5 不同配送模式下效果对比 Table 5 Comparison of the distribution effects under different modes |
图 3(Fig. 3)
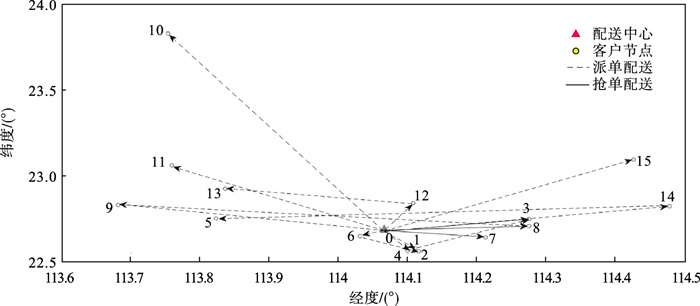 | 图 3 众包车辆配送路径Fig.3 Distribution paths of crowdsourcing vehicles |
4.2 结果分析由表 5可知, 众包的三种配送模型在成本、路径和时间上均优于传统配送模式.在三种众包配送模型中, “抢单”配送模型配送方式简单, 未能充分利用车辆容积进行配送, 虽然总配送路程最短, 但成本较高, 仅低于传统配送模式; “派单”配送模型在配送方式上更接近于传统配送, 车辆完全按照要求配送, 尽管完成配送任务后不用返回配送中心, 但配送路程仍较长, 配送成本仍较高; 本文提出的配送模型包含以上两种配送模型的特点, 并用算法对具体情况下的配送方式进行优化, 从配送结果上看, 仅配送路程略长于“抢单”配送模式, 而成本明显低于其他众包配送模型, 由此证明了本文配送模型的有效性.
由表 6可知, ACO-QPSO算法的平均最优值明显好于其他三种算法, 且算法方差最小, 算法稳定性最好, 证明了算法的有效性.
表 6(Table 6)
表 6 算法优化效果对比Table 6 Comparison of algorithm optimization effects
| 表 6 算法优化效果对比 Table 6 Comparison of algorithm optimization effects |
5 结论1) 本文对众包配送的“抢单”、“派单”模式进行了总结分析, 并将两种模式有机结合, 建立了众包配送车辆调度模型.
2) 针对本文提出的众包车辆调度模型, 设计了ACO-QPSO算法, 并对其中QPSO算法的原理和主要的求解步骤进行了说明, 同时给出了用ACO-QPSO算法求解模型的流程.
3) 以清湖冷链为例, 设置实验将本文模型与“抢单”配送模型、“派单”配送模型、传统配送模式进行了比较, 实验结果表明本文提出的模型可以更好地节约成本，减少配送距离和客户的等待时间; 将ACO-QPSO算法与蚁群、粒子群等算法进行了比较, 实验结果表明ACO-QPSO算法在平均最优解、方差、运行时间等指标上明显好于其他算法, 证明了算法的有效性.
参考文献
| [1] | Wang Y, Zhang D X, Liu Q, et al. Towards enhancing the last-mile delivery: an effective crowd-tasking model with scalable solutions[J]. Transportation Research Part E: Logistics and Transportation Review, 2016, 93: 279-293. DOI:10.1016/j.tre.2016.06.002 |
| [2] | Dupljanin D, Mirkovic M, Dumnic S, et al. Urban crowdsourced last mile delivery: mode of transport effects on fleet performance[J]. International Journal of Simulation Modelling, 2019, 18(3): 441-452. DOI:10.2507/IJSIMM18(3)481 |
| [3] | Akeb H, Moncef B, Durand B. Building a collaborative solution in dense urban city settings to enhance parcel delivery: an effective crowd model in Paris[J]. Transportation Research Part E: Logistics and Transportation Review, 2018, 119: 223-233. DOI:10.1016/j.tre.2018.04.007 |
| [4] | 王文杰, 陈颖, 蒋帅杰. 考虑平台竞争的众包物流社会配送服务最优定价策略[J]. 运筹与管理, 2020, 29(10): 11-20. (Wang Wen-jie, Chen Ying, Jiang Shuai-jie. Optimal design of a service system with free experience service under a dedicated service discipline[J]. Operations Research and Management Science, 2020, 29(10): 11-20.) |
| [5] | 刘悦秋, 李军, 潘旭. 基于大众参与度的众包物流定价策略研究[J]. 西南交通大学学报(社会科学版), 2019, 20(1): 107-115. (Liu Yue-qiu, Li Jun, Pan Xu. Research on pricing strategy of crowdsourcing distribution based on public participation[J]. Journal of Southwest Jiaotong University(Social Sciences), 2019, 20(1): 107-115. DOI:10.3969/j.issn.1009-4474.2019.01.014) |
| [6] | Castillo V E, Bell J E, Rose W J, et al. Crowdsourcing last mile delivery: strategic implications and future research directions[J]. Journal of Business Logistics, 2018, 39(1): 7-25. DOI:10.1111/jbl.12173 |
| [7] | Li L X, Wang X, Rezaei J. A Bayesian best-worst method-based multicriteria competence analysis of crowdsourcing delivery personnel[J]. Complexity, 2020(6): 1-17. |
| [8] | Devari A, Nikolaev A G, He Q. Crowdsourcing the last mile delivery of online orders by exploiting the social networks of retail store customers[J]. Transportation Research Part E: Logistics and Transportation Review, 2017, 105: 105-122. DOI:10.1016/j.tre.2017.06.011 |
| [9] | Sampaio A, Savelsbergh M, Veelenturf L P, et al. Delivery systems with crowd-sourced drivers: a pickup and delivery problem with transfers[J]. Networks, 2020, 76(2): 1-24. |
| [10] | Rechavi A, Toch E. Crowd logistics: understanding auction-based pricing and couriers' strategies in crowdsourcing package delivery[J/OL]. Journal of Intelligent Transportation Systems, 2020[2020-11-29]. https://doi.org/10.1080/15472450.2020.1797503. |
| [11] | Kafle N, Zou B, Lin J. Design and modeling of a crowdsource-enabled system for urban parcel relay and delivery[J]. Transportation Research Part B: Methodological, 2017, 99: 62-82. DOI:10.1016/j.trb.2016.12.022 |
| [12] | Alnaggar A, Gzara F, Bookbinder J H. Crowdsourced delivery: a review of platforms and academic literature[J]. Omega, 2021, 98: 102139. DOI:10.1016/j.omega.2019.102139 |
| [13] | Meng S, Kang J S, Chi K, et al. Gearbox fault diagnosis through quantum particle swarm optimization algorithm and kernel extreme learning machine[J]. Journal of Vibroengineering, 2020, 22(6): 1399-1414. DOI:10.21595/jve.2020.21550 |
| [14] | Zhang Z J, Wang W L, Xia R F, et al. Achieving large and distant ancestral genome inference by using an improved discrete quantum-behaved particle swarm optimization algorithm[J/OL]. BMC Bioinformatics, 2020[2020-11-18]. https://bmcbioinformatics.biomedcentral.com/articles/10.1186/s12859-020-03833-7. |
| [15] | Su X Y, Wei S W. Sliding mode control design for active suspension systems using quantum particle swarm optimisation[J/OL]. International Journal of Vehicle Design, 2020, 81(1/2)[2020-11-18]. http://dx.doi.org/10.1504/IJVD.2019.10033091. |
| [16] | Zhao X G, Liang J, Meng J, et al. An improved quantum particle swarm optimization algorithm for environmental economic dispatch[J]. Expert Systems with Applications, 2020, 152: 113370. DOI:10.1016/j.eswa.2020.113370 |
| [17] | Gan W Y, Zhu D Q, Ji D X. QPSO-model predictive control-based approach to dynamic trajectory tracking control for unmanned underwater vehicles[J]. Ocean Engineering, 2018, 158: 208-220. DOI:10.1016/j.oceaneng.2018.03.078 |
| [18] | Liu R C, Li J X, Fan J. A dynamic multiple populations particle swarm optimization algorithm based on decomposition and prediction[J]. Applied Soft Computing, 2018, 73: 434-459. DOI:10.1016/j.asoc.2018.08.015 |
| [19] | Zhang D G, Wang J X, Fan H R, et al. New method of traffic flow forecasting based on quantum particle swarm optimization strategy for intelligent transportation system[J]. International Journal of Communication Systems, 2020, 34(1): 1-20. |
