, 胡科, 陈丕峰, SIYAJEU Yannick
, 胡科, 陈丕峰, SIYAJEU Yannick 东北大学 机械工程与自动化学院, 辽宁 沈阳 110819
收稿日期:2021-01-07
基金项目:国家自然科学基金资助项目(51705068);中央高校基本科研业务费专项资金资助项目(N180703009,N170302001)。
作者简介:姜世杰(1985-), 男, 辽宁营口人, 东北大学副教授。
摘要:针对熔丝成型(fused filament fabrication, FFF)产品的表面质量缺陷问题, 提出了一种FFF产品表面粗糙度的理论建模方法.以材料丝表面轮廓为研究对象, 考虑样件表面的实际情况, 分别建立了FFF产品垂直和平行于纤维方向的表面粗糙度理论模型; 与此同时, 利用激光显微镜完成了相关样件表面粗糙度的实验研究; 通过对比理论分析与实验结果, 验证了所建模型的正确性; 理论模型的敏感性分析研究表明, 增大挤出宽度或打印层厚度会增大FFF产品的表面粗糙度, 而增大重叠区域宽度则会降低表面粗糙度.
关键词:熔丝成型表面粗糙度表面轮廓理论模型实验测试
Theoretical Model and Experimental Verification of Surface Roughness of Fused Filament Fabrication Plates
JIANG Shi-jie

 , HU Ke, CHEN Pi-feng, SIYAJEU Yannick
, HU Ke, CHEN Pi-feng, SIYAJEU Yannick School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China
Corresponding author: JIANG Shi-jie, E-mail: jiangsj@me.neu.edu.cn.
Abstract: Aiming at the surface quality defects of fused filament fabrication(FFF)products, a theoretical modeling method of the surface roughness of FFF products was proposed. Taking into account the actual conditions of the samples, the surface profile of the material filament was investigated, and the surface roughness theoretical models of FFF samples in two different directions(vertical and parallel to the fiber direction) were established respectively. At the same time, a series of corresponding experimental tests were performed using a laser microscope. Based on the comparison between theoretical and experimental results, the proposed model was verified. The sensitivity analysis of the theoretical model shows that increasing the extrusion width or printing layer thickness will increase the surface roughness of FFF products, while increasing the overlapping area width will decrease the surface roughness.
Key words: fused filament fabrication(FFF)surface roughnesssurface profiletheoretical modelexperimental test
快速成型是将材料逐层累加、堆积成型的一种新兴技术[1].其中, 熔丝成型(fused filament fabrication, FFF)因其成本低廉、原材料范围广、环境污染小等优点, 已成为当今使用最为广泛的快速成型技术之一[2].其工作原理是材料丝通过热熔喷头加热至熔融状态, 喷头按照预先设计好的打印路径和轨迹运动, 将熔融状态的材料挤出到指定位置并迅速冷却与周围材料黏结, 逐层累加最终堆积成三维实体或模型[3].然而, 由于逐层制造而产生的气孔、夹杂、层间分离等缺陷, 严重影响了FFF产品的表面质量, 进而限制了该技术的应用和发展[4].本文以表面粗糙度来表征FFF产品的表面质量, 表面粗糙度影响FFF产品的耐磨性、疲劳强度和耐腐蚀性等.在实际生产中, 对于应用于汽车、航空航天等关键部位的FFF零件, 需要其表面粗糙度值尽量小以提高配合质量、减少磨损并延长零件的使用寿命; 对于非关键部位的FFF零件, 表面粗糙度值可以大一些以节省生产成本.
近几年, ****们的研究主要集中在过程参数和后处理对FFF产品表面质量的实验分析方面[5-7].但随着FFF技术的发展, 其产品的应用领域越来越广泛, 对其表面质量的要求也越来越高, 需要明确FFF产品表面粗糙度的产生机理, 以提出切实可行的改进措施.Lalehpour等[8]假设FFF产品表面轮廓为正方形, 提出了一种在熔丝成型过程中基于材料层的表面粗糙度理论模型, 然后通过实验验证了理论模型的准确性.结果表明, 该理论模型能准确计算特定的FFF产品表面粗糙度.Angelo等[9]考虑阶梯效应对表面轮廓的影响, 在Ahn等[10]模型的基础上进行改进, 提出用于评估FFF产品表面质量的新参数Ra(表面粗糙度).将模型预测的Ra值与文献中的理论和实验结果进行比较发现, 改进后的模型预测结果与实验更加吻合.Li等[11]提出了一种FFF产品表面粗糙度预测的新方法, 即以数据驱动的表面粗糙度预测模型.该模型应用了机器学习算法, 可以较为准确地预测成型产品的表面粗糙度.Kaji等[12]通过对FFF产品表面轮廓几何形状的实际观察和分析, 提出了产品表面粗糙度的经验模型.Li等[13]基于抛物线曲线和线性直线的表面轮廓表示方法建立了FFF产品的表面粗糙度模型, 经与实验对比发现, 该模型可以提高表面粗糙度的预测精度.Ahn等[14]根据表面粗糙度的实际分布和轮廓特征获得了FFF产品的粗糙度表达式.针对FFF产品, 上述研究虽然提出了不同形式的表面粗糙度理论模型或经验公式, 但是普遍都忽略了产品的各向异性特点,即只考虑了单一方向的表面粗糙度.
本文根据FFF产品的实际截面形状分别建立了垂直和平行于纤维方向的表面粗糙度理论模型, 以更为准确地描述产品的表面质量情况.
1 FFF产品表面粗糙度理论模型基于FFF产品表面轮廓的实际截面形状, 考虑了表面角度、重叠区域等因素, 首先建立了垂直于纤维方向的表面粗糙度(the surface roughness vertical to the fiber direction, SRVFD)模型; 然后以SRVFD理论模型为基础, 考虑了成型精度的影响, 建立了FFF产品平行于纤维方向的表面粗糙度(the surface roughness parallel to the fiber direction, SRPFD)模型.
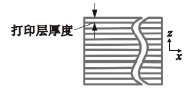
1.1 SRVFD模型FFF产品是由逐层累加的挤出材料丝构成, 由于重力影响, 材料丝的表面轮廓截面形状近似为椭圆, 如图 1所示.
图 1(Fig. 1)
 | 图 1 挤出材料丝横截面Fig.1 Cross section of the extruded material filament |
根据FFF产品横截面的实际情况(图 1), 确定垂直于纤维方向的表面粗糙度模型原理图, 如图 2所示.
图 2(Fig. 2)
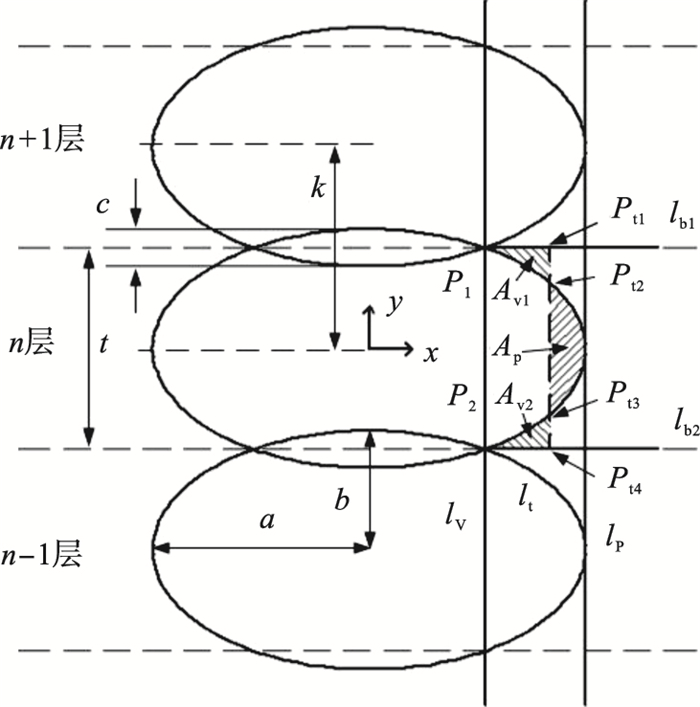 | 图 2 SRVFD模型原理图Fig.2 SRVFD model schematic |
以第n层材料丝横截面及其中心点建立xoy坐标系, 该截面轮廓可表示为
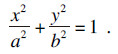 | (1) |
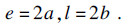 | (2) |
 | (3) |
 | (4) |
如图 2所示, P1, P2为第n层与第n+1层和第n-1层轮廓交点, 联立式(1)与式(4), 并取其中x, y较大值求解即可得到点P1(x1, y1).P1与P2相对于x轴对称, 则可确定点P2(x2, y2).
边界线由两条平行于表面法向量的lb1和lb2确定, lb1, lb2的表达式分别为
 | (5) |
 | (6) |
 | (7) |
则lt的表达式为
 | (8) |
每个封闭区域的面积Ap和Av都是由直线lt、峰廓线、谷廓线以及各自的边界线组成的封闭区域.在确定4个交点坐标值后, 即可通过式(9)~式(12)计算出面积Ap和Av.
 | (9) |
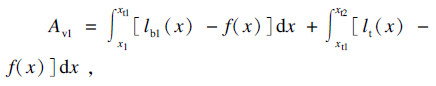 | (10) |
 | (11) |
 | (12) |
当lt处于某个位置使Ap=Av时, 联立式(9)~式(12), 可求得直线lt的表达式, 此时的lt即为轮廓算数平均中线.
在截面轮廓上获得n个取样点, 相邻取样点之间的间隔m=0.001mm, 取样点数量n由直线lv, lp之间的距离和取样点间隔决定, 其表达式为
 | (13) |
 | (14) |
根据定义确定SRVFD的表达式为
 | (15) |
1.2 SRPFD模型考虑到FFF设备的成型精度对表面粗糙度的影响, 假设FFF产品平行于纤维方向的表面轮廓是一条起伏波动的曲线, 如图 3所示.表面轮廓最大高度R取决于h, 表达式为
 | (16) |
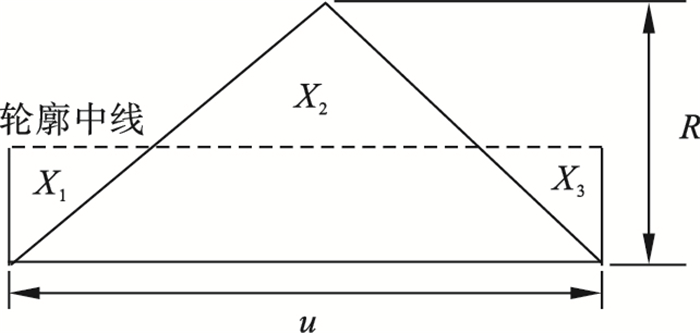 | 图 3 SRPFD模型原理图Fig.3 SRPFD model schematic |
根据SRVFD模型假设平行于纤维方向的表面轮廓宽度u=0.89mm, 进而确定平行于纤维方向的表面粗糙度Ra, p为
 | (17) |
 | (18) |
 | (19) |
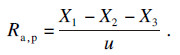 | (20) |
图 4(Fig. 4)
 | 图 4 样件示意图(单位: mm)Fig.4 Sample diagram(unit: mm) |
表 1(Table 1)
| 表 1 样件参数 Table 1 Processing parameters for the samples |
2.2 粗糙度实验本文利用3D测量激光显微镜(型号: LEXT OLS4100)针对每个样件进行了20组数据的测试, 其中垂直和平行于纤维方向的数据各10组.该设备采用405 nm半导体激光光源的双共焦光学系统, 平面最高分辨率为0.12 μm; 结合高精度的光栅读取能力, 可以生成高画质的影像, 实现精确的三维测量.测试过程如图 5所示.
图 5(Fig. 5)
 | 图 5 粗糙度测试设备和样件Fig.5 Roughness test equipment and samples |
实验过程中, 首先利用50倍镜头分别对样件进行焦距调节, 并设置测量区域, 然后对样件进行观察, 获得表面轮廓曲线, 进而获得表面粗糙度值.需要注意的是, 为保证粗糙度实验结果的准确性及其后续处理的便捷性, 需要对原始表面轮廓曲线进行降噪处理.
3 结果分析本节将分别针对FFF样件垂直和平行于纤维方向的表面轮廓以及粗糙度情况进行对比分析, 以验证理论模型的正确性.
3.1 垂直于纤维方向图 6绘制了样件(Ri, i=1~3)垂直于纤维方向的表面轮廓理论与平均实验结果, 可以发现, 实际表面轮廓具有随机性特点, 而理论轮廓是周期性的, 造成两者在长度为1 000 μm之后的部分偏差比较大, 但整体趋势基本一致, 吻合度较好, 因此本文提出的理论模型(SRVFD模型)能够准确预测出FFF样件垂直于纤维方向的表面轮廓.
图 6(Fig. 6)
 | 图 6 垂直于纤维方向的表面轮廓理论与实验结果Fig.6 Theoretical and experimental results of the surface profile vertical to the fiber direction |
图 7为样件(Ri, i=1~3)垂直于纤维方向的平均表面粗糙度与模型预测结果.表面粗糙度平均值分别为43.76, 42.22,42.37 μm, 理论模型预测结果为48.60μm, 误差分别为11.06%, 15.11%,14.70%.可见, 理论与实验结果的误差处于允许范围之内, 验证了理论模型的正确性.因此, 本文提出的SRVFD模型能够较准确地进行FFF样件SRVFD的分析与预测.
图 7(Fig. 7)
 | 图 7 垂直于纤维方向实验与模型预测结果Fig.7 Experimental and predicted surface roughness vertical to the fiber direction |
3.2 平行于纤维方向图 8绘制了样件(Ri, i=1~3)平行于纤维方向的表面轮廓理论与平均实验结果, 通过对比分析发现, 两者较为吻合, 因此本文提出的理论模型(SRPFD模型)能够准确预测出FFF样件平行于纤维方向的表面轮廓.
图 8(Fig. 8)
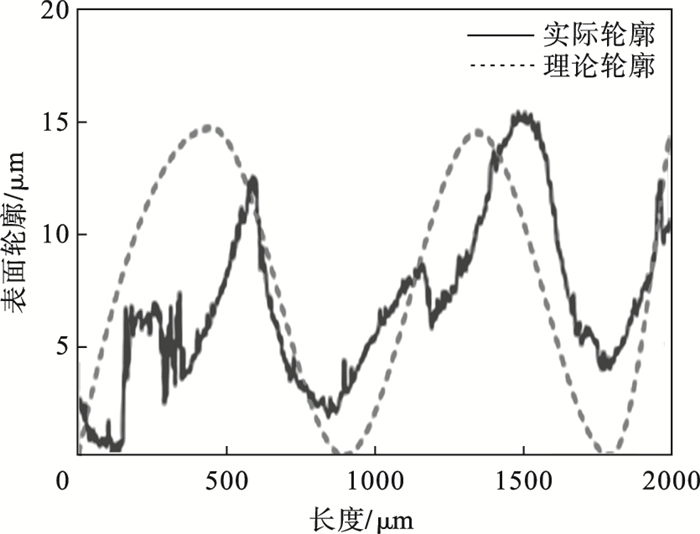 | 图 8 平行于纤维方向的表面轮廓理论与实验结果Fig.8 Theoretical and experimental results of the surface profile parallel to the fiber direction |
图 9为样件(Ri, i=1~3)平行于纤维方向的平均表面粗糙度与模型预测结果.其中表面粗糙度平均值分别为10.18, 10.32,9.17 μm, 模型预测结果为9.65 μm, 误差分别达到5.21%, 6.49%,5.23%.可见, 理论与实验结果的误差处于允许范围内.因此, SRPFD模型可以实现FFF样件SRPFD的预测, 且预测结果准确.
图 9(Fig. 9)
 | 图 9 平行于纤维方向实验与模型预测结果Fig.9 Experimental and predicted surface roughness parallel to the fiber direction |
4 敏感性分析为了分析所提出模型的敏感性, 选择了3个参数进行研究, 如表 2所示.每次分析只改变1个参数, 其他参数保持不变, 将不同过程参数下的表面粗糙度预测值进行比较, 可以确定模型的敏感性.
表 2(Table 2)
| 表 2 敏感性测试参数 Table 2 Parameters for testing sensitivity |
图 10为不同挤出宽度(0.2, 0.4和0.6mm)对FFF产品SRVFD和SRPFD预测值的影响.以SRVFD为例, 当挤出宽度为0.2, 0.4, 0.6mm时, 相对应的预测值分别为28.3, 48.6和63.3 μm.可见, 增大挤出宽度会增大产品的表面粗糙度.因此, 降低挤出宽度将有助于改善FFF产品的表面质量.
图 10(Fig. 10)
 | 图 10 不同挤出宽度对表面粗糙度的影响Fig.10 Effect of different extrusion width on the predicted surface roughness (a)—SRVFD预测;(b)—SRPFD预测. |
图 11为不同打印层厚度(0.1, 0.15和0.2mm)对FFF产品SRVFD和SRPFD预测值的影响.以SRVFD为例, 当打印层厚度为0.1, 0.15,0.2mm时, 对应的预测值分别为45.1, 48.6和53.5 μm.可见, FFF产品表面粗糙度预测值随着打印层厚度的增大而变大.因此, 降低打印层厚度将有助于改善FFF产品的表面质量.
图 11(Fig. 11)
 | 图 11 不同打印层厚度对表面粗糙度的影响Fig.11 Effect of different printing layer thickness on the predicted surface roughness (a)—SRVFD预测;(b)—SRPFD预测. |
图 12为不同重叠区域宽度(0.005, 0.01和0.015mm)对FFF产品SRVFD和SRPFD预测值的影响.以SRVFD为例, 当重叠区域宽度为0.005, 0.01和0.015mm时, 对应的预测值分别为58.0, 48.6和45.1 μm.可见, 增大重叠区域宽度会降低产品表面粗糙度值.
图 12(Fig. 12)
 | 图 12 不同重叠区域宽度的表面粗糙度预测值Fig.12 Effect of different overlapping area width on the predicted surface roughness (a)—SRVFD预测;(b)—SRPFD预测. |
以SRVFD为例, 当挤出宽度增大一倍时, 表面粗糙度预测值增大了71.73%;当打印层厚度增大一倍时, 表面粗糙度预测值增大了18.63%;当重叠区域宽度增大一倍时, 表面粗糙度预测值降低了16.21%, 详见表 3.综上所述, 挤出宽度对表面粗糙度的影响较大; 而打印层厚度和重叠区域宽度对表面粗糙度的影响基本一致.
表 3(Table 3)
| 表 3 过程参数对模型预测结果的影响 Table 3 Effect of the processing parameters on the prediction results |
5 结论1) 以材料丝表面轮廓为研究对象, 考虑了截面形状、表面角度和重叠区域宽度等因素的影响, 建立了FFF样件SRVFD理论模型, 其预测结果与实验结果吻合度较好, 验证了SRVFD模型的正确性.
2) 以SRVFD理论模型为基础, 考虑成型精度的影响, 建立了FFF产品SRPFD理论模型, 其预测结果与相关实验结果基本一致, 验证了SRPFD模型的正确性.
3) 对比分析了两个不同方向的表面轮廓理论与实验数据, 吻合度较好, 进一步验证了理论模型的正确性.
4) 理论模型敏感性分析表明, 增大挤出宽度或打印层厚度可以增大表面粗糙度; 但增大重叠区域宽度却可以降低表面粗糙度.
5) 本文提出的理论模型有助于为今后改善FFF产品表面质量的研究提供重要的参考和技术支持.
参考文献
| [1] | Ford S, Despeisse M. Additive manufacturing and sustainability: an exploratory study of the advantages and challenges[J]. Journal of Cleaner Production, 2016, 137: 1573-1587. DOI:10.1016/j.jclepro.2016.04.150 |
| [2] | Jami H, Masood S H, Song W Q. Dynamic response of FDM made ABS parts in different part orientations[J]. Advanced Materials Research, 2013, 748: 291-294. DOI:10.4028/www.scientific.net/AMR.748.291 |
| [3] | Chen L, He Y, Yang Y X, et al. The research status and development trend of additive manufacturing technology[J]. The International Journal of Advanced Manufacturing Technology, 2016, 89(9/10/11/12): 3651-3660. |
| [4] | Priya M S, Naresh K, Jayagnthat R, et al. A comparative study between in-house 3D printed and injection molded ABS and PLA polymers for low-frequency applications[J]. Materials Research Express, 2019, 6(8): 1-22. |
| [5] | Kim M K, Lee I H, Kim H C. Effect of fabrication parameters on surface roughness of FDM parts[J]. International Journal of Precision Engineering and Manufacturing, 2018, 19(1): 137-142. DOI:10.1007/s12541-018-0016-0 |
| [6] | Jayanth N, Senthil P, Prakash C. Effect of chemical treatment on tensile strength and surface roughness of 3D-printed ABS using the FDM process[J]. Virtual and Physical Prototyping, 2018, 13(3): 155-163. DOI:10.1080/17452759.2018.1449565 |
| [7] | Yang L P, Li S J, Li Y, et al. Experimental investigations for optimizing the extrusion parameters on FDM PLA printed parts[J]. Journal of Materials Engineering and Performance, 2018, 28(1): 169-182. |
| [8] | Lalehpour A, Barari A. A more accurate analytical formulation of surface roughness in layer-based additive manufacturing to enhance the product's precision[J]. The International Journal of Advanced Manufacturing Technology, 2018, 96(9/10/11/12): 3793-3804. |
| [9] | Angelo L D, Stefano P D, Marzola A. Surface quality prediction in FDM additive manufacturing[J]. The International Journal of Advanced Manufacturing Technology, 2017, 93(9/10/11/12): 3655-3662. DOI:10.1007/s00170-017-0763-6 |
| [10] | Ahn D, Kweon J H, Kwon S, et al. Representation of surface roughness in fused deposition modeling[J]. Journal of Materials Processing Technology, 2009, 209(15/16): 5593-5600. |
| [11] | Li Z X, Zhang Z Y, Shi J C, et al. Prediction of surface roughness in extrusion-based additive manufacturing with machine learning[J]. Robotics and Computer-Integrated Manufacturing, 2019, 57: 488-495. DOI:10.1016/j.rcim.2019.01.004 |
| [12] | Kaji F, Barari A. Evaluation of the surface roughness of additive manufacturing parts based on the modelling of cusp geometry[J]. International Federation of Automatic Control, 2015, 48(3): 658-663. |
| [13] | Li L, Hanghighi A, Yang Y R. Theoretical modelling and prediction of surface roughness for hybrid additive-subtractive manufacturing processes[J]. IISE Transactions, 2018, 51(2): 124-135. |
| [14] | Ahn D, Kim H, Lee S. Surface roughness prediction using measured data and interpolation in layered manufacturing[J]. Journal of Materials Processing Technology, 2009, 209(2): 664-671. DOI:10.1016/j.jmatprotec.2008.02.050 |