郭永春, 郑海燕, 胡心光, 沈峰满
东北大学 冶金学院, 辽宁 沈阳 110819
收稿日期：2020-09-09
基金项目：国家自然科学基金资助项目(NSFC51774071, NSFC51974073, NSFC51874080, NSFC51604069)；中央高校基本科研业务费专项资金资助项目(N182504008)；辽宁省自然科学基金资助项目(2019-MS-132)。
作者简介：郭永春(1992-), 男, 陕西咸阳人, 东北大学博士研究生;
沈峰满(1958-), 男, 黑龙江密山人, 东北大学教授, 博士生导师。

摘要：高炉渣系各组元活度对高炉冶炼和产品质量具有重要的影响作用. 基于分子-离子共存理论, 建立CaO-SiO₂-MgO-Al₂O₃四元渣系Al₂O₃活度预测模型; 结合试验测定值对其进行验证与修正, 最终建立了修正的CaO-SiO₂-MgO-Al₂O₃四元渣系Al₂O₃活度预测模型; 同时, 依据模型计算结果探究R(w(CaO)/w(SiO₂)), w(MgO)/w(Al₂O₃)和w(Al₂O₃)对Al₂O₃活度的影响. 研究结果表明: 修正后的CaO-SiO₂-MgO-Al₂O₃四元渣系Al₂O₃活度预测模型具有较高的预测精度, 能够很好地预测熔渣Al₂O₃活度; 当w(MgO)/w(Al₂O₃)=0.40, w(Al₂O₃)=20 % 时, 随着R增加, Al₂O₃活度逐渐减小; 当R=1.25, w(Al₂O₃)=20 % 时, 随着w(MgO)/w(Al₂O₃)增加, Al₂O₃活度逐渐减小; 当w(MgO)/w(Al₂O₃)=0.40, R=1.25时, 随着w(Al₂O₃)增加, Al₂O₃活度逐渐增大.
关键词：分子-离子共存理论质量浓度高炉渣预测模型Al₂O₃活度
Prediction Model of Al₂O₃ Activity in CaO-SiO₂-Al₂O₃-MgO Quaternary Slag System
GUO Yong-chun, ZHENG Hai-yan, HU Xin-guang, SHENG Feng-man
School of Metallurgy, Northeastern University, Shenyang 110819, China
Corresponding author: SHENG Feng-man, E-mail: shenfm@mail.neu.edu.cn.

Abstract: Since the activity of each component of the blast furnace slag has great effects on blast furnace smelting and product quality, a model was built to predict Al₂O₃ activity in CaO-SiO₂-Al₂O₃-MgO quaternary slag system, based on the molecule and ion coexistence theory. After the prediction model was validated by the experimental results, the effects of the R(w(CaO)/w(SiO₂)), w(MgO)/w(Al₂O₃) and w(Al₂O₃) on Al₂O₃ activity were explored. The results indicate that the model can predict the Al₂O₃ activity of molten slag accurately. When the w(Al₂O₃) was 20 % and w(MgO)/w(Al₂O₃) was 0.40, the Al₂O₃ activity decreased with the increasing R. When the w(Al₂O₃) was 20 % and R was 1.25, the Al₂O₃ activity decreased with the increasing w(MgO)/w(Al₂O₃). With the R=1.25 and w(MgO)/w(Al₂O₃) =0.40, the Al₂O₃ activity increased with the increasing w(Al₂O₃).
Key words: molecule and ion coexistence theorymass concentrationblast furnace slagprediction modelAl₂O₃ activity
高铝铁矿石的使用使得高炉炉渣中Al₂O₃含量偏高, 不仅导致炉渣的黏度升高、流动性变差、脱硫能力降低, 而且也降低了参与脱硫反应的有效组元的活度^[1-3]. 硫元素主要是通过界面化学反应脱除的, 脱硫时, 进入渣中的CaS组元并不是以单一化合物的形式存在的, 而是与其他组元进一步反应形成固溶体, 而参与脱硫反应的各组元的活度是影响脱硫过程的根本原因. 但目前关于高Al₂O₃高炉渣组元活度的研究相对较少, 所以建立CaO-SiO₂-MgO-Al₂O₃四元渣系组元活度计算模型, 预测相关组元活度, 对进一步研究高炉炉渣脱硫能力具有重要意义.
迄今为止, 很多熔渣热力学模型已经被提出, 如正规溶液模型^[4]、离子模型^[5]、Wilson方程^[6]、新一代的溶液几何模型^[7]、KTH模型^[8-9]、MIVM模型^[10]、Montecarlo模型^[11]、电当量模型^[12]、分子-离子共存理论模型^[13]等. 然而, 大多数预测模型均涉及人工定义参数, 适用范围有限. 各种模型都有优缺点, 至今还没有一种模型能适用于所有熔渣体系, 因此热力学模型都有待于进一步的开发与改进.
前期工作^[4-13]表明, 分子-离子共存理论模型具有一定的适用性, 且计算过程中只使用相关反应的标准吉布斯自由能(ΔG^?), 计算过程简单, 具有良好的应用前景. 因此, 本文选择分子-离子共存理论, 建立CaO-SiO₂-MgO-Al₂O₃四元渣系Al₂O₃活度预测模型; 并结合试验测定值对其进行验证与修正, 以便削弱该理论基础假设带来的计算误差, 最终建立具有更高精度的CaO-SiO₂-MgO-Al₂O₃四元渣系Al₂O₃活度修正模型.
1 CaO-SiO₂-MgO-Al₂O₃渣系质量浓度的热力学模型1.1 热力学模型的假设条件分子-离子共存理论以渣系中结构单元或离子对的质量作用浓度代替传统意义上的活度, 用于表征其反应能力, 使得相关复杂问题简单化. 即CaO-SiO₂-MgO-Al₂O₃渣系中结构单元或离子对的质量作用浓度能够像传统意义上的活度一样表征其反应能力. 其基本假设为^[14]
1) 熔渣由简单离子(Ca²⁺, Mg²⁺, O^2-, S^2-等)和SiO₂、硅酸盐、磷酸盐、铝酸盐等分子组成;
2) 在全成分范围内, 离子和分子的共存是连续的;
3) 简单离子和分子间进行着动态平衡反应;
4) 表示MeO的活度时应采取的形式: a_MeO=N_MeO=N_Me²⁺+N_O^2-;
5) 炉渣内部的化学反应服从质量作用定律.
1.2 结构单元或离子对的质量作用浓度结合MgO-SiO₂, CaO-SiO₂, CaO-Al₂O₃, MgO-Al₂O₃, CaO-MgO-SiO₂, CaO-Al₂O₃-SiO₂相图^[15-17], 确定了1 873 K下CaO-SiO₂-MgO-Al₂O₃四元渣系中存在的结构单元如下:

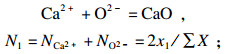(1)

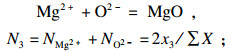(2)

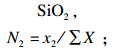(3)

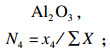(4)

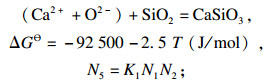(5)

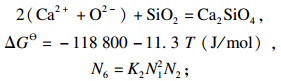(6)

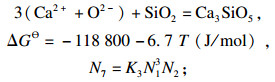(7)

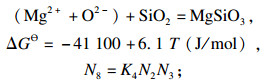(8)

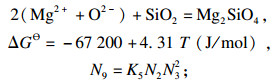(9)

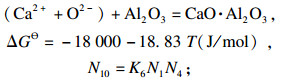(10)

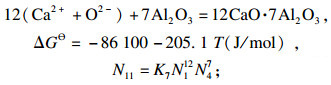(11)

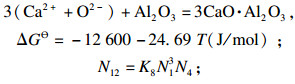(12)

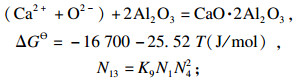(13)

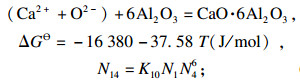(14)

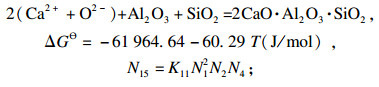(15)

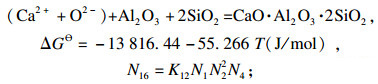(16)

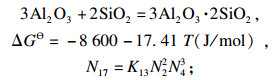(17)

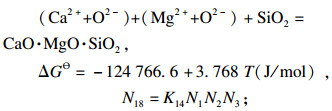(18)

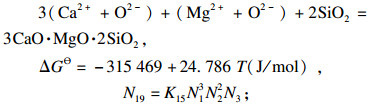(19)

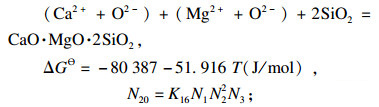(20)

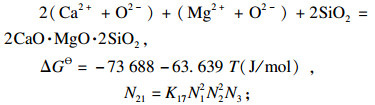(21)

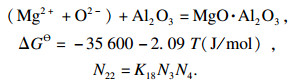(22)

式中: ∑X为平衡时的总物质的量; a_i为组元i的活度; N_i为组元i的质量浓度; x_i为组元i的物质的量; K_i为化学反应的平衡常数; ΔG^?为形成复杂分子i的化学反应标准吉布斯自由能变化(J/mol); 平衡前CaO-SiO₂-MgO-Al₂O₃渣系中CaO, SiO₂, MgO和Al₂O₃的摩尔分数分别为n₁=∑n_CaO, n₂=∑n_SiO2, n₃=∑n_MgO, n₄=∑n_Al2O3, n₅=∑n_CaS, n₆=∑n_MgS.
渣中所有结构单元的质量浓度之和为1:

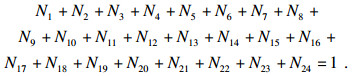(23)

反应前后CaO的总物质的量不变:

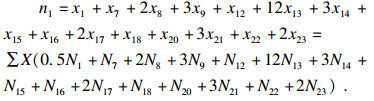(24)

反应前后SiO₂的总物质的量不变:

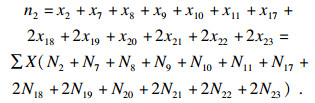(25)

反应前后MgO的总物质的量不变:

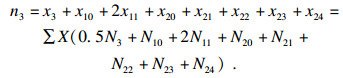(26)

反应前后Al₂O₃的总物质的量不变:

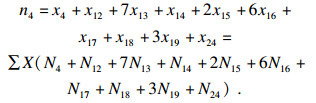(27)

联立消除∑X, 并将N_i(i=7~24)由N_i(i=1~6)代替, 化简得关于N₁，N₂，N₃，N₄，N₅，N₆的非线性方程组, 整理得

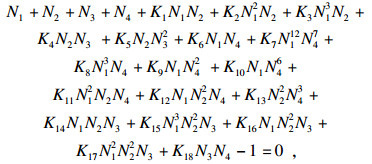(28)

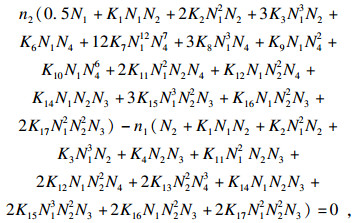(29)

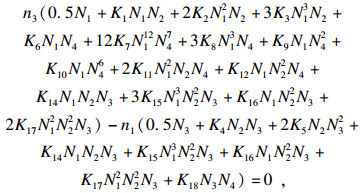(30)

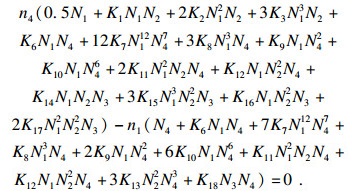(31)

式(28)~式(31)为CaO-SiO₂-Al₂O₃-MgO四元渣系结构单元或离子对的质量浓度预测模型. 预测模型采用Matlab进行编程并调用fsolve函数进行求解^[18].
2 CaO-SiO₂-MgO-Al₂O₃四元渣系活度模型验证为了验证模型的可靠性, 本文对比了1 873 K时CaO-SiO₂-Al₂O₃三元高炉渣系分子-离子共存理论预测模型得到的Al₂O₃活度值(N_(Al2O3))和文献参考的Al₂O₃活度值(a_(Al2O3))^[19], 结果参见图 1. 由图 1可知, 分子-离子共存理论预测的Al₂O₃活度值(N_(Al2O3))与文献参考的Al₂O₃活度值(a_(Al2O3))变化趋势一致, 其拟合度为0.84, 具有良好的线性关系. 因此CaO-SiO₂-Al₂O₃三元高炉渣系基于分子-离子共存理论活度预测模型可应用于计算组元Al₂O₃的活度.
图 1(Fig. 1)

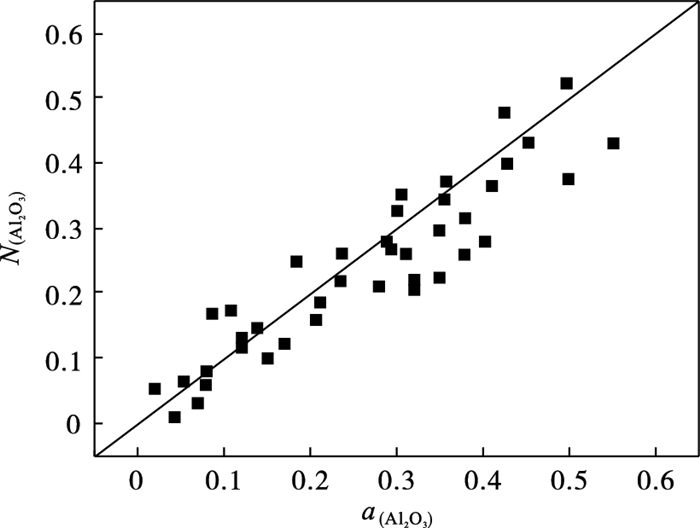图 1 CaO-SiO2-Al2O三元渣系模型验证Fig.1 Verification of CaO-SiO2-Al2O3 ternary slag system model

在前期的试验中, 以Al₂O₃-CaF₂作为参考渣, CO作为保护气体, Cu作为金属溶剂, 平衡时间24 h, 温度1 873 K时, 试验测定了CaO-SiO₂-MgO-Al₂O₃四元渣系中Al₂O₃的活度, 其渣系成分和Al₂O₃活度值如表 1所示^[20].
表 1(Table 1)

表 1 CaO-SiO2-MgO-Al2O3四元Al2O3的活度Table 1 Al2O3 activities in the CaO-SiO2-MgO-Al2O3 试样号 渣系成分/% R a(Al2O3) CaO SiO2 MgO Al2O3 1 47.78 38.22 4.0 10 1.25 0.008 0 2 6.22 36.98 4.8 12 1.25 0.009 8 3 43.89 35.11 6.0 15 1.25 0.016 7 4 41.56 33.24 7.2 18 1.25 0.026 5 5 37.71 34.29 8.0 20 1.10 0.042 3 6 8.51 33.49 8.0 20 1.15 0.033 6 7 39.27 32.73 8.0 20 1.20 0.026 5 8 40.70 31.30 8.0 20 1.30 0.024 4 9 40.56 32.44 7.0 20 1.25 0.047 0 10 39.44 31.56 9.0 20 1.25 0.043 0 11 38.89 31.11 10.0 20 1.25 0.040 4 12 38.33 30.67 11.0 20 1.25 0.036 6

表 1 CaO-SiO2-MgO-Al2O3四元Al2O3的活度 Table 1 Al2O3 activities in the CaO-SiO2-MgO-Al2O3

本文对比了CaO-SiO₂-MgO-Al₂O₃四元高炉渣系分子-离子共存理论预测模型得到的Al₂O₃活度值(N_(Al2O₃))和试验测定的Al₂O₃活度值(a_(Al2O3)), 结果见图 2. 由图 2a可知, 分子-离子共存理论预测的Al₂O₃活度值(N_(A2O3))与文献参考的Al₂O₃活度值(a_(Al2O3)) 变化趋势一致, 但计算值和实测值具有较大的偏离度. 公式(32)为相对误差函数, 计算表明: 基于分子-离子共存理论预测的Al₂O₃活度值(N_(Al2O3))与试验测定的Al₂O₃活度值(a_(Al2O3))相对误差为57 %. 分析认为分子-离子共存理论尚不完善, 未考虑在一定温度下某些化合物与炉渣实际的矿物组成是否一致, 也未考虑某些化合物在高温条件下解离可能会降低模型预测值的准确性, 因此为了提高模型预测值的可靠性和准确性, 在炉渣组成R=1.10~1.30，w(MgO)/w(Al₂O₃)=0.35~0.55, w(Al₂O₃)=10 % ~20 % 范围内, 结合试验测定值对其进行验证及修正, 并对模型预测值引入修正方程(公式(33)), 方程的拟合度为0.937 6. 修正后的结果对比如图 2b所示. 由图可知, 修正后预测的Al₂O₃活度值(N′_(Al2O3))与试验测定的Al₂O₃活度值(a_(Al2O3))变化趋势一致, 且具有良好的线性关系.修正后的相对误差为10 %, 较修正前的相对误差降低了47 %, 表明修正后的CaO-SiO-MgO-Al₂O₃四元渣系活度预测模型具有较好的预测精度, 可应用于计算R=1.10~1.30, w(MgO)/w(Al₂O₃)=0.35~0.55, w(Al₂O₃)=10 % ~20 % 范围内Al₂O₃活度值.

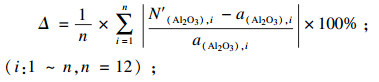(32)

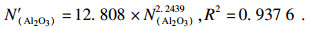(33)

图 2(Fig. 2)

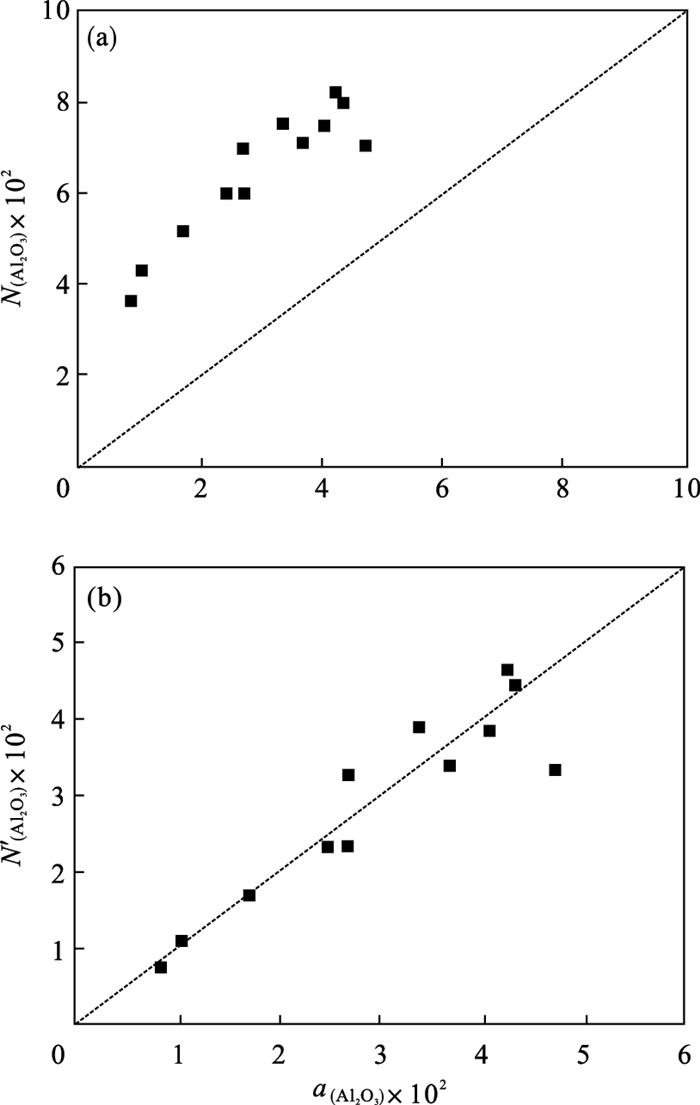图 2 CaO-SiO2-Al2O3-MgO四元渣系模型验证Fig.2 Verification of CaO-SiO2-Al2O3-MgO quaternary slag system model (a)—Δ=57 %；(b)—Δ=10 %.

式中: Δ为模型误差; n为对比试验数据数量; R²为拟合度.
3 结果与讨论3.1 R对Al₂O₃活度的影响图 3为当w(MgO)/w(Al₂O₃)=0.40, w(Al₂O₃)=20 % 时, R对Al₂O₃活度的影响.由图 3可知, 随着R增加, Al₂O₃活度逐渐减小.碱度增加, 渣中CaO的含量增加, SiO₂的相对含量减少, MgO和Al₂O₃的含量不变, CaO为强碱性氧化物, 能在渣中解离出O^2-: CaO→Ca²⁺+O^2-, 促使反应式(10)~式(14)正向进行.另一方面由于增加碱度, CaO含量增加, 解离出O^2-的含量增加, 酸性氧化物SiO₂的相对含量减少, 抑制了O^2-与SiO₂反应、促进了更多O^2-参加到铝酸根离子的生成中, 极大地消耗了酸性氧化物, 即随着R的增加, 渣中Al₂O₃活度越小.
图 3(Fig. 3)

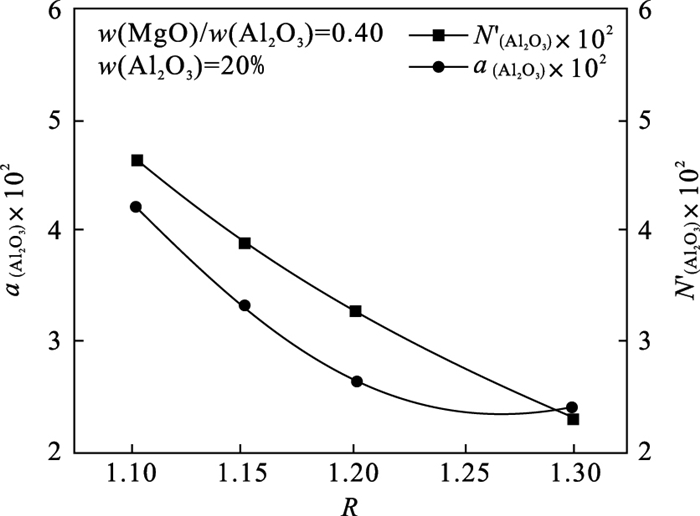图 3 R对Al2O3活度的影响Fig.3 Effect of R on activity of Al2O3

3.2 w(MgO)/w(Al₂O₃) 对Al₂O₃活度的影响图 4为当R=1.25, w(Al₂O₃)=20 % 时, w(MgO)/w(Al₂O₃)对Al₂O₃活度的影响.由图 4可知, 随着w(MgO)/w(Al₂O₃)增加, Al₂O₃活度逐渐减小.w(MgO)/w(Al₂O₃)的增加, 渣中MgO含量增加, MgO为碱性氧化物, 能在渣中解离出O^2-: MgO→Mg²⁺+O^2-, 提供了O^2-参加到铝酸根离子的生成中, 消耗了酸性氧化物, 因此渣中Al₂O₃活度不断减小.
图 4(Fig. 4)

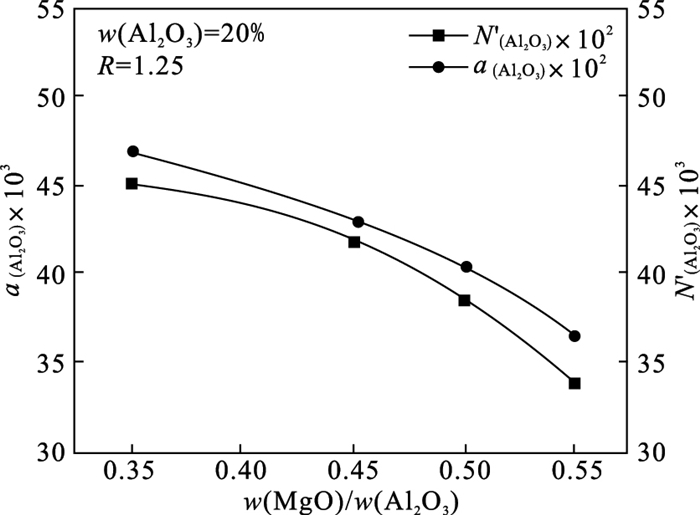图 4 w(MgO)/w(Al2O3)对Al2O3活度的影响Fig.4 Effect of w(MgO)/w(Al2O3) on activity of Al2O3

3.3 w(Al₂O₃) 对Al₂O₃活度的影响图 5为当w(MgO)/w(Al₂O₃)=0.40, R=1.25时, w(Al₂O₃)对Al₂O₃活度的影响.由图 5可知, 随着w(Al₂O₃)增加, Al₂O₃活度逐渐增大.Al₂O₃含量增加, MgO的含量也增加, CaO的含量相对减少, CaO为强碱性氧化物, 且CaO的碱性大于MgO, 碱性氧化物解离出的O^2-含量相对较少, 抑制了反应式(10)~式(14)正向进行, 渣中Al₂O₃活度不断增加.
图 5(Fig. 5)

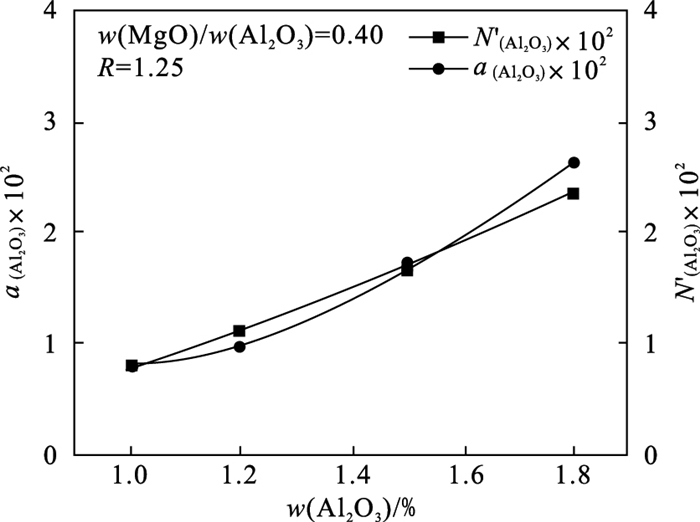图 5 w(Al2O3)对Al2O3活度的影响Fig.5 Effect of w(Al2O3) on activity of Al2O3

4 结论1) 在R=1.10~1.30，w(MgO)/w(Al₂O₃)= 0.35-0.55, w(Al₂O₃)=10 % ~20 % 范围内, 修正后的CaO-SiO₂-MgO-Al₂O₃四元渣系活度预测模型可应用于计算组元的活度.
2) 当w(MgO)/w(Al₂O₃)=0.40, w(Al₂O₃)=20 % 时, 随着R增加, Al₂O₃活度逐渐减小; 当R=1.25, w(Al₂O₃)=20 % 时, 随着w(MgO)/w(Al₂O₃)增加, Al₂O₃活度逐渐减小; 当w(MgO)/w(Al₂O₃)=0.40, R=1.25时, 随着w(Al₂O₃)增加, Al₂O₃活度逐渐增大.
参考文献

[1]	沈峰满, 郑海燕, 姜鑫, 等. 高炉炼铁工艺中Al2O3的影响及适宜w(MgO)/w(Al2O3)的探讨[J]. 钢铁, 2014, 49(1): 1-6. (Shen Feng-man, Zheng Hai-yan, Jiang Xin, et al. Influence of Al2O3 in blast furnace smelting and discussions on proper w(MgO)/w(Al2O3) ratio[J]. Iron and Steel, 2014, 49(1): 1-6.)
[2]	袁骧, 张建良, 毛瑞, 等. 镁铝比对高炉渣脱硫能力的影响[J]. 东北大学学报(自然科学版), 2015, 36(11): 1609-1613. (Yuan Xiang, Zhang Jian-liang, Mao Rui, et al. Effect of w(MgO)/w(Al2O3) ratio on desulfurization capacity of BF slag[J]. Journal of Northeastern University(Natural Science), 2015, 36(11): 1609-1613.)
[3]	Han H S, Shen F M, Jiang X, et al. Fundamental mechanism of effects of MgO on sinter strength[J]. Journal of Iron and Steel Research International, 2019, 26(11): 1171-1177. DOI:10.1007/s42243-019-00331-w
[4]	Shiro B Y. Mathematical expression of slag-metal reactions in steelmaking process by quadratic formalism based on the regular solution model[J]. ISIJ International, 1993, 33(2): 2-12.
[5]	Tijskens E, Viaene W A, Geerlings P. The ionic model: extension to spatial charge distributions, derivation of an interaction potential for silica polymorphs[J]. Physics & Chemistry of Minerals, 1995, 22(3): 186-199. DOI:10.1007/BF00202299
[6]	陶东平, 杨显万. 用Wilson方程估计多元液态合金在给定温度下的组元活度[J]. 金属学报, 1997, 33(10): 1079-1084. (Tao Dong-ping, Yang Xian-wan. Using Wilson equation to estimate the component activity of multi-element liquid alloy at a given temperature[J]. Acta Metallurgica Sinica, 1997, 33(10): 1079-1084.)
[7]	周国治. 新一代的溶液几何模型及其今后的展望[J]. 金属学报, 1997, 33(2): 126-132. (Zhou Guo-zhi. A new generation of solution geometry model and its future prospects[J]. Acta Metallurgica Sinica, 1997, 33(2): 126-132.)
[8]	Du S C, Nilsson R, Seetharaman S. A mathematical model for estimation of sulphide capacities of multi-component slags[J]. Steel Research, 1995, 66(11): 458-462. DOI:10.1002/srin.199501155
[9]	Nzotta M M, Du S C, Seetharaman S. A study of the sulfide capacities of iron-oxide containing slags[J]. Metallurgical & Materials Transactions B, 1999, 30(5): 909-920. DOI:10.1007/s11663-999-0096-4
[10]	Tao D P. Prediction of activities of three components in the ternary molten slag CaO-FeO-SiO2 by the molecular interaction volume model[J]. Metallurgical and Materials Transactions B, 2006, 37(6): 1091-1097. DOI:10.1007/BF02735033
[11]	Borgianni C, Granati P. Thermodynamic properties of silicates and of alumino-silicates from montecarlo calculations[J]. Metallurgical Transactions B, 1977, 8(1): 147-151. DOI:10.1007/BF02656363
[12]	沈峰满. 冶金物理化学[M]. 北京: 高等教育出版社, 2017: 133-134. (Shen Feng-man. Physical chemistry of metallurgy[M]. Beijing: Higher Education Press, 2017: 133-134.)
[13]	吕宁宁, 于景坤, 苏畅, 等. CaO-Al2O3和CaO-SiO2-Al2O3渣系中组元活度的计算[J]. 东北大学学报(自然科学版), 2013, 34(12): 1743-1746. (Lyu Ning-ning, Yu Jing-kun, Su Chang, et al. Activity calculation for the components in CaO-Al2O3 and CaO-SiO2-Al2O3 slags[J]. Journal of Northeastern University(Natural Science), 2013, 34(12): 1743-1746.)
[14]	张鉴. 冶金熔体和溶液的计算热力学[M]. 北京: 冶金工业出版社, 2017: 241-242. (Zhang Jian. Computational thermodynamics of metallurgical melts and solutions[M]. Beijing: Metallurgical Industry Press, 2017: 241-242.)
[15]	Verein D E. Slag atlas[M]. D-Düsseldorf: Verlag Stahleisen Gmbh, 1995.
[16]	梁英教, 车荫昌. 无机热力学数据手册[M]. 沈阳: 东北大学出版社, 1993. (Liang Ying-jiao, Che Yin-chang. Inorganic thermodynamics data book[M]. Shenyang: Northeastern University Press, 1993.)
[17]	Turchdogen E T. Physicalchemistry of high temperature technology[M]. New York: Acadamic Press, 1980.
[18]	Zhang D, Cao S Z. Series method for solving nonlinear control system based on MATLAB state equation and its realization[C]// Proceedings of 2013 3rd International Conference on Computer Science and Network Technology. Hangzhou: IEEE, 2014: 249-252.
[19]	Kousuke K, Kazuki M, Takahiro M, et al. Activity measurement of CaO-SiO2-AlO1.5-MgO slags equilibrated with molten silicon alloys[J]. ISIJ International, 2000, 40(6): 561-566. DOI:10.2355/isijinternational.40.561
[20]	Hu X G, Zheng H Y, Guo Y C, et al. Determination of Al2O3 activity by reference slag method in CaO-SiO2-Al2O3-MgO melts for blast furnace slag with high Al2O3 at 1873K[J]. Steel Research International, 2020, 91(3): 1-7.