
 , 田庄2, 张懿1
, 田庄2, 张懿1 1. 中国地质大学(武汉) 工程学院, 湖北 武汉 430074;
2. 四川电力设计咨询有限责任公司, 四川 成都 610041
收稿日期:2020-06-16
基金项目:国家自然科学基金资助项目(2019053086)。
作者简介:李兴明(1991-), 男, 四川绵竹人, 中国地质大学(武汉)博士研究生;
晏鄂川(1969-), 男, 四川成都人, 中国地质大学(武汉)教授,博士生导师。
摘要:土拱效应是抗滑桩工程发挥作用的关键内容.以土拱的应力变化为研究点, 首先明确了土拱拱轴线, 然后推导了新的土拱应力递减模型, 由此量化了土拱关键拱形参数的计算方法, 最后提出了新的滑坡荷载三级分担模型.研究结果表明: 桩间土拱和桩后土拱的应力呈指数递减规律, 基于土拱应力递减模型提出的拱迹线倾角和土拱厚度两个计算公式由于考虑影响因子全面因而更加切合实际; 依据计算的桩后土拱和桩间土拱极限承载力可知, 阶段划分的滑坡荷载三级分担模型与滑坡体-抗滑桩作用阶段特征相符合.研究可加强对土拱效应理论的理解, 也可为滑坡抗滑桩设计起指导作用.
关键词:土拱效应应力递减拱形参数荷载分担模型抗滑桩设计
Stress-Reduction Model for Soil Arch and Its Application in Load Sharing Model for Landslide
LI Xing-ming1, YAN E-chuan1

 , TIAN Zhuang2, ZHANG Yi1
, TIAN Zhuang2, ZHANG Yi1 1. Faculty of Engineering, China University of Geosciences, Wuhan 430074, China;
2. Sichuan Electric Power Engineering Co., Ltd., Chengdu 610041, China
Corresponding author: YAN E-chuan, E-mail: yecyec6970@163.com.
Abstract: Soil arching effect is the key research point for anti-slide piles coming into effect. Taking the stress change of soil arch as the research point, first, a reasonable arch axis for soil arch was specified, and then a new stress-reduction model for soil arch was further derived, based on which the calculation of the critical arch shape parameters of the soil arch was quantified, and last a new three-level load sharing model for landslide was proposed. Research shows that the model calculation has demonstrated an exponential reduction in the stress between and behind piles. The two equations of inclination angle at the foothold and the thickness of soil arch are more practical due to full consideration of effecting factors. According to the bearing capacity of soil arch behind and between anti-slide piles, the three-level load sharing model can be consistent with the phase characteristics of interaction between landslide mass and anti-slide pile. The research can deepen the understanding in soil arching effect theory, and can also provide theoretical guidance to the design of anti-slide piles in landslide programs.
Key words: soil arching effectstress reduceshape parameters of archload sharing modeldesign of anti-slide pile
抗滑桩作为一种有效的滑坡治理工程措施, 在全世界得到了广泛应用, 而土拱效应研究了抗滑桩与滑坡体的相互作用机理, 是抗滑桩发挥作用的关键内容, 因此土拱效应在工程实际中越来越受到重视[1].
通过活动门实验, Terzaghi[2]首先于1943年发现土拱效应, 随后Vardoulakis等[3]、Handy[4]、孙书伟等[5]进一步发展和验证了土拱效应, 并在抗滑桩工程中广泛应用.目前, 研究抗滑桩与土作用的方法之一是以分析土拱的应力分布规律为出发点, Janssen[6]首先发现粮仓效应堆积高度与仓底应力呈指数变化规律; 郑学鑫[7]解释了小主应力土拱内的应力规律, 证明土拱内应力变化符合指数规律; 张建勋等[8]采用数值模拟方法得出土拱内部应力沿推力方向呈递减分布特征; 但上述成果只是发现了土拱内部应力递减的现象, 却没有严格的数学推导或证明此现象; 另一种方法是分析抗滑桩与土之间的受力平衡, 建立了以桩间土拱和桩后土拱为主的物理模型[9], 如图 1所示, 通过概念性的拱形来解释土拱效应作用过程, 然而却缺少具体的物理模型来定义土拱拱形的关键参数.
图 1(Fig. 1)
 | 图 1 桩土相互作用系统Fig.1 Interaction between the soil and pile system |
从滑坡外力的角度来研究滑坡体与抗滑桩相互作用模型, 即是滑坡推力荷载分担模型, 不同的桩土作用阶段滑坡推力荷载由不同的介质承担.目前, 随着研究的深入,以单拱(桩后土拱或桩间土拱)模型为主的滑坡推力两级分担模型[10-11]不符合滑坡体与抗滑桩相互作用过程, 由该理论设计的抗滑桩尺寸结果误差较大; 基于桩后土拱和桩间土拱分段作用的滑坡荷载三级分担模型[12]考虑因素较全面, 符合滑坡相互作用过程与室内实验结果, 但如果有严格的数学推导过程, 这个模型将会更加完善.
本文以桩土作用下土拱效应为出发点, 首先明确滑坡土拱合理拱轴线形式, 接着分别推导桩间和桩后土拱的应力递减模型, 刻画了土拱的应力分布特征; 然后基于该土拱应力递减模型, 分别提出桩间和桩后土拱的关键拱形参数的计算公式; 最后推导桩土作用三阶段作用过程模式, 并提出基于土拱的极限承载力的滑坡荷载三级分担模型.
1 土拱拱轴线计算确定土拱合理的拱轴线是研究滑坡桩土作用的前提, 土拱一般被视为静定结构拱, 因为它能适应不均匀位移作用而不破坏[13].假设滑坡推力q均匀分布于桩间土体, 拱迹线的每一点均只存在与该处相切的压力, 而没有拉力、剪力和弯矩, 设拱脚跨度为l, 拱脚处反力分别为Fx, Fy, 以左侧拱脚为坐标原点建立直角坐标系, 土拱受力模型如图 2所示.
图 2(Fig. 2)
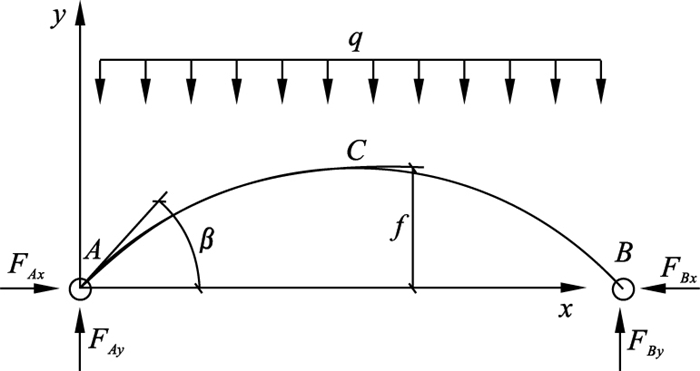 | 图 2 土拱受力模型Fig.2 Soil arch force model |
考虑土拱整体受力平衡, 则有
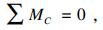 | (1) |
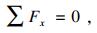 | (2) |
 | (3) |
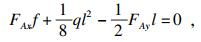 | (4) |
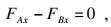 | (5) |
 | (6) |
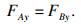 | (7) |
 | (8) |
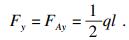 | (9) |
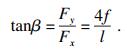 | (10) |
 | (11) |
 | (12) |
2 新的滑坡土拱应力递减模型2.1 桩间土拱应力递减模型图 3为桩间土拱受力模型.假设桩处滑面水平, y方向与滑体运动方向一致, 设滑体厚度为h, 桩后水平均布推力为q0, 桩间土拱净跨度为s0, 拱高为f.对于y轴方向厚度为dy的微拱单元, 对应推力分别为q和q+dq.
图 3(Fig. 3)
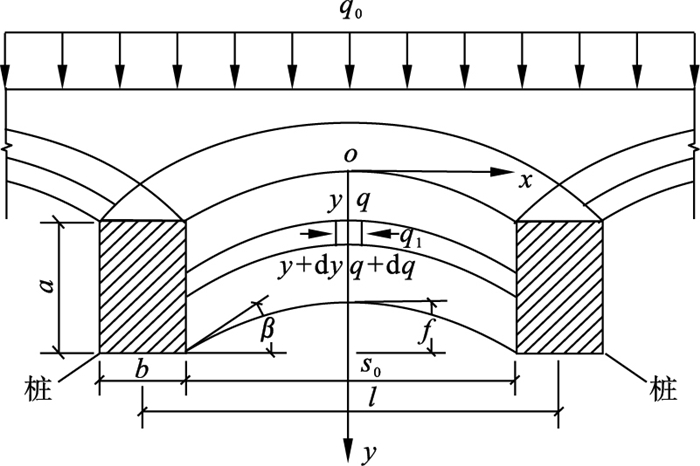 | 图 3 桩间土拱模型Fig.3 Model of soil arch between piles |
由式(9)知微拱单元的拱脚反力dFy满足
 | (13) |
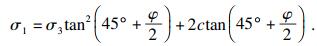 | (14) |
 | (15) |
将式(15)代入式(14)得
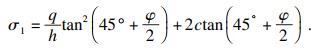 | (16) |
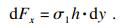 | (17) |
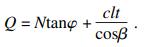 | (18) |
将式(13)、式(16)、式(17)代入式(18)得
 | (19) |
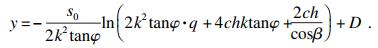 | (20) |
 | (21) |
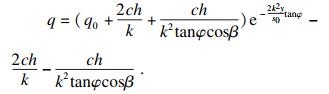 | (22) |
 | (23) |
 | (24) |
式(24)即为桩间土拱应力递减模型.
2.2 桩后土拱应力递减模型桩后土拱模型如图 4所示, 拱脚处的三角形“土核”的斜边与水平线夹角为α, 设桩宽为b, 桩高为a, 拱受水平均布推力q0, 滑体厚度h沿y方向, 各微拱单元拱脚处倾角β不变, 桩间净距为s0.
图 4(Fig. 4)
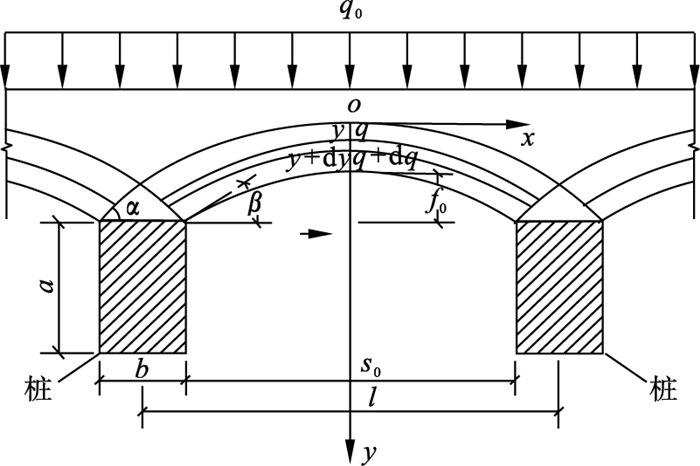 | 图 4 桩后土拱模型Fig.4 Model of soil arch behind piles |
对于厚度为dy的微拱单元, 其跨度为
 | (25) |
 | (26) |
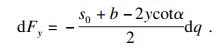 | (27) |
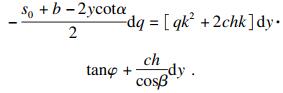 | (28) |
 | (29) |
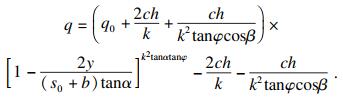 | (30) |
 | (31) |
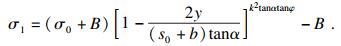 | (32) |
由式(30)和式(32)可知, 滑坡推力和桩后土拱应力皆符合指数递减规律, 验证了室内实验和数值模拟实验结果.式(32)为推导的桩后土拱应力递减模型.
3 拱形参数计算自土拱效应发现以来, 通过室内实验和数值模拟方法使土拱效应理论得到了进一步发展, 其中大多数研究定性描述了土拱的演化过程, 却很少有模型来定量刻画土拱的拱形.本节将依据推导的土拱应力递减模型, 分别获取桩间土拱和桩后土拱拱形参数的计算方程, 这将有助于从拱形的角度来理解土拱效应的发展.
由于在工程实际中土拱跨度和拱脚位置相对确定, 下面主要探讨拱高和厚度的计算方法.
3.1 桩间土拱拱形参数计算由式(8)可知, 图 2拱脚处横向支撑反力满足:
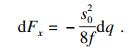 | (33) |
 | (34) |
 | (35) |
 | (36) |
 | (37) |
为尽可能反映土拱的整体特征, 本文建议桩间土拱的拱迹线倾角β均按土拱后缘处的微拱单元的拱迹线倾角计算, 设y=0处, 滑坡推力为q0, 则β计算式为
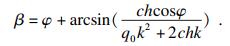 | (38) |
由于抗滑桩截面尺寸的限制, 桩间土拱厚度存在最大值tmax, 其大小由抗滑桩高a和拱迹线倾角β确定:
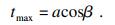 | (39) |
 | (40) |
3.2 桩后土拱拱形参数计算桩后土拱与桩间土拱的区别在于桩后土拱的跨度s是变化的, 而桩间土拱是固定的.对于微拱单元, 二者的强度控制条件没有区别.
如前文推导, 厚度为dy的微拱单元满足式(25)和式(26), 由式(8)可知微拱单元拱脚反力dFx满足:
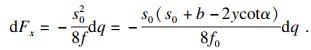 | (41) |
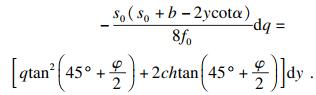 | (42) |
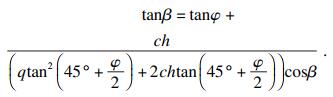 | (43) |
同桩间土拱一样, 受截面尺寸限制, 桩后土拱厚度也存在最大值tmax, 其大小由抗滑桩宽度b、桩后三角形土核斜边倾角α和拱迹线倾角β确定, 计算公式为
 | (44) |
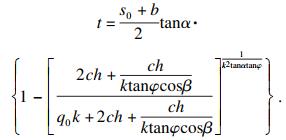 | (45) |
4 滑坡荷载三级分担模型滑坡的演化过程被分为三个阶段, 此演化过程从滑体与抗滑桩相互作用阶段性角度理解即为不同土拱效应之间的转化, 而土拱的活动门实验发现了这一作用过程也呈三阶段演化; 从滑坡推力荷载角度理解即为不同土拱对滑坡荷载的不同阶段分担.本节在利用数学推导验证桩土作用三阶段过程基础上, 计算了土拱极限承载力, 并由此提出与土拱效应阶段性相关的滑坡荷载三级分担模型.
4.1 桩土作用三阶段过程的数学推导活动门实验的土拱效应印证了滑坡过程演化的阶段性特征.土拱效应起源于太沙基(Terzaghi)活动门实验, 基于此众****作了更深入的研究.其中Vardoulakis等通过实验方法提出了土拱效应中“过渡阶段”的概念[3]; 而Chevalier等[14]通过实验研究验证了Vardoulakis等提出的“过渡阶段”.以上研究表明活动门实验实际分为三个过程[12-14]:
1) 初始阶段: 出现在活动门位移非常小过程内, 伴随活动门上方颗粒材料膨胀直到活动门上竖向荷载减到最小值(δ为1~3 mm);
2) 过渡阶段: 活动门上方形成的膨胀区范围不断扩大直至延伸至土体表面, 膨胀区呈楔形(δ为3~40 mm);
3) 最后阶段: 对应2个竖向滑动面的形成(δ为40~100 mm).
该活动门三阶段过程如图 5~图 7所示.
图 5(Fig. 5)
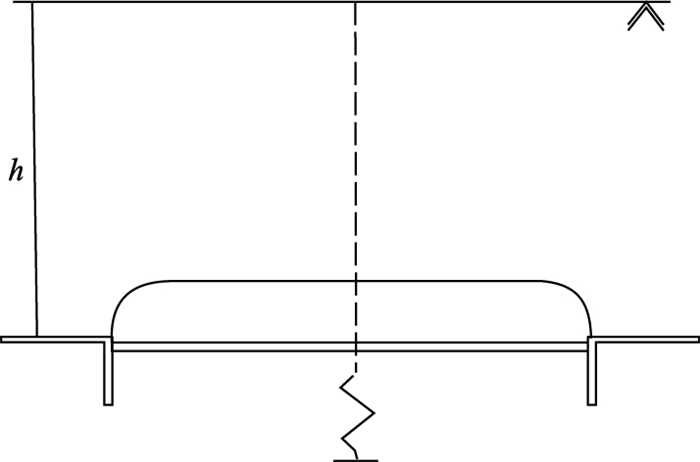 | 图 5 初始阶段Fig.5 Initial stage |
图 6(Fig. 6)
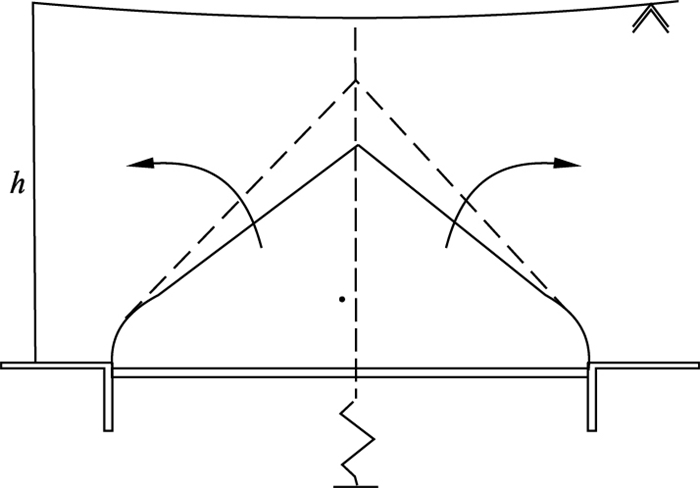 | 图 6 过渡阶段Fig.6 Transitory stage |
图 7(Fig. 7)
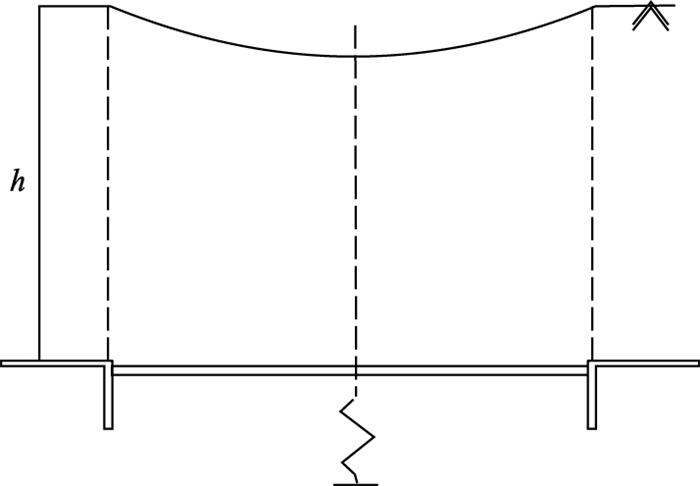 | 图 7 最后阶段Fig.7 Final stage |
活动门实验的三阶段过程表明土拱效应具有明显的阶段性特征, 其与活动门宽度、土体深度和性质等因素有关.在过渡阶段中的土拱为Handy[4]提出的小主应力拱, 在最后阶段出现大主应力拱.
与活动门实验中土拱效应相似, 抗滑桩与滑坡体间的相互作用中土拱效应也应满足三阶段特征, 土拱效应应与桩间距、滑体深度和力学参数相关.在滑坡体与抗滑桩作用的过渡阶段出现最小主应力拱, 此阶段桩后土拱首先起作用, 并占主导作用; 在最后阶段出现最大主应力拱, 由桩间土拱起主导作用.
基于土拱应力递减模型, 在过渡阶段, 桩后土拱应力分布方程如式(31)所示, 其应力值受滑坡推力q0、抗滑桩截面宽度b、土核的斜边与水平线夹角α、滑体厚度h、滑体抗剪强度黏聚力c和内摩擦角φ的影响; 在最后阶段, 桩间土拱应力方程式如式(23)所示, 应力值受滑坡推力q0、滑体厚度h、滑体抗剪强度影响.不同模型的土拱影响因素与图 6和图 7活动门实验过渡阶段至最后阶段演化过程相符合.另一方面, 阶段变化典型现象为实验膨胀破坏区与水平线夹角逐渐增大, 当破坏夹角趋近90°时实验由过渡阶段进入最后阶段.
基于以上分析, 滑坡体与抗滑桩作用由过渡阶段至最后阶段的明显变化是: ①起主导作用的土拱由桩后土拱变为桩间土拱; ②应力影响因素土核斜边与水平线夹角α逐渐趋近于90°, 抗滑桩截面宽度b逐渐失去作用.因此, 对式(31)桩后土拱应力式取b=0, α→90°求极限有
 | (46) |
4.2 滑坡荷载三级分担模型抗滑桩与滑坡体的相互作用、滑坡荷载分担作用分别从内外不同角度印证了滑坡过程演化的阶段性特征, 二者联系紧密.在滑坡体与抗滑桩相互作用三阶段中, 桩后土拱和桩间土拱分别在不同作用阶段起主导作用.基于土拱应力递减方程, 定量推导桩后土拱和桩间土拱的极限承载力, 可以此划分滑坡推力不同阶段分担模型.
1) 桩后土拱极限承载力计算.对式(30)求解q0得
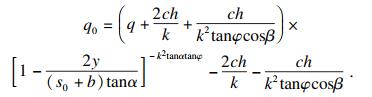 | (47) |
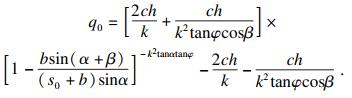 | (48) |
2) 桩间土拱承载极限值.对式(22)求解, 得
 | (49) |
 | (50) |
3) 滑坡荷载三级分担模型.令桩后土拱极限承载力为q1, 按式(48)计算, 令桩间土拱极限承载力为q2, 按式(50)计算, 故可划分基于土拱效应作用的滑坡荷载三级分担模型.当滑坡推力q < q1时, 滑坡推力主要由桩后土拱承担, 此时滑坡体与抗滑桩相互作用主要处于过渡阶段, 由桩后土拱传递滑坡推力至抗滑桩; 而当滑坡推力处于2个土拱极限承载力间即q1 < q < q2时, 滑坡推力的承担由桩间土拱起主导作用, 此时滑坡体与抗滑桩的相互作用处于最后阶段, 主要由桩间土拱传递滑坡推力至抗滑桩; 当滑坡荷载q > q2时, 此时土拱效应已经不存在, 抗滑桩基本失效, 滑坡荷载直接由桩前土体和抗滑桩后壁承担.
本文提出的滑坡荷载三级分担模型具以下优点: ①它同时从滑坡荷载和土拱效应两个方面演化了桩土作用的不同阶段; ②在不同阶段, 定量刻画了土拱应力值大小, 分析了土拱效应的关键影响因素; ③定量化了滑坡荷载三级分担模型, 且与滑坡体与抗滑桩作用阶段特征相符合.
5 结论1) 提出的桩间土拱和桩后土拱的应力解析解模型表明其应力满足指数递减规律, 这与已有室内实验与数值模拟成果相符合.
2) 依据土拱应力递减模型, 提出了土拱拱迹线倾角和土拱厚度的具体计算公式, 该公式不仅考虑了滑坡推力的影响, 也综合考虑了土体强度参数, 较传统方法更加切合实际.
3) 滑坡体与抗滑桩相互作用可分为三个阶段, 其中过渡阶段到最后阶段的两个显著变化一是起主导作用的由桩后土拱变为桩间土拱, 二是土斜边夹角α逐渐趋近于90°, 抗滑桩截面宽度b逐渐失去作用, 该过程和变化规律可由本文的土拱应力递减模型得到数学验证.
4) 本文基于桩间土拱和桩后土拱极限承载力(q1, q2)提出滑坡荷载三级分担模型: 当滑坡推力q < q1时, 滑坡推力主要由桩后土拱承担, 此时滑坡体与抗滑桩相互作用主要处于过渡阶段; 而当滑坡推力处于2个土拱极限承载力之间即q1 < q < q2时, 滑坡推力的承担由桩间土拱起主导作用, 此时滑坡体与抗滑桩相互作用主要处于最后阶段; 当滑坡荷载q > q2时, 此时土拱效应已经不存在, 抗滑桩基本失效, 滑坡荷载直接由桩前土体和抗滑桩后壁承担.
5) 研究对提升土拱效应的理论水平和开展滑坡抗滑桩设计工作有积极作用.
参考文献
| [1] | Tang H, Hu X, Xu C, et al. A novel approach for determining landslide pushing force based on landslide-pile interactions[J]. Engineering Geology, 2014, 182: 15-24. DOI:10.1016/j.enggeo.2014.07.024 |
| [2] | Terzaghi K. Theoretical soil mechanics[M]. New York: John Wiley & Sons, 1943: 76-85. |
| [3] | Vardoulakis L, Graf B, Gudehus G. Trap-door problem with dry sand: a statical approach based upon model test kinematics[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1981, 5: 57-78. DOI:10.1002/nag.1610050106 |
| [4] | Handy R L. The arch in soil arching[J]. Journal of Geotechnical Engineering, 1985, 3: 302-318. |
| [5] | 孙书伟, 马宁, 胡家冰, 等. 抗滑桩土拱演化特征及机理分析[J]. 铁道工程学报, 2019, 11: 7-12. (Sun Shu-wei, Ma Ning, Hu Jia-bing, et al. Evolution characteristics and mechanism analysis of soil arch of anti-slide pile[J]. Journal of Railway Engineering Society, 2019, 11: 7-12.) |
| [6] | Janssen H A. Versuche uber getreidedruck in silozellen[J]. Zeitschrift des Vereins Dtsch Ingenieure, 1895, 39: 1045. |
| [7] | 郑学鑫. 抗滑桩间土拱效应及其有限元模拟研究[D]. 南京: 河海大学, 2007. (Zheng Xue-xin.Analysis and simulation of soil arching effects on anti-slide piles[D].Nanjing: Hohai University, 2007. ) |
| [8] | 张建勋, 陈福全, 简洪钰. 被动桩中土拱效应问题的数值分析[J]. 岩土力学, 2004, 25(2): 174-178. (Zhang Jian-xun, Chen Fu-quan, Jian Hong-yu. Numerical analysis of soil arching effects in passive piles[J]. Rock and Soil Mechanics, 2004, 25(2): 174-178.) |
| [9] | Li C, Wu J, Tang H, et al. A novel optimal plane arrangement of stabilizing piles based on soil arching effect and stability limit for 3D colluvial landslides[J]. Engineering Geology, 2015, 195: 236-247. DOI:10.1016/j.enggeo.2015.06.018 |
| [10] | 周德培, 肖世国, 夏雄. 边坡工程中抗滑桩合理桩间距的探讨[J]. 岩土工程学报, 2004, 26(1): 132-135. (Zhou De-pei, Xiao Shi-guo, Xia Xiong. Discussion on rational spacing between adjacent anti-slide piles in some cutting slope projects[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(1): 132-135.) |
| [11] | 张玲, 陈金海, 赵明华. 考虑土拱效应的悬臂式抗滑桩最大桩间距确定[J]. 岩土力学, 2019, 40(11): 4497-4505. (Zhang Ling, Chen Jin-hai, Zhao Ming-hua. Maximum cantilever anti-slide piles spacing determination with consideration of soil arching effect[J]. Rock and Soil Mechanics, 2019, 40(11): 4497-4505.) |
| [12] | 李长冬. 抗滑桩与滑坡体相互作用机理及其优化研究[D]. 武汉: 中国地质大学(武汉), 2009. (Li Chang-dong.Study on interaction mechanism between anti-slide pile and landslide mass and pile optimization[D].Wuhan: China University of Geosciences (Wuhan), 2009. ) |
| [13] | 贾海丽, 王成华, 李江洪. 关于土拱效应的几个问题[J]. 西南交通大学学报, 2003, 38(4): 398-402. (Jia Hai-li, Wang Cheng-hua, Li Jiang-hong. Discussion on some issues in theory of soil arch[J]. Journal of Southwest Jiaotong University, 2003, 38(4): 398-402.) |
| [14] | Chevalier B, Combe G, Villard P. Experimental and numerical study of the response of granular layer in the trap-door problem[J]. AIP Conference Proceedings, 2009, 1145: 649-652. |
