
 , 刘阳2
, 刘阳2 1. 天津工业大学 天津市自主智能技术与系统重点实验室, 天津 300387;
2. 华晨宝马汽车有限公司, 辽宁 沈阳 110098
收稿日期:2021-03-23
基金项目:国家重点研发计划项目(2018YFB1701802);国家自然科学基金资助项目(61802280, 61806143, 61772365, 41772123);天津市自然科学基金资助项目(18JCQNJC77200);天津市教委科研计划项目(2017KJ094);采矿冶金过程自动化国家重点实验室/北京矿冶过程自动化重点实验室研究基金项目(BGRIMM-KZSKL-2019-08)。
作者简介:刘芳(1983-),女,辽宁沈阳人,天津工业大学副教授;
苏卫星(1980-),男,辽宁盘锦人,天津工业大学教授。
摘要:基于等效电路模型的一类车载动力电池剩余荷电状态(state of charge, SOC)的估算方法, 其估算精度高度依赖于模型精度, 模型精度又正比于模型复杂度, 以至于难以较好地应用于嵌入式控制单元.提出复杂度相对较低、能够自适应确定最优模型阶次的全新等效电路模型——基于阶次自适应AR模型的车载动力电池等效电路灰箱模型.基于此灰箱模型, 给出锂离子电池SOC的滑模观测器设计推导及能观性、收敛性证明.结果表明, 本文提出的基于阶次自适应AR等效电路灰箱模型的滑模观测器SOC估算方法(adaptive autoregressive-sliding mode observer, AAR-SMO)具有低模型复杂度、高精度、强鲁棒性及快速收敛等性能.
关键词:车载动力电池荷电状态AR模型等效电路模型滑模观测器
Sliding Mode Observer of Lithium Battery SOC Based on Order Adaptive AR Equivalent Circuit Model
LIU Fang1, LI Zhuo1, SU Wei-xing1

 , LIU Yang2
, LIU Yang2 1. Tianjin Key Laboratory of Autonomous Intelligence Technology and Systems, Tiangong University, Tianjin 300387, China;
2. BMW Brilliance Automotive Ltd., Shenyang 110098, China
Corresponding author: SU Wei-xing, E-mail: satelliteer@126.com.
Abstract: Based on the equivalent circuit model, the estimation method of the remaining state of charge (SOC) of a type of vehicle power battery shows that the estimation accuracy is highly dependent on the model accuracy and the model accuracy is directly proportional to the model complexity, so that it is difficult to be better applied to the embedded control unit problem. A new equivalent circuit model with relatively low complexity and capable of adaptively determining the optimal model order, i.e., a gray box model of the equivalent circuit of the vehicle power battery based on the order adaptive AR model is proposed. Based on this gray box model, the design derivation of the sliding mode observer for the state of lithium-ion battery SOC and the proof of observability and convergence are given. The results show that the sliding mode observer SOC estimation method (adaptive autoregressive-sliding mode observer, AAR-SMO) based on the order-adaptive equivalent circuit gray box model proposed in this paper has low model complexity, high accuracy, strong robustness and fast convergence performance.
Key words: vehicle power batterystate of chargeautoregressive modelequivalent circuit modelsliding mode observer
电池技术是制约电动汽车发展的关键因素, 为了提高电池的使用效率, 延长使用寿命, 降低运行成本, 提高可靠性, 除电池本体技术外, 电池管理系统(battery management system, BMS)也发挥着重要作用[1].车载电池的SOC作为BMS的重要参数, 成为BMS在效率、寿命、安全可靠等多方面精准管理的重要基础, 因此, 精准的SOC估计对车载动力电池乃至整个电动汽车的安全、可靠、高效运行至关重要.
目前较为主流的电池SOC估算方法有库伦积分法、基于电池模型一类的滤波族算法[2]、滑模观测器方法[3]及机器学习一类的智能算法等[4].其中, 库伦积分算法简单且易于实施, 但其属于开环的SOC估算方法, 存在累计误差无法消除的问题, 一般在实际应用中需要结合矫正环节以保证误差维持在合理范围内[5].机器学习一类的智能算法(例如模糊逻辑[6]、神经网络[7]、支持向量机[8]等)将电池视为黑箱, 完全利用数据驱动, 无需任何电池相关先验知识即可直接建立电池变量之间的关系, 由于数据集在这类SOC估算方法中的高度参与而导致的问题, 例如异常数据、高噪声及传感器漂移等会严重影响SOC的估算精度[9].完全基于数据的智能算法对于训练数据集的广泛性要求较高[10], 广泛性不足会导致欠拟合或过拟合现象.基于电池模型一类的SOC估算方法为目前最主流的SOC估算方法.此类算法的研究主要从两方面开展: ①具体SOC估算方法, 如滤波族、滑模观测器算法等本身性能的提高及复杂度的降低[11]; ②电池模型的精度、复杂度及适用性等问题的研究.在电池模型中, 电化学机理模型占有相当的比重, 其中具有代表性的单颗粒(single particle, SP)模型[12]、具有电解质的单粒子模型(single particle model with electrolyte, SPMe)[13]等均需要利用全局优化方法识别大量未知参数, 这将导致模型过度拟合或陷入局部优化等问题[14]; 在缺少准确且详细的模型参数时, 基于此类机理模型的SOC估算精度并不理想.基于电池外在电气特性的等效电路模型, 由于其简化的模型结构、具有意义明确且可在线估算的参数及能够直观反映出的电池特性, 使其在实时应用中引起科研人员的极大兴趣.这也直接导致各种等效电路模型的出现, 包括rint模型、戴维南(thevenin)模型、新一代车辆合作伙伴关系(partnership for a new generation of vehicles, PNGV)模型[15]及nRC模型等.其中, rint模型仅适用于稳态分析[16], thevenin模型和PNGV模型由于加入适当的电容等元件能够对电池的瞬态过程进行描述, 但模型精度不足, 不能满足科研人员对模型高精度的追求, 因此, nRC模型等各类改进模型应运而生.文献[17]通过对不同阶次的nRC模型进行仿真验证后指出nRC模型的模型精度会随阶次n的增加而提高, 但当模型阶次达到一定值(n=3)后, 模型精度提高的速度远低于模型复杂度提高的速度, 因此该文献认为此临界模型阶次(n=3)应定义为最佳的nRC模型的模型阶次.由于nRC模型本身为非线性模型, 即使模型阶次为3, 其模型复杂度也相对较高, 模型复杂度的高低将直接影响基于此模型的SOC估算方法的复杂度.
基于以上对于电池等效电路模型现状的分析, 以及车载电池对于SOC估算高精度、低复杂度、在线快速估计的需求, 首先提出了一种全新的锂离子电池等效电路灰箱模型——阶次自适应AR(adaptive autoregressive, AAR)等效电路模型.该模型的优势在于: 提出的阶次自适应AR等效电路模型能够实现AR模型阶次的自适应自动调整, 从而使基于此的等效电路能够以最优的模型阶次高精度拟合电池的电气特性; 在提出的阶次自适应AR等效电路模型中, 利用AR模型本身的线性结构有效降低模型复杂度, 避免传统非线性电池等效电路模型参数辨识过程中遇到的陷入局部最优的问题, 能够实现最优参数的快速辨识, 因此更适用于车载电池的状态估计问题; 提出利用BDT算法实现电池内部参数的在线实时辨识, 从而实现精确跟踪电池内阻随温度、SOC及老化等因素的变化情况, 从模型精度角度保证SOC估算的精度; 本文基于阶次自适应AR等效电路模型, 提出了阶次自适应AR等效电路模型的锂离子电池的SOC滑模观测算法.
1 阶次自适应AR等效电路模型1.1 AR等效电路模型结构阶次自适应AR等效电路模型如图 1所示.
图 1(Fig. 1)
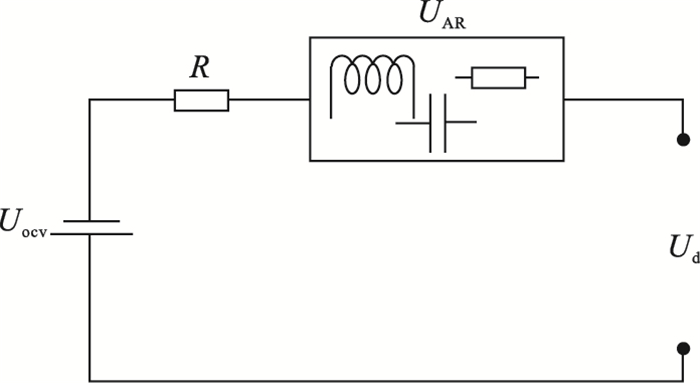 | 图 1 AAR等效电路模型Fig.1 Adaptive autoregressive equivalent circuit model |
Ud为电池的端电压, Uocv为电池的开路电压, R为电池欧姆内阻, UAR为电池内部除欧姆内阻压降外的“其他全部压降”, 一般称之为极化内阻产生的压降, 其受温度、放电倍率、SOC及电池老化等因素影响而动态变化, 对于锂离子电池而言属于快时变参数.
考虑AR模型相对简单的线性结构及当模型阶次适当时能够无限逼近任意非线性模型的能力[18], 提出将电池复杂的极化过程所产生的压降视为以电池电流I(t)(t=1, 2, …)为输入, 以极化内阻产生的压降UAR为输出的黑箱模型, 并利用AR模型对其进行拟合:
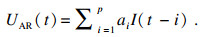 | (1) |
将黑箱模型与图 1中开路电压Uocv及欧姆内阻R一起组成“灰箱”的等效电路模型结构.其等效电路模型表达式为
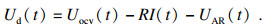 | (2) |
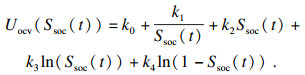 | (3) |
由于锂离子电池的开路电压与SOC的函数关系式主要随电池老化而改变, 而在一次充放电循环过程内几乎不变, 因此假设式(3)中参数k0, k1, k2, k3, k4在一次充放电循环内恒定不变.
1.2 阶次自适应AR等效电路模型参数辨识在Uocv(Ssoc(t))中, 参数k0, k1, k2, k3, k4在充放电循环中恒定不变, 具有仅随电池老化而改变的缓慢时变特征, 本文提出对其采用间歇式更新原则: 当电池充放电循环次数Num>Vset时, 利用最后一次循环得到的Ud(t), I(t)及计算得到的Ssoc(t), R及AR模型系数a1, a2, …, ap对其进行线性拟合以确定最新的参数k0, k1, k2, k3, k4.以下仅介绍实时更新欧姆内阻R及AR模型系数a1, a2, …, ap的辨识方法.
式(1)改写为式(2):
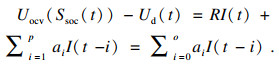 | (4) |
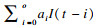
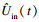
图 2(Fig. 2)
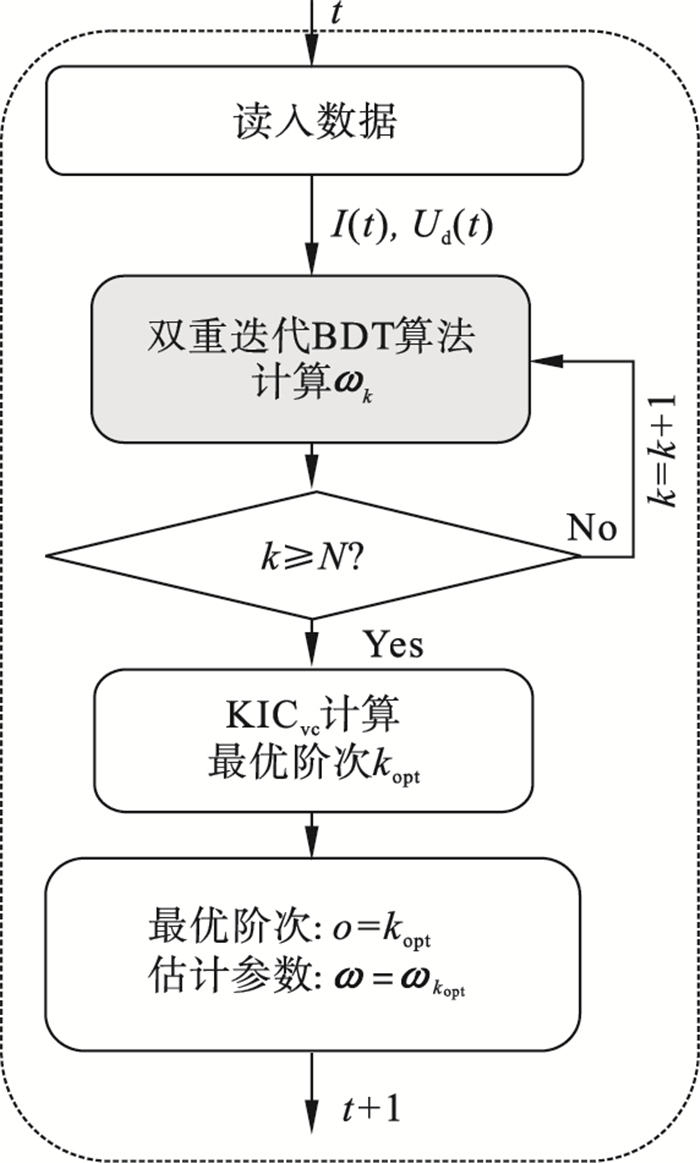 | 图 2 参数辨识流程图Fig.2 Parameter identification flowchart |
在图 2中:t为时间; k为当前迭代的阶次; ωk表示AR模型阶次为k时的待辨识参数ω值; N表示设定的AR模型最大迭代阶次; kopt表示利用KICvc准则确定的最优模型阶次kopt=opt{k}, k=1, 2, …, N; ωkopt表示待辨识参数ω在最优模型阶次kopt下的值.
KICvc准则式[21]为
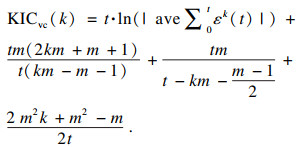 | (5) |
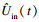
最优阶次kopt计算式为
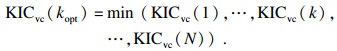 | (6) |
图 3(Fig. 3)
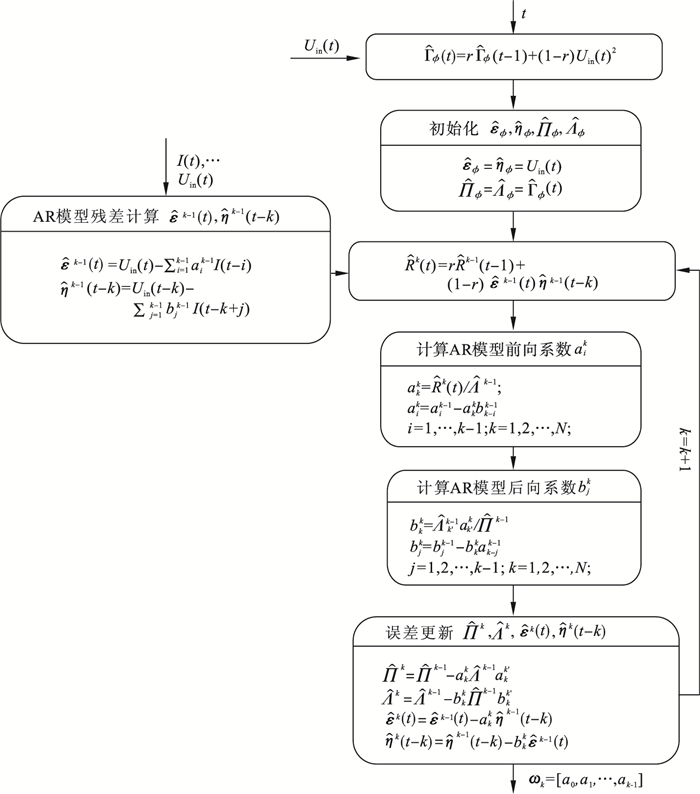 | 图 3 双重迭代BDT算法流程图Fig.3 Double iteration BDT algorithm flowchart |
在图 3中, Uin(t)表示电池内部电压降, Uin(t)=Uocv(
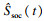
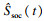
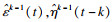
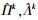
2 滑模观测器设计2.1 动态系统模型依据式(3), 开路电压Uocv(Ssoc)的动态模型为
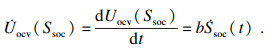 | (7) |
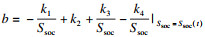
由于Ssoc可以表示为电流I(t)对时间的积分:
 | (8) |
式(7)可改写为
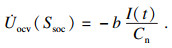 | (9) |
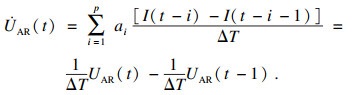 | (10) |
依据式(7)、式(9)得到AAR等效电路模型的动态表达式:
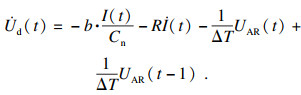 | (11) |
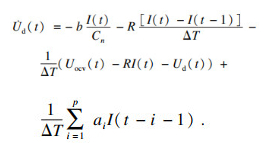 | (12) |
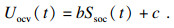 | (13) |
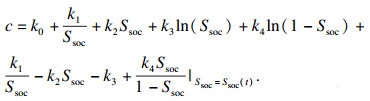 | (14) |
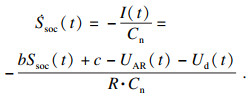 | (15) |
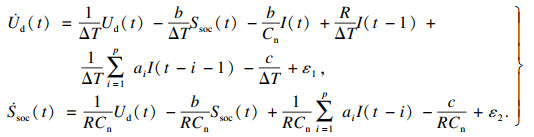 | (16) |
2.2 滑模观测器设计式(16)可用矩阵简写为
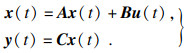 | (17) |
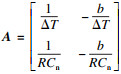
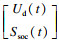
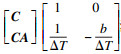
依据式(16)构造观测器:
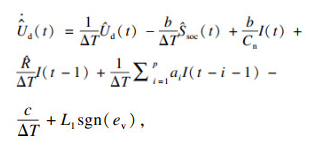 | (18) |
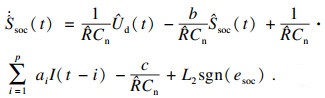 | (19) |
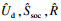
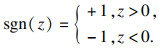 | (20) |
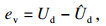 | (21) |
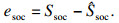 | (22) |
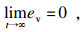 | (23) |
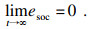 | (24) |
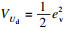
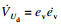
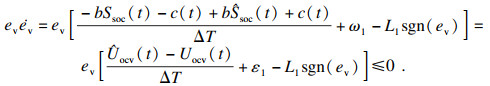 | (25) |
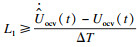
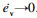
由于状态变量x(t)中Ud可测, 而Ssoc不可测, 建立ev和esoc之间的关系:
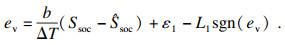 | (26) |
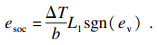 | (27) |
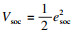
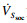
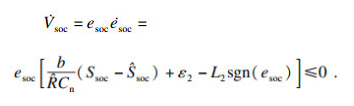 | (28) |
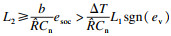
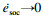
滑模观测器为
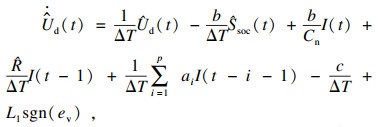 | (29) |
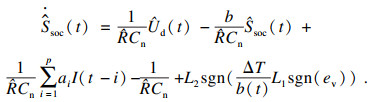 | (30) |
图 4(Fig. 4)
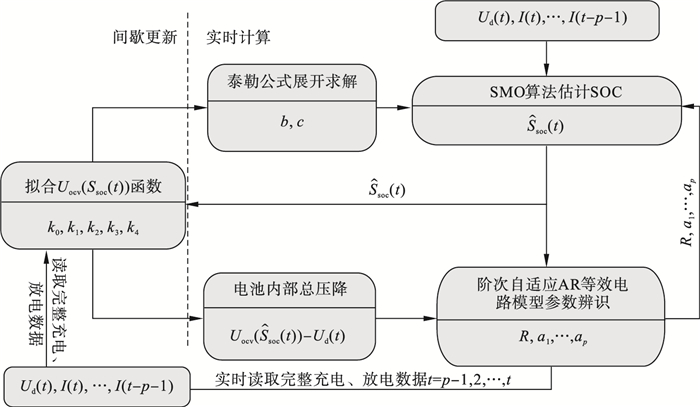 | 图 4 基于AAR等效电路模型结合滑模观测器的SOC估计流程Fig.4 Flow chart of estimation based on equivalent circuit model combined with sliding mode observer |
4 算法验证与比较4.1 验证与比较方案为了更贴近实际车载电池放电特征, 选取马里兰大学CALCE电池实验实测开放数据集中的A123型电池在动态应力测试工况(dynamic stress test, DST)下运行所采集的数据对提出的基于阶次自适应AR等效电路模型的SOC滑模观测算法进行有效性及适用性验证.其中A123的标称电压为3.3 V, 标称容量为1.1 Ah, 充、放电截止电压分别为3.6, 2.0 V, 最大放电电流为30 A的LiFePO4电池.
DST工况由美国高级电池协会(USABC)提出[22], 主要用于研究电池的瞬态特性, 因此更贴近于车载动力电池瞬态的随机放电特征.算法验证与比较分两步:
1) 模型精度验证与比较: 利用CALCE数据集DST工况数据验证本文提出的AAR等效电路模型的精度, 并与传统Thevenin模型进行精度比较.
2) 基于模型的SOC估算精度验证与比较: 利用CALCE数据集DST工况数据验证本文提出的AAR-SMO算法估算的SOC精度, 并与基于传统Thevenin模型的滑模观测算法(定义为Thevenin-SMO)估算SOC的精度进行比较.
为了更贴近实际情况, 本文在两步验证过程中, 均从无噪声环境和高斯白噪声环境下对算法的精度进行比较验证.
4.2 模型精度验证与比较4.2.1 无噪声下的验证与比较为了验证本文提出的阶次自适应AR等效电路模型的精确性, 在DST工况下分别利用AAR等效电路模型与传统Thevenin模型对端电压进行估算.Thevenin模型表达式为
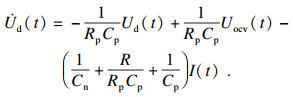 | (31) |
分别利用本文提出的AAR等效电路模型及传统Thevenin等效电路模型估算A123电池端电压, 结果如图 5所示.
图 5(Fig. 5)
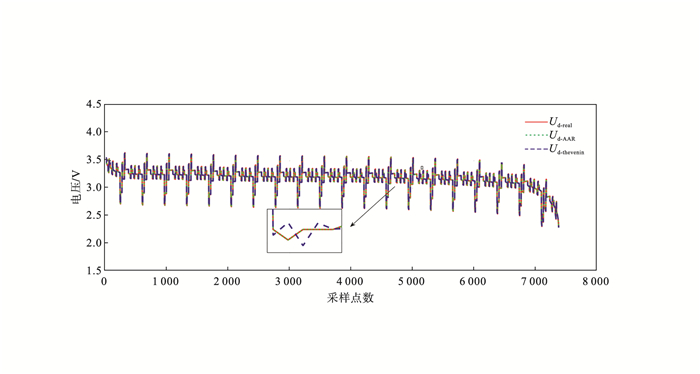 | 图 5 AAR模型与Thevenin模型精度比较Fig.5 Accuracy comparison between ARR model and Thevenin model |
在图 5中, Ud-real为真实端电压, Ud-AAR为本文提出的AAR模型估算的端电压, Ud-thevenin为Thevenin模型估算的端电压.从图中可以看出本文提出的AAR模型的估算精度最高, 且具有较高的稳定性, 更接近于真实端电压.
4.2.2 白噪声下的验证与比较为了更贴近实际, 在电流I(t)和端电压Ud(t)上分别加入30 db的高斯白噪声, 并利用含有噪声的电流、电压数据对本文提出的AAR等效电路模型精度进行验证, 同时与传统Thevenin模型进行精度比较, 结果如图 6所示, 与Thevenin模型的估算偏差比较如图 7所示..
图 6(Fig. 6)
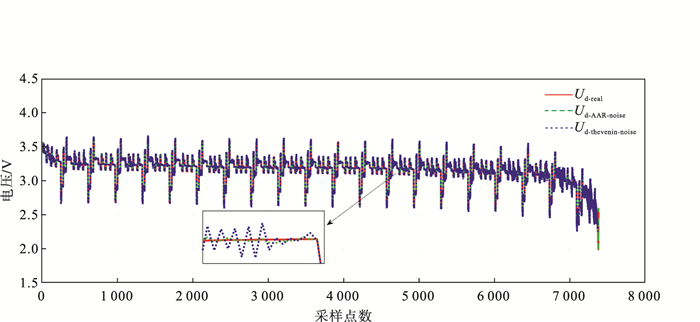 | 图 6 高斯白噪声下AAR模型与Thevenin模型精度比较Fig.6 Accuracy comparison of AAR model and Thevenin model under Gaussian white noise |
图 7(Fig. 7)
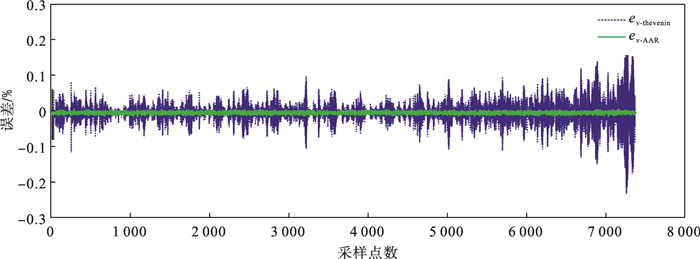 | 图 7 高斯白噪声下AAR模型与Thevenin模型的估算偏差比较Fig.7 Comparison of estimated deviation between AAR model and Thevenin model under Gaussian white noise |
在图 6中, 红色实线表示实测的真实端电压Ud-real; 绿色虚线表示高斯白噪声干扰下AAR模型估计的端电压, 用Ud-AAR-noise表示; 蓝色虚线为基于传统Thevenin模型得到的端电压拟合曲线, 用Ud-thevenin-noise表示.从图 6的局部放大图可以看出, 在噪声环境下, 本文提出的AAR模型能更好地反映出实际的电池电气特性, 且较传统Thevenin模型要稳定, 波动较小, 具有较好的鲁棒性.图 7为本文提出的AAR模型与传统Thevenin模型估算端电压的误差图.在相同白噪声干扰下, 本文提出的AAR模型能够以更高的精度逼近真实的端电压值, 且波动较小, 鲁棒性较好, 误差基本在0.01 V以下, 而传统Thevenin模型在噪声环境下的误差最大值大于0.2 V.
4.3 基于模型的SOC估算精度验证与比较4.3.1 无噪声下的验证与比较为了验证本文提出的基于AAR等效电路模型的电池剩余电量滑模观测估计器的实用性、有效性及估算精度, 本文依然利用马里兰大学CALCE电池实验实测开放的DST工况数据集来模拟车载动力电池的瞬态放电过程, 对本文提出的AAR-SMO算法进行SOC估算精度验证, 同时基于传统Thevenin模型, 采用相同思路的SMO观测器设计, 经过推导得到以下滑模观测器模型:
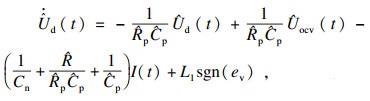 | (32) |
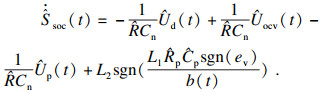 | (33) |
图 8(Fig. 8)
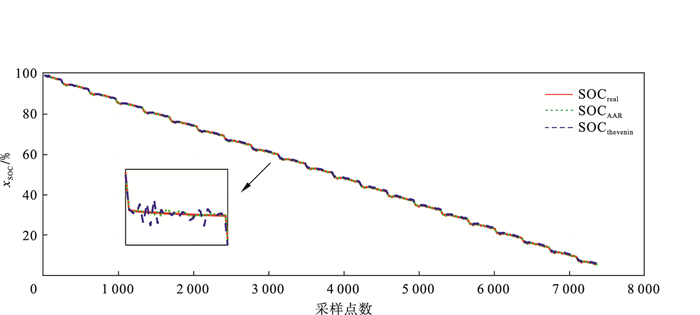 | 图 8 无噪声下AAR-SMO算法与Thevenin-SMO算法的SOC估算对比Fig.8 Comparison of SOC estimation between AAR-SMO algorithm and Thevenin-SMO algorithm under noiseless conditions |
在图 8中, SOCreal代表马里兰大学CALCE电池实验室给出的实测真实SOC值, SOCAAR为利用本文提出的AAR-SMO算法估算的SOC曲线, SOCthevenin为利用Thevenin-SMO算法估算的SOC曲线.从图 8中可以看出, 由于此次验证为无噪声理想环境下的SOC估算, 因此精度均较高.从局部放大图可以看出, 本文提出的AAR-SMO算法估算的SOC结果曲线更贴近真实SOC曲线, 精度略高, 在3000采样点以后收敛速度显著提升, 具有更高的稳态跟踪精度.
4.3.2 白噪声下的验证与比较在噪声环境下(电流I(t)和端电压Ud(t)上分别加入30 db的高斯白噪声), 分别用本文提出的AAR-SMO算法与Thevenin-SMO算法对SOC进行估算, 所得结果如图 9所示, 偏差分别如图 10, 图 11所示.
图 9(Fig. 9)
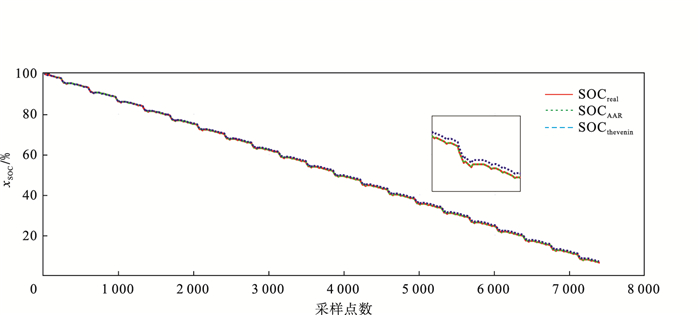 | 图 9 高斯白噪声下AAR-SMO算法与Thevenin-SMO算法的SOC估算对比Fig.9 Comparison of SOC estimation between AAR-SMO algorithm and Thevenin-SMO algorithm under Gaussian white noise |
图 10(Fig. 10)
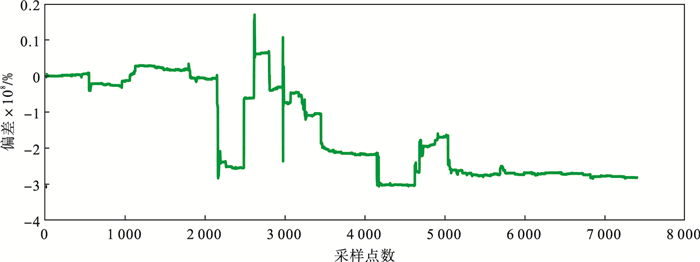 | 图 10 高斯白噪声下AAR-SMO算法估计的SOC的偏差Fig.10 Deviation of SOC estimated by AAR-SMO algorithm under Gaussian white noise |
图 11(Fig. 11)
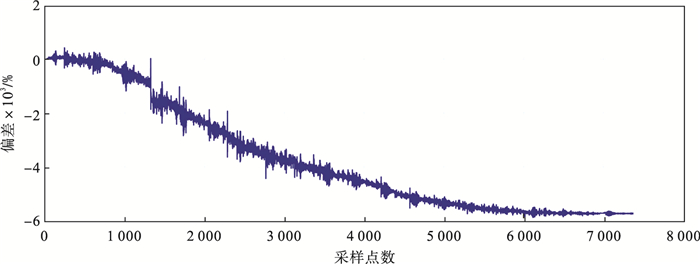 | 图 11 高斯白噪声下Thevenin-SMO算法估计的SOC的偏差Fig.11 Deviation of SOC estimated by Thevenin-SMO algorithm under Gaussian white noise |
在图 9中, 红色实线为真实实测SOC值, 用SOCreal表示; 绿色虚线为高斯白噪声干扰下基于AAR-SMO算法估计的SOC值, 用SOCAAR-noise表示; 蓝色虚线为白噪声干扰下基于传统Thevenin-SMO算法估算的SOC值, 用SOCthevenin-noise表示.通过局部放大图可以看出, 本文提出的基于AAR-SMO的SOC估算方法得到的估算结果更贴近真实值, 具有更高的估算精度, 更好的抗干扰性.
对比图 10与图 11的误差图可以更清晰地看出, 本文提出的AAR-SMO算法在噪声环境下估算的SOC精度高于基于传统Thevenin-SMO算法估算的SOC精度.可以验证本文提出的基于阶次自适应AR等效电路模型的SOC滑模观测器无论在理想环境下还是在噪声环境下都具有较高的估算精度及较强的鲁棒性.
5 结论1) 本文提出了一种阶次自适应AR等效电路模型, 该模型具有计算复杂度较低的线性结构, 能够自适应调整AR模型阶次, 使其能够以最优的AR模型阶次高精度模拟电池的瞬态电气特性, 有效避免传统电池等效电路模型在车载动力电池一类瞬态尖峰放电时, 存在电气特性难以精确跟随的问题,实现高精度与低复杂度的平衡.
2) 基于阶次自适应AR等效电路模型, 提出了阶次自适应AR等效电路模型锂离子电池SOC滑模观测算法, 给出滑模观测器的设计过程、稳定性及收敛性证明.
3) 通过基于马里兰大学CALCE电池实验实测开放数据集的验证, 以及与基于传统Thevenin模型的滑模观测器SOC算法进行比较, 结果表明本文提出的基于阶次自适应AR等效电路模型的SOC估算滑模观测器能够适应电流剧烈变化的充放电工况, 在较大测量噪声的情况下仍能保持高估算精度, 为提高电动汽车电池管理系统电池荷电状态估计的有效性和实用性提供了途径.
参考文献
| [1] | Liu F, Liu X Y, Su W X, et al. An online state of health estimation method based on battery management system monitoring data[J]. International Journal of Energy Research, 2020, 44(3): 6338-6349. |
| [2] | 章军辉, 李庆, 陈大鹏, 等. 基于自适应UKF的锂离子动力电池状态联合估计[J]. 东北大学学报(自然科学版), 2020, 41(11): 1557-1563. (Zhang Jun-hui, Li Qing, Chen Da-peng, et al. State co-estimation algorithm for li-ion power batteries based on adaptive unscented Kalman filters[J]. Journal of Northeastern University(Natural Science), 2020, 41(11): 1557-1563. DOI:10.12068/j.issn.1005-3026.2020.11.006) |
| [3] | Ning B, Cao B G, Wang B, et al. Adaptive sliding mode observers for lithium-ion battery state estimation based on parameters identified online[J]. Energy, 2018, 153: 732-742. DOI:10.1016/j.energy.2018.04.026 |
| [4] | Vidal C, Malysz P, Kollmeyer P, et al. Machine learning applied to electrified vehicle battery state of charge and state of health estimation: state-of-the-art[J]. IEEE Access, 2020, 8: 52796-52814. DOI:10.1109/ACCESS.2020.2980961 |
| [5] | 许元武, 吴肖龙, 陈明渊, 等. 基于变参数模型的锂电池荷电状态观测方法[J]. 控制理论与应用, 2019, 36(3): 443-452. (Xu Yuan-wu, Wu Xiao-long, Chen Ming-yuan, et al. Li-ion batteries state-of-charge observation method based on model with variable parameters[J]. Control Theory and Applications, 2019, 36(3): 443-452.) |
| [6] | Wang B, Qin F, Zhao X, et al. Equalization of series connected lithiumion batteries based on back propagation neural network and fuzzy logic control[J]. International Journal of Energy Research, 2020, 44(6): 4812-4826. DOI:10.1002/er.5274 |
| [7] | Chen C, Xiong R, Yang R X, et al. State-of-charge estimation of lithium-ion battery using an improved neural network model and extended Kalman filter[J]. Journal of Cleaner Production, 2019, 234: 1153-1164. DOI:10.1016/j.jclepro.2019.06.273 |
| [8] | Kashkooli A G, Fathiannasab H, Mao Z, et al. Application of artificial intelligence to state-of-charge and state-of-health estimation of calendar-aged lithium-ion pouch cells[J]. Journal of The Electrochemical Society, 2019, 166(4): A605-A615. DOI:10.1149/2.0411904jes |
| [9] | Zahid T, Xu K, Li W M. Machine learning an alternate technique to estimate the state of charge of energy storage devices[J]. Electronics Letters, 2017, 53(25): 1665-1666. DOI:10.1049/el.2017.2677 |
| [10] | Zhang S, Guo X, Zhang X. Multi-objective decision analysis for data-driven based estimation of battery states: a case study of remaining useful life estimation[J]. International Journal of Hydrogen Energy, 2020, 45(27): 14156-14173. DOI:10.1016/j.ijhydene.2020.03.100 |
| [11] | How D, Hannan M A, Lipu M, et al. State of charge estimation for lithium-ion batteries using model-based and data-driven methods: a review[J]. IEEE Access, 2019, 7(99): 136116-136136. |
| [12] | Cen Z, Kubiak P. Lithium-ion battery SOC/SOH adaptive estimation via simplified single particle model[J]. International Journal of Energy Research, 2020, 44(15): 12444-12459. DOI:10.1002/er.5374 |
| [13] | Pang H, Mou L, Guo L, et al. Parameter identification and systematic validation of an enhanced single-particle model with aging degradation physics for li-ion batteries[J]. Electrochimica Acta, 2019, 307: 474-487. DOI:10.1016/j.electacta.2019.03.199 |
| [14] | Brivio C, Musolino V, Merlo M, et al. A physically-based electrical model for lithium-ion cells[J]. IEEE Transactions on Energy Conversion, 2019, 34(2): 594-603. DOI:10.1109/TEC.2018.2869272 |
| [15] | Wei X, Mo Y M, Zhang F. Lithium-ion battery modeling and state of charge estimation[J]. Integrated Ferroelectrics, 2019, 200(1): 59-72. DOI:10.1080/10584587.2019.1592620 |
| [16] | Zheng Y, Gao W, Ouyang M, et al. State-of-charge in consistency estimation of lithium-ion battery pack using mean-difference model and extended Kalman filter[J]. Journal of Power Sources, 2018, 383: 50-58. DOI:10.1016/j.jpowsour.2018.02.058 |
| [17] | 熊瑞. 基于数据模型融合的电动车辆动力电池组状态估计研究[D]. 北京: 北京理工大学, 2014. (Xiong Rui. Estimation of battery pack state for electric vehicles using model-data fusion approach[D]. Beijing: Beijing Institute of Technology, 2014. ) |
| [18] | Liu F, Ma J, Su W X. Unscented particle filter for SOC estimation algorithm based on a dynamic parameter identification[J]. Mathematical Problems in Engineering, 2019(6): 1-14. |
| [19] | Yang D, Wang Y Y, Pan R, et al. State-of-health estimation for the lithium-ion battery based on support vector regression[J]. Applied Energy, 2018, 227: 273-283. DOI:10.1016/j.apenergy.2017.08.096 |
| [20] | 刘芳, 毛志忠. 应用阶数自学习自回归隐马尔可夫模型对控制过程异常数据的在线检测[J]. 控制理论与应用, 2011(5): 631-638. (Liu Fang, Mao Zhi-zhong. On-line detection of outliers in control process data based on autoregressive hidden Markov model with order self-learning[J]. Control Theory and Technology, 2011(5): 631-638.) |
| [21] | Seghouane A K. Vector autoregressive model-order selection from finite samples using kullback's symmetric divergence[J]. IEEE Transactions on Circuits & Systems, 2006, 53: 2327-2335. |
| [22] | Xing Y J, He W, Pecht M, et al. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures[J]. Applied Energy, 2014, 113(1): 106-115. |
