
 , 黄小斌, 陈百玲
, 黄小斌, 陈百玲 东北大学 资源与土木工程学院, 辽宁 沈阳 110819
收稿日期:2021-04-28
基金项目:国家自然科学基金青年基金资助项目(51808100)。
作者简介:张耀升(1994-), 男, 广西南宁人,东北大学博士研究生;
王连广(1964-), 男, 辽宁鞍山人,东北大学教授, 博士生导师。
摘要:为了明确注浆岩锚在半无限锚固长度下的受力机理, 分析了锚杆界面的受力关系, 给出相应的锚杆拔出方程.然后假定锚杆弹性部分沿锚固深度方向的剪应力分布呈四分之一椭圆弧, 进而给出了注浆锚杆临界锚固长度的计算公式.对4根锚固长度分别为6.0 m和8.5 m的锚杆进行了原位拉拔试验, 以验证所给公式的正确性.结果表明, 计算得到的轴向应变分布曲线与试验结果一致, 轴向应变随着锚固深度的增加呈非线性减小.计算得到的临界锚固长度为5.3 m, 与试验结果相差3.6%.最后, 通过与前人研究进行比较后发现, 本文所给公式具有一般性, 且通过本文所给公式计算得到的结果相对保守.
关键词:岩石锚杆注浆界面应力临界锚固长度拔出试验
Analysis of Interface Stress of Grouting Rockbolt and Calculation of Critical Anchorage Length
ZHANG Yao-sheng, WANG Lian-guang

 , HUANG Xiao-bin, CHENG Bai-ling
, HUANG Xiao-bin, CHENG Bai-ling School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: WANG Lian-guang, E-mail: wanglianguang@mail.neu.edu.cn.
Abstract: To clarify the mechanism of the grouting rockbolt with a semi-infinite anchorage length, the interface mechanical property of the rockbolt was analyzed and the corresponding pull-out equations were present. Assuming that the shear stress distribution of the elastic part of the anchor rod along the anchoring depth was a quarter elliptical arc, and then the calculation formula of the critical anchorage length of the grouting rockbolt was given. To verify the correctness of the present method, in-situ pull-out tests were carried out on 4 anchor rods with anchoring lengths of 6.0 m and 8.5 m, respectively. The results showed that the axial strain distribution curve calculated by the present method was consistent with the experimental results, and the axial strain decreases nonlinearly with the anchoring depth. The critical anchorage length calculated by the present method was 5.3 m, which was 3.6% different from the test result. The method presented in the manuscript was universal, and the calculation results obtained by the present method were relatively conservative compared with the results obtained by previous research.
Key words: rockboltgroutinginterface stresscritical anchorage lengthpull-out test
由于注浆锚杆在土木和采矿工程中得到了广泛的应用[1], 其剪切滑移性能和临界锚固长度一度成为学界研究的热点.自1980年以来, ****们对界面剪切滑移性能进行了大量研究, 在试验中发现注浆锚杆的剪切滑移性能与钢筋从混凝土中拔出、FRP从混凝土中拔出以及混凝土桩从地面中拔出桩的情况类似[2-3], 且研究表明锚杆与锚固体界面的破坏先于锚固体与岩石界面[4-6].****们基于试验提出了许多剪切滑移模型, 主要有三阶段线性模型、BPE模型、粘结滑移简化模型、CMR模型和连续曲线模型[7].基于剪切滑移模型,提出了多种计算方法, 用于预测锚杆的临界锚固长度[8].但是, 现有锚杆模型主要基于室内试验, 试验环境、灌浆材料及锚固长度与实际工程不同, 从这些模型获得的计算结果与实际结果有很大的出入.
本文根据前人现场试验结果, 给出注浆锚杆拔出方程, 并假设锚杆弹性段沿锚固深度方向的剪应力分布为四分之一椭圆弧, 进而给出注浆锚杆临界锚固长度的计算公式.然后, 通过现场拉拔试验, 验证计算结果的正确性.最后, 通过与前人研究结果对比后发现, 本文公式预测的结果与前人研究结果接近, 且本文方法预测的结果相对保守.
1 理论分析1.1 基本假定1) 锚杆的破坏形式为钢筋断裂, 即锚杆的长度足够长;
2) 忽略锚固体和围岩间的相对滑移;
3) 锚杆变形满足胡克定律.
1.2 界面受力分析沿锚杆长度方向截取长度为dz的锚杆微元, 并假设其距离原点的坐标为z.锚杆微元, 见图 1.
图 1(Fig. 1)
 | 图 1 锚杆微元Fig.1 Micro-element of rockbolt |
由静态平衡条件可得
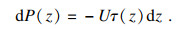 | (1) |
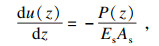 | (2) |
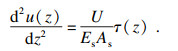 | (3) |
在锚杆拉拔过程中, 锚杆和锚固体之间存在剪切滑移s(z).根据载荷传递规则[9-10], 相对滑移等于锚杆的轴向位移u(z), 则有
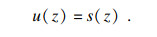 | (4) |
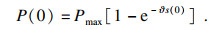 | (5) |
根据式(5), 当锚固长度足够长时, P(0)趋近于Pmax.此时, 锚杆尚未被拔出, 其破坏形式为钢筋断裂.因此, 公式(5)适用于半无限长锚杆.式(5)可以改写为[9]
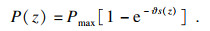 | (6) |
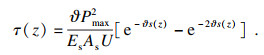 | (7) |
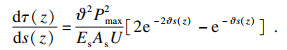 | (8) |
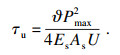 | (9) |
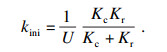 | (10) |
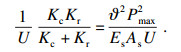 | (11) |
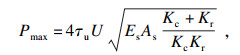 | (12) |
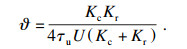 | (13) |
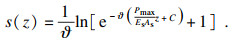 | (14) |
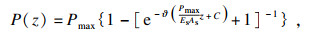 | (15) |
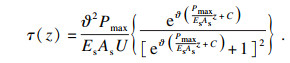 | (16) |
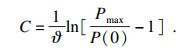 | (17) |
图 2(Fig. 2)
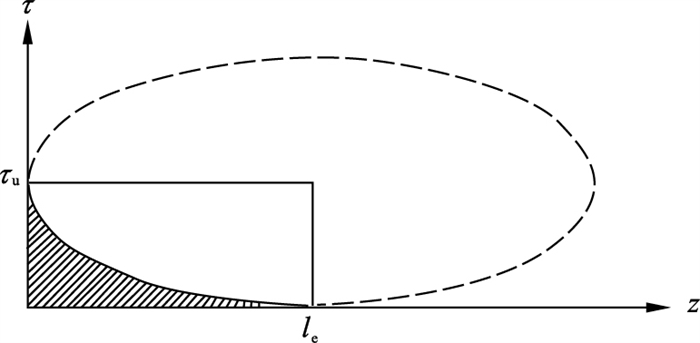 | 图 2 剪应力的近似分布Fig.2 Approximate distribution of shear stress |
为了确定锚杆的临界锚固长度, 可以先分别确定弹性段和塑性软化段的长度, 然后将它们相加.根据前述假设和平衡关系, 可得
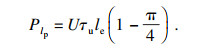 | (18) |
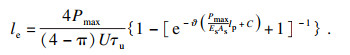 | (19) |
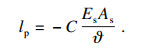 | (20) |
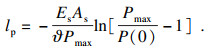 | (21) |
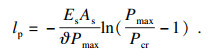 | (22) |
将式(19)和式(22)相加, 求得临界锚固长度:
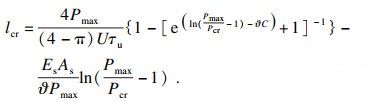 | (23) |
2.2 计算结果由式(12)计算得, 锚杆的最大拉拔力为2 447.3 kN, 计算得到的剪应力-滑移曲线见图 3.求得的剪应力-滑移曲线的趋势与文献[14-16]所给曲线相似, 这说明本文给出的计算公式合理.P(0)为400, 800, 1 200, 1 600, 2 000, 2 200, 2 400 kN时, 分别计算锚杆轴力分布和切应力分布.轴力分布见图 4,剪切应力分布见图 5.
图 3(Fig. 3)
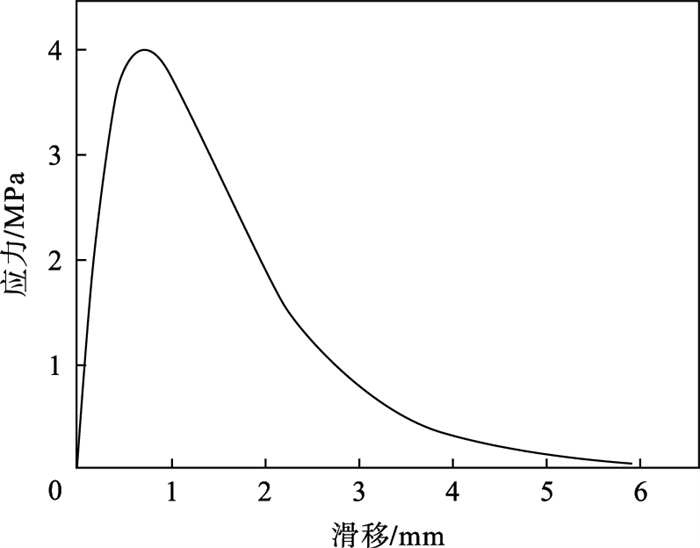 | 图 3 剪应力-滑移曲线Fig.3 Shear stress-slip curve |
图 4(Fig. 4)
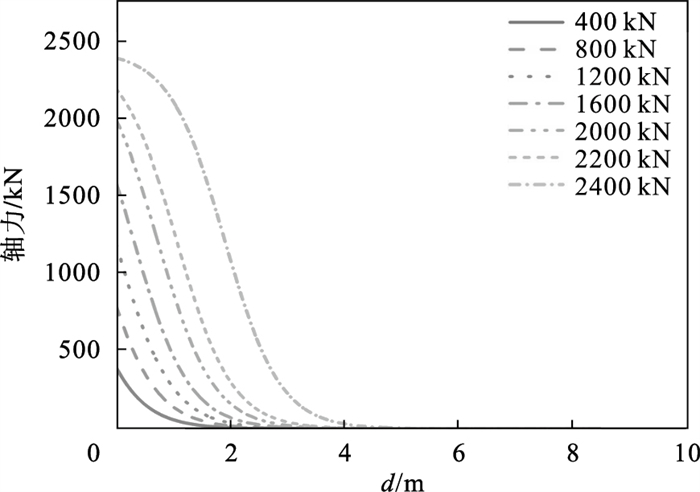 | 图 4 轴力分布Fig.4 Axial force distribution |
图 5(Fig. 5)
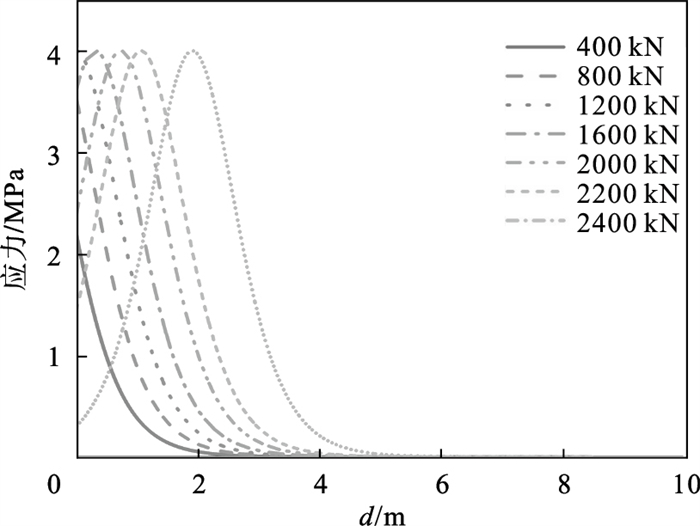 | 图 5 剪应力分布Fig.5 Shear stress distribution |
锚杆轴力分布曲线之间相互平行, 且轴力沿锚固深度呈指数减小.随着载荷的增加, 轴力的影响深度逐渐增大.当荷载超过2 000 kN后, 随着荷载的进一步增大, 锚杆顶部附近轴力的增长率明显降低.从图 5可以看出, 当荷载不超过1 200 kN时, 剪应力分布曲线沿锚固深度呈指数减小, 锚杆顶部的剪应力值最大, 锚固界面处于弹性状态.当荷载达到1 200 kN时, 锚杆顶部的剪应力达到锚固界面的剪切强度τu=4 MPa.随着载荷的进一步增加, 剪应力的峰值锚杆顶部向锚固深度方向移动, 且锚杆顶部的剪应力逐渐减小.假设锚杆的使用极限为2 000 kN(Pcr=2 000 kN), 则根据式(22)可求得临界锚固长度为5.3 m(lcr=5.3 m).
3 试验与验证3.1 原位试验1) 场地条件.为了验证理论的正确性, 对锚固长度为6.0 m和8.5 m的灌浆锚杆进行了拉拔试验.试验地点选在成分主要为花岗岩的基岩区, 且基岩裸露在地表或仅有风积土覆盖.围岩属性见表 1.现场岩石见图 6.
表 1(Table 1)
| 表 1 围岩属性 Table 1 The properties of surrounding rock |
图 6(Fig. 6)
 | 图 6 现场花岗岩Fig.6 The granite at the test site |
2) 试验材料.试验所用锚杆由4根直径为25 mm的PSB1080级螺纹钢筋组成, 具体见图 7.由于钢筋长度有限, 故采用连接器连接钢筋, 且连接器纵向间距大于1.0 m.锚杆组装完成后, 沿着锚杆长度方向粘贴应变片, 并做好防水处理.试验采用抗压强度为80 MPa的水泥灌浆料进行灌注, 灌浆速度控制在2 m/min以内.钢筋和水泥浆属性见表 2,锚杆参数见表 3.
图 7(Fig. 7)
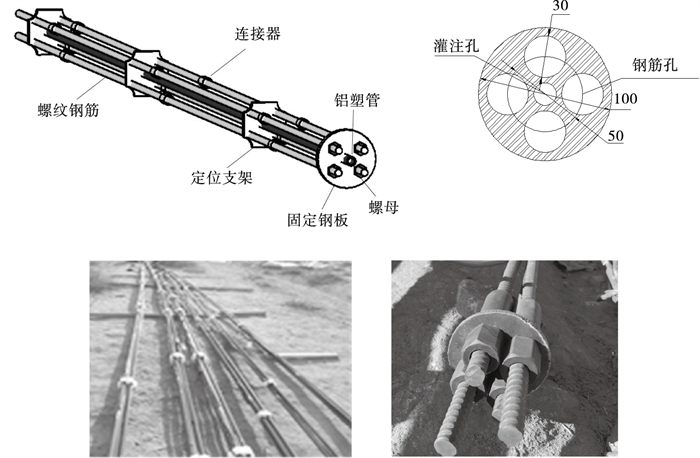 | 图 7 锚杆Fig.7 Rockbolt |
表 2(Table 2)
| 表 2 钢筋及灌浆料属性 Table 2 The properties of reinforcement and grout |
表 3(Table 3)
| 表 3 锚杆参数 Table 3 The parameters of rockbolts | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3) 安装及加载.根据要求, 在岩层中钻孔并清除孔中的残留物.然后通过吊车, 安装锚杆, 接着采用直径为16 mm的铝塑管进行灌浆, 最后采用液压千斤顶对锚杆进行分级加载, 每级加载200 kN, 待该级荷载数值稳定后, 再施加下一级荷载, 直至锚杆被拉坏.锚杆吊装及加载见图 8.
图 8(Fig. 8)
 | 图 8 锚杆吊装及加载Fig.8 The installation and loading of the rockbolt |
3.2 试验结果及理论验证1) 试验结果对比.试验结果表明, 锚杆以钢筋屈服断裂的形式破坏, 且没有出现钢筋被拔出的现象, 这说明试验符合半无限锚固长度的假设.锚杆破坏形式见图 9.由于试验中无法直接测得轴力, 而只能获得轴向应变, 且钢筋屈服前, 轴力与轴向应变成正比.因此, 这里研究荷载为2 000 kN时, 轴向应变的分布.荷载为2 000 kN时的轴向应变分布曲线见图 10.由图 10可知, 计算得到的轴向应变分布曲线与试验结果一致, 轴向应变随着锚固深度的增加呈非线性减小, 且最大应变出现在加载端.对于锚固长度为6 m的锚杆, 加载端附近轴向应变的计算值略大于试验值.根据图 10, 对计算应变和实测应变求Pearson相关系数, 分别求得试件1#1、试件1#2、试件2#1和试件2#2的相关系数为0.998, 0.988, 0.987和0.993.由计算结果可知, 相关系数均大于0.98, 这说明计算应变和实测应变显著性相关.试件1#1不同锚固深度下(a-3, a-5, a-7, a-9)的载荷与轴向应变曲线见图 11.随着荷载的增大, 不同锚固深度位置的轴向应变都会呈非线性增加.在相同载荷下, 轴向应变的试验结果要略小于计算结果.锚固深度超过5.5 m的应变基本可以忽略.由式(23)计算得到的临界锚固长度为5.3 m, 与试验测得的结果吻合, 二者相差3.6%.这说明, 采用式(23)计算得到的临界锚固长度满足工程要求.
图 9(Fig. 9)
 | 图 9 锚杆破坏模式Fig.9 The failure mode of the rockbolt |
图 10(Fig. 10)
 | 图 10 2 000 kN时的轴向应变分布曲线Fig.10 Axial strain distribution curve at 2 000 kN (a)—1#1; (b)—2#1; (c)—1#2; (d)—2#2. |
图 11(Fig. 11)
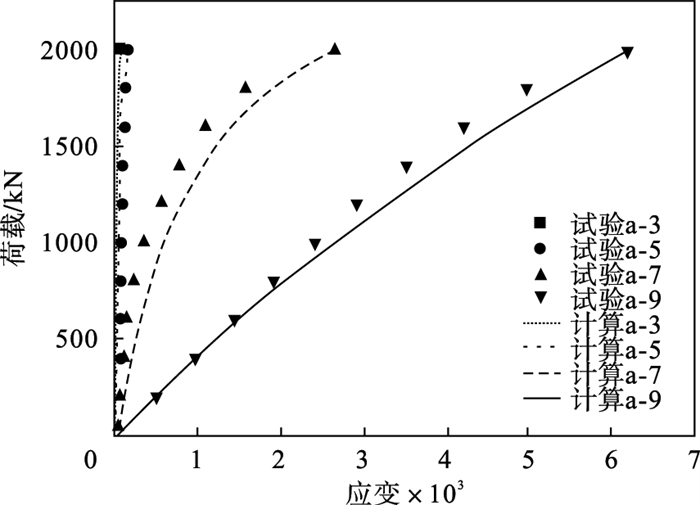 | 图 11 1#1荷载与轴向应变曲线Fig.11 Load and axial strain curves of 1#1 |
2) 研究对比.文献[3]和文献[17]分别进行了锚杆拉拔试验, 且分别给出了各自锚杆的计算模型.现采用文献[3]和文献[17]中的结果, 验证本文所给公式.结果对比见图 12.由对比可知, 本文所给出的预测结果与文献[3]和文献[17]中的试验结果吻合良好, 与文献[3]和文献[17]中的预测结果接近, 这说明本文所给出的计算方法具有一般性. 由图 12还可知, 当荷载为250kN时, 本文的预测方法较文献[3]中的预测方法更接近试验结果.本文求得远离加载点处的轴力要大于文献[17]的计算结果, 这说明本文的预测结果较文献[17]保守.
图 12(Fig. 12)
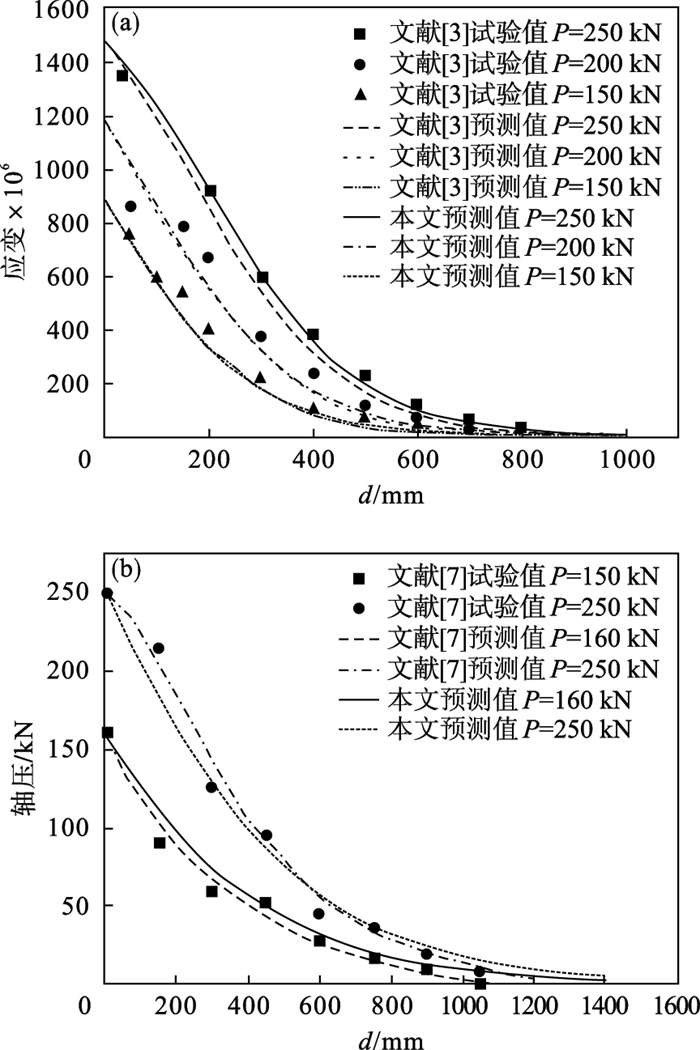 | 图 12 结果对比Fig.12 Comparison of results (a)—文献[3];(b)—文献[17]. |
4 结论1) 计算得到的轴向应变分布曲线与试验结果一致, 计算结果与试验结果的相关系数均大于98%.轴向应变随着锚固深度的增加呈非线性减小, 且最大应变出现在加载端.
2) 当锚杆顶部剪应力不超过锚固界面的剪切强度时, 剪应力沿锚固深度呈指数减小, 锚固界面处于弹性状态; 当锚杆顶部剪应力超过锚固界面的剪切强度后, 随着载荷的增加, 剪应力的峰值逐渐向锚固深度移动, 且锚杆顶部的剪应力逐渐减小.
3) 计算得到的临界锚固长度为5.3 m, 试验测得的临界锚固长度为5.5 m, 二者相差3.6%.
4) 本文所给出的计算方法具有一般性, 采用本文方法得到的结果与文献[3]和文献[17]中的试验结果吻合良好, 与文献[3]和文献[17]中的预测结果接近, 且相对保守.
参考文献
| [1] | Xu S, Hou P Y, Cai M. An experiment study on a novel self-swelling anchorage bolt[J]. Rock Mechanics and Rock Engineering, 2019, 52(11): 4855-4862. DOI:10.1007/s00603-019-01854-0 |
| [2] | Wu Q H, Chen L, Shen B T, et al. Experimental investigation on rockbolt performance under the tension load[J]. Rock Mechanics and Rock Engineering, 2019, 52(1): 4605-4618. DOI:10.1007/s00603-019-01845-1 |
| [3] | Zou J F, Zhang P H. Analytical model of fully grouted bolts in pull-out tests and in situ rock masses[J]. International Journal of Rock Mechanics and Mining Sciences, 2019, 113: 278-294. |
| [4] | Blanco M L, Michel T, Faouzi H H, et al. Assessment of the bolt-grout interface behavior of fully grouted rock bolts from laboratory experiments under axial loads[J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 63: 50-61. |
| [5] | Li C C, Gisle S, Arne M. A review on the performance of conventional and energy-absorbing rockbolts[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2014, 6: 315-327. |
| [6] | Feng B, Wang X, Wu Z S. Evaluation and prediction of carbon fiber-reinforced polymer cable anchorage for large capacity[J]. Advances in Structural Engineering, 2019, 22(8): 1952-1964. |
| [7] | 高丹盈, 朱海堂, 谢晶晶. 纤维增强塑料筋混凝土黏结滑移本构模型[J]. 工业建筑, 2003, 33(7): 41-43. (Gao Dan-ying, Zhu Hai-tang, Xie Jing-jing. The constitutive models for bond slip relation between FRP rebars and concrete[J]. Industrial Construction, 2003, 33(7): 41-43.) |
| [8] | 龙照, 赵明华, 张恩祥, 等. 锚杆临界锚固长度简化计算方法[J]. 岩土力学, 2010, 31(9): 2991-2994, 3011. (Long Zhao, Zhao Ming-hua, Zhang En-xiang, et al. A simplified method for calculating critical anchorage length of bolt[J]. Rock and Soil Mechanics, 2010, 31(9): 2991-2994, 3011.) |
| [9] | Seed H B, Reese L C. The action of soft clay along friction piles[J]. Transactions of the American Society of Civil Engineers, 1957, 122(1): 731-754. |
| [10] | 张乾青, 张忠苗. 抗拔单桩受力性状的解析算法[J]. 岩土工程学报, 2011, 33(sup2): 308. (Zhang Qian-qing, Zhang Zhong-miao. Analytical prediction approach for response of single pile under tension[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(sup2): 308.) |
| [11] | Van der Veen C. The bearing capacity of a pile[C]// Proceedings of the Third International Conference of Soil Mechanical and Foundation Engineering. [s. l. ], 1953: 84-90. |
| [12] | 黄明华, 周智, 欧进萍. 拉力型锚杆锚固段拉拔受力的非线性全历程析[J]. 岩石力学与工程学报, 2014, 33(11): 2190-2199. (Huang Ming-hua, Zhou Zhi, Ou Jin-ping. Nonlinear full-range analysis of load transfer in fixed segment of tensile anchors[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(11): 2190-2199.) |
| [13] | 朱训国. 地下工程中注浆岩石锚杆锚固机制研究[D]. 大连: 大连理工大学, 2006. (Zhu Xun-guo. Study on anchoring mechanism of grouted rock bolt in underground engineering[D]. Dalian: Dalian University of Technology, 2006. ) |
| [14] | Ma S Q, Nemcik J, Aziz N. An analytical model of fully grouted rock bolts subjected to tensile load[J]. Construction and Building Materials, 2013, 49: 519-526. |
| [15] | Zhang W L, Huang L, Juang C H. An analytical model for estimating the force and displacement of fully grouted rock bolts[J]. Computers and Geotechnics, 2020, 117: 103222. |
| [16] | Ma S Q, Zhao Z Y, Nie W, et al. An analytical model for fully grouted rockbolts with consideration of the pre-and post-yielding behavior[J]. Rock Mechanics and Rock Engineering, 2017, 50(11): 3019-3028. |
| [17] | 刘波, 李东阳, 段艳芳, 等. 锚杆-砂浆界面黏结滑移关系的试验研究与破坏过程解析[J]. 岩石力学与工程学报, 2011(sup1): 2790-2797. (Liu Bo, Li Dong-yang, Duan Yan-fang, et al. Experimental study of bond-slip relationship between bolt and mortar and theoretical solution to failure process[J]. Chinese Journal of Rock Mechanics and Engineering, 2011(sup1): 2790-2797.) |
