 , 欧阳治华2
, 欧阳治华2 1. 东北大学 资源与土木工程学院, 辽宁 沈阳 110819;
2. 武汉科技大学 资源与环境工程学院, 湖北 武汉 430081
收稿日期:2020-10-28
基金项目:国家重点研发计划项目(2016YFC0801601);国家自然科学基金重点资助项目(51534003)。
作者简介:张?晶(1990—),男,湖北荆州人,东北大学博士研究生;任凤玉(1956-),男,内蒙古赤峰人,东北大学教授,博士生导师。
摘要:Mohr-Wedge(MW)岩石强度准则是基于岩石楔形破坏力学模型及主应力间的偏微分方程等的理论性公式推导.利用量纲分析整理该准则所含的多个参数, 并赋予参数相应的物理意义, 可使该准则简单易懂.为分析包含岩石临界状态的MW准则适用性, 选取Mohr-Coulomb准则、Hoek-Brown准则和指数准则为比较对象, 以平均绝对误差MAE为评价指标, 量化比较4个准则预测岩石强度的准确度.结果表明: 当围压小于岩石临界状态围压σcr-M时, MW准则具有一定的适用性; 当围压大于σcr-M时, 4个准则预测的岩石强度因岩石临界状态围压不同而发生偏差.基于此, 提出了不同岩石临界状态围压预测岩石强度的方法, 可为岩石临界状态围压的取值提供一定的借鉴意义.
关键词:岩石临界状态Mohr-Wedge准则量纲分析岩石强度准则围压
Research on Applicability of the Mohr-Wedge Criterion Including Rock Critical State
ZHANG Jing1, REN Feng-yu1, HE Rong-xing1
 , OUYANG Zhi-hua2
, OUYANG Zhi-hua2 1. School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China;
2. College of Resources and Environmental Engineering, Wuhan University of Science and Technology, Wuhan 430081, China
Corresponding author: HE Rong-xing, E-mail: herongxing@mail.neu.edu.cn.
Abstract: The Mohr-Wedge (MW) strength criterion is a theoretical formula, which is derived based on the rock wedge failure mechanics model and the partial differential equation related to the principal stresses. The MW criterion can be easily understood by using the dimensional analysis to arrange the multiple parameters with corresponding physical meanings. To analyze the applicability of the MW criterion including the rock critical state, the Mohr-Coulomb criterion, the Hoek-Brown criterion and the exponential criterion were selected as the comparison objects, and the average absolute error MAE was used as the evaluation index in order to quantitatively compare the accuracy of the four criteria in predicting rock strength. The results show that when the confining pressure is less than the rock critical state confining pressure σcr-M, the MW criterion has certain applicability. When the confining pressure is greater than σcr-M, the rock strength predicted by the four criteria is different due to the different rock critical state confining pressure. Therefore, a method to predict rock strength under different rock critical state confining pressures was proposed, which can provide some reference for choosing the value of rock critical state confining pressure.
Key words: rock critical stateMohr-Wedge criteriondimensional analysisrock strength criterionconfining pressure
岩体因开挖扰动造成原岩应力场的二次分布, 在二次分布应力场的力系平衡前, 岩体可能发生变形和破坏[1-2].岩石强度准则是岩石力学中的基本理论之一, 表征岩石在极限应力状态下的应力状态和岩石强度参数之间的关系, 可作为复杂应力状态下天然岩体的破坏判据, 亦可定义各种应力场下岩石的强度和确定岩石破坏时塑性区的范围[3].因此, 岩石强度准则对实际岩石开挖工程具有非常重要的指导意义.
追溯岩石强度准则研究的起始可知, Mohr[4]借助大量试验提出岩石剪切破坏面上的剪应力τ和正应力σ存在某种函数关系τ=f(σ)(即摩尔包络线), 其不局限于Coulomb于1773年提出的τ和σ呈正比例关系.当摩尔包络线为曲线时, Balmer[5]借助几何关系得到用最大主应力σ1和最小主应力σ3来表示τ和σ的偏微分表达式.该偏微分表达式构建了非线性强度准则与摩尔包络线之间的桥梁, Ucar[6]和Kumar[7]先后求解出狭义Hoek-Brown准则[8]和广义Hoek-Brown准则[9]的剪切包络线表达式.Vutukuri等[10]引入岩石破坏角Φ与包线的坡角β之间的关系, 利用Balmer的结论推导出应力间的偏微分方程, 可作为岩石强度准则公式推导的基础[11-12].借助岩石破坏的微观剪切试验和Vutukuri等[10]推导的应力间的偏微分方程, Ouyang[13]提出了Mohr-Wedge(MW)岩石强度准则[14].
文献[15-21]基于试验观察或理论分析提出了很多实用的岩石强度准则, 但MW准则是基于微观试验的理论性公式推导, 其岩石楔形破坏力学模型符合岩石剪切破环力学特征, 具有一定的研究价值.该准则认为岩样在三轴荷载作用下, 当内部微裂隙被压密时, 岩样进入临界状态, 此时σ1和σ3的关系由非线性变化转变为线性变化, 这种变化与岩石在三轴荷载作用下的变形特征相符.为探讨该准则的适用范围和应用条件, 本文利用多种岩石三轴试验数据, 选取Mohr-Coulomb(MC)准则[4]、Hoek-Brown(HB)准则[9]和指数(EXP)准则[20]为比较对象, 试图通过对比分析研究MW准则的适用性.此外, 文献[22-25]认为岩石临界状态围压与单轴抗压强度σc存在一定的数量关系, 但MW准则提出的岩石临界状态围压σcr-M与σc无关, 其主要取决于岩石内部微裂隙的密度及闭合性, 故本文亦探讨了三轴条件下岩石临界状态围压的合理取值.
1 包含岩石临界状态的MW准则1.1 MW准则简介岩石在临界破坏状态时, 其内部特定区域会形成一条集中大量锯齿状裂隙[26-27]的潜在破坏带, 在此基础上, 基于对岩石微观剪切破坏机制的研究, Ouyang[13]提出了岩样的楔形破坏力学模型, 如图 1所示.
图 1(Fig. 1)
 | 图 1 岩样楔形破坏力学模型[13]Fig.1 The wedge failure mechanical model of rock sample |
在三轴荷载作用下, 潜在破坏带传递的力集中在楔块顶端, 破坏带内全部楔块端部集中力P1和P2之和与各自对应面积的比值可等效于岩石宏观破坏面上正应力σΦ和剪应力τΦ, 由此可以构建相应的力学条件求解岩石破坏角Φ与应力间的关系式.
Vutukuri等[10]借助曲线型摩尔包络线推导了应力间的偏微分方程:
 | (1) |
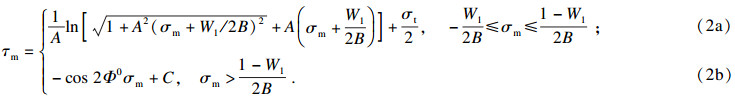 |
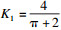

记MW准则提出的岩石临界状态围压为σcr-M, 如图 2所示, 岩样三轴受载条件下, 当σ3≤ σcr-M时, 受内部微裂隙的影响, 早期σ1和σ3会呈现非线性变化(式2a); 当σ3>σcr-M时, 岩样内部微裂隙被压密, 岩样表现为线性弹性材料, 此时σ1和σ3呈线性变化(式2b), 这表明MW准则符合三轴条件下岩石变形特征.
图 2(Fig. 2)
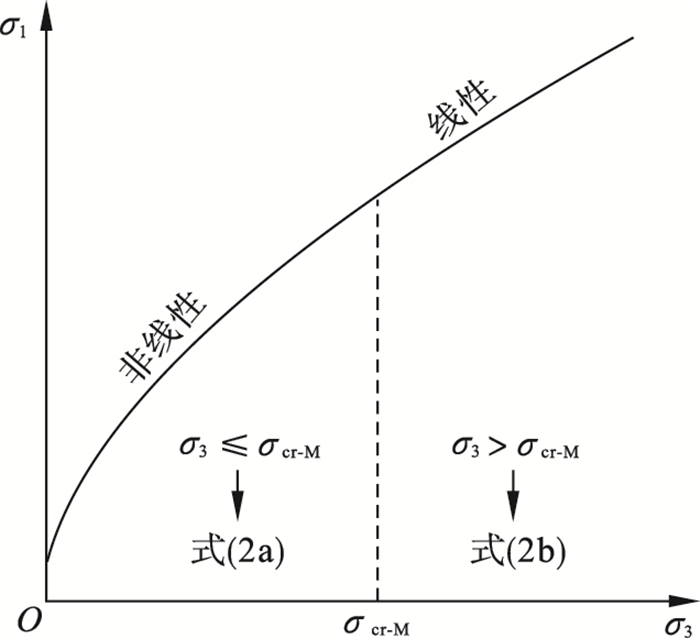 | 图 2 岩石加载过程中σ1和σ3的变化趋势Fig.2 Variation trend of σ1 and σ3 during rock loading |
HB准则自1980年提出以来[8], 被广泛应用于岩土工程领域, 该准则已成为岩土工程界影响最大的岩石强度准则之一, 完整岩石的HB准则可表示为[9]
 | (3) |
对式(3)两边求σ3的微分可知:
 | (4) |
1.2 MW准则参数物理意义由式(2)可知, MW准则包含的参数较多, 分析各个参数的量纲后得知, 该准则的参数可利用量纲分析进行整理.
1) 参数K1和K2: K1和K2为弹性力学计算得到的常量, 其量纲为1, 可引入参数K代替K1和K2:
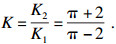 | (5) |
 |
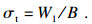 | (7) |
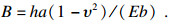 | (8) |
由式(8)所含参数的量纲可知, 参数B的量纲应为M-1LT2, 又A=-2K2B/K1, 可知参数A的量纲亦为M-1LT2, W和Φ的量纲均为1, 因此, 可引入量纲为ML-1T-2的参数σw来整理这4个参数:
 | (9) |
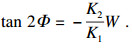 | (10) |
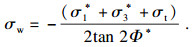 | (11) |
将式(5), 式(7)和式(9)代入式(2)可知:
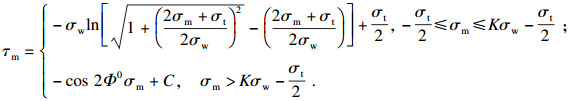 |
为探讨σw的物理意义, 将式(8)及A=-2K2B/K1代入式(9)可知:
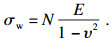 | (13) |

将

 | (14) |
由式(14)可知, σw与弹性模量、剪切模量和参数N有关, 故可定义σw为裂隙模量, 用以衡量岩石内部裂隙生成的难易程度.此外, 由式(12)的边界条件可知, 参数K为常量, σt的取值一般不大, 因此参数σw决定了岩石临界状态围压的大小, 即岩石进入临界状态的难易程度.
2 MW准则对岩石三轴强度的预测2.1 岩石三轴试验数据岩石三轴试验数据取自公开发表的文献, Dunham白云岩[28]、Westerly花岗岩[29]、Mizuho粗面岩[15]、Jinping砂岩[30]、Carrara大理岩[31]及Cedar闪长岩[29]的岩石三轴试验数据中围压σ3均小于σcr-M, 这几种岩石的三轴试验数据可参考文献[17].Yamaguchi大理岩[28]、Solenhofen石灰岩[28]及Indiana石灰岩[22]的岩石三轴试验数据中有部分围压σ3大于σcr-M.
2.2 岩石强度预测为研究MW准则预测岩石强度的准确度, 以MC准则、HB准则和EXP准则为比较对象, 对比分析4个准则预测的岩石强度.
以主应力表示的MC准则可表示为[4]
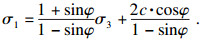 | (15) |
HB准则选用完整岩石的HB准则(见式(3)), EXP准则可表示为[20]
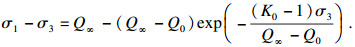 | (16) |
4种准则参数由最小二乘法拟合准则表达式与岩石三轴试验数据获取, 如表 1所示.图 3为4种准则预测岩石强度与试验强度之间的对比, 由图 3可以直观看出, 当围岩σ3小于σcr-M时, MW准则可较好地预测岩石强度; 当围岩σ3大于σcr-M时, MW准则可较好地预测Yamaguchi大理岩强度.为量化比较4种准则预测的岩石三轴强度与试验强度之间的差异, 引入平均绝对误差(MAE)作为评价指标:
 | (17) |
| 表 1 4种准则的参数值 Table 1 Parameter values for the four criteria | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
图 3(Fig. 3)
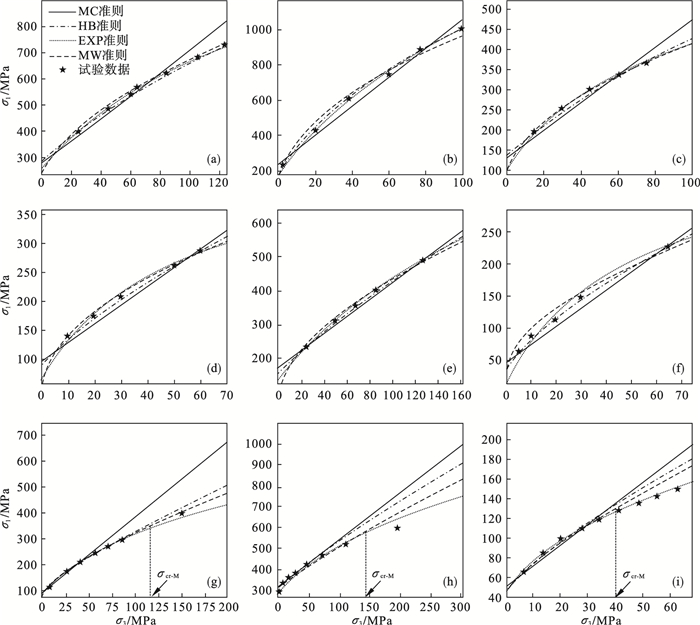 | 图 3 4种准则预测的岩石强度与试验强度之间的对比Fig.3 Comparison between rock strength predicted by 4 criteria and test strength (a)—Dunham白云岩; (b)—Westerly花岗岩; (c)—Mizuho粗面岩; (d)—Jinping绿片岩; (e)—Carrara大理岩; (f)—Cedar闪长岩; (g)—Yamaguchi大理岩; (h)—Solenhofen石灰岩; (i)—Indiana石灰岩. |
式中: N为某种岩石三轴试验数据的组数, i=1, 2, 3, …, N1; σ1icalc为I-HB准则在围压为σ3i时计算的岩石三轴强度; σ1itest为围压为σ3i时岩石的试验强度.
当围岩σ3小于σcr-M时, 4种准则预测岩石强度的平均绝对误差如表 2所示, 平均绝对误差越小, 说明准则预测岩石强度的准确度越高.由表 2可知, MW准则在围岩σ3小于σcr-M时可较好地预测岩石强度.当围岩σ3大于σcr-M时, 相较MC准则和HB准则, MW准则预测的岩石强度更接近于试验强度.对于Indiana石灰岩而言, 当围岩σ3大于σcr-M时, EXP准则可较好地预测该岩石强度, 但不能较好地预测Yamguchi大理岩和Solenhofen石灰岩的强度.这说明岩石进入临界状态后, 岩石强度及变形特征发生改变, 此时σ1和σ3的关系式亦随之变化.此外, 不同岩石对应的岩石临界状态不同, σcr-M不一定是Yamaguchi大理岩、Solenhofen石灰岩和Indiana石灰岩最适用的岩石临界状态围压, 故接下来需要研究σcr-M的适用性.
表 2(Table 2)
| 表 2 4种准则预测岩石强度的平均绝对误差(σ3<σcr-M) Table 2 Average absolute errors of 4 criteria for predicting rock strength (σ3 < σcr-M) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 岩石临界状态围压3.1 不同岩石的临界状态围压岩石临界状态指曲线型摩尔包络线[2]经过剪应力轴时斜率较大, 随后斜率增长率随围压增加呈负增长, 在某一高围压条件下, 摩尔包络线表征为水平线时的一种岩石破坏状态[32].针对三轴试验条件下临界状态围压的研究, 多数****认为其与单轴抗压强度σc存在数量关系.Hoek[22]认为当围压超过σc时岩石进入脆性向延性转化阶段, Singh等[16]通过对比分析201组完整岩石的三轴试验数据, 建议临界状态围压近似等于σc; 徐松林等[23]通过岩石三轴压缩全过程试验, 认为大理岩的临界围压约为(0.85~1.0)σc; 杨圣奇等[24]通过分析粗粒大理岩的常规三轴压缩下的强度和变形特征, 认为其临界围压宜取0.47σc; Barton[25]提出当临界状态围压超过3σc时, 岩石进入临界破坏状态, 此时岩石进入延性破坏阶段.由此可见, 岩石的临界状态围压虽与σc相关, 但数量关系却并不一致.
杨圣奇等[24]、徐松林等[23]、Singh等[16]和Barton[25]提出的岩石临界状态围压分别为σcr-Y, σcr-X, σcr-S和σcr-B:
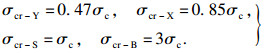 | (18) |
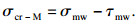 | (19) |
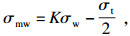 | (20) |
 | (21) |
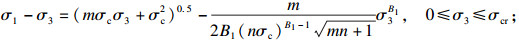 | (22) |
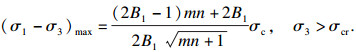 | (23) |
式(22)和式(23)成立的条件是岩石的临界状态围压σcr与岩石单轴抗压强度σc存在某种数量关系, 但MW准则包含的岩石临界状态围压与岩石单轴抗压强度并无关系.若假定σcr与σc无直接联系, 按文献[33] 的I-HB准则的推导方式, 令σcr=nσc进行反推, 可得到包含岩石临界状态围压的I-HB准则:
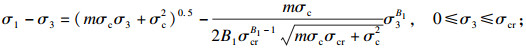 | (24) |
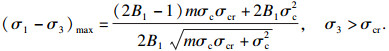 | (25) |
图 4(Fig. 4)
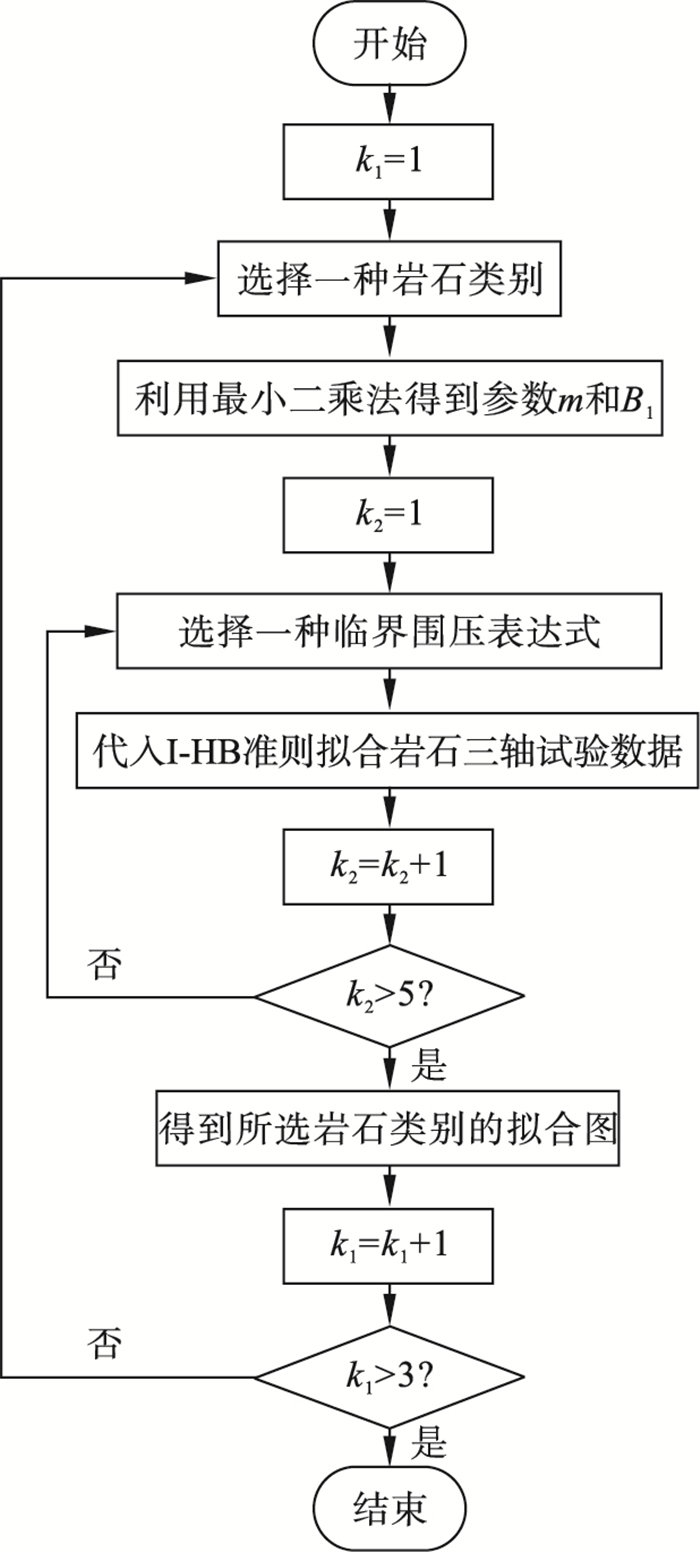 | 图 4 不同岩石临界状态围压下I-HB准则拟合岩石三轴试验数据流程图Fig.4 The flow chart of fitting rock triaxial test data under different rock critical state confining pressures based on I-HB criterion |
图 5(Fig. 5)
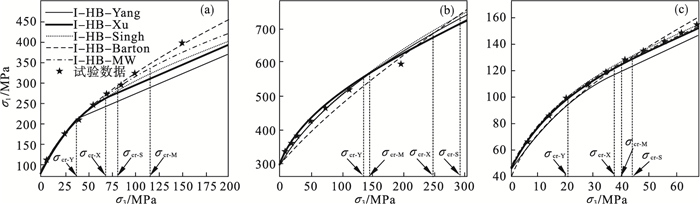 | 图 5 不同岩石临界状态围压下I-HB准则预测强度与试验强度之间的比较Fig.5 Comparison between strength predicted by I-HB criterion and experimental strength under different rock critical conditions (a)—Yamaguchi大理岩;(b)—Solenhofen石灰岩;(c)—Indiana石灰岩. |
在表 3中, I-HB准则参数m和B1通过最小二乘法拟合I-HB准则表达式与岩石三轴试验数据,单轴抗压强度σc直接取自试验数据, 则对应的σcr-Y, σcr-X, σcr-S, 和σcr-B均可得.关于MW准则对应的σcr-M, 需利用最小二乘法拟合MW准则表达式与岩石三轴试验数据得到参数σw, σt, C, 和Φ0, 再代入式(19)~式(21)即可求得σcr-M.
表 3(Table 3)
| 表 3 不同岩石临界状态围压下I-HB准则对应的参数 Table 3 Parameters corresponding to I-HB criterion under different rock critical state confining pressures | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
参考图 5a和图 5b中σcr-S和σcr-M的位置关系可知, Yamaguchi大理岩对应的σcr-M > σcr-S, Solenhofen石灰岩对应的σcr-M<σcr-S, 这表明MW准则提出的岩石临界状态围压σcr-M不同于其他4种岩石临界状态围压, 其与单轴抗压强度σc在数量关系上并无联系.
岩石临界状态围压取值不同时, I-HB准则预测岩石强度的准确度相差较大, 且没有一种岩石临界状态围压对应的I-HB准则可较好地预测这3种岩石的强度.这表明岩石的临界状态因岩石类别而异, 其对应的围压取值应根据相应的评价方式获取.为评价不同岩石临界状态下I-HB准则预测岩石三轴强度的准确度, 依旧采用平均绝对误差(MAE)作为评价指标, 得到的不同岩石临界状态围压下I-HB准则预测强度的平均绝对误差如表 4所示.
表 4(Table 4)
| 表 4 不同岩石临界状态围压下I-HB准则预测强度的平均绝对误差 Table 4 The average absolute error of prediction strength based on I-HB criterion under different rock critical conditions | |||||||||||||||||||||||||||||||||
由表 4可知, 适用的岩石临界状态围压按平均绝对误差MAE最小的原则进行选取(仅针对文中提到的5种临界围压表达式), 可见不同岩石类别, 其对应的岩石临界状态围压表达式不同.Yamaguchi大理岩的最适用岩石临界状态围压为σcr-B; Solenhofen石灰岩的最适用岩石临界状态围压为σcr-M; Indiana石灰岩的最适用岩石临界状态围压为σcr-S.比较表 4中的MAE值可知, I-HB-MW准则预测岩石强度的平均绝对误差均较小, 这表明基于微观剪切试验得到的岩石临界状态围压具有一定的合理性.
4 结论1) 包含岩石临界状态的MW准则是基于微观剪切试验的理论性公式推导, 其岩石楔形破坏力学模型符合岩石剪切破坏力学特征.该准则认为岩石进入临界状态后, σ1和σ3的关系由非线性转换为线性变化, 这与三轴条件下岩石的变形特征相符.
2) 包含较多参数的MW准则可利用量纲分析整理为2个参数σw和σt, 其中参数σw可定义为裂隙模量, 用以衡量岩石内部裂隙生成的难易程度, 同时, 该参数亦决定了岩石进入临界状态的难易程度.
3) 对比MC准则、HB准则和EXP准则可知, 当围岩σ3小于岩石临界状态围压σcr-M时, MW准则可较好地预测岩石强度, 表明MW准则具有一定的适用性, 且适用于岩石楔形破坏情形.当围岩σ3大于σcr-M时, 4个准则预测的岩石强度因岩石临界状态围压不同而发生偏差.
4) 岩石临界状态围压与单轴抗压强度之间不一定存在数量关系, 其取值因岩石类别而异.本文提出的不同岩石临界状态围压下I-HB准则预测岩石强度的方法, 可为岩石临界状态围压的取值提供一定的借鉴意义.
参考文献
| [1] | Shou Y, Zhou X, Qian Q. A critical condition of the zonal disintegration in deep rock masses: CrossMark strain energy density approach[J]. Theoretical and Applied Fracture Mechanics, 2018, 97: 322-332. DOI:10.1016/j.tafmec.2017.05.024 |
| [2] | Matthew D, Joseph P, Mary M, et al. Pseudo-static failure modes and yield accelerations in rock slopes[J]. International Journal of Rock Mechanics and Mining Sciences, 2018, 102: 1-14. DOI:10.1016/j.ijrmms.2017.11.001 |
| [3] | 蔡美峰, 何满潮, 刘东燕. 岩石力学与工程[M]. 北京: 科学出版社, 2010. (Cai Mei-feng, He Man-chao, Liu Dong-yan. Rock mechanics and engineering[M]. Beijing: Science Press, 2010.) |
| [4] | Mohr O. Welche umstande bedingen die elastizitatsgrenze und den bruch eines materials[J]. Zeitschrift des Vereins Deutscher Ingenieure, 1900, 44: 1524-1530. |
| [5] | Balmer G. A general analytical solution for Mohr envelope[J]. American Society for Testing and Materials, 1952, 52: 1260-1271. |
| [6] | Ucar R. Determination of shear failure envelope in rock masses[J]. International Journal of Rock Mechanics Engineering, 1986, 112(3): 303-315. |
| [7] | Kumar P. Shear failure envelope of Hoek-Brown criterion for rockmass[J]. Tunnelling and Underground Space Technology, 1998, 13(4): 453-458. DOI:10.1016/S0886-7798(98)00088-1 |
| [8] | Hoek E, Brown E T. Empirical strength criterion for rock masses[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1980, 106(GT9): 1013-1035. |
| [9] | Hoek E, Wood D, Shah S. A modified Hoek-Brown failure criterion for jointed rock masses[C]//Proceedings of the Rock Characterization. London: British Geotechnical Society, 1992: 209-214. |
| [10] | Vutukuri V S, Lama R D, Saluja S S. Handbook on mechanical properties of rocks[M]. Clausthal: Transform Technology Publications, 1974. |
| [11] | Sankhaneel W, Gabriel W. A progressive S-shaped yield criterion and its application to rock pillar behavior[J]. International Journal of Rock Mechanics and Mining Sciences, 2018, 105: 98-109. DOI:10.1016/j.ijrmms.2018.03.014 |
| [12] | Shen J Y, Jimenez R, Karakus M, et al. A simplified failure criterion for intact rocks based on rock type and uniaxial compressive strength[J]. Rock Mechanics and Rock Engineering, 2014, 47: 357-369. DOI:10.1007/s00603-013-0408-5 |
| [13] | Ouyang Z, Elsworth D. A phenomenological failure criterion for brittle rock[J]. Rock Mechanics and Rock Engineering, 1991, 24: 133-153. DOI:10.1007/BF01042858 |
| [14] | 张晶, 欧阳治华, 郭宏强, 等. Mohr-Wedge岩石破坏准则适用性研究[J]. 矿业研究与开发, 2016, 36(11): 19-25. (Zhang Jing, Ouyang Zhi-hua, Guo Hong-qiang, et al. Research on the applicability of Mohr-Wedge rock failure criterion[J]. Mining Research and Development, 2016, 36(11): 19-25.) |
| [15] | Mogi K. Fracture and flow of rocks under high triaxial compression[J]. Journal of Geophysical Research Atmospheres, 1971, 76(5): 1255-1269. DOI:10.1029/JB076i005p01255 |
| [16] | Signh M, Raj A, Singh B. Modified Mohr-Coulomb criterion for non-linear triaxial and polyaxial strength on intact rocks[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 48(4): 546-555. |
| [17] | Al-Ajmi A M, Zimmerman R W. Relation between the Mogi and the Coulomb failure criteria[J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42: 431-439. DOI:10.1016/j.ijrmms.2004.11.004 |
| [18] | 俞茂宏. 线性和非线性的统一强度理论[J]. 岩石力学与工程学报, 2007, 26(4): 662-669. (Yu Mao-hong. Linear and nonlinear unified strength theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(4): 662-669. DOI:10.3321/j.issn:1000-6915.2007.04.002) |
| [19] | 周小平, 钱七虎, 杨海清. 深部岩体强度准则[J]. 岩石力学与工程学报, 2008, 27(1): 117-123. (Zhou Xiao-ping, Qian Qi-hu, Yang Hai-qing. Strength criteria of deep rock mass[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(1): 117-123. DOI:10.3321/j.issn:1000-6915.2008.01.018) |
| [20] | You M Q. Mechanical characteristics of the exponential strength criterion under conventional triaxial stresses[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(2): 195-204. DOI:10.1016/j.ijrmms.2009.12.006 |
| [21] | Yamaji A, Sato K. Stress inversion meets plasticity theory: a review of the theories of fault-slip analysis from the perspective of the deviatoric stress-strain space[J]. Journal of Structural Geology, 2019, 125: 296-310. DOI:10.1016/j.jsg.2019.03.003 |
| [22] | Hoek E. Strength of jointed rock masses[J]. Geotechnique, 1983, 23(3): 187-223. |
| [23] | 徐松林, 吴文, 王广印, 等. 大理岩等围压三轴压缩全过程研究Ⅰ: 三轴压缩全过程的峰前、峰后卸围压全过程实验[J]. 岩石力学与工程学报, 2001, 20(6): 763-767. (Xu Song-lin, Wu Wen, Wang Guang-yin, et al. Study on complete procedures of marble under triaxial compression Ⅰ: testing study on complete procedure of triaxial compression and the processes of unloading confining at the pre-peak and post-peak[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(6): 763-767. DOI:10.3321/j.issn:1000-6915.2001.06.002) |
| [24] | 杨圣奇, 苏承东, 徐卫亚. 大理岩常规三轴压缩下强度和变形特性的试验研究[J]. 岩土力学, 2005, 26(3): 475-478. (Yang Sheng-qi, Su Cheng-dong, Xu Wei-ya. Experimental investigation on strength and deformation properties of marble under conventional triaxial compression[J]. Rock and Soil Mechanics, 2005, 26(3): 475-478. DOI:10.3969/j.issn.1000-7598.2005.03.028) |
| [25] | Barton N. Shear strength criteria for rock, rock joints, rockfill and rock masses: problems and some solutions[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2013, 5: 249-261. DOI:10.1016/j.jrmge.2013.05.008 |
| [26] | Peng S, Johnson A M. Crack growth and faulting in cylindrical specimens of chelmsford granite[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1972, 9(1): 37-86. DOI:10.1016/0148-9062(72)90050-2 |
| [27] | Walter J. Failure of granite under compression[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1977, 14(4): 209-215. DOI:10.1016/0148-9062(77)90950-0 |
| [28] | Mogi K. Experimental rock mechanics[M]. London: Taylor and Francis, 2007. |
| [29] | Swanson S R, Brown W S. An observation of loading path independence of fracture in rock[J]. International Journal of Rock Mechanics and Mining Sciences, 1971, 8: 277-281. DOI:10.1016/0148-9062(71)90023-4 |
| [30] | 汪斌, 朱杰兵, 邬爱清, 等. 高应力下岩石非线性强度特性的试验验证[J]. 岩石力学与工程学报, 2010, 29(3): 542-548. (Wang Bin, Zhu Jie-bing, Wu Ai-qing, et al. Experimental validation of nonlinear strength property of rock under high geostress[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(3): 542-548.) |
| [31] | Von K T. Festigkeitsversuche unter all seitigem Druck[J]. Zeit Vereins Deutscher Ingenieure, 1911, 55: 1749-1759. |
| [32] | Barton N. The shear strength of rock and rock joints[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1976, 13: 255-279. |
| [33] | 李斌, 王大国, 刘艳章, 等. 三轴条件下改进的Hoek-Brown准则的修正[J]. 煤炭学报, 2017, 42(5): 1173-1181. (Li Bin, Wang Da-guo, Liu Yan-zhang, et al. Improvement of modified Hoek-Brown criterion under conventional triaxial compression conditions[J]. Journal of China Coal Society, 2017, 42(5): 1173-1181.) |
