摘要:神经细胞的尺寸与太赫兹波的波长处于同一数量级, 因此, 神经细胞可等效为微型介质谐振器从而起到增强细胞内的太赫兹信号的作用. 基于此现象, 本文提出神经细胞弱谐振效应的新概念. 建立了三层结构的球形神经细胞胞体模型, 用太赫兹时域光谱仪系统测量了神经细胞生理液的相对介电常数, 并用双德拜模型对实验结果进行拟合; 利用时域有限差分法对太赫兹波在神经细胞中的传播特性进行研究. 结果表明, 当神经细胞的相对介电常数高于外部媒质时, 太赫兹波可以在神经细胞内部形成弱的谐振峰, 并且随着细胞与外部媒质的相对介电常数差值的减小, 谐振峰会向细胞膜侧偏移, 细胞对太赫兹波的聚焦特性会随着两侧相对介电常数差值的减小而逐渐增强, 这种现象称为弱谐振效应. 同时, 弱谐振效应也表现出与细胞尺寸和频率的相关性. 神经细胞的弱谐振效应在增强细胞内太赫兹信号强度的同时, 也会进一步增强太赫兹信号在神经纤维中的传输. 这些结果为解释太赫兹波与神经细胞的相互作用提供了新模型, 有助于研究太赫兹波在生物神经系统中的传递机制.
关键词: 太赫兹/
神经细胞/
传输/
弱谐振

English Abstract

全文HTML

--> --> -->

神经元是神经系统的基本结构和功能单元, 可以感受和传导兴奋. 神经元的结构特征主要包括细胞体和突起两部分, 较短的突起称为树突, 较长的突起成为轴突; 轴突与靶细胞相连, 实现动作电位在神经元之间的传导. 对于神经轴突而言, 其外围会形成由施万细胞包裹形成的髓鞘结构, 该结构不仅可以加快动作电位的传导, 同时由于髓鞘在太赫兹频段乃至光学频段具有较高的折射率, 对于特定频率的太赫兹波和光波可以看作介质波导^[1,2]. 另外, 太赫兹生物学和光遗传学的兴起, 也激发了众多****的思考, 生物体中是否存在高频信号传导通路, 可以实现太赫兹波作为载波的生物体内的信号传输?
在光学波段, 已有研究表明电磁波在透过生物细胞时, 可以发生聚焦现象. 2015年, Miccio等^[3]报道了无核的悬浮红细胞在光学频段表现出自适应液体透镜的特征, 并展示了其成像能力和可调谐焦距特性; 随后Johari等^[4,5]证明神经元的体细胞和细胞核同样具有这种聚焦效应, 理论和实验研究表明, 神经元能够聚焦光的传输, 使其能够通过组织传到目标细胞. 细胞的这种现象也被应用于体内光遗传纳米网络的研究^[6-8]. 在毫米波频段, 有研究表明, 具有这种球体以及椭球体结构的生物组织可以增强局部的电磁波传输, 尤其是当目标样品的尺寸与电磁波的波长在同一个数量级时, 这种相互作用会更加强烈. 有研究报道称, 当两颗葡萄之间存在窄带隙时, 葡萄的高相对介电常数可以在GHz频率下产生表面等离子体^[9]. 而在太赫兹波段, 神经细胞尺寸与太赫兹波波长都处于微米量级, 具备太赫兹波与细胞相互作用的条件, 但由于生物体内较高的含水量对太赫兹波的强吸收特性^[10], 使得该领域的研究鲜有报道.
基于现有的文献对神经细胞的特征描述, 我们发现了神经细胞在太赫兹波段弱谐振效应的新现象, 即尺寸在微米量级的神经元胞体, 对太赫兹频段(波长微米量级)的电磁波传输具有增强效应. 本文利用时域有限差分法(FDTD)建立了三层结构的神经细胞胞体模型, 对太赫兹波在神经细胞中的传输特性进行了分析, 同时考虑到神经细胞结构的特异性, 计算了细胞体-轴突中太赫兹波的传输特性, 以探索神经元中的太赫兹信号传输性能. 本研究为构建神经系统中的太赫兹波传输提供了一种可能的物理机理阐释, 为实验工作提供了一种理论预期.

2

-->

2.1.神经细胞胞体模型构建

神经元细胞是神经系统最基本的结构和功能单元, 根据功能的不同, 其形态也有所差异, 细胞体的形状大致分为椭球形、三角形和不规则形状. 鉴于单个神经细胞的相对介电常数难以精确测量, 本文建立了包含细胞膜、细胞内生理液以及细胞核的简化三层结构的球体细胞模型来模拟神经细胞胞体, 如图1所示.
图 1 细胞膜、细胞内生理液和细胞核三层媒质构建的神经细胞体模型
Figure1. Nerve cell body model constructed by three layers of membrane, intracellular fluid and nucleus.

一般细胞膜的结构特点为中间的磷脂双分子层构成基本骨架, 蛋白质分子嵌入在磷脂双分子层中或表面. 而神经细胞膜与一般细胞膜不同之处是膜表面分布着大量的离子通道和特异性受体, 能够感受和传导兴奋. 由于神经细胞膜组分的复杂性以及提取制备过程中难以保证其完整的结构功能, 本文采用细胞膜的主要组分磷脂的相对介电常数来表征神经细胞膜的相对介电常数. 磷脂在太赫兹频段的相对介电常数可以由文献[11]得到, 通过二阶德拜模型拟合后, 德拜参数如表1所列. 细胞内生理液的相对介电常数本文通过实验测量得到.

	$ {\varepsilon }_{\infty } $	$ {\varepsilon }_{\mathrm{s}} $	$ {\varepsilon }_{2} $	$ {\tau }_{1} $/ps	$ {\tau }_{2} $/ps
细胞膜	2.37	11.77	3.28	7.19	0.11

表1细胞膜二阶德拜模型参数拟合结果
Table1.Fitting results of membrane second-order Debye model parameters.

由于细胞核内的溶剂分子与细胞质中的相同, 在太赫兹波在神经元细胞中传输过程的模拟计算中, 采用细胞内生理液的相对介电常数来代表细胞核的相对介电常数. 另外, 由于线粒体等细胞器半径为1 μm左右, 远远小于广义太赫兹波的波长(3—100 μm), 太赫兹波经过微小细胞器时, 只表现为衍射和绕射行为, 因此计算中也忽略了其影响.
2 -->

2.2.细胞内生理液的相对介电常数的测量

细胞内生理液由非极性盐离子和营养物质组成, 在神经细胞中起着重要作用. 采用太赫兹时域光谱仪(THz-TDS)系统(Tera View TPS 3000)测量细胞内生理液体在生理浓度下的太赫兹光谱^[12], 实验环境为一个大气压, 温度为292 K. 通过实验配制得到等效的神经细胞生理液: KCl (1.043 g/100 mL), MgCl₂·6H₂O (0.041 g/100 mL), CaCl₂ (0.011 g/100 mL), Na₂ATP (0.11 g/100 mL), EGTA (0.38 g/100 mL), HEPES (0.238 g/100 mL)^[13]. 在测量过程中, 样品溶液被注入两个材料为聚四氟乙烯的太赫兹窗片之间, 窗片对太赫兹波的吸收可以忽略. 在0.3—2 THz的频率范围内, 细胞内生理液体的折射率以及吸收系数的测量结果如图2(a)和图2(b)所示.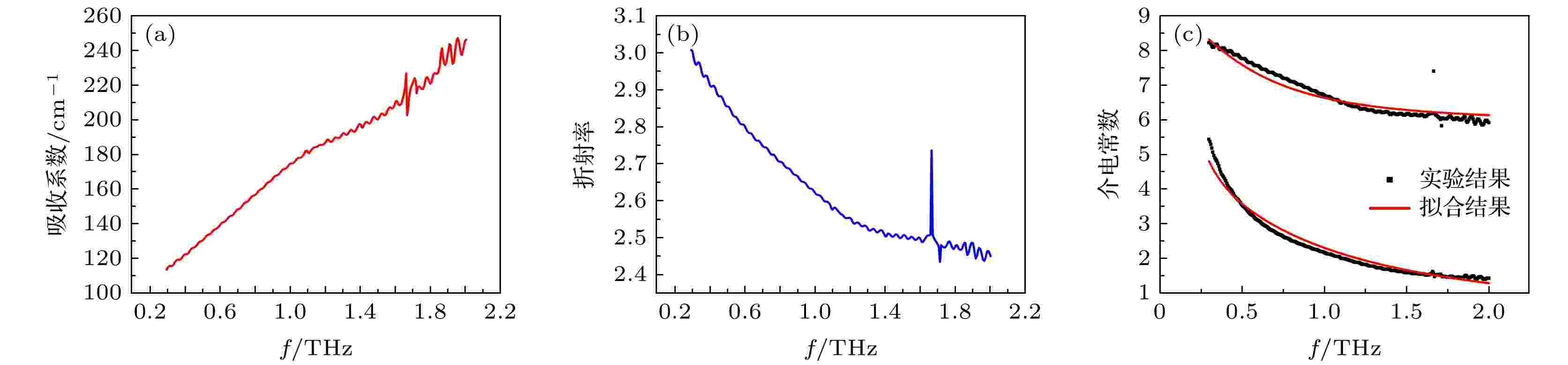
图 2 等效细胞内生理液体在0.3?2 THz频率范围内的(a) 吸收系数, (b)折射率, (c)相对介电常数实部和虚部(黑色圆点)以及二阶德拜模型拟合结果(红色实线)
Figure2. (a) Absorption coefficient, (b) refractive index, and (c) the real and imaginary parts of the dielectric constant of the effective intracellular fluid in the frequency range of 0.3?2 THz.

利用实验测量得到的折射率以及吸收系数, 采用(1)式与(2)式计算可以得到神经细胞内生理液在0.3—2 THz频率范围内的相对介电常数.

$ \hat \varepsilon \left( \omega \right) = \hat n{(\omega )^2} = {\left( {n\left( \omega \right) - {\rm{i}}\frac{c}{{2\omega }}\alpha \left( \omega \right)} \right)^2}, $

$ \varepsilon ' + \varepsilon '' = n{(\omega )^2} - \frac{{{c^2}\alpha {{(\omega )}^2}}}{{4{\omega ^2}}} - {\rm{i}}\frac{c}{\omega }n\left( \omega \right)\alpha \left( \omega \right), $

式中, $ \hat{n}$为复折射率, n为折射率, α为吸收系数, c为光速, ω为频率, $ \hat{\varepsilon } $为复相对介电常数, ${\varepsilon }' $为相对介电常数实部, ${\varepsilon }''$为相对介电常数虚部. 对于神经细胞内生理液在0.3—2 THz频率范围的相对介电常数, 可以采用二阶德拜模型^[14]对实验测得的相对介电常数进行拟合求得:

$ \hat \varepsilon \left( \omega \right) = {\varepsilon _\infty } + \frac{{{\varepsilon _{\text{s}}} - {\varepsilon _2}}}{{1 + {\text{i}}\omega {\tau _1}}} + \frac{{{\varepsilon _2} - {\varepsilon _\infty }}}{{1 + {\text{i}}\omega {\tau _2}}}{, } $

式中, $ {\varepsilon }_{\infty } $为高频极限相对介电常数, $ {\varepsilon }_{\mathrm{s}} $为静态相对介电常数, $ {\varepsilon }_{2} $为中间值, $ {\tau }_{1} $和$ {\tau }_{2} $为两次弛豫时间. 慢弛豫时间$ {\tau }_{1} $主要与氢键有关, 它反映了从$ {\varepsilon }_{\mathrm{s}} $到$ {\varepsilon }_{2} $的变化. 快速弛豫时间$ {\tau }_{2} $与单个分子的重定向有关, 它反映了从$ {\varepsilon }_{2} $到$ {\varepsilon }_{\infty } $的变化. 神经细胞内生理液拟合参数如表2所列.

	$ {\varepsilon }_{\infty } $	$ {\varepsilon }_{\mathrm{s}} $	$ {\varepsilon }_{2} $	$ {\tau }_{1} $/ps	$ {\tau }_{2} $/ps
细胞内生理液	5.685	77.34	8.990	12.6	0.243

表2等效神经细胞内生理液相对介电常数的二阶德拜模型参数拟合结果
Table2.Second-order Debye model parameter fitting results of dielectric constant of the effective intracellular fluid in nerve cells.

从图2(c)可以看出, 实验结果与0.3—2 THz的拟合结果符合较好. 等效神经细胞内生理液体的相对介电常数随频率的增加而减小, 在高频THz范围内接近光学相对介电常数$ {\varepsilon }_{\infty } $. 同时, 随着频率的增加, 相对介电常数的虚部与实部的比值会减小, 说明太赫兹波在神经细胞中传播时损耗更小. 然后采用二阶德拜模型模拟得到了等效神经细胞内生理液在0.3—50 THz范围内的介电响应特性, 如图3所示.
图 3 由二阶德拜模型模拟等效细胞内生理液在0.3?50 THz范围内的相对介电常数　(a)实部; (b)虚部
Figure3. Dielectric constant of intracellular fluid in the range of 0.3?50 THz simulated by second-order Debye model: (a) Real part; (b) imaginary part.

2 -->

2.3.太赫兹波在神经细胞中传输特性的计算方法

为了计算太赫兹波在神经细胞中的传输, 采用FDTD方法求解麦克斯韦方程组, 该方法是在Yee单元^[15]形成的离散时空网格上时域求解Maxwell方程的一种常用方法. 在直角坐标系中, Maxwell方程可以转化为6个偏微分方程.

$ \left\{ \begin{aligned} &\frac{{\partial {H_z}}}{{\partial y}} - \frac{{\partial {H_y}}}{{\partial z}} = \varepsilon \frac{{\partial {E_x}}}{{\partial t}} + \sigma {E_x}, \hfill \\ &\frac{{\partial {H_x}}}{{\partial z}} - \frac{{\partial {H_z}}}{{\partial x}} = \varepsilon \frac{{\partial {E_y}}}{{\partial t}} + \sigma {E_y}, \hfill \\ &\frac{{\partial {H_{{y}}}}}{{\partial x}} - \frac{{\partial {H_x}}}{{\partial y}} = \varepsilon \frac{{\partial {E_z}}}{{\partial t}} + \sigma {E_z}, \end{aligned} \right. $

$ \left\{ \begin{aligned} &\frac{{\partial {{E}_{{z}}}}}{{\partial {{y}}}} - \frac{{\partial {{E}_{{y}}}}}{{\partial {{z}}}} = - \mu \frac{{\partial {H_x}}}{{\partial t}} + {\sigma _{\rm{m}}}{H_x}, \hfill \\& \frac{{\partial {{E}_{{x}}}}}{{\partial z}} - \frac{{\partial {{E}_z}}}{{\partial x}} = - \mu \frac{{\partial {H_y}}}{{\partial t}} + {\sigma _{\rm{m}}}{H_y}, \hfill \\& \frac{{\partial {{E}_{{y}}}}}{{\partial {{x}}}} - \frac{{\partial {{E}_x}}}{{\partial y}} = - \mu \frac{{\partial {H_z}}}{{\partial t}} + {\sigma _{\rm{m}}}{H_z},\end{aligned} \right. $

式中, H, E, ε, μ, σ分别为磁场强度、电场强度、介质介电常数、介质磁导率、电导率.
利用FDTD方法计算太赫兹波在神经细胞中传播特性的模型包括信号源、背景介质、神经细胞模型和完美匹配层(PML) 4部分, 如图4(a)所示. 模型中采用的太赫兹信号源为正弦形式的太赫兹波, 其波形如图4(b)所示.
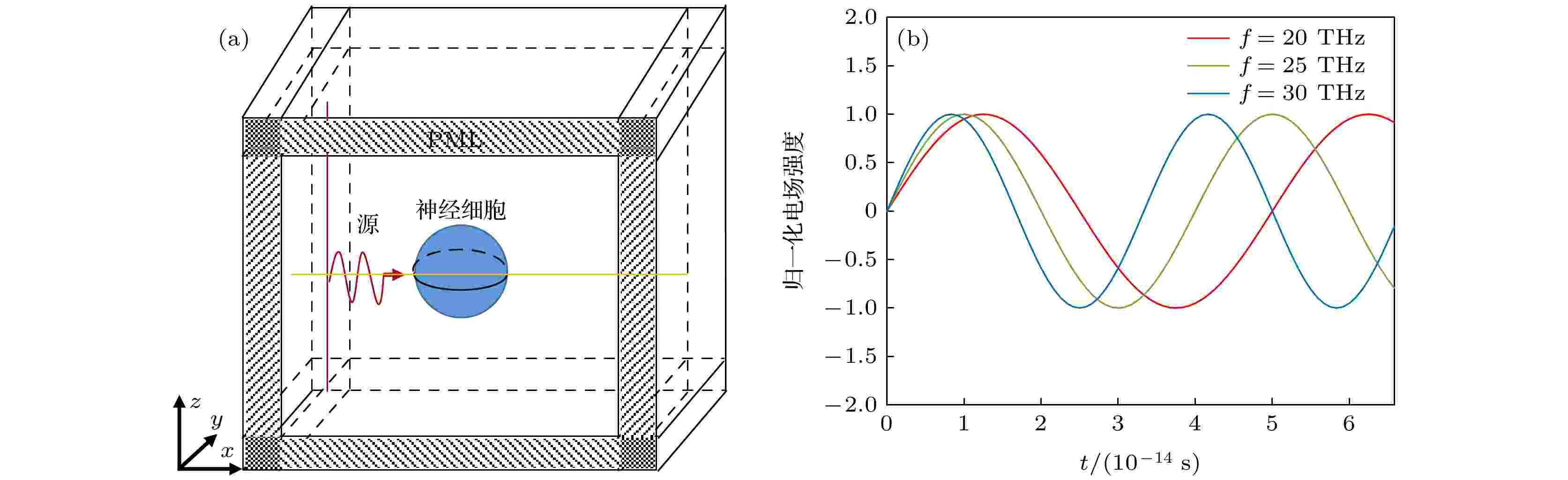图 4 (a)太赫兹波在神经细胞中传输的三维FDTD模型, 太赫兹波由线源产生, 以柱面波的形式向三维空间传输; (b)模拟过程中用到的3种频率(20, 25, 30 THz)的太赫兹辐射源波形
Figure4. (a) Three-dimensional FDTD model of THz wave transmission in the nerve cell. THz wave is generated by line sources and transmitted to three-dimensional space in the form of cylindrical wave. (b) THz source waveforms for the three frequencies (20, 25, 30 THz) used in the simulation.

神经细胞胞体由图1所示模型描述, 细胞膜厚度为9 nm, 细胞半径为8 μm, 细胞核半径为1 μm. 仿真中使用了单轴PML用于吸收入射到边界的太赫兹波以避免反射波的影响^[16]. 电场和磁场的本构关系可以表示为

$ {\boldsymbol{D}} = \varepsilon {\boldsymbol{E}}, $

$ {\boldsymbol{B}} = \mu {\boldsymbol{H}}. $

神经细胞可视为非磁性材料($ {\mu }_{\mathrm{r}}=1 $), 其介电常数可表示为$ \varepsilon ={\varepsilon }_{0}[{\varepsilon }_{\mathrm{r}}+\sigma /(\mathrm{i}\omega \left)\right] $. 由于神经细胞内生理液为极性液体, 因此可以不考虑欧姆损耗(σ = 0), $ {\varepsilon }_{\mathrm{r}} $用二阶德拜模型表示. 考虑到细胞膜厚度(9 nm)远小于太赫兹波长(30 THz时为10 μm), 采用元胞计算法^[17]将厚度为9 nm的细胞膜等效到单个网格上进行模拟, 这样可以在保证计算准确的同时节省大量的计算时长. 因此, (6)式和(7)式可以写成如下形式:

$ {\boldsymbol{D}} = \alpha {\varepsilon _{{\text{membrane}}}}\left( \omega \right){\boldsymbol{E}} + \left( {1 - \alpha } \right){\varepsilon _0}{\boldsymbol{E}}, $

$ {\boldsymbol{B}} = \alpha {\mu _{{\text{membrane}}}}\left( \omega \right){\boldsymbol{H}} + \left( {1 - \alpha } \right){\mu _0}{\boldsymbol{H}}, $

式中, α为单个网格中细胞膜的体积分数, $ {\varepsilon }_{\mathrm{m}\mathrm{e}\mathrm{m}\mathrm{b}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{e}} $为细胞膜的相对介电常数, 如(3)式所示, 其中参数如表1所列. 由于仿真所用的单元模型是球形的, 可以采用梯形网格处理方法来描述曲面边界; 同时考虑了元胞算法, 边界描述如图5所示.
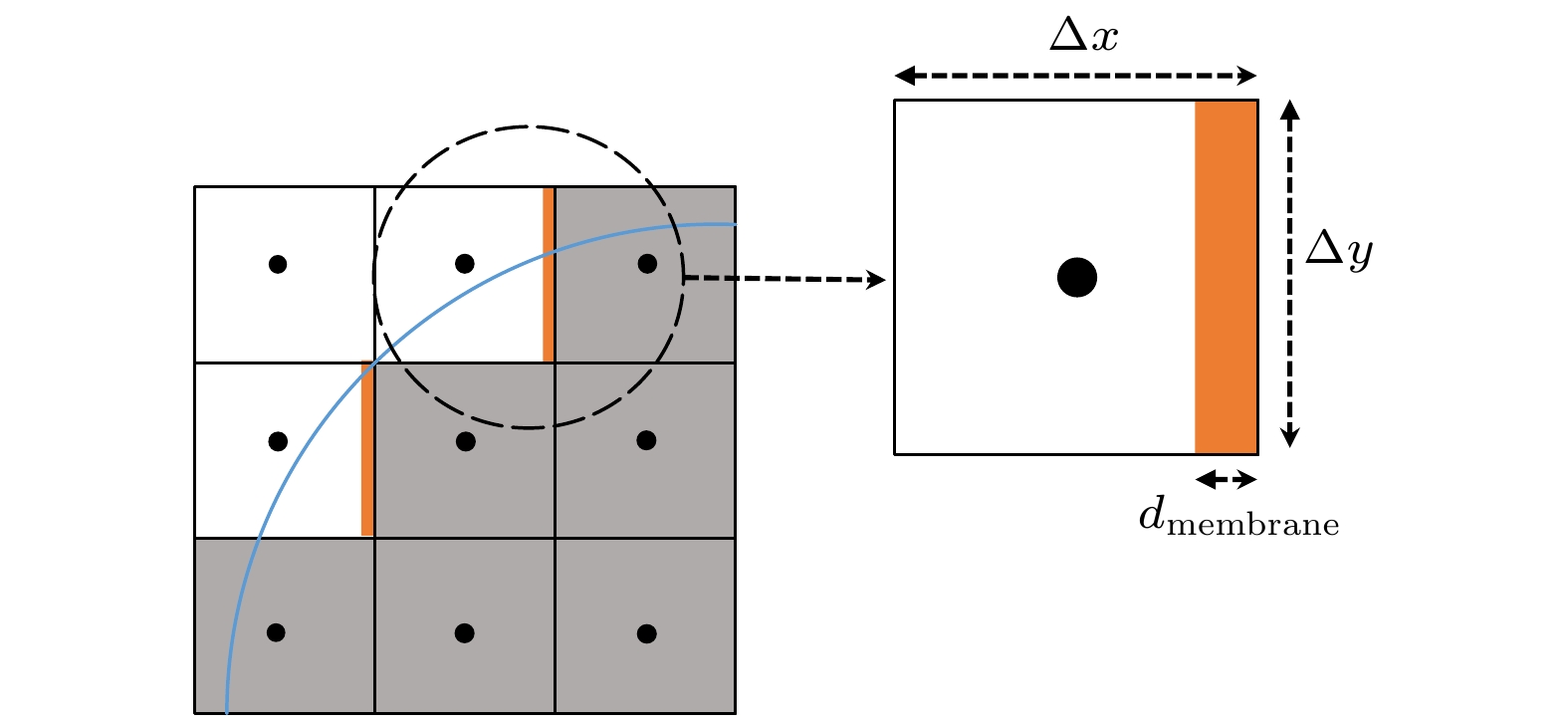图 5 曲面边界的梯形网格处理方法, 橙色的区域是细胞膜
Figure5. Surface boundary trapezoidal mesh treatment, the orange area is the cell membrane.

细胞膜的体积分数$ \alpha $可表示为$\alpha = {d}_{\mathrm{m}\mathrm{e}\mathrm{m}\mathrm{b}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{e}}/\Delta x$, 其中, $ {d}_{\mathrm{m}\mathrm{e}\mathrm{m}\mathrm{b}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{e}} $为膜的厚度, $ \Delta x $为单个网格的尺寸. 灰色区域表示细胞所在的区域, 白色区域表示细胞外部的背景媒质. 当网格中心与细胞中心之间的距离小于或等于细胞半径时, 则被认为是细胞的内部. Yee网格的空间步长与频率有关, 可以表示为$ \mathrm{d}x = \mathrm{d}y = \mathrm{d}z = {\lambda }_{0}/10 $, 其中$ {\lambda }_{0} $为空气中的波长, c为真空中的光速. 时间步长可以表示为$ \mathrm{d}t = \mathrm{d}x/(2c) $.

由于神经细胞(1—100 μm)的尺寸与太赫兹波长(3—100 μm)可比拟, 太赫兹波与神经细胞可能会发生明显的相互作用. 在实验测量结果的基础上, 利用FDTD方法建立了一个物理模型, 以研究太赫兹波在神经细胞中的传输特性、不同背景媒质与神经细胞的相对介电常数差异以及细胞尺寸和太赫兹波频率对弱谐振效应的影响. 另外, 在球形神经细胞结构的基础上, 考虑到神经细胞结构上的特异性, 建立了细胞体-轴突的神经细胞的物理模型, 并进一步研究太赫兹在包含神经纤维的神经细胞中的传输特性.
2

-->

3.1.不同背景媒质中的神经细胞弱谐振效应

采用FDTD方法计算了图4(a)所示的三维数学物理模型, 同时, 模型中电场的相对变化用增益系数G表示:

$ G = 10\log \Big|\frac{{{E_1}}}{{{E_{{\text{reference}}}}}}\Big|, $

其中$ {E}_{1} $为包含神经细胞的模型中的电场幅值, $ {E}_{\mathrm{r}\mathrm{e}\mathrm{f}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}} $为不包括神经细胞的背景环境中的电场振幅. 首先计算并分析了背景媒质的相对介电常数为1时, 由点源产生的频率为30 THz的太赫兹波在半径为8 μm的神经细胞中的传输特性, 结果如图6(a)所示.
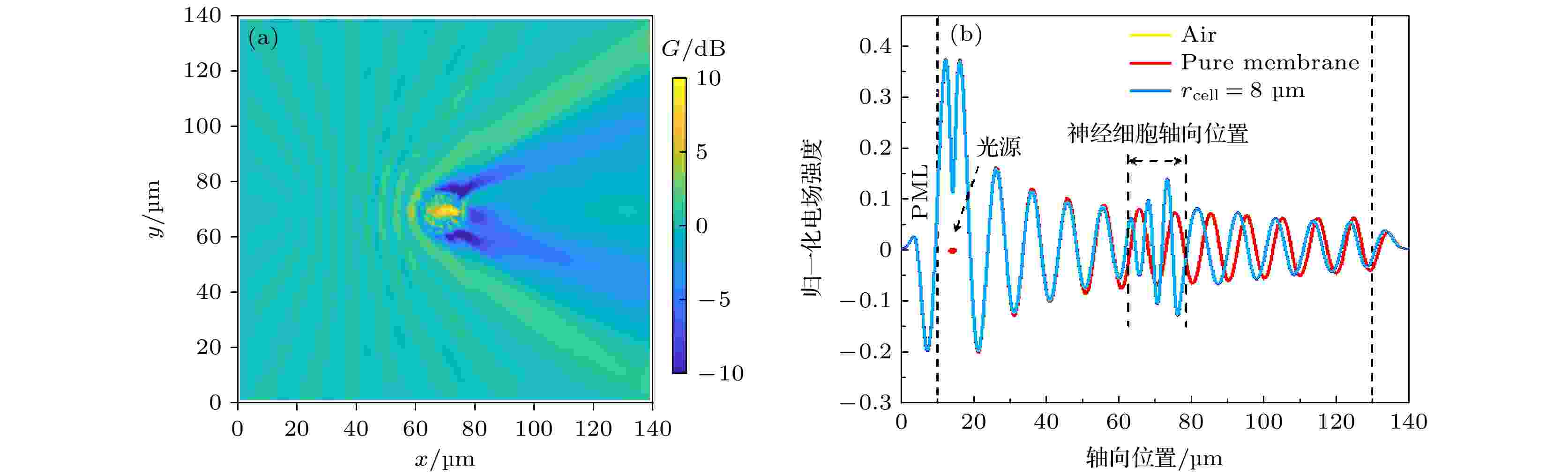图 6 (a)频率为30 THz的太赫兹波在神经细胞中传输的增益G; (b)太赫兹波在空气(黄色曲线)中、无神经细胞内生理液的模型(红色曲线)以及含有神经细胞内生理液的细胞模型(蓝色曲线)的一维场分布结果, 其中黄色曲线与红色曲线发生重叠
Figure6. (a) Gain of the THz wave transmission in nerve cells at a frequency of 30 THz; (b) one-dimensional field distribution results of the THz wave in air (yellow curve), a model without intracellular fluid (red curve), and a cell model with intracellular fluid (blue curve). The yellow curve overlaps with the red curve.

由图6(a)可看出: 增益G的最大值(> 10 dB)位于神经细胞内部, 太赫兹波与神经细胞相互作用可以在神经细胞内部产生较大的场增强效应; 在神经细胞外边界处, 增益系数G出现了小于0的情况, 表明细胞内的太赫兹波只有极少的一部分透射出去而大部分的能量都被集中在了细胞内部, 我们将这种效应称为神经细胞的弱谐振效应.
为进一步分析细胞膜以及细胞核对弱谐振效应的影响, 计算了只包含神经元细胞核以及细胞膜而无细胞内生理液的神经元细胞物理模型以及太赫兹波在纯背景媒质中的传输模型, 如图6(b)中的红色和黄色曲线所示. 结果表明, 对于细胞核等尺寸远小于太赫兹波波长的细胞器来说, 太赫兹波的绕射行为使得其对太赫兹波的传输影响可以忽略不计.
由于神经元分布在人脑组织的不同位置处发挥着不同的功能, 而不同功能区的含水量以及组成成分不同, 使得该部位的相对介电常数会有明显的不同, 因此, 计算了不同相对介电常数的背景媒质中, 神经细胞内部的太赫兹能量的变化. 这里讨论了背景媒质的相对介电常数分别为1, 2, 3, 4, 5和6时的传播情况, 结果如图7所示.
图 7 (a)—(f)背景媒质的相对介电常数分别为1, 2, 3, 4, 5和6时, 神经细胞中的场增益G结果, 太赫兹波的频率为30 THz
Figure7. (a)?(f) Field gain results in the nerve cell when the dielectric constant of background medium is 1, 2, 3, 4, 5, 6. The frequency is 30 THz.

频率为30 THz时, 由二阶德拜模型可以得到神经细胞的相对介电常数的实部为5.69, 虚部为0.1, 由图7(a)—(d)的计算结果可以看出, 随着膜内外两侧相对介电常数差异的逐渐减小, 弱谐振效应的峰值逐渐向后偏移, 与此同时, 神经细胞对太赫兹波的聚焦效应愈发明显. 当膜内外两侧相对介电常数的差值进一步减小时, 由图7(e)可以看出, 球形的神经细胞可以看作是凸透镜, 可以使得细胞后侧的电场进一步得到增强. 当神经细胞的相对介电常数低于外部媒质时, 弱谐振效应随之消失. 图8给出了计算模型轴线上的场增益, 其结果可以定量反映上述结论.
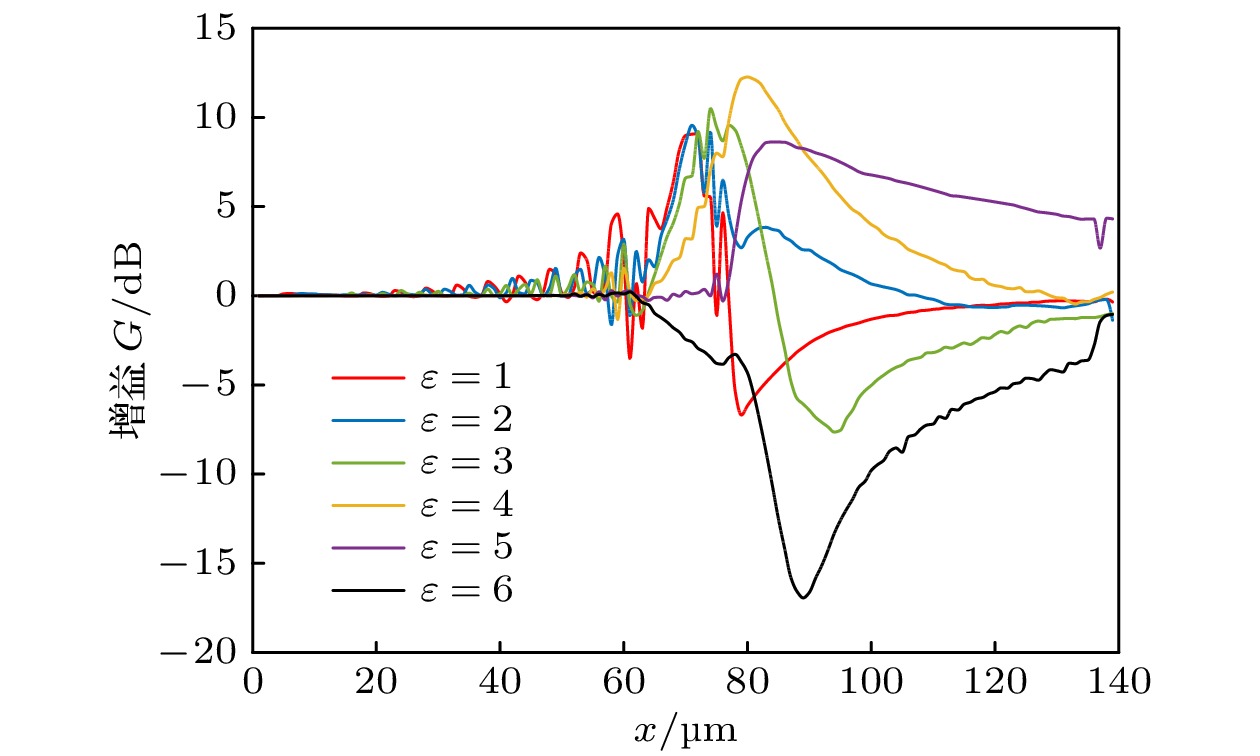图 8 背景媒质的相对介电常数分别为1, 2, 3, 4, 5和6时, 频率为30 THz的太赫兹波在神经细胞中轴线上的增益G曲线
Figure8. Gain curves on axis when dielectric constant of background medium is 1, 2, 3, 4, 5, 6, and the frequency is 30 THz.

神经细胞不仅分布在脑组织等中枢神经系统中, 在心肌、乳腺等组织中也发挥着重要的作用. 有研究表明, 乳腺癌转移瘤的生长与周围神经元的刺激有关^[18], 文献[19]给出了乳腺和癌变的乳腺组织的太赫兹频段的二阶德拜模型参数, 如表3所列.

	$ {\varepsilon }_{\infty } $	$ {\varepsilon }_{\mathrm{s}} $	$ {\varepsilon }_{2} $	$ {\tau }_{1} $/ps	$ {\tau }_{2} $/ps
正常乳腺组织	2.1	76.5	3.9	10.3	0.07
癌变乳腺组织	2.5	77.9	4.3	9.1	0.08

表3正常的乳腺组织以及癌变的乳腺组织的二阶德拜模型参数
Table3.Second-order Debye model parameters of normal and cancerous breast tissues.

用正常的乳腺组织和癌变的乳腺组织来代替原有的背景媒质, 并分别计算了半径为8 μm的神经细胞在这两个不同的媒质中的弱谐振效应的变化, 计算结果如图9所示.
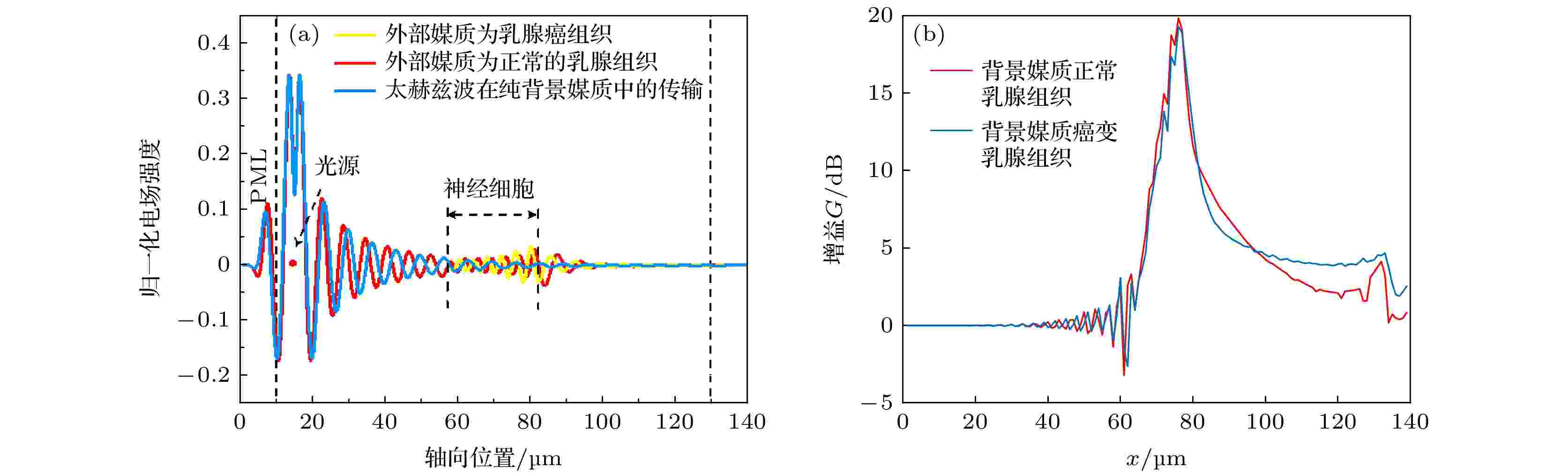图 9 背景媒质为乳腺和癌变的乳腺组织时, 频率为30 THz的太赫兹波在神经细胞中的(a)电场分布和(b)轴线上的增益
Figure9. (a) Electric field distribution and (b) gain of the 30 THz terahertz wave in nerve cells under the condition of breast and cancerous breast tissue in the background medium.

用二阶德拜模型描述乳腺以及癌变的乳腺组织时, 既可以反映媒质的相对介电常数, 同时也可以很好地反映太赫兹波在生物组织中传输的衰减. 计算结果表明, 当无神经细胞时, 由于乳腺组织对太赫兹波的吸收特性, 电磁波快速衰减, 当传输距离为100 μm时, 太赫兹波几乎衰减为0; 而当背景媒质为乳腺和癌变的乳腺组织时, 由于神经细胞的相对介电常数高于两种背景媒质, 使得细胞内部的电场得到增强, 进而传输距离也有所增加. 同时, 研究还表明, 正常的乳腺组织中的神经细胞的增益系数G高于癌变的乳腺组织中神经细胞的增益系数G, 说明正常乳腺组织中的神经细胞对太赫兹波的增强效应更为明显.
2 -->

3.2.神经细胞的弱谐振效应与细胞尺寸的关系

实际中, 生物体的不同功能区以及不同分化阶段的神经细胞的尺寸大小具有一定的差异, 神经细胞体的尺寸小到几微米, 大到几十微米, 因此, 需要研究不同尺寸的神经细胞(半径分别为8, 12.5和20 μm)中的弱谐振效应. 对于太赫兹波频率为30 THz, 背景媒质的相对介电常数为1的情况, 计算结果如图10所示.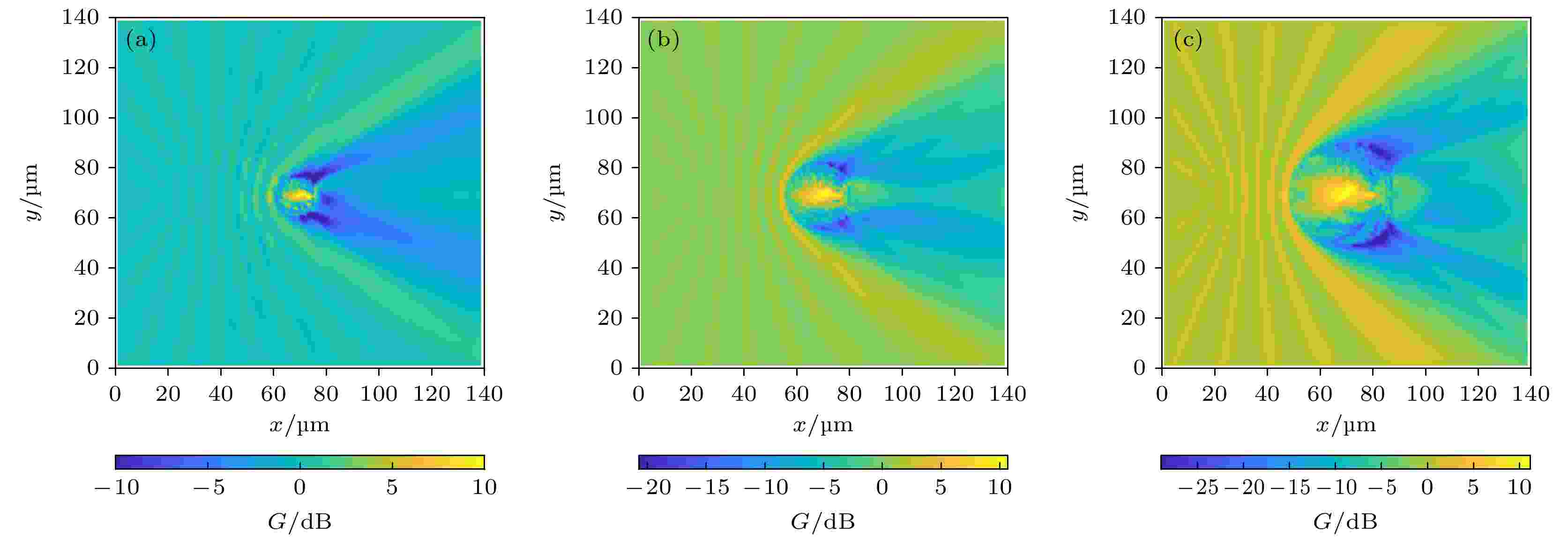
图 10 (a)—(c)神经细胞的半径为8, 12.5和20 μm时, 太赫兹波在神经细胞中传输的增益G
Figure10. (a)?(c) Gain of THz wave transmission in nerve cells with the radius of 8, 12.5, 20 μm.

研究表明, 在给定频率(30 THz)下, 随着细胞尺寸的增加, 场增益也有一定程度的增强, 一维轴线上的增益系数G如图11所示.
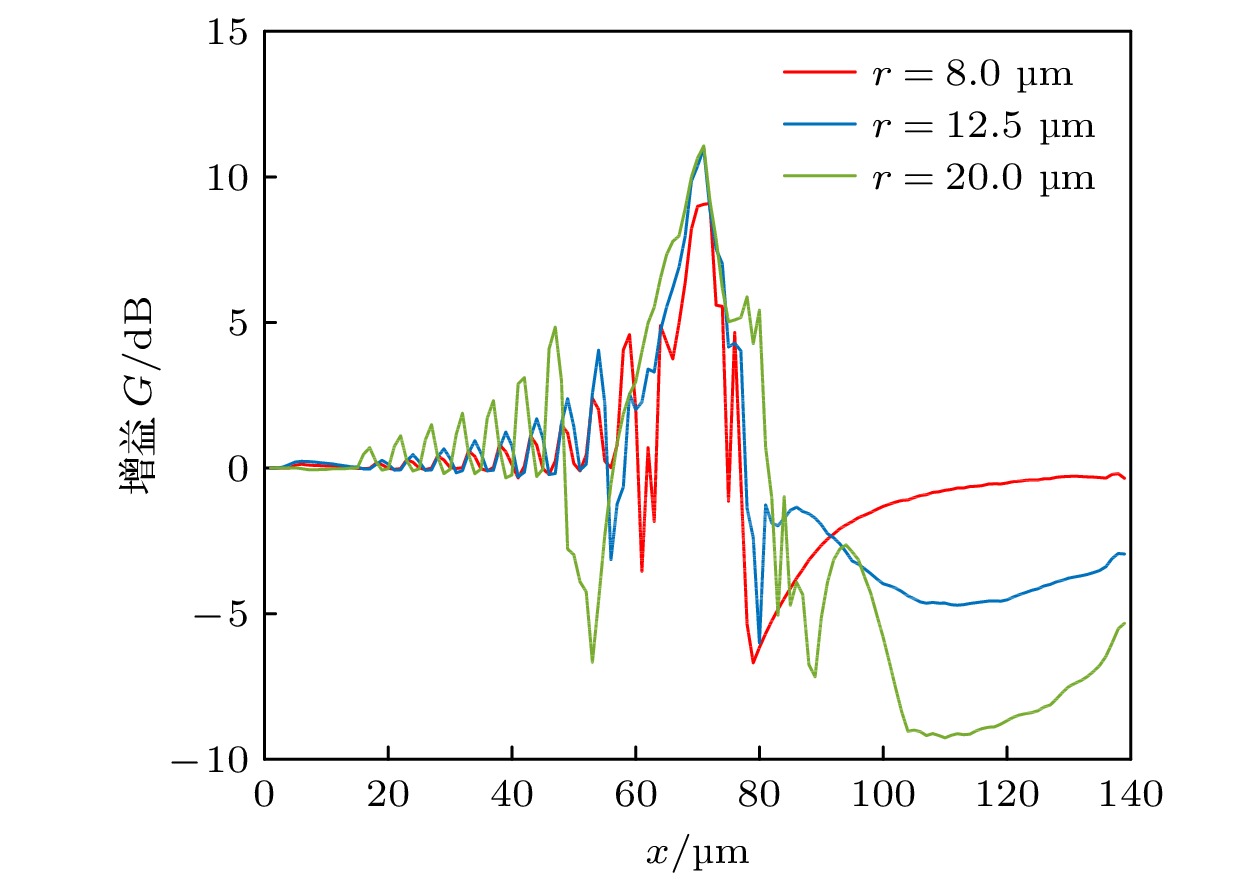图 11 神经细胞的半径为8, 12.5和20 μm时, 轴线上的场增益曲线
Figure11. Field gain curves along the axis of nerve cells with radius of 8, 12.5 and 20 μm.

细胞内部电场的增强通常会导致细胞外侧的电场的减弱. 从图11可以看出, 神经细胞的半径为8, 12.5和20 μm时, 细胞内部电场的最大增益分别为11.1, 11, 9.1 dB, 即随着细胞尺寸的增大, 增益系数G逐渐增强; 细胞内部电场增强的同时, 细胞两侧的反射波随之增大, 透射波也相应地减弱. 由于水对太赫兹波的强吸收特性, 当神经细胞的尺寸远大于太赫兹波波长时, 由膜一侧透射进入到细胞内部的太赫兹波会被水吸收而衰减, 导致难以与膜对侧的反射波相互叠加产生驻波增强效应. 进而弱谐振效应也会随之消失. 因此, 无论对于尺寸远小于太赫兹波长和尺寸远大于太赫兹波长的神经细胞体来说, 都难以产生弱谐振效应.
2 -->

3.3.神经细胞的弱谐振效应与频率的关系

由图2(c)的实验测量结果可以看出, 随着频率的增加, 相对介电常数的虚部与实部之比减小. 计算当神经细胞尺寸一定(r = 8 μm)时20, 25, 30 THz这3种不同频率下的太赫兹波在神经细胞模型中的传播特性, 结果如图12所示.
图 12 3种不同频率的太赫兹波通过神经元细胞传播的特性　(a) 20 THz; (b) 25 THz; (c) 30 THz
Figure12. Characteristic of three THz waves of different frequencies transmitting through the neuron cell: (a) 20 THz; (b) 25 THz; (c) 30 THz.

随着太赫兹波频率的增加, 细胞内部的场增强效应愈发明显, 图13给出了图12轴线上的电场增益系数G, 当频率为20, 25, 30 THz时, 细胞内部的最大增益分别为12.2, 10.3和8.3 dB. 结果表明, 当细胞尺寸一定时, 随着频率的升高, 细胞内的增益明显提升, 细胞对太赫兹波的束缚效果也更加明显. 当场主要集中在细胞内部时, 透射波的能量也相应减弱.
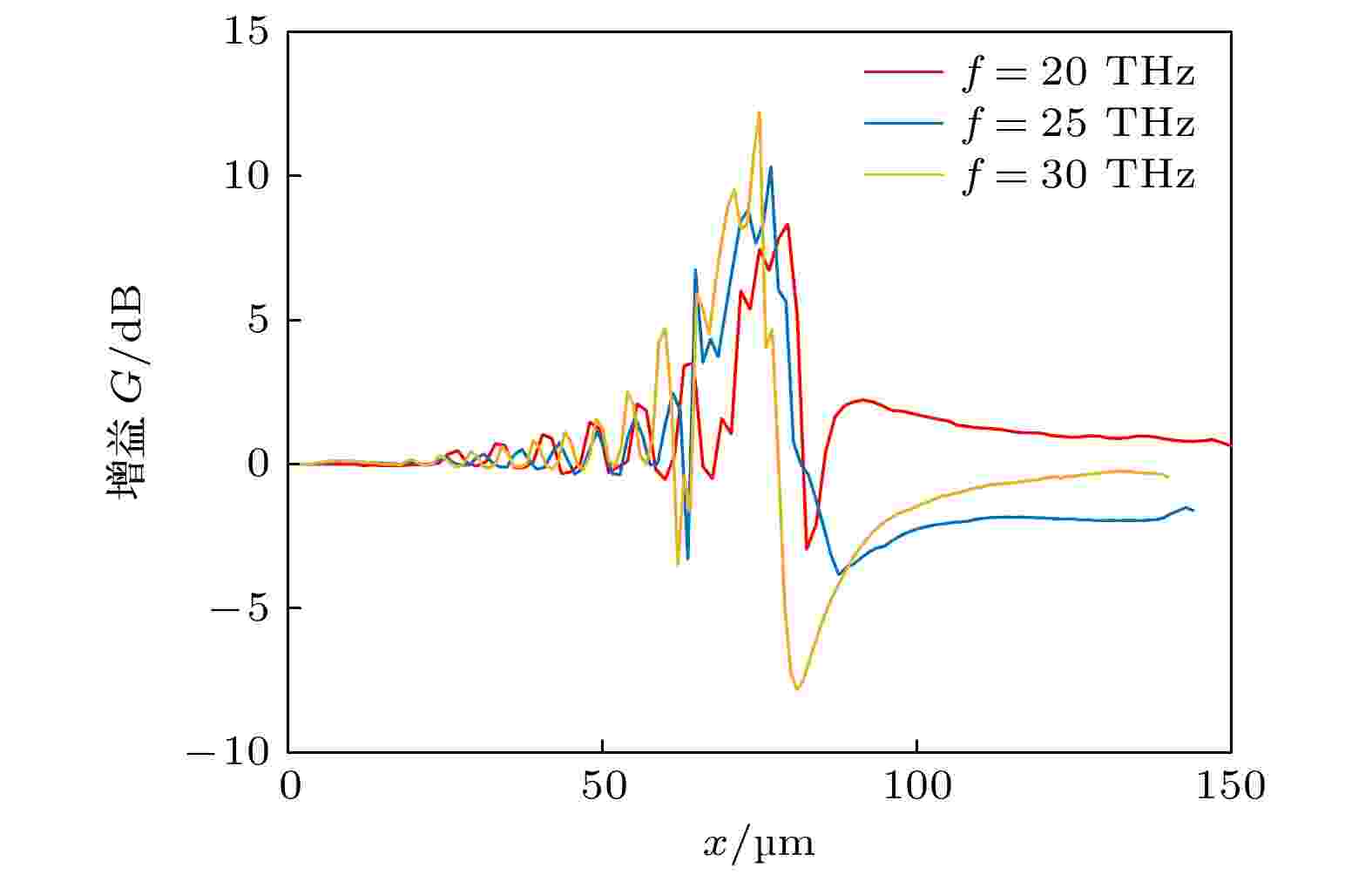图 13 神经细胞弱谐振效应与太赫兹波频率的关系, 细胞中心位于70 μm处
Figure13. Relation between weak resonance effect and THz frequency of nerve cells, cell center at 70 μm.

介质谐振器能使电磁波在介质中反射, 形成谐振结构. 高相对介电常数的介质确保大部分的场在谐振腔中, 不受辐射或泄漏的影响. 神经细胞的弱谐振效应也可以通过固有品质因数Q值得到解释:

$ Q = \frac{1}{{{\text{tan}}\delta }}, $

式中, tanδ与媒质的损耗有关, 由于神经细胞内部的生理液主要是以水为主要成分的极性液体, 因此, 媒质的损耗主要为极化损耗, 可以表示为$\mathrm{t}\mathrm{a}\mathrm{n}\delta ={\varepsilon }''/{\varepsilon }'$. 由图3可以看出, 随着频率的升高, 细胞的极化损耗逐渐降低, 当频率高于30 THz时, 神经细胞的Q值大于50, 说明神经细胞能够将电磁能量集中到细胞内部. 当频率分别为20, 25, 30 THz时, 细胞体的Q值分别为37.8, 47.2, 56.6. 由于细胞的Q值随着频率的增加而增加, 细胞将更多的高频太赫兹场的能量集中在细胞内, 产生谐振特性.
2 -->

3.4.太赫兹波在神经细胞-轴突中的传输特性

为研究神经元胞体的弱谐振效应对太赫兹波在神经纤维中传输的影响, 在图1所示的神经元胞体模型后增加了一段长为50 μm、半径为5 μm的神经轴突, 其中包括2 μm厚的髓鞘结构. 随后计算了频率为30 THz时的场增益, 结果如图14所示, 其中髓鞘的相对介电常数为9, 轴突的相对介电常数为4, 参数可以由文献[2]得到. 这里讨论背景媒质的相对介电常数为2和4的情况, 细胞体的相对介电常数由二阶德拜模型来描述.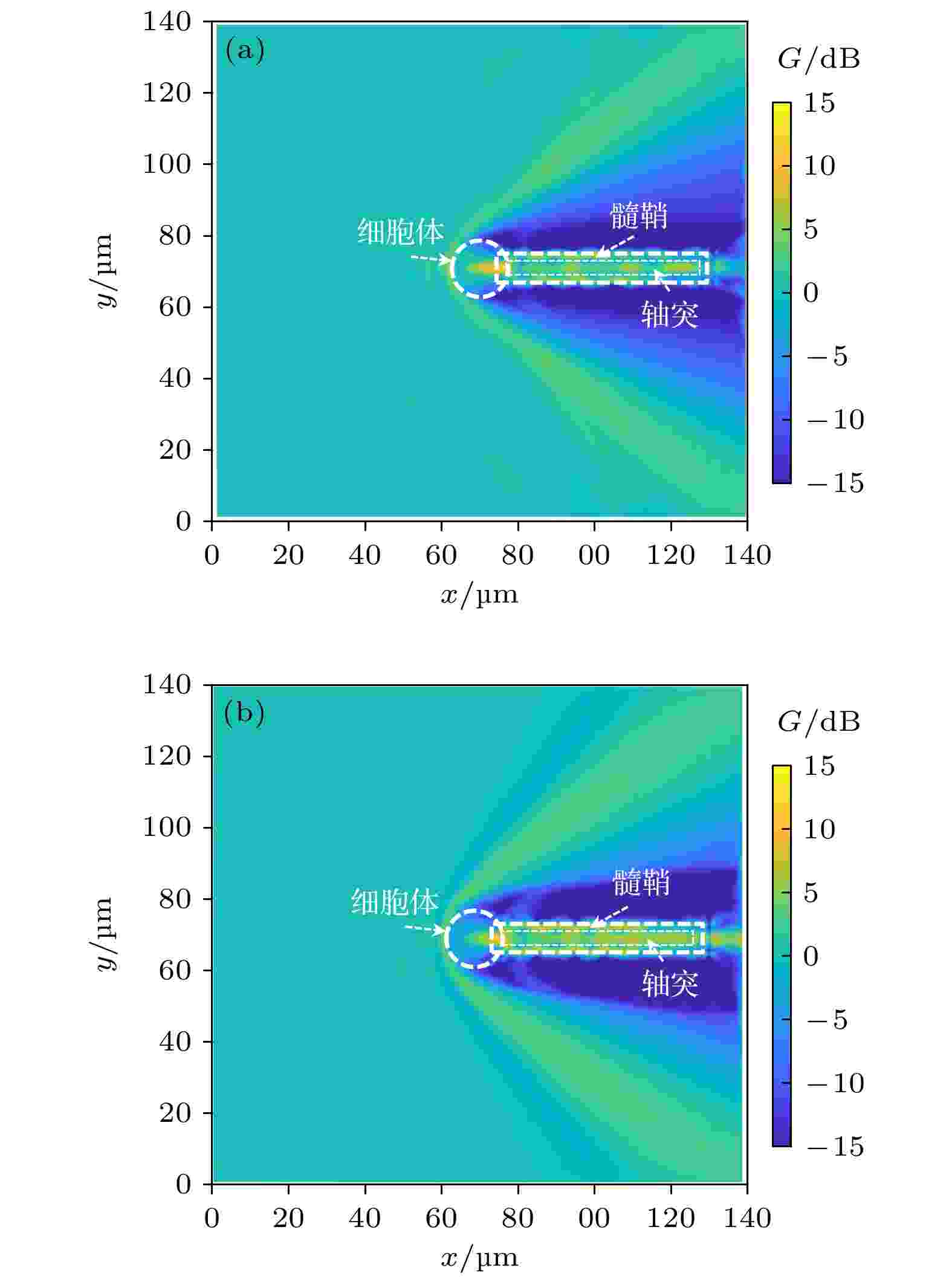
图 14 背景媒质的相对介电常数为(a) 2, (b) 4时, 神经细胞-轴突模型中的场增益G结果
Figure14. Field gain results in the neuron-axon model, when the relative permittivity of background medium is (a) 2 and (b) 4.

由计算结果可以看出, 神经细胞的弱谐振效应使得太赫兹波在细胞内得到增强并沿着神经纤维继续传输, 弱谐振效应随着膜两侧介电常数的差值减小而逐渐增强. 同时, 太赫兹波的能量被主要局限在细胞体以及髓鞘中, 说明了太赫兹波在神经细胞中传输的可能性.

本文建立了包含细胞膜、细胞内生理液以及细胞核的三层结构的神经细胞胞体的物理模型来研究太赫兹波在神经细胞中的传输特性. 由于单细胞的相对介电常数难以精确测量, 利用THz-TDS系统测量了等效的神经细胞内部生理液的相对介电常数, 并用二阶德拜模型对测量结果进行拟合, 拟合结果与实验结果保持一致. 利用FDTD方法从理论上研究了太赫兹波在神经细胞中的传输特性, 结果表明, 细胞器以及细胞核等尺寸远小于波长的小目标物体对太赫兹波传输过程产生的影响可以忽略不计. 由于神经细胞遍布周身, 包括脑组织在内不同组织的相对介电常数都有明显的差异, 研究了不同背景媒质中的神经细胞对太赫兹波传输的影响. 结果发现, 随着膜内外两侧相对介电常数差异的逐渐减小, 弱谐振效应的峰值逐渐向后偏移; 当细胞与背景媒质的相对介电常数相差无几, 且细胞的相对介电常数高于背景媒质时, 神经细胞对太赫兹波会产生聚焦效应. 通过研究不同频率的太赫兹波以及不同尺寸的神经细胞发现, 频率一定时, 随着细胞尺寸的增加, 弱谐振效应有一定程度的增强; 尺寸一定时, 随着太赫兹波频率的升高, 弱谐振效应也有一定程度的增强. 在神经元球形结构的基础上, 考虑了神经细胞结构上的特异性, 建立了细胞体-轴突物理模型, 通过分析细胞体-轴突中的场增益, 发现神经细胞的弱谐振效应也会进一步增强太赫兹信号在神经纤维中的传输.
本文通过理论分析提出了神经细胞的弱谐振效应, 为研究太赫兹波与神经细胞的相互作用提供了一种策略. 由于人体内不同组织中的细胞对太赫兹波传输的增强效应不同, 使得这一结论有助于解释人体内太赫兹信息传输的途径.