摘要:水是万物生命之源, 认识水的太赫兹吸收谱是太赫兹技术在生物医学上应用的前提, 太赫兹频率的选择对高效、低能耗地实现太赫兹的生物效应至关重要. 水的复杂氢键网络使得其具有较宽的太赫兹吸收峰, 因此有必要研究水的氢键网络动力学与其太赫兹吸收谱之间的关系, 然而这方面的研究仍然非常缺乏. 采用分子动力学模拟方法, 本文研究了不同水模型在常温常压下的太赫兹吸收谱, 并且进一步基于温度研究了水的太赫兹吸收谱对氢键网络强弱的依赖性, 发现温度的升高会使氢键网络的太赫兹吸收谱发生红移, 这表明氢键网络的太赫兹吸收谱的中心频率与氢键相互作用的强弱具有强关联, 更进一步的研究表明水中氢键网络的氢键寿命与氢键网络振动的吸收峰的中心频率之间存在线性关系. 这一现象背后的物理能够通过将氢键网络中的氢键类比为弹簧借助弹簧振子模型加以描述. 本文的发现将有利于理解水中复杂的氢键网络动力学, 以及促进太赫兹的生物效应研究.
关键词: 太赫兹/
水/
氢键

English Abstract

全文HTML

--> --> -->

水是生命之母^[1]. 水在分子细胞生物学中表现出不同的结构和功能, 它作为溶剂帮助细胞内的化学和信息传递过程, 决定并参与生物分子的相互作用和运动^[2-7]. 因此, 研究水的动力学性质对于理解生化反应以及大分子的生物功能等科学问题至关重要^[8-12]. 随着计算机的普及和计算能力的提升, 使用计算机进行分子动力学模拟已经成为与实验研究平行的一种研究方法. 1971年Rahman和Stillinger^[13]首次基于计算机模拟研究了具有分子团簇行为的水的性质. 为研究生物分子在溶液中的相互作用, 研究人员提出了许多水模型. 1981年, Berendsen等^[14]基于简单性的要求提出了SPC水模型, 设计了一种新的液态水的有效对势, 采用由尽可能少的点电荷组成的模型, 在保证足够的计算精度的前提下, 使得分子动力学模拟研究体相水的动力学性质成为了可能. 尽管该模型在大多数情况下的表现令人满意, 但仍有改进的余地. 1983年, Jorgensen等^[15]提出了TIP3P和TIP4P水模型, TIP3P能够很好地描述生物分子在水溶液中的动力学性质, 因此常用于生物系统^[16], TIP4P是四点水模型, 负电荷位于氢氧氢平分线上距离氧原子0.015 nm的虚原子, 而非氧原子上, 这有效地改善了水分子周围的静电分布, 它也常用于生物体系. 1987年, Berendsen等^[17]对SPC模型进行了重新参数化, 以获得正确的密度和能量, 由此得到了SPC/E水模型. 2004年Horn等^[18]在TIP4P的基础上又提出了TIP4P-Ew水模型, 被广泛使用于Ewald求和方法. 尽管如此, Guillot^[19]对不同水模型进行了深入的研究, 发现特定水模型只能反映水在某一方面的性质, 迄今没有一个令人完全满意的水势模型.
最近的研究表明, 水的动力学过程与太赫兹之间有着密切的关系. 太赫兹(terahertz, THz) 波的波段能够覆盖生物大分子、有机体、半导体和等离子体等物质的特征谱, 利用该频段可以加深和拓展人类对物理学、化学、天文学、信息学和生命科学中一些基本科学问题的认识^[20-24]. 在生物医学上, 生物大分子相互作用是重大生命现象与病变产生的关键动因, 然而太赫兹光子的能量覆盖了生物大分子空间构象的能级范围 (如图1(a) 所示), 该频段包含了其他电磁波段无法探测到的直接代表生物大分子功能的空间构象等重要信息^[25]. 2018年, 刘国治院士^[26]推断生物神经信号物理场应为太赫兹到红外区域的高频电磁场, 最可能频率范围应在0.5—100 THz, 并且将此波段称为广义太赫兹. 这预示着广义太赫兹波有望调控生物分子的结构和功能. 生物分子在水溶液中发挥活性和功能, 然而水是极性液体, 它在部分太赫兹频率下有异常高的吸收损失, 表现出热效应, 给太赫兹技术在生物体系中的应用蒙上了一层乌云^[27]. 通常来说, 水的太赫兹光谱有3个主峰 (图1(b)), 第1个峰位于5—30 THz区间, 对应水中氢键网络的振动模式(图1(c)), 第2个峰位于45—50 THz, 对应水分子内部键角的弯曲振动 (图1(c)), 第3个峰则位于90—105 THz, 它对应于水分子内部键长的拉伸振动 (图1(c)). 这意味着在广义太赫兹波段存在4个水的太赫兹弱吸收窗口, 可用于非热地调控生物大分子的结构和功能. 得益于此, 近3年, 太赫兹在水溶液中非热地调控细胞动力学过程取得重要的进展^[28-35] (图1(d)). 2019年, 我们提出1.39或4.66 THz的电磁刺激能够非热地引发一维水通道内受限水的超级渗透, 促使受限水由一维冰相向一维相干气相转变^[28]. 2020年, Wu等^[29]发现44.0 THz的电磁刺激能够共振地加速DNA分子的解旋过程, 并且有效地降低DNA的熔解温度. 同年, Wang等^[30]观察到太赫兹辐射能够引起DNA碱基对中氢键的瞬态质子转移. Li等^[31]证实细胞内ATP水解能够释放频率约为34 THz的内源光子, 进而调控生化反应. 2021年, Li等^[32]发现42.55 THz的电磁刺激能够非热地加速钙离子通道内钙离子的渗透. 同年, Liu等^[33]演示了53.7 THz的电磁刺激能够非热、可逆地调控神经信号和动物的行为. 以上研究表明, 为了避免太赫兹电磁波被体相水强吸收, 理论上预测既能够调控生物大分子的功能, 又对体相水产生有限热效应的太赫兹波段非常关键, 因此, 有必要深入地对体相水的太赫兹吸收谱进行理论研究.
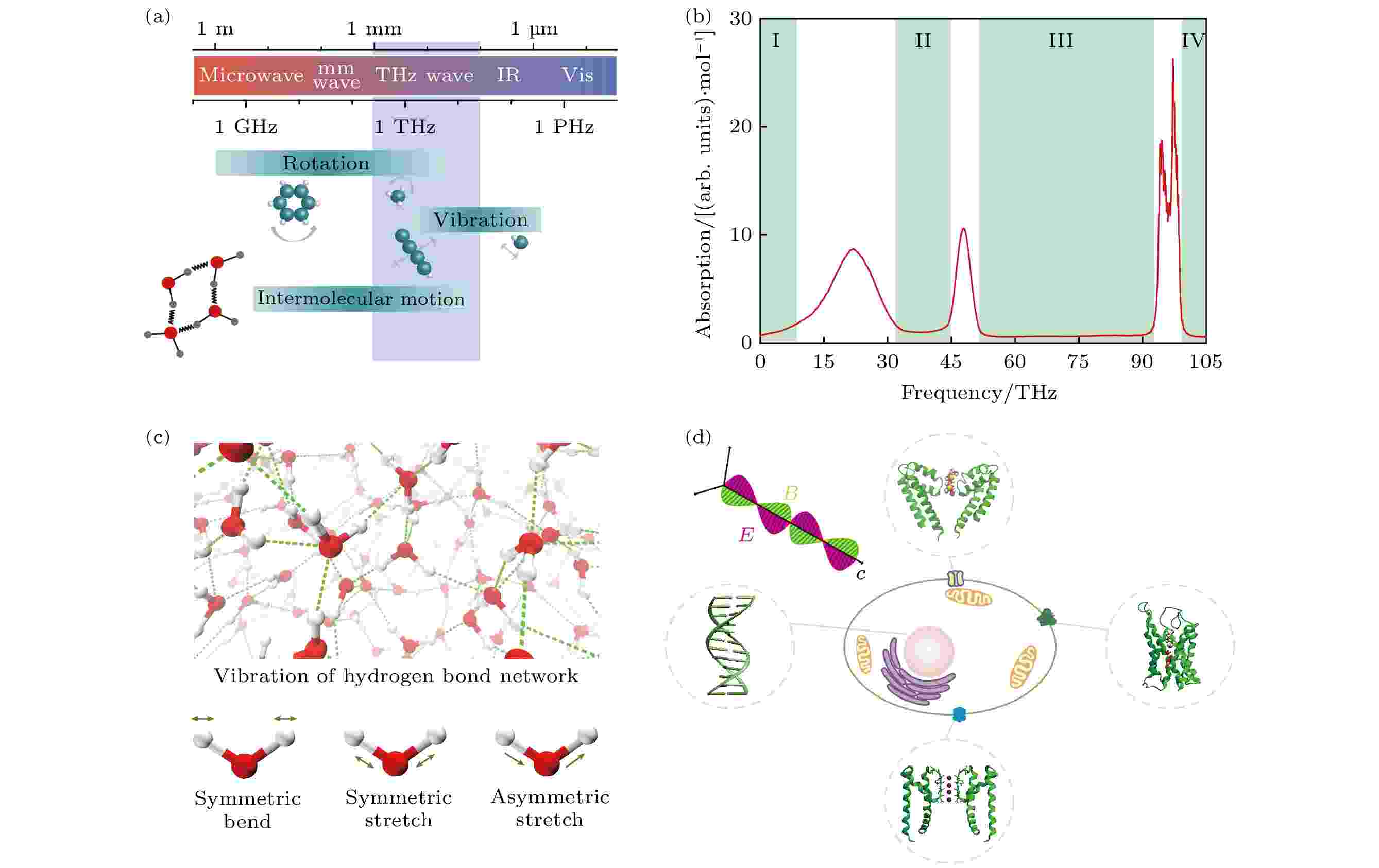图 1 太赫兹与生物分子的密切关系以及太赫兹调控细胞动力学　(a) 生物大分子的转/振动的频率在THz频段; (b) 水的太赫兹吸收谱, 绿色区域是有望非热地调控生物分子的广义太赫兹频率的4个窗口; (c) 水的太赫兹吸收谱的振动模式^[36]; (d) 太赫兹波非热调控细胞动力学, 涉及发挥细胞生物功能的水通道蛋白、DNA、钾离子通道、钙离子通道
Figure1. Close relationship between terahertz and biomolecules and the regulation of cell dynamics by terahertz: (a) Frequency of rotation/vibration of biological macromolecules is in the THz frequency band; (b) terahertz absorption spectrum of water, the green region is the four frequency windows in which electromagnetic wave is expected to non-thermally regulate biomolecules; (c) vibration modes of water corresponding to its terahertz absorption spectrum^[36]; (d) terahertz waves non-thermally regulate the dynamics of a cell, involving aquaporins, DNA, potassium and calcium channels that perform biological functions of the cell.

本文利用分子动力学模拟方法基于不同水模型和温度, 研究了水的太赫兹吸收谱以及与氢键网络动力学的关系, 发现水形成的氢键网络越强, 其太赫兹吸收峰越倾向于蓝移, 进一步发现了水的氢键寿命与其太赫兹吸收峰的频率之间存在线性关系, 并利用弹簧振子模型对这一现象的机理加以解释, 也就是将水的氢键等同于弹簧, 如果水的氢键越强, 其等效弹簧的劲度系数就越大, 进而使得氢键网络具有较大的振动频率.

2

-->

2.1.模拟方法

首先, 建立大小为4 nm × 4 nm × 4 nm的立方体模拟盒子, 然后在常温常压的情况下分别用水分子个数为2165的柔性SPC, SPC/E, TIP3P水分子模型和水分子个数为2211的柔性的TIP4P, TIP4P-Ew水分子模型将模拟盒子填充满. 水分子间的相互作用为

$ U({\boldsymbol{r}}_{i},{\boldsymbol{r}}_{j})=f\frac{{q}_{i}{q}_{j}}{{\boldsymbol{r}}_{ij}}+4{\varepsilon }_{ij}\bigg[{\left(\frac{{\sigma }_{ij}}{{\boldsymbol{r}}_{ij}}\right)}^{12}-{\left(\frac{{\sigma }_{ij}}{{\boldsymbol{r}}_{ij}}\right)}^{6}\bigg], $

式中第一项为长程静电相互作用, 第二项为短程Lennard-Jones作用. 其中 $ f=1/\left(4{\text{π}}{\varepsilon }_{0}\right) $, $ {\varepsilon }_{0} $是真空中的介电常数; r_ij是原子i和j之间的距离; q_i是原子i的电荷; $ {\varepsilon }_{ij} $, $ {\sigma }_{ij} $是原子i和原子j之间的Lennard-Jones作用参数. 这些水模型的力场参数差异如表1所列, 其中, r_H—O, θ分别表示O—H的键长、$ {\rm{\angle }} $HOH的键角, q_O (q_vir), q_H为氧原子(虚原子)、氢原子所带电荷量, ε和σ为Lennard-Jones作用参数. 模拟使用的软件是GROMACS 5.1.4, 采用OPLS/AA力场处理原子间的相互作用, 其中不同原子间的Lennard-Jones参数基于几何平均法计算, 使用跳蛙算法求解粒子的运动方程. 模拟过程采用周期性边界条件, 模拟系综为恒温恒压系综, 使用Nose-Hoover热浴控制系统温度保持在设定的参考温度, 温度弛豫时间为0.2 ps, 使用Parrinello-Rahman压强耦合器控制系统压强维持在1 bar (1 bar = 10⁵ Pa). 使用Particle-Mesh-Ewald方法处理静电相互作用, 静电和范德瓦耳斯相互作用的截断半径均为1 nm. 每次模拟时长为100 ns, 时间步长为1 fs, 其中最后5 ns的轨迹数据用于分析水的光谱和动力学性质.

Water model	σO—O/?	εOO/(kJ·mol–1)	qH/e	qO or qvir/e	θ/(°)	rH—O/?
SPC	3.166	0.650	0.410	–0.820	109.470	1.000
SPC/E	3.166	0.650	0.424	–0.848	109.470	1.000
TIP3P	3.151	0.636	0.417	–0.834	104.520	0.957
TIP4P	3.154	0.649	0.520	–1.040	104.520	0.957
TIP4P-Ew	3.164	0.681	0.524	–1.048	104.520	0.957

表1所用水模型的力场参数的比较
Table1.Comparison of the force field parameters of different water models employed.

2 -->

2.2.分析方法

3 -->

2.2.1.频谱解析

在经典近似的情况下, 分子与频率相关的光谱强度(I?)可以通过对水的总电荷流的自相关函数进行傅里叶变换获得, 它的表达式为

$ I\left(f\right)=\int \frac{\langle {\boldsymbol{J}}\left(t\right)\cdot {\boldsymbol{J}}\left(0\right) \rangle }{ \langle {\boldsymbol{J}}\left(0\right)\cdot {\boldsymbol{J}}\left(0\right)\rangle }{\rm{cos}}\left(ft\right){\rm{d}}t , $

其中$ \boldsymbol J(t)?=?\displaystyle\sum\nolimits_i q_i \boldsymbol v_i (t) $(q_i和v_i分别表示第i个原子的电荷和速度)是系统中水分子在t时刻的总电荷流^[37,38].
3 -->

2.2.2.径向分布函数

径向分布函数表示了与某个原子距离为r的单位体积元内出现的分子数密度, 表达式为^[39,40]

$ g\left(r\right)= \left\langle \frac{1}{{\rho }_{N}}\sum _{i=1}^{N}\sum _{j=1}^{N}\delta ({{r}}_{ij}-r) \right\rangle , $

其中, N 是系统中水分子的个数, $ {\rho }_{N} $是水的平均密度, r_ij是第i号分子和第j号分子之间的距离.
3 -->

2.2.3.自扩散系数

根据Einstein关系, 自扩散系数与粒子的均方根位移(MSD)成正比, 表达式为^[41]

$ {D}_{{\rm{s}}{\rm{e}}{\rm{l}}{\rm{f}}}=\lim _{t \rightarrow \infty}\frac{1}{6Nt}\left({\sum _{i=1}^{N}\left|{\boldsymbol{r}}_{i}\left(t\right)-{\boldsymbol{r}}_{i}\left(0\right)\right|^{2}}\right) , $

其中, N是粒子数目, ${\boldsymbol{r}}_{i}{(}{t}{)} - {\boldsymbol{r}}_{i}{(0)}$是第i个粒子在时间间隔t内的运动位移.
3 -->

2.2.4.氢键寿命

通常氢键采用纯几何准则进行定义: 若两个水分子的氧原子 (O···O) 间的距离小于0.35 nm, O···O—H之间的夹角小于30°, 则认为两水分子之间形成氢键. 氢键的自相关函数为^[42-44]

$ C\left(t\right)= \left\langle \frac{h\left(0\right)\cdot h\left(t\right)}{h\left(0\right)\cdot h\left(0\right)} \right\rangle . $

若一对水分子i和j在t时刻形成氢键, 则h(t)的值为1, 否则为0. 氢键自相关函数C(t) 统计在0时刻形成氢键的两个水分子在t时刻仍然成氢键的概率. 氢键寿命通过对自相关函数拟合得到, 常用指数函数 $ C\left(t\right)={\rm{e}}{\rm{x}}{\rm{p}}(-t/\tau ) $ 进行拟合, 式中$ \tau $为氢键的寿命^[45].

理论计算结果表明, 不同水模型计算得到的体相水的吸收谱与实验测量所得的吸收谱均存在一定程度的偏差, 并且体相水的氢键网络振动的吸收谱对温度敏感 (如图2所示). 首先, 计算由不同水模型(SPC, SPC/E, TIP3P, TIP4P, TIP4P-Ew)构成的体相水的太赫兹吸收谱, 并将结果与实验测量结果^[46]进行对比. 在定性分析上, 理论计算结果与实验测量结果具有相同性, 但是在定量分析上它们存在差异性. 具体来说, 如图2(a)所示, 由SPC, SPC/E, TIP3P, TIP4P, TIP4P-Ew水模型构成的体相水的太赫兹吸收谱都具有氢键网络振动的吸收峰、水分子内部弯曲振动的吸收峰和水分子内部氢氧键拉伸振动的吸收峰, 这就意味着这些水模型能够定性地描述体相水的各种振动模式. 定量上, 虽然由SPC和SPC/E水模型构成的体相水的氢键网络振动的吸收峰的中心频点在(20.11 ± 0.06) THz和(21.83 ± 0.04) THz, 略大于实验测量值 (19.5 THz), 但是这两种水模型的弯曲(45—50 THz)和拉伸振动的吸收峰(90—105 THz)的位置确与实验测量值接近(图2(a)上部). 相反的是, 由TIP3P, TIP4P, TIP4P-Ew水模型构成的体相水的弯曲(60—65 THz)和拉伸振动的吸收峰 (110—120 THz)的位置远偏离实验测量值, 但是它们的氢键网络振动的吸收峰的中心频点((18.52 ± 0.06) THz对应于TIP3P水模型; (19.28 ± 0.05) THz对应于TIP4P水模型; (20.77 ± 0.05) THz对应于TIP4P-Ew水模型)却更接近实验测量值(图2(a)下部). 以上结果表明, SPC和SPC/E相比于TIP3P, TIP4P和TIP4P-Ew更能反映水的单分子振动特性, 然而TIP3P, TIP4P和TIP4P-Ew相比于SPC和SPC/E更能反映水的氢键网络的集体振动特性. 因为水的独特性质, 例如较高的沸点和热容量, 来自于其复杂的氢键网络, 所以研究水的复杂氢键网络结构对于确定水的性质至关重要. 接下来, 比较由不同水模型组成的体相水的氢键网络振动的吸收谱(如图2(b) 所示). 理论模拟结果表明, 相比于SPC/E, SPC水模型的氢键网络振动的吸收峰的中心频率发生了红移. 这归因于SPC的氢氧原子电荷量的绝对值比SPC/E小 (如表1所列), 减小的电荷会影响偶极矩, 从而降低介电常数, 进而影响分子间的相互作用^[47], 最终导致SPC的氢键网络振动的吸收峰相比SPC/E发生了红移. 因为SPC和SPC/E水模型具有相同的键长r_H—O、键角$ {\rm{\angle }} $HOH参数, 所以它们弯曲和拉伸振动的吸收峰的频率是一致的. 同样地, TIP3P, TIP4P与TIP4P-Ew的氢氧原子电荷量的绝对值的大小依次是TIP3P < TIP4P < TIP4P-Ew, 随着电荷的增大, 氢键网络振动的吸收峰逐渐发生蓝移, 它们弯曲和拉伸振动的吸收峰的频率是一致的, 归因于它们也采用了相同的键长r_H—O、键角$ {\rm{\angle }} $HOH参数. 接下来, 通过观察不同水模型的氢键网络振动的吸收谱之间的差异 (图2(b)), 发现它们的中心频率依次是TIP3P ((18.52 ± 0.06) THz) < TIP4P ((19.28 ± 0.05) THz) < SPC ((20.11 ± 0.06) THz) < TIP4P-Ew ((20.77 ± 0.05)THz) < SPC/E ((21.83 ± 0.04) THz), 这预示着水的氢键网络的振动吸收峰的中心频率与水的相互作用之间存在一定的关系.
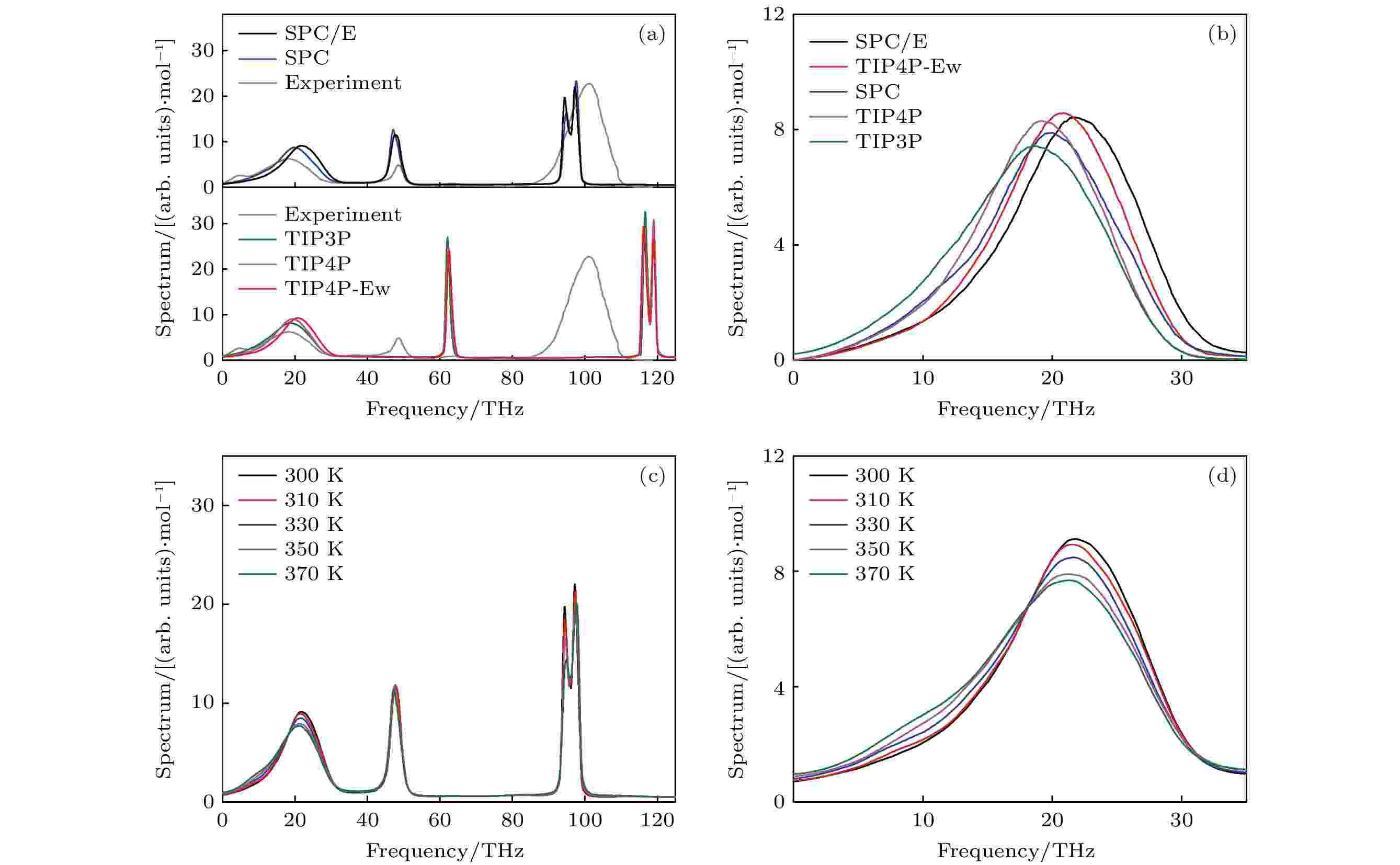图 2 不同水模型建模的体相水的太赫兹吸收谱和温度对其太赫兹吸收谱的影响　(a) 不同水模型建模的体相水的太赫兹吸收光谱以及实验测量所得体相水的太赫兹吸收谱之间的对比; (b) 对于不同水模型构成的体相水, 其氢键网络的太赫兹吸收谱; (c) 不同温度下, SPC/E水模型建模的体相水的太赫兹吸收谱; (d) 不同温度下, 对于SPC/E水模型构成的体相水, 其氢键网络的太赫兹吸收谱
Figure2. THz absorption spectra of bulk water modeled by different water models and effects of temperature on its spectra: (a) Comparison of THz absorption spectra of bulk water under different water models and its spectra from experimental measurement; (b) THz absorption spectra of hydrogen bond network of bulk water under different water models; (c) THz absorption spectra of bulk water modeled by SPC/E water model at different temperatures; (d) THz absorption spectra of hydrogen bond network of bulk water modeled by SPC/E water model at different temperatures.

因为温度会改变氢键网络的结构, 进而影响氢键网络的相互作用. 较高的温度更利于破坏氢键网络, 降低氢键的相互作用. 为了研究氢键网络的振动吸收峰的中心频率与水的相互作用之间的关系, 选择特定的水模型(SPC/E), 进一步计算了体相水在不同温度下的太赫兹吸收谱. 从图2(c)可知, 温度对水的氢键网络的振动吸收峰有显著的影响, 然而对水的弯曲和拉伸振动的吸收峰的影响有限. 特别地, 随着温度从300 K逐渐升高到370 K, 水的氢键网络振动的吸收峰的中心频率逐步发生了红移(如图2(d) 所示), 也就是300 K下为(21.83 ± 0.04) THz, 310 K下为(21.73 ± 0.05) THz, 330 K下为(21.39 ± 0.05) THz, 350 K下为(21.03 ± 0.06) THz, 370 K下为(20.81 ± 0.07) THz. 因此, 可以初步得出结论: 水具有越强的氢键, 其氢键网络振动的吸收峰的中心频率越大.
为了进一步研究水的氢键网络强弱与其振动吸收峰的中心频率之间的关系, 分析了体相水的结构和动力学性质(图3). 首先, 计算了由不同水模型构成的体相水的径向分布函数g(r), 如图3(a)所示. 可以看出, 随着r的增加, g(r)函数值逐渐减小并收敛到1.0, 这说明水分子表现出短程有序、长程无序的微观结构特征, 符合液体分子的排列规则. 此外, 由SPC/E, TIP4P和TIP4P-Ew构成的体相水的g(r)具有两个峰, 跟实验结果一致^[48], 但由SPC, TIP3P构成的体相水的g(r)只有1个峰. 特别地, 由不同水模型构成的体相水的第一水合层的密度是不一样的, 具体表现为g(r)的第1个峰的峰值高度的差异, 其峰值高度的大小关系依次为TIP3P (2.86) < TIP4P (3.13) < SPC (3.18) < TIP4P-Ew (3.43) < SPC/E(3.51); 然而, 由不同水模型构成的体相水的g(r)的第1个峰值所处的位置(r值)具有相反的关系: TIP3P (0.274 nm) > TIP4P (0.273 nm) = SPC (0.273 nm) > TIP4P-Ew (0.272 nm) > SPC/E (0.271 nm). 值得注意的是, g(r)的第1个峰值高度值越大以及g(r)的第1个峰值所处的r值越小, 水的氢键网络振动的太赫兹吸收峰的中心频率越大. 这归因于水分子与周围的第一水合层内的水分子形成氢键, g(r)的第1个峰的峰值高度越大以及它的r越小, 说明水分子与第一水合层内的水分子结合得越紧密, 从而具有越强的氢键相互作用, 对周围水分子的束缚也越强. 粒子的扩散系数能够说明周围粒子对其的束缚情况. 然后, 计算了由不同水模型构成的体相水的扩散系数D, 如图3(b)所示, 各D值的大小关系为TIP3P > TIP4P ≈ SPC > TIP4P-Ew > SPC/E, D的值依次是(3.97 ± 0.09) ×10^–5, (2.36 ± 0.04) × 10^–5, (2.34 ± 0.07) × 10^–5, (1.25 ± 0.07) × 10^–5和 (1.12 ± 0.01) × 10^–5 cm²/s. 将各D值的大小关系与其氢键网络振动的吸收峰的中心频率的大小关系联系起来, 发现水的氢键对水的束缚越强 (D值越小), 水的氢键网络振动的太赫兹吸收峰的中心频率越大. 同样地, 基于SPC/E水模型, 计算了温度对体相水g(r)和D的影响. 如图3(c) 所示, 随着温度的升高, g(r)的第1个峰值高度不断减小(300 K下为3.51, 310 K下为3.39, 330 K下为3.20, 350 K下为3.01, 370 K下为2.88), 它的第1个谷值却不断升高, 以及第2个峰的峰值也逐步降低甚至消失, 这表明水的长程有序性逐渐减小. 不仅如此, 随着温度升高, 体相水的D逐渐增大, 如图3(d) 所示, 表现为: D的值在300 K时为(1.12 ± 0.01) × 10^–5 cm²/s, 310 K时为 (1.54 ± 0.07) × 10^–5 cm²/s, 330 K时为 (2.47 ± 0.07) × 10^–5 cm²/s, 350 K时为 (3.54 ± 0.03) × 10^–5 cm²/s, 370 K时为 (4.80 ± 0.12) × 10^–5 cm²/s. 这是因为温度升高使得水分子的运动加剧, 削弱了水分子之间的氢键. 以上结果表明: 水分子具有越紧束缚的氢键网络, 其氢键网络的振动吸收峰的中心频率越大.
图 3 不同水模型构成的体相水的结构和动力学性质的分析　(a) 不同水模型构成的体相水的径向分布函数; (b) 不同水模型构成的体相水的扩散系数; (c) 特定的水模型(SPC/E)下, 温度对体相水的径向分布函数的影响; (d) 不同温度下SPC/E的扩散系数
Figure3. Analyses of structure and dynamic behavior of bulk water modeled by different water models: (a) Radial distribution function of bulk water under different water models; (b) diffusion coefficient of bulk water under different water models; (c) under specific water model (SPC/E), the effect of temperature on the radial distribution function of bulk water; (d) diffusion coefficient of bulk water at different temperatures.

最后, 定量研究水的氢键强弱与其振动吸收峰的中心频率之间的关系(如图4所示). 水分子之间的氢键处于动态变化, 它可能在某一时刻断裂, 随后又与其他水分子形成氢键, 氢键动态变化导致体系总偶极距的变化, 因此, 根据涨落耗散定理^[49], 氢键动态变化的快慢将直接影响氢键网络振动的太赫兹吸收谱. 氢键的平均寿命能够衡量氢键动态变化的快慢, 它由氢键的自相关函数C(t)拟合得到. 如图4(a)所示, 不同水模型的C(t)都近似于指数衰减, 但是它们衰减的快慢不一样, 表明氢键寿命大小不一样. 从图4(b)可知, SPC/E, TIP4P-Ew, SPC, TIP4P, TIP3P的氢键寿命依次为(7.09 ± 0.03), (5.46 ± 0.02), (3.23 ± 0.02), (3.11 ± 0.02)和(1.66 ± 0.01) ps. 将由不同水模型构成的体相水的氢键网络振动的吸收谱的中心频率v与它们的氢键寿命 τ联系起来 (如图4(c)所示), 发现它们之间呈线性关系$v=a_1 \cdot \tau +b_1$, 其中a₁ = (0.37 ± 0.05), b₁ = (18.60 ± 0.22). 不仅如此, 氢键寿命随着温度升高逐渐减小, 如图4(d) 所示, 体相水的τ在300 K时为(7.09 ± 0.03) ps, 310 K时为(5.14 ± 0.02) ps, 330 K时为(3.27 ± 0.01) ps, 350 K时为(2.32 ± 0.01) ps, 以及370 K时为(1.70 ± 0.01) ps. 同样地, 将不同温度下的体相水的氢键网络振动的吸收谱的中心频率v与它们的氢键寿命τ联系起来(如图4(e)所示), 发现τ越大, v也越大, 它们之间也呈线性关系$v=a_2 \cdot \tau +b_2$, 其中a₂ = (0.33 ± 0.04), b₂ = (19.78 ± 0.12). 值得注意的是, a₁ ≈ a₂, 这表明体相水的氢键网络振动的吸收谱的中心频率与它的氢键寿命之间的线性关系具有普适性. 更进一步剖析其中的机理, 将水分子之间的氢键比作弹簧 (如图4(f) 所示), 氢键网络中的水分子之间的氢键相互作用越弱, 说明弹簧的刚性越软, 即劲度系数k越小, 具体表现为水分子对周围水分子的束缚越弱, 水分子的随机扩散越强, 根据弹簧简谐振动的频率计算公式$ \omega =\sqrt{k/m} $可知, ω随k的减小而减小, 表现为氢键网络振动的太赫兹吸收峰发生红移.
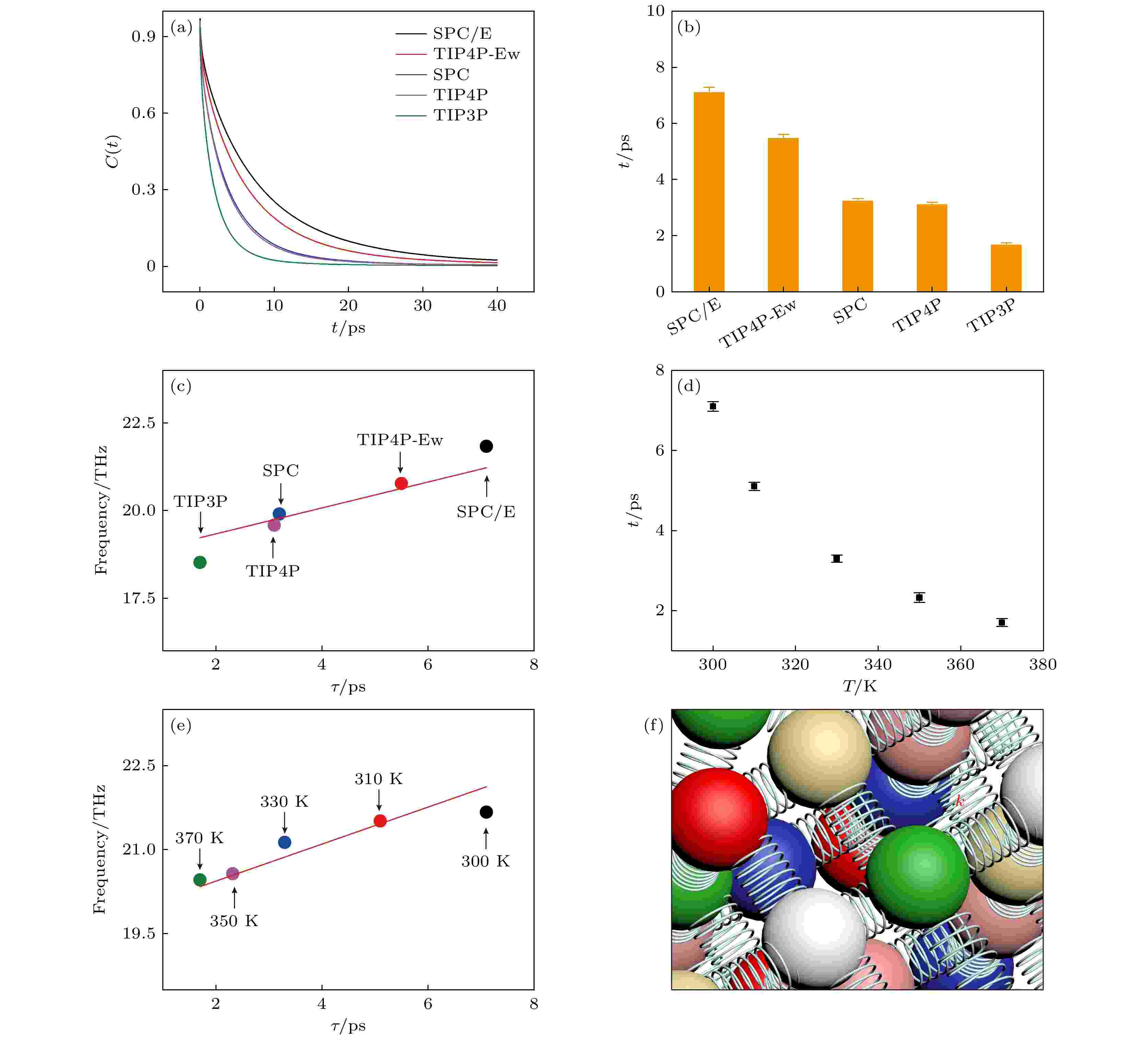图 4 氢键动力学与氢键网络振动的太赫兹吸收峰的中心频率之间的关系　(a) 由不同水模型构成的体相水的氢键的自相关函数; (b) 由不同水模型构成的体相水的氢键寿命; (c) 不同水模型下, 氢键网络振动的太赫兹吸收谱的中心频率与氢键寿命的对应关系; (d) 不同温度下, 体相水的氢键寿命; (e) 不同温度下, 水的氢键网络振动的太赫兹吸收峰的中心频率与氢键寿命的关系; (f) 氢键网络示意图
Figure4. Relationship between hydrogen bond dynamics and the center frequency of THz absorption spectra for the vibration of hydrogen bond network: (a) Hydrogen bond autocorrelation functions of bulk water under different water models; (b) lifetime of hydrogen bond of bulk water under different water models; (c) for bulk water under different water models, the relationship between the center frequency of THz absorption spectra for the vibration of hydrogen bond network and the lifetime of hydrogen bond; (d) lifetime of hydrogen bond for bulk water at different temperatures; (e) at different temperatures, the relationship between the center frequency of THz absorption spectra for the vibration of the hydrogen bond network and the lifetime of the hydrogen bond; (f) schematic diagram of the hydrogen bond network.

基于经典分子动力学模拟, 首先研究了不同水模型的太赫兹吸收谱, 以及温度对太赫兹吸收光谱的影响. 发现不同水模型均能够定性地描述体相水的各种振动模式, 然而定量分析振动吸收峰对应的太赫兹频率值却有差异. 进一步研究了水的氢键网络振动的吸收峰的中心频率与水的相互作用之间的关系, 发现水的氢键相互作用越强, 其氢键网络的振动吸收峰的中心频率越大, 即表现出蓝移现象. 为了更进一步研究水的氢键网络强弱与其振动吸收峰的中心频率的关系, 计算了径向分布函数和扩散系数, 研究结果表明水分子具有越紧束缚的氢键网络, 其氢键网络的振动吸收峰的中心频率就越大. 最后, 基于以上分析, 发现水的氢键寿命的大小与氢键网络振动的吸收峰的中心频率之间存在线性关系. 这些发现将有利于认识水中复杂的氢键网络动力学性质和加深在分子尺度对水的振动运动的理解, 同时促进太赫兹技术在生物医学上的应用.