摘要: 基于网格的数值方法(如有限元、有限体积、有限差分等)在大变形、不连续等问题中遇到挑战, 因此人们提出了多种无网格方法. 最优输运无网格方法是一种新型拉格朗日无网格方法, 但是继承了有限元方法在边界表征、边界处理等方面的优势, 在表面张力模拟中具有较大潜力. 基于拉格朗日方程, 通过将表面张力势能加入拉格朗日函数, 得到的表面张力广义力精确地作用在流体表面, 而且表面张力系数是唯一的输入参数. 给出了最优输运无网格方法轴对称离散格式. 通过对二维/三维泊肃叶流、静止和振动的液滴、液滴变形等典型问题的仿真分析, 验证了最优输运无网格方法在表面张力问题模拟中的精度和收敛性.
关键词: 最优输运无网格方法 /
表面张力 /
拉格朗日方程 /
轴对称 English Abstract Optimized transportation meshfree method and its apllication in simulating droplet surface tension effect Zhou Hao Li Yi Liu Hai Chen Hong Ren Lei-Sheng Hypervelocity Impact Research Center, China Aerodynamics Research and Development Center, Mianyang 621000, China Received Date: 07 June 2021Accepted Date: 17 August 2021Available Online: 30 August 2021Published Online: 20 December 2021Abstract: Owing to challenges encountered by mesh-based CFD methods when simulating large material deformation, a number of meshfree methods have been presented. The optimized transportation meshfree method is a newly developed meshfree method, but it inherits the advantage of the finite element method in boundary treatment and thus having great potential applications in surface tension effect simulation. By adding the surface tension potential into the Lagrangian, the resulting generalized force acts on fluid surfaces exactly. The axial symmetry treatment is also discussed. By simulating several benchmark cases such as two- and three-dimensional Poiseuille flow, static and vibrating drop and drop deformation, the advantages like precision and convergence of the optimized transportation meshfree method in simulating surface tension effect are verified.Keywords: optimized transportation meshfree method /surface tension /Lagrangian equations /axial symmetry 全文HTML --> --> --> 1.引 言 精确可靠的模拟表面张力对液滴变形与运动的影响在环境工程、微纳米工程以及医药工程等领域有着十分重要的应用. 采用基于网格的数值方法模拟此类问题往往需要复杂的界面追踪算法, 典型的如流体体积函数法[1 ,2 ] 和水平集方法[3 ] 等. 因此, 越来越多的研究者采用拉格朗日粒子类方法模拟表面张力相关现象, 利用粒子本身实现对边界的自动追踪, 极大地简化了算法, 其中最常用的数值方法是光滑粒子动力学(smoothed particle hydrodynamics, SPH)[4 ,5 ] 方法. 在SPH方法中, 主要有两种方法来考虑表面张力的影响: 粒子间相互作用力(inter-particle interaction force, IIF)方法[6 -10 ] 和连续力方法(continuum surface force, CSF) [11 ] . IIF方法来源于如下思想, 即表面张力来自于液体表面分子之间和内部分子之间作用力的差异. 受此启发, 在SPH方法中, 可以通过在宏观粒子之间加入额外远程吸引力和近程排斥力来近似模拟表面张力. 这种方法简单灵活, 粒子之间的额外作用力形式非常多. 这种方法的缺点是表面张力系数不是输入参数, 而是需要先模拟某个标准算例, 然后测量与这种宏观粒子之间吸引力等价的表面张力系数. 此外, 这种方法往往存在不收敛的问题. CSF方法通过给不同的流体赋以不同的色值(color)来区分不同的流体, 利用不连续的色函数(color function)求解表面法向以及曲率来计表面张力, 然后将只作用在表面的力转换为连续的体积力. SPH方法中, 界面法向向量及其曲率的计算误差一般较大. 无论哪种表面张力模拟方法, SPH方法都存在如下固有缺点: 1) SPH形函数不能严格满足1阶精度(特别是粒子分布不均匀或者自由界面处), 导致收敛性不好, 常常需要对形函数及其导数进行修正[12 ,13 ] ; 2)形函数不满足Kronecker delta性质, 因此位移边界条件处理复杂, 一般需要通过各种虚粒子处理边界条件. 因此, 本文尝试采用一种新型无网格方法模拟表面张力问题, 即最优输运无网格(optimized transportation meshfree, OTM)方法[14 ] .[15 -17 ] 形函数构造连续场, 并结合数学中的最优输运理论计算系统的动能积分. 相比于其他无网格方法, OTM方法在精度、收敛性、边界处理以及数学理论基础上均具有优势. OTM方法具有无网格方法能够处理大变形的优点, 同时又继承了有限元方法的部分优点, 如形函数严格满足一阶精度、形函数在边界处满足弱Kronecker delta性质等. 当前, OTM方法已经成功应用于金属侵彻[18 ] 、超高速碰撞[19 -21 ] 、裂纹扩展[22 ] 以及热传导等问题[23 ] , 但是将其应用于表面张力模拟还未见文献报道.2.OTM方法 22.1.连续介质离散 2.1.连续介质离散 OTM方法中的连续介质离散介于拉格朗日有限元与SPH方法之间. OTM方法将有限元网格中每个小网格转换为1个粒子, 位于小网格形心. 对于三角形, 形心为三条中线的交点. 粒子存储所有的物理量, 与SPH方法类似. 同时, 保留所有的网格节点, 其中存储了速度和位置, 如图1 所示. 初始时刻, 边界上只有节点, 且节点随着流场运动. 边界节点很好地表征了连续介质的边界位置, 与拉格朗日有限元方法类似. 此外, 由于局部最大熵形函数满足弱Kronecker delta性质, 边界条件处理简单. 抛弃有限元方法中单元和节点之间的固定连接关系, 而是采用近邻粒子搜索方式动态确定, 从而可以处理大变形, 这与SPH方法类似.图 1 利用有限元网格将连续介质离散为粒子和节点 (a)有限元网格; (b)用粒子与节点离散连续介质Figure1. Continuum discretized by particles (red symbols) and nodes (white symbols) in the OTM method by means of finite element mesh: (a) Finite element mesh; (b) continuum discretized by particles and nodes.2.2.LME形函数 -->2.2.LME形函数 最优输运无网格方法与更新拉格朗日有限元方法最大的1个区别是采用LME形函数, 因此不需要网格, 属于无网格方法. 给定1个节点集$ {\boldsymbol{x}}_{a}(a= $ $ 1, 2, \cdots , n) $ , 每个节点的形函数记为$ {N_a}({\boldsymbol{x}}) $ . 利用形函数可以从离散数值插值出1个连续场:$ {u^h}({\boldsymbol{x}}) $ 是插值出来的连续场, $ {u_a} $ 是物理量u 在节点a 处的值. 在有限元和SPH等方法中, 形函数及其导数都具有简单解析表达式, 但是LME形函数没有显式的解析表达式, 而是需要数值求解.1 )式可以精确重构常数场, 那么有$\displaystyle \sum\nolimits_a {{N_a}({\boldsymbol{x}}) = 1}$ , 即形函数满足归一化条件. 此外, 对于固定的x $ {N}_{a}(a=1, 2, \cdots , n) $ 可以看成是某个事件的概率分布, 其熵为x $ \left| {{\boldsymbol{x}} - {{\boldsymbol{x}}_a}} \right| $ 大于某一临界值时, 形函数$ {N_a}({\boldsymbol{x}}) $ 为零. 因此, 可以定义如下形函数影响域平均大小:β 是1个可调参数, 用于调节两个目标的权重. 最后1个约束条件表示形函数严格满足一阶精度. 上述优化问题解的存在性、唯一性以及求解方法文献[15 -17 ]中有详细论述, 本文只给出最后结果. LME形函数可以写成如下形式:Z 函数的定义为$ {{\boldsymbol{\lambda }}^*}({\boldsymbol{x}}) $ 是以下无约束优化问题的解:$ {{\boldsymbol{\lambda }}^*}({\boldsymbol{x}}) $ :$ {{\boldsymbol{\lambda }}^{(0)}} $ 一般取零. 流场发生变化后, $ {{\boldsymbol{\lambda }}^{(0)}} $ 一般取上1个时刻的$ {{\boldsymbol{\lambda }}^*} $ . 当β 等于零时, 得到的最大熵形函数是全局的, 不适合数值计算. 当β 趋于无限大时, 即不考虑熵最大, 只要求形函数影响域最小, 那么LME形函数可以连续过渡到有限元线性形函数. LME形函数具有以下特点: 1)满足一阶精度; 2)不依赖网格; 3)边界处满足弱Kronecker delta性质; 4)形函数非负.$ {{\boldsymbol{\lambda }}^*}({\boldsymbol{x}}) $ 与形函数后, 形函数导数为2.3.基本离散方程 -->2.3.基本离散方程 首先考虑无黏、可压缩以及等温流体. 当初始状态已知, 节点的位置描述了流场的形变的流动, 实际上完全描述了流场, 因此, 节点的位置可以当成系统的广义坐标. 本文下标p 表示粒子, 用下标a , b , c 表示节点. 由于无黏, 这是1个保守系统, 拉格朗日方程为E 是系统动能, V是 系统势能, $ {{\boldsymbol{f}}_a} $ 是广义节点力, $ {{\boldsymbol{v}}_a} $ 是节点速度, $ {{\boldsymbol{x}}_a} $ 是节点位置, N 是节点总数. 系统动能和势能为所有粒子动能和内能之和:$ {m_p} $ 表示粒子质量, $ {{\boldsymbol{v}}_p} $ 表示粒子速度, $ {e_p} $ 表示粒子单位质量内能, $ {\rho _p} $ 表示粒子密度.$ {\text{δ}} {{\boldsymbol{x}}_{p}} $ 和$ {\text{δ}} {{\boldsymbol{x}}_a} $ 分别为粒子和节点的虚位移, $ {N_a}({{\boldsymbol{x}}_{p}}) $ 表示节点a 处形函数在粒子p 处的值, $ \nabla {N_a}({{\boldsymbol{x}}_p}) $ 表示形函数梯度, 求和是对粒子的所有近邻节点. 粒子密度变化和位置变化的关系由连续性条件给出:14e )式代入(15 )式, 得到13 )式和(16 )式, 得到12a )式、(14c )式和(14d )式得到18 )式中交换求和顺序, 拉格朗日方程变成:M 19 )式与更新拉格朗日有限元格式有两点区别: 1)有限元格式中的单元积分对应了OTM中的粒子积分; 2)有限元中使用基于网格的形函数, 而OTM方法中使用无网格的局部最大熵形函数. 注意到局部最大熵形函数可以连续过渡到有限元线性形函数, 因此, OTM方法可以看成是一种特殊的单点积分拉格朗日有限元方法.23 )式代入(11 )式, 得到如下离散方程:20 )式和(21 )式可知, 节点质量刚好就是相容质量矩阵按行求和. 利用节点广义力和节点质量可以更新节点的速度和位置:25b )式更新节点位置后, 粒子位置根据(14a )式更新. 注意到节点位置变化代表了流场的形变, 因此两个相邻时刻的连续映射$\varphi :{{\boldsymbol{x}}^k} \to {{\boldsymbol{x}}^{k + 1}}$ 可以通过更新的节点位置插值得到28 )式可以用于更新粒子密度. 粒子密度更新后, 根据物态方程更新粒子压力.2.3.1.流体黏性的处理 -->2.3.1.流体黏性的处理 以上推导没有考虑黏性, 因而是保守系统. 处理非保守力的基本想法将其看成外力, 然后利用虚功原理推导对应的广义力. 假设$ {{\boldsymbol{f}}_p} $ 是作用在粒子p 上的外力, 那么此力的虚功为$ {{\boldsymbol{f}}_p} = {m_p}{\boldsymbol{g}} $ . 根据(30 )式得到广义力${{\boldsymbol{f}}_a} = \displaystyle \sum\nolimits_p {{m_p}{\boldsymbol{g}}{N_{a, p}}}$ . 考虑到重力实际上是保守力, 因此也可以将重力势能加入拉格朗日函数中, 得到重力对应的广义力. 简单计算可以证明两者是一致的.μ 为黏性系数.31 )式也能通过势能和拉格朗日方程得到. 从(33 )式可以看到, 1个粒子在无限短时间内受到的力只和应力张量本身有关, 而和应力应变关系无关. 因此, 可以临时假设1个线性应力应变关系, 从而得到简单的弹性势能. 对弹性势能求变分, 就得到了相应的广义力, 详细证明见附录A . 两种方法的结果是一致的.2.3.2.表面张力处理 -->2.3.2.表面张力处理 考虑二维情况, 液体边界被边界节点表征, 如图2 所示.图 2 二维条件下的边界节点(白点)Figure2. Boundary nodes (white symbols) in two-dimensional coordinate.$ {r_{ab}} = \left| {{{\boldsymbol{x}}_a} - {{\boldsymbol{x}}_b}} \right| $ , $ {r_{ac}} = \left| {{{\boldsymbol{x}}_a} - {{\boldsymbol{x}}_c}} \right| $ 为节点之间的间距. γ 是表面张力系数. 对(35 )式求变分, 得到广义力36 )式非常简洁, 可以解释为节点a 同时受到两个相邻节点b 和c 的吸引力, 吸引力大小刚好等于表面张力系数. (36 )式中没有可调参数, 表面张力系数是唯一的输入参数. 此外, 表面张力对应的广义力只作用在表面节点上, 即精确的作用在流体表面.2.3.3.轴对称处理 -->2.3.3.轴对称处理 记(r , θ , h )为柱坐标系, 并且假设环向没有位移, 而且所有物理量都和环向坐标无关, 即$ {\text{δ}} {u_\theta } = 0 $ , $ \partial /\partial \theta = 0 $ . 定义:11 )—(14 )式依然成立. 速度矢量散度在柱坐标下的表达式为15 )需要修改为$ {{\boldsymbol{n}}_r} $ 是径向单位向量. 于是, 轴对称条件下的广义力为18 )—(26 )式仍然成立. 注意(27 )式中的变形梯度张量的行列式表征的是粒子在(r , h )平面上的面积的变化:r , h )平面上的面积$ {S^{k + 1}} $ , 然后再更新密度:30 )式仍然成立. 黏性力对应的广义力也仍然成立, 详细证明见附录B .$ {\tilde r_{ab}} = {r_a} + {r_b} $ , $ {\tilde r_{ac}} = {r_a} + {r_c} $ . $ {r_k}(k = a, b, c) $ 为节点的径向坐标. 对(44 )式求变分, 得到表面张力对应的广义力:b 和节点c 对节点a 的吸引力, 后两项为对称轴对边界节点的吸引力. 可见, 笛卡尔坐标系下的OTM计算格式只需要经过微小改动, 就能计算三维轴对称问题.2.4.OTM方法详细步骤 -->2.4.OTM方法详细步骤 笛卡尔坐标系下, 采用OTM方法模拟表面张力的详细步骤总结如下.$ {N_{a, p}} $ 和形函数导数$ \nabla {N_{a, p}} $ .3.典型算例 所有的初始化借助于有限元网格. 网格节点变成节点, 网格形心放置粒子, 粒子体积即为网格大小. 物态方程如下:$ {\rho _0} $ 表示材料初始密度, ρ 表示当前密度, $ {c_0} $ 表示声速, p 表示压力.3.1.泊肃叶流 3.1.泊肃叶流 两块无限长的二维平板中间充满了静止液体, 液体在平行于平板方向的体积力作用下开始运动, 称之为泊肃叶(Poiseuille)流. 如果是无限长的三维圆管, 那么称之为Hagen-Poiseuille流. 对于二维泊肃叶, 参数和文献[24 ]一样, 解析解见文献[24 ]. 将平板距离变成圆管半径, 即为Hagen-Poiseuille流, 解析解见文献[25 ]. OTM模拟结果见图3 .图 3 速度分布的OTM模拟与解析解对比 (a) 二维泊肃叶流; (b) 三维轴对称泊肃叶流Figure3. Comparison of OTM (symbols) and analytic solutions (solid curves) for velocity profile: (a) Two-dimensional Poiseuilleflow; (b) axisymmetric Hagen-Poiseuille flow.3.2.静止液滴 -->3.2.静止液滴 二维液滴的半径R = 0.2 m, 密度ρ = 1 kg/m3 , 表面张力系数γ = 1 Pa·m, 黏性系数η = 0.5 Pa·s, 声速c 0 = 50 m/s. 静止状态下液滴的理论压力值可以根据Young-Laplace 公式得到ρ = γ /R = 5 Pa. 如果是三维液滴, 那么其理论压力值为ρ = 2γ /R = 10 Pa. OTM模拟的平均压力分别为 5.004 Pa和 9.967 Pa. 压力分布如图4 所示.图 4 静止液滴的压力场 (a) 二维液滴; (b) 轴对称三维液滴Figure4. Pressure field: (a) Two-dimensional rod; (b) axisymmetric three dimensional drop.3.3.液滴的周期振荡 -->3.3.液滴的周期振荡 在上1个算例的基础上, 将黏性减小到$ \eta = $ $ 5 \times {10^{ - 3}} $ Pa·s, 并且附加1个散度为0的初始速度场$ {v_x} = x $ , $ {v_y} = - y $ 给所有节点. 二维液滴的理论振荡周期为$ T = 2{\text{π }}\sqrt {\rho {R^3}/6\gamma } $ [26 ] . 为了验证OTM方法的收敛性, 采用不同的粒子总数模拟这个问题, 并且检查两条相互垂直线$ x = 0 $ 和$ y = 0 $ 上的物理量分布, 时刻$ t = T/2 $ , 如图5 所示.图 5 t = T /2时刻的压力和速度分布 (a) x = 0上的压力分布; (b) x = 0上的速度分布; (c) y = 0上的压力分布; (d) y = 0上的速度分布Figure5. Pressure and velocity profile at t = T /2: (a) Pressure profile at x = 0; (b) velocity profile at x = 0; (c) pressure profile at y = 0; (d) velocity profile at y = 0.图6 所示. 周期是根据液滴右上部分质心轨迹测量得到, 与文献[26 ]一样.图 6 二维液滴振荡 (a) 振荡周期理论解和数值解得对比; (b) 表面张力系数为$ \gamma = 1 $ 时液滴右上部分质心的轨迹Figure6. Two-dimensional rod oscillation: (a) Comparison of period between the numerical (symbols) and analytical (solid curve) results; (b) center of mass position history when $ \gamma = 1 $ .$ {v_{\text{r}}} = r $ , $ {v_h} = - 2 h $ , 其他物理量不变. 振荡周期的理论解为$ T = 2\pi \sqrt {\rho {R^3}/8\gamma } $ [27 ] . 模拟结果与理论的对比如图7 所示. 模拟的周期根据对称轴端点的位置轨迹测量. 可以看到, 两种情况下OTM计算结果和理论非常吻合.图 7 轴对称三维液滴振荡周期与理论的对比Figure7. Three-dimensional droplet oscillation, comparing of period between the numerical (symbols) and analytical (solid curve) results.3.4.液滴形变 -->3.4.液滴形变 将液滴半径扩大到 1 m, 表面张力系数扩大到10 Pa·m, 加上大小为10 m/s2 的重力. y = –1 m处放置1个光滑的固定平板. 液滴在重力、表面张力以及光滑平板的共同作用下产生变形, 如图8 所示.图 8 压力场 (a) t = 0 s; (b) t = 0.02 s; (c) t = 0.4 s; (d) t = 4 sFigure8. Pressure field at several typical times: (a) t = 0 s; (b) t = 0.02 s; (c) t = 0.4 s; (d) t = 4 s.图8(d) 中, 压力等值线与重力垂直, 和理论相符. 液滴内部的压力场需要满足两个条件, 一是压力沿Y 轴的线性分布规律$ {\text{δ}} p = \rho g{\text{δ}} Y $ , 另一个是自由表面附近的压力满足Young-Laplace方程$ p = \gamma /R $ . 这两个条件实际上决定了液滴的形状, 即液滴自由表面部分的微分方程为H 和p 0 分别为液滴最高点的Y 坐标和压力. 上述理论曲率半径在实际计算时误差太大, 因此, 本文采用如下方法计算曲率半径: 对于每个边界节点, 找到与其相邻的4个表面节点, 然后用1个圆来拟合这5个节点, 即$\mathop {\min }\limits_{{x_0}, r} \displaystyle \sum\nolimits_{i = 1}^5 {{{(\left| {{x_i} - {x_0}} \right| - r)}^2}}$ , 自由变量为圆的中心坐标和半径. 圆的半径即为此节点的曲率半径.图9(a) 所示. 采用曲率半径计算的边界压力和根据EOS计算的压力比较如图9(b) 所示.图 9 边界位置和压力 (a) 边界位置; (b) 边界压力与Y 轴坐标的关系, 压力根据表面曲率和EOS计算Figure9. Boundary position and pressure profile: (a) Boundary position; (b) boundary pressure versus Y coordinate, computed by Young-Laplace equation (circles) and EOS (points).Y 轴方向的线性分布和理论相符, 拟合直线的斜率也和理论$ {\text{d}}p/{\text{d}}Y = - \rho g = - 10 $ Pa/m相符.4.结 论 本文基于拉格朗日方程, 通过将表面张力势能加入拉格朗日函数, 得到了OTM方法框架下的表面张力效应表达式, 并且给出了轴对称的处理方式. 模拟了泊肃叶流, 静止和振荡的液滴, 液滴在重力、表面张力以及光滑平板共同作用下的形变等典型算例, 通过与解析解对比, 验证了OTM方法在模拟表面张力现象中具有如下优势: 1)表面边界节点精确的表征了边界的位置, 保证了表面张力势能的准确计算, 而且表面张力对应的广义力精确的作用在流体表面; 2)表面张力对应的广义力形式简洁, 具有直观的物理意义, 而且表面张力系数是唯一的输入参数, 不需要任何可调参数; 3)可以保证速度分布的空间收敛性.附录A.黏性应力张量对应广义力的势能方法推导 下面给出(33 )式的势能推导方法. 将应力和应变张量写成向量形式${:} $ L u 是位移. 广义胡克定律为c 16 )式写成矩阵形式:$ \nabla {N_{a, p}} $ 为列向量. 对于固定的应力张量$ {{\boldsymbol{\sigma}}_p} $ , 由于c A12 )式第二项中有应变, 因此是小量, 可以忽略A13 )式和 (33 )式一致.附录B.轴对称条件下黏性力对应的广义力 两个张量的双点乘是1个标量, 因此, 可以在柱坐标下求解37a )式和(37c )式, 虚功为B3 )式与(32 )式相同. 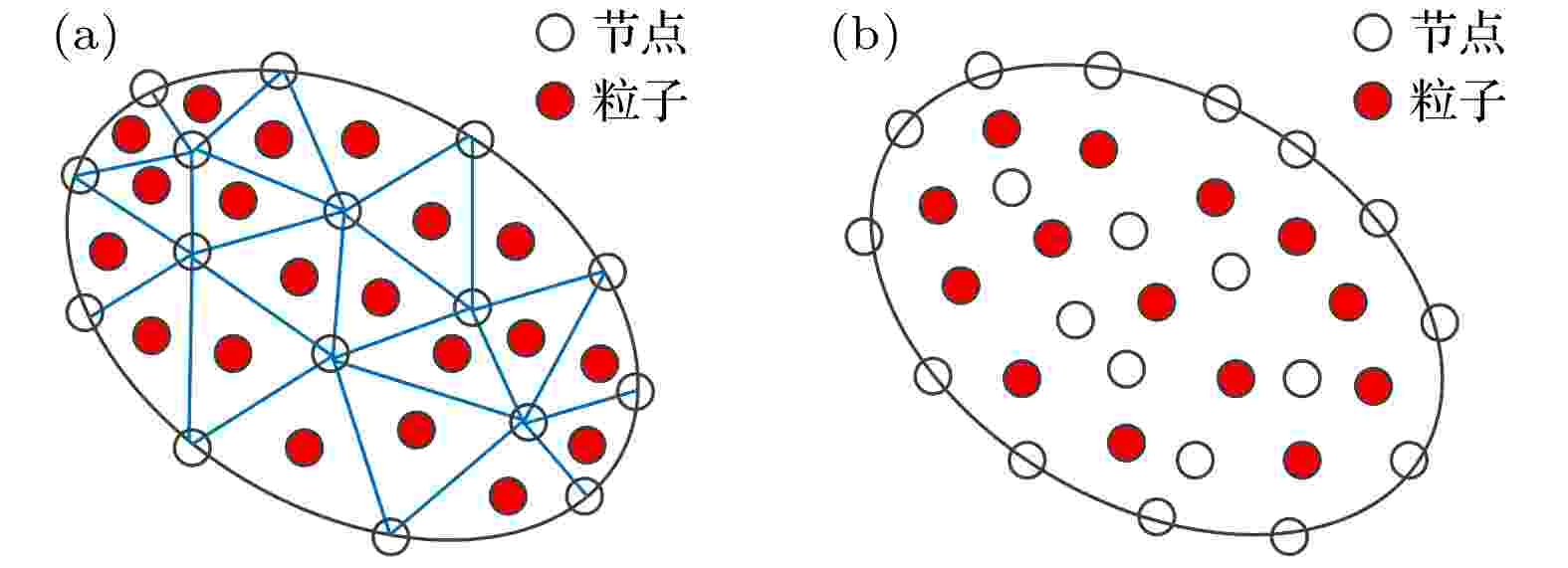 图 1 利用有限元网格将连续介质离散为粒子和节点 (a)有限元网格; (b)用粒子与节点离散连续介质
图 1 利用有限元网格将连续介质离散为粒子和节点 (a)有限元网格; (b)用粒子与节点离散连续介质































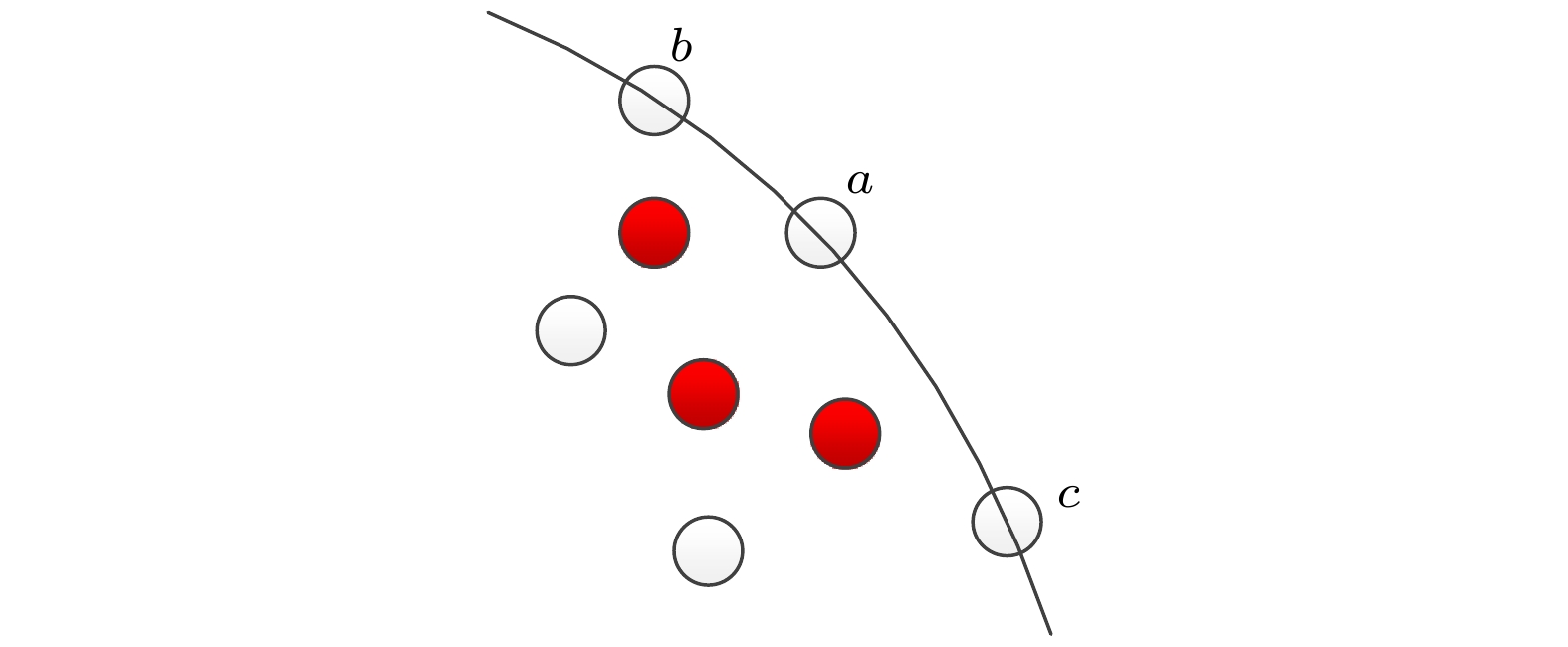 图 2 二维条件下的边界节点(白点)
图 2 二维条件下的边界节点(白点)












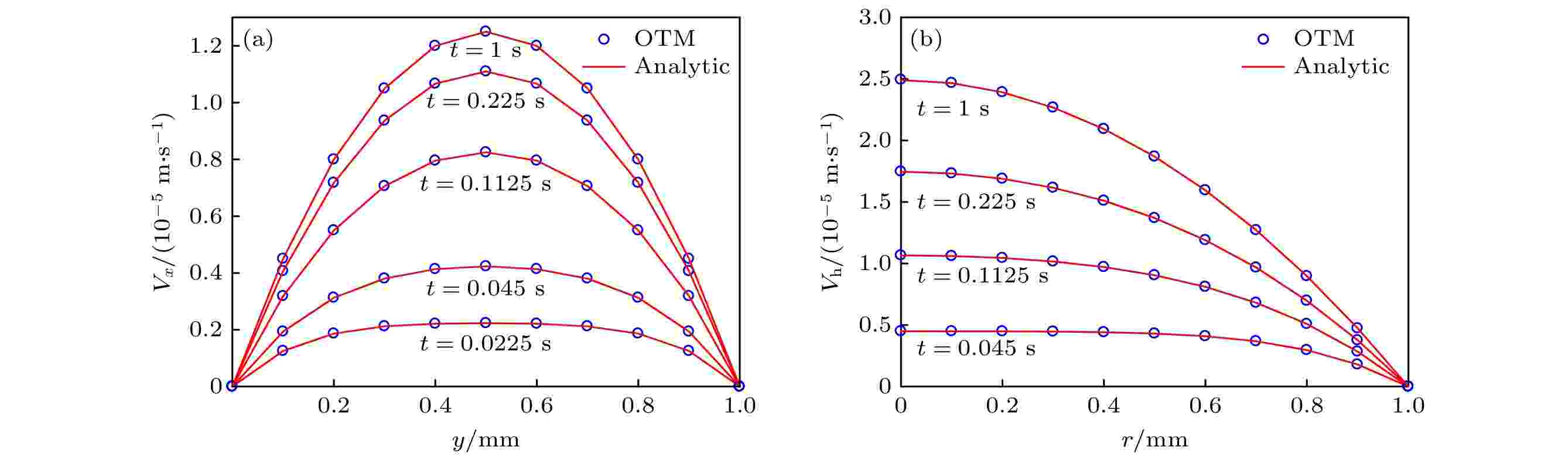 图 3 速度分布的OTM模拟与解析解对比 (a) 二维泊肃叶流; (b) 三维轴对称泊肃叶流
图 3 速度分布的OTM模拟与解析解对比 (a) 二维泊肃叶流; (b) 三维轴对称泊肃叶流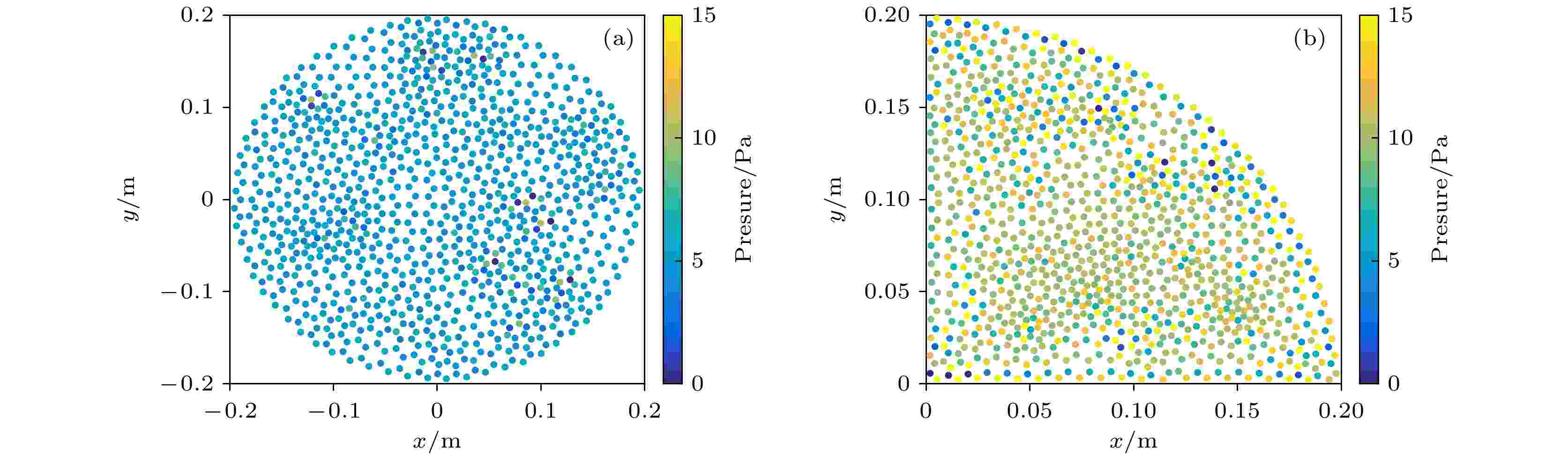 图 4 静止液滴的压力场 (a) 二维液滴; (b) 轴对称三维液滴
图 4 静止液滴的压力场 (a) 二维液滴; (b) 轴对称三维液滴







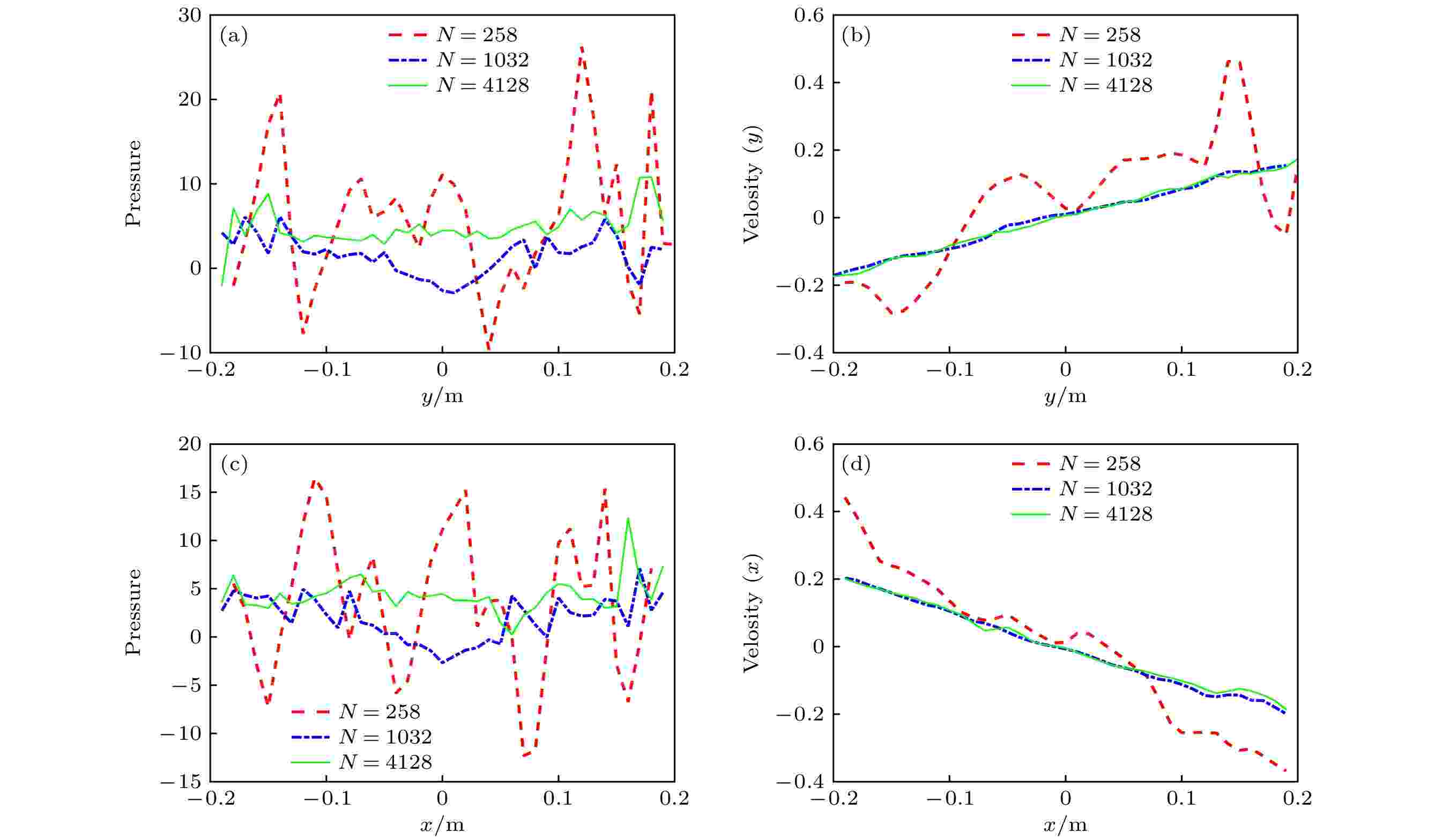 图 5 t = T/2时刻的压力和速度分布 (a) x = 0上的压力分布; (b) x = 0上的速度分布; (c) y = 0上的压力分布; (d) y = 0上的速度分布
图 5 t = T/2时刻的压力和速度分布 (a) x = 0上的压力分布; (b) x = 0上的速度分布; (c) y = 0上的压力分布; (d) y = 0上的速度分布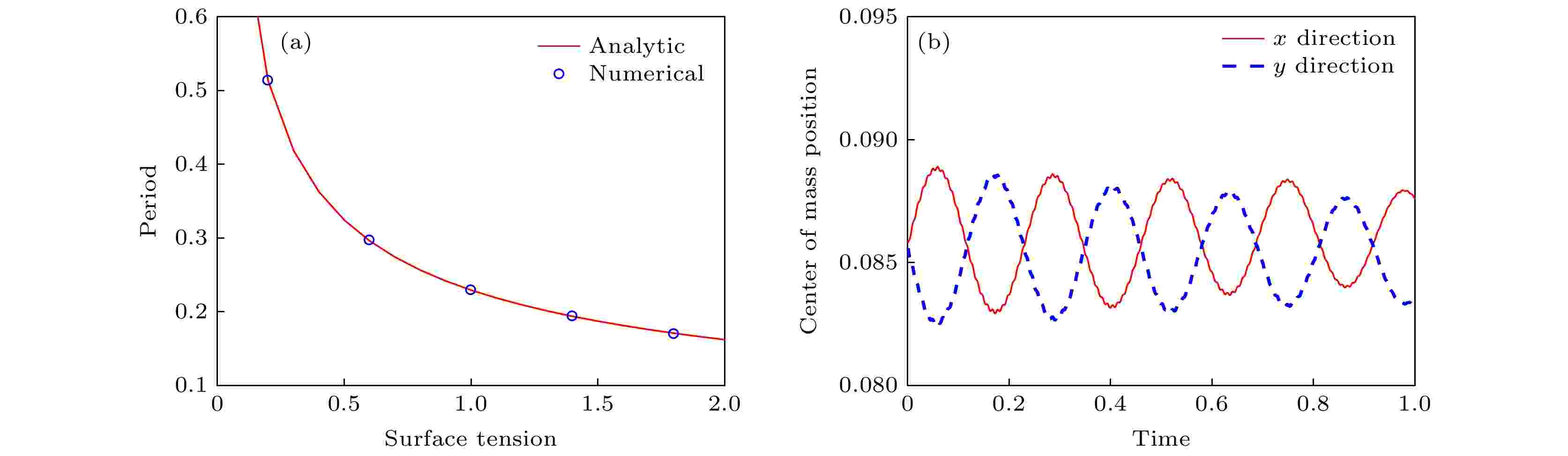 图 6 二维液滴振荡 (a) 振荡周期理论解和数值解得对比; (b) 表面张力系数为
图 6 二维液滴振荡 (a) 振荡周期理论解和数值解得对比; (b) 表面张力系数为




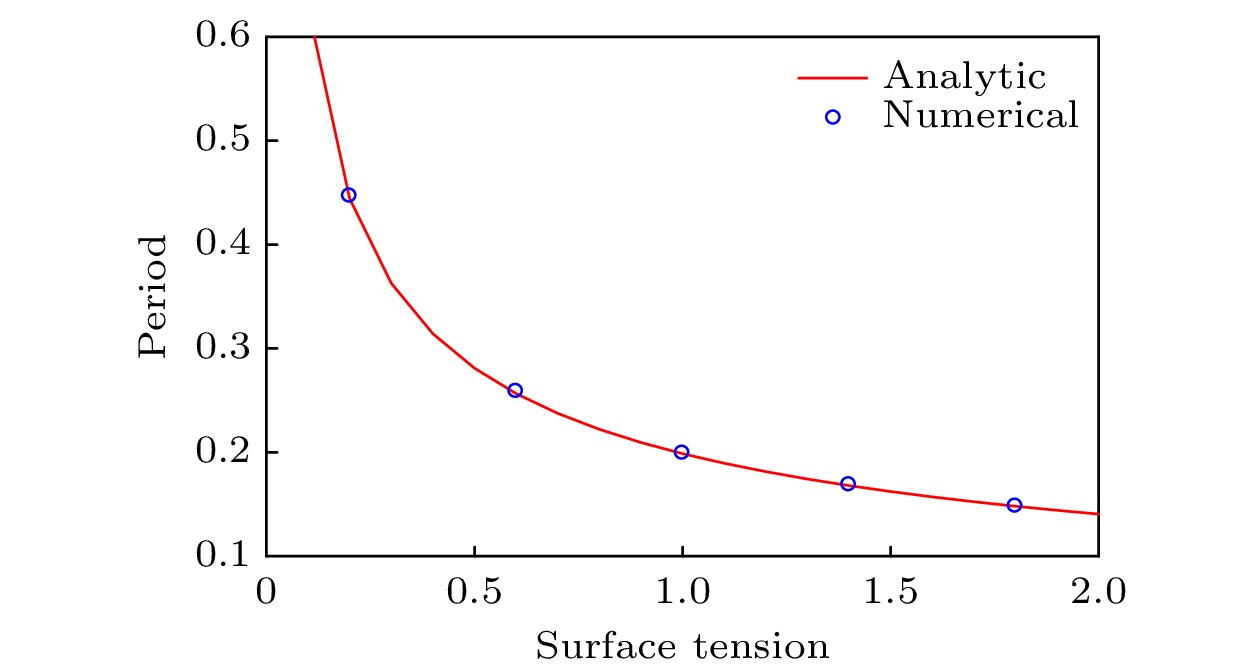 图 7 轴对称三维液滴振荡周期与理论的对比
图 7 轴对称三维液滴振荡周期与理论的对比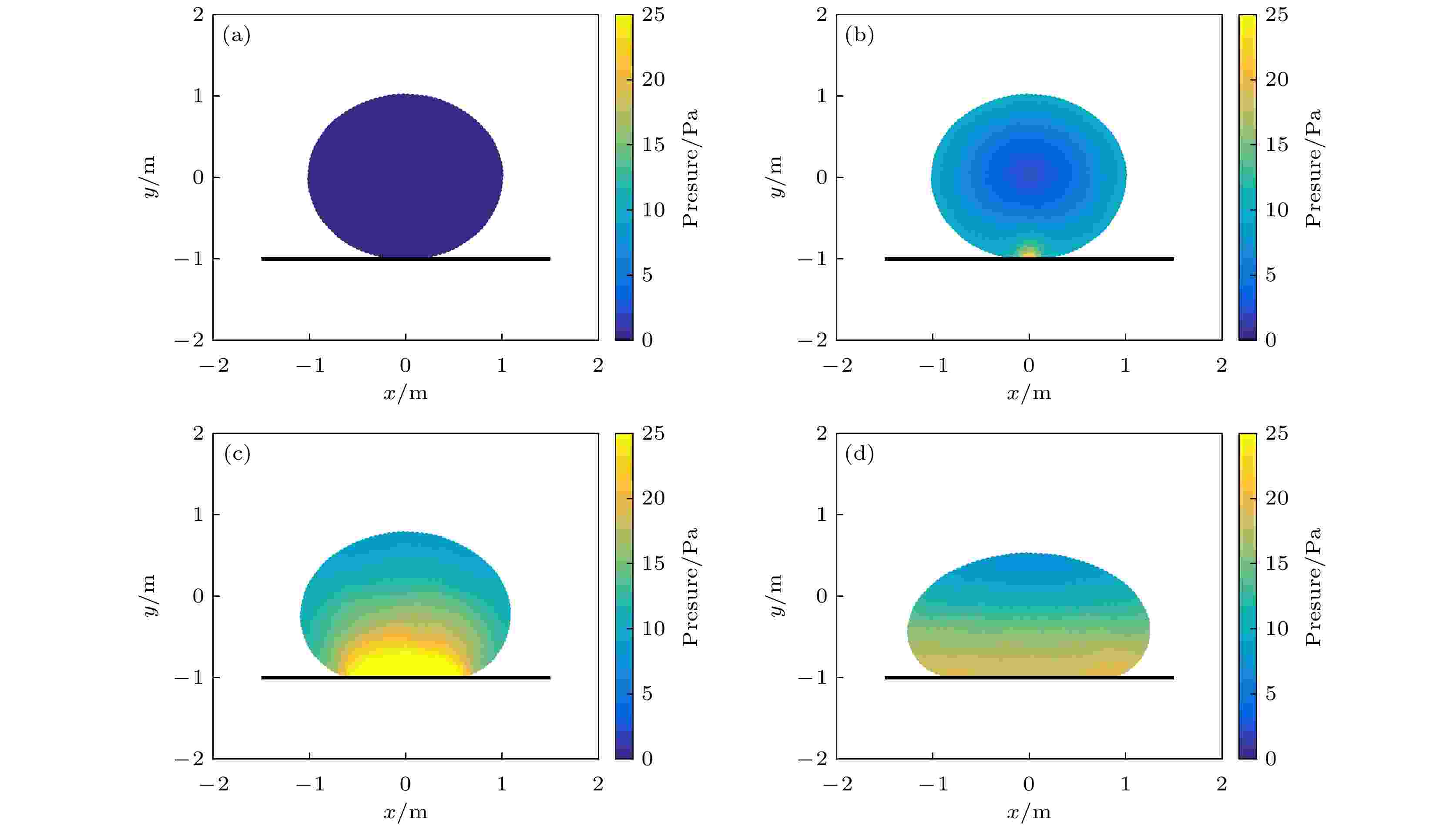 图 8 压力场 (a) t = 0 s; (b) t = 0.02 s; (c) t = 0.4 s; (d) t = 4 s
图 8 压力场 (a) t = 0 s; (b) t = 0.02 s; (c) t = 0.4 s; (d) t = 4 s


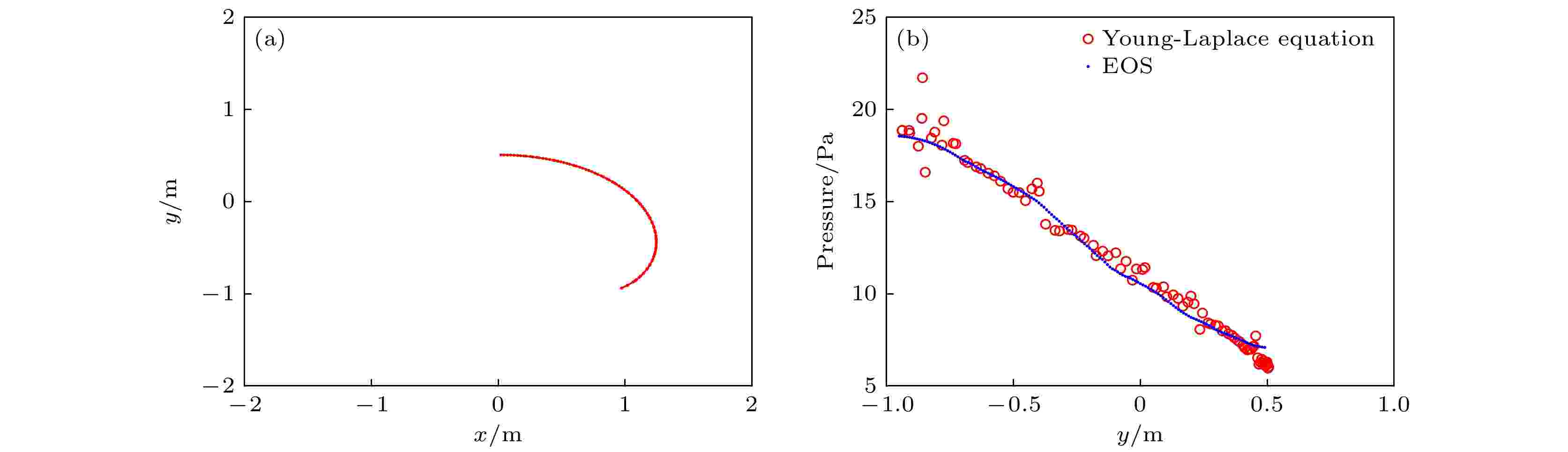 图 9 边界位置和压力 (a) 边界位置; (b) 边界压力与Y轴坐标的关系, 压力根据表面曲率和EOS计算
图 9 边界位置和压力 (a) 边界位置; (b) 边界压力与Y轴坐标的关系, 压力根据表面曲率和EOS计算



