摘要:将液滴沉积在高于Leidenfrost温度的表面上, 液滴将悬浮在自身的蒸汽垫上, 这使液滴具有惊人的移动性, 通常通过构造不对称的微纳结构表面对液滴下方的蒸汽流进行校正, 实现液滴自驱动. 但液滴运动方向和液滴输运速度(10—40 cm/s)具有局限性. 本实验构造Leidenfrost传热面和撞击面, Leidenfrost传热面用于悬浮液滴并为其提供足够的能量, 当Leidenfrsot液滴(燃料)与撞击面(点火器)接触时, 粗糙环的大量微/纳米腔不仅会向液滴产生额外的辐射热量, 而且还会提供成核点以在约10 ms内触发爆炸沸腾. 利用周期性爆炸沸腾产生的脉冲推力F_th实现液滴自驱动. 液滴运动初始阶段由于惯性力F_i占主导, 液滴撞击多为镜面反射, 液滴运动轨迹较为混乱, 随着液滴直径减小, 脉冲推力F_th占主导, 液滴轨迹通过Leidenfrost传热面中心. 同时液滴输运速度高达68.91 cm/s, 这是在以往微纳结构表面液滴自驱动从未实现的. 这一发现为高温下操纵液滴提供了新的思路, 有望在微流控和传热等两相系统中得到重要的应用.
关键词: Leidenfrost/
液滴动力学/
爆炸沸腾/
热量传递

English Abstract

全文HTML

--> --> -->

将液滴沉积在高于沸点温度的表面上, 液滴会悬浮在自身的蒸汽垫上, 这种现象称为Leidenfrost效应^[1]. 由于蒸汽层的有效润滑作用减少了液滴与固体表面的摩擦阻力, 因而液滴在热表面上方变得极易移动^[2], 使其在微流体机械技术和生物工程等领域具有重大应用前景. 如微齿轮泵^[3]、药物输运^[4]和生物芯片^[5]等. Leidenfrost液滴在自身蒸汽层上悬浮, 这使其具有长寿命化、超疏水性和高迁移率的特性, 在没有摩擦的情况下, Leidenfrost液滴具有随机运动特点. 采用壁面润湿性梯度^[6,7]、微结构梯度^[8,9]以及温度梯度^[10]等, 将液滴随机运动转换为定向运动, 使Leidenfrost液滴具有不对称受力, 实现液滴自驱动. 液滴、蒸汽和固体之间复杂的相互作用涉及影响液滴动力学的多种效应, 包括黏性力在蒸汽层中的重要作用^[11]、不均匀温度引起的Marangoni效应^[12,13]和在锯齿结构上不同的蒸汽压作用^[14,15]. Jia等^[14]注意到由于锯齿结构中蒸汽压分布不均匀, 液滴动力学行为表现为前进、后退甚至静止三种模式.
近年来, 与Leidenfrost有关的爆沸现象引起了关注, 爆沸指的是极短时间内, 汽泡在液体中快速长大, 对周围液体造成强烈扰动, 并伴随脉冲压力的输出. 在微流控领域, 采用爆沸产生的压力驱动流体是微泵的工作原理之一^[16]. 理论上, 最剧烈的爆沸发生在均质成核温度下, 在该温度下, 纯净液体也能形成汽化核心, 高过热度液体快速释放储存的能量, 形成爆沸. 采用小面积热源高热流密度(10—100 MW/m²量级)的超快脉冲加热, 可实现爆沸过程^[17]. Lyu等^[18]发现Leidenfrost液滴蒸发后期存在弹跳和爆沸两种可能, 指出初始液滴直径和颗粒浓度是决定Leidenfrost液滴蒸发后期动力学行为的关键参数. 随着液滴蒸发的进行, 液滴尺寸越来越小, 液滴中的颗粒浓度越来越大, 并在蒸发后期, 颗粒趋向于自组装在液滴表面, 充当核化穴角色, 是Leidenfrost液滴蒸发后期产生爆沸的机理.
综上, 尽管微/纳结构表面液滴自驱动已进行了较多研究, 但液滴在此类表面是否运动、如何运动、其运动方向的确定等均与表面几何结构参数、液滴工质种类、液滴尺寸及表面温度等有关, 具有不确定性, 蕴含的物理机理没有完全被揭示. 此外, 现有的构造微纳表面形貌的表面处理技术较为复杂、昂贵和费时. 而且, 在机械力和化学污染下表面形貌的稳定性对于表面设计而言始终是相当大的挑战. 迫切需要开发简单、有效且无成本的Leidenfrost液滴自驱动结构表面. 本实验充分利用Leidenfrost液滴随机运动特性, 通过制造简单的Leidenfrost传热面和撞击面, 控制液滴在Leidenfrost传热面上不发生沸腾, 而粗糙撞击环为液滴提供核化穴, 触发爆炸沸腾, 吸收撞击面热量, 并释放储存于液滴中的能量, 液滴快速膨胀诱导其脱离撞击面, 重新返回到Leidenfrost传热面, 并触发下一轮碰撞. 本文综合采用光学及声学同步测量方法, 探讨周期性爆沸式液滴自驱动现象、规律及机理, 阐明周期性爆沸式液滴如何转化为液滴动力学中的可控可调性.

火箭高速行进是由于热气流高速向后喷出, 利用产生的推力向前运动, 受火箭发射原理的启发, 本研究提出控制液滴动力学的新方法(见图1), 该装置由两种表面组成—Leidenfrost传热面及撞击面, Leidenfrost传热面用于液滴悬浮并为作为“燃料”的液滴提供足够的能量, 而撞击面作为“点火器”. 当Leidenfrsot液滴(燃料)与圆环(点火器)接触时, 撞击面为高温液滴提供大量核化穴, 触发液滴爆炸沸腾, 释放液体中储存的能量, 使液滴快速膨胀, 就像火箭发射一样, 获得向心推力, 产生自驱动, 并与撞击面再次碰撞, 实现液滴往复运动.
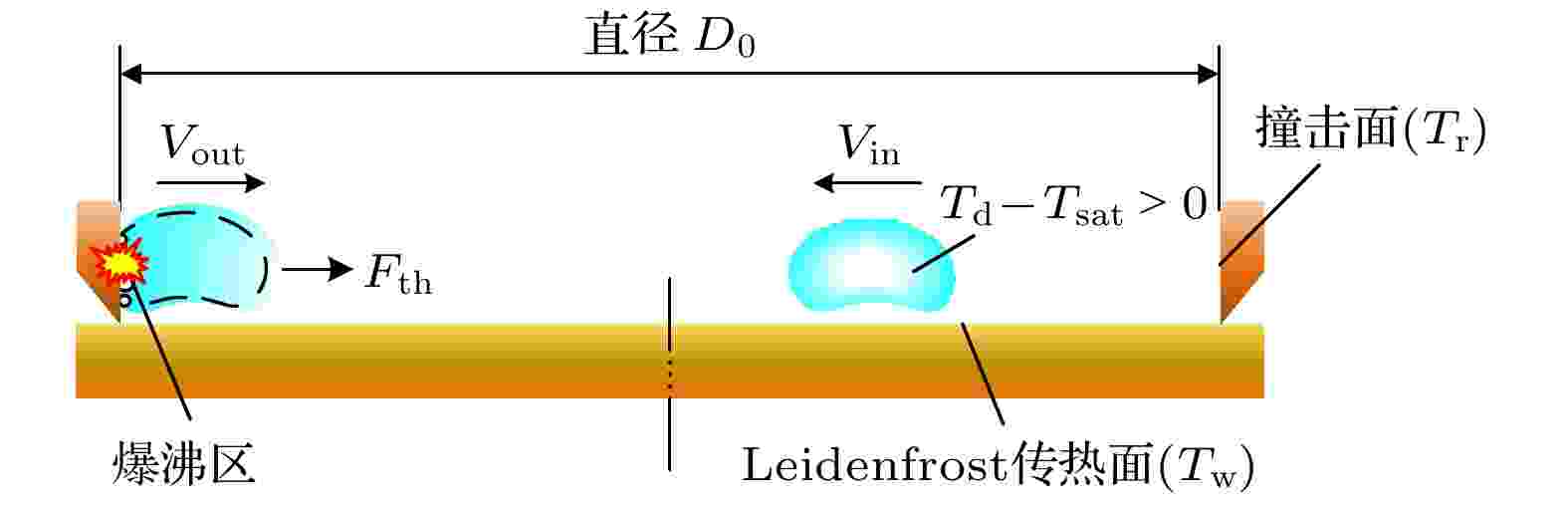图 1 爆炸沸腾触发液滴自驱动的新方法
Figure1. A new method of explosive boiling to trigger the self-propulsion of droplet.

2

-->

3.1.实验系统

为验证以上控制液滴动力学的想法, 建立如图2(b)所示的实验装置, 为更好地实现液滴在Leidenfrost传热面处于悬浮状态, 衬底温度T_w应高于Leidenfrost 转变温度T_t. 为使液滴撞击圆环发生爆炸沸腾, 圆环温度T_r应低于T_t. 因此T_w和T_r之间应该存在温差. 为此, 本研究采用异质结构: Leidenfrost传热面采用黄铜材质, 撞击圆环采用紫铜材质. 圆环外径为30 mm, 且紫铜圆环底部设置60°倒角, 使其与底板为线接触产生热阻从而形成温差. 实验开始前, 将Leidenfrost传热面调成水平, 并用角度仪测量, 传热面与水平方向的偏差为0.1°.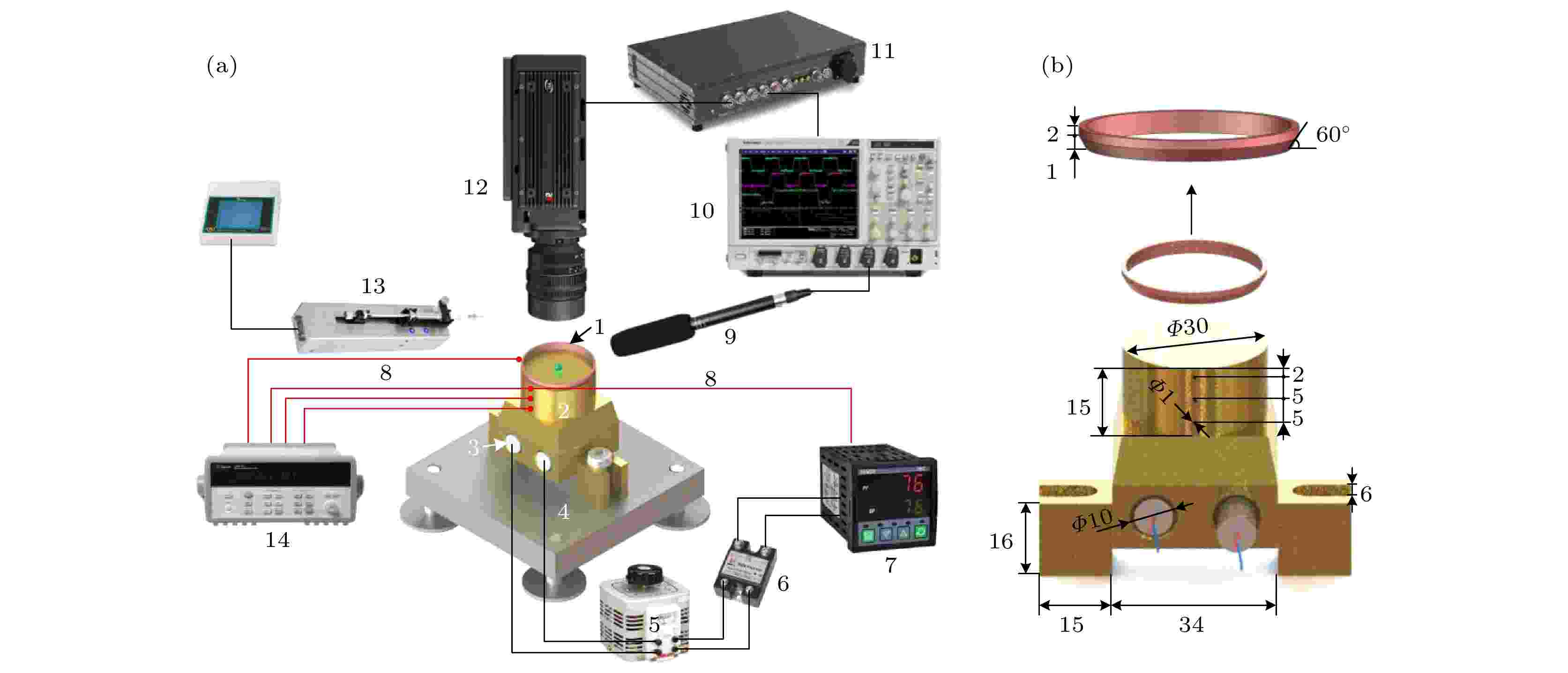
图 2 (a)实验装置图. 1, 紫铜环; 2, 黄铜加热块; 3, 加热棒; 4, 不锈钢底座; 5, 调压器; 6, 继电器; 7, PID温控仪; 8, K型热电偶; 9, 麦克风; 10, 高速数据采集仪(ScopeCorder DL750); 11, 同步器(MotionPro Timing Hub); 12, 高速相机(MotionPro Y4, IDT); 13, 微注射泵(RSP01-BDG); 14, 安捷伦34970A. (b) 黄铜加热块和紫铜环尺寸 (单位: mm)
Figure2. (a) Experimental setup. 1, copper skirt ring; 2, brass heating block; 3, cartridge heater; 4, stainless steel base; 5, voltage transformer; 6, electric relay; 7, PID temperature controller; 8, K thermocouple; 9, microphone; 10, high speed data acquisition system (ScopeCorder DL750; 11, synchronizer (MotionPro Timing Hub); 12, high speed camera (MotionPro Y4, IDT); 13, micro-syringe pump (RSP01-BDG); 14, Agilent 34970A. (b) Brass heating block and copper ring size (all dimensions are in mm).

实验系统由控温系统、实验件、微型注射泵(RSP01-BDG)、高速摄影系统(MotionPro Y4, IDT)、高速红外测温系统(InfrcTec, ImageIR 5380)、麦克风(SGC-578)、同步器(MotionPro Timing Hub, IDT)、高速数据采集系统(DL750 ScopeCorder, YOKOGAWA)等组成. 如图2(a)所示, 控温系统包括高精度温度控制器(控温误差0.5 ℃)、调压器及圆柱形加热棒. Leidenfrost传热面的温度由3根K型热电偶和2个筒式加热器控制. 3根K型热电偶的位置分布如图2(b)所示, 距离表面2 mm处的热电偶的温度由PID控制, 根据三根热电偶的温度采用最小二乘法外推Leidenfrost传热面的温度T_w. 撞击面的温度T_r通过焊接在撞击环外侧的K型热电偶丝实时监测, 热电偶的测量误差为0.2 ℃. 在实验过程中, 约2.8 mm的蒸馏水滴在20 mm高度下依靠自身重力滴落至Leidenfrost传热面中心位置. 液滴寿命至少测量了五次. 重复测试发现不确定度为0.5 s. Leidenfrost温度的不确定度估计为±5 ℃. 液滴爆炸沸腾的声音信号由麦克风收集, 采样频率为20 kHz, 通过高速数据采集系统将声信号转换为电压信号, 为保证实验的真实性, 本实验在安静的夜间环境下进行. 采用同步误差为20 ns同步器, 使麦克风和高速摄影系统协同工作, 高速相机分别以250和200 fps (frames per second)的帧率以俯拍的方式记录液滴运动轨迹, 其中T_r = 191.4 ℃下粗糙环的拍摄帧率为250 fps, T_r = 191.4 ℃下抛光环和T_r = 256.3 ℃下粗糙环的拍摄帧率为200 fps. 高速相机的空间分辨率为33.7 μm. 为更好地观察液滴撞击瞬间的演化过程, 对液滴撞击瞬间进行拍摄, 高速相机以4000 fps以俯拍的方式记录液滴撞击瞬间的微观过程.
2 -->

3.2.样品制备与表征

3 -->

3.2.1.样品制备

Leidenfrost传热面底座采用黄铜制造, 圆环撞击面由紫铜材料制成, 为验证撞击面粗糙度对控制液滴动力学行为的影响, 本实验采用两种表面—80#砂纸打磨粗糙表面和7000#砂纸打磨抛光表面. 在实验开始之前, 为确保打磨时表面平整, 将砂纸至于水平石英玻璃上, Leidenfrost传热面分别依次采用2000#, 3000#, 5000#, 7000#砂纸对其横向和纵向进行打磨, 随后再用抛光板抛光, 待加热面呈镜面后停止抛光. 将制备的样品分别放入稀盐酸、丙酮和酒精中各超声清洗3 min, 以去除铜表面的氧化层和油脂, 最后用去离子水冲洗并吹干.
3 -->

3.2.2.样品表征

对实验表面进行表征(见图3), 由于圆环内壁粗糙度测量困难, 采用与两个圆环样品相同的制作工艺, 制作了两个相应的平面. 用环境扫描电子显微镜 (FEI, Quanta 200, USA, 不确定度为3.7 nm)对粗糙紫铜表面和抛光紫铜表面进行表征, 采用三维光学显微镜(Bruker, Contour GT-K, USA)测量表面形貌, 光学轮廓仪的不确定度为0.2 nm. 两个表面的接触角由接触角测量仪(Dataphysics OCA15 plus, GER)测量, 不确定度为0.1°. 在正式实验开始前, 对两种表面粗糙度进行表征, 80#砂纸打磨的粗糙表面的平均粗糙度Ra = 1.49 μm, 接触角为β = 54.3°. 抛光表面的平均粗糙度Ra = 0.05 μm, 接触角为β = 62.3°.
图 3 采用与两个圆环样品相同的制造技术制备的两个平表面的表征　(a)抛光紫铜表面的扫描电子显微镜图像和接触角; (b)粗糙紫铜表面的扫描电子显微镜图像和接触角; (c), (d)抛光紫铜表面的表面形貌测量; (e), (f) 粗糙紫铜表面的表面形貌测量
Figure3. Characterization of two flat surfaces having the same fabrication technique as two skirt ring samples: (a) Scanning electronic microscope (ESEM) image and contact angles for polished copper surface; (b) ESME image and contact angles for rough copper surface; (c), (d) surface morphology measured for smooth copper surface; (e), (f) surface morphology measured for rough copper surface

2

-->

4.1.爆炸沸腾触发液滴动力学行为

对液滴整个生命周期内运动轨迹进行叠加, 结果如图4所示, 图中红色圆点为液滴初始滴落位置, 可以很明显地看出, 与抛光环和高温下的粗糙环的运动轨迹相比, 在T_w = 223.0 ℃, T_r = 191.4 ℃下粗糙环的运动轨迹呈现规则的直线运动, 根据整个寿命周期内液滴的运动行为将其分为三区: 液滴在第一区(1—40次撞击)时液滴运动轨迹较为混乱, 类似星形轨迹, 撞击后液滴多为入射角等于反射角的镜面反射, 液滴轨迹呈均匀分布, 几乎覆盖了整个Leidenfrost传热面; 随着液滴直径的减少, 液滴运动轨迹自调整为第二区(41—130次撞击)的细长矩形分布, 几乎全部过圆环中心, 且液滴撞击壁面后多为指向圆心的法线反射; 而第三区(131—150次撞击)的液滴运动轨迹在最终阶段又出现类似星形, 且最终液滴以直径0.105 mm停到黄铜底板上缓慢蒸发直至消失. 以上的结果表明, 通过调控液滴直径的大小可以很好地控制液滴运动轨迹.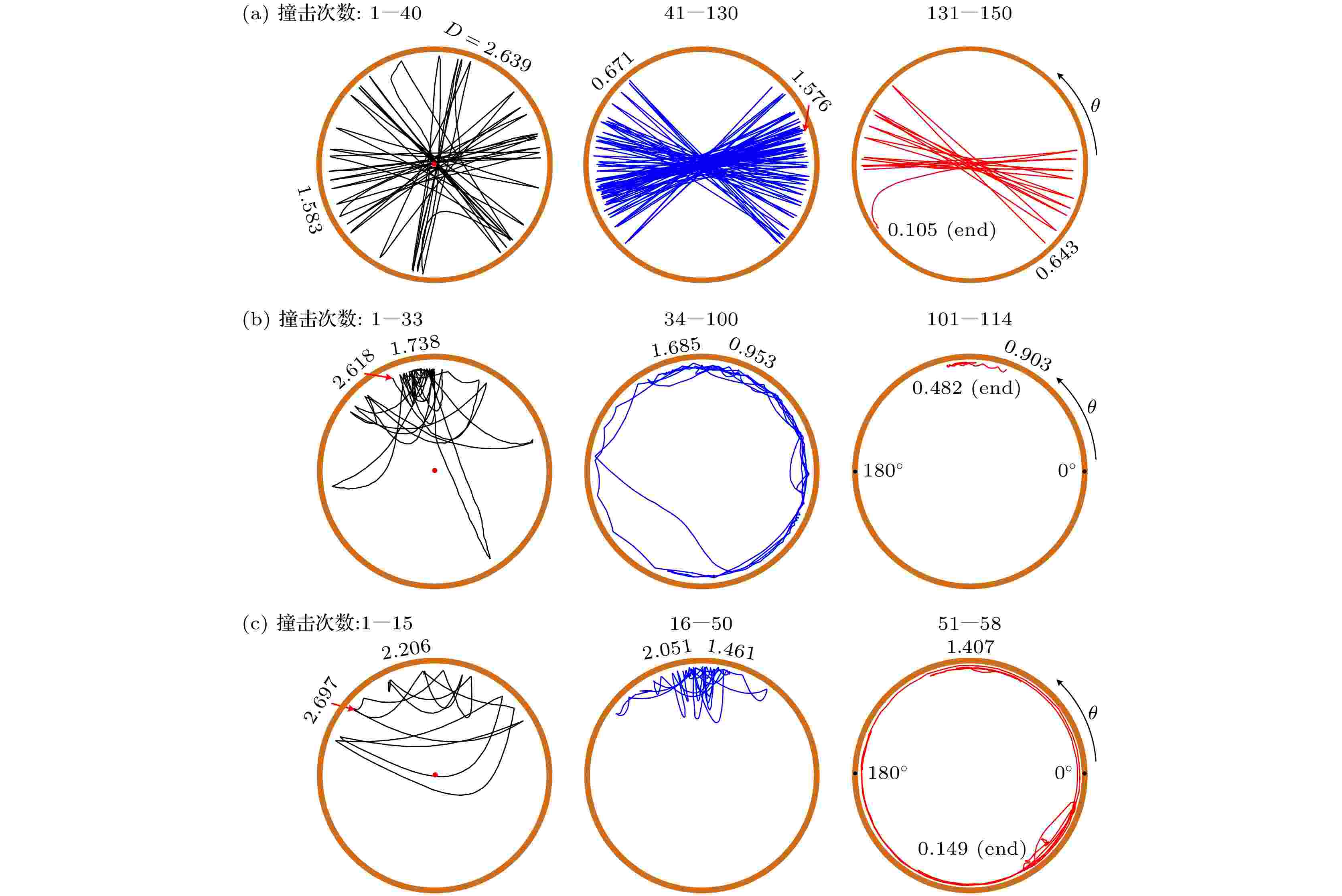
图 4 液滴整个寿命周期内液滴运动轨迹　(a)在T_w = 223.0 ℃, T_r = 191.4 ℃下, 液滴在粗糙环的运动轨迹; (b)在T_w = 223.0 ℃, T_r = 191.4 ℃下, 液滴在抛光环的运动轨迹; (c)在T_w = 304.5 ℃, T_r = 256.3 ℃下, 液滴在粗糙环的运动轨迹
Figure4. Droplet trajectory during the whole droplet lifetime: (a) Droplet trajectory on rough ring at T_w = 223.0 ℃, T_r = 191.4 ℃; (b) droplet trajectory on polished ring at T_w = 223.0 ℃, T_r = 191.4 ℃; (c) droplet trajectory on rough ring at T_w = 304.5 ℃, T_r = 256.3 ℃.

在相同的工况(T_w = 223.0 ℃和T_r = 191.4 ℃下, 记录了抛光环上的Leidenfrost液滴动力学行为, 结果如图4(b)所示. 与粗糙环相比, 抛光环液滴的撞击次数明显减少, 仅为114次, 多为弧形轨迹, 且在1—33次撞击呈现出在局部轻微反弹的规律, 但是由于能量不足以使液滴运动到与前一次碰撞相对的圆环内壁, 最终又返回到初始位置, 随着液滴直径的减少, 34—114次撞击的液滴在抛光环内壁做圆周运动, 最终以直径0.482 mm停在某处缓慢蒸发消失.
为比较温度对液滴动力学的影响, 在T_w = 304.5 ℃, T_r = 256.3 ℃下对粗糙环上液滴的动力学进行了研究, 结果如图4(c)所示, 在圆环温度较高时, 液滴运动轨迹与抛光环中的液滴类似, 且与以上两个工况相比, 高温环下的液滴撞击次数更少, 仅为58次, 在1—50次撞击时, 呈现出轻微反弹的轨迹, 且无法运动到环的另外一侧, 随后在51—58次出现液滴绕环内壁做圆周运动, 最终以直径0.149 mm停在某处缓慢蒸发直至消失.
为更好地理解液滴动力学行为, 对液滴在以上三种工况下的液滴撞击频率f, 液滴运动速度V, 声音信号进行了统计, 结果如图5—7所示.
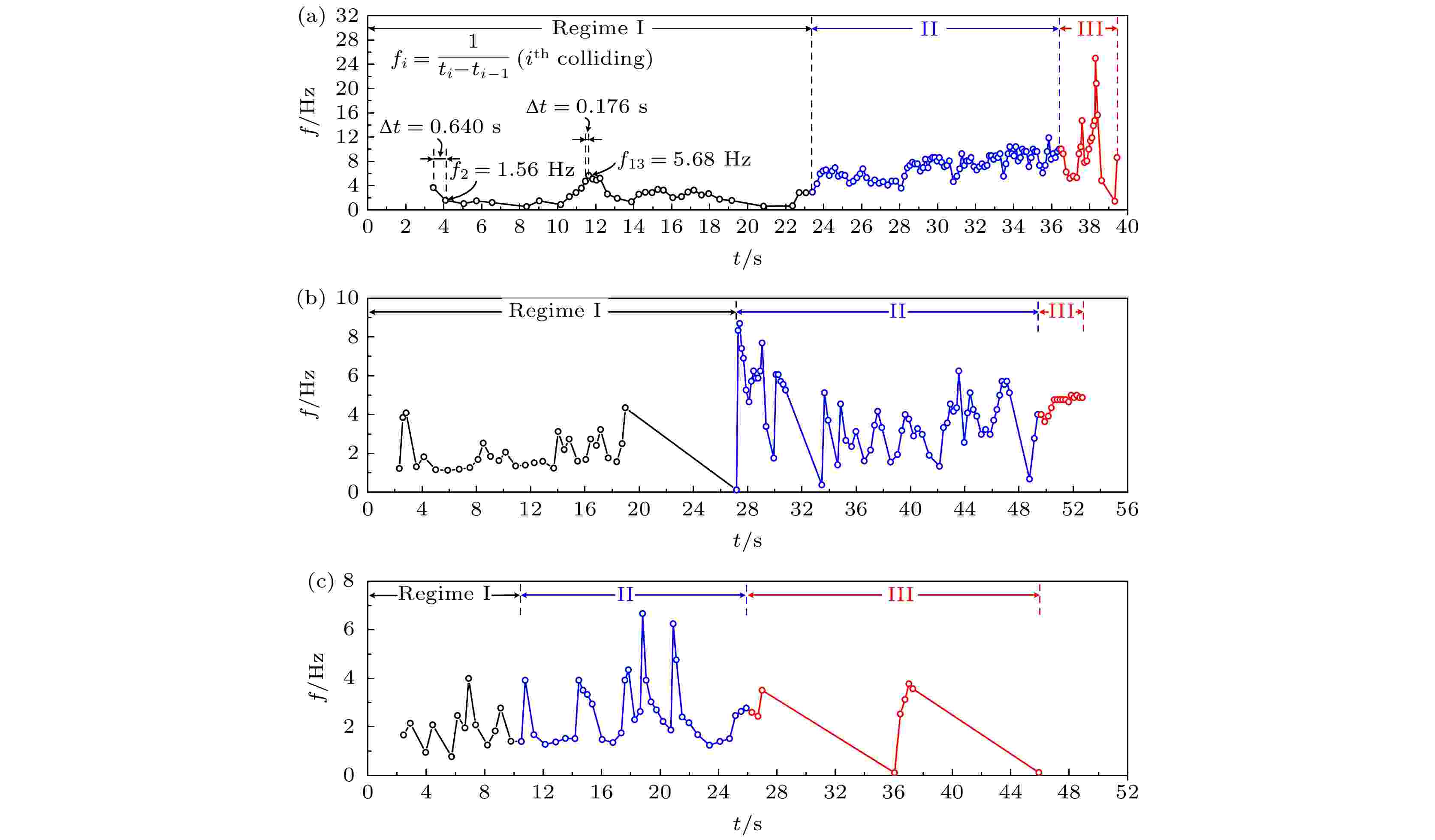图 5 液滴整个寿命周期内液滴撞击频率　(a)在T_w = 223.0 ℃, T_r = 191.4 ℃下, 粗糙环; (b)在T_w = 223.0 ℃, T_r = 191.4 ℃下, 抛光环; (c) T_w = 304.5 ℃, T_r = 256.3 ℃下, 粗糙环
Figure5. Droplet collision frequency during the whole droplet lifetime: (a) T_w = 223.0 ℃, T_r = 191.4 ℃, rough ring; (b) T_w = 223.0 ℃, T_r = 191.4 ℃, polished ring; (c) T_w = 304.5 ℃, T_r = 256.3 ℃, rough ring.

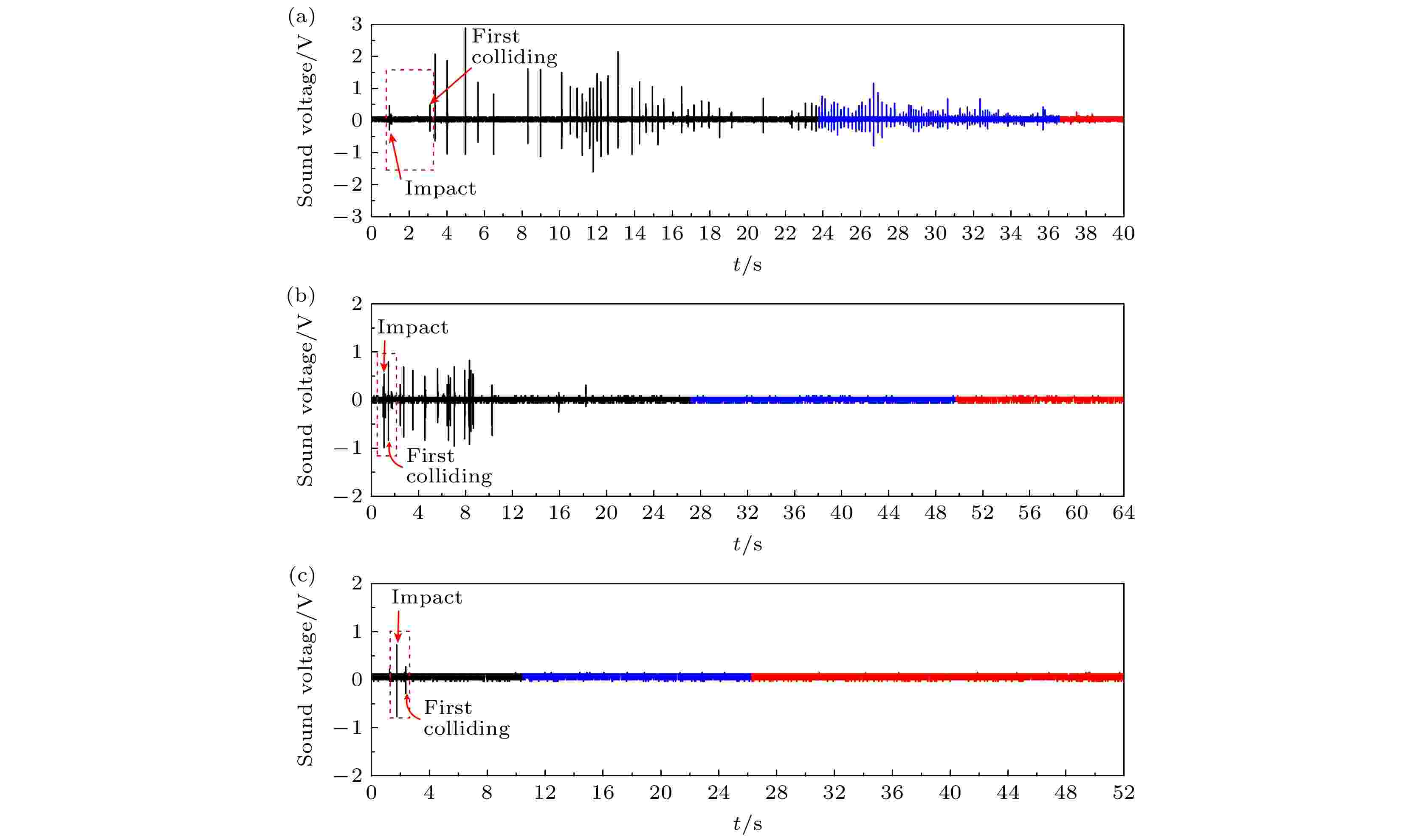图 7 液滴整个寿命周期内液滴的声音信号　(a)在T_w = 223.0 ℃, T_r = 191.4 ℃下, 粗糙环; (b)在T_w = 223.0 ℃, T_r = 191.4 ℃下, 抛光环; (c) T_w = 304.5 ℃, T_r = 256.3 ℃下, 粗糙环
Figure7. Droplet sound voltage during the whole droplet lifetime: (a) T_w = 223.0 ℃, T_r = 191.4 ℃, rough ring; (b) T_w = 223.0 ℃, T_r = 191.4 ℃, polished ring; (c) T_w = 304.5 ℃, T_r = 256.3 ℃, rough ring.

其中撞击频率为两个相邻撞击之间的时间差的倒数, 从图5可以看出, 在三种工况下, 液滴撞击频率依次减少, T_r = 191.4 ℃下粗糙环的频率在0.55—25.00 Hz范围内, 而T_r = 191.4 ℃下抛光环的频率明显减少, 在0.12—8.70 Hz范围内, T_r = 256.3 ℃下粗糙环的频率仅在0.11—6.67 Hz范围.
与抛光环和高温环相比, T_r = 191.4 ℃的粗糙环中的液滴撞击频率呈逐渐递增的趋势, 在第一区液滴撞击频率为0.55—5.68 Hz, 随后在第二区逐渐增加至11.90 Hz, 在第三区飙升至25.00 Hz. 与图4(b)和图4(c)的轨迹图相对应, 液滴在抛光环和高温环内多表现为局部反弹和绕环内壁运动, 因而液滴在抛光环和高温环内的撞击频率无明显规律, 且频率较低.
液滴运动速度是控制液滴动力学的重要参数, 如图6(a)所示, T_r = 191.4 ℃的粗糙环中的液滴运动速度在第一区为0.05—16.80 cm/s, 在第二区增加到37.58 cm/s, 随后飙升到68.91 cm/s. 这是以往微/纳结构表面自驱动从未达到的, 目前所报道的锯齿型自驱动液滴运动速度最高为40 cm/s^[19]. 通过以上简单的装置实现了锯齿型自驱动液滴运动的最大速度.
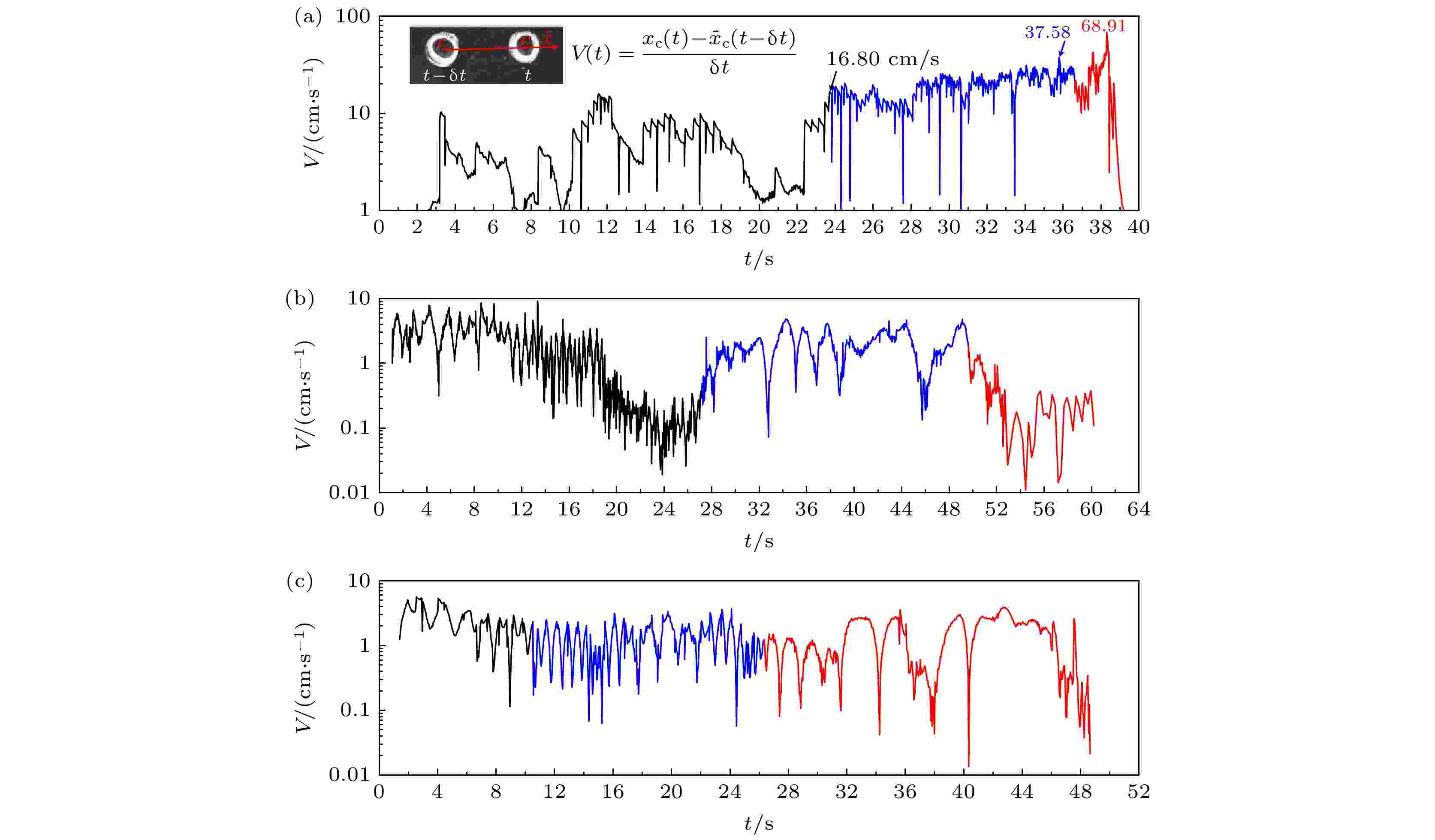图 6 液滴整个寿命周期内液滴运动速度　(a) 在T_w = 223.0 ℃, T_r = 191.4 ℃下, 粗糙环; (b)在T_w = 223.0 ℃, T_r = 191.4 ℃下, 抛光环; (c) T_w = 304.5 ℃, T_r = 256.3 ℃下, 粗糙环
Figure6. Droplet traveling velocity during the whole droplet lifetime: (a) T_w = 223.0 ℃, T_r = 191.4 ℃, rough ring; (b) T_w = 223.0 ℃, T_r = 191.4 ℃, polished ring; (c) T_w = 304.5 ℃, T_r = 256.3 ℃, rough ring.

其中撞击频率为两个相邻撞击之间的时间差的倒数, 从图5可以看出, 在三种工况下, 液滴撞击频率依次减少, T_r = 191.4 ℃下粗糙环的频率在0.55—25.00 Hz范围内, 而T_r = 191.4 ℃下抛光环的频率明显减少, 在0.12—8.70 Hz范围内, T_r = 256.3 ℃下粗糙环的频率仅在0.11—6.67 Hz范围.
在T_w = 304.5 ℃, T_r = 256.3 ℃下, 粗糙环内的液滴运动速度变化较为平缓(见图6(c)), 第一区液滴运动速度在0.11—5.68 cm/s范围内, 在第二区运动速度范围为0.06—3.71 cm/s, 第三区的运动速度明显减少, 运动速度范围为0.01—3.77 cm/s.
噪声检测广泛应用于相变传热以表征沸腾强度^[20,21]. 在T_w = 223.0 ℃, T_r = 191.4 ℃液滴撞击粗糙环的工况下, 整个寿命周期内液滴的声音信号如图7(a)所示, 每一个峰值代表一个脉冲噪声, 在该工况下涉及150个脉冲噪声, 对应于150次与圆环碰撞. 图7(a)中第一个噪声信号是指与Leidenfrsot传热面的碰撞, 但接下来的所有脉冲信号都是指与撞击环的碰撞. 在第一区的大液滴尺寸组中, 爆炸沸腾产生噪声达到0.13—2.85 V范围内的声压, 该声压很强, 人耳可以明显听到. 声压在第二区和第三区中衰减, 表明爆炸沸腾强度强烈依赖于液滴尺寸.
而在T_w = 223.0 ℃, T_r = 191.4 ℃液滴撞击抛光环时(如图7(b)所示), 可以很明显地看出, 液滴撞击发出的声音信号很少, 并且声音信号强度较弱, 在0.15—0.82 V范围内. 除第一区部分碰撞发生爆炸沸腾发生声音外, 其余两区并未产生声音信号, 说明随着液滴直径的减少, 液滴爆炸沸腾强度减弱.
在T_w = 304.5 ℃, T_r = 256.3 ℃下, 液滴撞击粗糙环时(见图7(c)), 除第一次撞击圆环发出声音信号外, 其余碰撞均未发出声响, 且此时的声音信号更弱, 仅为0.28 V, 说明此时的爆炸沸腾强度更弱, 在该工况下, 液滴撞击圆环时不能触发液滴发生爆炸沸腾.
为进一步验证液滴撞击圆环时是否发生了爆炸沸腾, 采用高速相机以4000 fps的拍摄频率对液滴撞击瞬间进行了捕捉, 结果如图8所示. 在T_w = 223.0 ℃, T_r = 191.4 ℃液滴撞击粗糙环的工况下(如图8(a)所示), 在液滴第22次撞击粗糙环时, 约在10 ms的时间尺度内, 液滴撞击瞬间液滴中产生小汽泡, 小汽泡在极短的时间内快速膨胀发生爆炸沸腾, 爆炸的能量足以克服液滴本身的表面能, 致使液滴两侧喷射出雾状小液滴, 如图8(a)中14.60925 s和14.61175 s. 同时可以看出, 在14.60925 s时液滴内部出现柱状汽泡, 随后14.61175 s时液滴与圆环接触部分变形, 柱状汽泡向左侧移动并呈圆形, 最终液滴在爆炸沸腾产生的推力F_th驱动下逃离撞击环. 液滴在推力F_th驱动下的运动将在4.2节进行详细阐述, 此处详细说明液滴中的汽泡向左运动的机理. 如图8(d)所示, 由于液滴周围温度不均匀, 液滴中的汽泡会有温度较高的向阳面和温度较低的背阳面, 由于汽泡膨胀, 汽泡周围液体会受到汽泡施加的力. 相应地, 液体对汽泡施加反作用力. 对于汽泡, 这些力在竖直方向相互抵消, 但产生一个指向左的合力F_m, 在该力的作用下汽泡更倾向于向左侧运动, 因而出现图8(a)中14.60925—14.61800 s液滴向左侧运动的现象. 值得说明的是, 在本实验中, 爆炸沸腾发生在14.60800—14.61800 s. 14.61800 s后液滴中的汽泡并不会发生爆炸沸腾, 直至液滴再次与圆环碰撞才会触发爆炸沸腾.
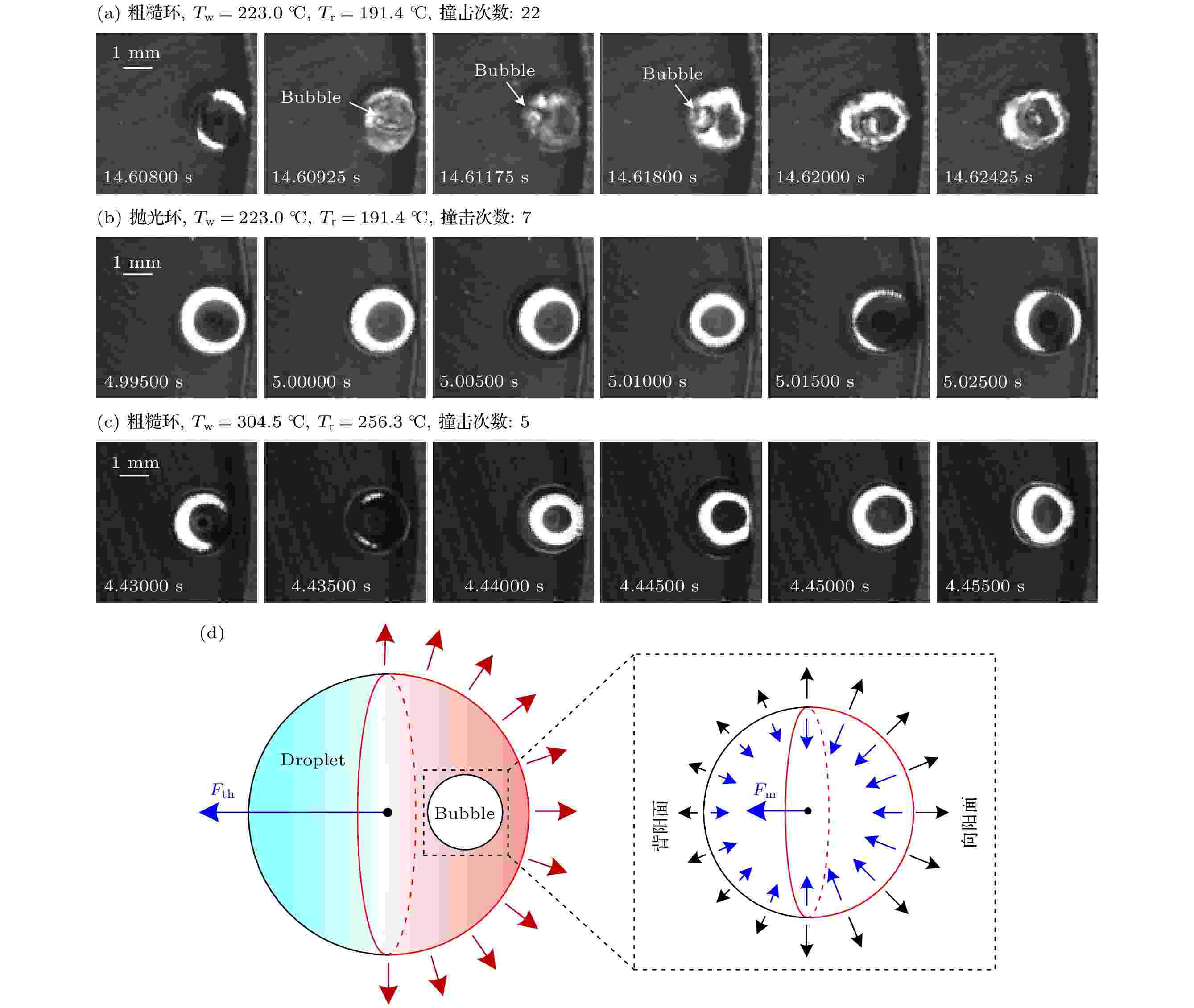图 8 液滴撞击瞬间　(a)在T_w = 223.0 ℃, T_r = 191.4 ℃下, 粗糙环; (b)在T_w = 223.0 ℃, T_r = 191.4 ℃下, 抛光环; (c) T_w = 304.5 ℃, T_r = 256.3 ℃下, 粗糙环; (d)液滴内汽泡运动机理
Figure8. Droplet impact moment: (a) T_w = 223.0 ℃, T_r = 191.4 ℃, rough ring; (b) T_w = 223.0 ℃, T_r = 191.4 ℃, polished ring; (c) T_w = 304.5 ℃, T_r = 256.3 ℃, rough ring; (d) movement mechanism of bubble in droplets.

而液滴撞击抛光环(T_w = 223.0 ℃, T_r = 191.4 ℃)和高温下粗糙环(T_w=304.5 ℃, T_r=256.3 ℃)时(见图8(b)和图8(c)), 液滴中没有小汽泡产生, 除液滴撞击环时发生轻微变形外, 液滴没有发生变形, 表明液滴在撞击抛光环和高温环时没有爆炸沸腾的现象.
2 -->

4.2.爆炸沸腾触发液滴自驱动机理分析

Leidenfrost状态下, 液滴悬浮于蒸汽膜上, 液滴受到Leidenfrost传热面辐射与对流加热, 但缺乏核化穴, 汽泡无法成核. 而撞击环与底板为线接触, Leidenfrost传热面T_w = 223.0 ℃时, 粗糙环温度T_r = 191.4 ℃, 温差ΔT = 31.6 ℃. 因而在Leidenfrost传热面达到液滴Leidenfrost温度(LFP)时, 撞击面并未达到LFP, 根据经典动力学核化理论, 汽泡临界半径r_c为^[22]

$ {r_{\text{c}}} = \frac{{4\sigma {T_{\text{s}}}}}{{{h_{{\text{fg}}}}{\rho _{\text{v}}}\left( {{T_{\text{r}}} - {T_{\text{s}}}} \right)}} , $

式中σ为表面张力, T_s为饱和温度, h_fg为液体汽化潜热, ρ_v为蒸汽密度, T_r为环表面温度. 取σ = 0.0589 N/m, T_s = 373.15 K, ρ_v = 0.598 kg/m³, h_fg = 2256.43 kJ/kg. 计算得到水的汽泡临界半径为0.71 μm, 本实验中粗糙环的粗糙度Ra = 1.49 μm, 大于汽泡临界半径, 因而液滴在撞击粗糙环时, 可以为高温液滴提供核化穴, 触发液滴爆炸沸腾, 而抛光环的平均粗糙度Ra = 0.05 μm, 远小于水的汽泡临界半径, 液滴无法在抛光环内核化, 无法触发爆炸沸腾. 而在高温粗糙环(T_w = 304.5 ℃, T_r = 256.3 ℃)时, 虽然粗糙环可以为液滴提供核化穴, 但此时的圆环温度已高达256.3 ℃, 已超过圆环的Leidenfrost温度, 液滴在撞击瞬间已达到Leidenfrost状态, 同样无法触发爆炸沸腾.
这里引入蒸发动量力F_e以更好地了解液滴动力学的控制, 实际上, 在本研究中, 蒸发动量力F_e作为推力F_th推动液滴运动(见图9). 蒸发动量力是在液体向蒸汽的转换过程中, 因质量传递引起汽液两相动量交换引起的. 在液滴均匀相变时, 由于液滴周围均匀蒸发, 净蒸发动量力为0. 而当沿界面不均匀相变时, 便会产生净蒸发动量力. Kandlikar^[23,24]指出F_e是由液体中汽泡周围的非对称蒸发引起的, 在这种情况下, 液体和蒸汽之间的质量传递导致动量交换. 对于加热壁上的汽泡生长, 在固-液-汽三相接触线附近蒸发更强, 汽泡周围的非对称蒸发延迟了汽泡离开壁面, 使其黏附在壁面上. 最近, Zhu等^[25]和张海松等^[26]通过对比蒸发动量力F_e和流体的惯性力F_i之间的竞争成功预测了超临界二氧化碳传热恶化开始的临界条件.
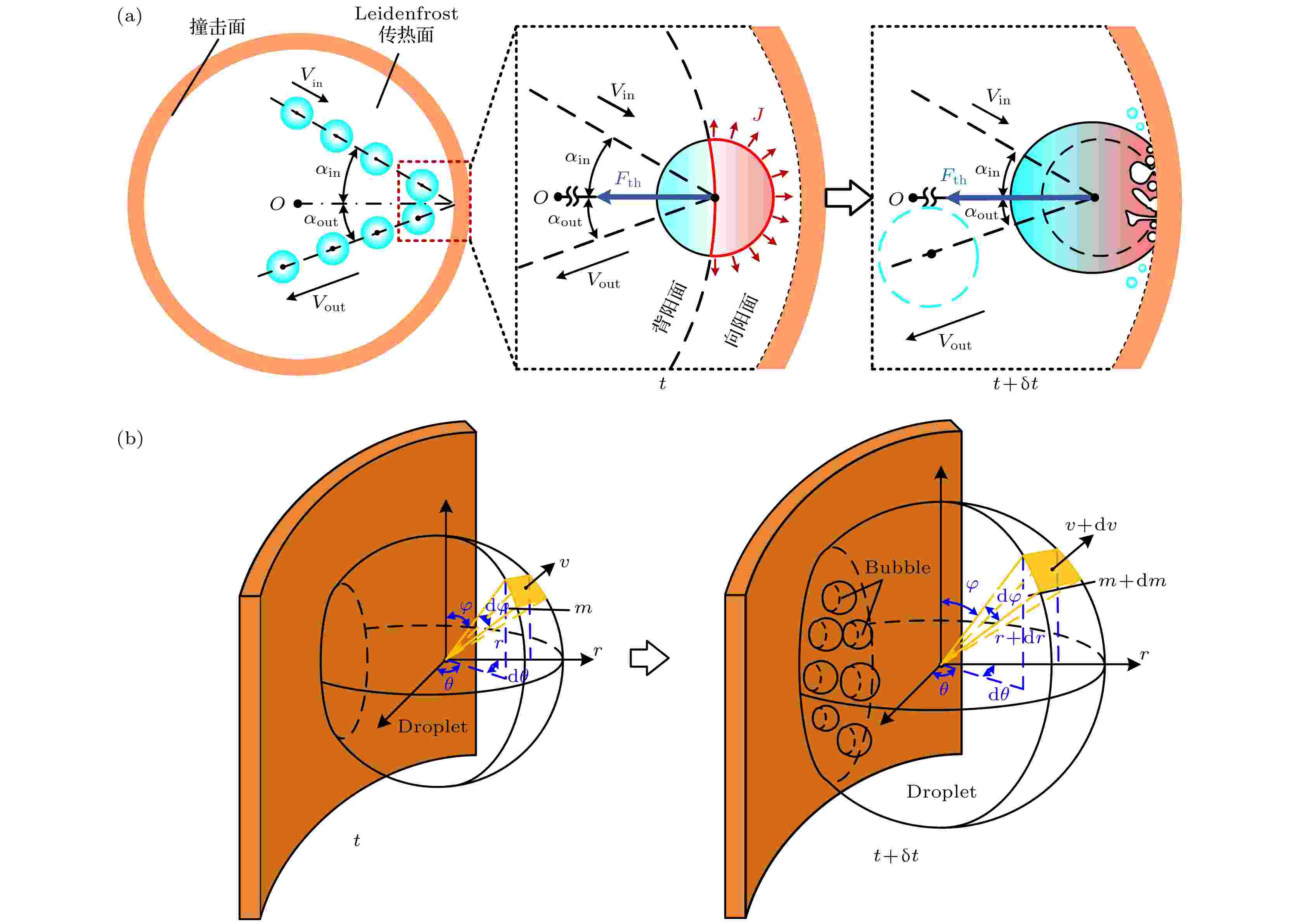图 9 爆炸沸腾触发液滴自驱动机理　(a)液滴自驱动机理; (b)蒸发动量力(即推力F_th)示意图
Figure9. Self-propulsion mechanism of droplet triggered by explosive boiling: (a) Self-propulsion mechanism of droplet; (b) schematic diagram of evaporative momentum force (thrust force F_th).

Shati等^[27]研究了表面粗糙度对辐射传热的影响, 结果表明, 与光滑表面相比, 大尺度粗糙度表面增加传热表面积和湍流强度. 锯齿状粗糙表面比使用光滑表面可提高约26%的传热. 考虑到这种粗糙度效应, 本研究中, 当Leidenfrost液滴接近圆环时, 粗糙的圆环表面增强了向液滴的辐射热传递, 从而提高了向阳侧的液滴温度和蒸发速率, 增强了向阳面和背阳面之间的对称性破坏. 这种非对称蒸发导致的推力F_th开始形成(见图9中的t时刻), 因该时刻F_th难以克服以V_in表征的液滴惯性力F_i, 液滴继续前进直到接触撞击面诱发爆炸沸腾(见图9中的t + δt时刻), 液滴中形成汽泡, 液滴界面快速膨胀, 在液滴与其周围气体(蒸汽和空气的混合物)之间产生足够的动量交换以形成推力F_th, 此时的推力F_th远大于t时刻推力, 驱动液滴逃离撞击面, 实现Leidenfrost传热面上的液滴自驱动. 在本文中, 非接触蒸发和接触沸腾都会引起蒸发动量力F_e, 但后者在文献中很少涉及. 非接触蒸发和接触沸腾的对称性破缺是推力F_th产生的原因.
Leidenfrost液滴以入射速度V_in和入射角α_in接近撞击环. 与壁面碰撞后, 以反射速度V_out和反射角α_out离开撞击环. 对于液滴-壁面碰撞, 存在两个限制条件, 即具有α_in = α_out的镜面反射和具有α_out = 0的法向反射. 实际碰撞在两个极限条件之间. 对于足够大的推力, 液滴可以在Leidenfrost表面上实现直线轨迹.
接下来对液滴运动过程进行受力分析以阐明液滴出现以上液滴动力学行为的原因, 液滴主要受推力F_th、惯性力F_i、重力F_g和拖曳力F_d的作用, 推力F_th可基于动量定理进行计算(见图9(b)), 液滴中汽泡的生长速率决定了液滴表面的膨胀速度, 对液滴表面取微元面, 对所有微元面上的蒸发动量力沿圆环直径方向积分, 获得向心推力F_th^[28]:

$ {F_{{\text{th}}}} = \frac{{{\text{d}}\left( {mv} \right)}}{{{\text{d}}t}} = v\frac{{{\text{d}}m}}{{{\text{d}}t}} + m\frac{{{\text{d}}v}}{{{\text{d}}t}}, $

其中m, v和t 分别为液滴质量、非对称相变引起的膨胀速度和时间. mv为液滴动量. 存在以下方程:

$ v = \frac{1}{2}\frac{{{\text{d}}D}}{{{\text{d}}t}},\;{\text{ }}\frac{{{\text{d}}v}}{{{\text{d}}t}} = \frac{1}{2}\frac{{{{\text{d}}^2}D}}{{{\text{d}}{t^2}}} . $

当液滴与圆环内壁接触时, 接触角为β, 由于壁面加热引起的热通量为q. 在碰撞过程中, 很难知道有多少能量用于从液体到蒸汽的相变. 这种能量包括从圆环吸收的热量和液滴中储存的能量. 由于爆炸沸腾, 前者被假定为汽泡增长的能量来源, 而后者被假定没有这种贡献. 根据液滴的质量守恒方程可得

$ m = \frac{{\text{π }}}{{24}}{\rho _{\text{l}}}{D^3}\left( {2 + 3\cos \beta - {{\cos }^3}\beta } \right) . $

将(4)式左右两侧对t求导可得

$ \frac{{{\text{d}}m}}{{{\text{d}}t}} = \frac{{{\text{π }}{\rho _{\text{l}}}{D^2}}}{8}\frac{{{\text{d}}D}}{{{\text{d}}t}}\left( {2 + 3\cos \beta - {{\cos }^3}\beta } \right) . $

液滴吸收撞击环的能量, 根据液滴的能量守恒方程可得

$ \frac{{{\text{d}}m}}{{{\text{d}}t}} = \frac{{q \cdot {\text{π }}{{(D{\sin}\beta )}^2}}}{{4{h_{{\text{fg}}}}}} , $

其中h_fg是液体汽化潜热. 联立(5)式和(6)式可得

$ \frac{{{\text{d}}D}}{{{\text{d}}t}} = \frac{{2q{\sin}{\beta ^2}}}{{{\rho _{\text{l}}}{h_{{\text{fg}}}}\left( {2 + 3\cos \beta - {{\cos }^3}\beta } \right)}} . $

将(3)—(5)式和(7)式代入(2)式可得

$ {F_{{\text{th}}}} = \frac{{{\text{π }}{D^2}{q^2}{\text{si}}{{\text{n}}^4}\beta }}{{4{\rho _{\text{l}}}h_{{\text{fg}}}^2\left( {2 + 3\cos \beta - {{\cos }^3}\beta } \right)}} \sim {D^2} . $

液滴所受惯性力F_i和重力F_g可表示为

$ {F}_{\text{i}}=\frac{\text{π}{\rho }_{\text{l}}{D}^{3}}{6}\frac{\text{d}V}{\text{d}t}\text{\,}{D}^{3}\text{, }\;\;{F}_{\text{g}}=\frac{\text{π}{\rho }_{\text{l}}{D}^{3}}{6}g\,{D}^{3} , $

其中V为液滴的运动速度, 而非液滴的膨胀速度v, g为重力加速度.
空气中液滴的拖曳力F_d为^[29]

$ {F_{\text{d}}} = \frac{1}{8}{\rho _{{\text{air}}}}{\left( {{V_{{\text{air}}}} - V} \right)^2}{\text{π }}{D^2}{C_{\text{d}}} , $

其中, ρ_air和V_air是空气密度和空气流动速度, 静止空气中V_air = 0, C_d为扰流阻力系数, 是空气流动雷诺数Re的函数. 对于流速较低的情况, C_d取斯托克斯阻力系数:

$ {C}_{\text{d}} =\frac{\text{24}}{Re}\text{, }\;\;Re =\frac{\left(V-{V}_{\text{air}}\right)D}{{\mu }_{\text{air}}} , $

其中μ_air为空气的黏度, 合并(10)式和(11)式可得

$ {F_{\text{d}}} = 3{\text{π }}{\mu _{{\text{air}}}}VD \sim D . $

由(8)式、 (9)式和 (12)式得出上述力的相对重要性如下:

$ \frac{{{F_{{\text{th}}}}}}{{{F_{\text{i}}}}}\sim{D^{ - 1}},\;\;\frac{{{F_{{\text{th}}}}}}{{{F_{\text{g}}}}}\sim{D^{ - 1}},\;\;\frac{{{F_{{\text{th}}}}}}{{{F_{\text{d}}}}}\sim D . $

综合以上液滴受力分析, 液滴受到的推力F_th总是背离撞击面, 指向Leidenfrost传热面圆心方向, 推力F_th倾向于调节液滴通过Leidenfrost传热面中心. 对于没有能量耗散的物体和墙壁之间的弹性碰撞, 物体在碰撞过程中镜面反射占主导地位, 即α_in = α_out和V_in = V_out. 在本研究中, 液滴的惯性力F_i倾向于满足镜面反射, 使其偏离Leidenfrost传热面中心的轨迹. 重力F_g倾向于使液滴在Leidenfrost表面的较低位置, 增加液滴相对于水平位置的敏感性. 拖曳力F_d与液滴运动方向相反并趋于减慢液滴运动. 因此, F_th/F_i, F_th/F_g和F_th/F_d的标度律支配着液滴动力学的控制. 当推力起主导作用时, 液滴轨迹通过圆心的可能性大, 对应于法向反射(α_out = 0); 当液滴惯性力起主导作用时, 液滴轨迹不通过圆心的可能性大, 对应于镜面反射(α_in = α_out). 当液滴在Leidenfrost传热上运动时, 以上各力共同制约着液滴运动. 液滴的运动轨迹绘制在图4(a)中. D^–1定律成功地解释了三区的液滴动力学行为, 在初始阶段(第一区), 液滴直径较大, 惯性力与重力占主导地位, 液滴运动更趋于镜面反射; 当液滴尺寸减小(第二区)时, 推力占主导地位, 入射角α_in和反射角α_out减少, 液滴运动轨迹接近Leidenfrost传热面中心. 应当注意, 在第三区内液滴(D$ \sim $0.105 mm)与圆环最后一次(第150次)碰撞后的运动轨迹为弯曲轨迹而不是直线轨迹, 这是因为对于非常小的液滴, 拖曳力占主导地位, 拖曳力阻止液滴继续运动随后停留在某处缓慢蒸发, 直到完全消失(见图4(a)).
对于抛光环(T_w = 223.0 ℃, T_r = 191.4 ℃)和高温粗糙环(T_w = 304.5 ℃, T_r = 256.3 ℃)的液滴, 虽然也会有局部反弹的运动, 但此时液滴运动的推力是由非对称蒸发而不是通过爆炸沸腾引起的. 对于直径较小的液滴绕圆环内壁运动, 这是由于本研究中的Leidenfrost衬底具有很大的热惯性, 可以保持恒定和均匀的温度, 但由于圆环和底板之间的线接触, 此时圆环的温度较低, 由于Marangoni效应, 圆环的较低温度会吸引液滴并将其黏附在圆环的侧壁周围, 但由于液滴具有一定的初速度, 因而出现液滴绕圆环内壁运动的现象. 实际上, 对于T_w = 223.0 ℃, T_r = 191.4 ℃下的粗糙环也存在Marangoni效应, 但Marangoni力被推力抑制, 因此, 液滴不能停留在圆环附近, 相反, 液滴所受的推力会像子弹一样将液滴推离圆环内壁.

通过简单地构造异质材料的Leidenfrost传热面和撞击面, 利用液滴撞击粗糙环时发生爆炸沸腾的方式实现液滴自驱动. 液滴全寿命周期内不同力的相对重要性制约着液滴运动, 在液滴初始阶段主要受惯性力F_i控制, 液滴撞击后更多地表现为镜面反射, 液滴轨迹近乎为星型, 且较为混乱. 随着液滴直径的逐渐减少, 液滴爆沸产生的推力F_th起主要作用, 而推力F_th方向指向圆心, 诱导液滴向圆心方向运动. 实验结果表明, 液滴在很宽的直径范围(D = 0.671—1.576 mm)内通过Leidenfrost传热面中心, 同时发现, 液滴输运速度可达68.91 cm/s, 这是以往微纳结构表面液滴自驱动从未实现的. 这一发现提供了一种在高温下操纵液滴运动的新方法, 并且将在传热系统、微流控设备和减阻等方面赋予更有前景的实际应用.