全文HTML
--> --> -->国外在基于碱金属原子自旋特性的光泵磁强计的研制和应用上发展显著[7-12], 其中Budker等[13,14]对磁强计的原理等进行了系统的阐述. 国内近年来也开展了光泵原子磁强计的研制[15-18], 孙伟民等[19]阐述了原子磁强计的基本原理、研究进展及应用情况; 王延辉等[20]研究了激光光强、激光频率、射频强度等参数对铯原子磁强计灵敏度的影响, 且达到的最优灵敏度为2.5 pT/Hz1/2; 近来, 本文的作者之一王彦华与北京计算科学研究中心赵楠研究组合作, 实验研究发现采用铷原子D1线和D2线通过光抽运过程极化铷原子时, 原子自旋极化的方向相反, 同等数密度、同等光强下, D1线对应的自旋极化度是D2线对应的自旋极化度的约2倍 [21].
对于碱金属原子光泵磁强计, 目前已经研制的大多是采用单束极化光(同时也是探测光)进行光抽运实现原子极化态的制备, 由于抽运过程中的不闭合跃迁, 只能实现部分原子自旋磁矩的定向排列, 这导致磁共振信号较弱, 限制了磁强计的灵敏度. 目前的商用磁通门磁强计大多存在准确度不高、零点漂移等问题, 所以对其进行校准是非常有必要的. 本文对比研究了不同类型铷原子气室的磁共振信号, 并在795 nm波长窄线宽单频连续极化光(同时也是探测光)下最优化铷原子磁共振信号各参数后, 引入铷原子D2线780 nm波长窄线宽单频连续反抽运光, 将更多原子制备到极化状态, 实现对光泵铷原子磁强计磁共振信号的增强及磁强计灵敏度的改善. 同时, 利用增强后的磁共振信号对一种商用磁通门磁强计在弱磁场测量时的准确度和偏差进行了评估和校准.
2.1.铷-85原子的自旋极化
单光束极化光(同时也是探测光)光泵磁强计的物理图像如图1所示。对于天然丰度的铷原子气室, 由于铷-85和铷-87原子丰度的差异, 相应的磁共振信号及灵敏度同样存在差异, 且文献[20]中的实验研究表明磁共振信号对应有最优的共振激光频率选择, 实验中我们以铷-85原子D1线














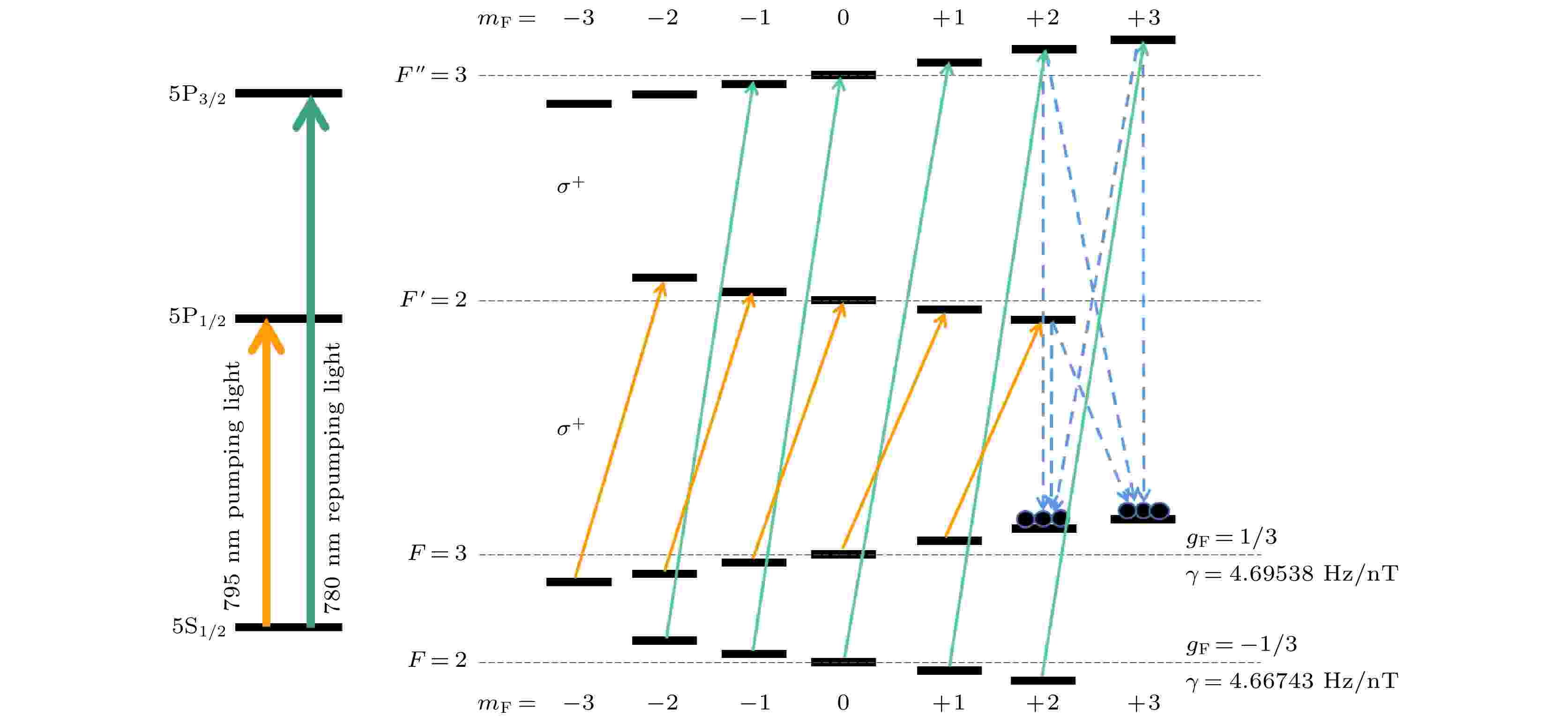 图 1 铷-85原子的相关能级图及有关的跃迁
图 1 铷-85原子的相关能级图及有关的跃迁Figure1. Relevant energy levels of rubidium-85 atoms and the related transitions.
同时我们也简单估算了780 nm波长窄线宽单频连续反抽运光对磁共振信号幅值的影响: 在原子气室处于热平衡状态时, 假设铷-85原子基态两个超精细态上各均匀分布N/2个原子, 当光强足够大, 795 nm σ+圆偏振光与(F = 3)态上的原子充分作用后, 不考虑相邻Zeeman态间的磁偶极跃迁, 由于超精细态光抽运效应与Zeeman态光抽运效应同时存在, 此时(F = 3, mF = +2, +3)态上布居的原子数极限值约为N/4, 若此时加入780 nm波长窄线宽单频连续反抽运光, 则(F = 3, mF = +2, +3)态上存在的原子数极限值为N, 即加入780 nm波长窄线宽单频连续反抽运光后处于极化态的原子数约为原来的4倍, 粗略估算磁共振信号幅值提高4倍.
2
2.2.相关理论分析
根据Bloch方程, 光泵原子磁强计中, 原子在直流偏置磁场B0和交变磁场Brf(
(1)式中Mz的稳态解为





光泵原子磁强计的灵敏度可表示为[23]

2
2.3.实验装置
实验装置如图2所示, 长度为5 cm、通光窗口直径为2 cm、高硼硅光学玻璃的圆柱形气室, 内部充有自然丰度的铷-85原子与铷-87原子, 且内表面镀有石蜡抗自旋弛豫膜, 以减弱原子与泡壁碰撞引起的自旋弛豫. 使用高频交流电流驱动的柔性薄膜电加热片对原子气室进行加热控温, 其通过特殊设计, 外加高频交流电流所产生的磁场在很大程度上相互抵消, 而且所加交变电流的频率远高于待测交流磁场的频率, 可进一步降低额外磁场的干扰. 使用四层高磁导率坡莫合金磁屏蔽筒为铷原子气室提供近零磁环境. 在磁屏蔽筒内放置无矩线圈, 用低噪声的电流源(Keysight B2961A)产生的电流驱动无矩线圈, 产生沿z轴方向的均匀直流磁场, 使原子发生Zeeman分裂; 同时沿x轴方向放置一组同向亥姆霍兹线圈对产生交变磁场, 用于驱动基态原子在相邻Zeeman态间的磁偶极跃迁, 实现磁共振. 795 nm波长窄线宽单频连续极化光(同时也是探测光)由分布布拉格反射器(DBR)式单频半导体激光器产生. 输出激光经过整形棱镜对和基于法拉第磁致旋光效应的光隔离器后分成两部分, 一部分用于饱和吸收光谱锁频, 另一部分通过格兰泰勒棱镜进一步提高激光束的线偏振度, 然后经过λ/4波片变换为圆偏振光, 通过开普勒望远镜系统对激光束进行扩束(扩束后光斑的高斯直径约为7.3 mm). 穿过铷原子气室后的透射光束经凸透镜聚焦后采用增益可调节的低噪声光电探测器(PD)接收. 780 nm波长窄线宽单频连续反抽运光由单频光栅外腔半导体激光器(ECDL)产生. 输出激光一部分用于偏振光谱锁频, 另一部分经过λ/4波片变换为圆偏振光, 经扩束(扩束后光斑的高斯直径约为10.1 mm)穿过原子气室后被双色镜滤除.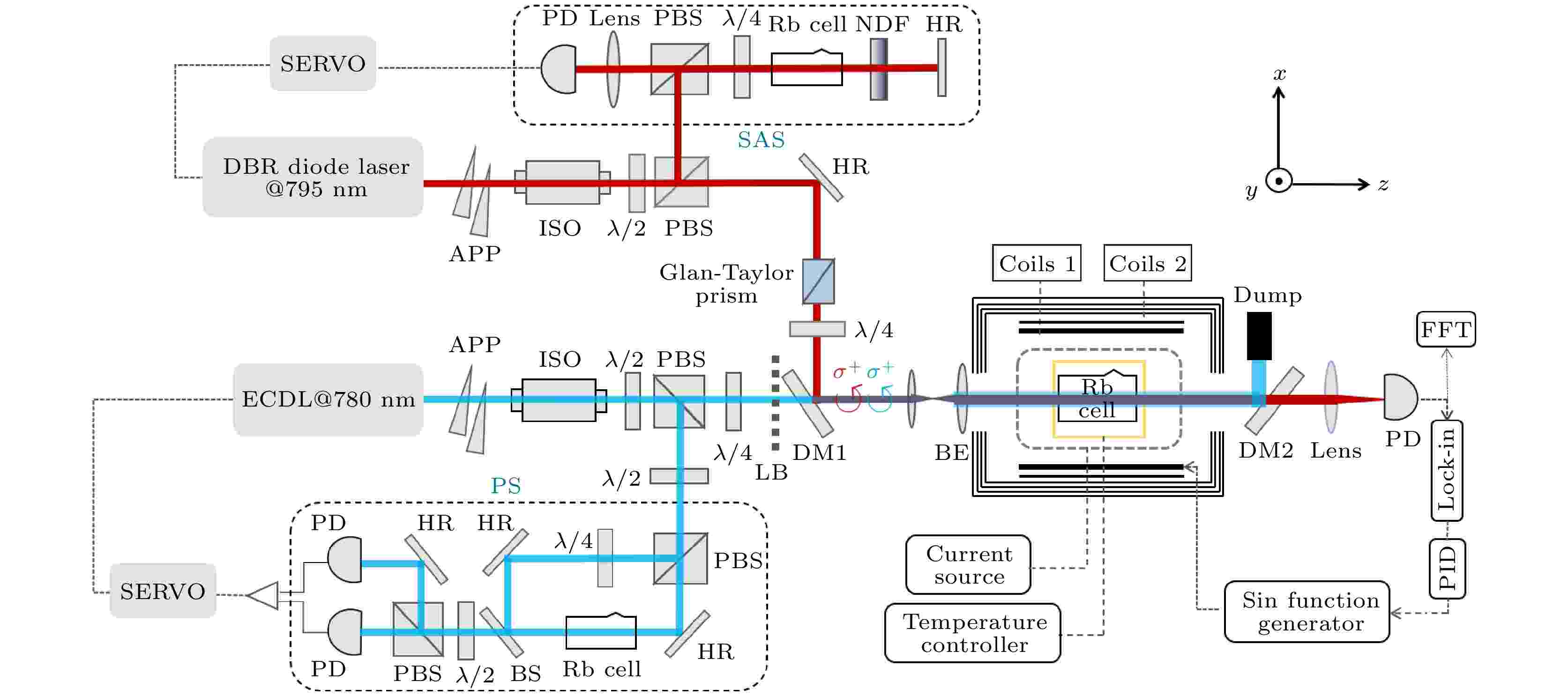 图 2 实验装置图 ECDL, 外腔半导体激光器; DBR, 分布布拉格反射激光器; APP, 整形棱镜对; ISO, 光隔离器; λ/2, 1/2波片; PBS, 偏振分光棱镜; HR, 高反镜; NDF, 衰减片; DM1, 双色镜(780 nm高透, 795 nm高反); DM2, 双色镜(795 nm高透, 780 nm高反); LB, 挡光板; BE, 扩束望远镜; PD, 光电探测器; Dump, 遮光器; Lock-in, 锁相放大器; PID, 比例积分微分放大器; SAS, 饱和吸收光谱装置; PS, 偏振光谱装置; FFT, 快速傅里叶变换动态信号分析仪
图 2 实验装置图 ECDL, 外腔半导体激光器; DBR, 分布布拉格反射激光器; APP, 整形棱镜对; ISO, 光隔离器; λ/2, 1/2波片; PBS, 偏振分光棱镜; HR, 高反镜; NDF, 衰减片; DM1, 双色镜(780 nm高透, 795 nm高反); DM2, 双色镜(795 nm高透, 780 nm高反); LB, 挡光板; BE, 扩束望远镜; PD, 光电探测器; Dump, 遮光器; Lock-in, 锁相放大器; PID, 比例积分微分放大器; SAS, 饱和吸收光谱装置; PS, 偏振光谱装置; FFT, 快速傅里叶变换动态信号分析仪Figure2. Schematic diagram of the experimental setup. ECDL, external-cavity diode laser; DBR, distributed-Bragg-reflector type diode laser; APP, anamorphic prism pairs; ISO, optical isolator; λ/2, half-wave plate; PBS, polarization beam splitter cube; HR, high-reflectivity mirror; NDF, neutral density filter; DM1, two-color mirror (high-transmittance@780-nm, high-reflection@795-nm); DM2, two-color mirror (high-transmittance@795-nm, high-reflection@780-nm); LB, light barrier; BE, the beam expanding telescope; PD, photodetector; Dump, laser dump; Lock-in, lock-in amplifier; PID, the proportional-integrational-differential amplifier; SAS, the saturation absorption spectroscopic device; PS, the polarization spectroscopic device; FFT, the Fast-Fourier-Transformation dynamic signal analyzer.
实验中磁共振信号的观察方法有两种, 一种为扫描交变磁场频率, 此时磁共振信号线宽的单位为频率; 另一种为扫描直流偏置磁场大小, 对应的磁共振信号线宽单位为磁场单位, 由拉莫尔频率公式可知两种磁共振线宽的表示方法可通过原子相应基态超精细态的旋磁比联系起来. 探测器输出的磁共振信号由锁相放大器(苏黎世仪器公司MFLI-5 MHz)进行调制解调得到同位相和正交位相信号. 随后通过比例-积分-差分放大器(PID) Servo电路实现沿x轴方向所加交变磁场的频率锁定(将交变磁场的频率锁定在磁共振信号的中心频率, 即拉莫尔频率), 实现光泵铷原子磁强计的闭环锁定.
3.1.铷原子气室的选择
首先定性分析对比不同原子气室产生的磁共振信号. 对于典型的充缓冲气体和镀石蜡的自然丰度铷原子气室的磁共振信号如图3所示. 实验中选用的缓冲气体为20 Torr (1 Torr = 133.3224 Pa) He和10 Torr Ne, 其典型的磁共振信号如图3(a)所示, 当激光频率调谐至铷-85原子共振频率时, 铷-85和铷-87的磁共振谱同时出现. 而对于只在原子气室内壁镀石蜡膜的气室, 相同参数下其磁共振信号如图3(b), 此时原子的基态旋磁比值可精确至该超精细跃迁线. 且从两种气室磁共振信号的对比中可以看出, 在相同的温度、轴向直流偏置磁场条件下, 对于充缓冲气体的铷原子气室, 缓冲气体带来的碰撞展宽使磁共振信号线宽明显展宽, 且文献[21]也分析了反抽运光对铷原子系综产生的退极化影响. 故充缓冲气体铷原子气室的这种特征不仅不利于磁强计灵敏度的提高, 而且严重影响实验中用磁共振谱对商用磁通门磁强计的校准(3.4节讨论). 对于只充有天然丰度铷原子、不充缓冲气体、气室内壁也不镀石蜡的铷原子气室, 由于铷原子与气室内壁的碰撞及铷原子之间的碰撞比较激烈, 铷原子的自旋弛豫时间短, 磁共振信号微弱, 实验中并没有看到较明显的磁共振信号. 故本实验中选择镀石蜡的铷原子气室进行后续实验操作.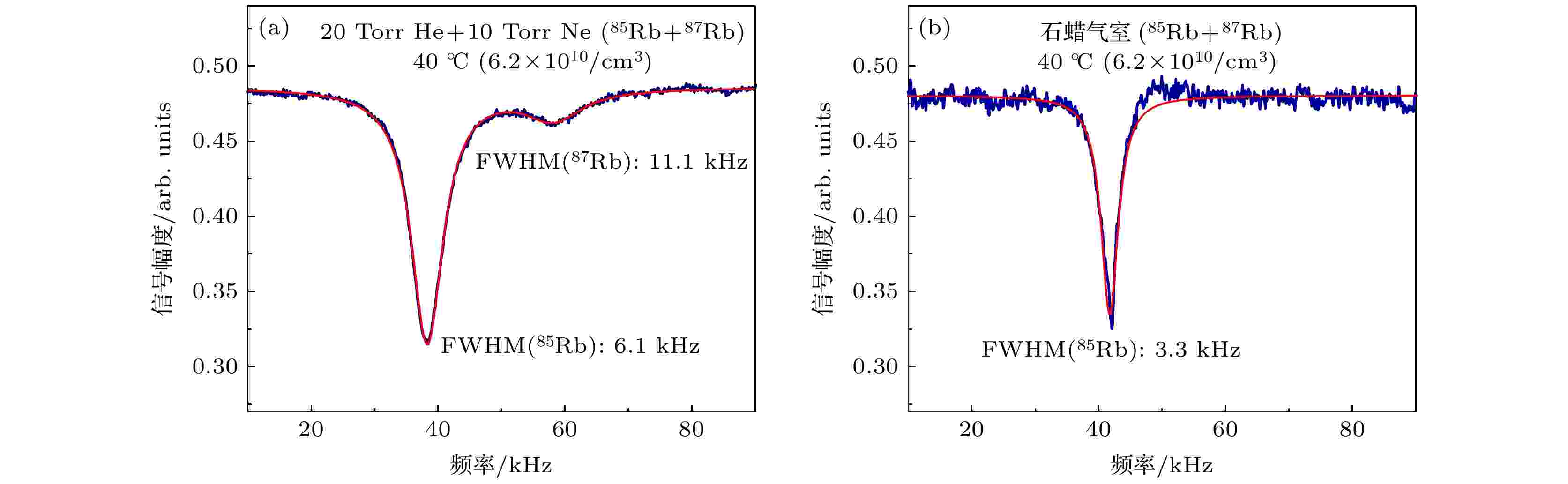 图 3 不同原子气室下的磁共振信号 温度40 ℃, 铷-85 (F = 3)对应的旋磁比为4.69538 Hz/nT, 轴向直流偏置磁场~8.87 μT, 795 nm波长窄线宽单频连续极化光(同时也是探测光)功率~200 μW, 光斑高斯直径~7.3 mm, 频率共振于铷-85原子
图 3 不同原子气室下的磁共振信号 温度40 ℃, 铷-85 (F = 3)对应的旋磁比为4.69538 Hz/nT, 轴向直流偏置磁场~8.87 μT, 795 nm波长窄线宽单频连续极化光(同时也是探测光)功率~200 μW, 光斑高斯直径~7.3 mm, 频率共振于铷-85原子

Figure3. Magnetic resonance signal at different rubidium vapor cells at temperature 40 ℃. The magnetogyric ratio of the 85Rb (F = 3) is 4.69538 Hz/nT, the static magnetic field is ~8.87 μT, the 795-nm pumping laser beam’s power is ~200 μW, the Gaussian diameter is ~7.3 mm and the frequency is locked to the 85Rb


2
3.2.仅采用795 nm波长窄线宽单频连续极化光(同时也是探测光)情形下的磁共振信号及参数优化
不同气室温度对磁共振信号的影响如图4所示. 795 nm波长窄线宽单频连续极化光(同时也是探测光)光强为200 μW, 共振于铷-85原子D1线的



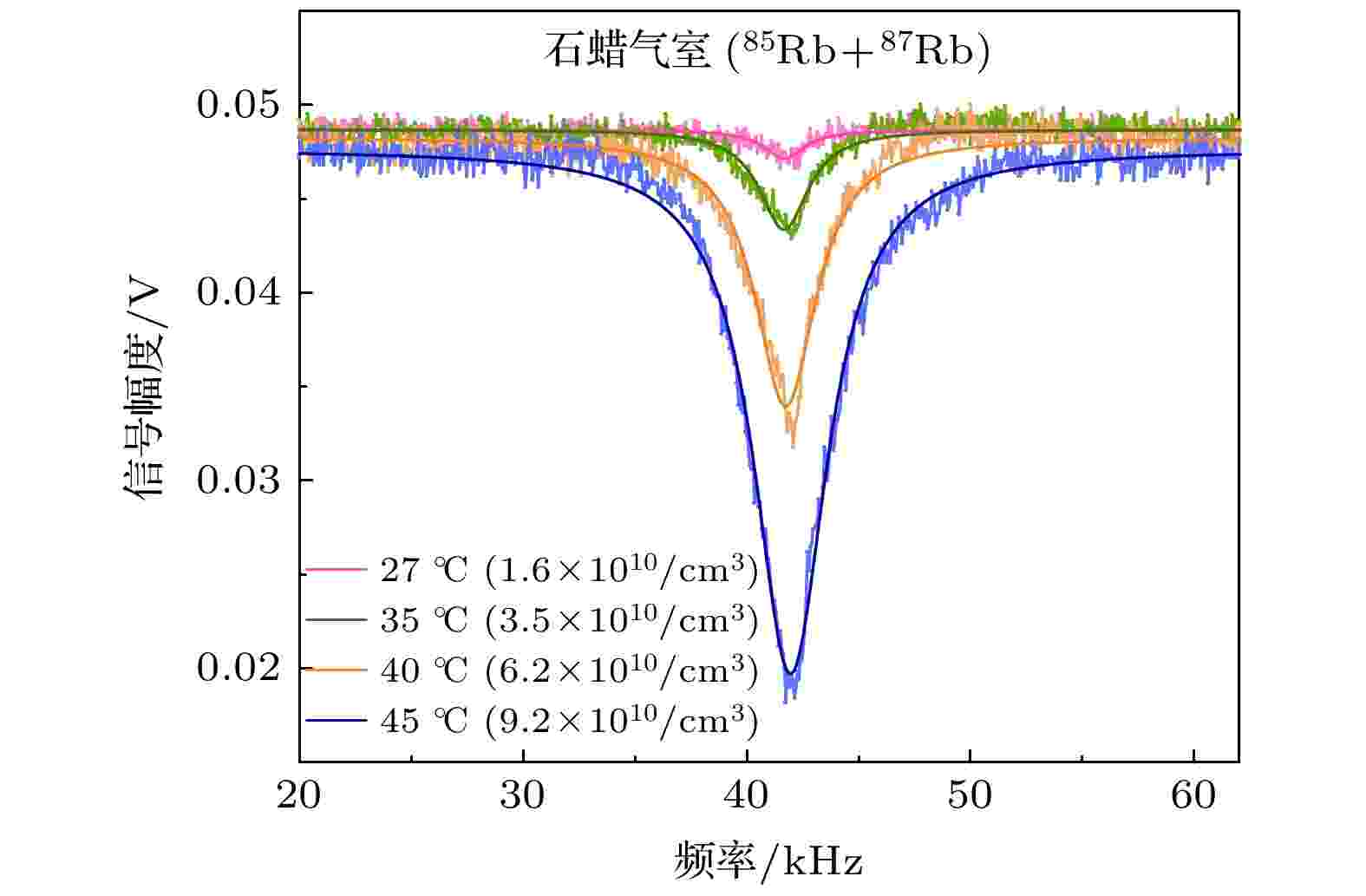 图 4 不同温度(27?45 ℃)下的磁共振信号 27, 35, 40, 45 ℃温度下磁共振信号的半高全宽分别为~2.2, ~2.7, ~3.3, ~4.0 kHz
图 4 不同温度(27?45 ℃)下的磁共振信号 27, 35, 40, 45 ℃温度下磁共振信号的半高全宽分别为~2.2, ~2.7, ~3.3, ~4.0 kHzFigure4. The magnetic resonance signals at different temperatures (27?45 ℃): The linewidth (FWHM) of the magnetic resonance signals are ~2.2 kHz@27 ℃, ~2.7 kHz@35 ℃, ~3.3 kHz@40 ℃, and 4.0 kHz@45 ℃, respectively.
内壁镀石蜡抗自旋弛豫膜的铷原子气室, 温度控制在45 ℃, 将795 nm波长窄线宽单频连续极化光(同时也是探测光)频率调谐至铷-85原子D1线的


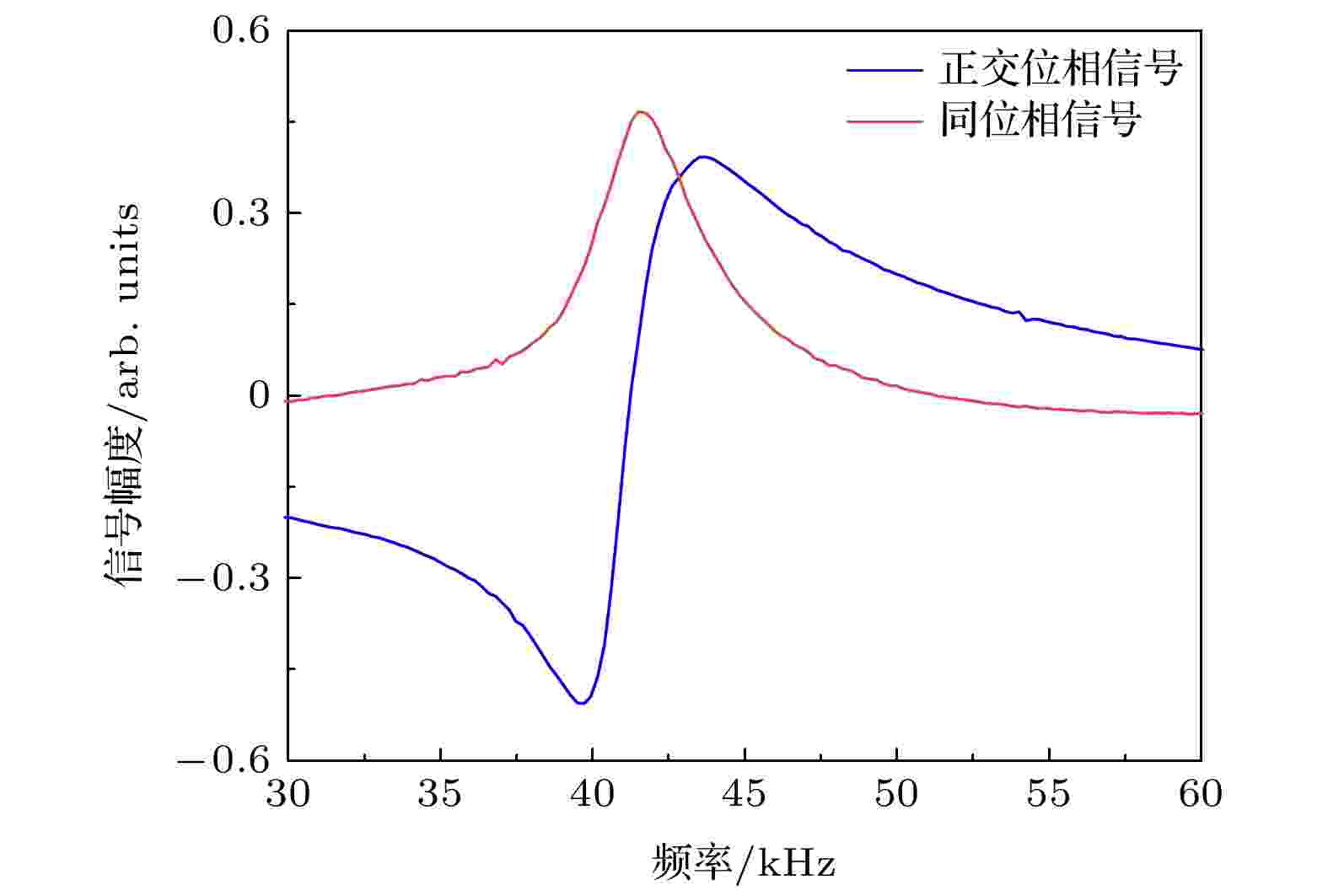 图 5 锁相放大器调制解调信号, 温度45 ℃, 795 nm波长窄线宽单频连续极化光(同时也是探测光)光强200 μW, 轴向直流偏置磁场~8.87 μT, 光斑高斯直径~7.3 mm, 频率共振于铷-85原子
图 5 锁相放大器调制解调信号, 温度45 ℃, 795 nm波长窄线宽单频连续极化光(同时也是探测光)光强200 μW, 轴向直流偏置磁场~8.87 μT, 光斑高斯直径~7.3 mm, 频率共振于铷-85原子

Figure5. The modulation and demodulation signal of the lock-in amplifier: the red curve is the demodulated in-phase signal. The blue curve is the out-of-phase gradient after demodulation. The 795-nm pumping laser beam’s power is ~200 μW, the static magnetic field is ~8.87 μT, the Gaussian diameter is ~7.3 mm and the frequency is locked to the 85Rb


2
3.3.引入780 nm波长窄线宽单频连续反抽运光情形下的实验结果及讨论
在仅采用795 nm波长窄线宽单频连续极化光(同时也是探测光)的最优参数基础上, 加入780 nm波长窄线宽单频连续反抽运光, 频率调谐至铷-85原子D2线

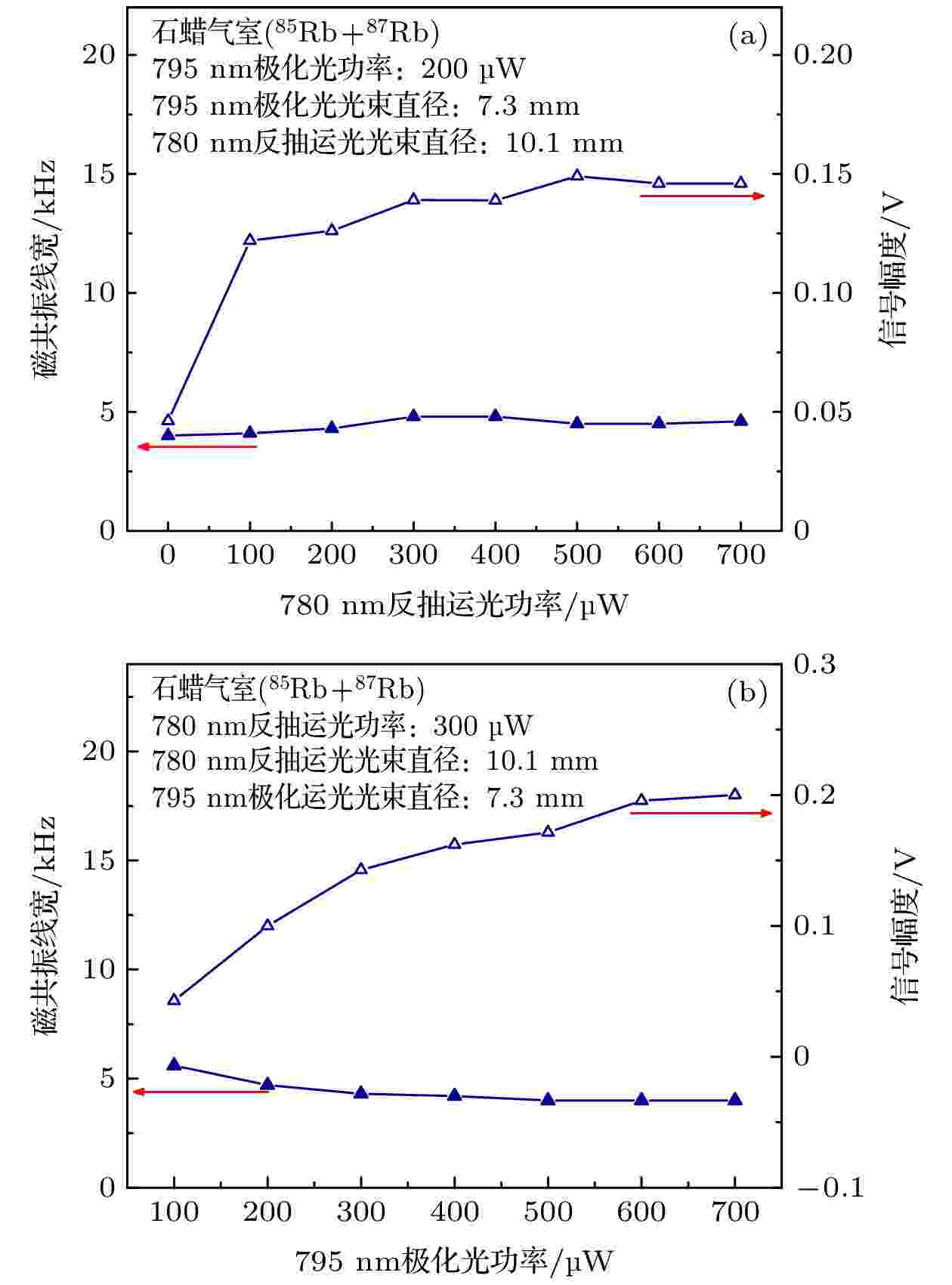 图 6 不同780 nm波长窄线宽单频连续反抽运光和795 nm波长窄线宽单频连续极化光(同时也是探测光)功率下磁共振信号的线宽、信号幅值的变化情况
图 6 不同780 nm波长窄线宽单频连续反抽运光和795 nm波长窄线宽单频连续极化光(同时也是探测光)功率下磁共振信号的线宽、信号幅值的变化情况Figure6. The variation of linewidth (FWHM) and signal amplitude of magnetic resonance signal under different power of pumping and repumping laser beam.
图6(a)中的结果显示, 加入780 nm波长窄线宽单频连续反抽运光后, 线宽并没有明显变化, 信号幅值增大到一定值后趋于稳定. 这主要受限于795 nm波长窄线宽单频连续极化光(同时也是探测光)的功率. 且加入780 nm波长窄线宽单频连续反抽运光后磁共振信号的幅值最大为原来的3.1倍, 比前面2.1节分析的理论值小, 这说明即使加入780 nm波长窄线宽单频连续反抽运光, 在一定程度上抑制了超精细态光抽运效应, 但仍不能将全部原子制备到极化状态. 图6(b)中, 选取780 nm波长窄线宽单频连续反抽运光功率为300 μW时, 随着795 nm波长窄线宽单频连续极化光(同时也是探测光)功率的增大, 磁共振信号的线宽先减小后变化不大, 信号幅值的增大趋势逐渐减缓. 实验中选择反抽运光功率300 μW作为后续实验条件.
2
3.4.铷-85原子光泵磁强计的灵敏度标定
磁强计的灵敏度也可表示为




典型的有无780 nm波长窄线宽单频连续反抽运光情况下的磁场灵敏度如图7所示, 其中定标频率为63 Hz. 如图7所示, 在仅有795 nm波长窄线宽单频连续极化光(同时也是探测光)存在时, 3—100 Hz的灵敏度为245.5 pT/Hz1/2; 加入780 nm波长窄线宽单频连续反抽运光后, 由于处于极化态的原子数增多, 标定场的信号幅值显著增大, 同时透射光子数的减小也使得背景噪声幅值明显减小, 两者综合作用下15—100 Hz磁场的灵敏度为26.4 pT/Hz1/2. 此时3—15 Hz处隆起的噪声本底可能是780 nm波长窄线宽单频连续反抽运光的额外强度噪声. 且从图7(a)和图7(b)对比中可以看出, 加入780 nml波长窄线宽单频连续反抽运光后, 可以清晰看到磁屏蔽筒内残余的50 Hz工频交变磁场信号, 强度约92.4 pT. 同时, 我们也将标定场频率放到103, 203, 503, 1003 Hz处进行标定, 结果表明, 在1.2 kHz频率范围内, 引入780 nm波长窄线宽单频连续反抽运光后的磁场灵敏度都有近1个数量级的提高.
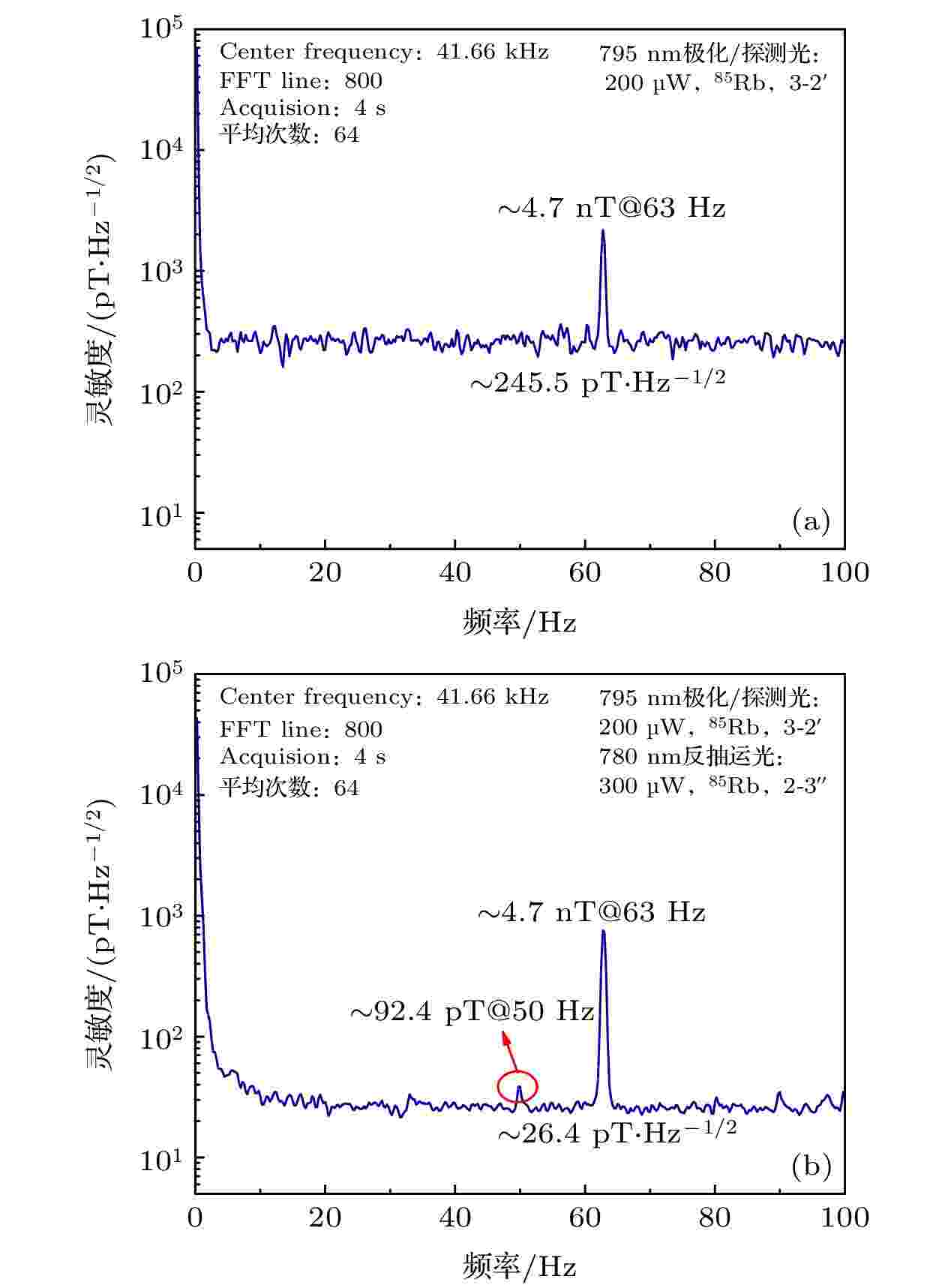 图 7 有无780 nm波长窄线宽单频连续反抽运光情况下磁场灵敏度, 标定场频率63 Hz, 磁场强度4.7 nT(a)在仅有795 nm波长窄线宽单频连续极化光(同时也是探测光)(功率200 μW, 共振于铷-85原子D1线
图 7 有无780 nm波长窄线宽单频连续反抽运光情况下磁场灵敏度, 标定场频率63 Hz, 磁场强度4.7 nT(a)在仅有795 nm波长窄线宽单频连续极化光(同时也是探测光)(功率200 μW, 共振于铷-85原子D1线



Figure7. The sensitivity of the magnetometer: The calibration field frequency is 63 Hz and the magnetic field strength is 4.7 nT: (a) The magnetic field sensitivity in the presence of pumping laser beam (the frequency is resonant with




对于光泵原子磁强计, 由于测量的碱金属原子的自旋进动频率与磁通量密度有直接的关联, 所以在对绝对磁场进行测量时不需要外部校准, 即此种光泵原子磁强计可用作校准元. 尤其本实验所用的在气室内壁镀石蜡抗自旋弛豫膜的铷原子气室, 同时使用铷-85和铷-87两种同位素原子进行标定和相互校验, 且已知不同超精细能级对应的精确旋磁比, 不存在中心频率漂移带来的不准确性问题, 同时结合数字采样系统可保证0.1 nT磁场精度的识别, 有能力对商用磁强计进行标定评估.
这里将要评估的商用磁强计是中国计量科学院研制的CTM-6 W型磁通门磁强计, 它适用于测量微弱恒定磁场、磁屏蔽装置内的磁场和材料的剩磁. 其工作原理及技术参数为: 采用低噪音长环形磁芯的磁通门探头输出的二次谐波信号正比于磁场, 经同步检波器和积分器转变为直流电流反馈回探头线圈, 再经数模转换器输出相应的磁场值, 其中反馈线圈磁场补偿外磁场, 构成一个闭环系统. 该磁通门磁强计标称的技术指标如下: 探头尺寸Φ8 mm × L40 mm, 测磁范围0.1—99999.9 nT, 分辨率0.1 nT, 不确定度0.05 % ± 10 nT.
在795 nm波长窄线宽单频连续极化光(同时也是探测光)和780 nm波长窄线宽单频连续反抽运光功率均为200 μW, 光斑直径均为7.3 mm, 原子气室内壁镀石蜡且温度控制在45 ℃, 795 nm波长窄线宽单频连续极化光(同时也是探测光)频率共振于铷-87原子D1线










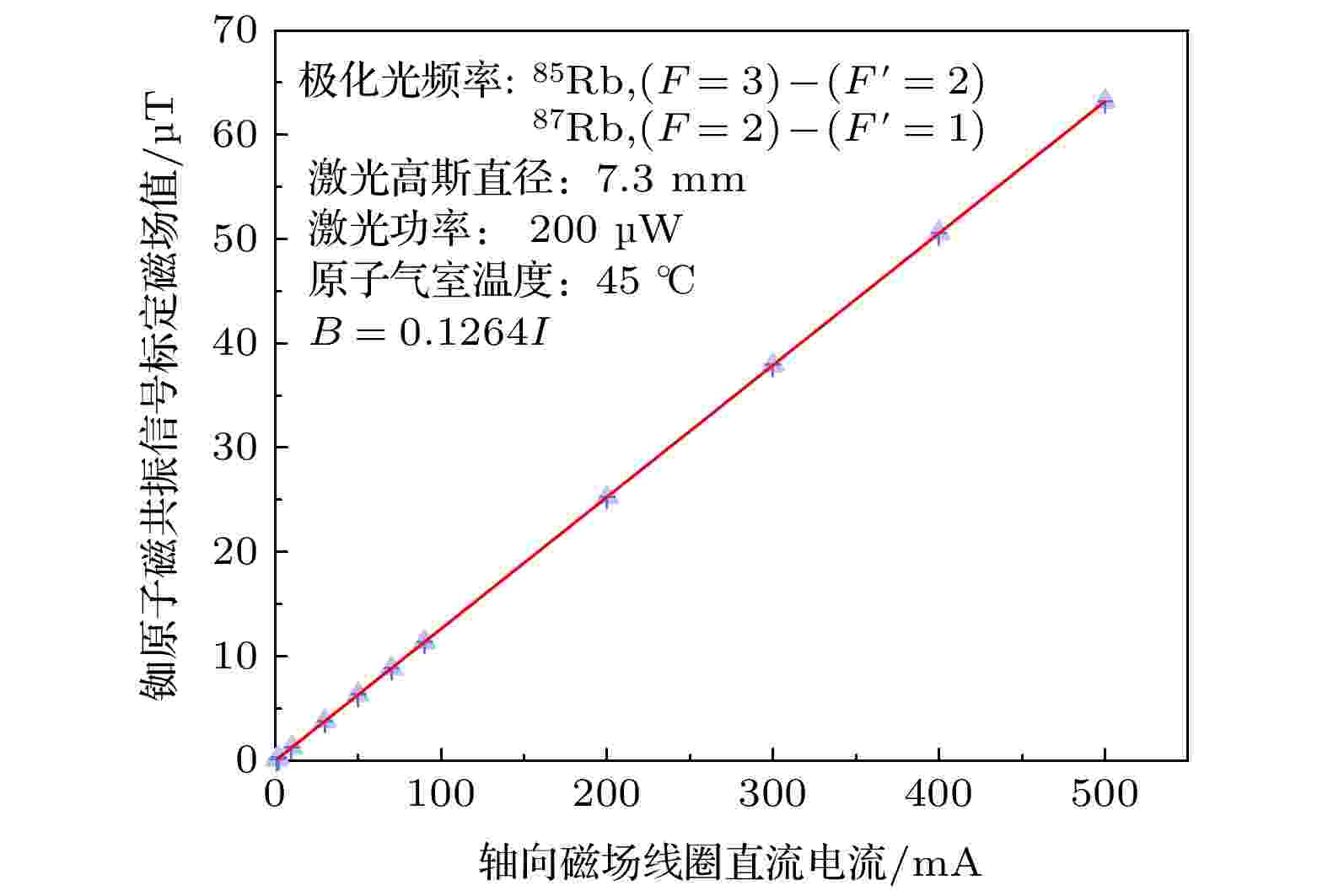 图 8 铷原子磁共振信号标定的磁场值
图 8 铷原子磁共振信号标定的磁场值Figure8. Magnetic field values calibrated by rubidium atomic magnetic resonance signals.
在相同的直流偏置磁场线圈电流下, 用磁通门磁强计测量得到的磁场值相对于用磁共振信号测量得到的磁场值的对比如图9所示.
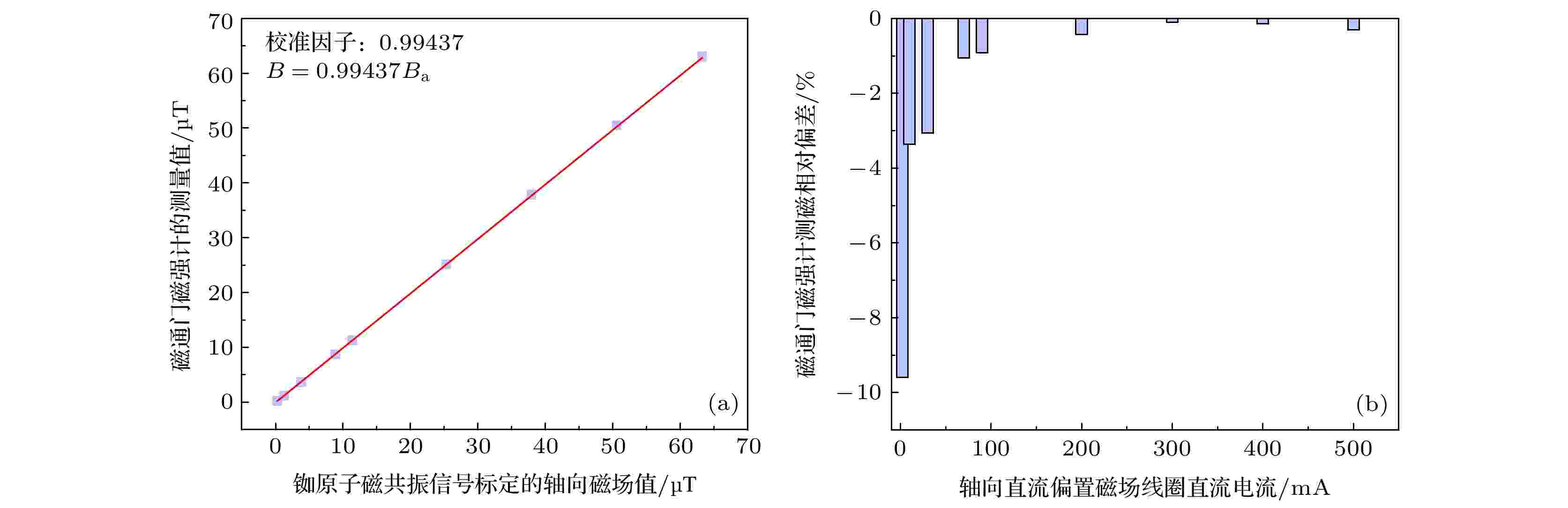 图 9 磁通门磁强计测量磁场值与磁共振信号测量磁场值的关系 (a)蓝红点线为磁通门磁强计测量磁场值相对于铷原子光泵磁强计测量磁场值的对比; (b) 磁通门磁强计测量磁场值相对磁共振信号测量磁场值的相对偏差
图 9 磁通门磁强计测量磁场值与磁共振信号测量磁场值的关系 (a)蓝红点线为磁通门磁强计测量磁场值相对于铷原子光泵磁强计测量磁场值的对比; (b) 磁通门磁强计测量磁场值相对磁共振信号测量磁场值的相对偏差Figure9. The relationship of the magnetic field measured by fluxgate magnetometer and magnetic resonance signal: (a) The blue and red dot lines are the comparison of the magnetic field measured by the fluxgate magnetometer and the rubidium atom optical pump magnetometer; (b) shows the relative deviation of the magnetic field measured by fluxhgate magnetometer compared with magnetic resonance signal.
在使用铷原子磁共振信号对轴向直流偏置磁场进行标定时, 由于磁屏蔽筒在消磁后剩余磁场小于1 nT, 可认为我们的系统近似处于无磁环境, 因此得到其拟合方程为B = 0.1264I. 磁通门磁强计测量磁场值与铷原子磁共振信号标定磁场值之间的关系为B = 0.99437Ba. 从图9可以看出, 磁通门磁强计测量值与真实磁场值相比偏低, 且磁通门磁强计测量磁场的相对偏差在轴向直流偏置磁场线圈电流值偏小时增大, 由此可见测量磁场越弱, 磁通门磁强计的准确度越差. 我们也给出了铷原子磁共振信号与磁通门磁强计在不同轴向直流偏置磁场线圈电流下分别标定磁场时的相对误差值, 如表1所示, 在各自标定磁场时, 磁通门磁强计的相对误差值较大, 标定磁场的准确度比较差, 且随着直流偏置磁场的增大, 磁通门磁强计测量磁场的误差值增大趋势明显.
| 直流偏置磁场线圈电流/mA | 2 | 10 | 30 | 70 | 90 | 200 | 300 | 400 | 500 |
| 铷原子磁共振信号标定磁场的相对误差/nT | ± 0.7 | ± 1.2 | ± 1.7 | ± 2.1 | ± 2.1 | ± 3.1 | ± 3.3 | ± 3.7 | ± 4.6 |
| 磁通门磁强计标定磁场的相对误差/nT | ± 1 | ± 2 | ± 2 | ± 4 | ± 5 | ± 6 | ± 9 | ± 13 | ± 12 |
表1磁通门磁强计与铷原子磁共振信号标定磁场的相对误差值
Table1.Relative error value of magnetic field calibration between fluxgate magnetometer and rubidium atomic magnetic resonance signal.
在后续实验中, 我们可通过以下几种方式进一步优化磁共振信号来提高灵敏度. 1)优化磁共振信号线宽. 本实验中轴向直流偏置磁场(沿极化光方向)的磁场梯度~20 nT/mm, 可能导致磁共振信号线宽展宽, 后续可通过优化轴向直流偏置磁场的均匀性使磁共振信号线宽更窄, 以及进一步优化横向交变磁场强度, 平衡磁共振信号信噪比与线宽的关系; 同时, 优化光束直径, 减小渡越展宽也会进一步减小线宽. 2)优化信噪比. 优化温度即原子数密度可进一步增大信噪比, 提高灵敏度; 激光的强度噪声也是信号幅值的影响因素之一, 后续可加入反馈回路抑制激光强度噪声, 提高信噪比. 本实验所使用的低噪声精密电流源的噪声~600 nA(对应量程为 ± 100 mA), 对应于拉莫尔进动频率的频率起伏约0.35 Hz, 故后续可使用秒稳约2 × 10–11 的铷原子钟(在1 s的探询时间尺度, 铷钟输出10 MHz钟信号的频率起伏小于0.0002 Hz)作为频率标准, 控制信号源产生稳定度更高的交变磁场, 对稳定度相对较差的轴向直流偏置磁场进行闭环锁定, 进一步减小噪声对磁强计的影响.
