摘要:本文设计了一种由两侧挖孔的六棱柱单胞周期性排列而成的新型光力晶体纳米梁谐振腔, 利用有限元法计算了该结构在不同缺陷态下的带隙特性. 基于移动边界效应和光弹性效应机制, 采用一阶微扰理论并借助光力耦合系数计算法获得了光力晶体纳米梁谐振腔的光力耦合率, 同时分析了谐振腔声学模态的对称性, 并对光力耦合机制进行了探索. 研究表明: 改变缺陷数量或优化几何结构均可改善光学模式和机械模式的重叠性; 对于同种缺陷不同数量的谐振腔结构, 缺陷数量只会影响光力耦合率中移动边界效应和光弹性效应的作用方式, 而几乎不会改变其耦合率的大小. 分析具有梯度缺陷的光力晶体纳米梁谐振腔的振动模态对称性发现, 只有关于x-y, x-z, y-z平面偶对称的振动模态才能与光学模态产生强耦合, 并得到高达2.25 MHz的光力耦合率.
关键词: 光力晶体/
缺陷态/
光力耦合效应/
有限元法

English Abstract

全文HTML

--> --> -->

光子晶体是指具有光子带隙特性的人造周期性电介质结构, 当电磁波在光子晶体中传播时, 会产生与半导体类似的能带结构^[1]. 电磁波可在特定频率范围的光子能带中传播而在带隙中无法传播, 凭借这一特性可以实现对电磁波的人工调控, 从而产生一些新颖的物理现象如电磁波的自准直、负折射、调谐滤波等^[2]. 与光子晶体类似, 声子晶体是一种弹性常数及密度周期性分布的人工复合结构, 可以对弹性波进行实时调控^[3]. 而当电磁波和弹性波被限制在微纳米尺度上时, 由于两者态密度的增加, 它们的相互作用剧烈增强, 可实现声对光的有效控制. 因此, 随着纳米技术近年来的不断进步, 微纳米结构中的声光相互作用受到了广泛关注.
光力晶体最重要的物理特性是同时具有声子带隙和光子带隙并对电磁波和弹性波进行调控. 与声子晶体、光子晶体分类类似, 光力晶体按空间周期性分类可分为一维、二维和三维体系^[4]. 一维体系中的梁结构和二维体系中的板结构在非周期性方向上具有有限尺寸, 凭借其相对成熟的加工工艺被广泛研究并加工制作. 2006年, Maldovan和Thomas^[5]第一次从理论上证实了在二维周期性结构中可同时产生光子和声子带隙, 引入缺陷实现了对电磁波和弹性波的同步局域并促进了声光相互作用. 光力晶体凭借带隙特性, 可对电磁波和弹性波进行调控, 进而实现滤波^[6,7]、单向传输^[8]、慢光慢声^[9]等效应, 也可作为传感器检测液体和气体的种类并对浓度、压强等参量进行测量^[10,11]. 2009年, Eichenfield等^[12]用两条光子晶体纳米梁构成了一种拉链式光子晶体腔结构, 从实验上证实了这种结构可凭借光力耦合作用实现较大的光弹簧效应; 同年, 该团队在拉链腔的基础上提出了光力晶体这一概念, 将具有声光子带隙的一维周期性结构开创性的引入到腔光力学领域并利用光力耦合特性提升了腔光力学系统对力变化的灵敏度^[13]. 相较于传统的腔光力学系统如法布里珀罗腔、回音壁腔^[14], 光力晶体谐振腔具有更高的光力耦合率和机械共振频率且其等效质量更小^[15]. 此外, 光力晶体谐振腔作为一种新的腔光力学系统, 凭借其极强的光力耦合效应可利用激光的辐射压力将谐振腔的机械振动冷却至量子基态, 从而为宏观尺度进行量子实验铺平了道路, 并且为集成光声子电路^[16]、弱力及微小位移测量^[17]、量子操纵和量子信息处理^[18-20]等实验提供了可行性思路. 因此, 获得具有高光力耦合率的光力晶体至关重要. 光力晶体中光力耦合率的计算方法主要分为两种, 分别是准静态方法^[21]和计算光力耦合系数的方法^[22]. Chan等^[22]首次提出了利用有限元模拟与数值优化相结合的方法计算光力晶体纳米梁的耦合率, 并考虑了移动边界和光弹性效应引起的光力耦合作用, 获得了1.1 MHz的光力耦合率; Gomis-Bresco等^[23]设计了一种具有光子模式带隙和声子完全带隙的振子型结构, 并在此基础上构建了光力晶体纳米梁谐振腔, 通过实验对谐振腔的声光耦合作用进行分析, 发现利用声子完全带隙能够降低力学模式的能量损耗并增强声光相互作用, 获得了1.8 MHz的光力耦合率; Oudich等^[24]发现光力晶体谐振腔声学本征模态的对称性是影响光力耦合率的关键因素; Li等^[25]优化了在一维硅波导中周期性挖孔的光力晶体纳米梁, 发现只需增加谐振腔中缺陷结构的气孔半径就可以改善光学模态和声学模态的重叠性, 显著提升光弹性效应对光力耦合率的影响, 获得了1.16 MHz的光力耦合率. 近年来, 狭缝型、鱼骨型光力晶体梁结构的提出同样提升了一维光力晶体纳米梁谐振腔的光力耦合率^[26-28], 这些结构可以作为微纳米光力系统中调制光学力的有效途径.
本文设计了一种相较于振子型^[29]、鱼骨型^[30]结构具有更宽声光子完全带隙的一维六角双孔型光力晶体. 利用有限元法计算了光力晶体纳米梁谐振腔在不同缺陷结构下的光学本征模态和声学本征模态, 通过耦合系数计算法分析了光弹性效应和移动边界效应对光力耦合率的贡献, 讨论了不同缺陷态下声学模态的对称性对光力耦合率的影响.

2

-->

2.1.光力晶体纳米梁谐振腔结构设计

具有声光子完全带隙的光力晶体通过引入缺陷结构能更好地局域电磁波和弹性波, 从而增强光力耦合效应, 但是目前对于改变缺陷结构来提高光力耦合率的研究较少. 图1(a)为本文所设计的一维光力晶体纳米梁谐振腔模型的三维示意图, 该结构利用一维硅波导形成, 通过改变纳米梁中心几个单胞的几何参数可形成缺陷区域构成光学谐振腔和声学谐振腔, 镜子区域是由光力晶体单胞周期性排列而成, 可实现对电磁波和弹性波的局域, 提高光力耦合率. 图1(b)为光力晶体单胞结构示意图, 其晶格常数用a表示, 气孔半径用r表示, 光力晶体纳米梁宽度用w表示, 厚度用s表示, 考虑到在通信方面的应用选取a为457 nm, r/a为0.262, s为250 nm, w为707 nm. 在缺陷区域, 本文研究了两种类型的谐振腔结构, 分别为不同缺陷数量的奇、偶对称型谐振腔和几何优化缺陷区域的梯度谐振腔. 图1(c)代表缺陷数量从单个增加到6个的光力晶体谐振腔, 图1(d)表示具有梯度腔的偶对称型光力晶体纳米梁谐振腔, 其中梁两侧的镜子结构由5个单胞构成, 中心缺陷区域由晶格常数先减小后增大的6个单胞组成. 图1(e)为奇对称型一维光力晶体纳米梁谐振腔, 镜子结构与图1(b)相同, 缺陷区域由晶格常数先减小后增大的7个单胞组成.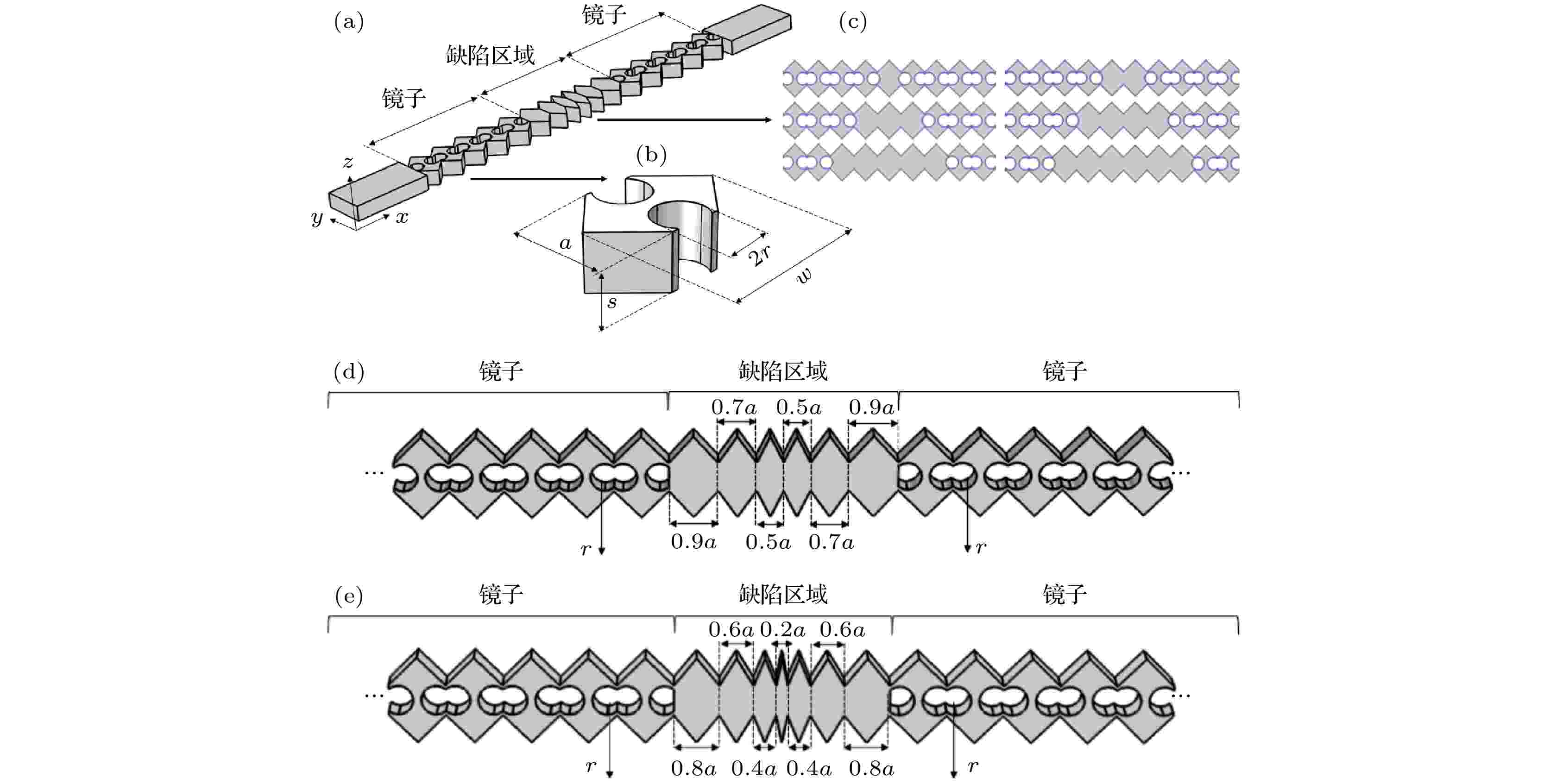
图 1 所设计的一维六角双孔型光力晶体纳米梁谐振腔:　(a)谐振腔结构; (b)光力晶体单胞; (c)不同缺陷数量谐振腔; (d)偶对称型梯度谐振腔; (e)奇对称型梯度谐振腔
Figure1. The model structures of the one-dimensional hexagonal double-hole type optomechanical crystal nanobeam cavity designed in the present work, where (a) is nanobeam cavity structure, (b) is optomechanical crystal unit cell, (c) represents the cavity with different number of defects, and (d) and (e) are the even-symmetric and odd-symmetric gradient nanobeam cavity, respectively.

2 -->

2.2.光力耦合率的计算方法

类比于腔光力学系统, 光力晶体的光力耦合是指谐振腔的光学谐振模式与谐振腔可形变结构形成的振动模态之间发生的相互作用. 在光力晶体谐振腔中, 机械振动会改变谐振腔的形状, 使光学谐振模式的频率$ {\omega _0} $发生变化而成为机械振动幅度α的函数. 在微纳米结构中, 机械振动幅度微弱, 因此可将光学谐振频率在机械谐振腔处于平衡时(α = 0)进行泰勒展开:

$ {\omega _0}\left( \alpha \right) = {\left. {{\omega _0}} \right|_{\alpha = 0}} + \alpha {\left. {\dfrac{{{\text{d}}{\omega _0}}}{{{\text{d}}\alpha }}} \right|_{\alpha = 0}} + \dfrac{1}{2}{\alpha ^2}{\left. {\dfrac{{{{\text{d}}^{\text{2}}}{\omega _0}}}{{{\text{d}}{\alpha ^2}}}} \right|_{\alpha = 0}} + \cdot \cdot \cdot {\kern 1pt} {\kern 1pt} .{\kern 1pt} {\kern 1pt} {\kern 1pt} $

目前对于光力耦合率的计算大多忽略(1)式的二次项及高次项, 只考虑线性的光力耦合, 可化简为

$\begin{split} \;& {\omega _0}\left( \alpha \right) = {\left. {{\omega _0}} \right|_{\alpha = 0}} + \alpha {\left. {\frac{{{\text{d}}{\omega _0}}}{{{\text{d}}\alpha }}} \right|_{\alpha = 0}}\\= \;&{\omega _0}\left( 0 \right) + \alpha {g_{{\text{OM}}}} = {\omega _0}\left( 0 \right) + \alpha \frac{{{\omega _0}}}{{{L_{{\text{OM}}}}}}{\kern 1pt} {\kern 1pt} , \end{split}$

式中: $ {\left. {{\omega _0}} \right|_{\alpha = 0}} = {\omega _0}(0) $代表光力晶体谐振腔处于平衡时的光学谐振频率; ${g_{{\text{OM}}}} = {\left. {\dfrac{{{\text{d}}{\omega _0}}}{{{\text{d}}\alpha }}} \right|_{\alpha = 0}}$称为色散光力耦合系数, 用来表征光力耦合的强度. 为了量化不同光子和不同声子之间的耦合强度, 所以将${g_{{\text{OM}}}}$与声子振动模态的零点涨落位移${\chi _{{\text{zpf}}}}$的乘积作为衡量谐振腔光力耦合强度的品质因子, 用${g_0}$表示即光力耦合率, 可用于不同声子振动模态之间耦合强度的比较, 其表达式为

$ {g_0} = {g_{{\text{OM}}}} \cdot {\chi _{{\text{zpf}}}} = {g_{{\text{OM}}}} \cdot \sqrt {\frac{\hbar }{{2{m_{{\text{eff}}}}{\omega _{\text{m}}}}}} {\kern 1pt} , $

式中, $\hbar$表示约化普朗克常数, m_eff为声子模式的谐振腔有效质量, ω_m表示声子模式的本征频率.
光力晶体纳米梁中的光力耦合率主要受移动边界效应和光弹性效应两部分影响, 移动边界效应为表面效应, 主要由机械模式位移影响不同材料界面处介电常数矩阵导致; 光弹性效应为体效应, 主要以机械模式变形导致电介质内部区域介电常数矩阵发生改变为主^[31]. ${g_0}$还可表示为

$ {g_0} = {g_{{\text{mb}}}} + {g_{{\text{pe}}}} = \left( {{{\left. {\frac{{{\text{d}}{\omega _0}}}{{{\text{d}}\alpha }}} \right|}_{{\text{mb}}}} + {{\left. {\frac{{{\text{d}}{\omega _0}}}{{{\text{d}}\alpha }}} \right|}_{{\text{pe}}}}} \right){\chi _{{\text{zpf}}}}{\kern 1pt} , $

式中, ${g_{{\text{mb}}}}$为移动边界效应光力耦合率, ${g_{{\text{pe}}}}$为光弹性效应光力耦合率.
利用微扰理论求解移动边界效应的Maxwell方程组^[32]可得:

$\begin{split} \,&{g_{{\text{mb}}}} = - \frac{{{\omega _0}}}{2}\dfrac{{\left\langle {{{{\boldsymbol{E}}}}\left| {\dfrac{{{\text{d}}\varepsilon }}{{{\text{d}}\alpha }}} \right|{{{\boldsymbol{E}}}}} \right\rangle }}{{\displaystyle\int {{\text{d}}V \cdot \varepsilon {{\left| {{{\boldsymbol{E}}}} \right|}^2}} }}{\chi _{{\text{zpf}}}} = \\ \,& - \frac{{{\omega _0}}}{2}\frac{{\displaystyle\int {{\text{d}}A \cdot {{{\boldsymbol{q}}}} \cdot {{{\boldsymbol{n}}}}\left( {\Delta \varepsilon {{| {{{{{\boldsymbol{E}}}}_{||}}} |}^2} - \Delta {\varepsilon ^{ - 1}}{{| {{{{{\boldsymbol{D}}}}_ \bot }} |}^2}} \right)} }}{{\displaystyle\int {{\text{d}}V \cdot \varepsilon {{\left| {{{\boldsymbol{E}}}} \right|}^2}} }}{\chi _{{\text{zpf}}}}{\kern 1pt} , \end{split}$

式中, ${{{\boldsymbol{q}}}} \cdot {{{\boldsymbol{n}}}}$表示位移分量与垂直于界面外的法向单位相量的点积, ${{{{\boldsymbol{E}}}}_{||}}$表示平行于界面的电场分量, ${{{{\boldsymbol{D}}}}_ \bot }$表示垂直于界面的电位移场分量, $\Delta \varepsilon = {\varepsilon _1} - $$ {\varepsilon _2}$被定义为电介质与空气介电常数之差, $\Delta {\varepsilon ^{ - 1}} = $$ {\varepsilon _1}^{ - 1} - {\varepsilon _2}^{ - 1}$为电介质与空气介电常数倒数之差, $\displaystyle\int {{\text{d}}A}$表示对光力晶体纳米梁谐振腔所有界面做面积分.
利用微扰理论求解光弹性效应的Maxwell方程组^[22]可得:

$ {g_{{\text{pe}}}} = - \frac{{{\omega _0}}}{2}\frac{{\left\langle {{{{\boldsymbol{E}}}}\left| {\delta \varepsilon } \right|{{{\boldsymbol{E}}}}} \right\rangle }}{{\displaystyle\int {{\text{d}}V \cdot \varepsilon {{\left| {{{\boldsymbol{E}}}} \right|}^2}} }}{\chi _{{\text{zpf}}}}{\kern 1pt} , $

式中$\left\langle {{{{\boldsymbol{E}}}}\left| {\delta \varepsilon } \right|{{{\boldsymbol{E}}}}} \right\rangle$可展开为

$\begin{split} &\left\langle {{{{\boldsymbol{E}}}}\left| {\delta \varepsilon } \right|{{{\boldsymbol{E}}}}} \right\rangle \\ =\;& -{\varepsilon _0}{n^4}\int {\text{d}}V \Big\{ 2{Re} \left\{ {E_x^*{E_y}} \right\}{p_{44}}{S_{xy}} \\ & + 2{Re} \left\{ {E_x^*{E_z}} \right\}{p_{44}} {S_{xz}} + 2{Re} \left\{ {E_y^*{E_z}} \right\}{p_{44}}{S_{yz}} \\ & + {\left| {{E_x}} \right|^2} \left[ {p_{11}}{S_{xx}} + {p_{12}}\left( {{S_{yy}} + {S_{zz}}} \right) \right] \hfill \\ & + {\left| {{E_y}} \right|^2}\left[ {p_{11}}{S_{yy}} + {p_{12}}\left( {{S_{xx}} + {S_{zz}}} \right) \right] \\ & + {\left| {{E_z}} \right|^2}\left[ {p_{11}}{S_{zz}} + {p_{12}}\left( {{S_{xx}} + {S_{yy}}} \right) \right]\Big\}, \end{split}$

式中, p为四阶光弹性张量, S为应变张量, 本文所用材料硅的光弹性张量为 (p₁₁, p₁₂, p₄₄) = (–0.094, 0.017, –0.051).

2

-->

3.1.声子和光子能带结构

本文利用有限元方法对光力晶体纳米梁谐振腔的声子和光子能带结构及声学传输损失进行了仿真计算, 并分析了声光相互作用. 有限元方法适用于模式的分析计算, 在确定光子晶体和声子晶体的电场和位移场分布中也被证明是有效的. 在计算中, 硅的密度设定为ρ = 2329 kg/m³, 并使用立方晶系各向异性弹性矩阵, 其中(C₁₁, C₁₂, C₄₄) = (166, 64, 80) GPa.
图2(a)表示声子能带结构, 其中蓝色区域表示声子带隙, 带隙范围为6.28 GHz到7.73 GHz, 归一化频率带隙范围为0.475到0.606; 图2(b)表示光子能带结构, 其中灰色区域表示光锥定义为ck/ω < 1, c是真空中光速, k是波矢, ω是角频率, 代表空气中电磁波的色散关系, 光子带隙范围为210.72 THz到245.35 THz. 因此, 本文所设计的光力晶体最高可同时对频率为10⁹ Hz的弹性波和频率为10¹⁴ Hz的电磁波进行调控. 图2(c)和图2(d)分别代表了声子带隙和光子带隙随单胞内孔半径线性变化的关系. 通过分析发现声子带隙和光子带隙的起始频率和截止频率都随几何结构变化显著, 只需改变单胞内孔半径就可在声子和光子带隙中产生缺陷模, 在带隙范围内打开通带.
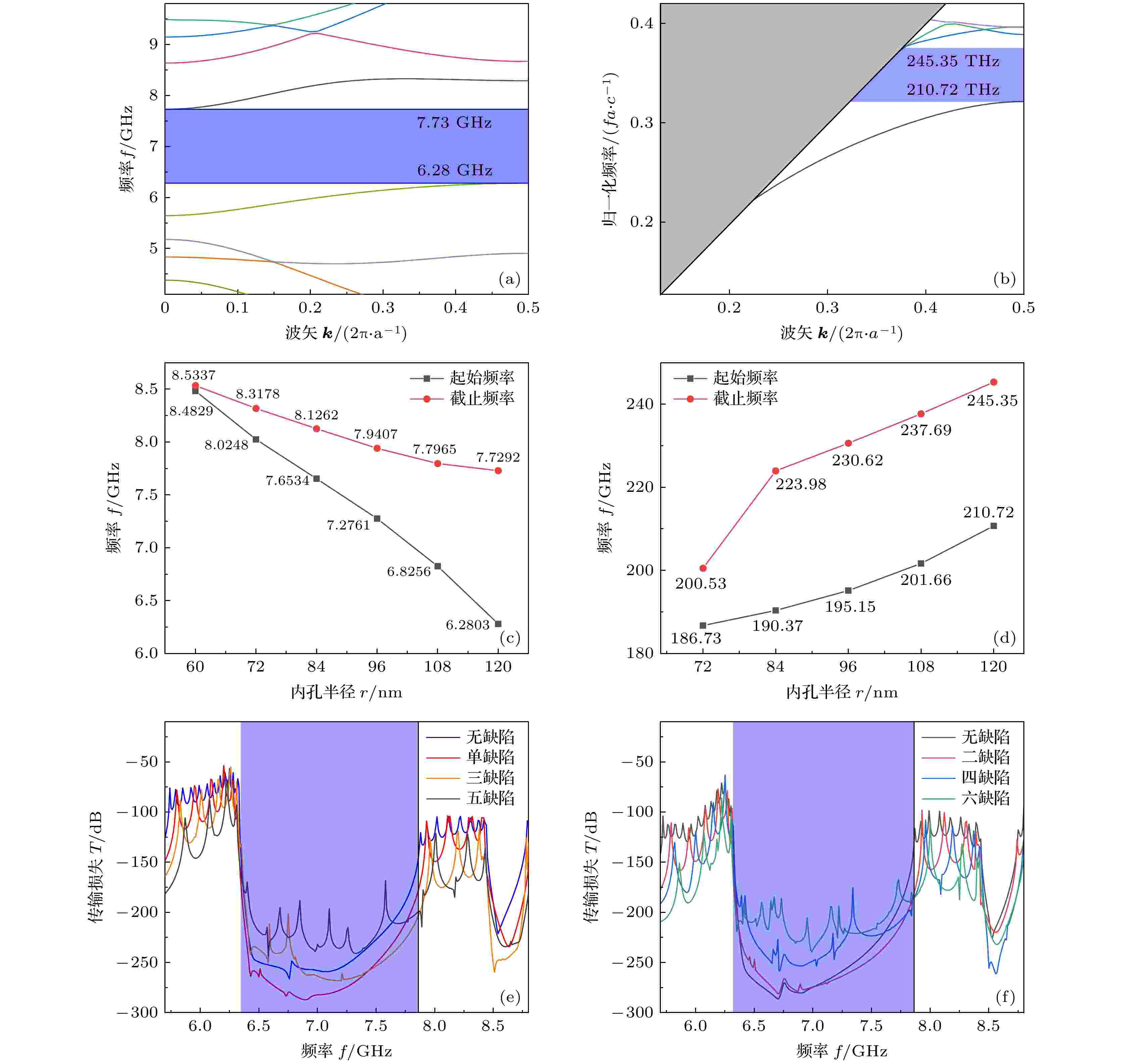图 2 六角双孔型光力晶体能带结构:　(a)声子能带结构; (b)光子能带结构; (c)声子带隙随内孔半径的改变; (d)光子带隙随内孔半径的改变; (e)无缺陷纳米梁与奇对称型谐振腔声透射谱; (f)无缺陷纳米梁与偶对称型谐振腔声透射谱
Figure2. The band structures of hexagonal double-hole type optomechanical crystal, where (a) and (b) represent the phononic and photonic band structure, respectively, (c) and (d) correspond to the change of the phononic and photonic band gap with the radius of the inner hole, and (e) and (f) are different defects acoustic transmission spectrum of optomechanical crystal nanobeam cavity.

本文通过移除光力晶体上的气孔作为缺陷引入到光力晶体纳米梁中构建谐振腔. 并将一、三、五数量的缺陷作为奇对称结构, 二、四、六数量的缺陷作为偶对称结构, 如图1(c)所示. 对不同数量缺陷的光力晶体纳米梁声透射谱进行了计算, 如图2(e)和图2(f)所示, 图中蓝色区域对应声子能量衰减范围与声子带隙完全吻合. 对比无缺陷、单缺陷、三缺陷、五缺陷结构透射谱可以发现, 随着缺陷数量的增加, 带隙范围内产生的缺陷模逐渐增多, 透射谱中共振峰的数量也在增加, 同理偶对称谐振腔也是如此, 缺陷数量的增多也为下一步寻找可产生高耦合率的声学共振模态提供了更多的可能性.
2 -->

3.2.光力耦合分析

本文利用光力耦合系数的计算方法, 根据(3)—(7)式计算了具有同种缺陷但数量不同的奇、偶对称型光力晶体纳米梁谐振腔的光力耦合率, 对比多组声学缺陷模和光学缺陷模找到了每种谐振腔所对应的具有最高耦合率的声学模态与光学模态. 其中在缺陷数量为一、三、五的谐振腔中找到了每种结构具有最高耦合率的电场和位移场分布模态如图3所示. 图3(a)为单缺陷的光力晶体纳米梁在241.5 THz下的电场分布图和6.51 GHz下的位移场分布图; 图3(b)为三缺陷的光力晶体纳米梁在232.7 THz下的电场分布图和7.18 GHz下的位移场分布图; 图3(c)为五缺陷的光力晶体纳米梁在237.61 THz下的电场分布图和7.18 GHz下的位移场分布图. 从模态图中看出无论缺陷数量多少, 电场和位移场都可以被很好地局域在谐振腔的缺陷区域中从而增强电场和位移场的重叠性, 提升光力耦合率. 从图3(g)中可以得到单缺陷、三缺陷和五缺陷下光力晶体纳米梁谐振腔的耦合率分别为–1.29, –1.24和1.27 MHz, 其中单缺陷下光力耦合率的光弹性效应和移动边界效应所占比重相近且相互促进, 而三缺陷中光弹性效应占主导地位, 五缺陷则主要以移动边界效应为主.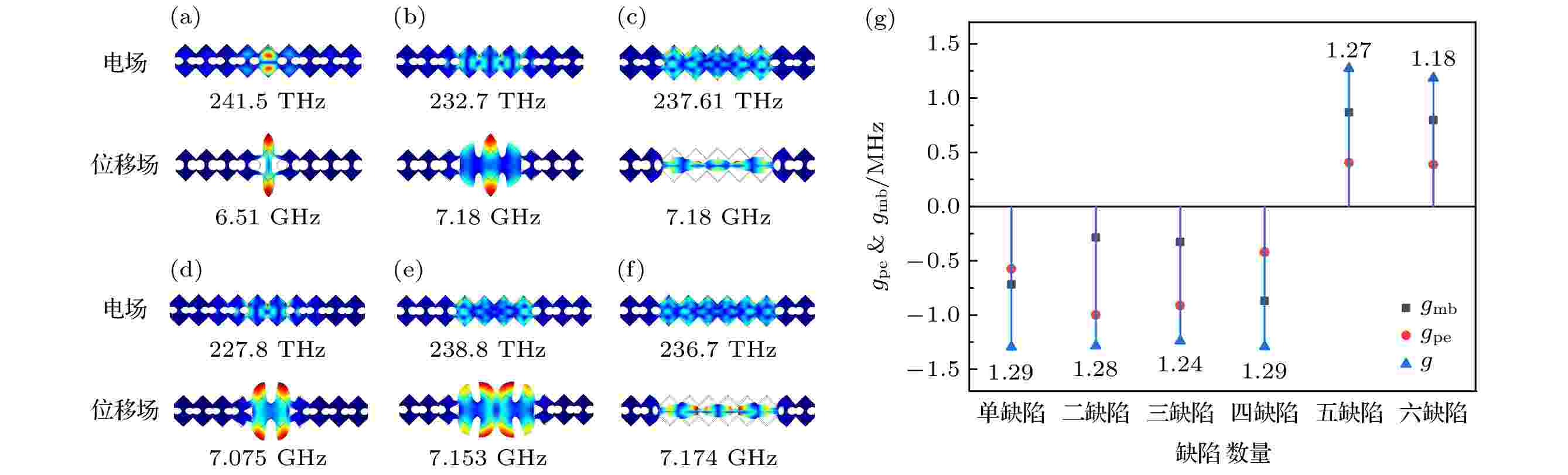
图 3 (a)?(f)不同缺陷数量光力晶体谐振腔的电场和位移场模态图; (g)不同缺陷数量谐振腔的光力耦合率
Figure3. The electric field and displacement field modes of optomechanical crystal cavities with different defect numbers are shown in (a) (f), and (g) is optomechanical coupling rates of nanobeam cavities with different numbers of defects.

经计算发现, 偶对称结构得到的耦合率与奇对称结构类似, 电场和位移场模态如图3(d)—(f)所示. 其中二缺陷的谐振腔电场模态与三缺陷电场模态十分相似, 主要集中在梁的中心区域, 光弹性效应占主导地位, 此外两者位移场分布也十分类似, 均为谐振腔向梁两侧拉伸振动, 且耦合率都为负值; 四、五、六缺陷谐振腔的电场模态主要集中在梁的两侧区域, 因此移动边界效应占主导地位. 通过对振动模态的分析, 四缺陷的振动模态为谐振腔向梁两侧拉伸, 五、六缺陷与其相反从而导致其耦合率正负值相反, 但不影响声光相互作用强度. 二、四、六缺陷下谐振腔的光力耦合率分别为–1.28, –1.29, 1.18 MHz. 因此在谐振腔中同种缺陷的数量对最高耦合率值的影响不显著, 但对耦合方式的影响较为明显.
因微纳米尺度的结构加工难度大, 为避免本文所设计的结构在加工时出现的误差和冗余导致光力耦合率降低, 我们对光力晶体梁的所有尖角都进行了圆角化处理来验证结构是否具有好的抗干扰能力. 以缺陷数量为两个的光力晶体梁为例, 该结构的圆角半径r' 以10 nm为步长, 分别从30 nm取到150 nm, 如图4(a)所示. 并计算了光力晶体梁在圆角处理后的光力耦合率, 如图4(b)所示, 当圆角半径小于100 nm时光力晶体梁的光力耦合率将会出现小幅降低, 其中圆角半径取30 nm时光力耦合率最低, 低至1.23 MHz; 当圆角半径大于100 nm时结构的光力耦合率将略高于原结构, 最高为1.36 MHz. 故在考虑加工冗余和误差后, 本文所设计的光力晶体梁仍能保持较高的光力耦合率, 受加工误差的影响较小且具有较强的误差适应性.
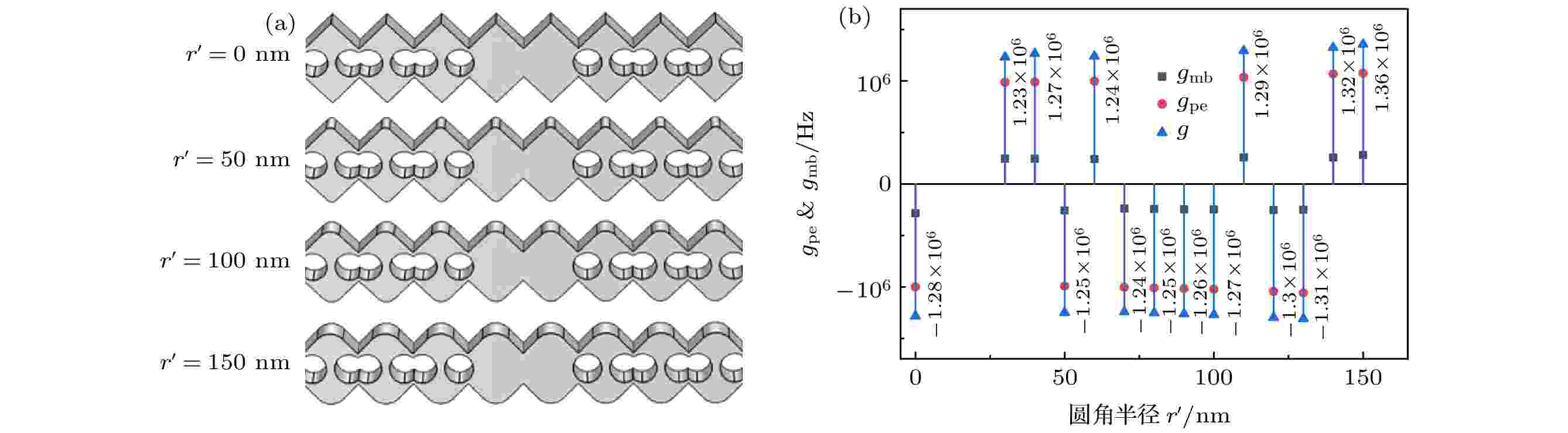图 4 具有不同圆角半径的两缺陷光力晶体纳米梁及其光力耦合率
Figure4. Two-defect optomechanical crystal cavities with different fillet radii and its optomechanical coupling rates.

基于以上分析发现, 所设计的光力晶体纳米梁只需引入单一缺陷就可得到较强的声光相互作用, 且等效质量为42.6 fg. 此外, 对于谐振腔均为同种缺陷组成的结构其每个缺陷单元的声学振动模态都十分相似, 可构成最简单的呼吸型振动模态^[13]. 对于空间传感器而言, 缺陷区域不能分布在任意大量的单元上, 因为空间分辨率会以增加感测面积为代价降低灵敏度, 所以此类结构为传感器设计提供了一种新思路, 且结构设计简单更容易进行加工制作与实验测试. 但同种缺陷构成的光力晶体纳米梁谐振腔因其结构设计的局限性, 仅通过改变缺陷数量无法获得更强的光力耦合效应.
为了继续提升所设计的光力晶体谐振腔的耦合率, 本文对光力晶体缺陷结构进行了几何优化, 如图1(d)和图1(e)所示. 偶对称谐振腔缺陷的晶格常数a_i按照${a_i} = a \times \left( {{\text{1}}{\text{.1}} - 0.{\text{2}}i} \right){\kern 1 pt} {\kern 1 pt} {\kern 1 pt} {\kern 1 pt} i = {\text{1}}—{\text{3}}$进行几何优化, 形成一个六缺陷的梯度腔结构; 奇对称谐振腔缺陷的几何优化方式与偶对称类似, 晶格常数a_i按照${a_i} = a \times \left( {{\text{1}} - 0.{\text{2}}i} \right){\kern 1 pt} {\kern 1 pt} {\kern 1 pt} i = {\text{1}}—{\text{4}}$进行几何优化, 形成一个具有七缺陷的梯度腔结构. 利用有限元方法对几何优化后的梯度腔缺陷的光力晶体纳米梁谐振腔声子能带结构进行了计算, 如图5(a)和图5(b)所示. 其中, 蓝色区域为光力晶体的声子带隙范围, 虚线A1-L1, A2-N2分别对应在声子带隙范围内, 偶对称型和奇对称型缺陷谐振腔所产生的声子缺陷模.
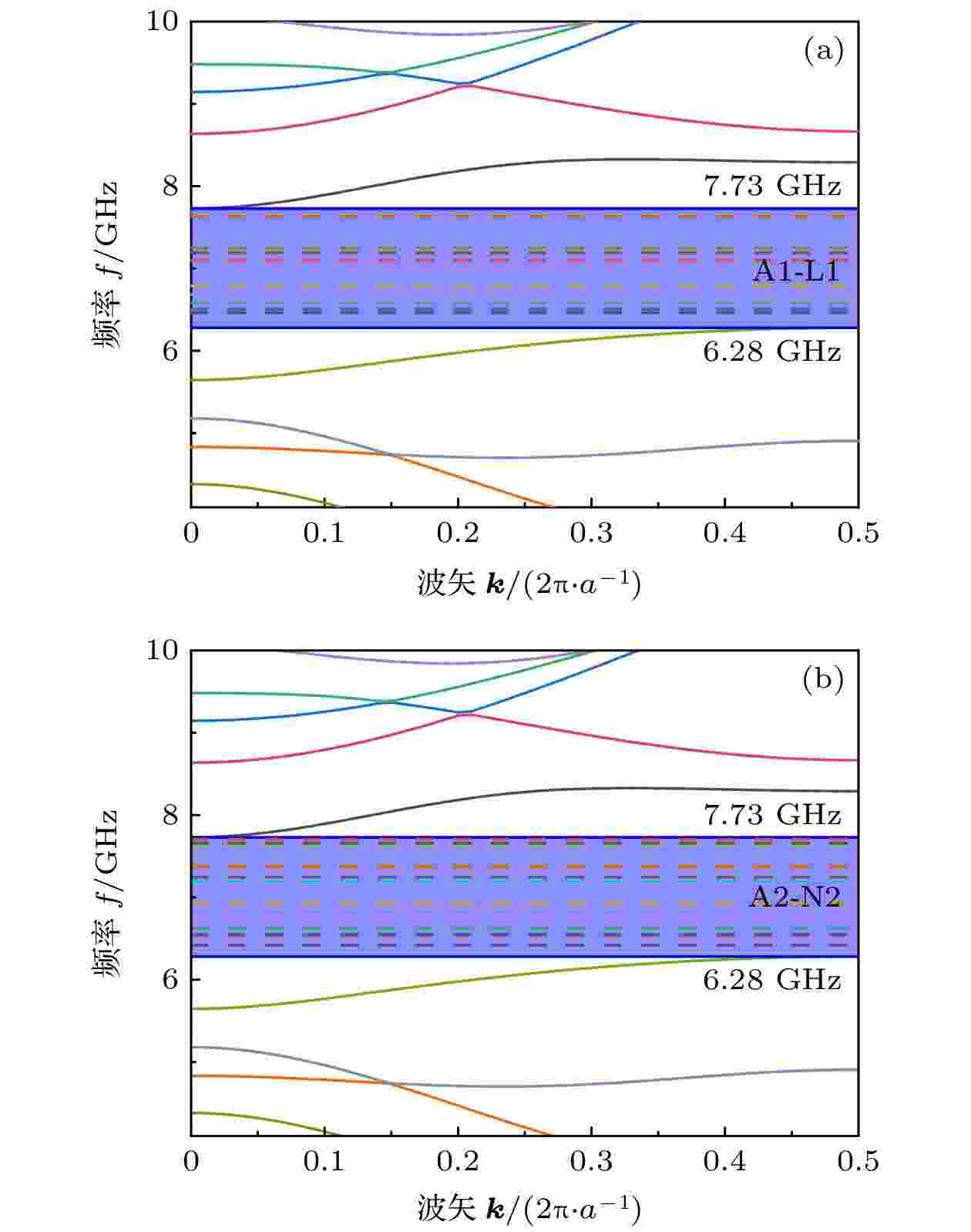图 5 几何优化谐振腔的声子能带结构:　(a)偶对称谐振腔的声子能带结构, A1-L1为带隙内产生的声子缺陷模; (b)奇对称谐振腔的声子能带结构, A2-N2为带隙内产生的声子缺陷模
Figure5. Phononic band structures of the geometrically optimized nanobeam cavities, where (a) is phononic band structure of the even symmetric cavity, in which A1-L1 are the defect modes generated in phononic band gap, and (b) is phononic band structure of the odd symmetric cavity, in which A2-N2 are the defect modes generated in phononic band gap.

图6(a)表示在声光子带隙范围内缺陷模的声学位移场A1-L1和电场P1分布图. 从图中可以看出在声子带隙范围内具有大量的缺陷模, 且每种缺陷模的振动能量都被很好地局域在缺陷区域内. 根据振动模态的对称性将不同频率下的声学缺陷模分成了四类: 具有关于x-y, x-z和y-z平面偶对称的三重偶对称性声学模态B1, F1, G1, K1; 具有关于x-y和x-z平面偶对称的二重偶对称性的声学模态A1, E1, J1; 具有关于y-z平面偶对称性的一重偶对称性的声学模态C1, D1; 不具有任何偶对称性的声学模态H1, I1, LI. 同样在多组电场缺陷模内找到了一个电磁波能量被很好局域在缺陷区域内的电场模态P1, 如图6(a)所示, 可以看出P1的电场分布主要集中在缺陷区域的表面, 本征频率为256.77 THz. 利用(3)—(7)式计算了所有声学缺陷模A1-L1和光学缺陷模P1之间的耦合.
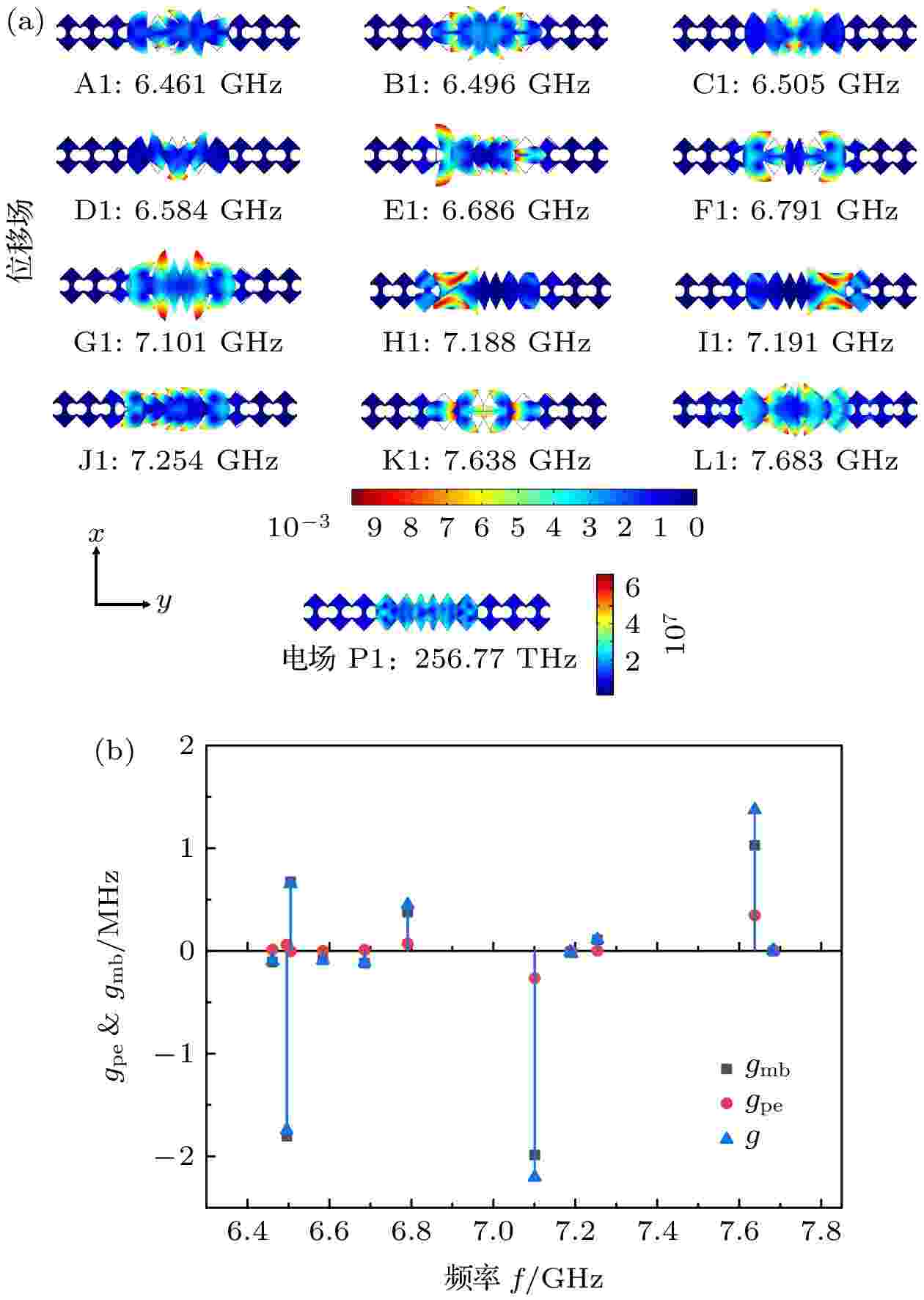图 6 几何优化偶对称谐振腔的电场和位移场模态及其光力耦合率:　(a)谐振腔的位移场模态图A1-L1与电场模态图P1; (b)光力耦合率及其分量g_mb和g_pe
Figure6. Geometrically optimize the electric field and displacement field modes of the even symmetric nanobeam cavity and optomechanical coupling rates, where (a) represents displacement field mode diagram A1-L1 and electric field mode diagram P1 of the nanobeam cavity, and (b) is optomechanical coupling rates of nanobeam cavities and its components g_mb and g_pe.

表1列出了光学缺陷模P1和十二个声学缺陷模之间的耦合率计算结果, 包括总耦合率${g_0}$、移动边界效应耦合率${g_{{\text{mb}}}}$、光弹性效应耦合率${g_{{\text{pe}}}}$及等效质量$ {m_{{\text{eff}}}} $, 其中在质量密度和弹性模量恒定的材料中$ {m_{{\text{eff}}}} $代表了机械模式的有效局域化. 在谐振传感应用中, 纳米机械谐振器的探测灵敏度通常反比于等效质量, 因此极低的等效质量使其拥有极高的探测灵敏度. 从图6(b)与表1可以看出, 对于所有缺陷模所产生的耦合率移动边界效应要远大于光弹性效应, 究其原因主要是在模态P1中电场主要分布在光力晶体梁表面且所有声学共振模的振动能量主要集中在梁的两侧, 从而导致移动边界效应占据主导地位. 由于移动边界效应是表面效应, 经过计算发现在同一电磁波频率下(5)式的分母项作为对电场的体积分, 无论如何改变声学共振模式都不会使其数值发生变化, 所以移动边界效应的耦合率主要受(5)式分子项面积分的影响, 如何使面积分的数值达到最大, 声学共振模式的对称性至关重要.

	A1		B1		C1		D1		E1		F1
gmb / Hz	–1.076×105		–1.805×106		6.721×105		–8.925×104		–1.204×105		3.790×105
gpe / Hz	1.130×104		6.104×104		–1.888×103		6.130×102		9.662×103		7.078×104
g0 / Hz	–9.626×104		–1.744×106		6.532×105		–8.864×104		–1.108×105		4.498×105
meff / 10–17 kg	2.429		4.072		1.657		1.719		6.816		4.698
	G1		H1		I1		J1		K1		L1
gmb / Hz	–1.987×106		–9.336×103		–1.745×104		1.102×105		1.028×106		–2.258×103
gpe / Hz	–2.661×105		–1.470×103		–6.952×103		1.425×103		3.462×105		7.341×103
g0 / Hz	–2.253×106		–1.081×104		–2.440×104		1.116×105		1.374×106		5.083×103
meff / 10–17 kg	7.086		2.879		2.949		3.320		8.115		3.701

表1偶对称型谐振腔声学共振模式与光学模式的耦合率
Table1.Optomechanical coupling rates of even symmetric nanobeam cavity

本文根据对称性分类发现偶对称性越高的声学共振模式所得到的耦合率越高, 以具有三重对称性的B1, F1, G1和K1为例, 这些模态的耦合率远高于其他共振模式, 其中B1, G1和K1三种谐振腔的耦合率都高达10⁶量级, 且声学模态G1具有最高的耦合率为2.253 MHz, 等效质量为70.86 fg. 而具有二重对称性或一重对称性的共振模态A1、E1、J1与C1、D1其耦合率相较于三重对称模态要低一个数量级, 大约为10⁵量级. 不具对称性的共振模态H1、I1、LI的耦合率将会更低, 只能达到10⁴和10³量级.
与偶对称结构类似, 本文同样对几何优化后的奇对称谐振腔缺陷模的声学本征频率进行了计算, 发现奇对称结构相较于偶对称结构缺陷数量增加, 产生了更多的缺陷模, 共14种, 分别为A2-N2, 这些模态的振动能量都很好的局域在缺陷区域内, 同样找到了一个电磁波能量被很好局域在缺陷区域中的电场模态P2, 如图7(a)所示. 表2与图7(b)列出了电场模态P2和十四种声学缺陷模之间的总耦合率, 按振动模态的对称性找到了三种三重偶对称性高的模态A2, E2和H2, 其中声学模态A2具有最高的耦合率为2.18 MHz, 等效质量为32.8 fg且移动边界效应占据主导地位. 而模态E2和H2由于移动边界效应和光弹性效应相抵消导致这两种高对称性模态不具备高耦合率. 此外, 其他低对称性声学模态与电场模态P2产生耦合率也非常低.
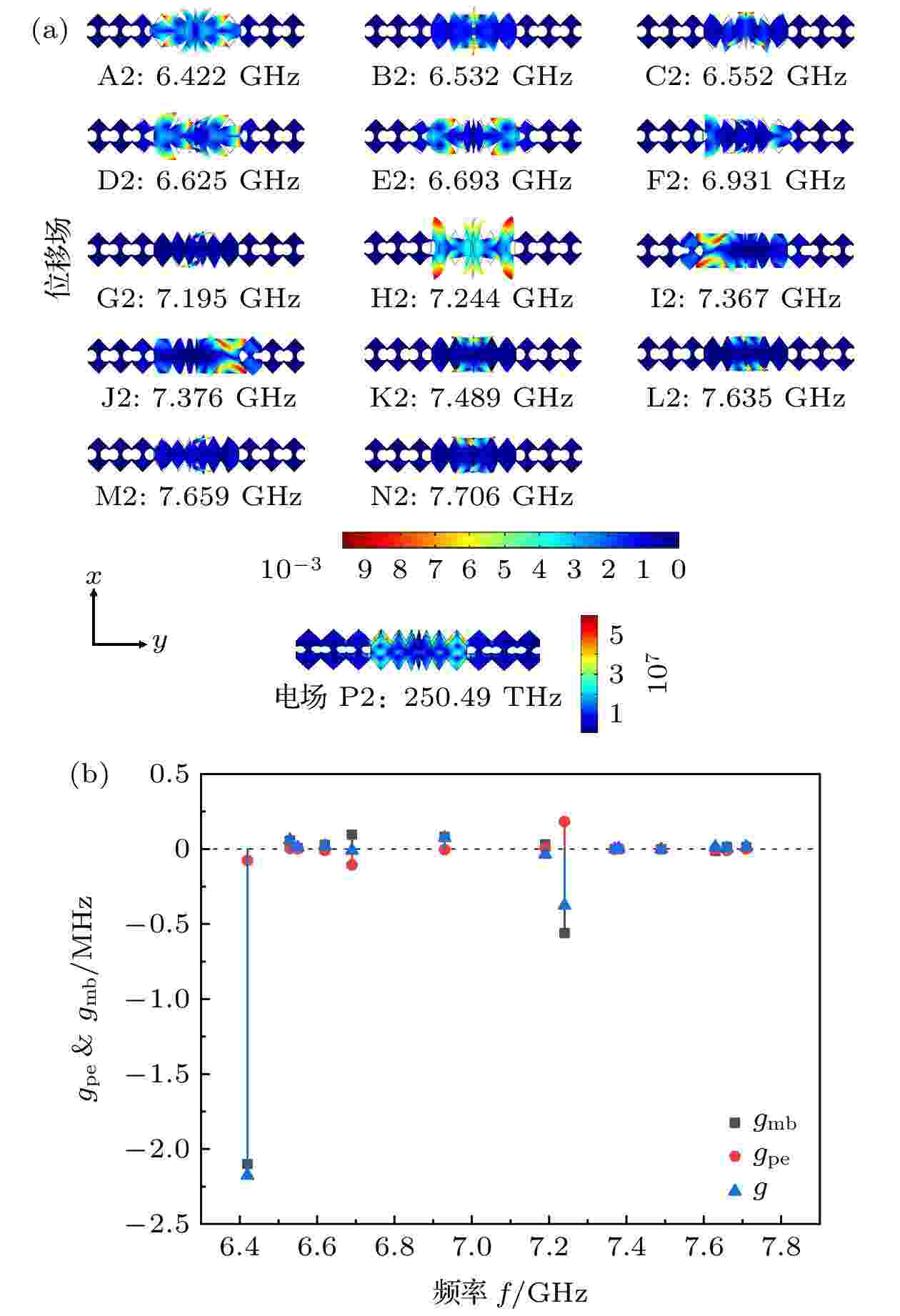图 7 几何优化奇对称谐振腔的电场和位移场模态及其光力耦合率:　(a)奇数谐振腔的位移场模态图A2-N2与电场模态图P2; (b)光力耦合率及其分量g_mb和g_pe
Figure7. Geometrically optimize the electric field and displacement field modes of the odd symmetric nanobeam cavity and optomechanical coupling rates, where (a) represents displacement field mode diagram A2-N2 and electric field mode diagram P2 of the nanobeam cavity, and (b) is optomechanical coupling rates of nanobeam cavity and its components g_mb and g_pe.

	A2	B2	C2	D2	E2	F2	G2
gmb/Hz	–2.100×106	5.629×104	7.079×103	2.795×104	9.599×104	8.016×104	3.082×104
gpe/Hz	–7.580×104	4.084×103	2.762×103	–8.579×103	–1.062×105	–4.091×103	5.240×103
g0/Hz	–2.176×106	6.037×104	9.840×103	1.937×104	–1.024×104	7.607×104	–3.606×104
meff /10–17 kg	3.28	0.991	1.05	3.65	2.79	1.41	0.110
	H2	I2	J2	K2	L2	M2	N2
gmb/Hz	–5.600×105	1.818×103	6.875×102	–1.391×103	–1.240×104	1.401×104	1.311×104
gpe/Hz	1.833×105	–2.254×103	1.972×103	–3.701×102	2.550×102	–8.942×103	9.903×102
g0/Hz	–3.767×105	–4.357×102	2.659×103	–1.761×103	1.266×104	5.066×103	1.410×104
meff /10–17 kg	9.16	1.96	1.89	0.296	0.233	0.287	0.260

表2奇对称型谐振腔声学共振模式与光学模式的耦合率
Table2.Optomechanical coupling rates of odd symmetric nanobeam cavity

为了进一步分析移动边界效应对光力耦合率的影响, 对谐振腔的移动边界效应表面密度${\zeta _{{\text{mb}}}}$进行了计算^[33], 由(8)式给出.

$ {\zeta _{{\text{mb}}}} = \frac{1}{4}{\text{d}}A \cdot {{{\boldsymbol{q}}}} \cdot {{{\boldsymbol{n}}}}\left( {\Delta \varepsilon {{\left| {{{{{\boldsymbol{E}}}}_{||}}} \right|}^2} - \Delta {\varepsilon ^{ - 1}}{{\left| {{{{{\boldsymbol{D}}}}_ \bot }} \right|}^2}} \right). $

所计算的偶对称型谐振腔声子腔模的${\zeta _{{\text{mb}}}}$如图8所示, 分别对应每个共振频率下梁两侧的${\zeta _{{\text{mb}}}}$, 其中三重偶对称性的声学共振模态B1, F1, G1和K1的${\zeta _{{\text{mb}}}}$同样具有偶对称性, 因此可以看出对称性越高的声学共振模态${\zeta _{{\text{mb}}}}$的面积分值越大. 移动边界效应表面密度的反对称分布导致其面积分的抵消, 但声学共振模态F1例外, 虽具有${\zeta _{{\text{mb}}}}$的对称性分布, 但模态F1的耦合率重叠积分值较低, 这意味着当正负${\zeta _{{\text{mb}}}}$值相邻出现时, 具有偶对称性的${\zeta _{{\text{mb}}}}$表面积分同样会相互抵消从而降低耦合率. 此外一些不具备对称性的声学模态如H1, I1和LI, ${\zeta _{{\text{mb}}}}$值十分微弱且不具备对称性, 其积分值将会远远小于具有对称性的模态, 从而验证了低对称性的声学共振模态难以与电场模态产生强耦合. 对于奇对称型光力晶体结构同样具有类似结论, 只有对称性高的声学共振模态才会与电场产生一个强烈的耦合获得极高的光力耦合率. 由于所设计结构的光力耦合率主要由移动边界效应提供, 因此${\zeta _{{\text{mb}}}}$可以捕捉到导致该结构具有强耦合率的主要潜在机制.
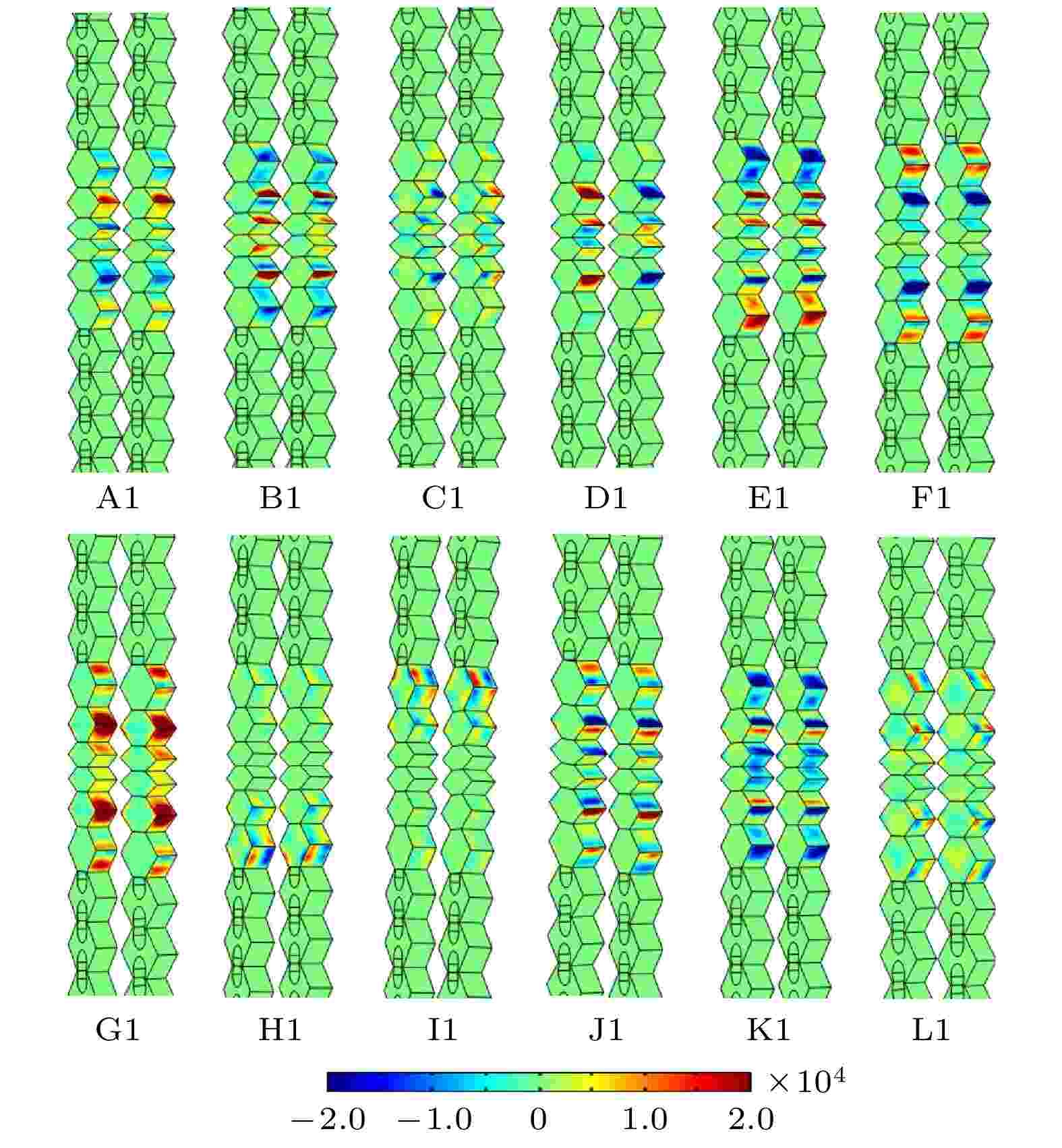图 8 偶对称型纳米梁谐振腔不同谐振频率下声子腔模${\zeta _{{\text{mb}}}}$的分布图
Figure8. The distribution diagram of the phononic cavity modes ${\zeta _{{\text{mb}}}}$ at different resonant frequencies of the even-symmetric nanobeam cavity.

虽然上文所设计的光力晶体梁具有较高的光力耦合率, 但因光力晶体梁的尖角结构对光的散射损耗较强, 导致光学Q因子较低. 为提升结构的光学品质因子, 我们对梯度腔型光力晶体梁的缺陷结构重新进行了几何优化, 如图9(a)所示. 该光力晶体梁的镜子区域同样是由六角双孔型光力晶体单胞构成, 缺陷区域是由10个中心挖孔的六角单胞做倒角实现, 结构的具体几何参数已在图9(a)中标明. 利用有限元方法计算了该结构的声学本征模态和光学本征模态, 并根据前文得出的结论选择了一个振动能量被局域在缺陷内且偶对称性最高的声学模态, 频率为7.545 GHz, 如图9(b)所示. 同样选择了一个电磁波能量被很好地局域在缺陷内的光学模态, 其频率为261.91 THz, 如图9(c)所示, 该模式的光学品质因子为11178.
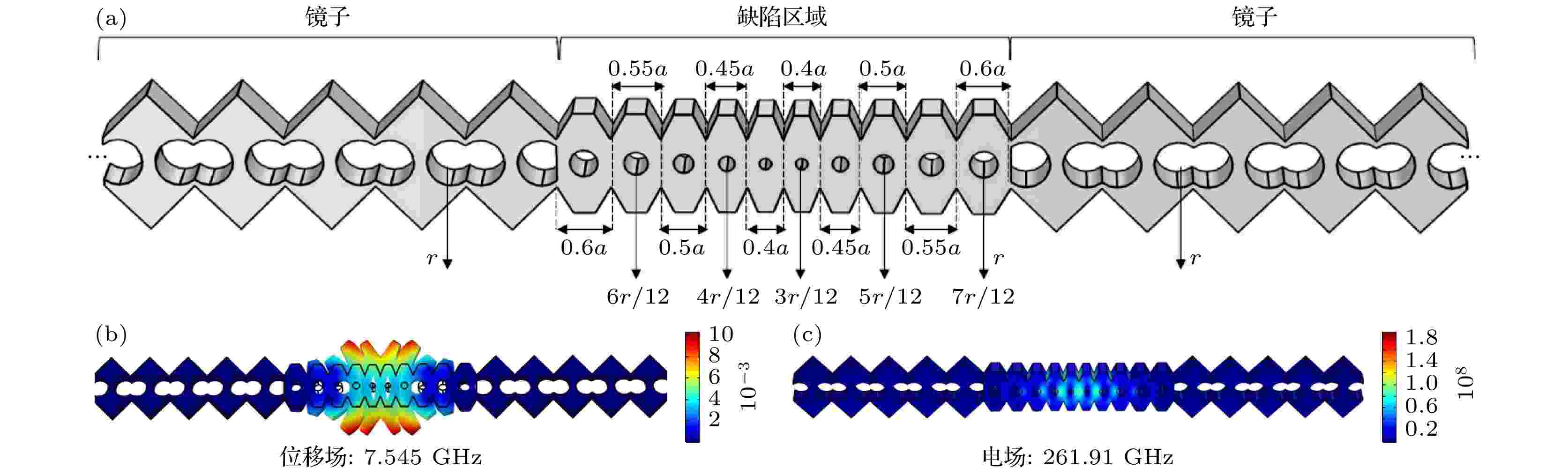图 9 新型梯度腔光力晶体梁及其声学模态和光学模态
Figure9. A new gradient cavity optomechanical crystal nanobeam and its acoustic and optical modes.

此外, 我们还对新型梯度腔光力晶体梁的光力耦合率进行了计算, 结果如表3所示, 该结构的光力耦合率主要为光弹性效应占主导地位且高达2.19 MHz. 因此, 我们所设计的光力晶体梁可通过对缺陷结构的合理设计来提升结构的光学品质因子并保持高光力耦合率.

f/GHz	gmb/Hz	gpe/Hz	g0/Hz	meff /kg
7.545	–1.093×105	–2.076×106	–2.185×106	7.383×10–17

表3新型梯度腔光力晶体梁的光力耦合率
Table3.Optomechanical coupling rates of a new gradient cavity optomechanical crystal nanobeam.

本文研究了一种新型一维六角双孔型光力晶体纳米梁谐振腔的声学与光学共振模之间的声光相互作用. 与传统光力晶体相比, 所设计的结构具有更宽的声子带隙和光子带隙, 且光力晶体梁缺陷的可设计性更强. 其中, 缺陷区域主要通过不同数量同种缺陷或经几何优化后的梯度缺陷构成. 考虑了移动边界效应和光弹性效应对光力耦合的影响, 本文基于一阶微扰理论并借助光力耦合系数计算法计算了结构的光力耦合率. 对于同种缺陷不同数量的谐振腔结构, 缺陷数量只会影响光力耦合的作用方式, 而对耦合率的大小几乎没有影响. 其中, 单缺陷光力晶体谐振腔耦合率最高可达–1.29 MHz, 此时等效质量为42.6 fg, 而单一缺陷设计简单、易于加工与制作, 且作为光力晶体空间传感器感测面积将会更小, 这为高精度传感器的设计提供了一种新的思路.
相对于单缺陷光力晶体谐振腔, 梯度腔缺陷可获得更高的耦合率. 基于梯度缺陷的偶对称光力晶体谐振腔耦合率最高可达2.25 MHz, 奇对称结构耦合率能达到2.18 MHz, 两种谐振腔的耦合方式均为移动边界效应占主导地位. 进一步分析声学共振模态后发现, 只有偶对称性高的声学共振模态才可能与光学模态产生强耦合; 同时, 计算并分析了其移动边界效应表面密度, 发现具备高对称性的声学共振模态的表面密度同样具有较好的对称性, 而当缺陷态中移动边界效应表面密度相邻出现且相互抵消时, 对称性无论高低均会破坏移动边界效应的耦合方式进而降低光力耦合率. 此外, 所设计的光力晶体梁还可以通过优化缺陷结构来同时达到保持高光力耦合率和提升谐振腔品质因子的效果. 因此, 本研究为设计液体浓度传感器、质量传感器和微小位移传感器等声光功能器件提供了模型参考.