全文HTML
--> --> -->众所周知, 纳米LaB6由于体等离子共振效应而对可见光具有高的穿透性, 这也有望将其应用在隔热玻璃中[11-15]. 本课题组在前期研究中首次发现[16,17], 对纳米LaB6进行二价Eu2+或Ba2+离子掺杂可有效改变体等离子共振频率能量, 从而实现对透射光波长可调. 但在制备过程中发现, 添加Ca2+或Ba2+离子存在易挥发、化学配比难控制等问题. 同时所制备纳米粉末尺寸较大, 不利于观察到明显光吸收现象[18-20]. 相比之下, Sr2+添加所合成粉末粒度小, 不易挥发, 化学成分稳定. 然而目前为止关于碱土金属Sr掺杂对LaB6光吸收的影响未见报道. Sr替代是否能改变LaB6体等离子共振频率能量等一系列问题值得进一步研究.
本文采用固相烧结法首先制备出了纳米多元稀土六硼化物La1–xSrxB6粉末. 并研究了Sr替代对LaB6透射光波长的影响. 其次, 为了进一步研究Sr替代对LaB6逸出功的影响, 对多晶块体进行了热发射性能的测试. 最终, 为了阐明Sr替代对LaB6光吸收及逸出功的影响规律, 采用密度泛函理论计算了体等离子共振频率能量和费米能级, 从而揭示光吸收和热发射机理.
2.1.样品制备及表征
将稀土氧化物La2O3 (包头稀土研究所, 纯度为99.99%), 金属氧化物SrO (Sigma-Aldrich, 纯度为99.9%)和NaBH4 (Aladdin, 纯度为99.99%)粉末以摩尔比为1–x∶x∶6 (x = 0, 0.2, 0.4, 0.6, 0.8和1)的比例混合研磨0.5 h. 随后将混合粉末压制成圆柱状, 放入石英管中进行真空烧结. 烧结温度设定为1000—1200 ℃, 保温时间为2 h. 对反应产物用盐酸、蒸馏水和无水乙醇进行3次洗涤, 去除杂质相.采用X射线衍射仪(Cu Kα射线, Philips PW1830)、场发射扫描电子显微镜(FESEM: Hitachi SU-8010)以及透射电子显微镜(TEM: FEI-Tecnai F20S-Twin 200 kV)分别对烧结后的纳米粉末物相、形貌及微观结构进行表征. 采用紫外-可见分光光度计(PerkinElmer Lambda 750S)测定纳米粒子的光吸收. 利用放电等离子烧结炉(型号为LABOX-2010 Khv)对所制备的纳米粉末进行真空烧结致密化. 烧结条件为: 轴向压力50 MPa, 烧结温度为1200 ℃, 保温时间为6 min, 升温速率为70 ℃/min. 随后将烧结块沿体线切割, 切成发射面积为1 mm2的正方形块体, 在阴极温度为1673和1773 K下测量热电子发射电流密度, 真空度为2 × 10–4 Pa, 外加电压为2000 V.
2
2.2.计算方法
为了定性解释Sr替代对LaB6透射光波长的影响, 采用CASTEP计算程序, 利用密度泛函理论[21]赝势平面波方法[22], 计算了LaB6的态密度、介电函数、体等离子频率能量. 计算时建立的2 × 2 × 2的La0.875Sr0.125B6超级晶胞, 如图1所示. 电子相互作用采用广义梯度近似[23]Perdew-Burke-Ernzerhof泛函描述. 平面波截止能量为400 eV. 收敛阈值为2 × 10–5 eV/atom, 对总能量进行几何优化, 最大作用力为0.05 eV/? (1 ? = 0.1 nm). 设k点为11 × 11 × 11, 对La0.875Sr0.125B6超胞电子结构和光学性质进行计算[24].
图 1 La0.825Sr0.125B6晶体结构示意图Figure1. Schematic diagram of the La0.825Sr0.125B6 crystal structure.
为了理论上预测SrB6及Sr替代对LaB6多晶块体逸出功的影响, 首先计算了单晶SrB6的(100), (110), (111), (210)晶面和单晶La1–x Srx B6 (x = 0.25和0.75)的(100)晶面的功函数. 计算中采用平面波基展开电子波函数, 截止能量设为400 eV[25]. 系统总能量的收敛值为2 × 10–5 eV/atom. 当真空高度设置为21 ?时, 可忽略不同原子层间的相互作用.
3.1.纳米La1–xSrxB6的物相、形貌和微观结构分析
首先为确定反应温度对物相的影响, 选择成分为La0.4Sr0.6B6的样品系统, 测试了反应温度为1000, 1150和1200 ℃时所制备样品的XRD图谱, 结果如图2(a)所示. 从图2(a)可知, 这3个反应温度下所有粉末物相均为CsCl-型立方晶体结构, 空间群为Pm
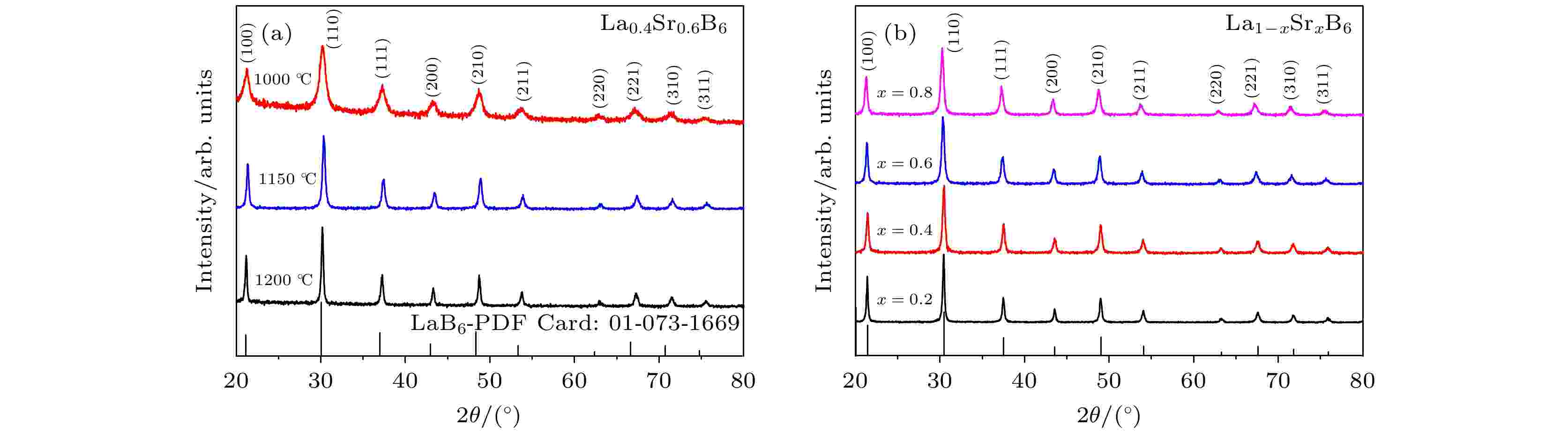图 2 (a)不同反应温度下制备的La0.4Sr0.6B6纳米颗粒的XRD谱图; (b) 1150 ℃下制备的La1–x Srx B6纳米颗粒的XRD谱图Figure2. (a) XRD pattern of La0.4Sr0.6B6 nanoparticles prepared at different reaction temperatures; (b) XRD pattern of La1–x Srx B6 nanoparticles prepared at 1150 ℃.
图3为在反应温度为1150和1200 ℃下纳米La1–x Srx B6粉末的SEM观察照片. 从图3(a)—(d)可以看出, 当反应温度为1150 ℃时, 制备的纳米颗粒分散性好, 平均尺寸为20 nm. 从图3(e)—(h)可知, 当反应温度升高到1200℃时, 纳米粉末平均晶粒尺度约为30 nm; 此外, 还发现在此反应温度下一些颗粒出现异常长大现象. 分析认为主要原因是高的反应温度有利于质量的扩散及迁移, 从而导致大晶粒吞并小晶粒导致晶粒长大. 图3最底层子图为纳米La0.4Sr0.6B6粉末元素分布及分析结果. 从中可知, La, Sr, B这3种元素均匀分布在选定区域的表面. 结合X射线能量色散光谱(EDS)分析, 未出现杂质元素峰表明所合成粉末纯度高、单相性好.
图 3 不同反应温度下所制备的纳米La1–x Srx B6 (x = 0.2, 0.4, 0.6, 0.8)粉末SEM照片 (a)—(d)反应温度为1150 ℃; (e)—(h)反应温度为1200℃. 最底层为纳米La0.4Sr0.6B6粉末元素分布及EDS分析Figure3. SEM image of La1–x Srx B6 (x = 0.2, 0.4, 0.6, 0.8) nanoparticles (a)?(d) prepared at 1150 ℃, (e)?(h) prepared at 1200 ℃. The lowest side shows the elements mapping and EDS analysis of La0.4Sr0.6B6 nanoparticles.
为了进一步分析所合成纳米粉末结晶度及微观结构, 以纳米La0.4Sr0.6B6粉末为例, 采用高分辨透射电子显微镜(HRTEM)对其进行详细表征. 图4(a)为纳米La0.4Sr0.6B6粉末在低倍镜下的TEM照片, 表明纳米颗粒呈立方形貌, 平均晶粒为30 nm. 图4(b)为所选择的单颗粒的形貌照片. 图4(c)为局部放大的HRTEM晶格相照片, 其中平行晶面间距d = 0.15 nm和d = 0.21 nm与(220)晶面和(200)相对应(图4(d)), 表明所选择的单颗粒为结晶质量良好的单晶体. 图4(e)—(g)为所选择的单晶颗粒的La, Sr, B这3种元素分布图, 可以清楚地看出, 这些元素均匀分布在纳米单晶表面, 说明Sr原子成功占据了纳米LaB6的晶格位.
图 4 纳米La0.4Sr0.6B6粉末的(a) TEM照片、(b)单颗粒形貌照片、(c) HRTEM照片; (d)图(c)的傅里叶(FFT)变换; (e)—(g)所选择的单晶颗粒的La, Sr, B元素分布图Figure4. (a) TEM image of La0.4Sr0.6B6 nanoparticles; (b) selected single crystal morphology; (c) HRTEM image for selected single crystal; (d) indexing FFT patterns from panel (c); (e)?(g) La , Sr , B element mapping for selected single crystal .
2
3.2.纳米La1–x Srx B6粉末的光吸收
图5为纳米La1–x Srx B6粉末的光吸收曲线. 如图5(a)所示, LaB6纳米颗粒的吸收谷在591 nm处, 吸收峰在近红外区域. 基于Xiao等[27]的计算结果和Kimura等[28]的实验研究结果可知, 在LaB6的吸收谷处存在最大的透射光和最小的反射光, 说明波长为591 nm的光透过了LaB6纳米粒子. 当Sr掺杂量增加到x = 0.2时, 透射光波长移动至602 nm (图5(b)). 当Sr添加量继续增大至x = 0.4, 0.6和0.8时, 透射光波长依次为608, 628和658 nm. 说明Sr掺杂使纳米LaB6透射光波长连续可调, 产生了“红移”现象.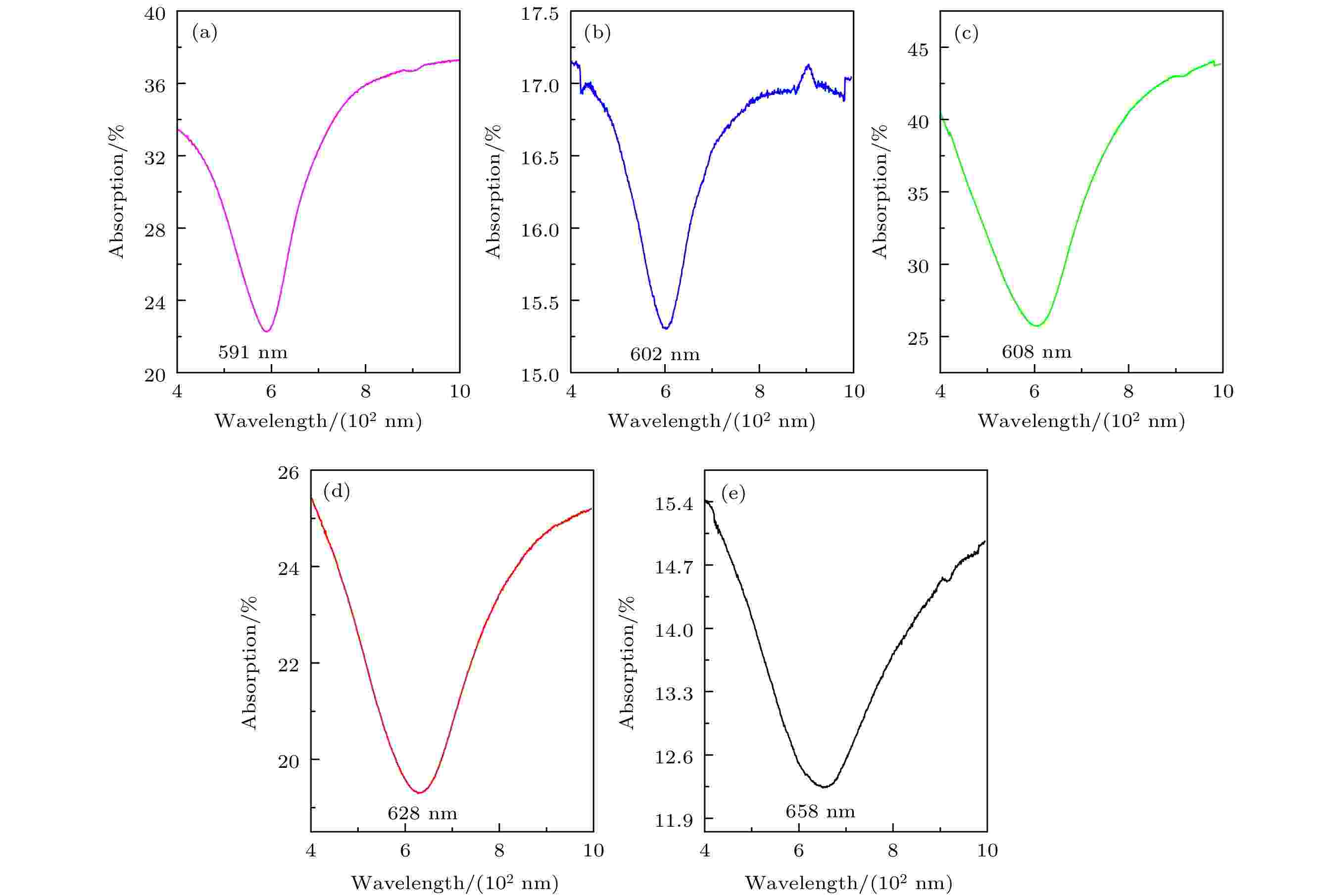
图 5 纳米La1–x Srx B6 (x = 0 (a), 0.2 (b), 0.4 (c), 0.6 (d), 0.8 (e))粉末的光学吸收曲线Figure5. Optical absorption spectrum of La1–x Srx B6 (x = 0 (a), 0.2 (b), 0.4 (c), 0.6 (d), 0.8 (e)) nanoparticles.
大量研究结果表明新型光吸收材料纳米LaB6的透射光波长是与体等离子振荡频率能量密切相关. Kauer[29]测量LaB6在波长为200—20000 nm 范围内的反射谱时发现, 在600 nm附近出现了反射率最小值. Kimura等[30]测量了LaB6单晶体在能量范围为1 meV—40 eV内的反射谱, 并通过Kramers-Kronig转换关系得到了光电导及能量损失谱等重要光学性质. 结果发现在反射谱上能量为2.0 eV附近有个急剧下降的等离子边. 随后Xiao等[27]结合实验结果, 采用第一性原理计算发现LaB6能量损失谱中的体等离子共振频率能量峰出现在2.0 eV处, 恰与实验测的反射谱及吸收谱最小值, 透射光最大值的波长610 nm对应. 这也充分证明了纳米LaB6透射光波长由体等离子共振频率能量所决定. 此外, 本课题组在纳米SrB6光吸收的前期研究中发现[31], 当波长为1935 nm时出现了吸收最小值. 根据光波能量与波长关系式: λ = 1240/E可断定其体等离子共振频率能量为0.64 eV. 基于上述研究, 为了进一步验证Sr掺杂能否改变LaB6体等离子共振频率能量, 采用第一性原理计算了La0.875Sr0.125B6超胞能带、态密度及能量损失谱等, 从而定性解释多元稀土六硼化物La1–xSrxB6透射光波长红移本质.
图6为La0.875Sr0.125B6晶体态密度计算结果, 选择零点为费米能级. 从图6(a)可以看出, La 6s, La 5p和La 5d的电子态主要位于–34.1 eV, –17.9 eV和2.9 eV. 图6(b)显示了Sr 5s, Sr 4p和Sr 4d电子态分别位于–36.2 eV, –17.8 eV和6.1 eV. 图6(c)显示B 2p和2s电子态分别位于–10—15 eV和10—20 eV. 结合图6(a)—(c)的计算结果可知, La0.875Sr0.125B6的导带由B 2p态、B 2s态、La 5p态和Sr 4p态贡献. 价带由B 2p态、Sr 5s态、La 6s态、La 5d态和Sr 4d态贡献.
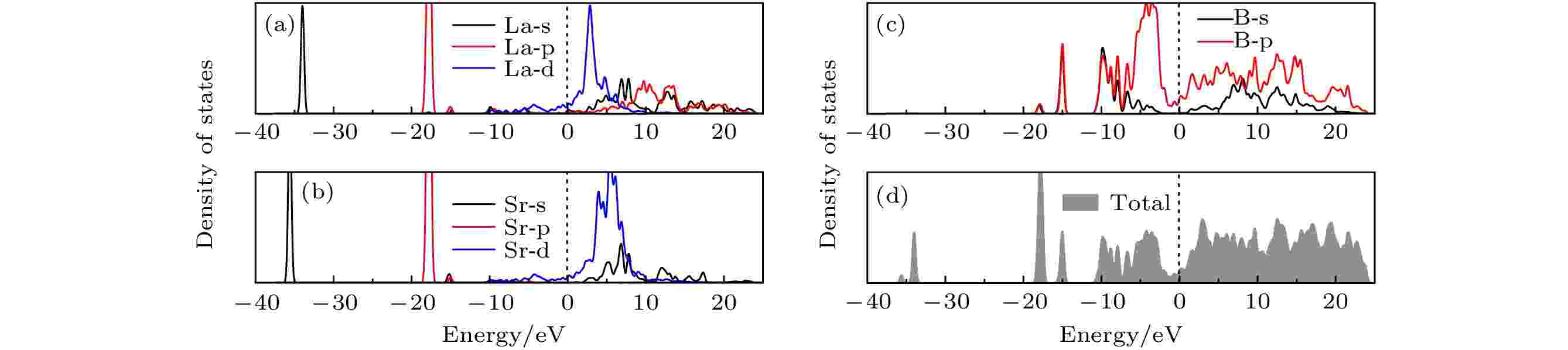图 6 La0.875Sr0.125B6晶体的态密度的第一性原理计算结果Figure6. First-principle calculation results of density of states of La0.875Sr0.125B6 crystal.
图7(a)为La0.875Sr0.125B6晶体的介电函数变化曲线. 从图7(a)可看出实部ε1(ω)从负值区域(ε1(ω)<0)突然增加到正的区域(ε1(ω)>0), 表明在ε1(ω) = 0零点处发生了由金属态到介电态的相变. 而这个零点位置(–1.6 eV)恰与能量损失函数的最低能量对应. La0.875Sr0.125B6的能量损失函数见图7(b). 在整个能量区发现了3个峰, 分别位于1.6 eV, 12.1 eV和21.2 eV. 其中1.6 eV的低能峰对应于体等离子频率激发能, 12.1 eV和21.2 eV的高能峰由B 2p, La 5d和Sr 4d的价带等离子体激元的激发贡献[26]. 相比与LaB6体等离子共振频率能量2.0 eV, La0.875Sr0.125B6的体等离子共振频率能量减小到1.6 eV. 由此可定性地解释, Sr掺杂后其透射光波长向高波段移动.
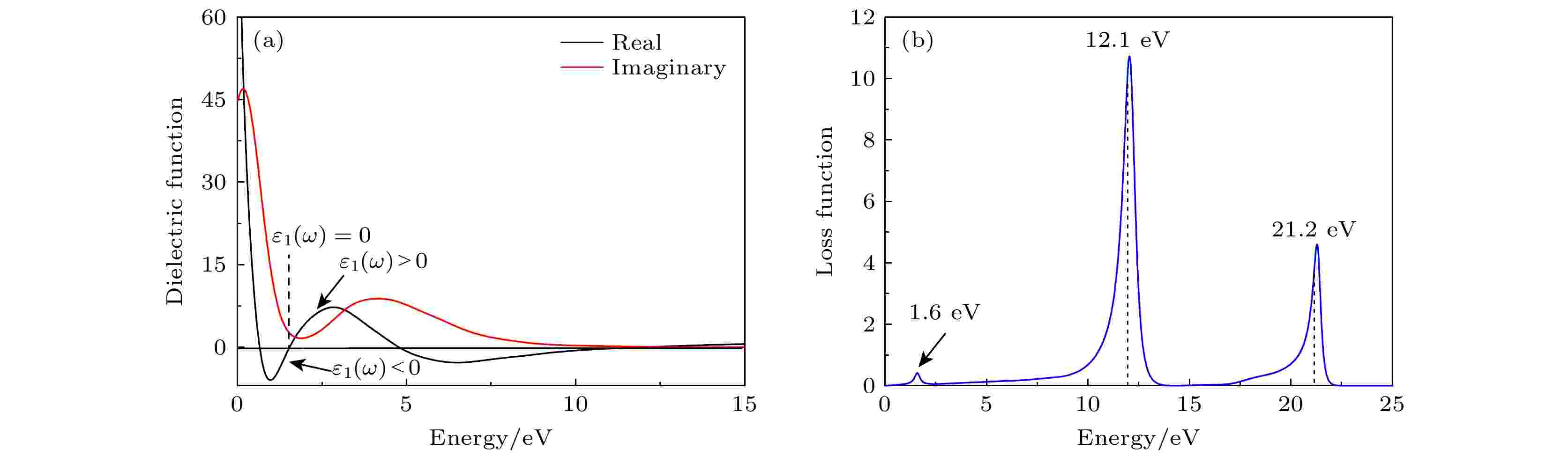图 7 La0.875Sr0.125B6晶体的(a)介电函数和(b)能量损失谱Figure7. (a) Dielectric function and (b) loss function spectra of La0.875Sr0.125B6 crystal.
2
3.3.LaxSr1–xB6多晶块体的热电子发射性能
大量研究表明, SrB6是一种窄带隙半导体、高温绝缘体和中子吸收材料[32,33]. 然而, 对热电子发射方面研究报道较少. 因此, 在本节中将重点围绕SrB6多晶块体的热发射性能而展开, 其次围绕La1–x Srx B6多晶块体展开. 由于多晶块体可视为单晶体不同晶面发射性能的平均效果, 因此在实验测量前, 采用第一性原理计算单晶SrB6的不同晶面的逸出功, 并与SrB6多晶块体实验测量结果进行比较. 烧结块体致密度及实物照片如
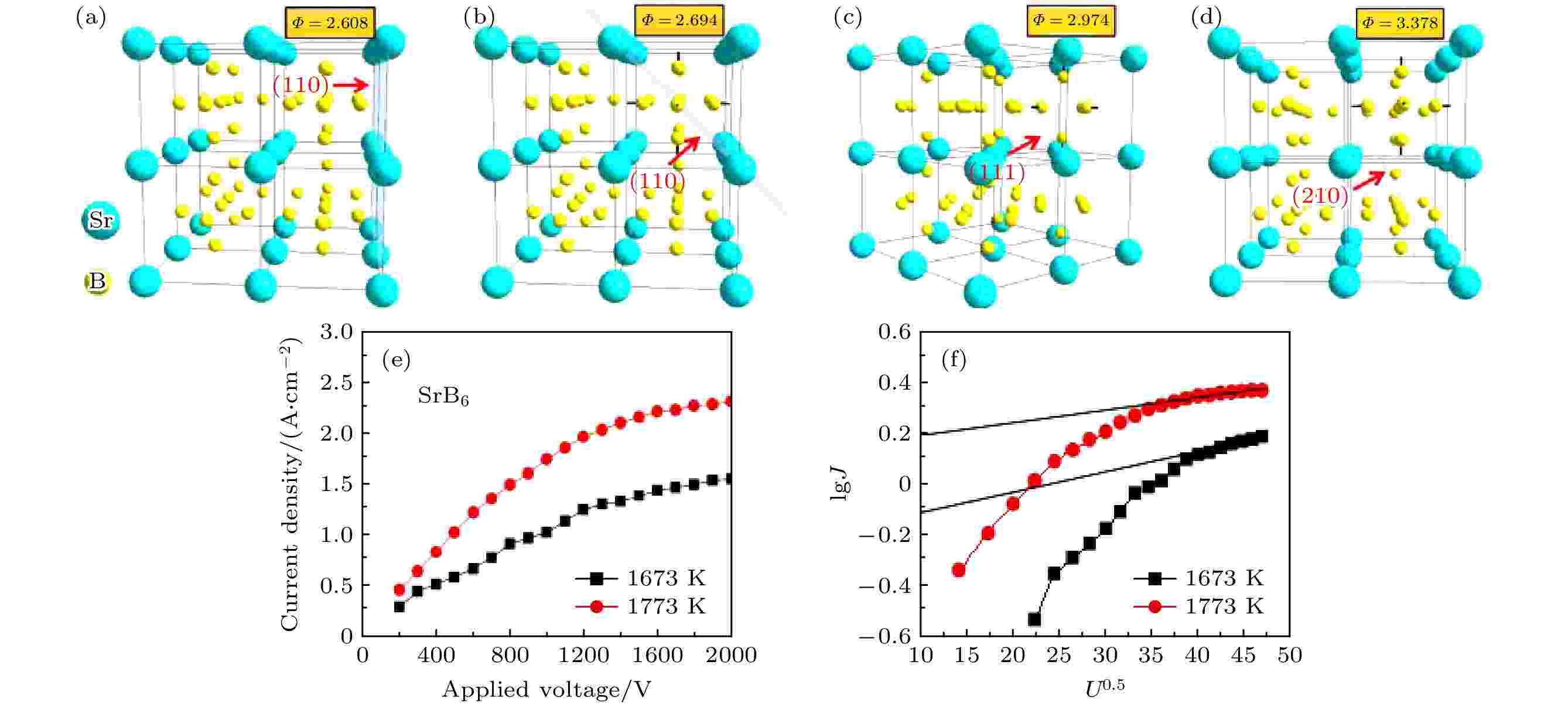图 8 单晶SrB6的(a) (100)面、(b) (110)面、(c) (111)面、(d) (210)面的结构示意图及逸出功计算结果; (e) SrB6多晶块体的热电子发射电流密度随外加电压变化曲线; (f) SrB6多晶块体的lgJ-U 0.5曲线Figure8. Schematic diagram of (a) (100) surface, (b) (110) surface, (c) (111) surface, (d) (210) surface of single crystal SrB6 and the calculated results of escape work; (e) thermionic emission current density of SrB6 polycrystalline bulk with applied voltage; (f) lgJ-U 0.5 curves of SrB6 polycrystalline bulk.
图9给出了La1–x Srx B6多晶块体的热电子发射电流密度随外加电场的变化曲线. 由图9(a)的测量结果可知, La0.2Sr0.8B6在1673 K和1773 K时的最大发射电流密度分别为2.45 A/cm2和5.39 A/cm2, 均高于单一SrB6的电流密度. 从图9(b)—(d)可知, La0.4Sr0.6B6, La0.6Sr0.4B6, La0.8Sr0.2B6多晶块体在阴极温度1673 K时的最大发射电流密度分别为4.45 A/cm2, 6.07 A/cm2, 6.84 A/cm2, 表现出了线性增大趋势. 当阴极温度升高至1773 K时, 这些多元硼化物最大发射电流密度整体增大至14.55 A/cm2, 15.34 A/cm2和19.36 A/cm2. 图10为La1–x Srx B6 (x = 0.8, 0.6, 0.4, 0.2)多晶块体的肖特基外延曲线, 零场发射电流密度(J0)和有效功函数(φe)列于表1. 可以看出, La1–xSrxB6多晶块体的逸出功随着Sr掺杂量的减少线性减小, 均保持在较低值2.552—2.845 eV之间, 表现出了良好的热电子发射性能. Futamoto等[35]和Swanson等[36]采用“铝溶剂”法制备的单晶LaB6 (100)晶面在1873 K下, 最大发射电流密度分别为8.5 A/cm2 和 2.1 A/cm2. 而区域熔炼法制备的LaB6 (100)晶面在1773 K时, 最大热发射电流密度为29.4 A/cm2. 周身林等[37]制备的LaB6多晶块体在1793 K时, 最大发射电流密度为17.41 A/cm2. 从上述发射性能可知, 本文所制备的 La0.8Sr0.2B6最大发射电流密度为19.36 A/cm2, 该值要高于“铝溶剂”法制备的单晶体, 低于区域熔炼法制备单晶体发射性能. 但多晶块体具有制作成本低, 可制备出大发射面积等优点而还是有很好的应用前景.
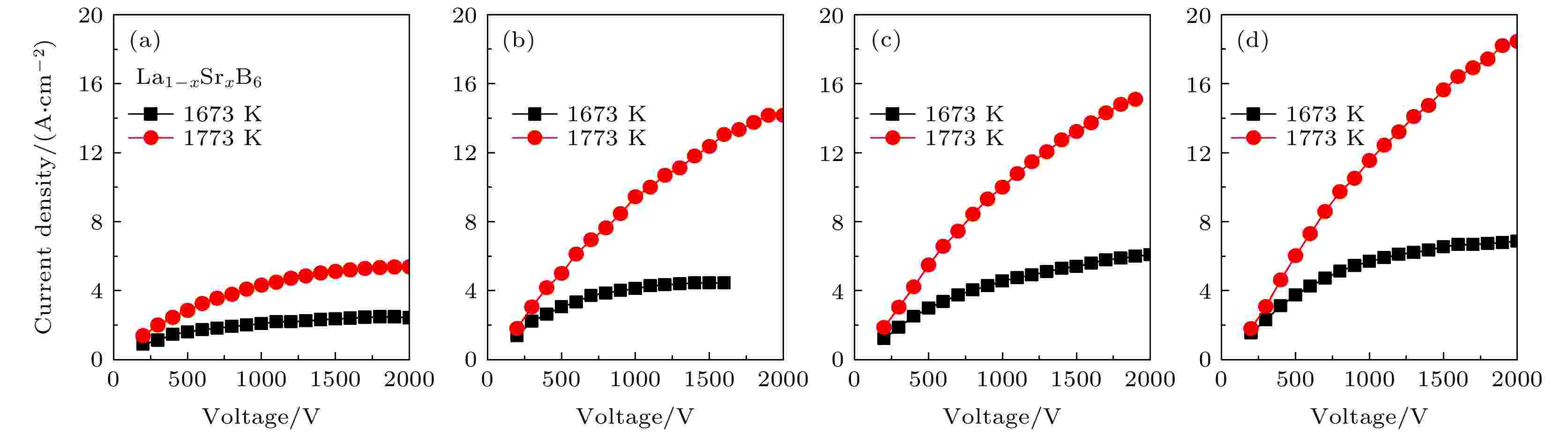图 9 La1–x Srx B6多晶块体的热电子发射电流密度 (a) x = 0.8; (b) x = 0.6; (c) x = 0.4; (d) x = 0.2Figure9. Thermionic emission current density of La1–x Srx B6 bulks: (a) x = 0.8; (b) x = 0.6; (c) x = 0.4; (d) x = 0.2.
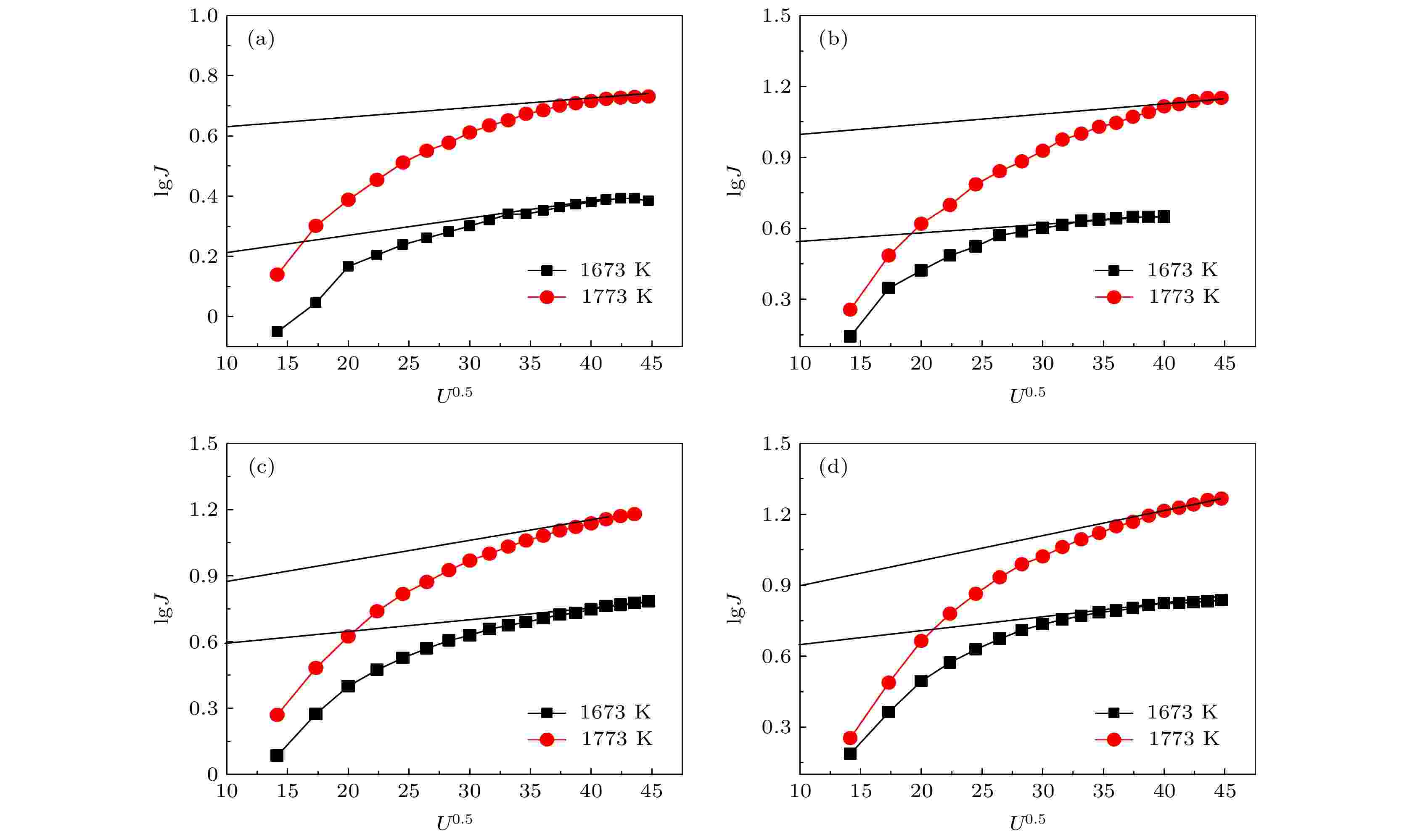图 10 La1–x Srx B6多晶块体肖特基外延曲线 (a) x = 0.8; (b) x = 0.6; (c) x = 0.4; (d) x = 0.2Figure10. Typical Schottky plots for La1–x Srx B6 bulks: (a) x = 0.8; (b) x = 0.6; (c) x = 0.4; (d) x = 0.2.
| Compound | 零场发射电流密度(J0) | 有效逸出功 φe/ eV | |
| 1673 K | 1773 K | ||
| SrB6 | 0.97 | 1.79 | 2.845 |
| La0.2Sr0.8B6 | 1.67 | 4.73 | 2.691 |
| La0.4Sr0.6B6 | 3.5 | 8.7 | 2.585 |
| La0.6Sr0.4B6 | 4.1 | 8.3 | 2.573 |
| La0.8Sr0.2B6 | 5.39 | 10 | 2.552 |
表1La1–x Srx B6 (x =1, 0.8, 0.6, 0.4, 0.2)多晶块体的零场发射电流密度J0和有效逸出功φe
Table1.Zero field emission current density J0 and the effective escape work φe of the polycrystalline block La1–x Srx B6 (x = 1, 0.8, 0.6, 0.4, 0.2).
通常而言, 逸出功可以理解为费米能级附近的电子从外加吸收能量后, 摆脱原子核的束缚从阴极表面逃离所需的能量. 因此, 可以推断出多元稀土六硼化物La1–x Srx B6多晶块体热电子发射增强机理同样与逸出功密切相关. 言外之意, 可以理解为La元素增加费米能级升高, 减小了电子跳跃至真空层的距离, 从而减小了逸出功, 增强了发射电流密度. 根据这个研究思路, 采用第一性原理计算了SrB6, La0.125Sr0.875B6和LaB6的费米能级. 结果发现它们的值分别为7.692 eV, 7.885 eV和8.016 eV, 表现出了线性增大规律, 与预测结果完全一致, 其机理总结于图11中.
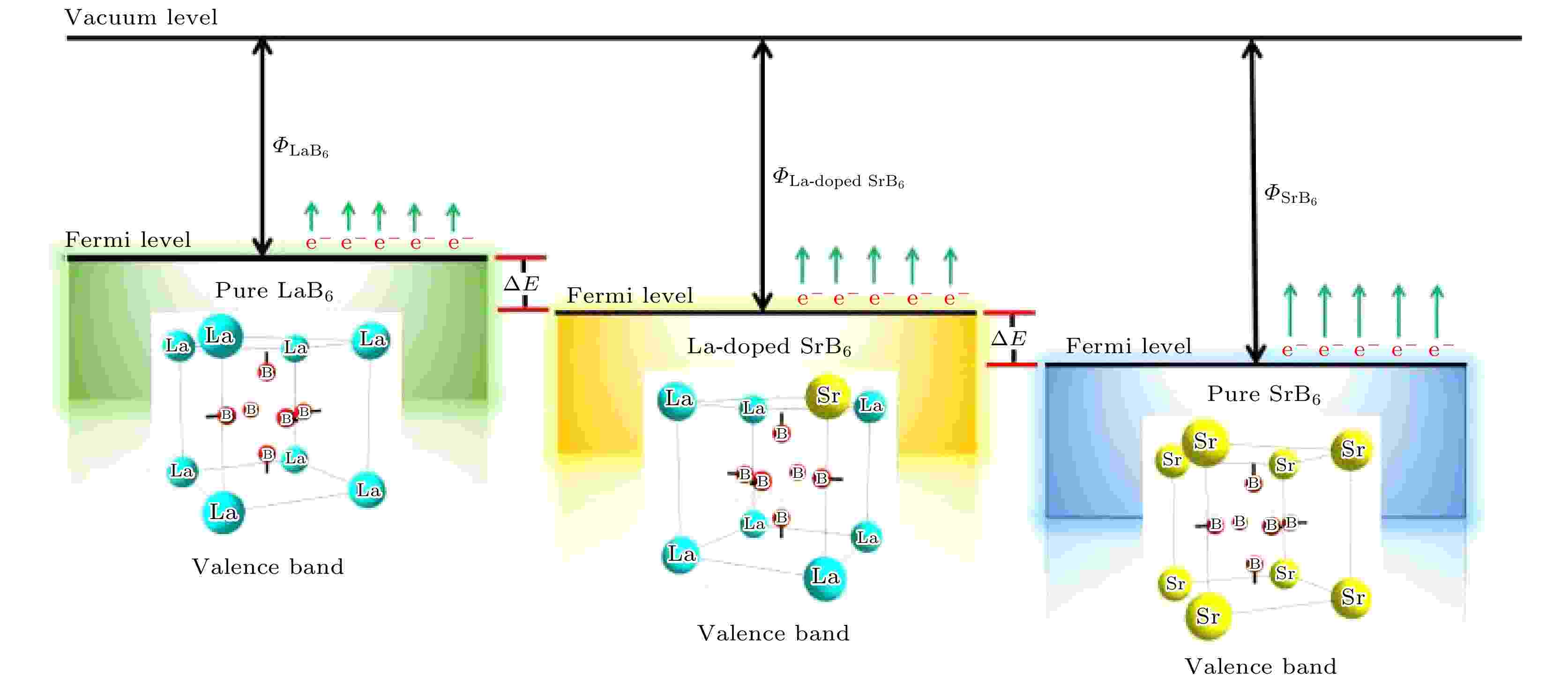图 11 所提出的La1–x Srx B6增强热电子发射机理示意图Figure11. Proposed mechanism of the La1–x Srx B6 enhanced thermionic emission.
