删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

侧向局域共振超构板声振特性

本站小编 Free考研考试/2021-12-29
摘要:以侧向局域共振超构板为研究对象, 基于布洛赫定理及弯曲波传播理论, 建立了侧向局域共振超构板的振动响应、声辐射功率及辐射效率理论计算模型, 同时建立了侧向局域共振超构板的有限元模型以验证理论模型的有效性. 进一步开展了有/无周期附加侧向局域共振结构超构板的模态分析, 探索了侧向局域共振超构板辐射声功率及辐射效率随频率变化的关系. 结果表明, 侧向局域共振超构板在两条特定频段(带隙)内的板面均方振速及辐射声功率远低于均匀平板, 而辐射效率却高于均匀平板. 本研究可为推进侧向局域共振超构板在减振降噪领域的工程应用奠定理论基础.
关键词: 侧向局域共振超构板/
板面均方振速/
辐射声功率/
带隙

English Abstract


全文HTML

--> --> -->
1.引　言
振动与声广泛存在于自然界中. 绝大多数振动与噪声是有害的. 例如, 飞机起飞及降落时的振动使得机身发生剧烈颤抖, 加之噪声使得舒适性降低; 工厂中设备运转产生的振动使得设备精度降低, 噪声还会干扰附近居民的生活与工人的高效工作等. 高频噪声由于波长短易于衰减, 而低频波波长较长, 易于发生衍射, 从而可以远距离传播, 这对于水下航行器的隐蔽性而言极为不利. 因此, 低频振动和噪声抑制已经成为实际工程中亟待解决的一项难题[1].
传统减振降噪手段因集中载荷大、抑振频段高等缺点在工程领域应用中有一定局限性. 通过人工构建结构形式并将其周期排布形成的周期结构在特定频段控制弹性波传播的特性吸引了众多研究者的目光[2]. 由于结构形式或材料周期变化的周期结构对弹性波产生散射作用, 可形成Bragg散射带隙; 结构内部具有局域共振现象的周期结构可形成局域共振带隙[3,4]. 两种机理形成的带隙均能够有效抑制弹性波的传播. 而局域共振型周期结构通过均质化等效, 其等效参数在特定频段呈现负值, 从而被称作声学超材料[5]. 2000年, 武汉大学Liu等[6]应用局域共振型声子晶体结构实现声学超材料的等效负质量密度, 把普通的声子晶体带隙频率降低了两个数量级, 突破了Bragg带隙与结构特征长度匹配的限制, 实现了小尺寸控制大波长的目的. 2006年, 美国伊利诺伊大学香槟分校的Fang等[7]利用亥姆赫兹共鸣器一维阵列, 实现了负等效模量. 2010年, “双负”声学超材料才首次被延世大学的Lee等[8]通过实验成功验证.
声学超构材料突破了传统材料的束缚, 极大地拓展了自然界中现有材料的声学属性, 为调控弹性波带来了全新的视角[9]. 将局域共振结构与工程中常用的经典梁、板结构结合可构成具有特殊声学性能的超构梁、板. 声学超构板结构相较于超构梁结构从一维转换至二维, 其运动方程的改变导致相关计算更加复杂. 而平板结构在工程实际中大量应用, 因此声学超构板的振动与声辐射特性具有非常重要的研究意义及工程价值. 国防科技大学温熙森教授课题组[10,11], 设计了一种局域共振超构板, 该超构板由周期排布的弹簧振子和均质板结构组成, 利用平面波展开法计算了超构板的带隙及振动特性, 获得了带隙内弯曲波传递被有效抑制的特性, 同时该超构板能够在特定频段内实现高效隔声. 美国普渡大学Sun教授课题组[12]提出了一种基于微结构设计的声学超构板, 理论和试验研究表明该超构板的等效质量密度具有强各向异性. 西安交通大学吴九汇教授课题组[13]提出了一种轻质局域共振超构板, 其隔声量在多个频段高于普通平板. 科罗拉多大学的Pai课题组[14-16]设计了周期附加多级弹簧振子的超构板, 总结出超构板抑振机理为振子惯性力与主结构剪力之间相互抵消, 为超构板抑制低频弹性波的优化设计提供了明确的思路. 西北工业大学盛美萍教授课题组[17,18]提出侧向局域共振超构板及夹芯声学超构板, 利用理论推导与数值仿真结合的方法研究了带隙内结构振动及辐射声功率被有效抑制的特性.
目前对于声学超构板的研究主要集中在结构振动、隔声、吸声等方面, 对于声学超构板的声辐射特性的文献却比较少见[19,20], 而声学超构板的声辐射特性研究对于工程结构的隐蔽性有着非常重要的意义. 由于侧向局域共振结构的特殊构造形式, 因此可以利用较小的空间产生多条带隙, 且多条带隙的位置可以通过四杆机构的几何参数灵活调控. 同时, 侧向局域共振超构板的振动及声辐射相比于平板结构在带隙内远低于带隙外水平, 有助于结构振动与噪声控制工程应用. 本文将进一步延续前期侧向局域共振超构板振动特性的工作[18], 采用模态叠加法及瑞利积分方法计算有限大侧向局域共振超构板的振动及声辐射, 并使用有限元仿真模型进行验证, 以揭示侧向局域共振超构板的声辐射特性及规律, 为工程实际结构中的噪声控制提供技术支撑.
2.建模与方法
图1所示为处于空气介质中的侧向局域共振超构板, 由于空气阻抗与平板阻抗相差较大, 因此可忽略空气负载对平板振动的影响. 对于周期附加侧向局域共振结构, 其垂向弹簧振子质量与刚度分别为${m_1}$和${k_1}$, 侧向弹簧振子质量与刚度分别为${m_2}$和${k_2}$, 四杆机构的垂向与水平距离比为L/D. 对于平板结构, 其密度为$\rho $, 厚度为h, 杨氏模量为E, 泊松比为$\nu $. 因此, 周期附加侧向局域共振结构的四边简支平板振动控制方程在频域可写为
图 1 浸润于空气中的侧向局域共振超构板　(a) 受外力激励的侧向局域共振超构板鸟瞰图; (b) 侧向局域共振超构板正视图
Figure1. Acoustic metamaterial plate with periodic local resonators submerged in air: (a) Perspective view of the acoustic metamaterial plate with external force applied; (b) front view of a single unit cell of the acoustic metamaterial plate.

$ \begin{split} &\tilde D\left[ {\dfrac{{{\partial ^4}w\left( {x,y} \right)}}{{\partial {x^4}}} + 2\dfrac{{{\partial ^4}w\left( {x,y} \right)}}{{\partial {x^2}\partial {y^2}}} + \dfrac{{{\partial ^4}w\left( {x,y} \right)}}{{\partial {y^4}}}} \right] \\ &- \rho h{\omega ^2}w\left( {x,y} \right) \hfill \\ =\;& F{\rm{\delta }}\left( {x - x'} \right){\rm{\delta }}\left( {y - y'} \right) \\ &+ \sum\limits_{s = 1}^S {\sum\limits_{t = 1}^T {f\left( {{x_s},{y_t}} \right){\rm{\delta }}\left( {x - {x_s}} \right){\rm{\delta }}\left( {y - {y_t}} \right)} }, \hfill \end{split} $
$\begin{split}& - {\omega ^2}{m_2}{w_{2st}} = {k_1}\left[ {w\left( {{x_s},{y_t}} \right) - {w_{2st}}} \right] \\&~~ + 2{k_2}\frac{L}{{2D}}\left\{ { - \frac{L}{{2D}}\left[ {{w_{2st}} - w\left( {{x_s},{y_t}} \right)} \right] - {w_{3st}}} \right\} {, } \end{split}$
$ - {\omega ^2}{m_3}{w_{3st}} = {k_2}\left\{ { - \frac{L}{{2D}}\left[ {{w_{2st}} - w\left( {{x_s},{y_t}} \right)} \right] - {w_{3st}}} \right\} {, } $
式中, $\omega $为角频率, s和t分别代表x和y方向侧向振子的个数, $\tilde D = {{E{h^3}} \mathord{\left/ {\vphantom {{E{h^3}} {[12\left( {1 - {\nu ^2}} \right)}}} \right. } {[12\left( {1 - {\nu ^2}} \right)}}]$为抗弯刚度, F为作用于平板上的垂向集中力, 而
$\begin{split} &f\left( {{x_s},{y_t}} \right) = - {k_1}\left[ {w\left( {{x_s},{y_t}} \right) - {w_{2st}}} \right] \\&- 2{k_2}\frac{L}{{2D}}\left\{ { - \frac{L}{{2D}}\left[ {{w_{2st}} - w\left( {{x_s},{y_t}} \right)} \right] - {w_{3st}}} \right\} \end{split}$
为周期附加侧向局域共振结构对平板结构的作用力.
因此, 简支平板振动位移可表示为
$ {w_1}\left( {x,y} \right) = \sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{W_{1mn}}\sin \left( {{\kappa _m}x} \right)\sin \left( {{{\bar \kappa }_n}y} \right)} } {, } $
式中, ${\kappa _m} = {{m{\text{π}}} \mathord{\left/ {\vphantom {{m{\text{π}}} a}} \right. } a}$, ${\kappa _n} = {{n{\text{π}}} \mathord{\left/ {\vphantom {{n{\text{π}}} b}} \right. } b}$分别表示沿x和y方向的波数.
对于由狄拉克函数所表示的点力可分解为
$\begin{split} &F{\rm{\delta }}\left( {x - x'} \right){\rm{\delta }}\left( {y - y'} \right) \\=\;& \sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{F_{mn}}\sin \left( {{\kappa _m}x} \right)\sin \left( {{{\bar \kappa }_n}y} \right)} } {, } \end{split}$
式中, ${F_{mn}}$为模态作用力. 由三角函数的正交性可知
$ {F_{mn}} = \frac{F}{{{L_{am}}{L_{bn}}}}\sin \left( {{\kappa _m}x'} \right)\sin \left( {{{\bar \kappa }_n}y'} \right){, } $
式中,
$ {L}_{am}=a/2{, }~~{L}_{bn}=b/2 . $
利用同样的方法对侧向局域共振结构与平板之间耦合作用力进行变换得
$\begin{split} &f\left( {{x_s},{y_t}} \right){\rm{\delta }}\left( {x - {x_s}} \right){\rm{\delta }}\left( {y - {y_t}} \right) \\=\;& \sum\limits_{m = 0}^M {\sum\limits_{n = 0}^N {{F_{mnst}}\sin {\kappa _m}x\sin {{\bar \kappa }_n}y} } {, } \end{split}$
$ {F_{mnst}} = \frac{{f\left( {{x_s},{y_t}} \right)}}{{{L_{am}}{L_{bn}}}}\sin {\kappa _m}{x_s}\sin {\bar \kappa _n}{y_t}. $
将(5)式、(6)式和(9)式代入(1)—(3)式中, 同时利用三角函数正交性可得

$ \begin{split} &\left[ {\tilde D{{\left( {\kappa _m^2 + \bar \kappa _n^2} \right)}^2} - {\omega ^2}\rho h} \right]{W_{mn}} - \dfrac1{{{L_{am}}{L_{bn}}}} {{\left[ {{k_1} + \dfrac{{{k_2}}}{2}{{\left( {\dfrac{L}{D}} \right)}^2}} \right]}} \sum\limits_{s = 1}^S {\sum\limits_{t = 1}^T {\sin {\kappa _m}{x_s}\sin {{\bar \kappa }_n}{y_t}} } {w_{2st}} \\ & - \dfrac1{{{L_{am}}{L_{bn}}}} {{\left[ { - {k_1} - \dfrac{{{k_2}}}{2}{{\left( {\dfrac{L}{D}} \right)}^2}} \right]}} \sum\limits_{s = 1}^S {\sum\limits_{t = 1}^T {\sum\limits_{p = 0}^M {\sum\limits_{q = 0}^N {\sin {\kappa _m}{x_s}\sin {{\bar \kappa }_n}{y_t}\sin {\kappa _p}{x_s}\sin {{\bar \kappa }_q}{y_t}{W_{pq}}} } } } \\ &- \dfrac{{{k_2}L}}{{{L_{am}}{L_{bn}}D}}\sum\limits_{s = 1}^S {\sum\limits_{t = 1}^T {\sin {\kappa _m}{x_s}\sin {{\bar \kappa }_n}{y_t}} } {w_{3st}} = \dfrac{{F\sin {\kappa _m}x'\sin {{\bar \kappa }_n}y'}}{{{L_{am}}{L_{bn}}}}, \hfill \end{split} $
$ \left[ { - {k_1} - \dfrac{{{k_2}}}{2}{{\left( {\dfrac{L}{D}} \right)}^2}} \right]\sum\limits_{q = 0}^M {\sum\limits_{p = 0}^N {\sin {\kappa _p}{x_s}\sin {{\bar \kappa }_q}{y_t}{W_{pq}}} } + \left[ {{k_1} + \dfrac{{{k_2}}}{2}{{\left( {\dfrac{L}{D}} \right)}^2}} \right]{w_{2st}} + \dfrac{{{k_2}L}}{D}{w_{3st}} - {\omega ^2}{m_2}{w_{2st}} = 0, $
$- \dfrac{{{k_2}L}}{{2D}}\sum\limits_{p = 0}^M {\sum\limits_{q = 0}^N {\sin {\kappa _p}{x_s}\sin {{\bar \kappa }_q}{y_t}{W_{pq}}} } + \dfrac{{{k_2}L}}{{2D}}{w_{2st}} + {k_2}{w_{3st}} - {\omega ^2}{m_3}{w_{3st}} = 0. $
将(11)—(13)式整理成矩阵形式
$ \left[ {{\boldsymbol{K}} - {\omega ^2}{\boldsymbol{M}}} \right]{\boldsymbol{\varPhi }} = {\boldsymbol{F}} {, } $
式中, K为刚度矩阵, M为质量矩阵, F为外力向量. 它们的具体表达式为
$ {\boldsymbol{\varPhi }} = {\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{W}}_{\text{1}}}}&{{{\boldsymbol{W}}_{\text{2}}}}&{{{\boldsymbol{W}}_{\text{3}}}} \end{array}} \right]^{{\rm{T}}} } = {\big[ {\begin{array}{*{20}{c}} {{{\left[ {{W_{mn}}} \right]}_{1 \times \left( {M \times N} \right)}}}&{{{\left[ {{w_{2st}}} \right]}_{1 \times \left( {S \times T} \right)}}}&{{{\left[ {{w_{3st}}} \right]}_{1 \times \left( {S \times T} \right)}}} \end{array}} \big]^{\text{T}}}, $
$ {\boldsymbol{F}} = \left[ {\begin{array}{*{20}{c}} {\boldsymbol{F}}&{\bf{0}}&{\bf{0}} \end{array}} \right] \hfill= \left[ {\begin{array}{*{20}{c}} {{{\left[ {{F_{mn}}} \right]}_{1 \times \left( {M \times N} \right)}}}&{\bf{0}}&{\bf{0}} \end{array}} \right], $
$ {\boldsymbol{K}} = \left[ {\begin{array}{*{20}{c}} {\tilde D{\boldsymbol{K'}} - \dfrac{{\left[ { - {k_1} - \dfrac{{{k_2}}}{2}{{\left( {\dfrac{L}{D}} \right)}^2}} \right]}}{{{L_{am}}{L_{bn}}}}{\boldsymbol{U}}}&{\dfrac{{4\left[ {{k_1} + \dfrac{{{k_2}}}{2}{{\left( {\dfrac{L}{D}} \right)}^2}} \right]}}{{{L_{am}}{L_{bn}}}}{\boldsymbol{P}}}&{ - \dfrac{{{k_2}}}{{{L_{am}}{L_{bn}}}}\dfrac{L}{D}{\boldsymbol{P}}} \\ {\left[ { - {k_1} - \dfrac{{{k_2}}}{2}{{\left( {\dfrac{L}{D}} \right)}^2}} \right]{\boldsymbol{P}}}&{\left[ {{k_1} + \dfrac{{{k_2}}}{2}{{\left( {\dfrac{L}{D}} \right)}^2}} \right]}&{\dfrac{{{k_2}L}}{D}} \\ { - \dfrac{{{k_2}L}}{{2D}}{\boldsymbol{P}}}&{\dfrac{{{k_2}L}}{{2D}}}&{{k_2}} \end{array}} \right], $

$ {\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} {\rho h{\boldsymbol{I}}}&0&0 \\ 0&{{m_1}}&0 \\ 0&0&{{m_2}} \end{array}} \right], $
$ {\boldsymbol{K'}} = \left[ {\begin{array}{*{20}{c}} {{{\left( {\kappa _1^2 + \bar \kappa _1^2} \right)}^2}}& \cdots &0 \\ \vdots & \vdots & \vdots \\ 0& \cdots &{{{\left( {\kappa _M^2 + \bar \kappa _N^2} \right)}^2}} \end{array}} \right], $
$\begin{split} {\boldsymbol P} =\,& \big[\sin{\kappa_1}{x_s}\sin{\bar\kappa}_1 y_t ~~~ {\sin {\kappa _m}{x_s}\sin {{\bar \kappa }_n}{y_t}} ~~~ \cdots~~ \\ &~~~ {\sin {\kappa _M}{x_s}\sin{{\bar\kappa}_N} {y_t}} \big]^{\rm T}, \\[-10pt]\end{split}$
$ {\boldsymbol{I}} = \left[ {\begin{array}{*{20}{c}} 1& \cdots &0 \\ \vdots & \vdots & \vdots \\ 0& \cdots &1 \end{array}} \right] . $
求解(14)式可获得外部激励力F作用下侧向局域共振超构板在简支作用下的位移系数, 将其代入(5)式可获得相应的振动位移. 因此, 对该平板振动位移进行求导可获得相应的速度响应为
$ v\left( {x,y} \right) = \sum\limits_{m = 0}^M {\sum\limits_{n = 0}^N {{V_{mn}}\sin \left( {{\kappa _m}x} \right)\sin \left( {{{\bar \kappa }_n}y} \right)} }, $
式中, $ {V_{mn}} = {\text{j}}\omega {W_{mn}} $. 该平板均方振速为
$ \left\langle {{{\bar v}^2}} \right\rangle = \sum\limits_{m = 0}^M {\sum\limits_{n = 0}^N {\frac{1}{8}{V_{mn}}V_{mn}^*} } {, } $
式中, *代表复数共轭. 在一远场观测点S, 该点相对于坐标系原点位置为$\left( {r, \theta, \varphi } \right)$, 其中r为坐标原点距观测点距离, $\theta $为观测俯仰角, $\varphi $为观测方位角. 利用瑞利积分可得该观测点处由侧向局域共振超构板辐射的声压为
$ p\left( {r,\theta,\varphi } \right) = \frac{{{\text{j}}{k_0}c{\rho _0}}}{{2{\rm{\pi}}}}\int_0^a {\int_0^b {\frac{{v\left( {x,y} \right){{\text{e}}^{ - {\text{j}}kr}}}}{r}{\text{d}}y{\text{d}}x} } . $
将(22)式代入(24)式可得
$ p\left( {r,\theta,\varphi } \right) = \sum\limits_{m = 0}^M {\sum\limits_{n = 0}^N {{V_{mn}}{T_{mn}}\left( {r,\theta,\varphi } \right)} } {, } $
式中,
$\begin{split} &{T_{mn}}\left( {r,\theta,\varphi } \right) = {\text{j}}{k_0}{\rho _0}c\dfrac{{{{\text{e}}^{ - {\text{j}}kr}}}}{{2{\rm{\pi}}r}}\dfrac{{ab}}{{mn{{\rm{\pi}}^2}}}\\&~~~~ \times \dfrac{{{{\left( { - 1} \right)}^m}{{\text{e}}^{ - {\text{j}}{\tau _x}}} - 1}}{{{{\left[ {{{{\tau _x}} \mathord{\left/ {\vphantom {{{\tau _x}} {\left( {m{\rm{\pi}}} \right)}}} \right. } {\left( {m{\rm{\pi}}} \right)}}} \right]}^2} - 1}} \dfrac{{{{\left( { - 1} \right)}^n}{{\text{e}}^{ - {\text{j}}{\tau _y}}} - 1}}{{{{\left[ {{{{\tau _y}} \mathord{\left/ {\vphantom {{{\tau _y}} {\left( {n{\rm{\pi}}} \right)}}} \right. } {\left( {n{\rm{\pi}}} \right)}}} \right]}^2} - 1}} {, } \end{split}$
其中,
$ {\tau _x} = ka\sin \theta \cos \varphi,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\tau _y} = kb\sin \theta \sin \varphi . $
因此, 该侧向局域共振超构板的辐射声功率可通过在远场某一球面对(25)式进行积分获得.
$ \begin{split} \Pi =\;& \int_0^{2{\rm{\pi}}} {\int_0^{{{\rm{\pi}} \mathord{\left/ {\vphantom {{\rm{\pi}} 2}} \right. } 2}} {\dfrac{{{{\left| {p\left( {r,\theta,\varphi } \right)} \right|}^2}}}{{2{\rho _0}c}}} } {r^2}\sin \theta {\text{d}}\theta {\text{d}}\varphi \hfill \\ =\;& \sum\limits_{m = 0}^M \sum\limits_{n = 0}^N \sum\limits_{p = 0}^M \sum\limits_{q = 0}^N {{\hat V}_{mn}}\hat V_{pq}^* \\ & \times\int\nolimits_0^{2{\rm{\pi}}} \int\nolimits_0^{{{\rm{\pi}}/ 2}} \dfrac{{{T_{mn}}\left( {r,\theta,\varphi } \right)T_{pq}^*\left( {r,\theta,\varphi } \right)}}{{2{\rho _0}c}}\\ & \times {r^2}\sin \theta {\text{d}}\theta {\text{d}}\varphi. \ \end{split} $
由此可得辐射效率为
$\begin{split} \sigma = &\dfrac{\Pi }{{\dfrac{1}{2}{\rho _0}cab \big\langle \overline{{{\hat v}^2}} \big\rangle }} = \dfrac{\displaystyle{\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {\sum\limits_{p = 1}^N {\sum\limits_{q = 1}^N {{{\hat V}_{mn}}\hat V_{pq}^*{\sigma _{mnpq}}} } } } }}{\displaystyle{\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{{\hat V}_{mn}}\hat V_{mn}^*} } }}. \end{split}$

3.结果与讨论
针对本文所提出的计算侧向局域共振超构板的振动及声辐射计算方法, 首先采用有限元方法对该方法有效性进行验证. 建立侧向局域共振超构板有限元模型, 使用SHELL181单元建立平板单元, MASS21单元建立垂直方向质量及侧向质量, COMBIN40单元建立垂直及侧向弹簧单元, BEAM188单元建立四杆机构. 设置垂直方向质量及弹簧沿垂直平板方向振动, 设置侧向质量及弹簧沿平行平板方向振动, 同时设置弹簧阻尼参数. 侧向局域共振超构板计算参数见表1. 在$x = 0.1\;{\kern 1 pt} {\kern 1 pt} {\text{m}}$, $y = 0.1{\kern 1 pt} {\kern 1 pt} \;{\text{m}}$处施加一简谐力, 并提取$x = 0.4{\kern 1 pt} {\kern 1 pt} \;{\text{m}}\;$, $ y = 0.3{\kern 1 pt} \;{\kern 1 pt} {\text{m}} $处的振动加速度, 采用参考加速度${a_{{\text{ref}}}} = 1 \times {10^{ - 6}}{\kern 1 pt} {\kern 1 pt} {\text{m}}/{{\text{s}}^{\text{2}}}$计算该平板的振动加速度级, 相应的理论分析及仿真分析结果如图2所示.
参数名称参数符号参数取值
平板杨氏模量E$2.1 \times {10^{11}}{\kern 1 pt} {\kern 1 pt} {\text{Pa}}$
平板密度$\rho $$7850{\kern 1 pt} {\kern 1 pt} {\text{kg}}/{{\text{m}}^3}$
平板泊松比$\nu $0.3
平板厚度h0.003 m
垂向振子刚度k1$1 \times {10^4}\;{\text{N}}/{\text{m}}$
垂向振子质量m10.005 kg
侧向振子刚度k2$0.5 \times {10^4}\;{\text{N}}/{\text{m}}$
侧向振子质量m20.002 kg
四杆机构几何参数比L/D1
空气密度${\rho _0}$$1.25\;{\text{kg}}/{{\text{m}}^3}$
空气中声速c$343\;{\text{m}}/{\text{s}}$


表1侧向局域共振超构板模型计算参数
Table1.Parameters for the metamaterial plate with periodic lateral local resonators.

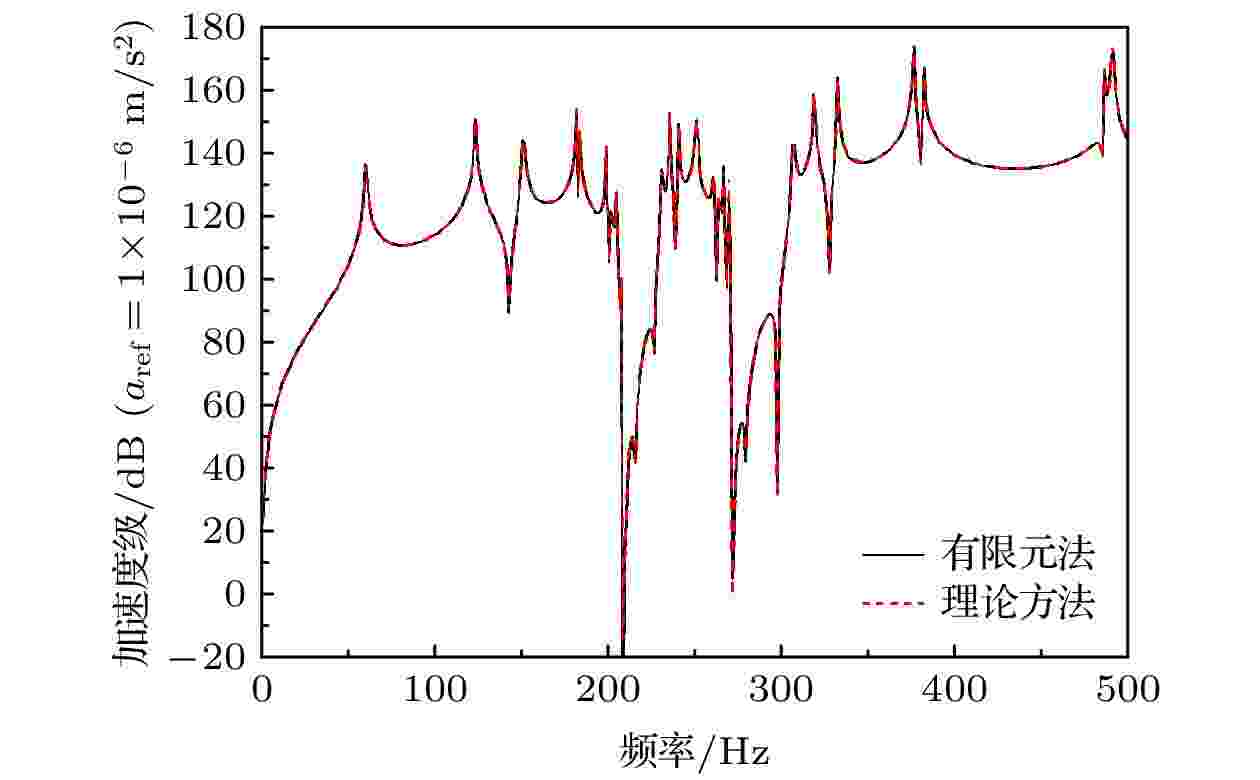图 2 侧向局域共振超构板振动加速度级的理论方法与有限元法结果对比
Figure2. Comparison of the theoretical and simulative results of the acceleration level for the metamaterial plate.

由图2可见, 理论方法及有限元方法计算的侧向局域共振超构板振动加速度级结果曲线吻合, 一致性较好, 验证了本文计算方法的有效性. 分析该加速度级曲线可知, 在207—234 Hz及270—329 Hz两个频段, 侧向局域共振超构板的振动加速度远低于其他频段, 这表明侧向局域共振超构板可在特定频段有效抑制弯曲波的传播. 参照文献[18]可知, 这两个频段被称作带隙, 带隙所处频段无相应的实数波数, 弹性波以指数形式快速衰减. 弹性波衰减的物理机理主要是由于附加侧向局域共振结构共振所产生的惯性力与弯曲波在平板内引起的剪力相平衡, 从而将弹性波能量暂时存储在侧向局域共振结构之中. 若侧向局域共振结构附带阻尼特性, 则部分弹性波能量将被阻尼所耗散.
为明确侧向局域共振超构板的抑振机理, 本文计算了平板振动模态频率及侧向局域共振超构板模态频率, 见表2和表3.
模态阶数1234567
频率/Hz75.8164.6214.6303.3312.6445.8451.4


表2平板模态频率
Table2.Modal frequency of the bare plate.

模态阶数1234567
频率/Hz70.8147.8179.9200.95201.7206.3206.4
模态阶数7—1112—130131132133134135
频率/Hz207.1—207.9208.1—208.9217.8223.7234.3259.3260.6
模态阶数136137138139140—260261262
频率/Hz267.9268.0269.1269.9270.0—271.1278.6282.0
模态阶数263264265266267
频率/Hz288.3329.8336.9456.9462.2


表3侧向局域共振超构板模态频率
Table3.Modal frequency of the metamaterial plate.

计算可得, 在500 Hz以下频段, 无周期附加侧向局域共振结构模态仅7阶, 如表2所列, 而侧向局域共振超构板则有267阶模态, 如表3所列, 其中207.1—207.9 Hz有5阶模态, 208.1—208.9 Hz有119阶模态, 271.0—271.1 Hz有121阶模态. 对比表2中平板模态频率可知, 周期附加侧向局域共振结构以后, 原平板结构模态改变. 低频模态向更低频移动, 这主要是由于周期侧向局域共振结构所带来的附加质量效应. 其他频段的频率改变主要是周期侧向局域共振结构振动改变了原平板的能量分布, 使得结构自身固有属性发生改变.
结合图2中所示侧向局域共振超构板振动响应可知, 第一带隙以下频段有五阶模态分别对应振动响应曲线的5个峰值, 而208.1—208.9 Hz的119阶模态及270.0—271.1 Hz的121阶模态均为附加侧向局域共振结构的模态, 此时, 主结构平板的振动能量以弹簧的势能及质量的动能的形式被暂时储存在侧向局域共振结构中, 从而使得主结构平板的振动响应在两带隙内较小, 表现出弯曲波被抑制的现象.
为具体分析附加周期侧向局域共振结构对平板振动特性的影响, 选取了平板和侧向局域共振超构板四阶代表性模态, 如图3和图4所示.
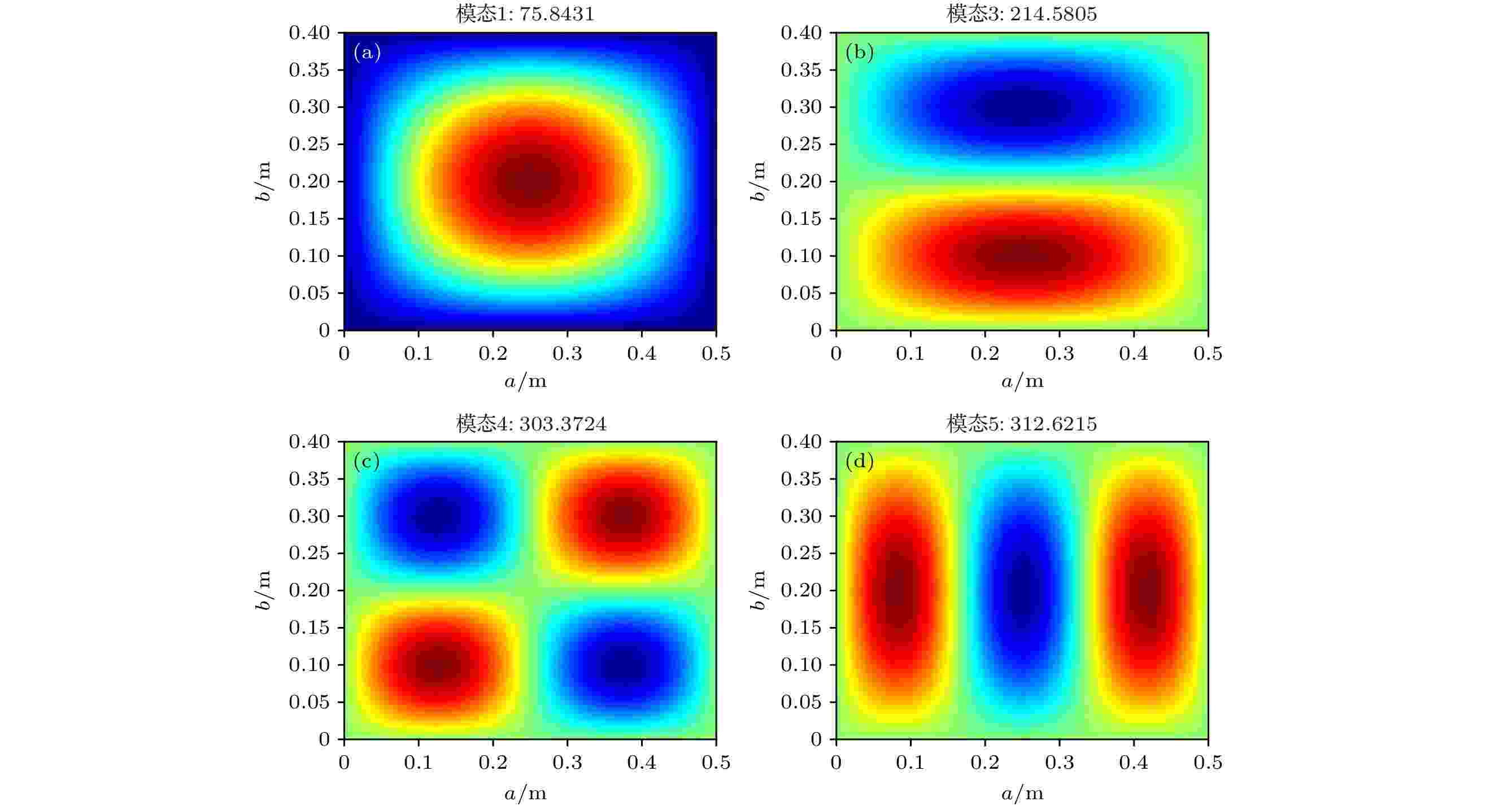图 3 平板第1, 3, 4, 5阶模态
Figure3. Modal analysis of bare plate: the 1st, 3rd, 4th and 5th modes.

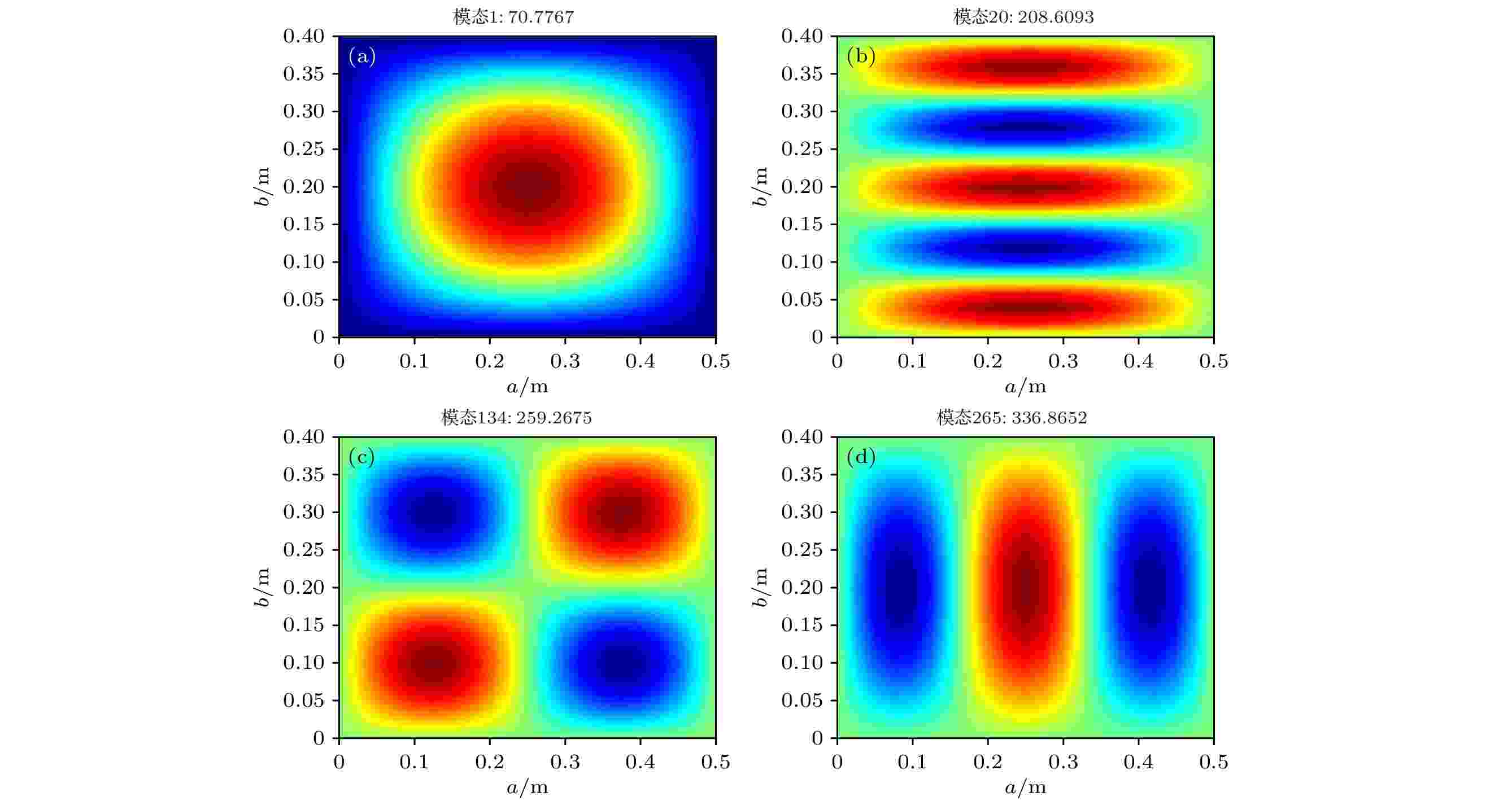图 4 侧向局域共振超构板第1, 20, 134, 265阶模态
Figure4. Modal analysis of the metamaterial plate: the 1st, 20th, 134th and 265th modes.

由图3和图4可见, 平板的第1阶模态振型与侧向局域共振超构板的第1阶模态振型一致, 平板的第4阶模态振型和侧向局域共振超构板的第134阶模态振型一致. 平板第1阶模态频率为75.8 Hz, 超构板的第1阶模态频率为70.8 Hz, 平板第4阶模态频率为303.4 Hz, 超构板的第134阶模态频率为259.3 Hz. 通过对比两种板结构的两阶模态频率及模态振型可以发现, 附加侧向局域共振结构后, 平板模态频率向低频移动, 同时由于侧向局域共振结构周期排布, 因此, 侧向局域共振超构板的振动模态是由原平板的结构的振动模态之间穿插许多侧向局域共振结构共振频率组成. 平板结构的第5阶模态振型(312.6 Hz)与侧向局域共振超构板的第265阶模态振型(336.9 Hz)相似, 但振动峰谷值不同, 其具体振动特性应仔细结合所有振动模态进行详细分析, 以明确附加侧向局域共振结构后平板振动模态的变化, 揭示侧向局域共振超构板抑振机理.
以下对侧向局域共振超构板辐射声功率开展计算, 以揭示结构声辐射特性及规律. 采用表2中结构参数及材料参数, 以(28)式和(29)式计算平板和侧向局域共振超构板的振动辐射声功率及辐射效率, 结果见图5和图6.
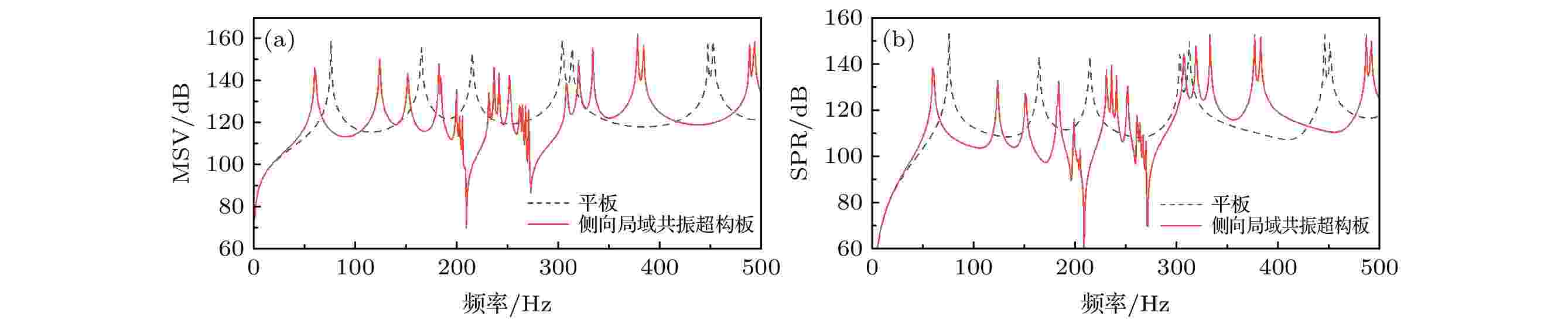图 5 平板与侧向局域共振超构板的(a)表面振速(MSV)与(b)辐射声功率(SRP)对比
Figure5. Comparison of (a) mean square velocity and (b) sound radiation power between the bare plate and the metamaterial plate.

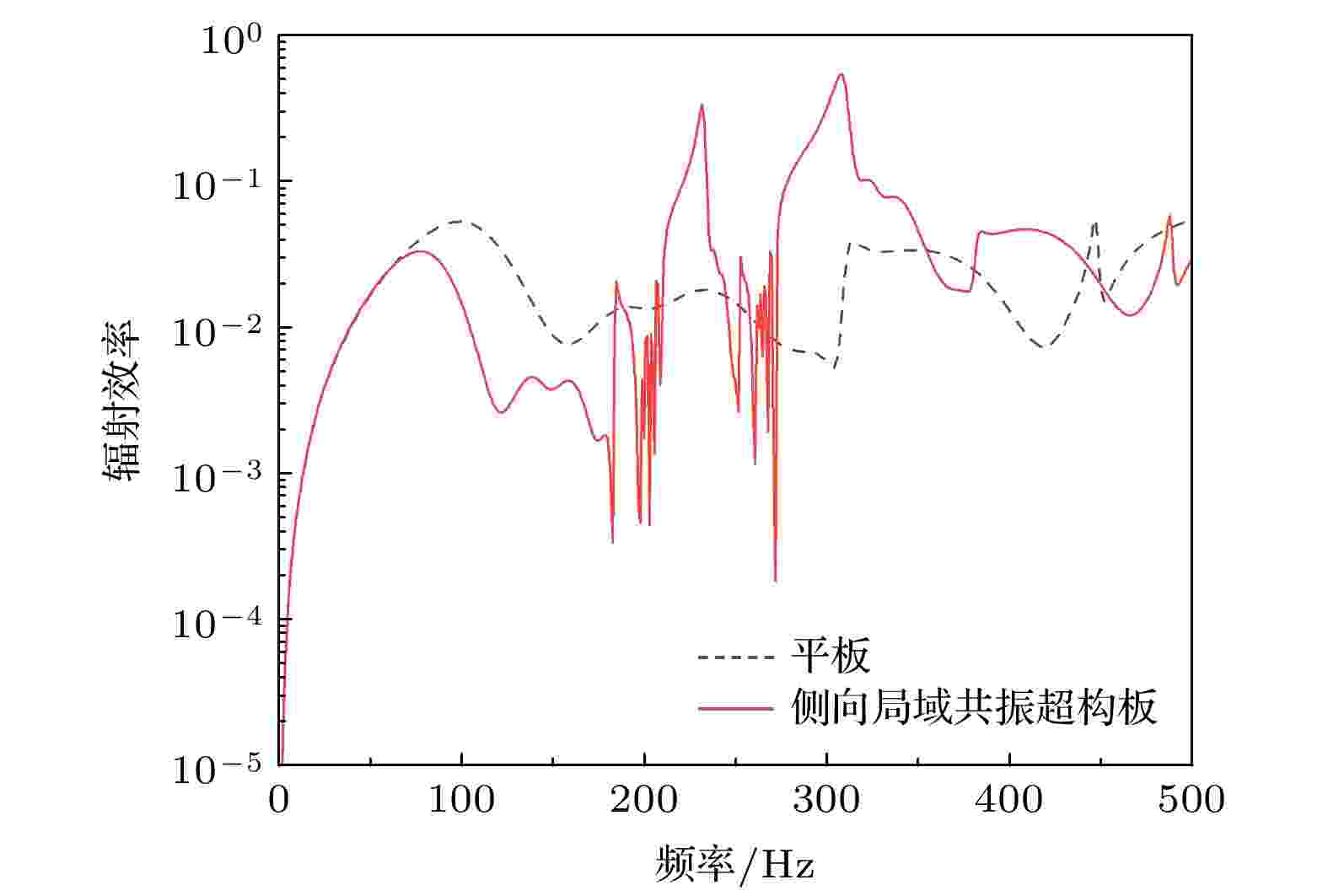图 6 平板与侧向局域共振超构板的辐射效率对比
Figure6. Comparison of radiation efficiency between the bare plate and the metamaterial plate.

图5中MSV表示板面均方振速, SRP表示辐射声功率. 对比平板, 侧向局域共振超构板的板面平均振速在带隙内远低于平板的板面振速, 这主要是由于侧向局域共振超构板在带隙内的抑振特性所导致. 进一步, 侧向局域共振超构板的振动辐射声功率在带隙内也远低于平板. 图6所示为平板与侧向局域共振超构板的辐射效率对比. 结果表明在0—Hz之间, 平板与侧向局域共振超构板辐射效率相同, 70—200 Hz侧向局域共振超构板辐射效率低于平板, 两带隙内侧向局域共振超构板的辐射效率远高于平板, 带隙以上频段, 两种曲线取值相当. 由(29)式可知, 辐射效率由远处辐射声能量除以板面振动能量计算而来, 表示结构向周围辐射声能量的能力. 结合图5和图6所示结果可知, 带隙内侧向局域共振超构板振动能量显著降低, 即使其辐射效率增大, 其计算所得辐射声功率仍然远低于带隙外, 即带隙内超构板振动模态辐射声能力强, 但超构板振动能量低, 导致超构板辐射声能量低.
4.结　论
本文采用理论分析方法及有限元法对侧向局域共振超构板的振动响应进行了分析, 同时推导了声辐射功率及辐射效率的计算表达式. 基于模态叠加法及布洛赫定理, 获得侧向局域共振超构板的加速度级及声辐射特性. 有限元方法计算所得超构板加速度级与理论计算结果吻合, 验证了本文所采用的理论方法的正确性. 同时, 结合文献, 侧向局域共振超构板能够产生两条带隙, 且带隙内超构板的板面均方速度及辐射声功率均远远低于均匀平板, 这主要是由于附加局域共振结构共振产生惯性力抵消了弯曲波在平板内引起的剪力. 而带隙内, 超构板的辐射效率却高于均匀平板, 这说明带隙内超构板的振动模态辐射声能力强, 但辐射的能量低, 结果导致带隙内超构板的辐射声功率较低. 本文所做研究表明侧向局域共振超构板在特定频段能够有效抑制振动能量的传播及声能量的辐射.
相关话题/结构 辐射 计算 质量 声学
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 基于辐射制冷-温室效应的热电系统性能分析
    摘要:基于辐射制冷和温室效应,设计了一种无需主动能量输入的温差发电系统:夜间利用辐射制冷降低热电模块的冷端温度,白天利用温室效应增加热端温度,以提高冷热端温差,达到全天候无间断的发电效果.实验研究了热电模块冷热端温差随时间的变化及其受环境湿度的影响.在中国陕西的夏季实验测量和分析结果表明:辐射制冷使 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 三元Hf-C-N体系的空位有序结构及其力学性质和电子性质的第一性原理研究
    摘要:采用第一性原理方法,研究了三元Hf-C-N体系的空位有序结构及其力学性质和电子性质.首先采用第一性原理和进化算法,预测得到8种可能存在的热力学稳定的Hf-C-N空位有序结构;这些结构都具有岩盐结构,与实验发现的无序固溶体的结构类型一致.本文的预测结果证明了Hf-C-N空位化合物能够以有序结构形 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于MXene涂层保护Cs<sub>3</sub>Sb异质结光阴极材料的计算筛选
    摘要:以锑化铯(Cs3Sb)为代表的碱金属型半导体光阴极具有高量子效率、低电子发射度、光谱响应快等特点,可作为理想的新型电子发射源.然而Cs3Sb中碱金属敏感于含氧气体,从而导致其结构不稳定,工作寿命低,影响电子发射效率.利用超薄层状的二维材料进行涂层保护Cs3Sb基底,有望构建新型高性能光阴极材料 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 渔网超结构的等离激元模式及其对薄膜电池的陷光调控
    摘要:渔网超结构具有平面、近光学无损、特定光场中可以激发表面等离激元等特点,在增强光子器件的响应效率方面极具潜力.本文基于时域有限差分方法和严格耦合波分析,系统研究了渔网超结构的等离共振模式及其对晶硅薄膜电池的光波调控性能.研究结果表明,渔网结构对光波的吸收、散射和消光特性强烈依赖金属层的厚度、线宽 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 单缺陷对Sc, Ti, V修饰石墨烯的结构及储氢性能的影响
    摘要:寻找稳定高效的储氢材料是实现氢经济的关键.过渡金属修饰石墨烯储氢材料在理论上被广泛研究,但存在H2解离和金属团聚的问题.本文基于密度泛函理论对Sc,Ti,V修饰单缺陷石墨烯的结构及储氢性能进行计算.结果表明:单缺陷使Sc,Ti,V与石墨烯的结合能提高4—5倍;Sc,Ti,V离子特性增强,可以通 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 二维共价键子结构Zintl相热电材料研究及进展
    摘要:热电材料可以实现热能和电能间的直接相互转换,在半导体制冷和热能回收方面有着重要应用.Zintl相热电材料由电负性差异较大的阴阳离子组成,其输运特征符合“声子玻璃,电子晶体”的概念,因此受到了广泛的研究,特别是具有二维共价键子结构Zintl相热电材料凭借优异的电性能更是被寄予厚望.本文综述了具有 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 用于提升有限口径辐射功率的紧耦合相控阵天线的设计
    摘要:电磁波的辐射功率对其传输距离起着决定性作用.传统上,可以通过增大辐射口径或增加天线单元输入功率来提升电磁波的辐射功率.但辐射口径由于受装配空间限制而无法持续增大,天线单元输入功率的增大也因信号源功率提升困难而难以实现.因此,在有限口径下,如何提升电磁波的辐射功率成了迫切需要解决的问题.通过在有 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 冲击波波后辐射效应对Richtmyer-Meshkov不稳定性增长影响的实验研究
    摘要:辐射冲击波波后物质具有辐射属性,它通过扰动界面引起的Richtmyer-Meshkov(RM)不稳定性的增长有别于通常的冲击波.在高功率激光装置上开展冲击波波后辐射效应对界面不稳定性增长影响的实验研究,认识波后辐射对界面增长的影响过程及规律,有助于提高高能量密度条件下RM不稳定性演化规律的认识 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 一种200 kV的多功能脉冲辐射系统研制
    摘要:研制了一套峰值电压200kV的多功能脉冲辐射系统,该系统具有产生脉冲电子束和脉冲X射线的功能,在两种运行状态中可以灵活切换.系统包括脉冲功率驱动源、真空二极管和实验腔体,其中,脉冲功率驱动源由Marx发生器、高储能的水介质传输线和脉冲压缩开关组成.系统负载等效阻抗2Ω、负载电流半高宽30ns, ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 二维双金属铁磁半导体CrMoI<sub>6</sub>的电子结构与稳定性
    摘要:二维磁性半导体由于兼具磁性、半导体性和特殊的二维结构而受到人们的广泛关注,为纳米级自旋电子和光电子器件的研发应用和相关的基础理论研究提供了新的思路和平台.基于第一性原理计算,在对一系列二维双金属碘化物CrTMI6的交换能进行初步筛选的基础上,选出了具有铁磁性的CrMoI6单层结构.进一步计算表 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.