摘要:近年来, 人类对火星的探索活动不断掀起新的热潮. 研究表明, 火星尘暴内的强电场可能引发CO₂大气放电现象. 对其中的放电机理进行分析不但有助于深化对火星地表演化的认识, 也为基于放电等离子体技术实现火星原位制氧提供了可能. 本文在深入分析火星CO₂放电过程的基础上, 基于图论与粒子依赖性分析的方法, 结合整体模型, 提出了一种定量确定火星大气条件下CO₂放电简化集合的方法. 首先从反应粒子构成的网络拓扑图及粒子间相互作用关系入手, 筛除C₂O, $ {\mathrm{C}}_{2}{\mathrm{O}}_{2}^{+} $, $ {\mathrm{O}}_{4}^{-} $等低活跃粒子, 得到CO, $ {\mathrm{C}\mathrm{O}}_{2}^{+} $, $ {\mathrm{C}\mathrm{O}}_{3}^{-} $等主要粒子, 实现对粒子种类的选取; 随后基于反应速率分析, 定量获得各反应对CO₂放电过程的贡献比重, 最终确定包含16种粒子、67种反应的基态CO₂放电反应简化集合. 数值模拟表明, 使用简化集合与初始集合的计算结果一致, 这也给出了火星大气条件下CO₂放电的关键过程. 从方法学上来讲, 本文的研究为进一步实现复杂化学等离子体体系中, 反应粒子与反应种类的自动化、精确化与智能化选择提供依据, 同时本文提供的方法能够定量分析反应粒子之间的相互关系, 从而为精确研究火星CO₂放电中的各种产物, 实现基于放电等离子体技术的火星原位制氧奠定理论基础.
关键词: CO₂放电/
火星大气/
反应集合/
原位制氧

English Abstract

全文HTML

--> --> -->

火星作为太阳系内与地球最为接近的行星, 一直吸引着人们探索的目光, 在过去的六十年中, 人类向火星发射了四十余颗火星探测器, 获取了大量的火星资料. 近年来, 新一轮的火星探测正在兴起, 中国于2020年7月发射火星探测器“天问一号”, 经过10个月的飞行, 已于2021年3月份进入火星轨道, 着陆火星表面并进行巡视探测. 已有的研究表明, 火星大气主要由体积比为95.32%的二氧化碳、2.7%的氮气、1.6%的氩气和大约0.13%的氧气组成, 表面气压在600—700 Pa左右, 不到地球大气压的1%^[1].
火星稀薄的大气在光照等因素的作用下携带沙尘形成强烈的尘暴, 沙尘颗粒在通过摩擦与碰撞等过程携带电荷后, 最终可以形成几十到几百千伏每米的沙尘电场, 可能使火星大气发生CO₂击穿放电现象^[2-9], 目前人们正对火星沙尘放电中独特的自激发与自熄灭等现象进行深入的研究^[10-13]. 从另一个角度来看, 火星大气中丰富的CO₂资源为人类空间探索进行火星原位制氧提供了可能. 2021年2月登陆的美国毅力号火星探测器已经携带基于热催化的CO₂制氧装置, 针对火星原位制氧进行了实地探索, 预计能以6 g/h的速率产生纯度高于98%的氧气^[14], 这意味着火星原位制氧问题的研究开始进入新的阶段. 由于等离子体低能耗、高效率的特点, 采用CO₂放电的方式进行火星原位制氧也成为人们关注的主要方向之一^[15]. 一方面, 借助于CO₂放电等离子体技术在火星上实现原位制氧有其独特的优势, 首先火星大气中的压力和温度范围有利于CO₂分子不对称拉伸模式的振动激发和随后的振动上移, 这可使更多的能量储存在CO₂的振动模式中, 有利于CO₂分解^[16]; 此外, CO₂通过振动激发解离比电子碰撞激发解离需要更少的能量, 因此在火星上采用CO₂的逐步振动激发方式能更有效地分解CO₂, 并提高能量利用效率^[17]. 另一方面, 由于CO₂是地球上主要的温室气体, 它经过转化的产物作为增值化学品和新燃料具有独特的优势, 因此人们对地球大气压下的CO₂放电已开展深入的研究, 并对脉冲介质阻挡放电(DBD)、微波放电、滑动弧放电等不同模式下的CO₂放电行为得到了一定的认识^[18-21]. 这些成果将有助于人们更深刻地理解火星环境中的CO₂放电.
进行火星上CO₂放电研究首先面临的一个重要问题是放电反应集合的确定, 由于火星上的放电环境与地球大气环境及实验室环境差别很大, 寻找完整的反应集合是火星原位制氧及火星沙尘放电等研究的重要前提, 这同时也涉及到对火星CO₂放电中主要与本质放电过程的认识. 一般来说, 出于计算的难易程度考虑, 首先选择零维模型^[22]或一维模型^[23,24]进行反应集合的分析, 并在将其应用于高维模型^[25-28]之前进行反应集合的简化, 此过程被称为骨架还原^[29]. 反应集合的主要分析方法有灵敏度分析(SA)、不确定性分析(UA)、主成分分析(PCA)和通径分析(PWA), SA与UA通过分析系统受到扰动后的响应来实现集合的化简, PCA着重于研究集合解耦后各粒子之间的耦合关系, PWA则以各路径的速率大小作为选择的标准^[30-33].
然而, 对于火星条件下CO₂放电这种复杂的反应过程而言, 上述方法通常非常耗时. 在实际研究中, 可以首先应用图形理论对初始集合进行预处理. 它通过构造数学图形的方式对节点间关系进行分析, 已被广泛用于各种复杂系统和多种领域^[34-38]. 在反应种类繁多、粒子间相互关系复杂的情况下, 图论方法能够确定在后续模拟中扮演中心角色的粒子, 并对等离子体化学过程做到迅速而准确的分类^[39,40]. 对于图论方法的处理结果, 可以在数值模拟之后, 借助粒子间依赖关系分析进行深入的探讨与验证, 它能够定量地求解粒子重要程度, 运用有向图对可以保留在简化集中的粒子进行标记, 从而产生还原骨架, 以一定的精度预测简化集中粒子的表现^[41,42]. 由于粒子间通过反应耦合, 因此依赖关系分析法需着重考虑粒子和反应的速率表达式. 在分析过程中, 它计算粒子间相互关系占用的时间只是进行常微分方程积分所需时间的一部分, 速度较快, 因此已被用于等离子体方面的研究^[21].
DBD是进行CO₂转化最常用的非热等离子体类型, 其设计简单, 并有利于在应用中扩大规模^[17,43]. 虽然振动激发能级在微波和滑动弧放电中对CO₂转化起到关键作用, 但在DBD大于200 Td (1 Td = 10^–17 V·cm²)的约化场范围下, 高能级振动态粒子的存在显得没那么重要, 电子在激发粒子的过程中造成的能量损失也可通过引入不会造成粒子变化的虚拟反应进行弥补^[17,19,4344]. 因此本文不考虑振动激发态粒子, 采用图论分析法与粒子依赖性分析法, 结合基于反应速率的反应比重分析, 致力于获得可应用于DBD形式下的基态CO₂放电简化集合.

由于目前缺乏类火星环境下CO₂放电的数值模拟与实验室结果, 为了验证初始反应体系的合理性, 首先将其应用于地球大气压条件下进行数值模拟^[45,46], 并将CO₂的计算转化率结果与Bogaerts等^[18,47]的基态集合的数值模拟结果和实验室结果进行对比论证, 如图1所示. 可以看到, 转化率结果具有比较好的一致性, 随着比能量输入(SEI)的升高, 转化率的上升率降低, 这一定程度上说明我们的反应体系与放电模型是合理可靠的. 关于大气压下模拟的计算模型与计算结果将另文发表, 本文仅集中讨论反应粒子与反应集合的精确化与自动化选择.
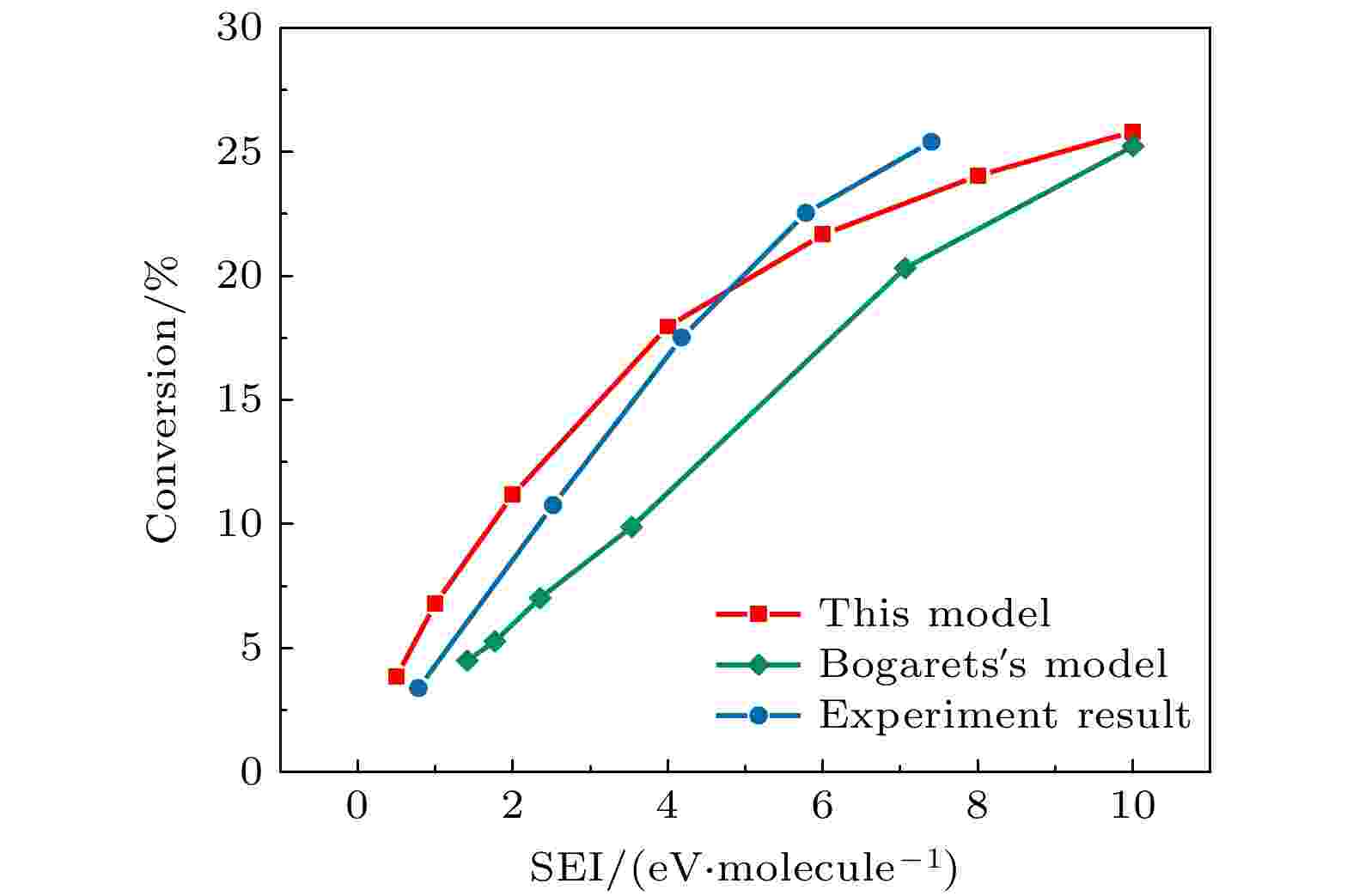图 1 地球大气环境下CO₂放电转化率对比
Figure1. Comparations of CO₂ discharge conversion in the earth atmosphere.

本文采用等离子体整体模型, 借助粒子平衡方程和能量平衡方程, 求解物质浓度及能量随时间的演化过程. 运用自编Matlab程序, 采用局部能量近似的方法, 耦合Bolsig+程序, 通过计算各粒子的浓度变化与能量的散失过程, 得出各反应间的相互关系; 运用Zdplaskin程序, 查看CO₂转化率与能量效率、能量损耗随比能量输入的变化, 并将粒子浓度变化与自编Matlab程序中的结果形成对照.
放电数值模拟中取火星气压为700 Pa, 火星表面平均温度为218 K, 并设置功率密度为20 W/cm³, 忽略背景气体CO₂及其产物O₂和CO的振动态与激发态形式, CO₂初始浓度与火星条件下保持一致, 初始的放电反应集合在借鉴Kozák和Bogaerts^[18]的研究后进行一定的补充, 定义粒子M为过渡粒子, 在本模型中可由CO₂, O₂, CO等中性粒子替代. 详情见附录A的表A1.

	初始集合粒子构成
中性粒子	CO2, CO, C, O, O2, O3, C2O
正离子	$ {\mathrm{C}\mathrm{O}}_{4}^{+} $, $ {\mathrm{C}\mathrm{O}}_{2}^{+} $, CO+, C+, O+, $ {\mathrm{O}}_{2}^{+} $, $ {\mathrm{O}}_{4}^{+} $, $ {\mathrm{O}}_{5}^{+} $, $ {\mathrm{C}}_{2}{\mathrm{O}}_{2}^{+} $, $ {\mathrm{C}}_{2}{\mathrm{O}}_{3}^{+} $, $ {\mathrm{C}}_{2}{\mathrm{O}}_{4}^{+} $
负离子	$ {\mathrm{C}\mathrm{O}}_{4}^{-} $, $ {\mathrm{C}\mathrm{O}}_{3}^{-} $, O–, $ {\mathrm{O}}_{2}^{-} $, $ {\mathrm{O}}_{3}^{-} $, $ {\mathrm{O}}_{4}^{-} $

表A1初始反应集合中的粒子构成
TableA1.Composition of particles in the original model.

数值模拟中的反应速率v定义为单位时间单位体积内各反应中化学计量数为1的粒子的浓度变化量:

$ v = K{n_1}{n_2}, $

其中$ {n}_{1} $, $ {n}_{2} $为反应中的粒子浓度; K为反应的速率系数, 由碰撞截面和粒子间的相对速度共同决定.
比能量输入$ {E}_{\mathrm{s}\mathrm{i}} $, CO₂转化率${X}_{\mathrm{C}\mathrm{O}_2}$, 能量效率η, 能量损耗$ {E}_{\mathrm{c}} $的表达式分别为^[48,49]

$ {E_{{\text{si}}}} = \frac{{{P_{\text{d}}}}}{{{n_{{\text{C}}{{\text{O}}_{\text{2}}}}}({t_{\text{r}}})}} \cdot {t_{\text{r}}}, $

$ {X_{{\text{C}}{{\text{O}}_{\text{2}}}}}({\text{%}} ) = \frac{{{n_{{\text{C}}{{\text{O}}_{\text{2}}}}}({t_0}) - {n_{{\text{C}}{{\text{O}}_{\text{2}}}}}({t_{\rm r}})}}{{{n_{{\text{C}}{{\text{O}}_{\text{2}}}}}({t_0})}} \times 100{\text{%}} , $

$ \eta (\text{%}) = \frac{{{X_{{\text{C}}{{\text{O}}_{\text{2}}}}}(\text{%}) \cdot \Delta {H_{{\text{C}}{{\text{O}}_{\text{2}}}}}}}{{{E_{\rm si}}}}, $

$ {E_{\text{c}}} = \frac{{{E_{{\text{si}}}}}}{{{X_{{\text{C}}{{\text{O}}_{\text{2}}}}}(\text{%})/100}} . $

这里$ {P}_{\mathrm{d}} $是能量密度; $ {t}_{0} $是反应初始时刻; $ {t}_{\mathrm{r}} $是气体驻留时间; $ \Delta {H}_{{\mathrm{C}\mathrm{O}}_{2}} $是1个CO₂分子分解成1个CO和1/2个O₂时所需的能量, 常为2.93 eV/molecule.
在简化集合的构建过程中, 首先运用图论对初始集合进行预处理, 将各粒子视为节点, 粒子间的碰撞反应由节点间的有向边表示, 并寻找节点间连通的最短路径, 从粒子间连通性、临近中心性、相间中心性、网络集聚度等方面共同分析反应集合特征. 在进行数值模拟之后, 采用粒子依赖性分析法, 探究不同粒子之间的相互关系, 定量地判断各粒子的重要程度, 并结合图论分析的相关结论确定粒子简化集. 最后对粒子简化集所涉及的各项反应基于反应速率进行反应比重分析, 化简反应种类, 形成最终的完整简化集. 具体的分析过程见第3节, 特别需要指出的是, 该分析方法在包含振动激发能级粒子种类的集合中同样具备可行性.

2

-->

3.1.图论分析

3 -->

3.1.1.粒子间连通性分析

由于不同粒子(即节点)间的碰撞反应类型存在差异, 因此首先统计各粒子参与反应的数目, 确定初始集合总体的反应构成情况, 如图2所示.
图 2 各粒子所参与的反应数目
Figure2. Number of reactions that each species participates in

背景气体分子CO₂参与了超过1/3的碰撞反应, CO, O₂和O是其放电的主要产物, 其中CO的碳氧成键较为稳定, 与之相比, O₂和O更具活泼性, 它们参与的反应数目已远超CO₂, 是初始集合中参与反应构成最多的粒子.
另一方面, 通过检索反应类型可以发现, 相比于其他正离子, $ {\mathrm{C}\mathrm{O}}_{4}^{+} $, $ {\mathrm{O}}_{4}^{+} $, $ {\mathrm{O}}_{5}^{+} $等正离子不会直接通过中性气体分子发生电子碰撞电离反应产生, 它们同C₂O与$ {\mathrm{O}}_{4}^{-} $一样, 一般作为重粒子碰撞反应的产物粒子出现, 且极少通过碰撞生成其他粒子, 在等离子体化学反应集中很难找到他们的存在, 涉及的反应数目较少.
图3描述了各粒子与其他粒子间可通过反应建立联系的数目. 在共25种粒子中, O₂可与23种粒子直接连通; 作为基本粒子的CO₂也具备显著的表现, 它可以通过碰撞反应生成其他粒子, 或由其他粒子经过逆反应补偿. 通过图2与图3的对比可以发现, 参与反应种类较少的$ {\mathrm{C}\mathrm{O}}_{4}^{+} $, $ {\mathrm{O}}_{4}^{+} $, $ {\mathrm{O}}_{5}^{+} $, C₂O与其他粒子的连通性同样较差, 它们只能与较少的粒子建立联系, 对完整粒子集合起间接影响作用, 粒子重要性不足; 而$ {\mathrm{C}\mathrm{O}}_{2}^{+} $, $ {\mathrm{O}}_{2}^{-} $等粒子参与的反应种类虽不多, 与之直接连通的粒子种类却处于较高的水平, 说明它们可以在有限的反应中与较多的粒子建立联系.
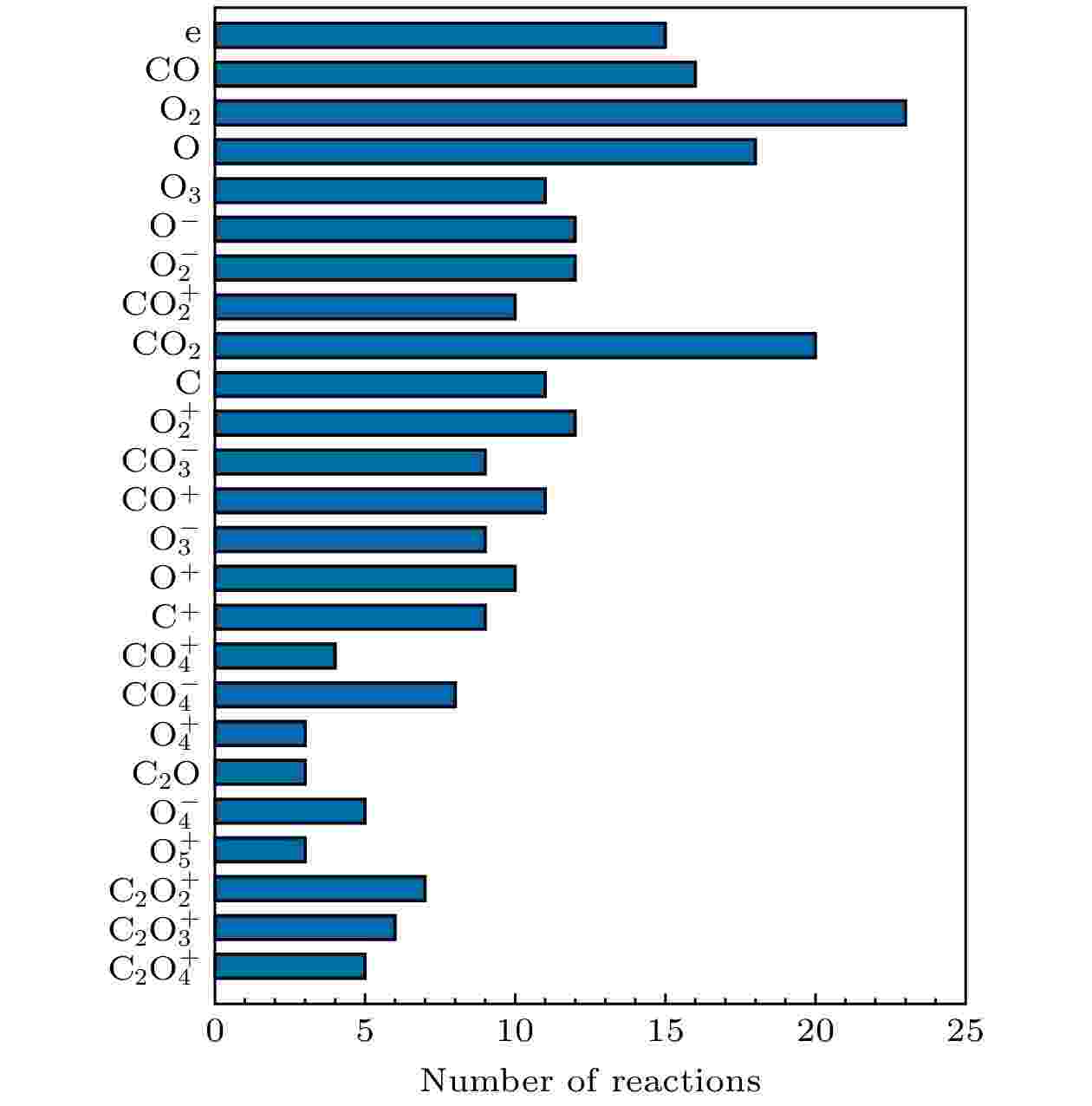图 3 可通过反应直接建立联系的粒子种类数目
Figure3. Number of species that can be directly connected by reactions.

为了更好地预测各粒子在放电行为中的实际参与情况, 研究了它们在反应中分别作为反应物与生成物出现时与其他粒子相沟通的频数, 如图4所示. 在这里, 引入了度(Degree)的概念, 定义汇入节点的边的总数为入度(In-degree), 背离节点的边的总数为出度(Out-degree). 比如, e, O^–, $ {\mathrm{O}}_{2}^{+} $等粒子的入度小于出度, 说明在基态集合的反应构成中, 它们往往以反应物的形式存在, 损失的途径多于生成的途径. 但出于反应速率的考虑, 这并不能预测它们在反应中的实际产生量与损耗量.
图 4 各粒子度数　(a)出度、入度的条形堆积图; (b)粒子在出度-入度空间的分布情况
Figure4. Degrees of species: (a) Stacked bars of in-degree and out-degrees; (b) distribution of species in the out-degree-in-degree space.

电子和O₂在度数图中均有显著的表现. 由于电子大量参与了与中性粒子间的碰撞反应(电子碰撞电离反应、电子碰撞解离反应、电子解离附着反应等), 因此出度值最高, 为114; O₂是CO₂放电的气体产物之一, 也是多种重粒子反应的主要生成物, 由于化学性质活泼, 它常在三体反应过程中作为中间粒子催化反应进行, 不发生浓度的改变. 在169个反应构成的初始集合中, O₂的入度和出度分别为159与86, 平均在每个反应中都能与至少一个粒子建立联系.
离子方面, O^–和$ {\mathrm{O}}_{2}^{+} $最为活跃. 它们主要经过CO₂, O₂, O₃等粒子与电子发生碰撞解离与碰撞电离反应产生, 并作为反应物在与其他重粒子的大量碰撞中损耗. 实际上, 与绝大多数中性粒子在度空间中的分布相反, 以O^–和$ {\mathrm{O}}_{2}^{+} $为代表的大部分带电粒子均具有更高的出度. 这说明集合中的绝大多数反应是各种离子经过碰撞重新生成中性粒子的过程, 尽管这些离子往往仅来自于为数不多的几种反应.
3 -->

3.1.2.粒子间信息传递速度分析

放电过程中, 某粒子浓度发生变化时, 其他粒子做出响应的快慢在拓扑网络中表现为信息的传递速度, 途经的过渡粒子越多, 则信息的传递速度越慢, 传递速度与路径长度成反比. 可以运用临近中心性$ {C}_{\mathrm{c}\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s}} $对信息传递速度进行描述, 如(6)式所示, 其中$ {d}_{i, j} $为粒子i与粒子j连通时最短路径上的有向边数目, $ {L}_{i} $即粒子i与其他粒子连通时的平均最短路径长度.

$ {C_{{\text{closeness}}}}(i) = \frac{{N - 1}}{{\displaystyle\sum\nolimits_{j = 1} {{d_{i,j}}} }} = \frac{1}{{{L_i}}} . $

为了直观地展现粒子关系, 将能够在反应中建立联系的粒子通过有向边连接, 并基于临近中心性绘制了图5所示的粒子网络拓扑图.
图 5 粒子网络拓扑图
Figure5. Species network topology.

该网络将各粒子按临近中心性数值大致分为三类: 以O₂为代表的高临近中心性粒子群置于网络中心, 以表示其在信息传递过程中的高效性; C₂O等边缘粒子数值较低, 被置于最外围; 数值居中的$ {\mathrm{O}}_{2}^{-} $等粒子位于二者之间. 每个粒子节点被给予了不同的色彩表示, 色温的高低对应粒子临近中心性的相对大小. 有向线首端的粒子能通过反应对末端粒子产生作用. 为了使绘图简洁, 未保留O₂, CO₂, CO, O, e, O^–之间的连接线, 而是将节点图形边缘相互融合, 表示它们之间可以两两通过反应产生与损耗.
CO₂虽是火星大气条件下放电过程中的背景气体粒子, 但其临近中心性弱于O₂, 在网络中并不位于正中位置. 这是因为在担任过渡粒子催化三体反应这方面, CO₂远没有O₂表现得更为活泼. 结合图3可以看出, 在25种粒子中, O₂只与C₂O无法直接连通, 而CO₂与$ {\mathrm{O}}_{3}^{-} $, $ {\mathrm{O}}_{4}^{+} $, $ {\mathrm{O}}_{4}^{-} $, $ {\mathrm{O}}_{5}^{+} $无法直接连通, 这导致在O₂或CO₂的浓度发生改变时, O₂可以直接通过单次反应将这一信息传递给几乎所有粒子, 而CO₂则更需要过渡粒子的参与. 比如, CO₂与$ {\mathrm{O}}_{3}^{-} $虽然可以在反应N07与I81中通过O₃建立联系, 也可以选择另外多达8种中间粒子, 但信息在节点间的过渡必然导致传递速度减慢, 即临近中心性的下降. 可是, 这并不意味着CO₂的重要程度低于O₂. 在火星大气环境中, 由于CO₂所占比重较高, 其他粒子受CO₂浓度变化的影响极大, 这在后面的粒子依赖性分析中已进行了论证.
在计算中发现, C₂O十分特殊. 其他粒子在相互建立联系的过程中, 最多只需途经一个过渡粒子, 而C₂O与$ {\mathrm{O}}_{3}^{-} $, $ {\mathrm{O}}_{4}^{+} $, $ {\mathrm{O}}_{4}^{-} $, $ {\mathrm{O}}_{5}^{+} $之间的路径长度为3, 即需要寻找两个粒子进行过渡才能将信息传递于后者. 这说明C₂O与它们之间的信息流动效率极低, C₂O通过碰撞反应带来的影响可能远不如其他粒子, 其他粒子的影响更为关键; 此外, 这种连通的低效性也说明该五种粒子与其他粒子间的联系较为疏远, 在粒子集合的化简中应予以适当考虑.
针对各粒子建立联系的方式, 引入了相间中心性$ {C}_{\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{w}\mathrm{e}\mathrm{e}\mathrm{n}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s}} $来细致研究各粒子担任过渡粒子时发挥的作用:

$ {C_{{\text{betweenness}}}}(i) = \sum\limits_{\scriptstyle j = 1,\atop \scriptstyle l = 1}^N {\frac{{{s_{j,l}}(i)}}{{{s_{j,l}}}}\frac{1}{{(N - 1)(N - 2)/2}}}, $

式中$ {s}_{j, l} $表示连通节点j, l的路径种类; $ {s}_{j, l}\left(i\right) $表示构成最短路径时需要节点i参与的数目. 在这里, 通过结合临近中心性的结果, 绘制了图6所示的各粒子在临近-相间中心性空间的分布图. 总的来说, 临近中心性越高的粒子, 往往具有越高的相间中心性, 更多地作为过渡粒子提高网络的稳定性. 对于不能直接连通的粒子对, O₂承担了接近一半的过渡粒子选择, 对拓扑网络的构建起到极大的支撑作用.
图 6 粒子在临近-相间中心性空间的分布图
Figure6. Distribution of species in the closeness-betweenness centrality space.

值得注意的是, C₂O与$ {\mathrm{O}}_{4}^{+} $的相间中心性为0, 这意味着它们不在其他任何一个粒子对的最短路径上, 换言之, 其余粒子间进行最快速的信息传递, 并不需要它们的参与. 此外, 与连通性分析中的数值相比, $ {\mathrm{C}\mathrm{O}}_{4}^{+} $的居间中心性表现较为显著. 其原因在于, $ {\mathrm{C}\mathrm{O}}_{4}^{+} $位于$ {\mathrm{O}}_{5}^{+} $粒子与CO₂, C₂O, $ {\mathrm{O}}_{2}^{+} $连通时的最短路径上, 说明$ {\mathrm{O}}_{5}^{+} $与上述3个粒子进行信息连通需要$ {\mathrm{C}\mathrm{O}}_{4}^{+} $作为过渡粒子; 同时, 在$ {\mathrm{O}}_{5}^{+} $与O₃产生相互关系的3个反应E18, I12, I40中, 反应I12与反应I40均涉及$ {\mathrm{C}\mathrm{O}}_{4}^{+} $的参与, 这也说明$ {\mathrm{O}}_{5}^{+} $对$ {\mathrm{C}\mathrm{O}}_{4}^{+} $存在着较强的依赖性.
3 -->

3.1.3.集聚度分析

在多数社会网络中, 各节点易与周围节点形成紧密的团状结构, 并倾向于向中心节点攀附. 在这里, 运用集聚系数$ {C}_{\mathrm{c}\mathrm{l}\mathrm{u}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{g}} $来探究火星大气条件下等离子体化学集所构成网络的紧密程度:

$ {C_{{\text{clustering}}}}(i) = \frac{{{b_i}}}{g} = \frac{{{b_i}}}{{{g_i}({g_i} - 1)/2}}, $

式中$ {g}_{i} $为与节点i直接相连的节点数目, $ {b}_{i} $为这些节点间能够直接相连的对数, g为该相连对数可能出现的最大值. 图7给出了各粒子在集聚系数-度数空间中的分布, 可以看出, 随着粒子度数的升高, 集聚系数整体呈现下降的趋势, 这表明集合中并不活跃的粒子周围可能会形成更为紧密的网络. 通过深入研究发现, 能够与具备高度数与中心性数值的O₂等粒子相连的粒子群中不乏$ {\mathrm{C}}_{2}{\mathrm{O}}_{2}^{+} $, $ {\mathrm{C}\mathrm{O}}_{4}^{+} $, $ {\mathrm{C}\mathrm{O}}_{4}^{-} $等低活跃粒子, 由于这些粒子间一般不具备通过反应直接连通的能力, 因此虽然以O₂为中心形成的网络体系足够大, 但孤立节点的存在会使O₂的集聚系数降低. 而由于粒子度数频率服从标准等离子体化学模型分布, 各低活跃性的边缘粒子会更多地直接攀附于活跃粒子, 并经过它们与其他粒子建立联系, 这使得以低活跃粒子为中心构成的邻居网络中有大量的活跃粒子参与, 进而形成复杂而稠密的网络.
图 7 粒子在集聚系数-度数空间的分布
Figure7. Distribution of species in the clustering coefficient-degree space.

这种稠密的网络反过来印证了这些粒子的低活跃性与低影响度. 比如, $ {\mathrm{O}}_{4}^{+} $和C₂O的集聚系数是1, 说明与它们直接相连的邻居粒子间能实现完全互联, 构成完整的网络结构, 这意味着$ {\mathrm{O}}_{4}^{+} $与C₂O重要性的下降—周围粒子进行信息的传递并不需要它们的过渡. 这样的粒子在集合中就显得多余了. 因此, 集聚系数偏高的粒子, 也是在构建简化集时值得注意的对象.
2 -->

3.2.粒子种类筛选

前面通过粒子的度数与中心性, 分析初始集合中各粒子的活跃水平、粒子间信息的传递速度, 并借助集聚系数探讨网络构成, 最终初步得出$ {\mathrm{O}}_{4}^{+} $, C₂O, $ {\mathrm{O}}_{4}^{-} $, $ {\mathrm{O}}_{5}^{+} $等粒子在集合中的低影响性. 但应强调的是, 图论的结果只能说明外部条件或某一粒子浓度发生改变时, 整个粒子集合做出反馈的速度, 而不能说明各粒子所受影响深度的大小. 本节将基于初始集合进行数值模拟, 定量分析粒子间相互依赖关系, 探究各粒子通过反应带来的影响, 验证图论分析的相关结果, 并结合附录A的表A2—A5^{[18,21,44,45,50-62]}中具体的反应过程, 化简粒子集合.

序号	反应	文献
(X01)	e + CO2 $ \Rightarrow $ $ {\mathrm{C}\mathrm{O}}_{2}^{+} $ + 2e	[50]
(X02)	e + CO2 $ \Rightarrow $ CO + O + e	[50]
(X03)	e + CO2 $ \Rightarrow $ CO + O–	[50]
(X04)	e + CO2 $ \Rightarrow $ 2e + O + CO+	[50]
(X05)	e + CO2 $ \Rightarrow $ 2e + CO + O+	[50]
(X06)	e + CO2 $ \Rightarrow $ 2e + C+ + O2	[50]
(X07)	e + CO2 $ \Rightarrow $ $ {\mathrm{O}}_{2}^{+} $ + C + 2e	[51, 52]
(X08)	e + CO $ \Rightarrow $ C + O–	[50]
(X09)	e + CO $ \Rightarrow $ e + C + O	[50]
(X10)	e + CO $ \Rightarrow $ 2e + CO+	[50]
(X11)	e + CO $ \Rightarrow $ 2e + C + O+	[50]
(X12)	e + CO $ \Rightarrow $ 2e + C+ + O	[50]
(X13)	e + O3 $ \Rightarrow $ $ {{\mathrm{O}}_{2}^{-}}^{-} $ + O	[50]
(X14)	e + O3 $ \Rightarrow $ O2 + O–	[50]
(X15)	e + O3 $ \Rightarrow $ O + O2 + e	[53]
(X16)	e + O3 $ \Rightarrow $ $ {\mathrm{O}}_{2}^{+} $ + O + 2e	[53]
(X17)	e + O3 $ \Rightarrow $ O+ + O– + O + e	[53]
(X18)	e + O2 $ \Rightarrow $ 2 O + e	[50]
(X19)	e + O2 $ \Rightarrow $ O + O–	[50]
(X20)	e + O2 $ \Rightarrow $ 2e + $ {\mathrm{O}}_{2}^{+} $	[50]
(X21)	e + O2 $ \Rightarrow $ 2e + O + O+	[50]
(X22)	e + O2 $ \Rightarrow $ e + O+ + O–	[50, 54]
(X23)	e + O $ \Rightarrow $ 2e + O+	[50]
(X24)	e + C $ \Rightarrow $ 2e + C+	[50]

表A2初始集合中由碰撞截面描述的电子碰撞反应
TableA2.Electron impact reactions described by collision cross sections in the original model.

序号	反应	反应速率系数	文献
(I01)	O– + CO2 $ \Rightarrow$ O + CO2 + e	4.0 × 10–18	[48]
(I02)	O– + CO2 + CO $ \Rightarrow$ $ {\mathrm{C}\mathrm{O}}_{3}^{-} $ + CO	1.5 × 10–40	[61]
(I03)	O– + CO2 + O2 $ \Rightarrow$ $ {\mathrm{C}\mathrm{O}}_{3}^{-} $ + O2	3.1 × 10–40	[61]
(I04)	O– + CO2 + CO2 $ \Rightarrow$ $ {\mathrm{C}\mathrm{O}}_{3}^{-} $ + CO2	9.0 × 10–41	[52]
(I05)	$ {\mathrm{O}}_{2}^{-} $ + CO2 + O2 $ \Rightarrow$ $ {\mathrm{C}\mathrm{O}}_{4}^{-} $ + O2	4.7 × 10–41	[52]
(I06)	$ {\mathrm{O}}_{3}^{-} $+ CO2 $ \Rightarrow$ $ {\mathrm{C}\mathrm{O}}_{3}^{-} $ + O2	5.5 × 10–16	[18]
(I07)	$ {\mathrm{O}}_{4}^{-} $ + CO2 $ \Rightarrow$ O2 + $ {\mathrm{C}\mathrm{O}}_{4}^{-} $	4.8 × 10–16	[18]
(I08)	O+ + CO2 $ \Rightarrow$ $ {\mathrm{O}}_{2}^{+} $ + CO	9.4 × 10–16	[18]
(I09)	O+ + CO2 $ \Rightarrow$ O + $ {\mathrm{C}\mathrm{O}}_{2}^{+} $	4.5 × 10–16	[18]
(I10)	C+ + CO2 $ \Rightarrow$ CO+ + CO	1.1 × 10–15	[18]
(I11)	$ {\mathrm{O}}_{2}^{+} $ + CO2 + M $ \Rightarrow$ $ {\mathrm{C}\mathrm{O}}_{4}^{+} $ + M	2.3 × 10–41	[18]
(I12)	$ {\mathrm{O}}_{5}^{+} $ + CO2 $ \Rightarrow$ $ {\mathrm{C}\mathrm{O}}_{4}^{+} $ + O3	1.0 × 10–17	[52]
(I13)	CO+ + CO2 $ \Rightarrow$ $ {\mathrm{C}\mathrm{O}}_{2}^{+} $ + CO	1.0 × 10–15	[56]
(I14)	$ {\mathrm{C}\mathrm{O}}_{2}^{+} $ + CO2 + M $ \Rightarrow$ $ {\mathrm{C}}_{2}{\mathrm{O}}_{4}^{+} $ + M	3.0 × 10–40	[18]
(I15)	O+ + CO $ \Rightarrow$ O + CO+	4.9 × 10–18(Tg/298)0.5exp(–4580/Tg)	[18]
(I16)	C+ + CO $ \Rightarrow$ CO+ + C	5.0 × 10–19	[18]
(I17)	$ {\mathrm{C}}_{2}{\mathrm{O}}_{3}^{+} $ + CO $ \Rightarrow$ CO2 + $ {\mathrm{C}}_{2}{\mathrm{O}}_{2}^{+} $	1.1 × 10–15	[18]
(I18)	$ {\mathrm{C}}_{2}{\mathrm{O}}_{4}^{+} $ + CO $ \Rightarrow$ CO2 + $ {\mathrm{C}}_{2}{\mathrm{O}}_{3}^{+} $	9.0 × 10–16	[18]
(I19)	$ {\mathrm{C}}_{2}{\mathrm{O}}_{3}^{+} $ + CO + M $ \Rightarrow$ CO2 + $ {\mathrm{C}}_{2}{\mathrm{O}}_{2}^{+} $ + M	2.6 × 10–38	[18]
(I20)	$ {\mathrm{C}}_{2}{\mathrm{O}}_{4}^{+} $ + CO + M $ \Rightarrow$ CO2 + $ {\mathrm{C}}_{2}{\mathrm{O}}_{3}^{+} $ + M	4.2 × 10–38	[18]
(I21)	O– + CO $ \Rightarrow$ CO2 + e	5.5 × 10–16	[44]
(I22)	$ {\mathrm{C}\mathrm{O}}_{3}^{-} $ + CO $ \Rightarrow$ 2CO2 + e	5.0 × 10–19	[58]
(I23)	$ {\mathrm{O}}_{2}^{+} $ + C $ \Rightarrow$ CO+ + O	5.2 × 10–17	[18]
(I24)	$ {\mathrm{O}}_{2}^{+} $ + C $ \Rightarrow$ C+ + O2	5.2 × 10–17	[18]
(I25)	CO+ + C $ \Rightarrow$ CO + C+	1.1 × 10–16	[18]
(I26)	O– + C $ \Rightarrow$ CO + e	5.0 × 10–16	[57]
(I27)	$ {\mathrm{C}\mathrm{O}}_{2}^{+} $ + O $ \Rightarrow$ $ {\mathrm{O}}_{2}^{+} $ + CO	1.638 × 10–16	[52]
(I28)	$ {\mathrm{C}\mathrm{O}}_{2}^{+} $ + O $ \Rightarrow$ CO2 + O+	9.62 × 10–17	[18]
(I29)	CO+ + O $ \Rightarrow$ CO + O+	1.4 × 10–16	[18]
(I30)	$ {\mathrm{C}\mathrm{O}}_{4}^{-} $ + O $ \Rightarrow$ $ {\mathrm{C}\mathrm{O}}_{3}^{-} $ + O2	1.1 × 10–16	[18]
(I31)	$ {\mathrm{C}\mathrm{O}}_{4}^{-} $ + O $ \Rightarrow$ CO2 + O2 + O–	1.4 × 10–17	[18]
(I32)	$ {\mathrm{C}\mathrm{O}}_{4}^{-} $ + O $ \Rightarrow$ CO2 + $ {\mathrm{O}}_{3}^{-} $	1.4 × 10–16	[18]
(I33)	$ {\mathrm{C}\mathrm{O}}_{3}^{-} $ + O $ \Rightarrow$ CO2 + $ {\mathrm{O}}_{2}^{-} $	8.0 × 10–17	[58]
(I34)	$ {\mathrm{C}\mathrm{O}}_{2}^{+} $ + O2 $ \Rightarrow$ $ {\mathrm{O}}_{2}^{+} $ + CO2	6.4 × 10–17	[52]
(I35)	CO+ + O2 $ \Rightarrow$ $ {\mathrm{O}}_{2}^{+} $ + CO	1.2 × 10–16	[18]
(I36)	C+ + O2 $ \Rightarrow$ CO + O+	6.2 × 10–16	[18]
(I37)	C+ + O2 $ \Rightarrow$ CO+ + O	3.8 × 10–16	[18]
(I38)	$ {\mathrm{C}}_{2}{\mathrm{O}}_{2}^{+} $ + O2 $ \Rightarrow$ 2CO + $ {\mathrm{O}}_{2}^{+} $	5.0 × 10–18	[18]
(I39)	$ {\mathrm{C}\mathrm{O}}_{4}^{-} $ + O3 $ \Rightarrow$ CO2 + $ {\mathrm{O}}_{3}^{-} $ + O2	1.3 × 10–16	[18]
(I40)	$ {\mathrm{C}\mathrm{O}}_{4}^{+} $ + O3 $ \Rightarrow$ $ {\mathrm{O}}_{5}^{+} $ + CO2	1.0 × 10–16	[52]
(I41)	$ {\mathrm{C}\mathrm{O}}_{2}^{+} $ + O– $ \Rightarrow$ O + CO2	1.0 × 10–13	[62]
(I42)	$ {\mathrm{C}\mathrm{O}}_{2}^{+} $ + $ {\mathrm{O}}_{2}^{-} $ $ \Rightarrow$ CO + O2 + O	6.0 × 10–13	[44]
(I43)	$ {\mathrm{C}\mathrm{O}}_{2}^{+} $ + $ {\mathrm{C}\mathrm{O}}_{3}^{-} $ $ \Rightarrow$ 2CO2 + O	5.0 × 10–13	[58]
(I44)	$ {\mathrm{C}\mathrm{O}}_{2}^{+} $ + $ {\mathrm{C}\mathrm{O}}_{4}^{-} $ $ \Rightarrow$ 2CO2 + O2	5.0 × 10–13	[18]
(I45)	CO+ + $ {\mathrm{O}}_{2}^{-} $ $ \Rightarrow$ CO + O2	2.0 × 10–13	[55]
(I46)	C+ + O– $ \Rightarrow$ C + O	5.0 × 10–14	[55]
(I47)	C+ + $ {\mathrm{O}}_{2}^{-} $ $ \Rightarrow$ C + O2	5.0 × 10–14	[55]
(I48)	O–+ CO+ $ \Rightarrow$ CO + O	1.0 × 10–13	[62]
(I49)	$ {\mathrm{C}\mathrm{O}}_{3}^{-} $ + $ {\mathrm{O}}_{2}^{+} $ $ \Rightarrow$ CO2 + O2 + O	3.0 × 10–13	[18]
(I50)	$ {\mathrm{O}}_{2}^{+} $ + $ {\mathrm{C}\mathrm{O}}_{4}^{-} $ $ \Rightarrow$ CO2 + 2O2	3.0 × 10–13	[18]
(I51)	$ {\mathrm{C}}_{2}{\mathrm{O}}_{2}^{+} $ + M $ \Rightarrow$ CO+ + CO + M	1.0 × 10–18	[18]
(I52)	$ {\mathrm{C}}_{2}{\mathrm{O}}_{2}^{+} $ + $ {\mathrm{C}\mathrm{O}}_{3}^{-} $$ \Rightarrow$ CO2 + 2CO + O	5.0 × 10–13	[18]
(I53)	$ {\mathrm{C}}_{2}{\mathrm{O}}_{2}^{+} $ + $ {\mathrm{C}\mathrm{O}}_{4}^{-} $ $ \Rightarrow$ CO2 + 2CO + O2	5.0 × 10–13	[18]
(I54)	$ {\mathrm{C}}_{2}{\mathrm{O}}_{2}^{+} $ + $ {\mathrm{O}}_{2}^{-} $$ \Rightarrow$ 2CO + O2	6.0 × 10–13	[18]
(I55)	$ {\mathrm{C}}_{2}{\mathrm{O}}_{3}^{+} $ + $ {\mathrm{C}\mathrm{O}}_{3}^{-} $ $ \Rightarrow$ 2CO2 + CO + O	5.0 × 10–13	[18]
(I56)	$ {\mathrm{C}}_{2}{\mathrm{O}}_{3}^{+} $ + $ {\mathrm{C}\mathrm{O}}_{4}^{-} $ $ \Rightarrow$ 2CO2 + CO + O2	5.0 × 10–13	[18]
(I57)	$ {\mathrm{C}}_{2}{\mathrm{O}}_{3}^{+} $ + $ {\mathrm{O}}_{2}^{-} $ $ \Rightarrow$ CO2 + CO + O2	6.0 × 10–13	[18]
(I58)	$ {\mathrm{C}}_{2}{\mathrm{O}}_{4}^{+} $ + M $ \Rightarrow$ $ {\mathrm{C}\mathrm{O}}_{2}^{+} $ + CO2 + M	1.0 × 10–20	[18]
(I59)	$ {\mathrm{C}}_{2}{\mathrm{O}}_{4}^{+} $ + $ {\mathrm{C}\mathrm{O}}_{3}^{-} $$ \Rightarrow$ 3CO2 + O	5.0 × 10–13	[18]
(I60)	$ {\mathrm{C}}_{2}{\mathrm{O}}_{4}^{+} $ + $ {\mathrm{C}\mathrm{O}}_{4}^{-} $ $ \Rightarrow$ 3CO2 + O2	5.0 × 10–13	[18]
(I61)	$ {\mathrm{C}}_{2}{\mathrm{O}}_{4}^{+} $ + $ {\mathrm{O}}_{2}^{-} $ $ \Rightarrow$ 2CO2 + O2	6.0 × 10–13	[18]
(I62)	O–+ O3 $ \Rightarrow$ 2O2 + e	3.0 × 10–16	[44]
(I63)	O–+ O3 $ \Rightarrow$ $ {\mathrm{O}}_{3}^{-} $ + O	8.0 × 10–16	[18]
(I64)	$ {\mathrm{O}}_{2}^{-} $ + O3 $ \Rightarrow$ $ {\mathrm{O}}_{3}^{-} $ + O2	4.0 × 10–16	[18]
(I65)	$ {\mathrm{O}}_{3}^{-} $ + O3 $ \Rightarrow$ 3O2 + e	3.0 × 10–16	[18]
(I66)	O+ + O3 $ \Rightarrow$ $ {\mathrm{O}}_{2}^{+} $ + O2	1.0 × 10–16	[18]
(I67)	O– + O2 $ \Rightarrow$ O3 + e	1.0 × 10–18	[44]
(I68)	O– + O2 $ \Rightarrow$ $ {\mathrm{O}}_{2}^{-} $ + O	1.5 × 10–18	[55]
(I69)	O– + O2 $ \Rightarrow$ O + e + O2	6.9 × 10–16	[52]
(I70)	O– + O2 + O2 $ \Rightarrow$ $ {\mathrm{O}}_{3}^{-} $ + O2	1.1 × 10–42(Tg/300)	[52]
(I71)	$ {\mathrm{O}}_{2}^{-} $ + O2 $ \Rightarrow$ 2O2 + e	2.7 × 10–16(Tg/300)0.5exp(–5590/Tg)	[52]
(I72)	$ {\mathrm{O}}_{2}^{-} $ + O2 + M $ \Rightarrow$ $ {\mathrm{O}}_{4}^{-} $ + M	3.5 × 10–43	[18]
(I73)	$ {\mathrm{O}}_{3}^{-} $ + O2 $ \Rightarrow$ O2 + O3 + e	2.3 × 10–17	[18]
(I74)	O+ + O2 $ \Rightarrow$ O + $ {\mathrm{O}}_{2}^{+} $	1.9 × 10–17(Tg/298)–0.5	[18]
(I75)	$ {\mathrm{O}}_{2}^{+} $ + O2 + O2 $ \Rightarrow$ $ {\mathrm{O}}_{4}^{+} $ + O2	4.0 × 10–42(Tg/300)–2.93	[52]
(I76)	$ {\mathrm{O}}_{4}^{+} $ + O2 $ \Rightarrow$ $ {\mathrm{O}}_{2}^{+} $ + O2 + O2	1.8 × 10–19	[52]
(I77)	O+ + O + O2 $ \Rightarrow$ $ {\mathrm{O}}_{2}^{+} $ + O2	1.0 × 10–41	[52]
(I78)	O– + O $ \Rightarrow$ O2 + e	2.3 × 10–16	[21]
(I79)	$ {\mathrm{O}}_{2}^{-} $ + O $ \Rightarrow$ O2 + O–	3.31 × 10–16	[21]
(I80)	$ {\mathrm{O}}_{2}^{-} $ + O $ \Rightarrow$ O3 + e	3.3 × 10–16	[18]
(I81)	$ {\mathrm{O}}_{3}^{-} $ + O $ \Rightarrow$ O3 + O–	1.0 × 10–19	[18]
(I82)	$ {\mathrm{O}}_{3}^{-} $ + O $ \Rightarrow$ 2O2 + e	1.0 × 10–19	[18]
(I83)	$ {\mathrm{O}}_{3}^{-} $ + O $ \Rightarrow$ $ {\mathrm{O}}_{2}^{-} $ + O2	2.5 × 10–16	[18]
(I84)	$ {\mathrm{O}}_{4}^{-} $ + O $ \Rightarrow$ $ {\mathrm{O}}_{3}^{-} $ + O2	4.0 × 10–16	[18]
(I85)	$ {\mathrm{O}}_{4}^{-} $ + O $ \Rightarrow$ O– + 2O2	3.0 × 10–16	[18]
(I86)	$ {\mathrm{O}}_{4}^{+} $ + O $ \Rightarrow$ $ {\mathrm{O}}_{2}^{+} $ + O3	3.0 × 10–16	[18]
(I87)	O– + $ {\mathrm{O}}_{2}^{+} $ $ \Rightarrow$ O2 + O	2.6 × 10–14(300/Tg)0.44	[21]
(I88)	O– + $ {\mathrm{O}}_{2}^{+} $ $ \Rightarrow$ 3O	4.2 × 10–13(300/Tg)0.44	[21]
(I89)	O– + $ {\mathrm{O}}_{2}^{+} $ + O2 $ \Rightarrow$ O3 + O2	2.0 × 10–37	[57]
(I90)	O– + O+ + O $ \Rightarrow$ O2 + O	2.0 × 10–37	[57]
(I91)	O– + O+ + O2 $ \Rightarrow$ 2O2	2.0 × 10–37	[57]
(I92)	O– + O+ $ \Rightarrow$ 2O	4.0 × 10–14	[18]
(I93)	$ {\mathrm{O}}_{2}^{-} $ + O+ $ \Rightarrow$ O + O2	2.7 × 10–13	[18]
(I94)	$ {\mathrm{O}}_{2}^{-} $ + O+ + O2 $ \Rightarrow$ O3 + O2	2.0 × 10–37	[57]
(I95)	$ {\mathrm{O}}_{2}^{-} $ + $ {\mathrm{O}}_{2}^{+} $ $ \Rightarrow$ 2O2	2.01 × 10–13(300/Tg)0.5	[21]
(I96)	$ {\mathrm{O}}_{2}^{-} $ + $ {\mathrm{O}}_{2}^{+} $ $ \Rightarrow$ O2 + 2O	4.2 × 10–13	[21]
(I97)	$ {\mathrm{O}}_{2}^{-} $ + $ {\mathrm{O}}_{2}^{+} $ + O2 $ \Rightarrow$ 3O2	2.0 × 10–37	[57]
(I98)	$ {\mathrm{O}}_{3}^{-} $ + O + M $ \Rightarrow$ O3 + O + M	2.0 × 10–37(Tg/300)–2.5	[57]
(I99)	$ {\mathrm{O}}_{3}^{-} $ + $ {\mathrm{O}}_{2}^{+} $ + M $ \Rightarrow$ O3 + O2 + M	2.0 × 10–37(Tg/300)–2.5	[57]
(I100)	$ {\mathrm{O}}_{3}^{-} $ + O+ $ \Rightarrow$ O3 + O	1.0 × 10–13	[18]
(I101)	$ {\mathrm{O}}_{3}^{-} $+ $ {\mathrm{O}}_{2}^{+} $ $ \Rightarrow$ O2 + O3	2.0 × 10–13	[18]
(I102)	$ {\mathrm{O}}_{3}^{-} $ + $ {\mathrm{O}}_{2}^{+} $ $ \Rightarrow$ 2O + O3	1.0 × 10–13	[18]
(I103)	$ {\mathrm{O}}_{4}^{-} $ + M $ \Rightarrow$ $ {\mathrm{O}}_{2}^{-} $ + O2 + M	4.0 × 10–18	[18]

表A5初始集合中的离子-中性和离子-离子反应, 其中T_g为气体温度, 单位是K, 速率系数的单位在二体或三体反应中分别是m³/s或m⁶/s
TableA5.Ion-neutral and ion-ion reactions in the original model. T_g is the gas temperature in K. The rate coefficients are in m³/s or m⁶/s for binary or ternary reactions.

对集合中不同的粒子A与B, 粒子A对粒子B的依赖性$ {r}_{AB} $为

$ {r_{AB}} = \frac{{\displaystyle\sum\nolimits_{i = 1} {|{R_{A,i}}{\delta _{B,i}}|} }}{{\displaystyle\sum\nolimits_{i = 1} {|{R_{A,i}}|} }}, $

其中$ {R}_{A, i} $表示粒子A在反应i中的产生率. 如果在粒子A生成的反应中, 粒子B作为反应物出现, 则取该反应的$ {\delta }_{B, i} $为1, 否则取0. 该数值是反应物对生成物浓度影响的时间积分归一化贡献率, 如果$ {r}_{AB} $为1, 则意味着粒子B参与了粒子A的所有生成反应. 在下面的分析过程中, 通过采用绘制有向图的方式进行分析, 箭头标示的数值即粒子间的依赖性. 为使绘图相对整洁, 将依赖性的最低阈值ε设为0.1, 此数值可以最大程度保留粒子间的相互关系.
首先关注在CO₂的产生与损耗过程中, 其他中性粒子的表现. 图8中, 除O₃经由O受到CO₂的影响外, 其他中性粒子均直接依赖于CO₂, 而CO₂可通过CO与O之间的逆反应产生. 对于无有向边汇入的粒子节点, 如O₃与C₂O, 可以认为它们对其他中性粒子的数值影响极其微弱; 此外, C₂O对CO, C, CO₂的依赖作用为1, 通过检索反应构成, 发现C₂O只通过反应N09产生, 涉及的反应数目极少, 可作为边缘粒子删除.
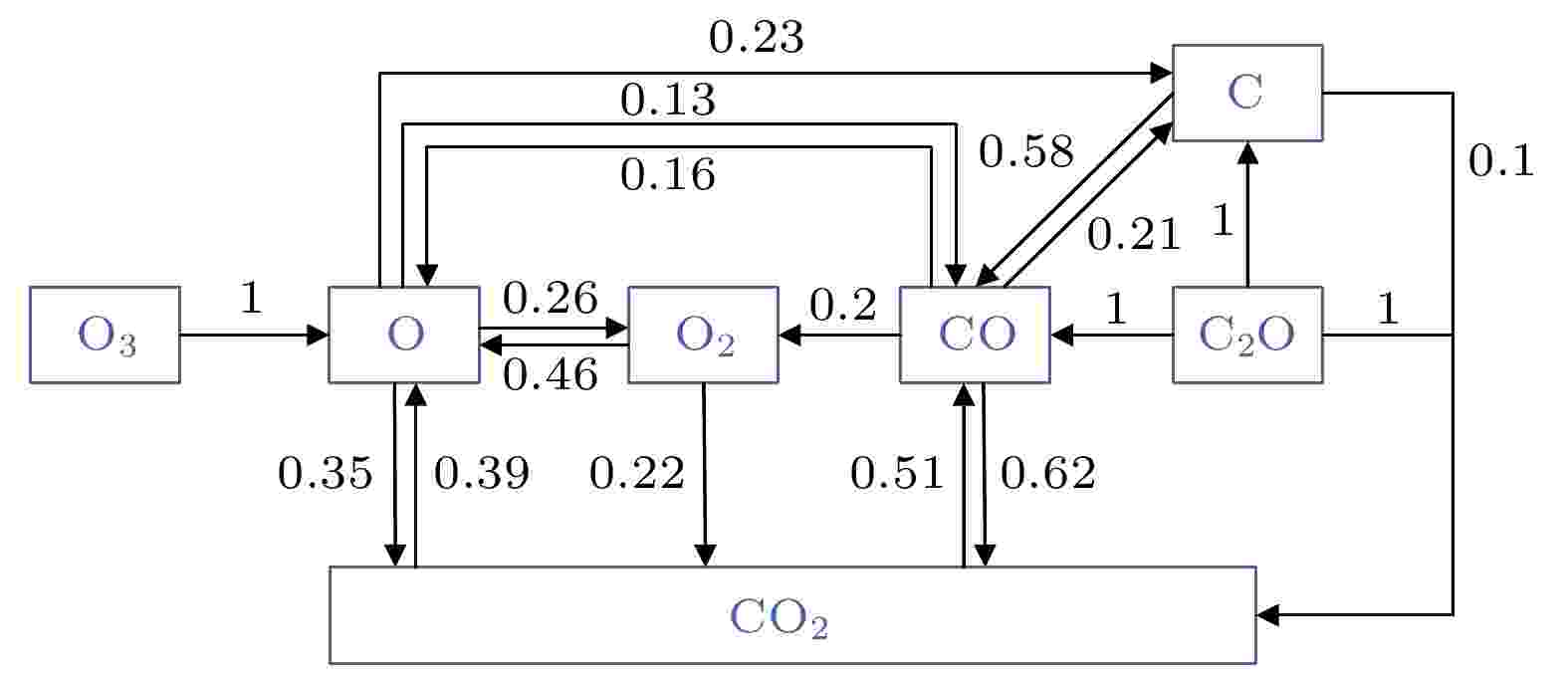图 8 基于CO₂的各中性粒子间的相互关系有向图
Figure8. Directed relation graph among neutral species based on CO₂.

在整体模型中, 认为外部能量首先传递于电子, 并通过电子与重粒子间发生碰撞进行能量传递. 因此, 研究电子与各离子的相互关系能明确具体的放电过程和电荷转移行为. 图9是基于电子的各带电粒子之间的有向关系图. 可以看到, $ {\mathrm{C}\mathrm{O}}_{2}^{+} $, O⁺, CO⁺, C⁺的产生均依赖于电子与CO₂, O, CO, C等中性粒子间发生碰撞电离反应; $ {\mathrm{O}}_{3}^{-} $, $ {\mathrm{C}\mathrm{O}}_{3}^{-} $, $ {\mathrm{O}}_{2}^{-} $, $ {\mathrm{O}}_{4}^{-} $, $ {\mathrm{C}\mathrm{O}}_{4}^{-} $对电子与CO₂发生附着反应的产物O^–的直接或间接依赖性较强, O^–浓度的改变将极大程度地影响它们的粒子浓度; $ {\mathrm{O}}_{2}^{+} $, $ {\mathrm{C}\mathrm{O}}_{2}^{+} $与其他多种带电粒子间均存在一定的依赖与被依赖关系, 在数值模拟过程中比较活跃, 对反应体系起调节作用.
图 9 基于e的各带电粒子间的相互关系有向图
Figure9. Directed relation graph among charged species based on electrons.

$ {\mathrm{O}}_{4}^{+} $, $ {\mathrm{O}}_{4}^{-} $, $ {\mathrm{O}}_{5}^{+} $, $ {\mathrm{O}}_{3}^{-} $, $ {\mathrm{C}\mathrm{O}}_{4}^{-} $和$ {\mathrm{C}}_{2}{\mathrm{O}}_{2}^{+} $在有向图中分别对某一粒子具有极强的依赖性, 且不具备足够影响其他粒子的能力. 其中$ {\mathrm{O}}_{4}^{+} $, $ {\mathrm{O}}_{4}^{-} $, $ {\mathrm{O}}_{5}^{+} $在前文的图论分析中同样表现不显著, 因此对于它们在粒子集合中低重要性的认识得以进一步加深. 而对于$ {\mathrm{O}}_{3}^{-} $, $ {\mathrm{C}\mathrm{O}}_{4}^{-} $和$ {\mathrm{C}}_{2}{\mathrm{O}}_{2}^{+} $, 它们在图论的中心性与集聚度等方面具有适中的表现, 为了深入研究像这样的粒子可能出现的行为, 并决定是否需要在简化粒子集合中保留, 绘制了图10所示的完整粒子集合的有向图, 查看各带电粒子与中性粒子间的关系, 并结合图论结果综合分析它们的实际表现.
图 10 初始集合所有粒子间相互关系有向图
Figure10. Directed relation graph of the original model among all species.

在前面的连通性分析中, $ {\mathrm{O}}_{3}^{-} $参与了18个反应, 与9个粒子直接连通; $ {\mathrm{C}\mathrm{O}}_{4}^{-} $参与了11个反应, 与8个粒子直接连通, 说明它们在反应体系中具备一定的活跃性. 由于数值较小, 在完整粒子集合有向图中未表示对它们具有依赖作用的粒子, 于是决定对它们以反应物形式参与的具体反应进行着重分析. 在反应I06中, 高浓度CO₂的参与使$ {\mathrm{O}}_{3}^{-} $大量损耗, 而作为该反应的产物, $ {\mathrm{C}\mathrm{O}}_{3}^{-} $主要在反应I04中产生, O₂主要在反应E03, N13, I78中产生, 这些反应的速率高于反应I06若干个量级, 使得$ {\mathrm{C}\mathrm{O}}_{3}^{-} $与O₂并不依赖$ {\mathrm{O}}_{3}^{-} $的存在; 对于$ {\mathrm{C}\mathrm{O}}_{4}^{-} $, 它在放电初期主要通过反应I44损耗, 随后反应I30, I32, I50开始占据主导地位, 与$ {\mathrm{O}}_{3}^{-} $类似, 这些反应的产物CO₂, O₂, $ {\mathrm{C}\mathrm{O}}_{3}^{-} $也均依赖于其他可提供更高产率的反应. 总的来说, 诸如$ {\mathrm{O}}_{3}^{-} $, $ {\mathrm{C}\mathrm{O}}_{4}^{-} $这样的粒子, 虽然它们在数值模拟中对其他粒子的浓度变化影响较小, 但它们在连通性中表现出的一般活跃性仍使其具备了足够的可选择性, 因此研究人员可以根据自身的实际情况来确定是否将其纳入简化集合.
对于$ {\mathrm{C}}_{2}{\mathrm{O}}_{2}^{+} $粒子, 通过研究其依赖性和反应构成, 发现它仅通过反应I17与I19产生, 完全依赖于$ {\mathrm{C}}_{2}{\mathrm{O}}_{3}^{+} $的粒子浓度, 这样的粒子在反应体系中会表现出极大的不稳定性. 与之相似的是, $ {\mathrm{C}}_{2}{\mathrm{O}}_{3}^{+} $粒子受到$ {\mathrm{C}}_{2}{\mathrm{O}}_{4}^{+} $浓度的影响, 而$ {\mathrm{C}}_{2}{\mathrm{O}}_{4}^{+} $粒子完全依赖于$ {\mathrm{C}\mathrm{O}}_{2}^{+} $粒子通过反应I14产生. 总的来看, $ {\mathrm{C}\mathrm{O}}_{2}^{+} $浓度的变化会依次影响到$ {\mathrm{C}}_{2}{\mathrm{O}}_{4}^{+} $, $ {\mathrm{C}}_{2}{\mathrm{O}}_{3}^{+} $, $ {\mathrm{C}}_{2}{\mathrm{O}}_{2}^{+} $的粒子浓度. 一旦$ {\mathrm{C}\mathrm{O}}_{2}^{+} $浓度出现大幅度波动, 或者反应的速率系数计算存在较大误差, 那么不确定性会逐步扩大, 使数值模拟结果出现问题, 因此在化简时应直接删除$ {\mathrm{C}}_{2}{\mathrm{O}}_{2}^{+} $, $ {\mathrm{C}}_{2}{\mathrm{O}}_{3}^{+} $, $ {\mathrm{C}}_{2}{\mathrm{O}}_{4}^{+} $.
$ {\mathrm{C}\mathrm{O}}_{4}^{+} $同样值得注意. 在粒子的依赖性分析中, 它仅对$ {\mathrm{O}}_{5}^{+} $的浓度有较大影响, 而$ {\mathrm{O}}_{5}^{+} $的不重要性已在前文中提及, 这使得$ {\mathrm{C}\mathrm{O}}_{4}^{+} $的重要性大大下降. 如果去除涉及$ {\mathrm{O}}_{5}^{+} $的反应, 这样$ {\mathrm{C}\mathrm{O}}_{4}^{+} $粒子便只参与了两个反应, 形成一个最简单的闭环路径, 易受到单个反应的速率系数的影响, 存在较高的不确定性.
2 -->

3.3.反应集合的最终简化

在前面, 针对初始粒子集合, 已从图形理论与粒子间依赖性两个角度进行了完整的分析, 对粒子在集合中的重要程度得到了明确的认识, 把$ {\mathrm{O}}_{4}^{+} $, $ {\mathrm{O}}_{4}^{-} $, $ {\mathrm{O}}_{5}^{+} $, C₂O归为不重要粒子, 把$ {\mathrm{C}\mathrm{O}}_{4}^{+} $, $ {\mathrm{C}}_{2}{\mathrm{O}}_{2}^{+} $, $ {\mathrm{C}}_{2}{\mathrm{O}}_{3}^{+} $, $ {\mathrm{C}}_{2}{\mathrm{O}}_{4}^{+} $归为不稳定与不确定性粒子, 决定在简化集合中将它们涉及的反应删除, 实现粒子种类的选择. 下一步, 需要研究简化粒子集合中的粒子所参与反应的重要性, 并基于反应速率的大小筛选掉不重要的部分, 实现反应集合的最终简化.
反应速率是衡量一个反应重要性最基本的指标. 下面以CO₂与电子发生碰撞电离反应的生成粒子$ {\mathrm{C}\mathrm{O}}_{2}^{+} $为例, 简要分析它在所参与反应中的具体表现.
如图11所示, 反应X1, 即电子与CO₂的碰撞电离反应, 是$ {\mathrm{C}\mathrm{O}}_{2}^{+} $的最主要来源; 反应E3, I27, I28是$ {\mathrm{C}\mathrm{O}}_{2}^{+} $损耗的主要途径. 总的$ {\mathrm{C}\mathrm{O}}_{2}^{+} $生成速率略低于损耗速率, 说明$ {\mathrm{C}\mathrm{O}}_{2}^{+} $浓度在这一时刻呈现下降趋势. 此外, I44, I58等反应的速率较低, $ {\mathrm{C}\mathrm{O}}_{2}^{+} $在这些反应中浓度变化较小, 在构建反应简化集时可予以适当考虑.
图 11 $ {\mathrm{C}\mathrm{O}}_{2}^{+} $在所参与的各项反应中的反应速率
Figure11. Reaction rates of $ {\mathrm{C}\mathrm{O}}_{2}^{+} $ in each reaction involved.

仅比较不同反应对单一粒子浓度的影响是不够的, 由于各粒子浓度不同, 不同粒子在同一反应中的化学计量数也可能存在差异, 所以需要分析各反应在整个放电过程中的参与. 对此, 引入了各反应的相对贡献$ {C}_{\mathrm{r}\mathrm{e}}\left(j\right) $与绝对贡献$ {C}_{\mathrm{a}\mathrm{b}\mathrm{s}}\left(j\right) $:

$ {C_{{\text{re}}}}(j) = \sum\limits_{i = 1}^{{n_j}} {\frac{{|{R_{i,j}}|}}{{\displaystyle\sum\nolimits_{j = 1}^m {|{R_{i,j}}|} }}}, $

$ {C_{{\text{abs}}}}(j) = \sum\limits_{i = 1}^{{n_j}} {|{R_{i,j}}|}, $

其中$ {R}_{i, j} $为反应j中第i个粒子的反应速率, m为反应数目, $ {n}_{j} $为反应j中包含的粒子种类. 相对贡献是反应对所涉及的具体粒子浓度变化的描述, 绝对贡献是对反应中粒子总浓度变化的数值描述. 在对二者进行归一化处理后, 可得到各反应的贡献比重, 数值越高则代表反应对整个数值模拟的贡献越大.
图12以初始集合中由碰撞截面描述的电子碰撞电离反应子集为例, 给出了各反应的贡献比重. 其中, 反应X01, X02, X03是造成CO₂损耗的主要反应, CO₂具备的高粒子浓度, 会使这些反应具有极高的反应速率, 为整个数值模拟带来足够的粒子浓度变化, 从而本身具有较高的绝对贡献比重与相对贡献比重.
图 12 初始集合中由碰撞截面描述的电子碰撞电离反应的比重
Figure12. Proportion of electron impact ionization reactions described by collision cross sections in the original model.

对于反应X13, X14, X15而言, 它们是消耗O₃的主要反应, 相对贡献会呈现较高的数值; 而由于速率系数相对较小、反应中所涉及的各反应物浓度偏低, 它们对粒子总浓度的数值影响并不大, 因此会表现出极小的绝对贡献. 这在已舍弃的$ {\mathrm{O}}_{5}^{+} $等粒子上也有着同样的表现.
在反应集合的筛选中, 应主要针对相对贡献和绝对贡献均较低的反应, 因为它们无论对单一粒子还是集合整体而言, 均具有极低的影响. 需要注意的是, 虽然用户可根据自身的情况选择简化集的精简度, 但仍需要保证每个粒子在反应中均包含足够的生成与损耗反应, 以大体符合实际的放电过程, 同时提高数值模拟的稳定性, 尽量避免因为单个反应的问题带来整个反应过程的不确定性. 最终, 本文在对简化粒子集合中相对贡献比重小于0.2, 绝对贡献比重小于0.002的反应去除后, 又补充了E11, I30, I44, I83等反应以使$ {\mathrm{O}}_{3}^{-} $及$ {\mathrm{C}\mathrm{O}}_{4}^{-} $所涉及的反应类型更加丰满, 最终形成16个粒子参与, 67个反应构成的简化集合, 见附录B^{[18,21,44,45,50-53,56-58,61,62]}的表B1—B5.

简化集合粒子构成
中性粒子	CO2, CO, C, O, O2, O3
正离子	$ {\mathrm{C}\mathrm{O}}_{2}^{+} $, CO+, C+, O+, $ {\mathrm{O}}_{2}^{+} $
负离子	$ {\mathrm{C}\mathrm{O}}_{4}^{-} $, $ {\mathrm{C}\mathrm{O}}_{3}^{-} $, O–, $ {\mathrm{O}}_{2}^{-} $, $ {\mathrm{O}}_{3}^{-} $

表B1简化集合中的粒子构成
TableB1.Composition of particles in the simplified model.

本节采用与初始集合相同的火星大气条件下的外部输入条件—气压700 Pa、温度218 K、功率密度20 W/cm³, 对简化集进行数值模拟验证, 并将部分结果同初始集合进行比较.
图13给出了简化集与初始集合的粒子浓度变化情况. 反应初期, 电子浓度较低, 平均电子能量较高, 电子雪崩不断发展, 大量电子同高浓度的CO₂发生电子碰撞反应, 在进行能量传递的同时, 伴随着CO₂的电离与解离过程, 产生大量电子与其他重粒子. 之后随着电子温度的下降与放电产物浓度的升高, 除电子碰撞反应外, 重粒子间的碰撞反应速率开始加快, 各粒子浓度在0.1 ms后开始趋于较稳定的状态, 简化集与初始集合的粒子浓度表现基本一致.
图 13 初始集合(实线)与简化集(虚线)关于粒子浓度的数值模拟结果比较　(a)中性粒子; (b)正离子; (c)电子与负离子
Figure13. Comparison of the numerical simulation results of particle concentration between the original model (solid line) and the simplified model (dashed line): (a) Neutrals; (b) positive ions; (c) electron and negative ions.

中性粒子方面, CO和O是电子与CO₂发生碰撞反应的主要产物, 浓度上升迅速, 与此同时, 大量的O会发生复合反应生成O₂, 导致O₂的浓度升高; C是CO₂不完全反应的产物, 在将来的实验过程中, 应尽量抑制生成C的副反应的发生, 以防颗粒物对装置造成损坏; O₃则是由于与CO₂的直接联系较少, 因此会呈现相对更少的变化.
离子方面, $ {\mathrm{C}\mathrm{O}}_{2}^{+} $由CO₂发生电子碰撞电离反应直接生成, 反应初期浓度最高, 之后由于O₂浓度上升, 会与电子发生碰撞电离反应加速$ {\mathrm{O}}_{2}^{+} $的生成, 反应I27速率的提升也会在损耗$ {\mathrm{C}\mathrm{O}}_{2}^{+} $的同时促进$ {\mathrm{O}}_{2}^{+} $的生成, 最终使$ {\mathrm{O}}_{2}^{+} $浓度高于$ {\mathrm{C}\mathrm{O}}_{2}^{+} $; 对于$ {\mathrm{C}\mathrm{O}}_{3}^{-} $, 在数值模拟进行1 ms之前, 由于CO₂充当三体反应I04的过渡粒子, 大大催化了该反应发生, 因此$ {\mathrm{C}\mathrm{O}}_{3}^{-} $的浓度剧烈升高, 这之后I33, I49的反应速率提高, 促进了$ {\mathrm{C}\mathrm{O}}_{3}^{-} $的损耗, 使其浓度开始下降, 最终低于CO₂电子附着反应产物O^–的浓度.
作为火星环境下CO₂放电的主要产物, CO可以用作燃料, O₂是生命所需, 同时也可以液氧的形式用于火箭推动. 图14已列出影响它们浓度变化的主要反应. 对于CO, 主要通过电子与CO₂的碰撞解离反应Y02、电子附着反应Y03、C与O₂间的中性粒子碰撞反应M02及$ {\mathrm{C}\mathrm{O}}_{2}^{+} $与O间的离子-中性粒子碰撞反应H16生成, 并可通过与电子的碰撞解离反应Y08, 以及与O^–作用生成CO₂的反应H11发生损耗. 对于O₂, 与C之间的中性粒子反应M02是它最主要的损耗途径, 此外, 它也可以通过电子与$ {\mathrm{C}\mathrm{O}}_{2}^{+} $的碰撞反应F01、单原子氧之间的复合反应M02、O^–与O间的粒子碰撞反应H33等多种途径生成.
图 14 3 ms时引起(a) CO和(b) O₂浓度变化的主要反应
Figure14. Main reactions at 3 ms which cause density changes of (a) CO and (b) O₂.

图15给出了简化集合与初始集合在CO₂转化率、能量效率和能量损耗方面的比较. 可以看到, 各曲线基本重合, 这证明了所构建的简化集的合理性. 图15(a)中, 随着反应进行, SEI提高, CO₂转化率也相应提高, 但上升率逐渐降低. 这是因为, CO₂分解产生的相对稳定的CO在足够长的反应时间后可以与O^–和O重新结合, 形成CO₂, 起到一定的逆补偿作用^[17]. 另一方面, 由(4)式和(5)式可以看到, 能量效率与能量损耗的变化也是合理的, 实际上, 当转化率不具备与SEI同速上升的能力时, 能量效率总是下降、能量损耗量总是上升的^[17]. 从反应速率的角度, 由于SEI的升高会使粒子温度增加, 进而导致部分反应的速率系数增加, 意味着更多的能量损失于各种重粒子的碰撞反应中, 进而导致能量效率与能量损耗产生相应的表现. 总的来说, 转化率与能量效率是无法同时兼顾的, 因此, 确定合适的放电条件, 使放电在保证CO₂转化率的基础上尽可能提高能量转化效率, 将会是下一步的目标.
图 15 作为比能量输入的函数, 简化集合与初始集合关于转化率与能量方面的比较　(a) CO₂转化率; (b)能量效率; (c)能量损耗
Figure15. As a function of SEI, comparations of original and simplified model on (a) conversion of CO₂, (b) energy efficiency, (c) energy cost.

近年来, 随着人类探索火星的热潮兴起, 火星CO₂大气放电现象也引起了人们极大的关注. 然而, 在火星大气条件下, CO₂放电现象极为复杂, 涉及到几十种粒子, 成百上千种反应. 为了精确描述火星大气的放电现象, 有必要使用定量准确的方法全面分析火星大气条件下的反应集合. 本文的研究提供了一种对火星大气条件下的复杂等离子体化学集进行分析与简化的准确方法, 为今后火星大气放电的研究奠定了前提与基础. 同时, 也有助于以定量的方式构建其他复杂气体的反应集合.
首先通过图论的方法, 寻找各目标粒子直接参与的反应数目和直接相关的粒子种类, 从入度与出度方面分析粒子对整个放电过程的参与程度与粒子间建立联系的方式. 在对粒子中心性的考察中, 发现O₂与其他绝大多数粒子具备直接相关性, 于是以O₂为中心粒子构建基于临近中心性的粒子间网络拓扑图, 并结合网络的紧密程度, 分析过渡粒子在其他粒子对连接中的关键作用, 通过粒子间信息流的传递速度推断各粒子的重要程度, 把$ {\mathrm{O}}_{4}^{-} $, $ {\mathrm{O}}_{5}^{+} $, C₂O等粒子归入边缘粒子的行列. 随后针对初始集合, 基于整体模型进行数值模拟工作, 通过粒子间的依赖性分析, 从各粒子对CO₂分解的依赖性和电荷转移过程等角度绘制有向关系图, 确定粒子间通过碰撞反应造成的实际相互影响, 并结合图论分析法, 针对边缘粒子进行细致考虑, 去除了对放电反应影响较小的$ {\mathrm{O}}_{4}^{+} $, $ {\mathrm{O}}_{4}^{-} $, $ {\mathrm{O}}_{5}^{+} $, C₂O和不确定程度较高的$ {\mathrm{C}}_{2}{\mathrm{O}}_{2}^{+} $, $ {\mathrm{C}}_{2}{\mathrm{O}}_{3}^{+} $, $ {\mathrm{C}}_{2}{\mathrm{O}}_{4}^{+} $, $ {\mathrm{C}\mathrm{O}}_{4}^{+} $, 最终得到参与反应的主要粒子种类. 然后分析这些关键粒子参与的化学反应, 计算各反应的速率大小, 通过反应的相对比重分析和绝对比重分析, 得出各反应分别对单一粒子的影响和对整体粒子浓度变化的作用, 将反应种类化简到67个, 实现最终的集合化简. 从方法学的角度来讲, 希望借助于上述反应选择策略及引入新的智能算法^[63], 在复杂化学等离子体体系中实现反应粒子与反应种类的自动化、精确化与智能化选择.
通过分别基于简化集合与初始集合进行数值模拟, 发现相应的粒子浓度、转化率、能量效率等数据的高度一致性, 从而对火星大气CO₂放电的具体过程得到了更深入的了解. 同时, 用简化集代替初始集合进行数值模拟工作, 能够极大地降低计算工作量. 由于包含振动能级的粒子集合与基态粒子集合相似, 均是通过粒子间的碰撞反应实现相互作用, 因此, 本文构建简化集的思路对于振动激发态集合同样适用. 下一步, 将纳入振动态集合, 并考虑火星沙尘颗粒的影响, 与类火星大气条件下的实验探究结果进行对比, 对反应集合进行进一步的完善与改进, 揭示火星CO₂放电中主要与本质的反应过程, 深化对火星大气的认识, 为火星CO₂放电及原位制氧的研究提供理论基础.

初始集合包含的粒子种类如表A1所列, 考虑到碰撞种类和反应速率系数计算方式的差异, 这些粒子构成的反应被划分为不同的碰撞反应子集, 如表A2—A5所列. 其中, 粒子M为中间三体粒子, 在模型计算过程中可由CO₂, CO, O₂等中性粒子代替.

序号	反应	反应速率系数	文献
(E01)	e + e + C+ $\Rightarrow $ C + e	5.0 × 10–39	[55]
(E02)	e + CO+ $\Rightarrow $ C + O	3.46 × 10–14Te–0.48	[56]
(E03)	e + $ {\mathrm{C}\mathrm{O}}_{2}^{+} $ $\Rightarrow $ C + O2	3.94 × 10–13Te–0.4	[21]
(E04)	e + $ {\mathrm{C}\mathrm{O}}_{2}^{+} $ $\Rightarrow $ CO + O	2.0 × 10–11Te–0.5Tg–1	[18]
(E05)	e + $ {\mathrm{C}\mathrm{O}}_{4}^{+} $ $\Rightarrow $ CO2 + O2	1.61 × 10–13Te–0.5	[18]
(E06)	e + $ {\mathrm{C}}_{2}{\mathrm{O}}_{2}^{+} $ $\Rightarrow $ 2CO	4.0 × 10–13Te–0.34	[18]
(E07)	e + $ {\mathrm{C}}_{2}{\mathrm{O}}_{3}^{+} $ $\Rightarrow $ CO2 + CO	5.4 × 10–14Te–0.7	[18]
(E08)	e + $ {\mathrm{C}}_{2}{\mathrm{O}}_{4}^{+} $ $\Rightarrow $ 2CO2	2.0 × 10–11Te–0.5Tg–1	[18]
(E09)	e + O2 + O2 $\Rightarrow $ $ {\mathrm{O}}_{2}^{-} $ + O2	2.2 × 10–41(300/Tg)1.5exp(-600/Tg)	[52]
(E10)	e + O + O2 $\Rightarrow $ O– + O2	1.0 × 10–43exp(300/Tg)	[52]
(E11)	e + O3 + O2 $\Rightarrow $ $ {\mathrm{O}}_{3}^{-} $ + O2	4.6 × 10–40	[52]
(E12)	e + O+ + M $\Rightarrow $ O + M	6.0 × 10–39(Te × 38.67)–1.5	[57]
(E13)	e + $ {\mathrm{O}}_{2}^{+} $ $\Rightarrow $ 2O	6.0 × 10–13Te–0.5(1/Tg)0.5	[21]
(E14)	e + $ {\mathrm{O}}_{2}^{+} $ + M $\Rightarrow $ O2 + M	6.0 × 10–39(Te × 38.67)–1.5	[57]
(E15)	e + $ {\mathrm{O}}_{2}^{+} $ + e $\Rightarrow $ O2 + e	1.0 × 10–31(Te × 38.67)–4.5	[57]
(E16)	e + O+ + e $\Rightarrow $ O + e	7.2 × 10–32(Te × 38.67)–4.5	[57]
(E17)	e + $ {\mathrm{O}}_{4}^{+} $ $\Rightarrow $ 2O2	2.25 × 10–13Te–0.5	[18]
(E18)	e + $ {\mathrm{O}}_{5}^{+} $ $\Rightarrow $ O2 + O3	5.0 × 10–12(Te × 38.67)–0.6	[52]

表A3初始集合中由反应速率系数描述的电子碰撞反应, 其中T_e为电子温度, 单位是eV; T_g为气体温度, 单位是K; 速率系数的单位在二体或三体反应中分别是m³/s或m⁶/s
TableA3.Electron impact reactions described by rate coefficients in the original model. T_e is the electron temperature in eV and T_g is the gas temperature in K. The rate coefficients are in m³/s or m⁶/s for binary or ternary reactions.

序号	反应	反应速率系数	文献
(N01)	CO2 + O $ \Rightarrow$ CO + O2	2.8 × 10–17exp(–26500/Tg)	[21]
(N02)	CO + O2 $ \Rightarrow$ CO2 + O	4.2 × 10–18exp(–24000/Tg)	[21]
(N03)	CO2 + C $ \Rightarrow$ 2CO	1.0 × 10–21	[21]
(N04)	C + O2 $ \Rightarrow$ O + CO	3.0 × 10–17	[21]
(N05)	C + O + M $ \Rightarrow$ M + CO	2.14 × 10–41(Tg/300)–3.08exp(–2114/Tg)	[21]
(N06)	CO + M $ \Rightarrow$ O + C + M	1.52 × 10–10(Tg/298)–3.1exp(–129000/Tg)	[58]
(N07)	CO + O3 $ \Rightarrow$ CO2 + O2	4.0 × 10–31	[52]
(N08)	CO2 + CO2 $ \Rightarrow$ CO + O + CO2	3.91 × 10–16exp(–49430/Tg)	[59]
(N09)	C + CO + CO2 $ \Rightarrow$ C2O + CO2	6.3 × 10–44	[59]
(N10)	C2O + O $ \Rightarrow$ 2CO	5.0 × 10–17	[18]
(N11)	C2O + O2 $ \Rightarrow$ CO2 + CO	3.3 × 10–19	[18]
(N12)	O + O2 + CO2 $ \Rightarrow$ O3 + CO2	1.7 × 10–42Tg–1.2	[48]
(N13)	O + O + CO2 $ \Rightarrow$ O2 + CO2	3.81 × 10–42Tg–1exp(–170/Tg)	[48]
(N14)	O + CO + CO2 $ \Rightarrow$ 2CO2	1.6 × 10–45exp(–1510/Tg)	[48]
(N15)	O + CO + CO $ \Rightarrow$ CO2 + CO	6.54 × 10–45	[60]
(N16)	O + O2 + CO $ \Rightarrow$ CO2 + O2	6.51 × 10–48	[60]
(N17)	O + O + CO $ \Rightarrow$ O2 + CO	2.76 × 10–46	[60]
(N18)	O + O + O $ \Rightarrow$ O2 + O	6.2 × 10–44exp(–750/Tg)	[52]
(N19)	O + O + O2 $ \Rightarrow$ 2O2	1.3 × 10–44(Tg/300)–1exp(–170/Tg)	[52]
(N20)	O + O3 $ \Rightarrow$ 2O2	3.1 × 10–20Tg0.75exp(–1575/Tg)	[18]
(N21)	O2 + O3 $ \Rightarrow$ 2O2 + O	7.26 × 10–16exp(–11400/Tg)	[48]
(N22)	O2 + O + O2 $ \Rightarrow$ O3 + O2	8.61 × 10–43Tg–1.25	[48]
(N23)	O2 + O2 $ \Rightarrow$ O + O3	2.1 × 10–17exp(–498000/Tg)	[57]
(N24)	O2 + M $ \Rightarrow$ O + O + M	3.0 × 10–12Tg–1exp(–59380/Tg)	[57]

表A4初始集合中的中性粒子反应, 其中 T_g 为气体温度, 单位是 K; 速率系数的单位在二体或三体反应中分别是 m³/s 或 m⁶/s
TableA4.Reaction of neutrals in the original model. T_g is the gas temperature in K. The rate coefficients are in m³/s or m⁶/s for binary or ternary reactions.

序号	反应	文献		序号	反应	文献
(Y01)	e + CO2 $\Rightarrow $ $ {\mathrm{C}\mathrm{O}}_{2}^{+} $ + 2e	[50]		(Y11)	e + O3 $\Rightarrow $ $ {\mathrm{O}}_{2}^{-} $ + O	[50]
(Y02)	e + CO2 $\Rightarrow $ CO + O + e	[50]		(Y12)	e + O3 $\Rightarrow $ O2 + O–	[50]
(Y03)	e + CO2 $\Rightarrow $ CO + O–	[50]		(Y13)	e + O3 $\Rightarrow $ O + O2 + e	[53]
(Y04)	e + CO2 $\Rightarrow $ 2e + O + CO+	[50]		(Y14)	e + O3 $\Rightarrow $ $ {\mathrm{O}}_{2}^{+} $ + O + 2e	[53]
(Y05)	e + CO2 $\Rightarrow $ 2e + CO + O+	[50]		(Y15)	e + O2 $\Rightarrow $ 2 O + e	[50]
(Y06)	e + CO2 $\Rightarrow $ $ {\mathrm{O}}_{2}^{+} $ + C + 2e	[51, 52]		(Y16)	e + O2 $\Rightarrow $ O + O–	[50]
(Y07)	e + CO $\Rightarrow $ C + O–	[50]		(Y17)	e + O2 $\Rightarrow $ 2e + $ {\mathrm{O}}_{2}^{+} $	[50]
(Y08)	e + CO $\Rightarrow $ e + C + O	[50]		(Y18)	e + O $\Rightarrow $ 2e + O+	[50]
(Y09)	e + CO $\Rightarrow $ 2e + CO+	[50]		(Y19)	e + C $\Rightarrow $ 2e + C+	[50]
(Y10)	e + CO $\Rightarrow $ 2e + C+ + O	[50]

表B2简化集合中由碰撞截面描述的电子碰撞反应
TableB2.Electron impact reactions described by collision cross sections in the simplified model.

简化集合包含的粒子种类如表B1所列, 考虑到碰撞种类和反应速率系数计算方式的差异, 这些粒子构成的反应被划分为不同的碰撞反应子集, 如表B2—B5所列.

序号	反应	反应速率系数	文献
(F01)	e + $ {\mathrm{C}\mathrm{O}}_{2}^{+} $ $\Rightarrow $ C + O2	3.94 × 10–13Te–0.4	[21]
(F02)	e + $ {\mathrm{C}\mathrm{O}}_{2}^{+} $ $\Rightarrow $ CO + O	2.0 × 10–11Te–0.5Tg–1	[18]
(F03)	e + O3 + O2 $\Rightarrow $ $ {\mathrm{O}}_{3}^{-} $ + O2	4.6 × 10–40	[52]
(F04)	e + $ {\mathrm{O}}_{2}^{+} $ $\Rightarrow $ 2O	6.0 × 10–13Te–0.5(1/Tg)0.5	[21]

表B3简化集合中由反应速率系数描述的电子碰撞反应, 其中T_e为电子温度, 单位是eV; T_g为气体温度, 单位是K; 速率系数的单位在二体或三体反应中分别是m³/s或m⁶/s
TableB3.Electron impact reactions described by rate coefficients in the simplified model. T_e is the electron temperature in eV and T_g is the gas temperature in K. The rate coefficients are in m³/s or m⁶/s for binary or ternary reactions.

序号	反应	反应速率系数	文献
(M01)	CO2 + C $ \Rightarrow$ 2 CO	1.0 × 10–21	[21]
(M02)	C + O2 $\Rightarrow $ O + CO	3.0 × 10–17	[21]
(M03)	O + O2 + CO2 $\Rightarrow $ O3 + CO2	1.7 × 10–42Tg–1.2	[48]
(M04)	O + O + CO2 $\Rightarrow $ O2 + CO2	3.81 × 10–42Tg–1exp(–170/Tg)	[48]

表B4简化集合中的中性粒子反应, 其中, T_g 为气体温度, 单位是 K; 速率系数的单位在二体或三体反应中分别是 m³/s 或 m⁶/s
TableB4.Reaction of neutrals in the simplified model. T_g is the gas temperature in K. The rate coefficients are in m³/s or m⁶/s for binary or ternary reactions.

序号	反应	反应速率系数	文献
(H01)	O– + CO2 $ \Rightarrow $ O + CO2 + e	4.0 × 10–18	[48]
(H02)	O– + CO2 + CO $ \Rightarrow $ $ {\mathrm{C}\mathrm{O}}_{3}^{-} $ + CO	1.5 × 10–40	[61]
(H03)	O– + CO2 + O2 $ \Rightarrow $ $ {\mathrm{C}\mathrm{O}}_{3}^{-} $ + O2	3.1 × 10–40	[61]
(H04)	O– + CO2 + CO2 $ \Rightarrow $ $ {\mathrm{C}\mathrm{O}}_{3}^{-} $ + CO2	9.0 × 10–41	[52]
(H05)	$ {\mathrm{O}}_{2}^{-} $ + CO2 + O2 $ \Rightarrow $ $ {\mathrm{C}\mathrm{O}}_{4}^{-} $ + O2	4.7 × 10–41	[52]
(H06)	$ {\mathrm{O}}_{3}^{-} $ + CO2 $ \Rightarrow $ $ {\mathrm{C}\mathrm{O}}_{3}^{-} $ + O2	5.5 × 10–16	[18]
(H07)	O+ + CO2 $ \Rightarrow $ $ {\mathrm{O}}_{2}^{+} $ + CO	9.4 × 10–16	[18]
(H08)	O+ + CO2 $ \Rightarrow $ O + $ {\mathrm{C}\mathrm{O}}_{2}^{+} $	4.5 × 10–16	[18]
(H09)	C+ + CO2 $ \Rightarrow $ CO+ + CO	1.1 × 10–15	[18]
(H10)	CO+ + CO2 $ \Rightarrow $ $ {\mathrm{C}\mathrm{O}}_{2}^{+} $ + CO	1.0 × 10–15	[56]
(H11)	O– + CO $ \Rightarrow $ CO2 + e	5.5 × 10–16	[44]
(H12)	$ {\mathrm{C}\mathrm{O}}_{3}^{-} $ + CO $ \Rightarrow $ 2CO2 + e	5.0 × 10–19	[58]
(H13)	$ {\mathrm{O}}_{2}^{+} $ + C $ \Rightarrow $ CO+ + O	5.2 × 10–17	[18]
(H14)	$ {\mathrm{O}}_{2}^{+} $ + C $ \Rightarrow $ C+ + O2	5.2 × 10–17	[18]
(H15)	O– + C $ \Rightarrow $ CO + e	5.0 × 10–16	[57]
(H16)	$ {\mathrm{C}\mathrm{O}}_{2}^{+} $ + O $ \Rightarrow $ $ {\mathrm{O}}_{2}^{+} $ + CO	1.638 × 10–16	[52]
(H17)	$ {\mathrm{C}\mathrm{O}}_{2}^{+} $ + O $ \Rightarrow $ CO2 + O+	9.62 × 10–17	[18]
(H18)	$ {\mathrm{C}\mathrm{O}}_{4}^{-} $ + O $ \Rightarrow $ $ {\mathrm{C}\mathrm{O}}_{3}^{-} $ + O2	1.1 × 10–16	[18]
(H19)	$ {\mathrm{C}\mathrm{O}}_{4}^{-} $ + O $ \Rightarrow $ CO2 + O2 + O–	1.4 × 10–17	[18]
(H20)	$ {\mathrm{C}\mathrm{O}}_{4}^{-} $ + O $ \Rightarrow $ CO2 + $ {\mathrm{O}}_{3}^{-} $	1.4 × 10–16	[18]
(H21)	$ {\mathrm{C}\mathrm{O}}_{3}^{-} $ + O $ \Rightarrow $ CO2 + $ {\mathrm{O}}_{2}^{-} $	8.0 × 10–17	[58]
(H22)	$ {\mathrm{C}\mathrm{O}}_{2}^{+} $ + O2 $ \Rightarrow $ $ {\mathrm{O}}_{2}^{+} $ + CO2	6.4 × 10–17	[52]
(H23)	$ {\mathrm{C}\mathrm{O}}_{2}^{+} $ + O– $ \Rightarrow $ O + CO2	1.0 × 10–13	[62]
(H24)	$ {\mathrm{C}\mathrm{O}}_{2}^{+} $ + $ {\mathrm{O}}_{2}^{-} $ $ \Rightarrow $ CO + O2 + O	6.0 × 10–13	[44]
(H25)	$ {\mathrm{C}\mathrm{O}}_{2}^{+} $ + $ {\mathrm{C}\mathrm{O}}_{3}^{-} $ $ \Rightarrow $ 2CO2 + O	5.0 × 10–13	[58]
(H26)	$ {\mathrm{C}\mathrm{O}}_{2}^{+} $ + $ {\mathrm{C}\mathrm{O}}_{4}^{-} $ $ \Rightarrow $ 2CO2 + O2	5.0 × 10–13	[18]
(H27)	$ {\mathrm{C}\mathrm{O}}_{3}^{-} $ + $ {\mathrm{O}}_{2}^{+} $ $ \Rightarrow $ CO2 + O2 + O	3.0 × 10–13	[18]
(H28)	$ {\mathrm{O}}_{2}^{+} $ + $ {\mathrm{C}\mathrm{O}}_{4}^{-} $ $ \Rightarrow $ CO2 + 2O2	3.0 × 10–13	[18]
(H29)	O– + O3 $ \Rightarrow $ 2O2 + e	3.0 × 10–16	[44]
(H30)	O– + O3 $ \Rightarrow $ $ {\mathrm{O}}_{3}^{-} $ + O	8.0 × 10–16	[18]
(H31)	$ {\mathrm{O}}_{2}^{-} $ + O3 $ \Rightarrow $ $ {\mathrm{O}}_{3}^{-} $ + O2	4.0 × 10–16	[18]
(H32)	O– + O2 $ \Rightarrow $ O + e + O2	6.9 × 10–16	[52]
(H33)	O– + O $ \Rightarrow $ O2 + e	2.3 × 10–16	[21]
(H34)	$ {\mathrm{O}}_{2}^{-} $ + O $ \Rightarrow $ O2 + O–	3.31 × 10–16	[21]
(H35)	$ {\mathrm{O}}_{2}^{-} $ + O $ \Rightarrow $ O3 + e	3.3 × 10–16	[18]
(H36)	$ {\mathrm{O}}_{3}^{-} $ + O $ \Rightarrow $ $ {\mathrm{O}}_{2}^{-} $ + O2	2.5 × 10–16	[18]
(H37)	O–+ $ {\mathrm{O}}_{2}^{+} $ $ \Rightarrow $ O2 + O	2.6 × 10–14(300/Tg)0.44	[21]
(H38)	O– + $ {\mathrm{O}}_{2}^{+} $ $ \Rightarrow $ 3O	4.2 × 10–13(300/Tg)0.44	[21]
(H39)	$ {\mathrm{O}}_{2}^{-} $ + $ {\mathrm{O}}_{2}^{+} $ $ \Rightarrow $ 2O2	2.01 × 10–13(300/Tg)0.5	[21]
(H40)	$ {\mathrm{O}}_{2}^{-} $ + $ {\mathrm{O}}_{2}^{+} $ $ \Rightarrow $ O2 + 2O	4.2 × 10–13	[21]

表B5简化集合中的离子-中性和离子-离子反应, 其中T_g为气体温度, 单位是K; 速率系数的单位在二体或三体反应中分别是m³/s或m⁶/s
TableB5.Ion-neutral and ion-ion reactions in the simplified model. T_g is the gas temperature in K. The rate coefficients are in m³/s or m⁶/s for binary or ternary reactions.