摘要: 采用Voronoi方法构建了50, 130和200 μm三种晶粒度的高纯铜靶板, 在晶界处随机预制损伤成核点, 建立了平板撞击高纯铜靶板的二维轴对称计算模型, 研究了晶粒度和加载应力对高纯铜层裂宏观力学响应和细观损伤演化的影响. 基于自由面速度剖面特征分析, 揭示了晶粒度和加载应力幅值对Pull-back速度回跳点位置、速度回跳斜率及回跳幅值的影响规律, 论证了层裂强度与损伤区拉伸应力峰值相对应 本质上表征微损伤早期长大临界应力; 基于损伤演化云图特征分析, 讨论了长大和聚集过程中微孔洞周围局域化塑性应变场的演变, 揭示了晶粒度和加载应力对微孔洞聚集和应力松弛行为的影响. 计算结果再现了层裂实验中材料内部的微孔洞长大、聚集的细观物理过程, 进一步揭示其与宏观力学响应之间的内禀关系, 这对认识层裂损伤演化机制和理论模型构建具有重要的意义.
关键词: 层裂 /
晶粒度 /
数值模拟 /
损伤演化 English Abstract Numerical simulation on dynamic damage evolution of high pure copper with different grain sizes Lin Qian 1 ,Xie Pu-Chu 1 ,Hu Jian-Bo 2 ,Zhang Feng-Guo 3 ,Wang Pei 3 ,Wang Yong-Gang 1 1.Key Laboratory of Impact and Safety Engineering, Ministry of Education of China, Ningbo University, Ningbo 315211, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 11972202) and the National Defense Basic Scientific Science Challenge Project, China (Grant No. TZ2018001)Received Date: 16 April 2021Accepted Date: 15 May 2021Available Online: 08 October 2021Published Online: 20 October 2021Abstract: High-purity (HP) copper targets with grain sizes of 50, 130 and 200 μm are constructed by using the Voronoi method. Damage nucleation points are randomly prefabricated at the grain boundaries. A two-dimensional axisymmetric finite element model is established to simulate the spallation experiment of HP copper target. The effects of grain size and loading stress on the macro- mechanical response and meso-damage evolution of HP copper spallation are studied and compared with the relevant experimental results. Based on the analysis of free surface velocity profiles, the effects of grain size on the location of pull back velocity rebound point, velocity rebound slope and velocity rebound amplitude are revealed. It is demonstrated that the spalling strength corresponds to the peak value of tensile stress in the damage zone, which essentially represents the critical stress of micro damage nucleation or early growth. Based on the characteristic analysis of damage evolution nephogram, the evolution process of localized plastic strain field around the micro-voids in the growth and coalescence process is reproduced, and the strong dependence of micro-void coalescence behavior on grain size is clarified. The loading stress amplitude has little effect on the location of pull back velocity rebound point, but has a significant effect on the growth and coalescence behavior of micro-voids. The slope and amplitude of pull back velocity rebound increase with loading stress increasing, which is consistent with the relevant experimental result. With the increase of the loading stress, the micro-voids grow from independent growth to coalescence, thus forming spalling surface. The physical process of damage evolution determines the wave oscillation characteristics after the pull-back rebound point. The numerical simulation results reproduce the physical process of damage evolution and its influence on the macroscopic mechanical response, which is of great significance for further understanding spall damage evolution mechanism and theoretical model construction.Keywords: spall fracture /grain size /numerical simulation /damage evolution 全文HTML --> --> --> 1.引 言 强冲击载荷下延性金属层裂是一个复杂的损伤演化过程, 在细观层次上它涉及微孔洞成核、长大和聚集过程, 最后形成宏观的层裂面[1 -3 ] . 国内外****对延性金属层裂问题已进行了系统、深入的实验研究, 重点关注了外载荷条件、微观组织结构的影响[4 -10 ] . 绝大多数层裂模型主要描述微孔洞成核、长大过程[1 ,11 ] , 关注微孔洞成核率及分布效应[12 ] 、微孔洞表面的位错发射[13 ] 、微孔洞长大速率依赖性[14 ] 、惯性效应[15 ,16 ] 等众多因素的影响, 但涉及多个微孔洞聚集行为的理论描述仍然比较少. 少量****尝试借助逾渗理论来考虑微孔洞簇之间相互作用[17 ,18 ] , 这也是在平均场理论上进行建模. 事实上, 微孔洞聚集行为具有高度的局域化变形特征, 将控制应力松弛速率以及层裂过程中消耗的总能量. 迄今还无法用实验手段来直接观测材料内部微孔洞长大、聚集过程.[19 -21 ] . 然而, 分子动力学模拟技术涉及的时空尺度非常小, 与实验结果很难进行对比. 为此, Becker等[22 -24 ] 尝试采用随机撒成核点的有限元方法对金属层裂行为开展数值模拟研究, 揭示了微孔洞长大、聚集过程中应变局域化流场和应力场的演化, 但未考虑材料晶粒度对微孔洞潜在成核点数量的影响. 许多实验结果已显示材料层裂损伤演化特性强烈依赖于晶粒度. Trivedi等[25 ] 通过实验分析了冲击加载强度在4—21 GPa之间不同晶粒尺寸高纯铝材料的损伤情况, 在较低冲击应力下晶粒度对层裂强度影响较弱, 而在高冲击应力下层裂强度随着晶粒度增大而增大. Schwartz等[26 ] 研究晶粒尺寸对高纯铜层裂强度的影响, 发现随着晶粒度增大层裂强度增大. Escobedo等[6 ] 对30, 60, 100和200 μm四种晶粒度的初始层裂高纯铜样品内部损伤分布及其对自由面速度剖面的影响规律进行了较系统研究, 揭示晶粒度对层裂强度的影响微弱, 但对自由面提前回跳点之后波形有比较显著的影响, 阐明了晶粒度明显影响微孔洞之间聚集行为. Chen等[27 ] 研究了78, 273和400 μm三种晶粒度的高纯铜层裂行为, 结果也显示晶粒度对层裂强度的影响微弱, 但随着晶粒度增大, 断裂机制从沿晶断裂向穿晶断裂转变. 张凤国和周洪强[28 ] 认为晶粒度的影响反映在材料内部潜在的孔洞成核总数上, 层裂损伤演化物理模型中引入了晶粒尺寸影响, 计算结果与相关实验结果定性上符合较好. 综上所述, 人们关于晶粒度对材料层裂行为的影响还没有取得共识, 晶粒尺寸的影响与冲击加载应力幅值的影响两者是耦合的. Schwartz等[26 ] 和Escobedo等[6 ] 的层裂实验得到晶粒度对层裂强度的影响规律不一致, 其原因应该是与加载应力幅值差别较大有关. 目前, 关于晶粒度对细观损伤演化过程的影响, 由于缺乏高时空分辨的直接观测手段, 这方面的实验研究工作非常少. 本文拟开展这方面的数值模拟工作, 进一步揭示晶粒度对损伤演化过程的影响规律和内在机制.[26 ] , 采用不同回火温度和持续时间, 可以实现对材料平均晶粒尺寸的调控, 但是当平均晶粒尺寸比较小时, 晶粒尺寸分布非常不均匀, 往往不是等轴晶, 而平均晶粒尺寸较大时, 晶粒尺寸分布相对比较均匀, 且绝大多数晶粒是等轴晶. 本文采用Voronoi方法构建了不同晶粒度的高纯铜几何模型, 在参考有关文献实验结果的基础上, 选择为50, 130和200 μm三种平均晶粒尺寸, 并在晶粒交界处随机布置一定数量的潜在成核点, 从而建立了平板撞击条件下高纯铜层裂损伤演化二维轴对称细观有限元计算模型, 重点关注晶粒度和加载应力对微孔洞长大、聚集的影响, 揭示微孔洞聚集相关的局域化应变场演化和应力松弛行为, 探讨其与自由面速度波剖面典型特征之间的内禀关系.2.有限元模型 采用Voronoi方法在Abaqus有限元软件中分别建立50, 130和200 μm三种不同晶粒尺寸高纯铜样品, 为了减少计算规模, 这里建立了平板撞击靶板的二维轴对称有限元模型, 如图1 所示, 其中飞片和靶体材料都是高纯铜, 飞片和靶体的宽度均为400 μm. 为了模拟一维应变条件, 对飞片和靶体的边界施加 Y 方向位移约束条件. 在对称碰撞条件下, 当飞片和样品的厚度之比为1∶2时, 由波传播分析易知, 靶体厚度中心层附近区域拉伸应力持续时间最长, 损伤主要集中在此区域, 这里选取400 μm宽, 400 μm长的正方形区域作为典型损伤区域(图1 中红色方框内). 在损伤区域内多个晶界交汇点处随机撒布半径为1 μm微孔洞作为初始成核源. 在预制微孔洞内填充了球形杂质或者第二相粒子以避免压缩冲击波作用下被压溃而发生网格畸变. 填充物在压缩力学性能与基体材料一致, 但其拉伸强度非常小, 仅设为10 MPa. 有限元计算中网格划分控制尺寸为0.5 μm, 网格单元类型为轴对称线性缩减积分单元CAX4 R, 网格数量134万, 计算中采用了ALE算法防止网格畸变. 微孔洞成核源网格划分局部放大图如图1 , 从中可以看到整个模型的网格划分是比较规则的, 可以比较好地保证计算精度.图 1 三种晶粒尺寸高纯铜靶体层裂实验的几何建模Figure1. Geometric modeling of high purity copper sample with three grain sizes.$ {\boldsymbol{\sigma }}_{ij} $ 为应力张量; P 为静水压力; $ {\boldsymbol{S}}_{ij} $ 为偏应力张量. 当von Mises屈服函数$\phi = \dfrac{1}{2}{S}_{ij}{S}_{ij}- \dfrac{{\sigma }_{Y}^{2}}{2} \leqslant 0$ 时, ${S}_{ij} = 2 G({\varepsilon }_{ij}-{\varepsilon }_{v})$ ; 而当$\phi = \dfrac{1}{2}{S}_{ij}{S}_{ij} - \dfrac{{\sigma }_{Y}^{2}}{2} > 0$ 时, ${S}_{ij}=\dfrac{{\sigma }_{Y}}{{S}^{*}}{S}_{ij}$ , 其中${s}^{*}={\left(\dfrac{2}{3}{S}_{ij}{S}_{ij}\right)}^{1/2}$ , 这里$ {\varepsilon }_{v} $ 为体积应变, G 为剪切模量, $ {\sigma }_{Y} $ 为屈服应力. $ {\sigma }_{Y} $ 满足Johnson-Cook(J-C)硬化准则[29 ] , 即${\varepsilon }_{{\rm{p}}}$ 是等效塑性应变, ${\dot{\varepsilon }}_{{\rm{p}}}$ 是等效塑性应变率, $ {\dot{\varepsilon }}_{0} $ 是参考等效应变率, A , B , n , C 和m 是材料参数. 采用J-C损伤断裂模型[29 ] 模拟微孔洞聚集行为, 即$ {\sigma }^{*}=-p/{\sigma }_{\mathrm{e}\mathrm{q}} $ , $ {\sigma }_{\mathrm{e}\mathrm{q}} $ 为Mises等效应力, d 1 , d 2 , d 3 , d 4 , d 5 为材料损伤参数. 静水压力P 由Mie-Grüneisen状态方程给出:$\eta = {\rho }/{{\rho }_{0}}{-1}$ , $ {\rho }_{0} $ 是材料初始密度, $ \rho $ 为当前密度, K 是体积模量, s 是一个参数, $ {\varGamma }_{0} $ 是材料的Grüneisen系数, $ {E}_{\mathrm{m}} $ 为材料比内能. 高纯铜的J-C本构、损伤断裂及状态方程参数如表1 所列.ρ /(kg·m–3 )A /MPaB /MPaC m n $ {\dot{\varepsilon }}_{0} $ T room T melt 8910 90 292 0.025 1.09 0.31 1 300 1356 $ {c}_{0} $/(m·s–1 ) s $ {\varGamma }_{0} $ $ G/\mathrm{G}\mathrm{P}\mathrm{a} $ d 1 d 2 d 3 d 4 d 5 3910 1.51 2 47 1.08 4.89 3.03 0.014 1.12
表1 高纯铜J-C本构、损伤断裂及状态方程参数[29 ] Table1. Parameters of equation of state for high-purity copper[29 ] .3.计算结果与分析 23.1.模型可靠性检验 3.1.模型可靠性检验 基于裴晓阳等[8 ] 的高纯铜层裂实验数据, 对构建的层裂实验损伤演化细观有限元计算模型进行可靠性检验, 具体的实验条件: 高纯铜的平均晶粒度50 μm, 飞片和靶板材料均为高纯铜, 厚度分别为3.10 mm和6.10 mm, 飞片撞击速度198 m/s. 实验中采用全光纤激光干涉测试技术对靶板自由面速度时程进行了实时监测. 计算边界条件与实验保持一致. 图2 给出了计算得到的自由面速度时程与实验结果的对比, 两者符合比较好, 这表明层裂损伤演化细观有限元模型以及采用的材料参数具有较好的可靠性.图 2 计算得到自由面速度时程曲线与实验结果的对比Figure2. Comparison of simulated free surface velocity profile with the experimental result.3.2.晶粒度的影响 -->3.2.晶粒度的影响 33.2.1.自由面速度 -->3.2.1.自由面速度 为了适当减小计算规模, 这里飞片和靶板的厚度分别选择为1和2 mm, 飞片撞击速度设定为90 m/s, 在靶板内部产生损伤状态, 考察晶粒度对损伤演化的影响. 图3 给出了三种晶粒度高纯铜靶体的自由面速度时程曲线, 结果显示: 随着晶粒度的增加, pull-back速度幅值$ \Delta {u}_{1} $ 增大, pull-back回跳点之后速度回跳斜率 $ {\dot{u}}_{\mathrm{f}\mathrm{s}} $ 稍有减小; 与50 μm相比, 130和200 μm高纯铜靶板的pull-back速度回跳幅值$ \Delta {u}_{2} $ 显著减小.图 3 不同晶粒度高纯铜靶体的自由面速度时程曲线及局部放大曲线Figure3. Free surface velocity profiles of HP copper with different grain sizes.$ \Delta {u}_{1} $ , Novikov[30 ] 在声学近似条件下给出了计算层裂强度公式:$ {\rho }_{0} $ 是材料密度, $ {c}_{0} $ 是材料的体积声速, 计算得到的不同晶粒度高纯铜层裂强度变化范围是0.85—1.00 GPa, 与裴晓阳等[8 ] 和Chen等[27 ] 给出的实验结果基本一致. 计算结果表明层裂强度随着晶粒度增大而增大, 这与Schwartz等[25 ] 和Trivedi等[26 ] 的实验结果在定性上保持一致. 图4 给出了50和200 μm晶粒度高纯铜靶板内部损伤区域典型单元的应力时程曲线, 同时也给出了没有损伤情况下的结果, 结果显示: 拉伸应力首先达到一个峰值, 随即开始应力松弛. 应力松弛的主导机制是损伤演化, 而损伤演化可分为微孔洞成核、长大和聚集几个阶段. 事实上, 一旦微孔洞成核之后, 微孔洞的弹塑性长大伴随着能量耗散, 造成了应力快速松弛, 从而导致了pull-back信号产生. 由此推断pull-back速度幅值$ \Delta {u}_{1} $ 与材料内部发生微孔洞成核与早期长大之间是强关联的, 层裂强度应该与损伤区拉伸应力峰值相对应. 下面首先从时间轴上来进行验证, 图4 中给出典型单元的拉伸应力峰值时间对应0.8 μs, 再根据典型单元距离自由面距离(约1 mm)除以高纯铜塑性波传播速度(约3978 m/s)得到损伤中心区应力波传播到自由面需要时间约0.25 μs, 最大拉伸应力波到达自由面的时间约在1.05 μs, 这与图3 中给出的pull-back回跳点对应时间是自洽的. 再从应力幅值来验证, 图4 给出拉伸应力峰值为1.15—1.25 GPa, 比基于pull-back速度幅值$ \Delta {u}_{1} $ 计算的层裂强度要大一些, 这是因为应力波从损伤区向自由面传播过程中发生了一定程度的衰减[31 ] , 但在简化层裂强度计算公式(1 )式中没有考虑这些因素的影响, 需要进行修正. Kanel[32 ] 提出了考虑层裂片厚度影响的修正公式:图 4 不同晶粒度高纯铜损伤区典型单元的应力时程曲线Figure4. Stress profiles of elements in the damage zone of HP copper with different grain sizes.$ {h}_{\mathrm{s}\mathrm{p}} $ 是完全层裂时层裂片厚度或初始损伤时损伤区到自由面之间距离; $ {c}_{l} $ 是纵波波速; $ {\dot{u}}_{f1} $ 是卸载段自由面速度变化率, 计算得到自由面速度的修正值$ \delta $ 约为12 m/s, 修正后的层裂强度为1.06—1.21 GPa, 这与拉伸应力峰值已非常接近, 偏差率在5%以内. 综上, 通过层裂实验的细观有限元模拟, 验证了层裂强度在物理内涵上代表了材料所承受的最大拉伸应力, 在细观层次上代表微孔洞成核和早期长大的临界应力. 回跳速度斜率$ {\dot{u}}_{f2} $ 与材料内部的损伤演化速率之间是相互强关联的, Kanel等[5 ] 基于特征线方法建立了$ {\dot{u}}_{f2} $ 和材料内部损伤演化速率${\dot V_V}$ 的定性关联, 即A 和B 为材料参数. 损伤演化速率决定了应力松弛速率, 从图4 中可以看到应力松弛率随着晶粒度增大而减小, 表明晶粒度小的靶板内部损伤演化速率高, 这与图3 自由面速度曲线上$ {\dot{u}}_{f2} $ 随着晶粒度的变化关系是一致的. 最后讨论一下速度回跳幅值$ \Delta {u}_{2} $ , 通常以$\varphi =\Delta {u}_{2}/{\Delta }{u}_{1}$ 来反映材料内部的损伤程度, 下面以图5 给出的X -t 波系图来进行简单分析. 飞片和靶板自由面反射的稀疏波首先在a 点相遇, 在靶板中心区域开始产生拉伸应力, 在b 点处材料内部开始出现初始微损伤, 稀疏波在微损伤区发生部分透射和部分反射, 反射形成压缩波到达自由面后速度开始回跳, 在c 点处材料内部损伤面形成, 后续稀疏波在损伤面全部反射成压缩波. 如果在a 点之后随即发生瞬时断裂形成完全层裂面, 则后续稀疏波在层裂面全部反射成压缩波, $ \varphi $ 应该接近于1, 这与许多脆性材料的层裂实验结果是一致. 事实上, 损伤演化是一个过程, 从a 点到c 点是一个损伤发展过程, 靶板自由面反射的左行稀疏波一部分穿越了损伤区, 一部分在损伤区反射形成较弱的压缩波, 从而导致$ \varphi $ 低于1; 损伤发展速度越快, 损伤程度越严重, 损伤区的波阻抗越低, 则损伤区反射的压缩波越强, 导致$ \varphi $ 越接近1. 以上从宏观角度讨论和推断了自由面速度典型特征与损伤演化之间的内在关系, 下面将基于损伤演化物理图像来进一步阐明.图 5 层裂实验中X -t 波系图Figure5. Schematic diagram of X - t wave interactions in spallation experiment.3.2.2.损伤演化分析 -->3.2.2.损伤演化分析 数值模拟结果可以提供丰富的损伤演化时空信息, 这在实验中是难以获得的. 图6 给出了90 m/s飞片速度撞击条件下不同晶粒度靶体内部损伤时空演化结果, 图中云图显示的是等效塑性应变. 微孔洞长大和聚集行为都强烈依赖于等效塑性应变, 因此可以借助等效塑性应变云图来间接反映损伤演化过程. 在T = 0.81 μs时刻, 当飞片后表面和靶体自由面两束稀疏波在靶体中间位置相遇时, 产生拉伸应力促使微孔洞开始长大, 微孔洞周围出现塑性变形区, 处于早期长大阶段; 在T = 0.92 μs时刻, 微孔洞在拉伸载荷作用下持续长大, 对于晶粒度50 μm的高纯铜, 观察到微孔洞周围的塑性应变场开始相互交叠, 形成了局域化塑性变形区, 而晶粒度130和200 μm的高纯铜内部微孔洞还处于独立长大阶段; 在T = 1 μs时刻, 晶粒度50 μm高纯铜内部的微孔洞之间形成了贯通性塑性变形区, 损伤已比较严重, 对于130和200 μm晶粒度高纯铜, 仅观察到部分微孔洞之间出现局域化塑性变形区, 还处于聚集初始阶段. 当T = 1.1 μs时刻, 对于50 μm高纯铜, 局域化塑性变形区出现贯通断裂面, 形成了层裂面, 但130和200 μm高纯铜内部微孔洞之间出现比较明显的局域化塑性变形区, 但没有形成贯通. 综上分析, 晶粒尺寸对微孔洞之间的聚集行为产生了显著影响, 对于晶粒度较小的高纯铜, 内部初始成核点的数量较多, 在微孔洞长大过程中其周围的塑性应变场易发生相互叠加, 形成局域化塑性变形区, 出现了贯通性断裂面, 从而形成最终的层裂面; 对于晶粒尺寸大的高纯铜, 内部初始成核点的数量较少, 微孔洞周围塑性应变场相互作用比较困难, 微孔洞主要是独立长大, 聚集的影响相对较弱.图 6 不同时刻下不同晶粒度高纯铜的细观损伤演化云图Figure6. Mesoscopic damage distribution of HP copper with different grain sizes at different times.D . 在实验中, 人们通过对层裂实验的靶板进行软回收, 然后对其内部损伤进行细观统计分析, 仅可以得到靶板内部损伤状态在空间上分布特征. 目前还无法用实验手段直接观测到材料内部微孔洞长大及聚集过程, 难以给出损伤度随着时间的演化行为, 而数值模拟恰好填补这个空白. 基于数值模拟结果, 采用Matlab软件对微孔洞长大过程中体积改变进行统计分析, 图7 给出了不同晶粒度的高纯铜内部损伤度演化时程曲线, 结果显示: 相比于130和200 μm, 50 μm晶粒度的高纯铜内部损伤发展较快, 并且出现了二次增长的现象. 基于图6 给出的损伤演化云图, 可以推断此二次增长现象是由于损伤演化后期微孔洞之间的聚集和贯通引起的.图 7 不同晶粒度高纯铜内部损伤度时程曲线Figure7. Damage degree evolution profiles of HP copper with different grain sizes.[33 ,34 ] . 对比分析图3 、图6 和图7 , 结果显示: 1) 与130和200 μm相比, 50 μm晶粒度高纯铜在拉伸载荷作用下其内部微孔洞成核点较多, 在孔洞长大过程中容易与相邻孔洞形成塑性流动带, 引起宏观损伤演化速率增大, 从而导致了应力松弛发生时间较早, 并且应力松弛的速率也较快, 由此引起了自由面速度回跳提前和回跳速度斜率增大; 2) 50 μm晶粒度高纯铜内部微孔洞周围塑性场快速交叠, 微孔洞加速长大, 很快形成了局域化损伤带, 从而阻止了大部分稀疏波穿越损伤带, 更多的稀疏波传播到损伤区域反射形成压缩波, 导致二次压缩波峰值较高, 即$ \varphi $ 值较高; 而130和200 μm晶粒度高纯铜内部在较长时间内处于孔洞独立长大阶段, 没有完全形成损伤带, 比较多的稀疏波穿越损伤区, 被损伤区反射的稀疏波较少, 导致二次压缩波峰值较低, 即$ \varphi $ 值较低. 由此来看, 在3.2.1 节讨论的靶板自由面速度和内部应力时程的典型特征对晶粒度的依赖性在内在机制主要归因于晶粒度对微孔洞聚集行为的影响. 因此, 微孔洞之间的聚集行为在整个损伤演化中占据重要地位.3.3.加载应力幅值的影响 -->3.3.加载应力幅值的影响 33.3.1.自由面速度 -->3.3.1.自由面速度 以50 μm晶粒度高纯铜靶体为例, 通过改变飞片撞击速度V 来调整加载应力幅值, 这里选择了60, 70, 80, 90, 和100 m/s五个飞片速度, 对应的加载应力分别为0.94, 1.12, 1.30, 1.48, 和1.66 GPa. 图8 给出了不同撞击速度下50 μm晶粒度高纯铜靶体自由面速度时程曲线. 为了对比分析需要, 把自由面速度峰值平台平移放在同一高度之后pull-back信号局部放大, 见图8 中右上角的局部放大图. 在撞击速度60 m/s条件下, 自由面速度剖面上没有观察到明显的pull-back信号, 此时加载应力低于层裂强度, 随着飞片撞击速度的增加, pull-back信号越来越明显. 然而, 飞片撞击速度对pull-back速度幅值$ \Delta {u}_{1} $ 几乎没有影响, 但对pull-back回跳点之后的波形有显著影响, pull-back回跳斜率$ {\dot{u}}_{f2} $ 和速度回跳幅值$ \Delta {u}_{2} $ 都随着撞击速度的增加而增大, 这里仿真结果与裴晓阳等[8 ] 给出的实验结果在定性上是一致的. 最后讨论加载应力与波形振荡周期之间关系. 当加载应力(V = 60 m/s)较低, $ \Delta t $ 约为1 μs, 即应力波在整个靶板来回传播需要的时间($\Delta t= {2{h}_{0}}/{D}$ , h 0 =2 mm为靶板厚度, D 为应力波传播速度, 约4000 m/s), 推测此时靶板基本处于无损伤状态; 随着加载应力增大(V = 70或80 m/s), pull-back回跳点之后的波形振荡较为复杂, 可明显区分为两个阶段, 见图8 所示, 第I阶段波形振荡幅值低且周期Δt 1 短, 而第II阶段幅值较高且周期Δt 2 长; 根据波形振荡特征, 可以推测靶板处于初始损伤状态, 即加载应力不足以在靶板中产生完全层裂面, 只能产生损伤区. 由于损伤区的波阻抗较低, 来自靶板自由面反射的左行稀疏波传播到损伤区会发生透射和反射, 部分反射形成右行压缩波, 产生第I阶段较弱的pull-back速度回跳信号, 而当透射的稀疏波在靶板前自由面反射的压缩波到达后自由面时即产生第II阶段较强的波形振荡信号, 因此, 总周期(Δt 1 + Δt 2 )应该与应力波在靶板来回传播时间保持一致; 随着加载应力进一步增大(V = 90或100 m/s), 自由面速度剖面上呈现稳定的波形振荡信号, 振荡周期约为0.5 ms, 这与应力波在层裂面和自由面之间来回传播的时间一致, 即$\Delta t= {2{h}_{\mathrm{s}}}/{D}$ , h s = 1 mm为层裂片厚度. 图9 给出了不同撞击速度下高纯铜靶体损伤区典型单元的应力时程曲线, 图中显示: 1) 随着撞击速度增大, 加载压缩应力峰值增大, 而拉伸应力峰值保持不变, 再次验证了拉伸应力峰值与pull-back速度幅值$ \Delta {u}_{1} $ 之间的对应关系; 2)随着撞击速度增大, 拉伸应力峰值之后的应力松弛速率增大, 如前所述应力松弛速率取决于损伤发展速率, 由此也再次验证了自由面速度剖面上pull-back信号之后的速度回跳斜率与损伤发展速率之间的对应关系; 3)当撞击速度较低时, 出现了二次压缩应力, 当靶板处于初始损伤状态, 损伤没有完全实现对拉伸应力的松弛, 随着速度增大, 损伤越来越严重, 二次压缩应力不断减小.图 8 不同撞击速度下高纯铜自由面速度时程曲线及局部放大Figure8. Free surface velocity profiles of HP copper at different impact velocities.图 9 不同撞击速度下高纯铜损伤区单元应力时程曲线Figure9. Stress profiles of damaged elements in HP copper spallation experiment.3.3.2.损伤演化分析 -->3.3.2.损伤演化分析 图10 给出了不同撞击速度下靶板内部细观损伤演化的物理过程. 当T = 0.81 μs时, 微孔洞处于早期长大阶段, 撞击速度对这一阶段影响比较微弱, 微孔洞周围出现了微弱的塑性变形区, 对应力波传播的影响非常有限; 当T = 1.0 μs时, 当60和70 m/s较低撞击速度下, 微孔洞直径和周围塑性变形场明显增大, 但仍然处于独立长大阶段, 而当撞击速度进一步增大, 明显观察到部分微孔洞之间的塑性应变场相互交叠, 形成了局域化塑性变形区, 但没有形成完成层裂面; 当T = 1.2 μs时, 在撞击速度60—80 m/s条件下, 多个区域观察到微孔洞之间发生相互作用, 并且微孔洞之间聚集行为表现出一定的随机性, 而当撞击速度提高到90和100 m/s条件下, 观察微孔洞之间的塑性应变局域化行为已非常严重, 应变局域化抑制了周围孔洞的增长, 进一步观察断裂面沿着局域化形变带发展, 导致了微孔洞之间完全贯通形成层裂面. 由此看来, 加载应力对孔洞长大和聚集行为产生了显著的影响, 在靶板中产生了不同的损伤状态, 当应力波在损伤区传播时, 损伤状态对波传播的影响必然体现在自由面速度剖面上.图 10 不同撞击速度下高纯铜细观损伤演化物理过程 (a) V = 60 m/s; (b) V = 70 m/s; (c) V = 80 m/s; (d) V = 90 m/s; (e) V = 100 m/sFigure10. Microscopic damage evolution process of high-purity copper under different impact velocities: (a)V = 60 m/s; (b) V = 70 m/s; (c) V = 80 m/s; (d) V = 90 m/s; (e) V = 100 m/s.4.结 论 本文构建了不同晶粒度的高纯铜层裂损伤演化细观有限元模型, 研究了晶粒度和加载应力幅值对高纯铜层裂特性的影响, 讨论了宏观力学响应与损伤演化动力学之间的关联性. 加载应力恒定条件下, 高纯铜的层裂强度随着晶粒度增大而增大, 而损伤演化速率随着晶粒度增大而减小, 本质上归因于晶粒度对微孔洞聚集行为的影响; 晶粒度保持不变条件下, 随着加载应力幅值增加, 高纯铜的层裂强度基本不变, pull-back回跳斜率和回跳幅值均增大, 微孔洞从独立长大演变到多孔洞聚集形成层裂面, 损伤演化细观动力学过程决定了pull-back回跳点之后波形振荡的典型特征. 
图 1 三种晶粒尺寸高纯铜靶体层裂实验的几何建模
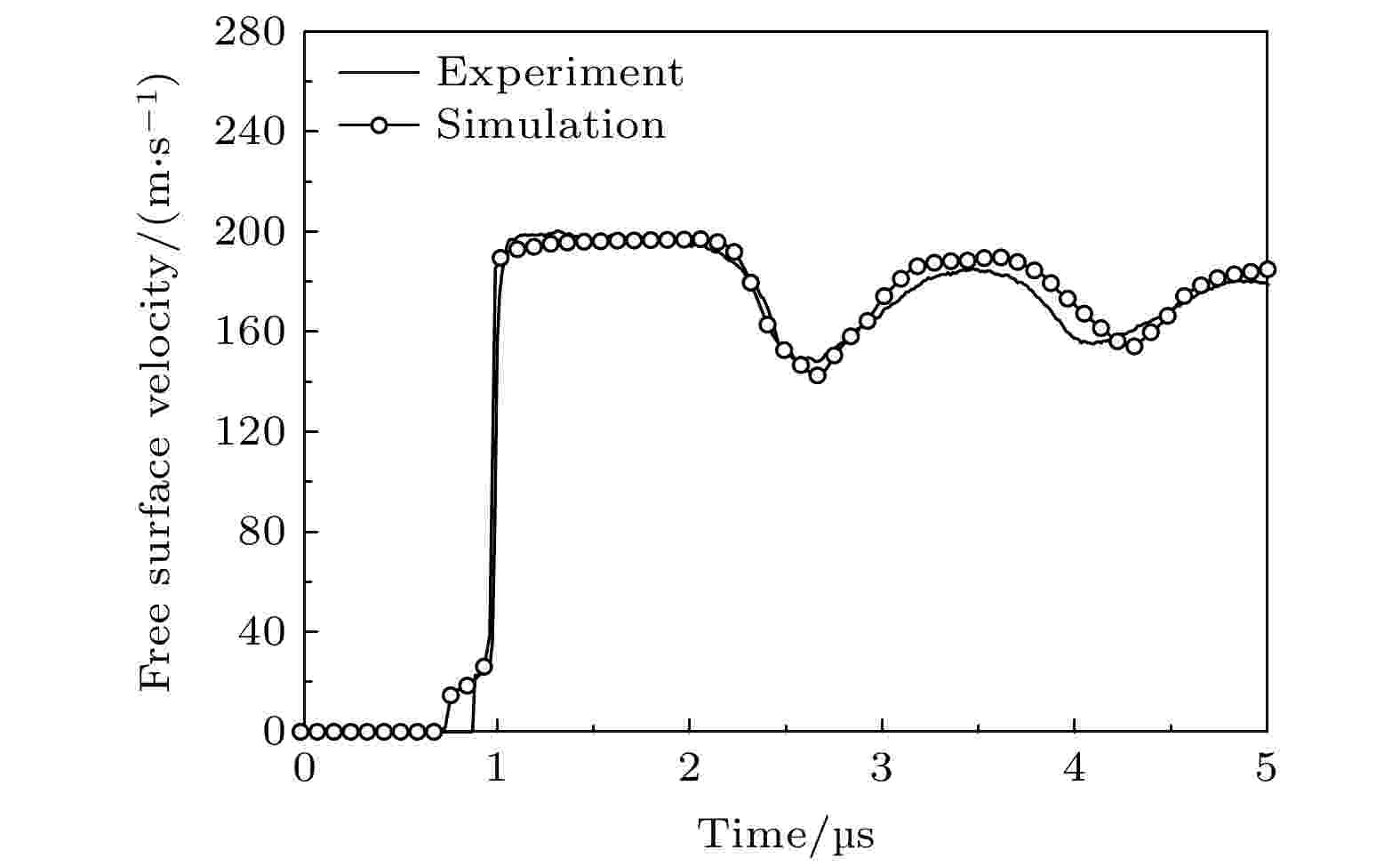图 2 计算得到自由面速度时程曲线与实验结果的对比
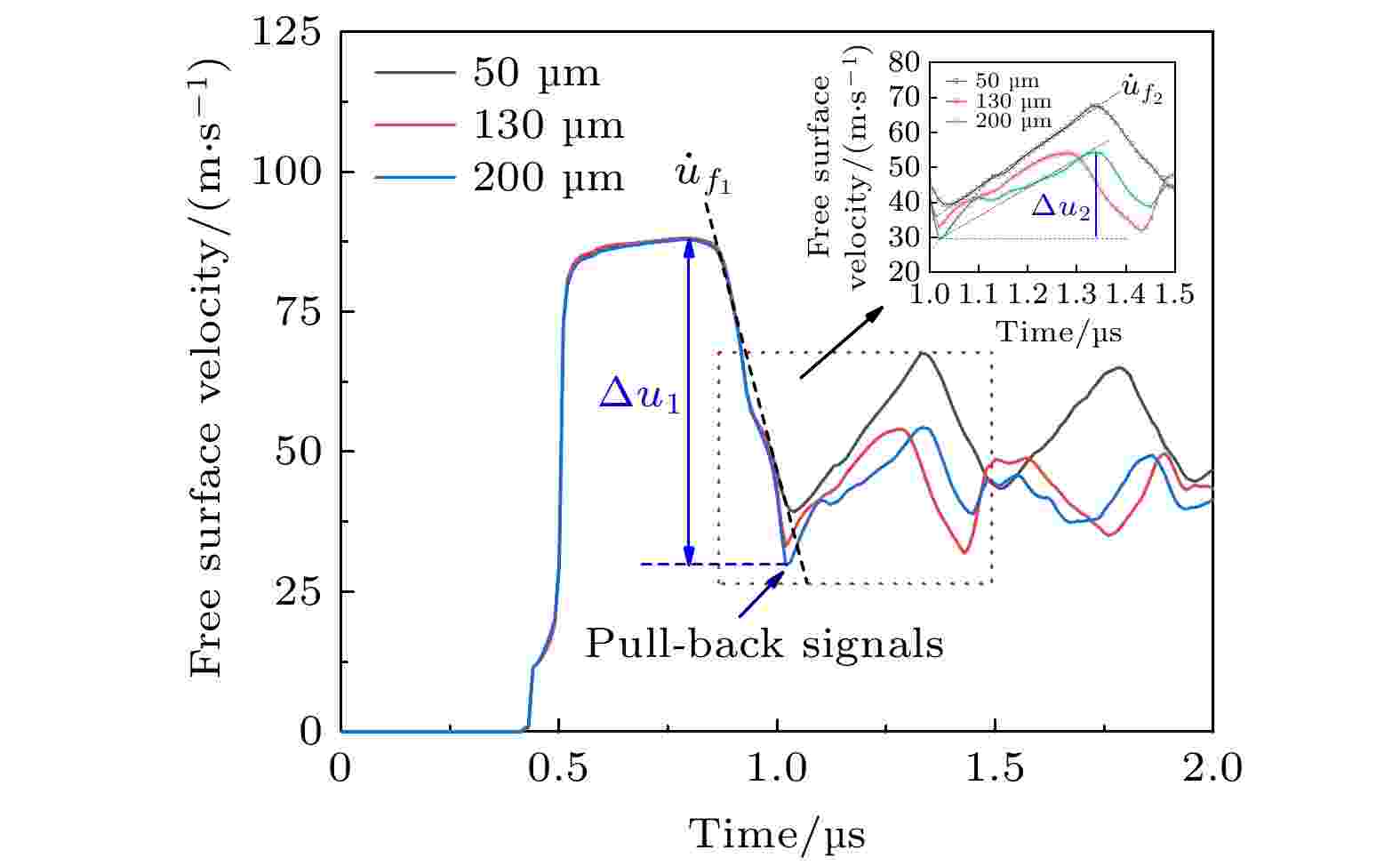图 3 不同晶粒度高纯铜靶体的自由面速度时程曲线及局部放大曲线
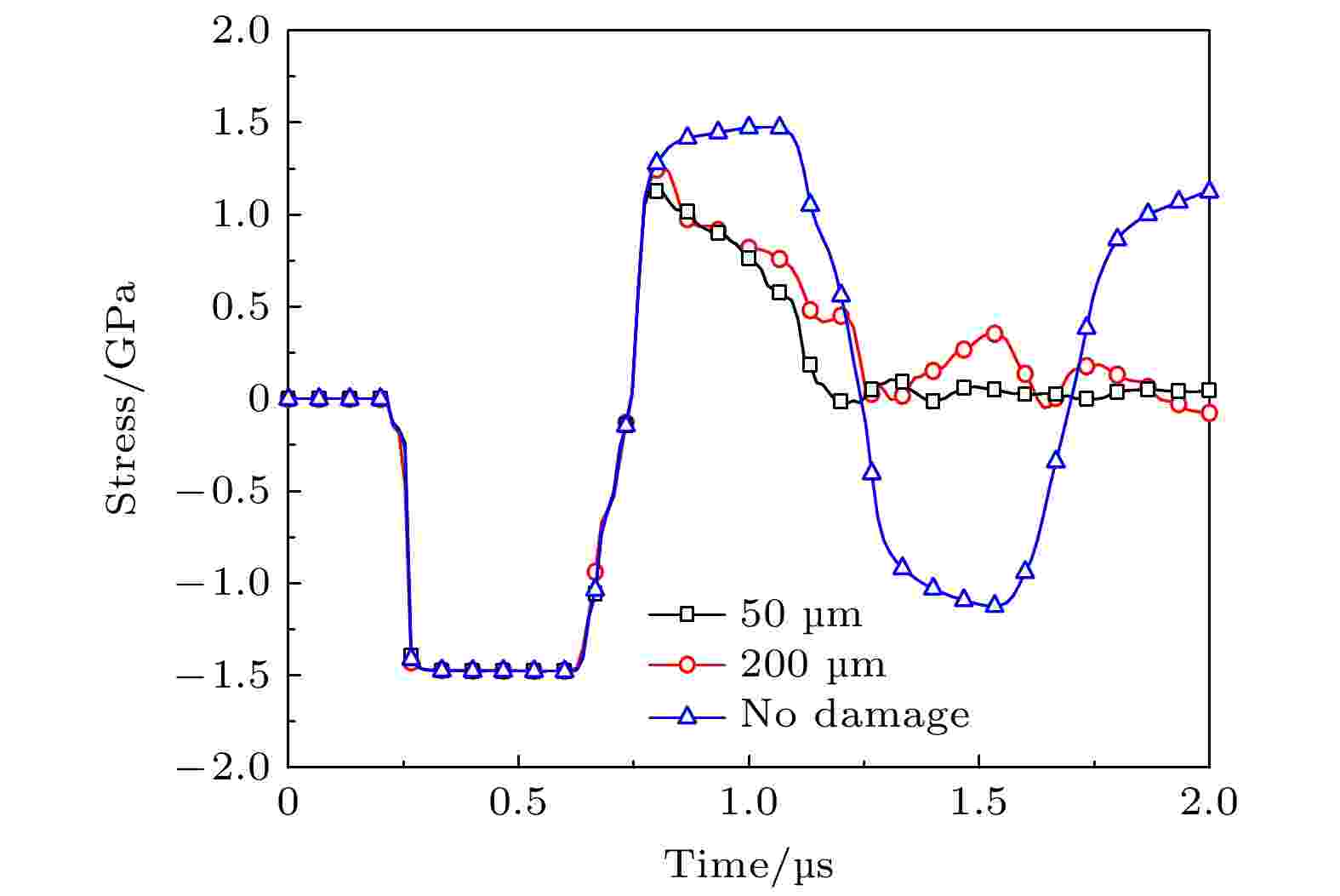图 4 不同晶粒度高纯铜损伤区典型单元的应力时程曲线
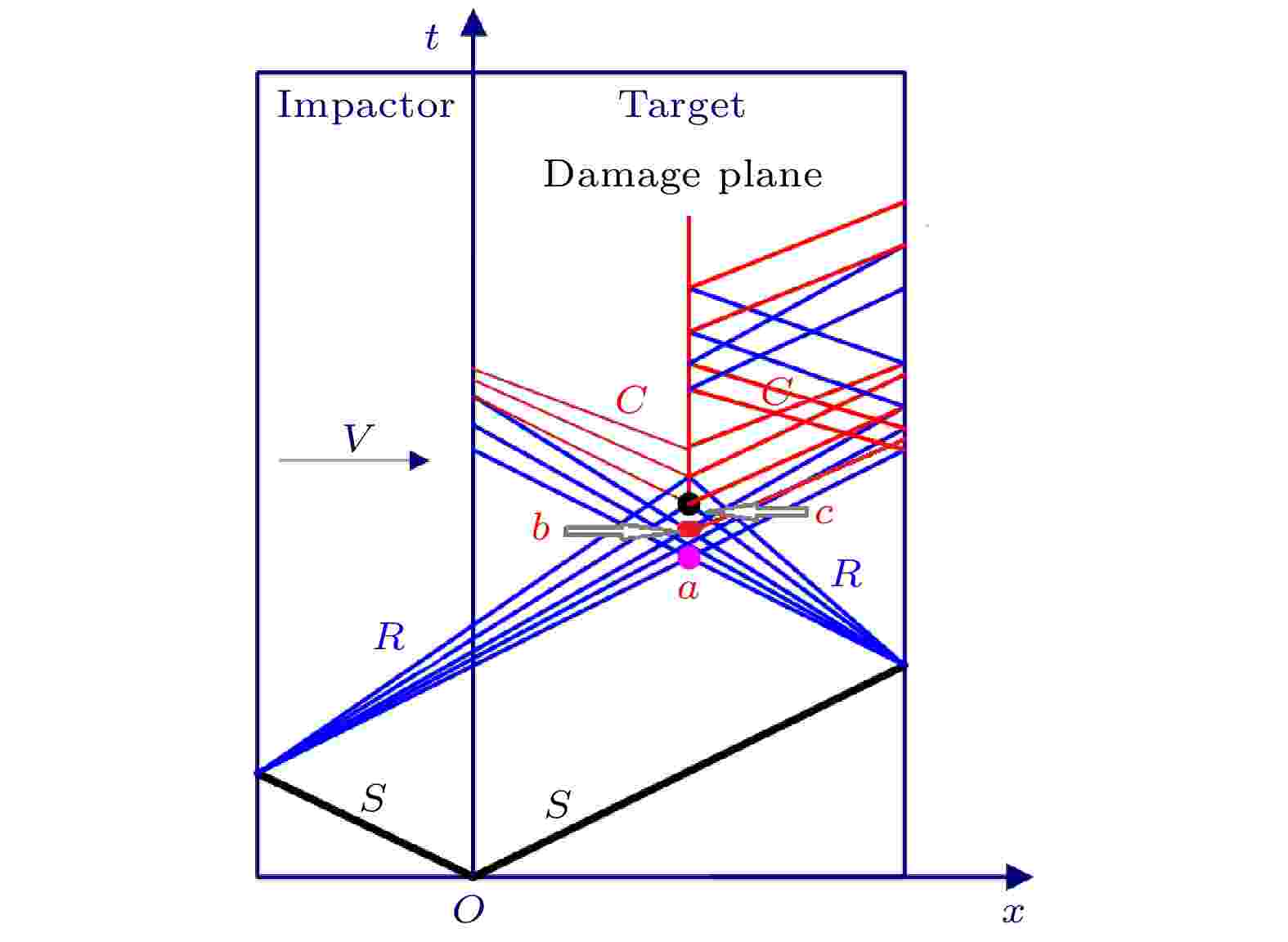图 5 层裂实验中X-t波系图
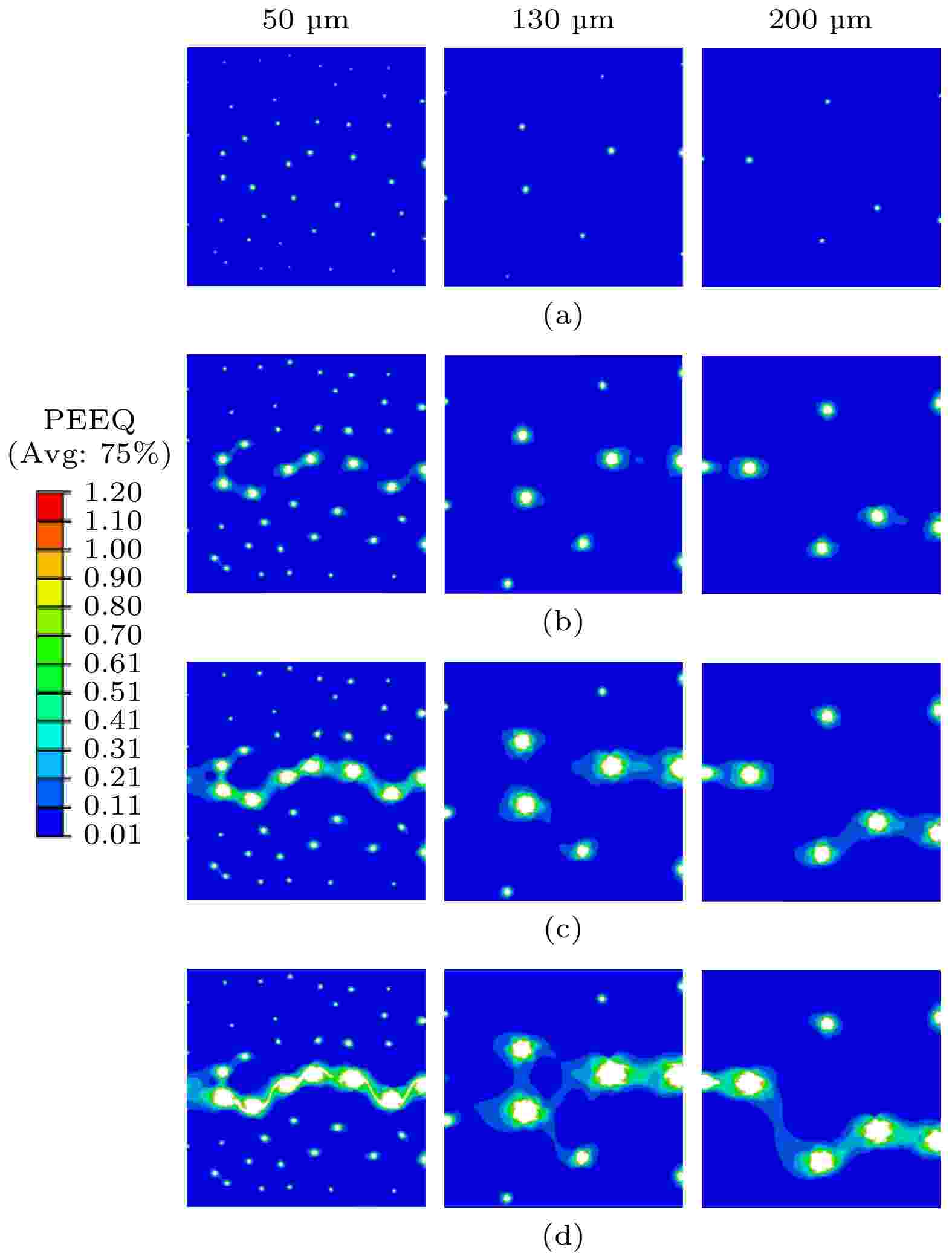图 6 不同时刻下不同晶粒度高纯铜的细观损伤演化云图
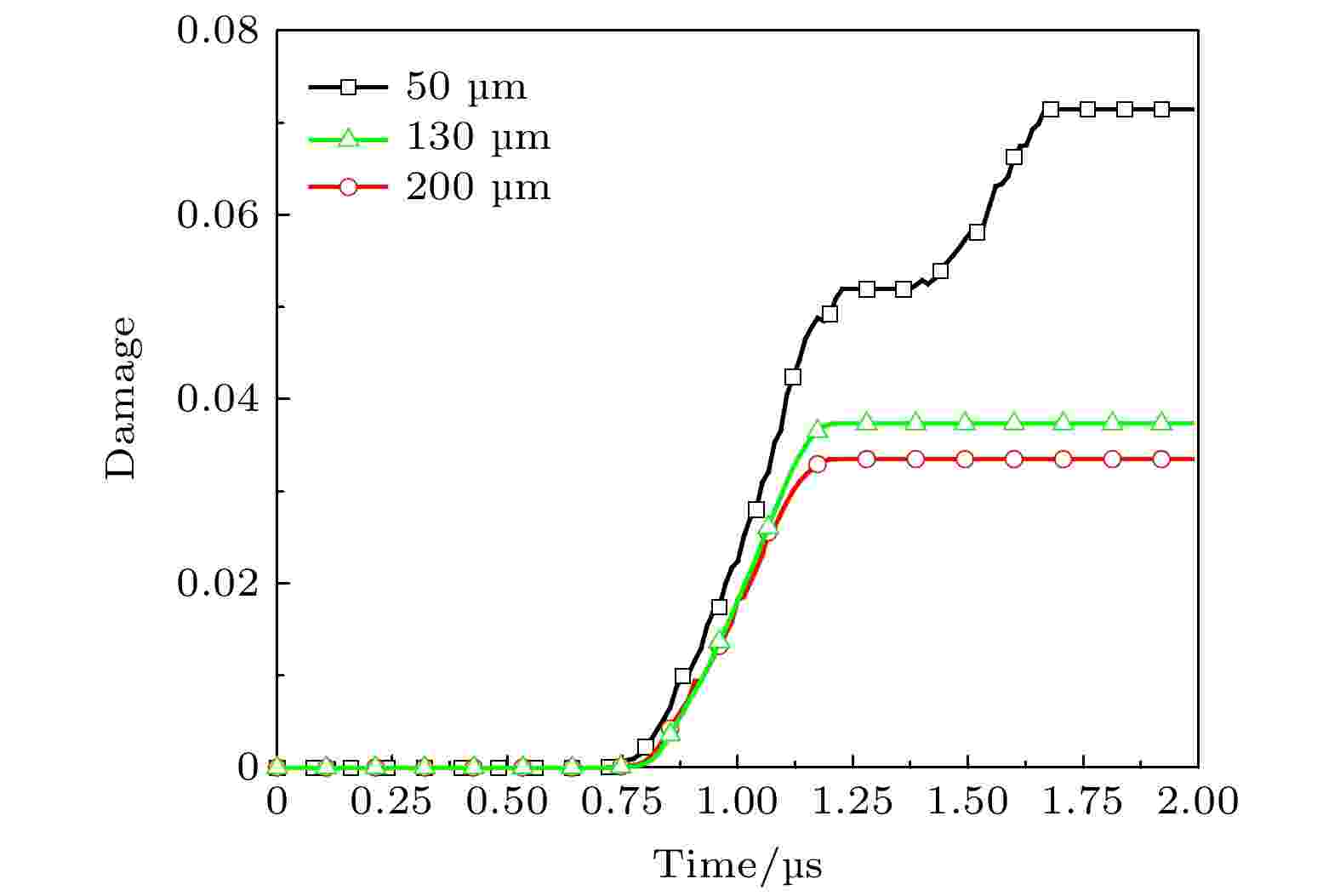图 7 不同晶粒度高纯铜内部损伤度时程曲线
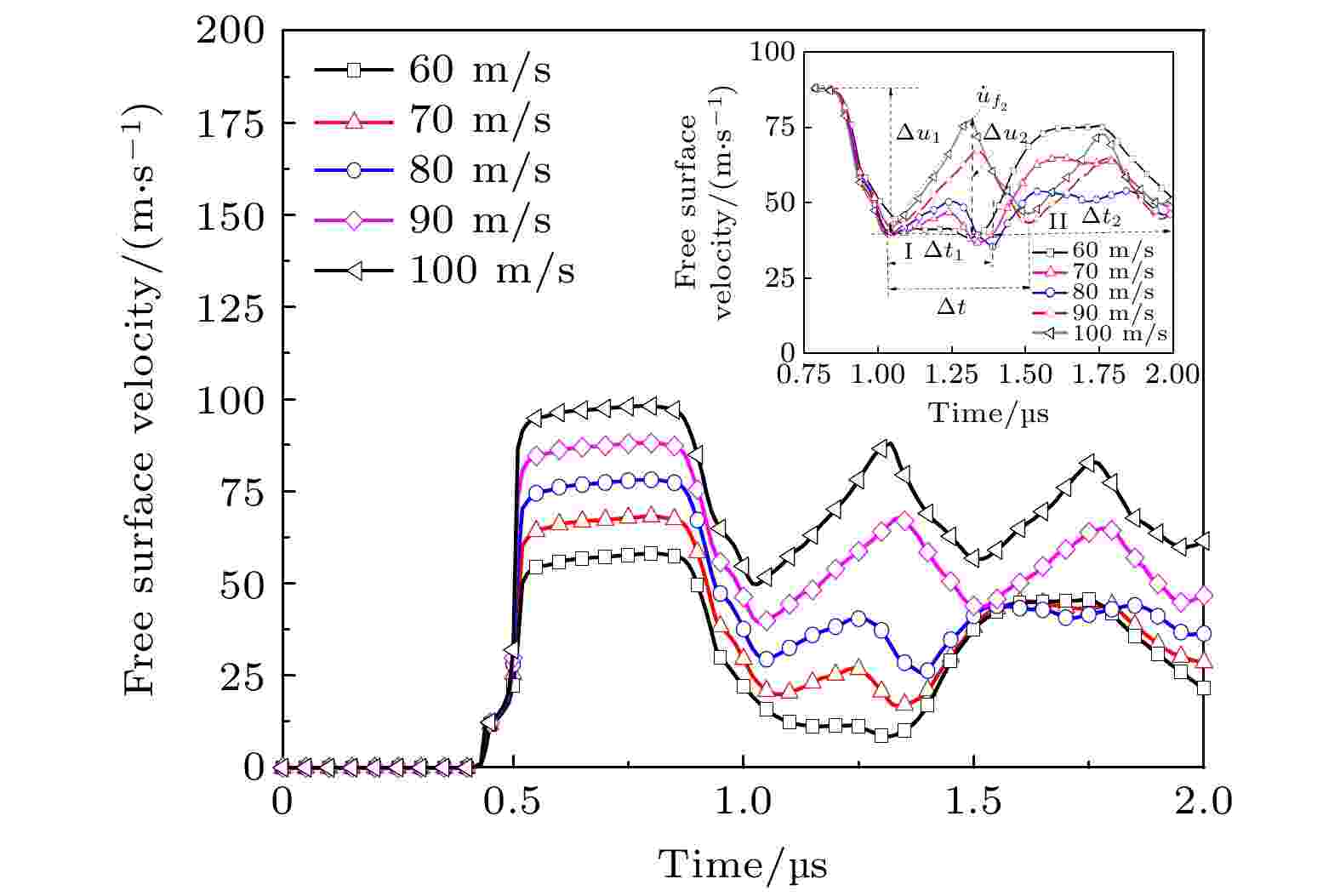图 8 不同撞击速度下高纯铜自由面速度时程曲线及局部放大
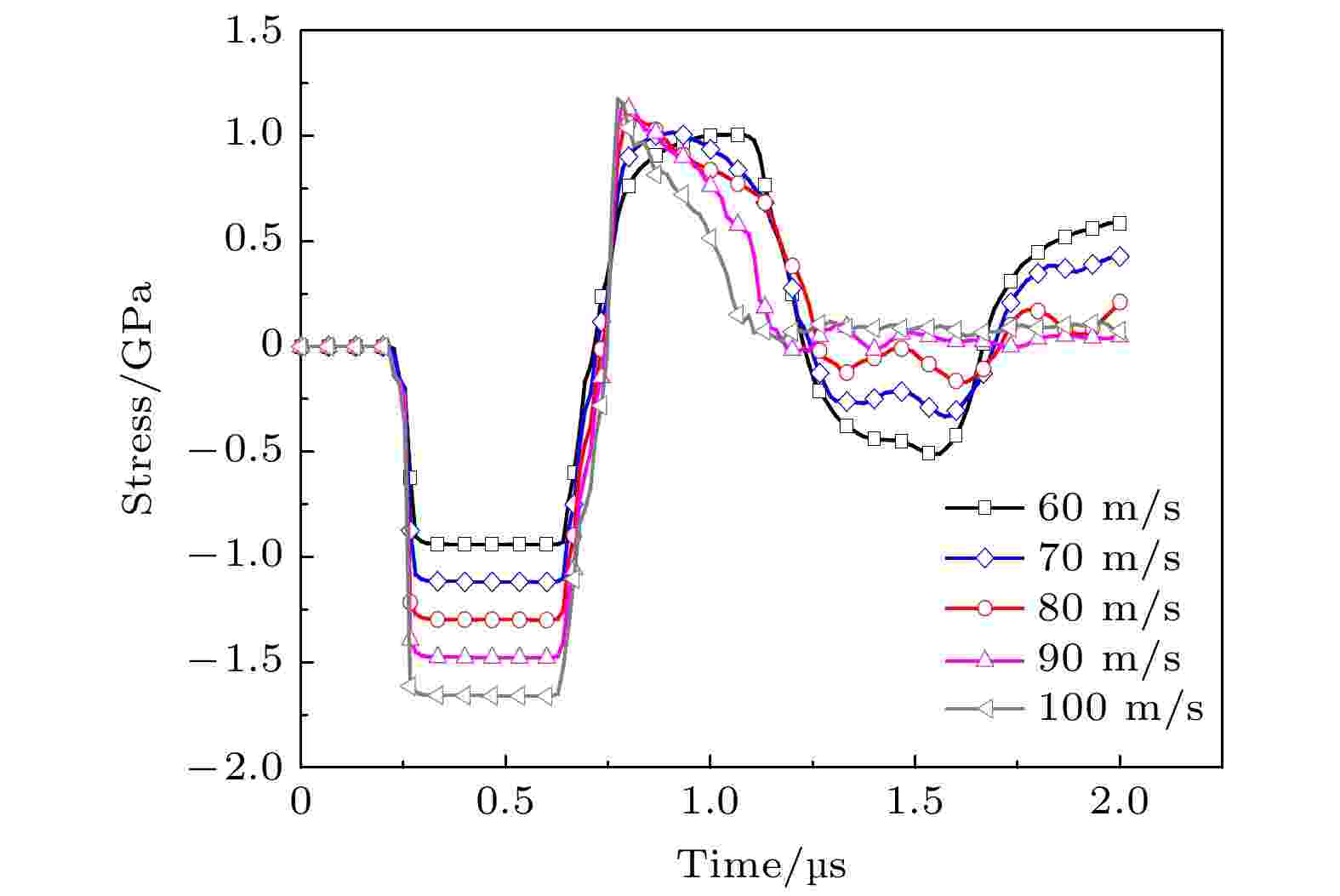图 9 不同撞击速度下高纯铜损伤区单元应力时程曲线
图 10 不同撞击速度下高纯铜细观损伤演化物理过程 (a) V = 60 m/s; (b) V = 70 m/s; (c) V = 80 m/s; (d) V = 90 m/s; (e) V = 100 m/s