全文HTML
--> --> -->界面电流的介入可能会改变材料原有的摩擦磨损性能. 例如, 高铁受电弓滑板服役时其表面产生的摩擦热和焦耳热加剧了滑板材料的磨损, 同时离线状态时电弧放电恶化了表面接触状态, 严重威胁到高铁运行的安全性[5]. 目前已有许多****针对材料的载流摩擦磨损行为开展了相关研究: Yasar等[6]研究了接触压降对铜-石墨复合材料载流摩擦行为的影响, 发现摩擦力随接触压力呈“U”型变化; 沈向前等[7]认为载流摩擦过程中产生的电弧热是表面局部温度升高的原因, 破坏了接触表面的润滑膜, 进而提高了摩擦力; 王一帆[8]分析了Cu/QCr0.5的磨损率与电流密度的关系, 当电流密度持续增大时, 界面表面的粗糙程度会显著提高, 加剧了材料的磨损. 这些研究说明了材料的载流摩擦受到力、电和热等多场耦合因素的影响, 比传统摩擦更为复杂, 其磨损形式也更为丰富[9].
电接触下石墨烯的摩擦性能研究也取得了长足进步. Jiang等[10]观察到负偏压时氧化石墨烯薄膜的载流摩擦力迅速增大, 而正偏压时摩擦力几乎保持不变. Berman等[11]发现带电氮化钛球与金基底相对载流摩擦时, 表面涂覆石墨烯可以提供良好的减摩作用, 且该润滑性能不受测试环境和摩擦历史的影响. Lee等[12]使用导电原子力显微镜研究了动态电接触下石墨烯的纳米载流摩擦特征, 认为摩擦力与针尖滑动速率和接触应力均有联系. 然而, 由于试验工况多样、石墨烯化学修饰多元, 电流对石墨烯本征摩擦特性的影响机制尚未清晰. 分子动力学作为一种基于牛顿力学的模拟方法, 具有易于操作、成本低廉、参数可控、运动过程可视等优点, 能够作为有效研究手段来阐明石墨烯的载流摩擦机理, 促进现代层状低维材料摩擦理论的发展[2].
本文使用分子动力学方法建立单晶硅针尖在弹性基底支撑石墨烯表面滑移的分子模型, 研究载流条件下石墨烯的摩擦性能, 分析石墨烯的载流摩擦行为与模拟工况之间的联系, 并通过绘制石墨烯的表面形貌、接触界面的电荷分布和表面势能对石墨烯的载流摩擦机理进行系统地讨论.
图 1 分子构型 (a) 半球形针尖与石墨烯相对滑移; (b) 弹性基底Figure1. Molecular configuration of (a) hemisphere-shaped tip sliding against graphene and (b) elastic substrate.
石墨烯是体状石墨材料的组成基元, 继承了石墨的高导电性, 当石墨烯两端产生电压时其内部会自然地产生定向电流. 针尖的刚性层和石墨烯的固定层分别当作电极, 含有总量相等但方向相反的电荷. 载流过程中电极的电荷保持不变, 而其余原子根据其临近原子的相互作用对所带电荷的大小和方向进行调整. 待体系达到稳定的电平衡状态后, 电极间的电势差可导致体系内部电荷的定向移动, 从而在针尖电极-接触界面-石墨烯电极间产生电流. 规定使电流从针尖电极流出的电压为正偏压, 反之流入的为负偏压.
石墨烯由弹性基底支撑. 之前的分子模拟研究中一般使用以AB方式堆积的多层石墨烯作为弹性基底. 最近, Chang等[13]为提升计算效率提出了一种更为简洁的弹性基底设置方法. 他们将基底简化成刚性墙和面外弹簧, 能够精准地复现石墨烯低载荷下的本征摩擦行为[14]. 类似于上述方法, 载流摩擦过程中刚性墙的位置被固定, 将石墨烯的碳原子与刚性墙通过面外弹簧(弹簧常数ks)进行连接, 如图1(b)所示. 但需指出的是, 该简化方法无法模拟高应力下石墨烯的摩擦性能. 这是由于石墨烯层间实则为非线性相互作用, 急剧增加的层间支撑作用无法等效成固定的弹簧刚度, 因此应控制模拟过程中石墨烯的低应力接触状态.
本文中所有的模拟仿真均适用开源代码LAMMPS[15], 而通过软件OVITO[16]对分子的运动轨迹进行可视化. 使用ReaxFF势函数[17]来描述原子间的相互作用, 该势函数具有基于距离相关的键序函数形式, 能够模拟带电体系的动态行为. 此外, COMB3与ReaxFF势函数所获取的载流摩擦机理保持一致, 排除了力场类型对载流摩擦的影响. 在仿真过程中, 等间隔时间计算一次体系内的静电相互作用, 当相邻静电势能差大于1 × 10–4 kcal/mol收敛精度时, 调整参与电平衡原子的带电量. 分子模型在载流摩擦过程前先100 ps的系统驰豫达到能量最小值. 每个时间步都记录针尖所受的阻力, 并将最后30 ?滑动距离内的阻力取平均作为摩擦力. 整个系统的温度通过Nose-Hoover温控器保持在300 K.
3.1.石墨烯的偏压载流摩擦行为
图2所示为最后30 ?滑动距离内石墨烯载流摩擦力的变化, 摩擦力的负号表示该力方向与针尖滑移方向相反. 为了对比载流前后石墨烯摩擦行为的变化, 统计无载流时石墨烯的摩擦力(见图2(a)). 从图2(a)中可以发现, 摩擦力曲线展示出较为平稳的黏滑特征, 其周期(2.4 ?)接近于石墨烯的晶格常数. 偏压时石墨烯的黏滑运动形式未发生变化, 但每个黏滑周期内的波动幅值却显著增大. 该幅值受偏压方向的影响, 负偏压的幅值要高于正偏压.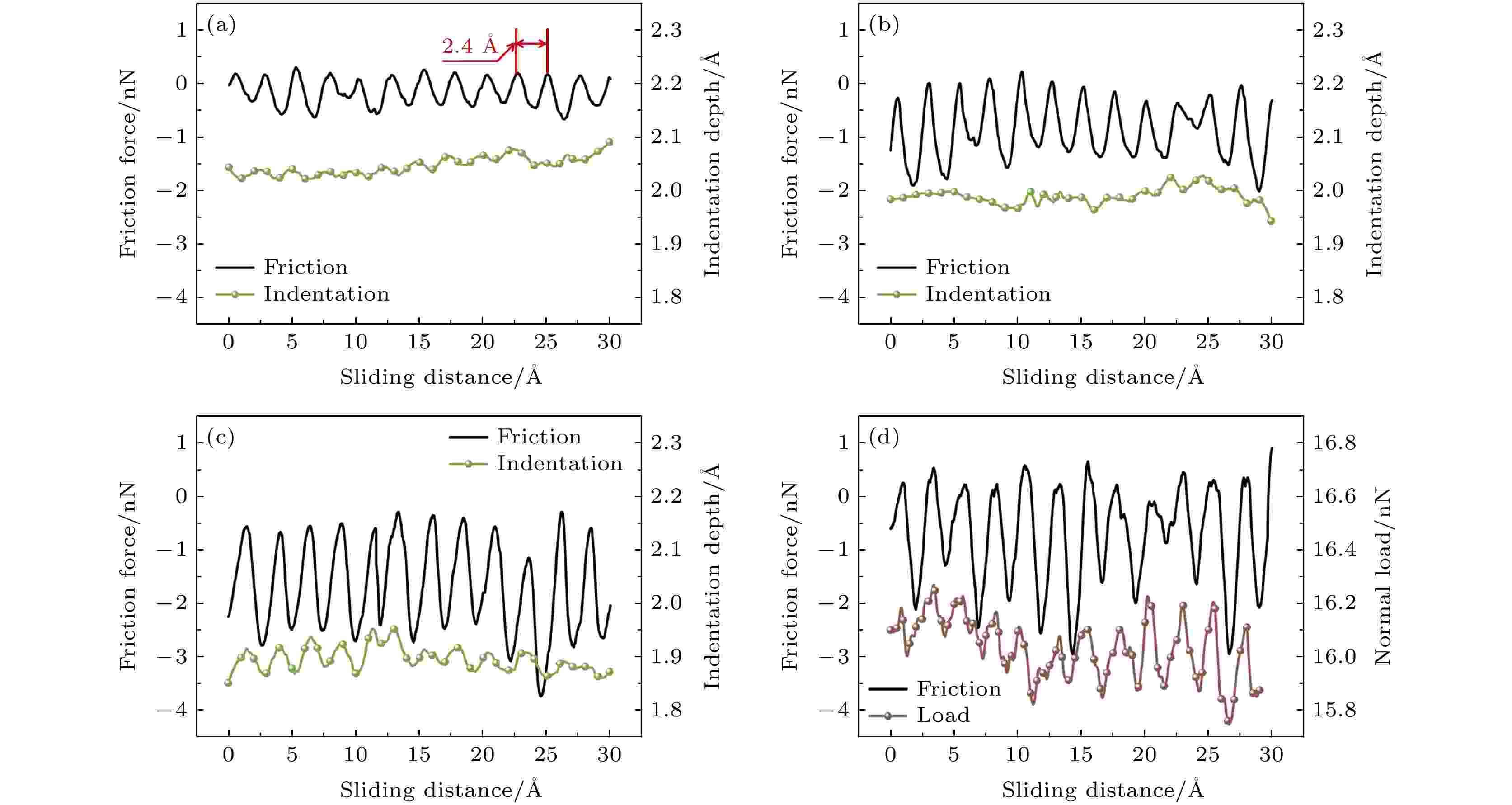
图 2 摩擦力随摩擦距离的变化 (a) 无偏压; (b) 正偏压; (c), (d)负偏压. (a)?(c)恒定fn, (d)恒定压痕深度Figure2. Variations of friction force with sliding distance: (a) Without bias voltage, (b) with positive-bias; (c), (d) negative-bias voltage. (a)?(c) constant fn, (d) constant indentation depth.
通过滑动过程中针尖压痕深度的变化来分析电流对石墨烯摩擦行为的影响机制. 定义压痕深度为滑动针尖在初始滑移时刻与当前滑动时刻之间的面外距离, 更大的压痕深度意味着石墨烯的面外变形程度得到提高. 从图2(a)看出, 当石墨烯内部无载流时, 压痕深度在2.05 ?附近轻微波动, 其稳定的压痕深度变化确保了黏滑运动中微弱的摩擦力振荡. 偏压状态下压痕深度的波动程度加剧, 导致摩擦力震荡幅值的增大. 通过对比图2(b)和图2(c), 发现负偏压下的压痕深度波动明显强于正偏压, 能够解释偏压方向对摩擦力波动幅值的影响.
摩擦过程中平均压痕深度与摩擦力之间也存在相关性. 平均压痕深度的变化满足无载流 > 正偏压 > 负偏压的变化趋势, 而摩擦力则遵循无载流 < 正偏压 < 负偏压的关系, 压痕深度的减小对应于摩擦力的增加. 这种对应关系表明石墨烯的载流摩擦行为与其面外变形相关[3]. 然而, 之前的文献报道中一般认为摩擦力与面外变形呈正相关关系, 即增大压痕深度可提高摩擦力. 这种差异说明基于面外变形的摩擦机理无法解释石墨烯的载流摩擦特征, 下文将载流摩擦机理进行详细讨论. 相较于图2(c)(平均压痕深度1.89 ?), 图2(d)所示的载流摩擦力在恒定压痕深度(1.8 ?)时发生下降, 表明只有在相同的载流条件下面外变形机理才具有适用性. 此外, 由于限制了针尖的自由度, 使得接触界面在相对滑动时难以动态调整, 进而加剧黏滑周期内摩擦力的振动[18].
图3所示为正负偏压下石墨烯的载流摩擦力. 一旦石墨烯内部存在电流, 其摩擦力会成倍的上升. 例如, 0.9 V负偏压时石墨烯的载流摩擦力为(1.96 ± 0.12) nN, 高于无载流时摩擦力((0.23 ± 0.05) nN)将近8.5倍. 石墨烯的载流摩擦力也受偏压大小和方向的影响, 当偏压从0.1 V增加到2.0 V时, 正偏压的载流摩擦力增幅为0.38 nN, 而负偏压的增幅为2.11 nN. Lang等[19]利用水分子在石墨烯电极表面的吸附行为以及石墨烯与针尖之间的本征势能差异来解释摩擦力在不同偏压方向的上升速率. 由于本文的真空模拟体系中未掺杂水分子, 可忽略前者对石墨烯摩擦特征的影响. 而后者的影响实际上来源于石墨烯表面静电能的变化. 综上所述, 石墨烯在摩擦过程中呈现出明显的黏滑运动特征, 且该特征与载流方向无关; 电流通过时石墨烯的摩擦力会迅速上升, 负偏压的上升速率高于正偏压.
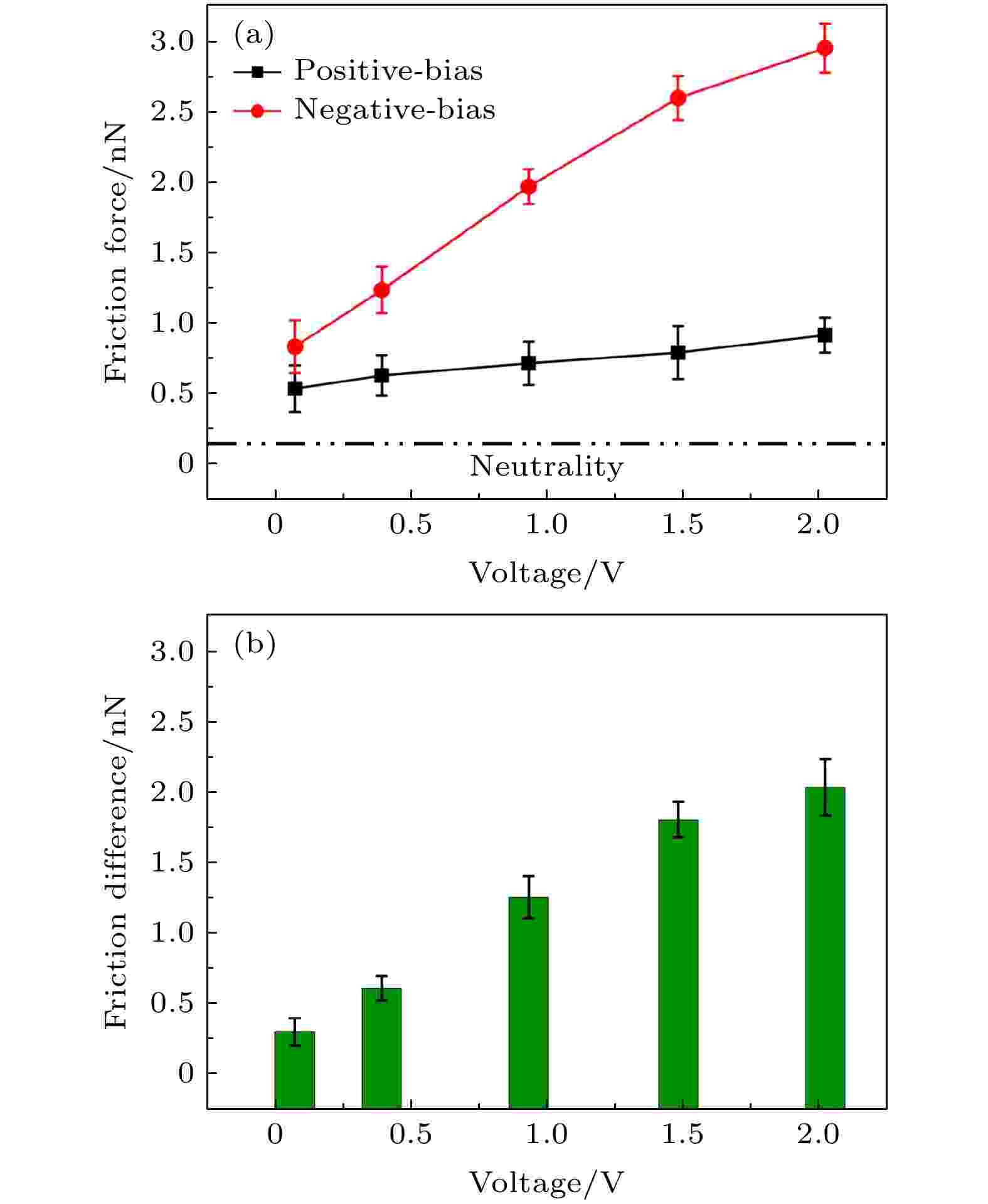图 3 (a) 载流摩擦力随偏压的变化; (b) 摩擦力差异Figure3. (a) Variation of current-carrying friction with voltages; (b) friction difference.
2
3.2.模拟工况对载流摩擦的影响
研究表明[20,21]石墨烯的摩擦行为呈现出高度的环境敏感性, 不同试验条件下石墨烯可能具有截然相反的摩擦特征. 基于上述考虑, 首先分析不同fn下石墨烯的载流摩擦力(ks = 0.27 nN/?), 如图4所示. 对于相同的fn, 正偏压时载流摩擦力随着偏压的增大而上升. 负偏压时也得到相似的载流摩擦力-偏压关系, 表明石墨烯在低应力接触条件下具有稳定的载流摩擦行为. 当保持偏压不变时, 载流摩擦力与fn也呈现出正相关关系. 例如, 对于偏压大小为0.9 V, fn为8 nN的正偏压载流摩擦力为0.51 nN, 而负偏压则为0.74 nN; 随着fn上升到24 nN, 正偏压载流摩擦力增大0.43 nN, 而负偏压则增大2.44 nN. 不同的增长数值说明石墨烯的载流摩擦性能与其内部载流特征(偏压大小和方向)密切相关.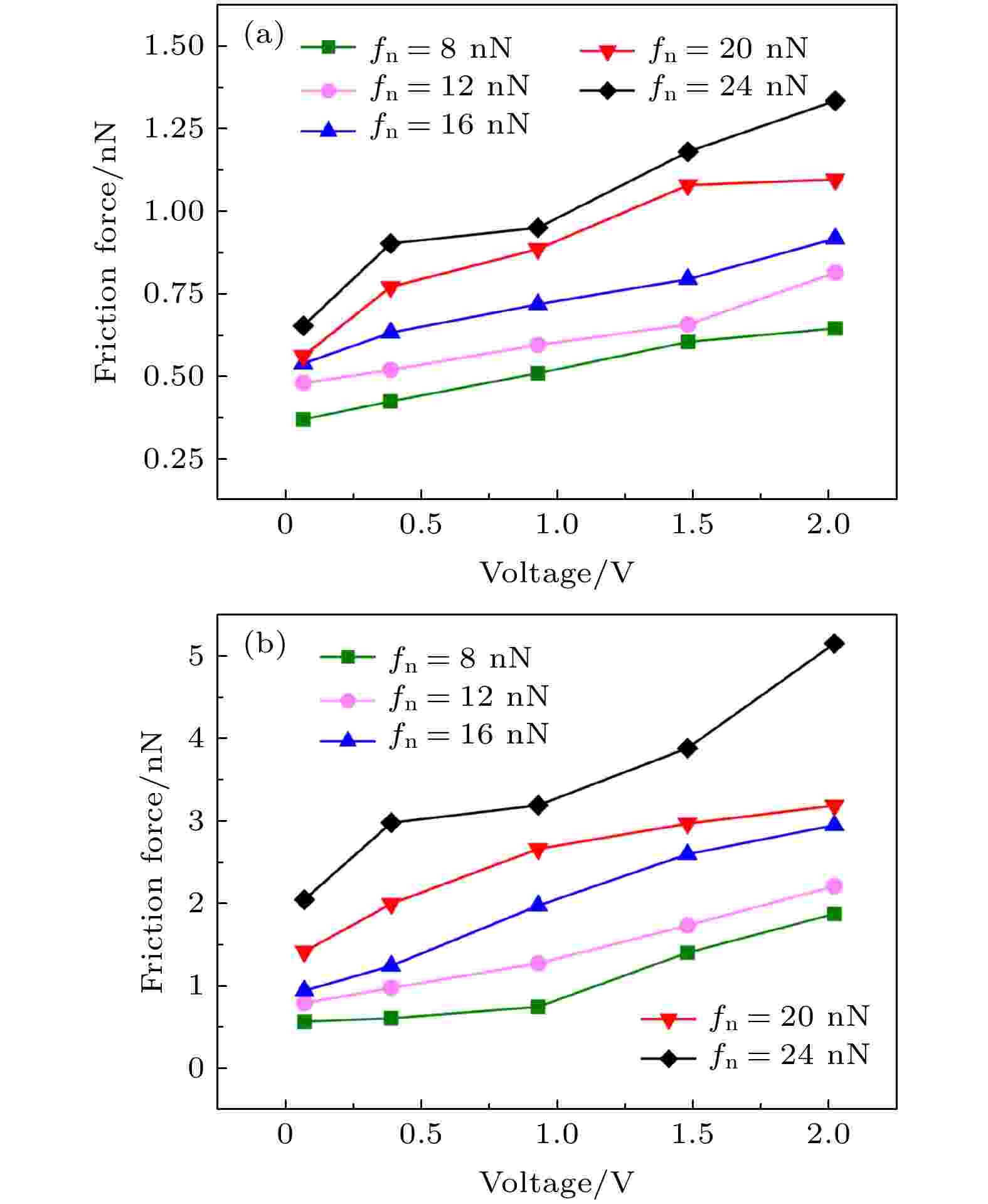
图 4 在(a)正偏压和(b)负偏压下不同fn的载流摩擦力Figure4. Current-carrying friction with different fn under (a) positive-bias and (b) negative-bias voltage.
接着研究ks对石墨烯载流摩擦特征的影响(fn = 16 nN). 图5所示为ks分别等于0.22, 0.27和0.32 nN/?时石墨烯的载流摩擦力随负偏压的变化. 类似于图4中的结果, 在不同的ks下石墨烯也具有相似的载流摩擦力-偏压曲线. 同时, 由于ks的减小, 石墨烯面外变形程度的增大也会提高其载流摩擦力, 因此对石墨烯的摩擦性能可实现精准调节. 由此可以看出, 石墨烯表现出稳定的载流摩擦特征, 不受模拟工况(fn和ks)的影响, 能够较好地胜任复杂多变的载流服役工况, 为制备兼具高导电、高强度、耐磨损的涂层材料提供崭新的解决思路.
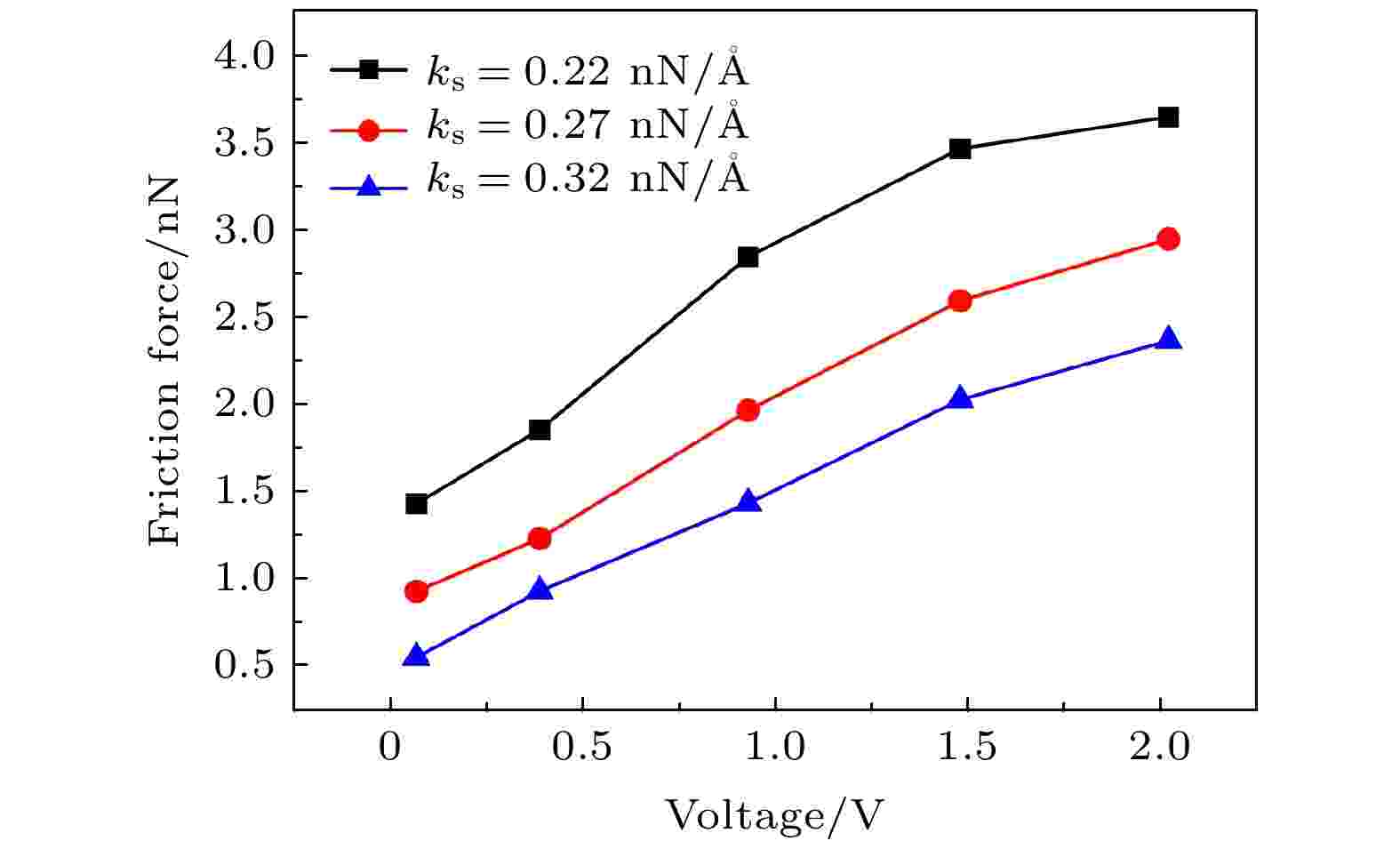图 5 负偏压下不同ks的载流摩擦力Figure5. Current-carrying friction under different ks with negative-bias voltage.
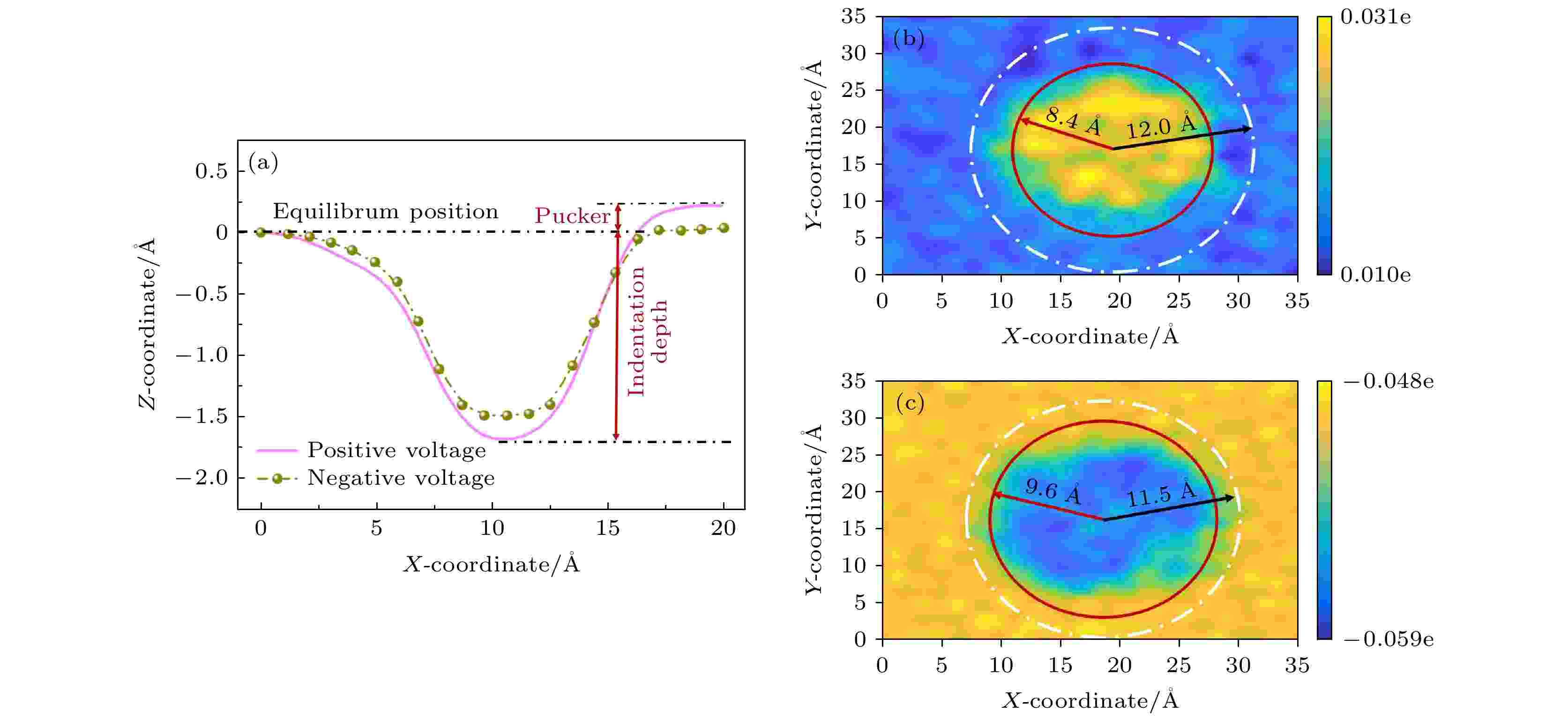图 6 (a) 针尖周围的石墨烯原子坐标; (b)正偏压和(c)负偏压下石墨烯的电荷分布Figure6. (a) Coordinate of atoms in graphene near tip; charge distribution of graphene under (b) positive-bias and (c) negative-bias voltage.
电流热效应能显著改善石墨烯的摩擦性能, 然而石墨烯具有较高的载流迁移率和导热系数, 导致电流热效应在石墨烯的载流过程中不明显[25], 因此该效应未在石墨烯的载流摩擦机理分析中加以讨论. 统计相对滑动物体之间的接触面积也是纳米摩擦理论分析的重要研究手段. 考虑到带电针尖与石墨烯之间满足弹性Hertz接触, 所以将石墨烯的接触区域近似成圆球形状(见图6(b)白点虚线). 从表1的统计结果中看出, 正偏压、负偏压和无偏压下接触半径的变化趋势也无法解释石墨烯的载流摩擦机理. 然而, 在石墨烯的接触区域内, 无论偏压方向如何, 其中心位置的原子带电量均高于外部原子. 这种独特的表面形貌给载流摩擦机理的研究提供了新思路[26]. 定义高带电量所围成的范围为载流区域(见图6(b)红实线), 统计正负偏压下该载流区域的半径(见表1), 发现载流半径从正偏压下的8.4 ?增加到负偏压下的9.6 ?, 说明石墨烯的载流摩擦机理与载流面积挂钩.
| 正偏压 | 负偏压 | 无偏压 | |
| 接触半径/? | 12.0 | 11.5 | 10.2 |
| 载流半径/? | 8.4 | 9.6 | — |
表1石墨烯的接触和载流半径
Table1.Contact and current-carrying radius of graphene
接触与载流区域的耦合变化会直接影响到石墨烯与针尖之间的相互作用. 摩擦界面的吸附能等于体系的整体势能减去体系中各独立部分的势能和, 描述为[27]
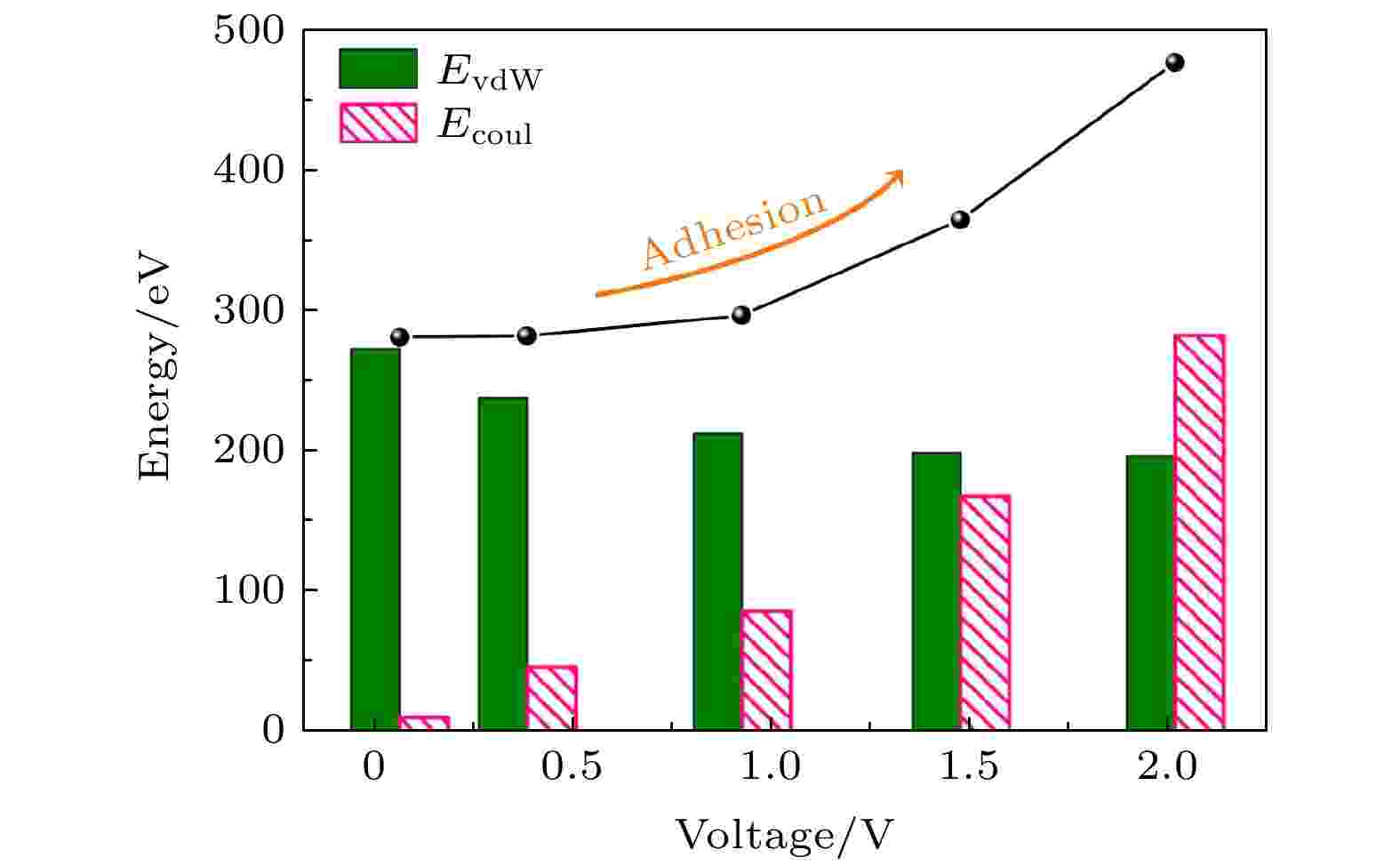图 7 接触界面处的EvdW, Ecoul和吸附能Figure7. EvdW, Ecoul and adhesion at the contact interface.
Prandtl-Tomlinson模型指出[28], 当具有规则晶体结构排列的低维材料在摩擦界面产生非键合相互作用时, 其摩擦行为遵循能量势垒理论体系. 针尖滑动时需要克服摩擦材料表面所形成的能量势垒, 成为摩擦过程中能量耗散的主要起因[29]. 该理论已应用于纳米级摩擦机理研究中[30], 表明石墨烯的表面特征可反应其载流摩擦机理. 通过刚性原子以一定的面外距离扫描石墨烯的表面来绘制其表面势能形貌, 如图8所示. 载流摩擦过程中摩擦界面的EvdW和Ecoul分别表示为
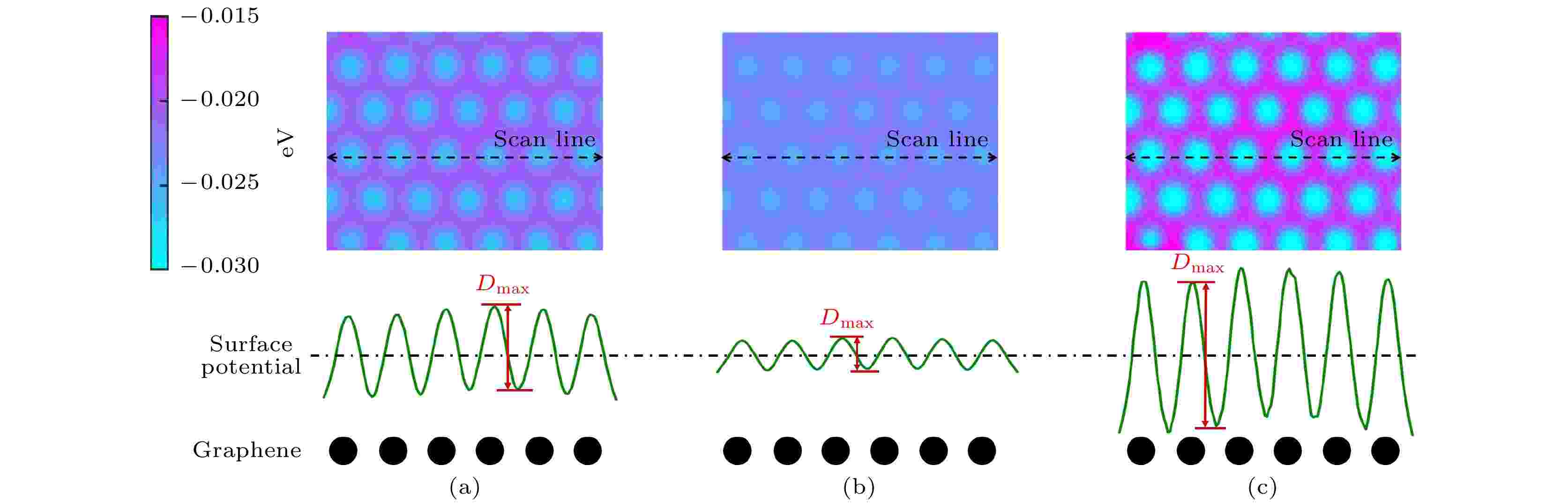图 8 (a) 参考、(b) 低应力和(c) 载流时石墨烯的表面势能Figure8. Surface potential of graphene at: (a) Reference; (b) low stress; (c) current-carrying.
图8(a)—(c)分别描绘了石墨烯在参考、低应力和载流状态时的表面势能面. 低应力状态是通过提升扫描原子的面外位置实现的, 而增大LJ势函数中的参数 来表达载流影响. 由于石墨烯规则的晶体结构, 参考状态的表面势能图呈现出均匀的周期性特征, 导致石墨烯具有稳定的黏滑运动趋势[31]. 对于低应力下的表面势能图, 尽然该图维持了原有的周期性特征, 但能量势垒受到摩擦界面吸附作用的影响. 载流介入后, 表面势能图的色差增大, 表明针尖在滑动过程中需要克服更大的能量势垒, 从而导致摩擦力的增加.
为了定量分析低应力与载流状态对石墨烯表面性能的影响, 统计沿特定方向石墨烯势能线的变化, 如图8所示. Dmax代表势能曲线中某一黏滑周期内波峰与波谷的最大差值. 相比于参考状态, 低应力时的Dmax发生明显的下降, 而施加偏压载流时的Dmax却显著上升. 因此石墨烯的内部载流特征能够加剧摩擦时滑动针尖的能量耗散, 进而提高摩擦力. 基于上述的载流机理分析, 可以总结石墨烯载流摩擦的上升是由于载流区域半径的扩大, 导致摩擦界面之间的Ecoul显著提高; 基于Prandtl-Tomlinson模型的分析发现, 载流可提高针尖滑移时所需克服的能量势垒, 进而影响到石墨烯的载流摩擦行为.
2) 石墨烯的载流摩擦行为不受模拟工况(fn和ks)的影响, 但其摩擦力数值依赖于模拟工况;
3) 在石墨烯的载流区域内, 范德瓦耳斯力略微下降而静电力却显著提高, 导致摩擦界面之间的吸附相互作用增大. 低应力时针尖在石墨烯表面滑移过程中所需要克服的能量势垒减小, 而载流时其能量势垒却得到提高, 加剧了摩擦过程中针尖滑移的能量耗散, 进而增大石墨烯的载流摩擦力.
感谢中南大学高性能计算平台提供计算资源.
