摘要: 基于Hill动力学与Michaelis-Menten方程, 建立理论模型研究CDK1(细胞周期蛋白依赖性蛋白激酶)/APC(后期促进复合物) 系统振荡过程中, 时间延迟对系统振荡动力学的影响. 理论模型考虑CDK1-Plk1 (Polo样蛋白质激酶)-APC通路中的时间延迟效应, 研究发现, 在不同时间延迟条件下, CDK1, Plk1和APC随时间演化呈现了周期性振荡特性, 表明了细胞周期进程. 随着时间延迟的增加, CDK1, Plk1和APC随时间演化的振荡周期变长、振幅增大, 表明了时间延迟会改变体系的动力学特性. 通过考察在高斯白噪声环境中的时间延迟效应, 研究发现, 噪声扰动明显地改变了CDK1随时间演化的动力学特性. 在较小噪声环境中, CDK1/APC系统通过自调节时间延迟, 改变振幅或振荡周期, 重新自调控, 使系统恢复稳定的周期性振荡. 在较大噪声环境中, CDK1呈现了阻尼振荡模式. 由此表明了较强的噪声, 会使得CDK1/APC系统周期性振荡动力学出现较大改变, 由于时间延迟, CDK1/APC振荡系统表现为从原有的周期性振荡转变为阻尼振荡, 系统原有的振荡模式很难再恢复. 理论结果进一步揭示了诸如非洲爪蟾胚胎等细胞周期过程中的时间延迟效应, 可为设计调控细胞周期、阻断肿瘤转变的通路治疗方案提供理论依据.
关键词: 时间延迟 /
细胞周期 /
振荡动力学 English Abstract Influence of time delay on dynamics of cell cycle Zhao Xin-Jun 1,2 ,Li Jiu-Zhi 3 ,Jiang Zhong-Ying 2 1.Xinjiang Laboratory of Phase Transitions and Microstructures of Condensed Matter Physics, Yi Li Normal University, Yining 835000, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 21764015), the Yi Li Normal University Doctoral Research Startup Foundation, China (Grant No. 2020YSBS008), and the Joint Funds of Xinjiang Natural Science Foundation, China (Grant No. 2019D01C333)Received Date: 15 February 2021Accepted Date: 25 May 2021Available Online: 03 October 2021Published Online: 20 October 2021Abstract: In this work, based on the Hill dynamics and Michaelis-Menten equation, a theoretical model is built to study the influence of time delay on the oscillation dynamics of a cyclin-dependent kinase 1 (CDK1)/ anaphase-promoting complex (APC) system. The theoretical model considers the time delay in the CDK1- polo-like protein kinase (P1K1)-APC pathway. We find that under different time delay conditions, the CDK1, Plk1 and APC exhibit periodic oscillation characteristics over time, indicating cell cycle progression. With the increase of time delay, the oscillation periods and amplitudes of CDK1, Plk1 and APC increase, which indicates that the time delay will change the dynamic characteristics of the system. It implies that during the cell cycle, the status of the CDK1/APC oscillation system will show a long-term correlation with the biochemical reaction time of each component, such as CDK1, Plk1 and APC. This correlation is influenced by its past, and there is a time-delay effect. The additional correction will be made due to time delay. By investigating the time-delay effect in Gaussian white noise environment, we find that in the Gaussian white noise environment, the noise disturbance obviously changes the dynamic characteristics of CDK1 evolution with time. In a low-noise environment, the CDK1/APC system changes the oscillation amplitude or period through self-adjusting time delay, so that the system can restore the stable periodic oscillation, while in a high noise environment, CDK1 exhibits a damped oscillation, indicating that the periodic oscillation dynamics of the CDK1/APC system will be significantly changed by strong noise. In the CDK1/APC system oscillation process, the system adjusts the physiological response through a feedback mechanism. There is a time delay between the perception of the noise effect and the establishment of an appropriate physiological response. By different time delays, the system can adjust complex non-periodic chaotic rhythms with different time delays, and recover to produce a stable periodic physiological process. Owing to the time delay, the CDK1/APC oscillation system changes from the original stable oscillation to a damped oscillation, but the original oscillation mode is difficult to recover. The theoretical results further reveal the time-delay effect in cell cycle processes such as Xenopus embryos, and provide a theoretical basis for designing pathway treatment plans that regulate cell cycle and block tumor transformation.Keywords: time delay /oscillatory dynamics /cell cycle 全文HTML --> --> --> 1.引 言 细胞周期(cell cycle)进行过程中与调控其按一定顺序发生生化事件的基因、蛋白密切相关[1 ,2 ] , 例如, 核苷酸代谢与细胞周期之间存在明显的相关性, 足够的嘌呤可以促进细胞周期进程并在复制过程中保持DNA保真度[3 ] 、RNA结合蛋白ZFP36L1会抑制细胞周期信号转导等[4 ] . 在许多真核细胞中, 细胞周期作为一系列偶然事件进行, 新细胞首先生长到足够的大小后进行DNA复制, 然后开始有丝分裂, 最后, 细胞必须成功组织中期纺锤体才能完成有丝分裂并重新开始循环.[5 -7 ] . 但是, 细胞生物学的最新进展也导致了对细胞周期认识上的重大突破, 其中, 两栖非洲爪蟾的早期胚胎细胞周期的研究已经被广泛开展[8 -10 ] . 研究发现, 该细胞周期DNA复制并非取决于细胞的生长, 有丝分裂进入并不取决于DNA复制的完成, 有丝分裂退出也不取决于中期纺锤体的成功组装[11 ,12 ] , 并且细胞周期都是由以细胞周期蛋白依赖性蛋白激酶CDK1和后期促进复合物(APC)为中心的蛋白回路驱动, CDK1的激活使细胞进入有丝分裂, 而通常落后于CDK1的APC激活则使细胞周期停滞. 两栖非洲爪蟾的早期胚胎细胞周期呈现出了仅每25 min一次脉冲[13 ] , 这是由自主生化振荡器驱动, 振荡器的核心是CDK1/APC正负反馈回路, 其中活跃的CDK1通过不完全了解的机制激活了APC, 反过来, 活性的APC将CDK1聚泛素化, 该细胞周期类似于由自主生化振荡器驱动时钟效应[7 ,14 ,15 ] . 在非洲爪蟾胚胎细胞周期振荡系统中, Yang等[16 ] 发现该系统具有延时数字开关效应, 在CDK1和APC激活之间存在时间延迟, 并且具有极高的超灵敏性. Doedel等[17 ] 通过计算建模揭示了这些体系周期振荡的鲁棒性(robustness), 类似于时钟产生的稳定振荡.[18 -22 ] 在诸如非洲爪蟾胚胎系统的细胞周期如何工作方面已经取得了重要的成果, 并发现在不同种情况下, 细胞周期均由以CDK1和APC为中心的蛋白回路驱动机理. 但是尚要完全解CDK1激活APC的机制, 是一个多步骤的过程, 具有许多中间物种, 例如, APC/CCdc20的激活取决于CDK1多个位点被磷酸化, 这种多步机制在CDK1/APC通路系统中还会产生时间延迟性. 其中, Polo样蛋白质激酶1(Polo-like kinase1, Plk1)是一种保守的丝氨酸-苏氨酸激酶, 作为CDK1激活APC通路中的中间物, 在细胞周期中起着关键的作用[23 ] . 时间延迟可以在多个尺度上显著影响生理系统的动力学, 并且还可能导致生理学和生物医学感兴趣的具体动力学系统内的可靠性丧失[24 ] . 在遗传调节网络水平上, 转录、翻译和翻译后步骤导致几分钟的延迟, 从而导致功能调节蛋白的产生. 时间延迟还可以加速前馈架构中的信号传输[25 ,26 ] , 改变噪声引起的开关现象的统计[27 ,28 ] . 在生物系统中, 噪声可源于细胞自然生长率, 以及基因选择过程中的遗传因子、变异因子等涨落, 还可能是由于生化反应随机性引起的内部涨落[29 ,30 ] . 迄今为止, 大多数理论研究都集中在考察CDK1/APC系统的稳态性[18 -22 ] , 以及可能出现的稳态对细胞周期的影响方面, 但是没有将时间延迟导致的APC的活动变化与CDK1的早期活动(例如, 有源APC对CDK1的灭活、抑制自身的生产或激活)联系起来, 也没有考虑到噪声引发的CDK1/APC系统振荡模式的改变, 以及时间延迟对细胞周期适应噪声环境的调控作用. 因此在细胞周期过程中, 时间延迟对细胞周期动力学的影响还有待于进一步探究. 另外, 在噪声环境中, 生物系统往往可以保持相当稳定的周期进程, 那么, 生物系统如何通过自调控, 实现在噪声环境中依然能保持生理功能的稳定性, 以及是否可以通过时间延迟调控细胞周期适应自然噪声环境的节奏, 其物理机制需要更进一步全面深刻的探究.2.理论模型 在CDK1-Plk1-APC信号驱动的细胞周期过程中, 活跃的CDK1激活APC, 然后导致细胞周期蛋白降解并使CDK1失活. 基于Ferrell等[21 ] 的研究, 考虑Plk1介于CDK1/APC振荡系统的模型示意如图1 所示.图 1 CDK1-Plk1-APC信号通路模型示意图.Figure1. Schematic depiction of the model on CDK1-Plk1-APC pathway.[31 ,32 ] , 可以获得各组分反应速率时间延迟的动力学方程组为t 时的CDK1, Plk1和APC活性的变化率分别取决于早期的APC, CDK1和Plk1的活性. 基于之前的实验、理论研究[14 ,16 ,21 ] , 以上方程组中, 取各参数值为: $ {k_1} = {\text{0}}.{\text{1}} $ , $ {k_2} = {\text{3}} $ , $ {k_3} = {\text{3}} $ , $ {d_{\text{1}}} = 3 $ , $ {d_{\text{2}}} = {d_{\text{3}}} = 1 $ , $ {K_1} = {K_2} = {K_3} = {\text{0}}.{\text{5}} $ , Hill系数为$ {n_1} = {n_2} = {n_3} = {\text{8}} $ . Ferrell等[16 ,21 ] 已经通过拟合实验数据, 确定了应用Hill函数量化体系的模型参数. 生物系统具有很强的稳定性, 这使得合理的数学模型能够在较大的参数范围内有效描述系统的特性, 也可以通过考察模型对参数变化的敏感性检测参数设置的合理性.3.结果与讨论 时间延迟将CDK1, Plk1, APC活性的变化与APC, CDK1, Plk1的早期活性联系在一起, 反之亦然. 通过考察不同的$ {\tau _{\text{C}}} $ , $ {\tau _{\text{A}}} $ 和$ {\tau _{\text{P}}} $ , 可以确定Plk1介于CDK1-Plk1-APC振荡系统的时间延迟效应.图2 呈现了在不同时间延迟条件下, $ [{\text{CDK1}}] $ , $ [{\text{Plk1}}] $ 和$ [{\text{APC}}] $ 随时间演化的周期特性, 由此表明了细胞周期进程. 从图2 可以看出, $ [{\text{CDK1}}] $ , $ [{\text{Plk1}}] $ 和$ [{\text{APC}}] $ 随时间的演化显示了较为稳定的周期演化振荡特性. 比较图中不同时间延迟$ {\tau _{\text{C}}} $ , $ {\tau _{\text{A}}} $ 和$ {\tau _{\text{P}}} $ , 可以发现, 随着$ {\tau _{\text{C}}} $ , $ {\tau _{\text{A}}} $ , $ {\tau _{\text{P}}} $ 的增大, $ [{\text{CDK1}}] $ , $ [{\text{Plk1}}] $ 和$ [{\text{APC}}] $ 随时间演化的振荡周期变长, 振幅略微增大. 这是由于, 正负反馈回路中各基因、蛋白质激活合成的时间延迟, 导致各组分出现了较长时间的信号响应性, 致使各组分反应周期时间变长, 相当于在正负反馈回路中添加中间物种使得各组分量积蓄增多. 因此, $ [{\text{CDK1}}] $ , $ [{\text{Plk1}}] $ 和$ [{\text{APC}}] $ 随时间演化的振幅略微增大, $ [{\text{CDK1}}] $ , $ [{\text{Plk1}}] $ 和$ [{\text{APC}}] $ 随时间演化的振幅增大, 意味着其量的增多, 生化反应需要较长时间才能反应完全, 因此周期变长. 由此进一步表明了在细胞周期过程中, CDK1/APC振荡系统状态会表现出CDK1, Plk1, APC等各组分生化反应(APC激活、循环降解以及多聚化等)时间上的长期关联性, 这种关联性受到其过去的影响, 出现了时间延迟效应, 并且由于时间延迟会产生额外的修正.图 2 不同时间延迟条件下, $ [{\text{CDK1}}] $ , $ [{\text{Plk1}}] $ 与$ [{\text{APC}}] $ 随时间的演化.Figure2. Temporal evolutions of the levels of $ [{\text{CDK1}}] $ , $ [{\text{Pik1}}] $ and $ [{\text{APC}}] $ at different time delays.图2 中$ {\tau _{\text{C}}} $ , $ {\tau _{\text{A}}} $ , $ {\tau _{\text{P}}} $ 的变化对$ [{\text{CDK1}}] $ , $ [{\text{Plk1}}] $ , $ [{\text{APC}}] $ 随时间演化动力学的影响, 还可以发现, $ {\tau _{\text{A}}} $ 和$ {\tau _{\text{P}}} $ 对$ [{\text{CDK1}}] $ , $ [{\text{Plk1}}] $ , $ [{\text{APC}}] $ 的振荡影响有几乎相同的效应, 但不同于$ {\tau _{\text{C}}} $ 的影响效应, 较大的$ {\tau _{\text{C}}} $ 明显改变了$ [{\text{Plk1}}] $ 和$ [{\text{APC}}] $ 的振荡模式. 源于模型的数学微分方程组(1 )—(3 )中, $ [{\text{Plk1}}] $ 和$ [{\text{APC}}] $ 随时间演化的数学形式相似, 但其演化形式不同于$ [{\text{CDK1}}] $ , $ [{\text{Plk1}}] $ 作为一种中间反应物, 在数学描述中可以将其等效于CDK1和APC反应物间的时间延迟效应. 因此在分析CDK1-Plk1-APC信号回路中的时间延迟效应方面, 可以只考虑引起振荡的基本元素正反馈反应物CDK1, 以及负反馈反应物APC间的时间延迟($ {\tau _{\text{C}}} $ 和$ {\tau _{\text{A}}} $ )效应, 确定时间延迟($ {\tau _{\text{C}}} $ 和$ {\tau _{\text{A}}} $ )对$ [{\text{CDK1}}] $ 和$ [{\text{APC}}] $ 的影响, 即可明确时间延迟效应对CDK1-Plk1-APC信号通路的影响特性. 为了进一步理解时间延迟对CDK1-Plk1-APC信号通路稳定性的影响, 可以分析时间延迟对$ [{\text{CDK1}}] $ 和$ [{\text{APC}}] $ 相空间轨迹的影响.图3 显示了不同时间延迟$ {\tau _{\text{C}}} $ 条件下, $ [{\text{CDK1}}] $ 和$ [{\text{APC}}] $ 对应的相空间轨迹, 从图3 可以看出, 较小的$ {\tau _{\text{C}}} $ 条件下的相空间轨迹朝着极限循环螺旋上升, 形成稳定的极限循环圈, 并且存在稳定点, 意味着系统呈现了持续稳定的周期性振荡. 随着$ {\tau _{\text{C}}} $ 的增大, 振荡模式有了逐渐的改变, 致使较大$ {\tau _{\text{C}}} $ 条件下的相空间轨迹循环圈出现“锐化”现象, 随着$ {\tau _{\text{C}}} $ 的进一步增大, 相空间轨迹圈呈现出更加显著的“锐化”尖点. 由此表明, 通过时间延迟的调控作用, 可以不同程度地改变CDK1和APC的振荡模式, 这种调控作用源于生物系统固有的生化特性. 其中包括APC的细胞周期不同阶段活性的增强或降低, 以及中间反应物Plk1等在关键的途径点的协同调节作用. Vodermaier等[33 ] 的研究已经发现, APC的活性在G1期和S期之间的边界处最小化, 在M期结束时达到最大值以完成有丝分裂, 在G1期逐渐降低, 并达到最小值. Plk1作为有丝分裂事件的关键调节剂, 不仅可以控制中心体成熟、双极纺锤体形成、姐妹染色单体分离、后期促进复合物/环体 (APC/C) 活化和有丝分裂退出, 还可以调节许多非有丝分裂事件, 例如DNA复制、DNA损伤应答和DNA损伤检查点恢复、染色体动力学和微管动力学等[34 ] .图 3 不同$ {\tau _{\text{C}}} $ 条件下, $ [{\text{CDK1}}] $ 与$ [{\text{APC}}] $ 对应的相图.Figure3. Phase plots of $ [{\text{CDK1}}] $ vs . $ [{\text{APC}}] $ at different $ {\tau _{\text{C}}} $ .图4(a) 显示较小的$ {\tau _{\text{A}}} $ 对应着的稳定循环圈暗含了$ [{\text{CDK1}}] $ 和$ [{\text{APC}}] $ 振荡的稳态性. 随着$ {\tau _{\text{A}}} $ 的增大, 在$ {\tau _{\text{A}}} = 1.5 $ 和$ {\tau _{\text{A}}} = 2.0 $ 时, $ [{\text{CDK1}}] $ 和$ [{\text{APC}}] $ 对应的相空间轨迹循环圈出现“锐化”尖点. 在$ {\tau _{\text{A}}} = 2.0 $ 时, 图4(b) 中$ [{\text{APC}}] $ 随时间演化出现了双峰振荡模式, 相对图1 中τ A = 0—1.5时$ [{\text{APC}}] $ 单峰振荡模式有所改变. 由此可以确定, 时间延迟效应可以使得CDK1-Plk1-APC通路中基因激活、蛋白质合成或多聚化周期性振荡模式改变, 从单峰周期性振荡态转变为双峰振荡态, 进而在一程度上改变着细胞周期动力学, 调节细胞周期进程.图 4 不同$ {\tau _{\text{A}}} $ 条件下, $ [{\text{CDK1}}] $ 与$ [{\text{APC}}] $ 对应的相图, 以及$ {\tau _{\text{A}}} = 2.0 $ 时, $ [{\text{CDK1}}] $ 与$ [{\text{APC}}] $ 随时间的演化Figure4. Phase plots of $ [{\text{CDK1}}] $ vs $ [{\text{APC}}] $ different $ {\tau _{\text{A}}} $ , and temporal evolutions of the levels of $ [{\text{CDK1}}] $ and $ [{\text{APC}}] $ for $ {\tau _{\text{A}}} = 2.0 $ .[26 -28 ] , 为了考察在噪声环境中, 时间延迟如何影响CDK1-Plk1-APC信号通路, 在这里考虑高斯白噪声对体系中正反馈CDK1的扰动, 基于Steuer等[27 ] 的研究, 在高斯白噪声扰动环境下, CDK1反应速率时间延迟的动力学方程由方程(1 )变为$ \xi {{(}}t{{)}} $ 为高斯白噪声, 且$\langle \xi {{(}}t{{) \rangle = 0}}$ , $\langle \xi {{(}}t{{)}}\xi {{(}}t'{{) \rangle = }} $ $ \delta {{(}}t - t'{{)}}$ , D 为噪声幅.图5 显示了噪声幅为D = 0.01和D = 0.05时, $ [{\text{CDK1}}] $ 随时间的演化, 以及$ [{\text{CDK1}}] $ 和$ [{\text{APC}}] $ 对应的相图. 从图5 可以看出, 噪声扰动明显地改变了$ [{\text{CDK1}}] $ 随时间演化的动力学特性, $ [{\text{CDK1}}] $ 和$ [{\text{APC}}] $ 对应的相空间轨迹不再是稳定的循环圈, 稳定点不再存在, 尤其是噪声幅较大时, 噪声扰动效应增强, 体系稳定性显著改变, 这时, CDK1/APC系统振荡动态环节失稳, 将可能遇到Hopf分岔(Hopf bifurcation)现象[35 -37 ] . 因此, 噪声的存在不仅通过增加更多的无序性(例如系统中CDK1基因激活、循环降解、多聚化的涨落等)来改变系统的动力学行为, 而且还可能导致其明显的质的改变.图 5 噪声幅D = 0.01和D = 0.05时, $ [{\rm{CDK1}}]$ 随时间的演化, 以及与$ [{\rm{APC}}]$ 相对应的相图Figure5. Temporal evolutions of the levels of $ [{\rm{CDK1}}]$ , and phase plots of $ [{\rm{CDK1}}]$ vs. $ [{\rm{APC}}]$ for D = 0.01 and D = 0.05.图6 呈现了在不同时间延迟条件下, 噪声幅为D = 0.01和D = 0.05时, $ [{\text{CDK1}}] $ 随时间的演化, 以及与$ [{\text{APC}}] $ 相对应的相图. 从图6 可以看出, 在噪声幅为D = 0.01条件下, $ [{\text{CDK1}}] $ 随时间演化的周期性振荡模式的改变, 通过减少时间延迟, 降低振荡幅度, 逐渐调节振荡频率, $ [{\text{CDK1}}] $ 被噪声扰动改变了的周期性振荡, 几乎可以被完全调节恢复($ [{\text{CDK1}}] $ 随时间的演化, 在较小时间延迟条件下均呈现了周期性稳定的振荡, 以及与$ [{\text{APC}}] $ 相对应的相图, 最终形成了稳定的极限循环圈). 由此表明, 系统通过反馈机制调节生理反应, 从感知某种干扰(噪声效应)到建立适当的生理反应也会存在时间延迟, 在较小噪声环境中, CDK1/APC系统通过自调节时间延迟(激活或灭活通路中相关的基因激活, 以促进或抑制相关的蛋白合成), 改变振荡幅度或振荡周期, 重新自调控, 使系统恢复稳定的周期性振荡, 细胞周期重新恢复周期性分裂功能, 这样, 在某些情况下, 生物系统通过生化特性固有的时间延迟增强了自身对噪声的抗性, 确保了体系的鲁棒性.图 6 不同时间延迟条件下, 噪声幅为D = 0.01和D = 0.05时, $ [{\text{CDK1}}] $ 随时间的演化, 以及与$ [{\text{APC}}] $ 相对应的相图Figure6. Temporal evolutions of the levels of $ [{\text{CDK1}}] $ , and phase plots of $ [{\text{CDK1}}] $ vs . $ [{\text{APC}}] $ for D = 0.01 and D = 0.05 at different time delays.图6 也显示了在较大在噪声幅条件下(D = 0.05), $ [{\text{CDK1}}] $ 呈现了一种阻尼振荡模式, 其随时间的演化周期性不能再被恢复. 由此表明了较强的噪声, 会使得CDK1/APC系统周期性振荡动力学出现较大改变, 通过体系中的时间延迟, 系统周期性动力学演化为阻尼振荡模式, 系统原有的振荡模式很难再恢复. $ [{\text{CDK1}}] $ 和$ [{\text{APC}}] $ 相对应的相图也显示了不稳定的渐进式循环圈, 应证了体系振荡模式的改变. 另外, 相图中渐进式循环极限圈表明了体系在太大的噪声信号的扰动下, 动力学特性已经被显著改变, 这样使得Hopf分叉到达另一稳定振荡态, 在CDK1/APC振荡系统表现为从原有的稳定周期性振荡模式转变为阻尼振荡. 这是由于, 源于细胞自然生长率、遗传因子、变异因子、生化反应的噪声信号[29 ,30 ] , 在时间上的突然, 会损害细胞周期蛋白或者破坏相关基因激活, 以至干扰有丝分裂退出和DNA复制[38 ] , 从而影响细胞周期进程.图7 呈现了在不同时间延迟、噪声幅条件下, $ [{\text{CDK1}}] $ , $ [{\text{Plk1}}] $ , $ [{\text{APC}}] $ 的功率谱密度(PSD)分布. 从图7 可以看出, 在低噪声幅(D = 0.01) 条件下, $ [{\text{CDK1}}] $ , $ [{\text{Plk1}}] $ , $ [{\text{APC}}] $ 的PSD呈现了单峰(当$ {\tau _{\text{C}}} = $ $ {\tau _{\text{P}}} = {\tau _{\text{A}}} = {\text{0}}.{\text{5}} $ )和双峰(当$ {\tau _{\text{C}}} = {\tau _{\text{P}}} = {\tau _{\text{A}}} = {\text{0}}.{\text{01}} $ )频带分布. 比较不同的时间延迟, 可以发现, 相对较长的时间延迟, 较短的时间延迟使得PSD分布频带由低频(单峰)向高频(双峰)转移. 由此表明, 在CDK1/APC系统振荡过程中, 通过具有不同时间延迟的正负反馈, 改变细胞周期振荡频带分布, 在一定程度上消除噪声影响, 以此调节细胞周期过程, 进而调节复杂非周期性的混沌节律, 帮助确保依赖于CDK1的有丝分裂事件的完成, 使系统恢复生成稳定的周期性生理进程.图 7 不同时间延迟、噪声幅条件下, $ [{\text{CDK1}}] $ , $ [{\text{Plk1}}] $ , $ [{\text{APC}}] $ 的功率谱密度(PSD)Figure7. power spectral density of $ [{\text{CDK1}}] $ , $ [{\text{Plk1}}] $ and $ [{\text{APC}}] $ at different time delays and noise amplitudes.图7 也显示了在较高噪声幅(D = 0.05) 条件下, $ [{\text{CDK1}}] $ , $ [{\text{Plk1}}] $ , $ [{\text{APC}}] $ 的PSD呈现了较为紊乱的多峰频段分布, 由此表明了CDK1/APC系统周期性振荡动力学特性的改变, 对应着图6 中呈现的系统由周期性动力学演化为阻尼振荡. 对于较小的噪声幅, CDK1/APC系统出现围绕其稳态的微小涨落(系统中CDK1基因激活、循环降解、多聚化的涨落等), 相空间本身的偏移受到噪声的影响不大, 通过时间延迟等自调节, 可以使得系统维持原有的稳定周期性振荡态. 但是, 随着噪声强度的增加, 系统一回到稳定状态, 便立即进行下一次较强的激活波动, 对于较大的噪声幅度, CDK1/APC系统的动态受到激活涨落的支配, 在这种情况下, 噪声会引起较大的偏离原来稳定周期性振荡态的偏移, 在很大程度上影响细胞周期进程.4.结 论 本文建立动力学理论模型, 研究CDK1/APC系统振荡过程中, 时间延迟对系统动力学的影响, 以及系统在噪声环境中的时间延迟效应. 研究发现, 在不同时间延迟条件下, $ [{\text{CDK1}}] $ , $ [{\text{Plk1}}] $ 和$ [{\text{APC}}] $ 随时间演化呈现了周期演化振荡特性, 表明了细胞的周期性进程. 随着$ {\tau _{\text{C}}} $ , $ {\tau _{\text{A}}} $ , $ {\tau _{\text{P}}} $ 的增大CDK1-Plk1-APC信号通路中各基因、蛋白质激活合成的时间延迟, 导致各组分出现较长时间的信号响应性, 使得各组分量积蓄增多, $ [{\text{CDK1}}] $ , $ [{\text{Plk1}}] $ 和$ [{\text{APC}}] $ 随时间的演化的振荡周期变长、振幅增大. 通过分析$ {\tau _{\text{C}}} $ , $ {\tau _{\text{A}}} $ , $ {\tau _{\text{P}}} $ 的变化对$ [{\text{CDK1}}] $ , $ [{\text{Plk1}}] $ , $ [{\text{APC}}] $ 随时间演化的振荡影响, 研究发现, 微分方程组模型化体系的演化, 中间反应物(例如Plk1), 在数学描述中等效于正反馈与负反馈反应物间的时间延迟效应. 通过考察不同$ {\tau _{\text{C}}} $ 条件下$ [{\text{CDK1}}] $ 和$ [{\text{APC}}] $ 对应的相空间轨迹, 可以发现, 较小的$ {\tau _{\text{C}}} $ 条件下的相空间轨迹朝着极限循环螺旋上升. 并形成稳定的极限循环圈, 意味着系统呈现了持续的稳定循环振荡, 随着时间延迟的改变, 相空间轨迹循环圈出现“锐化”尖点, 体系振荡模式呈现出了相应的变化, 由此表明了时间延迟会改变体系的动力学特性.[27 ,28 ] . 通过考察高斯白噪声对体系中CDK1的扰动, 可以发现, 噪声扰动明显地改变了$ [{\text{CDK1}}] $ 随时间演化的动力学特性, $ [{\text{CDK1}}] $ 和$ [{\text{APC}}] $ 对应的相空间轨迹不再是稳定的循环圈. 在较小噪声环境中, CDK1/APC系统通过自调节时间延迟, 改变振荡幅度或振荡周期, 重新自调控, 使系统恢复稳定的周期性振荡, 细胞周期重新恢复周期性分裂功能. 生物系统通过自调节, 使其具有很强的稳定性, 变化体系中的时间延迟效应, 可以在一定程度上消除噪声引起的扰动, 从而再次恢复形成稳定的信号通路, 表明了时间延迟效应还可能防止噪声引起的CDK1/APC系统相空间轨迹的改变, 稳定振荡相位. 在较大噪声幅条件下, 由于时间延迟效应, $ [{\text{CDK1}}] $ 呈现了阻尼振荡模式, 其随时间演化的周期性不能再被恢复. 由此表明了较强的噪声, 会使得CDK1/APC系统周期性振荡动力学特性呈现较大变化, 体系稳定性显著改变, 这时, CDK1/APC系统振荡动态失稳, 可能出现Hopf分岔现象[33 ,34 ] . 鞍结分岔(saddle-node bifurcation)决定了自激活[35 ] , 通过改变体系中的时间延迟, 在CDK1/APC振荡系统表现为从原有稳定的周期性振荡模式转变为阻尼振荡, 系统原有的动力学模式很难再恢复. Pomerening等[38 ] 对细胞周期振荡器系统的剖析, 已经证明正反馈的缺失会产生阻尼振荡, 这为我们理解源于细胞自然生长率、遗传因子、变异因子、生化反应等涨落引发的噪声信号, 损害细胞周期进程提供了一个示例.[39 ,40 ] . 本文的理论模型与结果揭示了时间延迟如何影响CDK1-Plk1-APC通路信号, 进一步深刻理解了诸如非洲爪蟾胚胎等细胞周期中的时间延迟效应, 揭示的原理也可适用于其他种类细胞的细胞周期, 有助于设计可靠的合成时钟, 并可为设计调控细胞周期、阻断肿瘤转变的通路治疗方案提供理论依据. 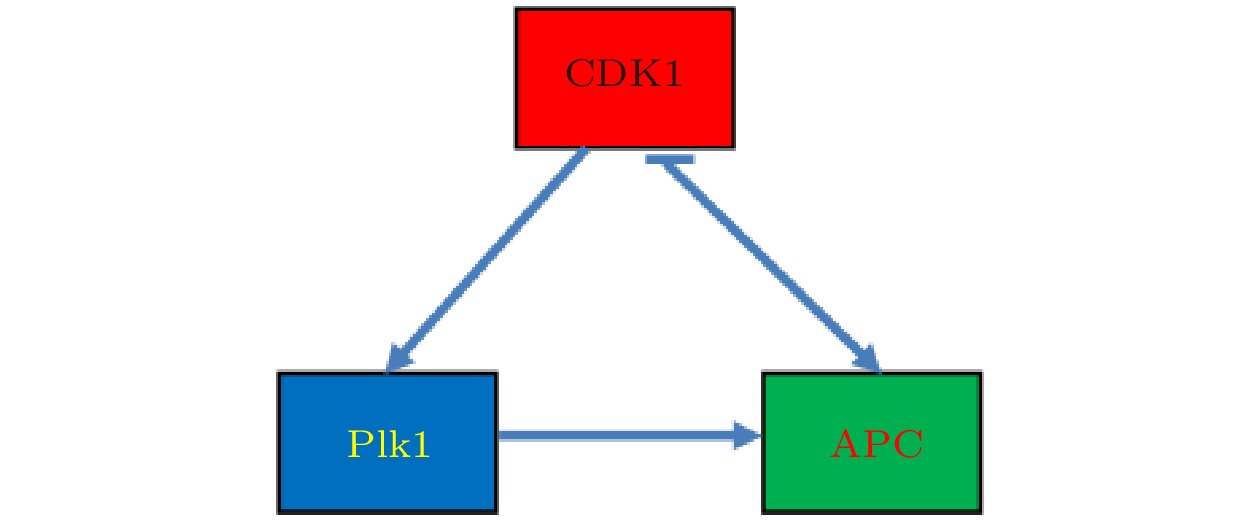 图 1 CDK1-Plk1-APC信号通路模型示意图.
图 1 CDK1-Plk1-APC信号通路模型示意图.
































































































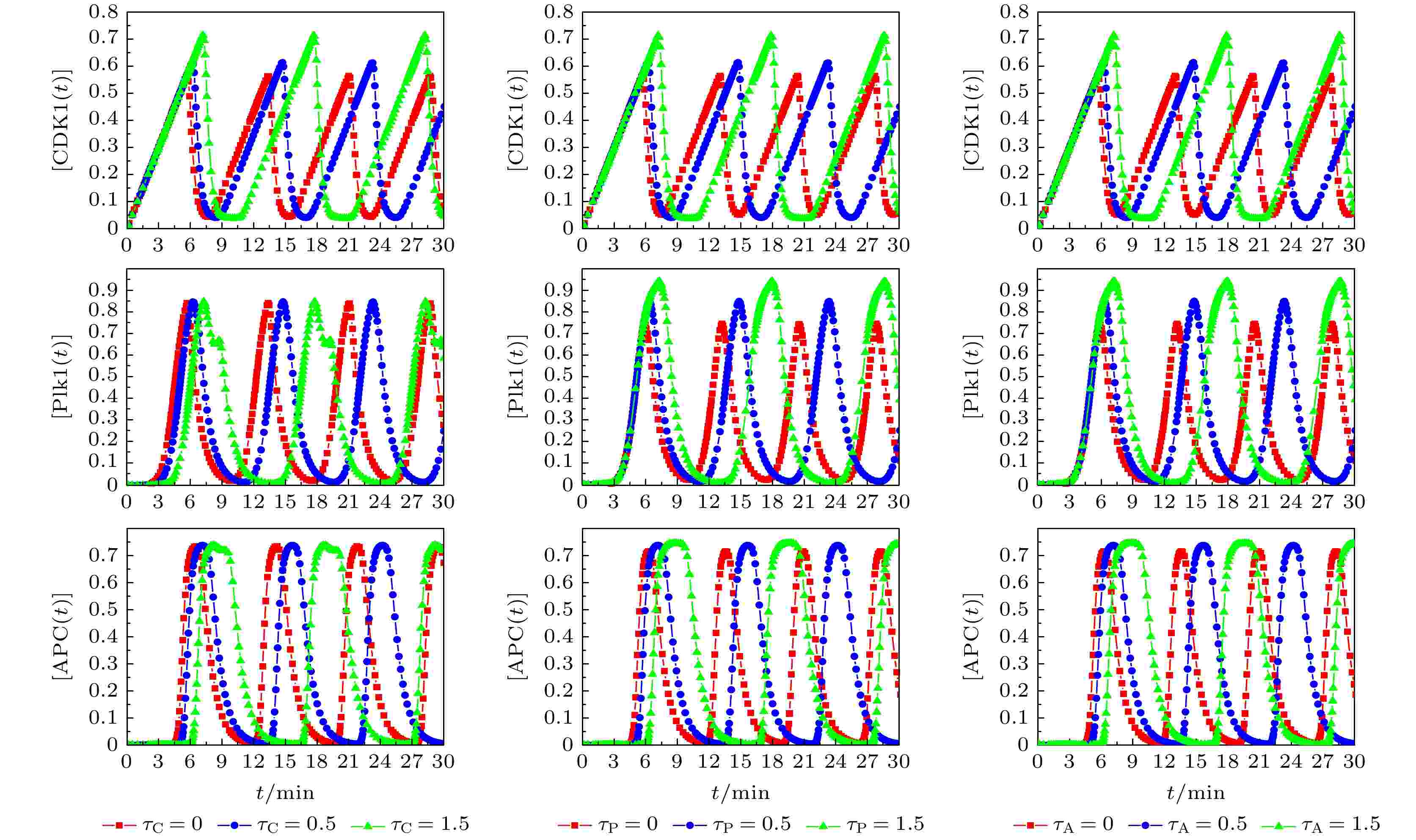 图 2 不同时间延迟条件下,
图 2 不同时间延迟条件下, 



































































































































































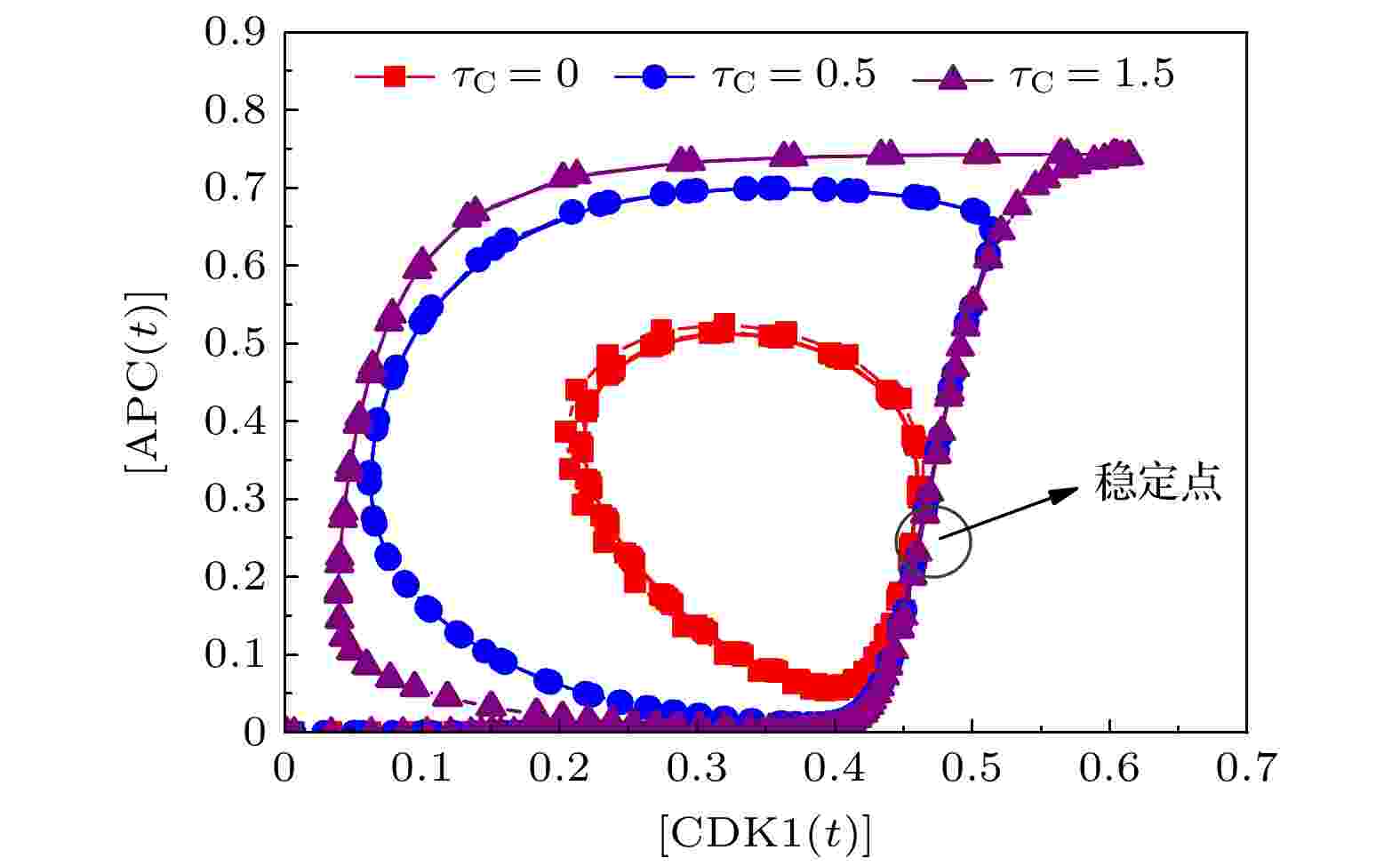 图 3 不同
图 3 不同


































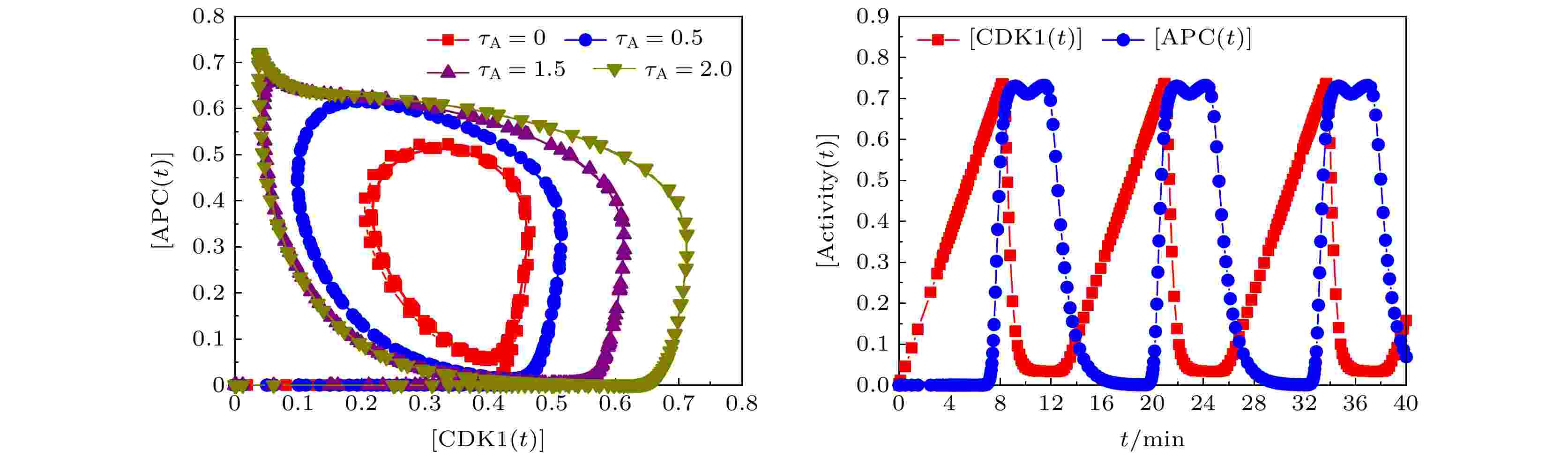 图 4 不同
图 4 不同











































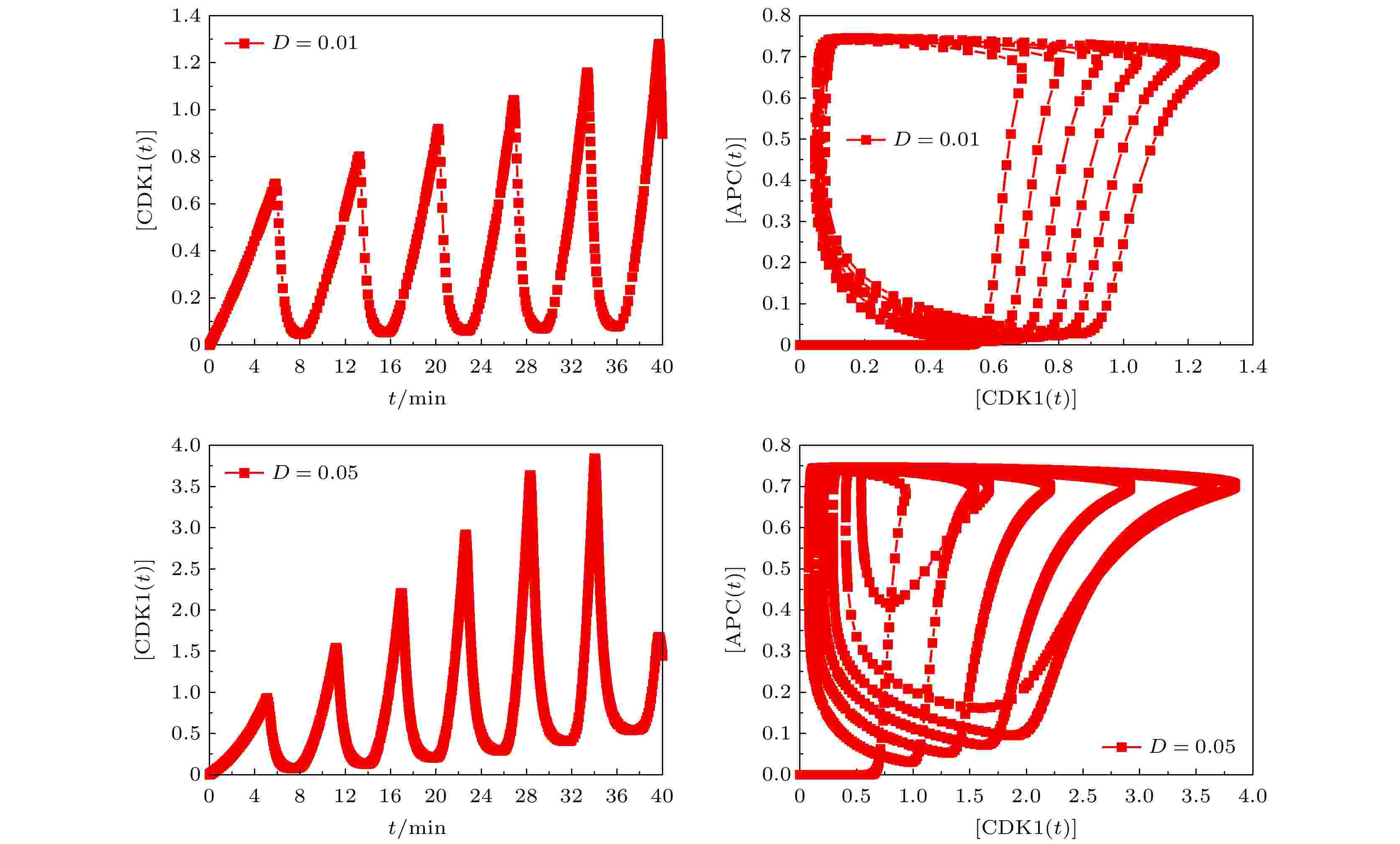 图 5 噪声幅D = 0.01和D = 0.05时,
图 5 噪声幅D = 0.01和D = 0.05时, 


























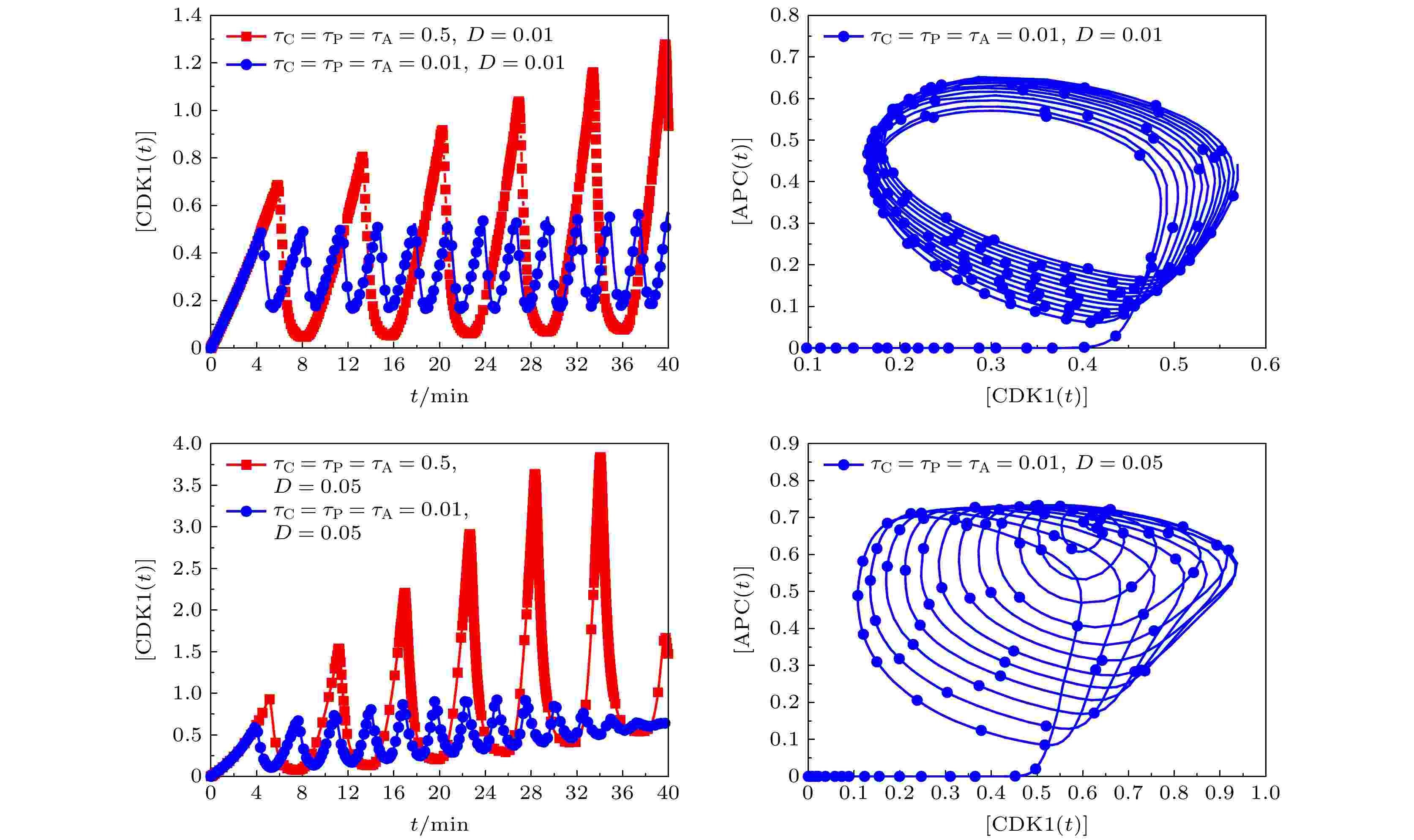 图 6 不同时间延迟条件下, 噪声幅为D = 0.01和D = 0.05时,
图 6 不同时间延迟条件下, 噪声幅为D = 0.01和D = 0.05时, 


























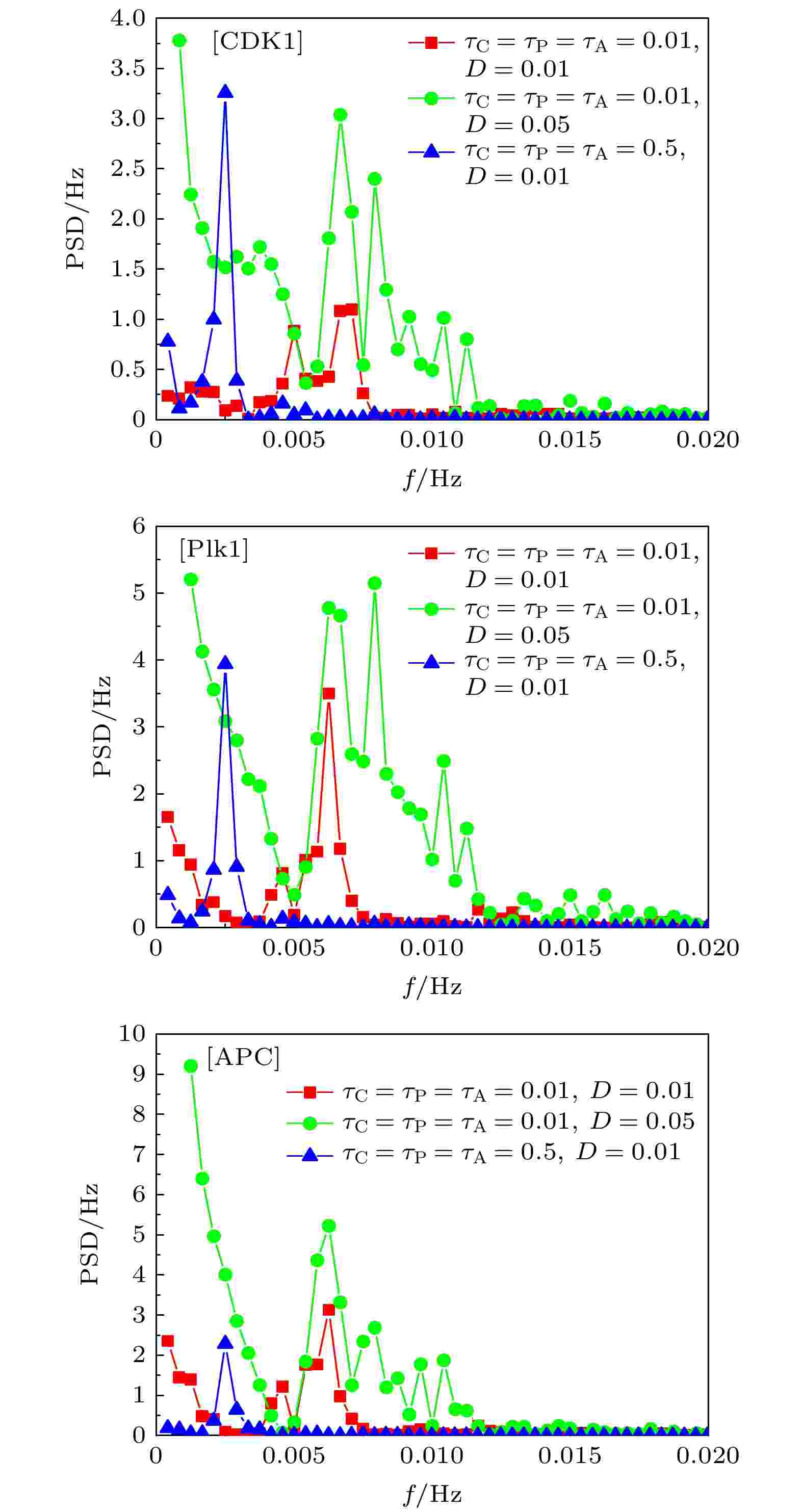 图 7 不同时间延迟、噪声幅条件下,
图 7 不同时间延迟、噪声幅条件下, 



















































































