摘要:为了深入探究空化泡群中气泡的动力学特性, 建立了超声驱动下考虑水蒸气的蒸发和冷凝的泡群中泡的动力方程. 基于该方程, 研究了泡群中泡的位置、泡的数量、泡的初始半径对其动力学特性的影响, 探究了超声作用下球状泡群中气泡半径、能量、温度、压力和气泡内水蒸气分子数的变化规律. 结果表明: 泡群中泡的运动受到周围气泡的抑制作用; 泡群中泡的初始半径大小对泡群中泡的半径、能量、温度、压力和气泡内水蒸气分子数有显著影响; 泡群中泡的位置距离泡群中心越远, 泡的膨胀半径越大; 随着泡群中泡的数目增加, 泡的振幅减小; 超声频率增加, 泡群中泡的空化效应减弱; 超声声压增加, 泡群中泡的空化效应增加. 研究结果为超声空化泡群的研究提供了理论参考.
关键词: 超声空化/
球状泡群/
蒸发和冷凝/
动力学特性

English Abstract

全文HTML

--> --> -->

超声空化是指液体中的微小泡核在声波作用下被激活, 表现为泡核的振荡、生长、收缩乃至崩溃等一系列动力学过程^[1]. 空化气泡在崩溃时, 泡内会形成高温高压现象^[2-7]. 空化气泡崩溃的同时, 还会伴随着声致发光、强烈的冲击波以及微射流等现象的发生^[2]. 利用空化气泡崩溃瞬间产生的高温高压以及冲击射流等极端物理条件, 超声空化在石油开发、癌症治疗、超声清洗和废水处理等领域得到了广泛应用^[8-12].
在超声空化研究中, 为了更好地理解空化效应发生的物理机理, 人们基于Rayleigh空化泡的运动方程发展了单气泡动力学模型来分析空化泡的动力学特性^[13-19]. 文献[13]考虑了动态声空化泡气液分界面处的气体扩散. 文献[14]考虑了动态声空化泡的气液界面上的相变过程. 文献[15]考虑了化学变化对动态声空化泡内外质量交换特性的影响. 文献[16, 17]提出了关于动态声空化泡内外质量交换的唯象模型, 得到了考虑内外质量交换时空化泡的平衡半径. 文献[18]考虑空化泡径向速度很大时对外边界压力梯度的影响. 文献[19]在考虑动态声空化泡的气液界面上的相变情况下, 研究了双频超声对空化泡的动力学特性影响.
但是在实际应用中的空泡总是以多泡(空化泡群)形式存在, 为了探究实际情况下多泡中空化泡的动力学特性, 许多课题组开展了对空化泡群^[20-25]的有关研究. 文献[20]建立了链式泡群和球状泡群内气泡的动力学方程, 分析了泡群内气泡的运动行为和多泡声致发光特征. 文献[21]建立了由不同尺寸气泡组成的泡群的动力学模型, 研究了泡群内气泡初始半径、气泡数量、声频率及声压对气泡动力学特性的影响. 文献[22]从均匀球状泡群内气泡非线性振动方程出发分析了驱动声压幅值、声波频率和液体环境对空化气泡振动特性的影响. 文献[23]从泡群中气泡动力学方程出发, 对泡壁运动方程进行线性约化, 得到球状泡群中气泡谐振频率的表达式, 并给出了泡群中气泡谐振频率与单泡 Minnaert 频率的修正系数. 讨论了泡群中气泡初始半径、气泡数量、气泡之间距离对谐振频率的影响. 文献[24]考虑了气泡壁上的质量交换、热传导和化学反应等效应, 研究了声压幅值、频率和气泡数对球状泡群内的温度和氧化剂生成量的影响. 文献[25]利用气泡群及群内任一气泡的Rayleigh-Plesset 方程并结合van der Waals过程方程, 研究了不同类型气泡组成的混合泡群中的气泡半径、泡内温度和群内压力脉冲变化规律.
以上关于空化泡群的研究, 有的在不考虑气泡内外质量交换的情况下, 建立多气泡动力学模型, 或者在考虑气泡内外质量交换的情况下, 求解气泡群内物理特性变化. 本文在考虑气泡内水蒸气的蒸发和冷凝的前提下, 结合气泡之间的相互作用, 建立了球状泡群中泡的动力学模型, 并探讨了泡在泡群中的不同位置以及泡群中泡的数量、初始半径对泡的动力学特性的影响. 进一步研究了不同声场作用下泡群中气泡半径、能量、温度、压力和气泡内水蒸气分子数的变化.

2

-->

2.1.理论模型

为了建立考虑内外质量交换的球状泡群中空化泡的振动模型, 先作出如下假设: 1) 不考虑球状泡群边界运动对泡群内压力分布的影响; 2) 泡群内空化泡始终为球形, 只做径向运动; 3) 气泡在泡群中分布均匀且初始半径相同; 4) 忽略泡内空气分子数量的改变; 5) 忽略液体密度和液体中超声传递速度的变化; 6) 液体为可压缩性流体, 其表面张力、黏滞性不可忽略; 7) 考虑水蒸气的蒸发和冷凝的影响.
在考虑空化泡内水蒸气的蒸发和冷凝情况下, 距离球状泡群中心r₀处的气泡振动方程可近似表示为^[14,20]

$ \begin{split}&R\ddot{R}\left(1-\frac{\dot{R}}{c}+\frac{\dot{m}}{\rho c}+\frac{3}{2}{M}_{0}\right)\\ & +\frac{3}{2}{\dot{R}}^{2}\left(1-\frac{\dot{R}}{3c}+\frac{2\dot{m}}{3\rho c}+2{M}_{0}\right)\\=\;&\frac{1}{\rho }\left(1+\frac{\dot{R}}{c}\right)\left[{P}_{\text{out}}-A\mathrm{sin}\left(2\text{π}ft\right)-{P}_{0}\right] \\& +\frac{\ddot{m}R}{\rho }\left(1-\frac{\dot{R}}{c}+\frac{\dot{m}}{\rho c}\right) \\&+\frac{\dot{m}}{\rho }\left(\dot{R}+\frac{\dot{m}}{2\rho }+\frac{\dot{R}\dot{m}}{2\rho c}\right)+\frac{R}{\rho c}\frac{\text{d}{P}_{\text{out}}}{\text{d}t},\end{split} $

式中, R, $ \dot R $和$ \ddot R $分别表示泡的半径、半径随时间的变化速度和加速度. $ \dot m $和$ \ddot m $分别代表单位时间内空化气泡单位面积上水蒸气蒸发和冷凝的速度和加速度. c 为水中的声速, P₀ 为水中静压, ρ 为水的密度, A 为超声波的振幅, f 为超声波的频率. ${M_0} = N\dfrac{R}{{{r_{{\text{clust}}}}}}\left( {1 - \dfrac{{{r_0}^2}}{{3{r_{{\text{clust}}}}^2}}} \right)$, 其中r₀为该气泡在球状泡群中的相对位置, N为泡群中气泡总数, r_clust为球状泡群的半径.
P_out (t)为空化气泡外边界处的液体压力, 其表达式为

$ {P_{{\text{out}}}}\left( t \right) = {P_{{\text{in}}}}\left( t \right) - \frac{{2\sigma }}{R} - \frac{{4\mu }}{R}\left( {\dot R - \frac{{\dot m}}{\rho }} \right) - {\dot m^2}\left( {\frac{1}{\rho } - \frac{1}{{{\rho _{\text{a}}}}}} \right), $

其中, P_in (t)为空化泡的泡内压强, $ \sigma $为水的表面张力, $\mu $ 为水的黏性系数, $ {\rho _{\text{a}}} $为气泡内气体分子的密度, 其表达式为

$ {\rho _{\text{a}}} = \frac{{{M_{{{\text{H}}_{\text{2}}}{\text{O}}}}{n_{{{\text{H}}_{\text{2}}}{\text{O}}}} + {M_{{\text{air}}}}{n_{{\text{air}}}}}}{{V{N_{\text{A}}}}}, $

其中, $ {M_{{{\text{H}}_{\text{2}}}{\text{O}}}} $和$ {M_{{\text{air}}}} $分别为水蒸气和空气的摩尔质量, $ {n_{{{\text{H}}_{\text{2}}}{\text{O}}}} $和$ {n_{{\text{air}}}} $分别为气泡内水蒸气分子和空气分子的总数量, V 为空化泡的体积, $ {N_{\text{A}}} $为阿伏伽德罗常数.
计算P_in (t)时, 采用van der Waals状态方程:

$ {P_{{\text{in}}}}\left( t \right) = \frac{{{R_{\text{g}}}Tn}}{{\left( {V - nb} \right)}} - \frac{{a{n^2}}}{{{V^2}}}, $

式中, $ n = \left( {{n_{{\text{air}}}} + {n_{{{\text{H}}_{\text{2}}}{\text{O}}}}} \right)/{N_{\text{A}}} $, a 和b 是van der Waals量(二者会随着泡内水蒸气分子数的变化而改变), R_g是气体常数, T是气泡内的温度. a 和b 的变化方程为

$\begin{split}a = \;&{a_{{\text{air}}}}{\left( {\frac{{{n_{{\text{air}}}}}}{{{n_{\text{t}}}}}} \right)^2} + 2{a_{{\text{air}} \text- {{\text{H}}_{\text{2}}}{\text{O}}}}\left( {\frac{{{n_{{\text{air}}}}}}{{{n_{\text{t}}}}}} \right)\left( {\frac{{{n_{{{\text{H}}_{\text{2}}}{\text{O}}}}}}{{{n_{\text{t}}}}}} \right)\\&+ {a_{{{\text{H}}_{\text{2}}}{\text{O}}}}{\left( {\frac{{{n_{{{\text{H}}_{\text{2}}}{\text{O}}}}}}{{{n_{\text{t}}}}}} \right)^2},\end{split}$

$\begin{split}b =\;& {b_{{\text{air}}}}{\left( {\frac{{{n_{{\text{air}}}}}}{{{n_{\text{t}}}}}} \right)^2} + 2{b_{{\text{air}} - {{\text{H}}_{\text{2}}}{\text{O}}}}\left( {\frac{{{n_{{\text{air}}}}}}{{{n_{\text{t}}}}}} \right)\left( {\frac{{{n_{{{\text{H}}_{\text{2}}}{\text{O}}}}}}{{{n_{\text{t}}}}}} \right)\\&+ {b_{{{\text{H}}_{\text{2}}}{\text{O}}}}{\left( {\frac{{{n_{{{\text{H}}_{\text{2}}}{\text{O}}}}}}{{{n_{\text{t}}}}}} \right)^2},\end{split}$

其中, ${a_{{\text{air}}\text-{{\text{H}}_{\text{2}}}{\text{O}}}} = \sqrt {{a_{{\text{air}}}} \times {a_{{{\text{H}}_{\text{2}}}{\text{O}}}}}$, $\sqrt[\root{5}3]{{b_{{\text{air-}}{{\text{H}}_{\text{2}}}{\text{O}}}}} = \Big(\sqrt[\root{5}3]{{b_{{\text{air}}}}} \;+ $$ \sqrt[\root{5}3] {b_{\rm{H_2O}}}\Big)/2$, $ {a_{{\text{air}}}} $和$ {b_{{\text{air}}}} $, $ {a_{{{\text{H}}_{\text{2}}}{\text{O}}}} $和$ {b_{{{\text{H}}_{\text{2}}}{\text{O}}}} $分别为空气、水蒸气的van der Waal量, $ {n_{\text{t}}} = {n_{{{\text{H}}_{\text{2}}}{\text{O}}}} + {n_{{\text{air}}}} $.
空化气泡内的温度(T)可以用如下方程计算:

$ T = \frac{{{N_{\text{A}}}^2EV + {{\left( {{n_{{{\text{H}}_{\text{2}}}{\text{O}}}} + {n_{{\text{air}}}}} \right)}^2}a}}{{\left( {{n_{{{\text{H}}_{\text{2}}}{\text{O}}}}{C_{v,}}_{{{\text{H}}_{\text{2}}}{\text{O}}} + {n_{{\text{air}}}}{C_{v,}}_{{\text{air}}}} \right){N_{\text{A}}}V}}, $

其中, E 是气泡的内能, $ {C_{v, {\text{air}}}} $和$ {C_{v, {{\text{H}}_{\text{2}}}{\text{O}}}} $是空气和水蒸气的等体摩尔热容. 气泡内能 E 在单位时间的变化为

$ \Delta E = -{P_{{\text{in}}}}\left( t \right)\Delta V\left( t \right) + \frac{{{N_{\text{A}}}}}{{{M_{{{\text{H}}_{\text{2}}}{\text{O}}}}}}4{{\text{π}}^2}\dot me\Delta t, $

式中, 等式右端第一项表示泡内压强在$ \Delta t $时间内导致的空化泡内能变化, $ \Delta V\left( t \right) $表示气泡体积在$ \Delta t $时间内的变化. 等式右端第二项表示泡内的水蒸气分子数量变化在$ \Delta t $时间内产生的气泡内能变化. 其中e 是水蒸气蒸发或冷凝所携带的能量^[14].
空化气泡单位时间单位面积上水蒸气蒸发和冷凝的速率$ \dot m $表示为

$ \dot m = \frac{{{\alpha _{\text{M}}}}}{{{{\left( {2{\text{π}}{R_{\text{v}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}}}\left( {\frac{{{P_{\text{v}}}^ * }}{{{T_0}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}} - \frac{{K{P_{\text{v}}}}}{{{T^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}}}} \right), $

其中, $ {\alpha _{\text{M}}} $为常数^[14], ${R_{\text{v}}} = {{{R_{\text{g}}}} \mathord{\left/ {\vphantom {{{R_{\text{g}}}} {{M_{{{\text{H}}_{\text{2}}}{\text{O}}}}}}} \right. } {{M_{{{\text{H}}_{\text{2}}}{\text{O}}}}}}$为水蒸气的气体常数, $ {P_{\text{v}}}^ * $为气泡内的饱和蒸气压, T₀ 为液体温度, ${P_{\text{v}}} = {{\left( {{n_{{{\text{H}}_{\text{2}}}{\text{O}}}} \times {P_{{\text{in}}}}\left( t \right)} \right)} \mathord{\left/ {\vphantom {{\left( {{n_{{{\text{H}}_{\text{2}}}{\text{O}}}} \times {P_{{\text{in}}}}\left( t \right)} \right)} {\left( {{n_{{{\text{H}}_{\text{2}}}{\text{O}}}} + {n_{{\text{air}}}}} \right)}}} \right. } {\left( {{n_{{{\text{H}}_{\text{2}}}{\text{O}}}} + {n_{{\text{air}}}}} \right)}}$为气泡内的水蒸气分压. K 的表达式为

$ K = {e^{\left( { - {\Omega ^2}} \right)}} - \Omega \sqrt {\text{π}} \int_0^\Omega {{e^{\left( { - {x^2}} \right)}}} {\text{d}}x, $

其中$\Omega = \dfrac{{\dot m}}{{{P_{\text{v}}}}}{\left( {\dfrac{{{R_{\text{v}}}T}}{2}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}$.
$ t + \Delta t $时刻气泡内水蒸气分子数量为

$ {n_{{{\text{H}}_{\text{2}}}{\text{O}}}}\left( {t + \Delta t} \right) = {n_{{{\text{H}}_{\text{2}}}{\text{O}}}}\left( t \right) + \frac{{{N_{\text{A}}}}}{{{M_{{{\text{H}}_{\text{2}}}{\text{O}}}}}}4{{\text{π}}^2}\dot m\Delta t . $

本文在求解空化泡的动力学方程式时, 选择Runge-Kutta法. 计算初始条件为R = R₀, $ \dot R $ = 0, $ \ddot R $ = 0, T = T₀, $ \dot m $ = $ \ddot m $ = 0, P_out = P₀. 水的物性参数为c = 1500 m/s, σ = 0.0725 N/m, μ = 1 × 10^–3 Pa·s, ρ = 1000 kg/m³, P₀ = 1 × 10⁵ Pa. 本文主要研究功率超声作用下, 泡群内不同位置处空化泡的归一化半径、泡内压力、泡内能量、泡内温度以及泡内水蒸气分子数随时间的变化特性.
2

-->

3.1.单泡与泡群中泡的动力学特性

为了研究泡群中泡的动力学特性, 根据(1)式分别计算了单泡、泡群中心的泡和泡群表面的泡的动力学特性, 计算结果如图1所示. 单泡和泡群中泡的初始半径R₀ = 4.5 μm, 根据文献[20-22], 泡群内空化泡个数N = 300, 泡群半径r_clust = 1 × 10^–3 m, 超声波的振幅A =1.5 × P₀, 超声波的频率f = 20 kHz.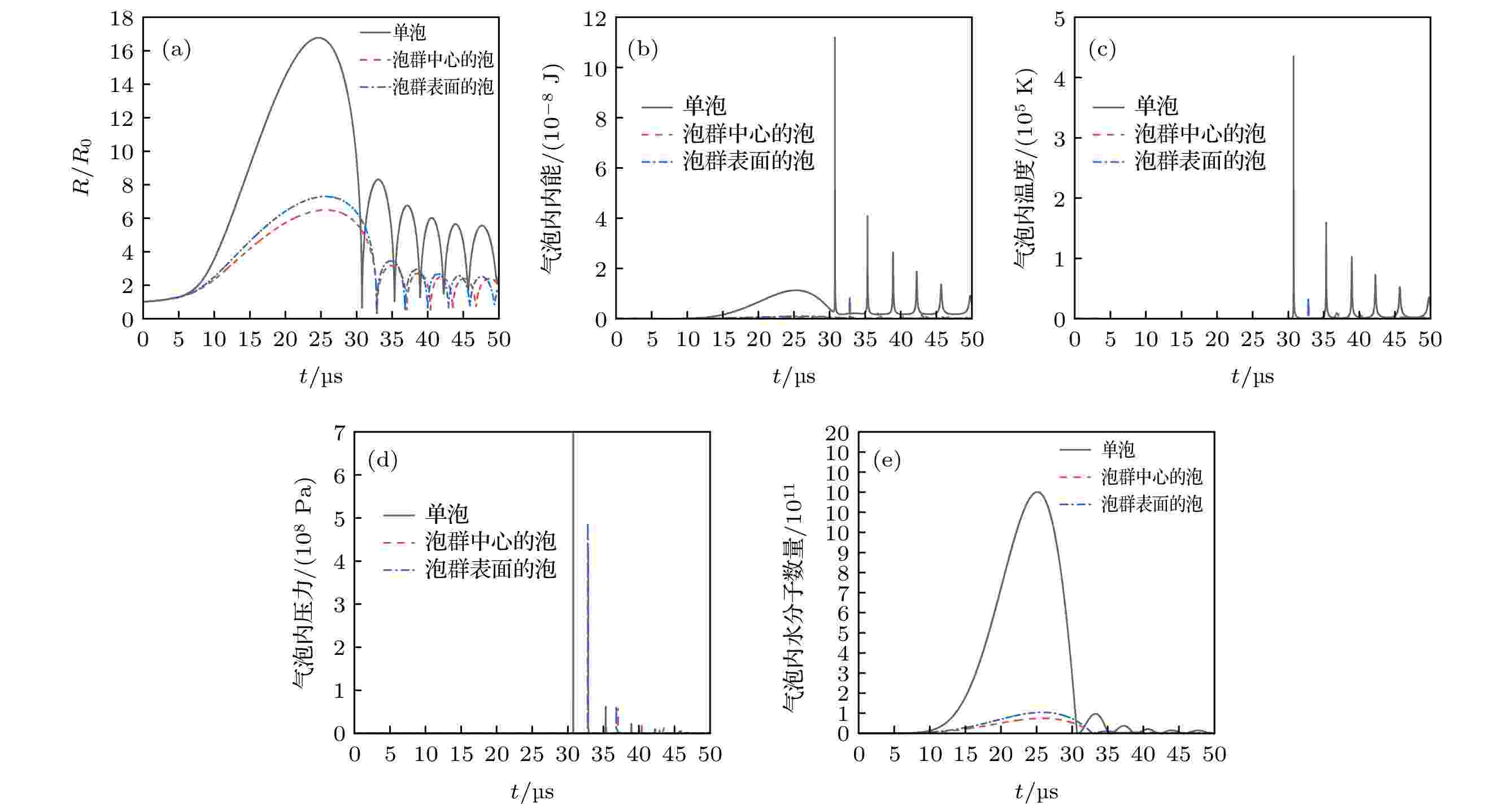
图 1 单泡、泡群中心的泡和泡群表面的泡的动力学特性　(a) 气泡归一化半径随时间的变化曲线; (b) 气泡内内能随时间的变化曲线; (c) 气泡内温度随时间的变化曲线; (d) 气泡内压力随时间的变化曲线; (e) 气泡内水分子数量随时间的变化曲线
Figure1. Dynamical behaviors of a single bubble, a bubble at the center of a bubble group and a bubble on the surface of a bubble group: (a) Change curve of the normalized radius with the time for the bubble; (b) change curve of the internal energy in the bubble with the time; (c) change curve of the temperature in the bubble with the time; (d) change curve of the pressure in the bubble with the time; (e) change curve of the number of water molecules in the bubble with the time.

图1(a)为气泡归一化半径随时间的变化曲线. 比较发现, 单泡的振动幅度明显高于泡群中的泡, 位于泡群表面泡的振动幅度大于位于泡群中心泡的振动幅度; 单泡的膨胀和崩溃时间比泡群中泡的膨胀和崩溃时间更短, 泡群表面的泡比泡群中心的泡先崩溃. 图1(b)为气泡内内能随时间的变化曲线. 可以看出, 单泡的泡内内能远大于位于泡群表面和泡群中心泡的泡内内能. 图1(c)为气泡内温度随时间的变化曲线. 图1(d)为气泡内压力随时间的变化曲线. 结合图1(c)和图1(d)可以看出, 单泡的泡内最高温度和最大压力都要高于位于泡群中泡的泡内最高温度和最高压力, 且位于泡群中心的泡和位于泡群表面的泡的泡内最高温度和最大压力较接近. 图1(e)为气泡内水分子数量随时间的变化曲线, 它的曲线形状与气泡归一化半径随时间的变化曲线趋势一致. 可以看出, 单泡泡内水分子数量最大值远大于位于泡群中泡的泡内水分子数量最大值.
由此可知, 位于泡群中的泡由于受到周围气泡的作用, 其振动幅度更小, 崩溃时间更长, 泡内内能、泡内最高温度、泡内最大压力和泡内水分子数量更小.
2 -->

3.2.初始半径对泡群中心泡的动力学特性的影响

图2给出了泡群中不同初始半径泡的动力学特性. 泡群中泡的初始半径R₀取值分别为4.5, 10.5, 15.5和20.5 μm, 相应的泡内初始水分子个数和空气分子个数也会改变^[14,18]. 泡群内泡的个数N = 300, 泡群半径r_clust = 1 × 10^–3 m, 超声波的振幅A = 1.5 × P₀, 超声波的频率 f = 20 kHz.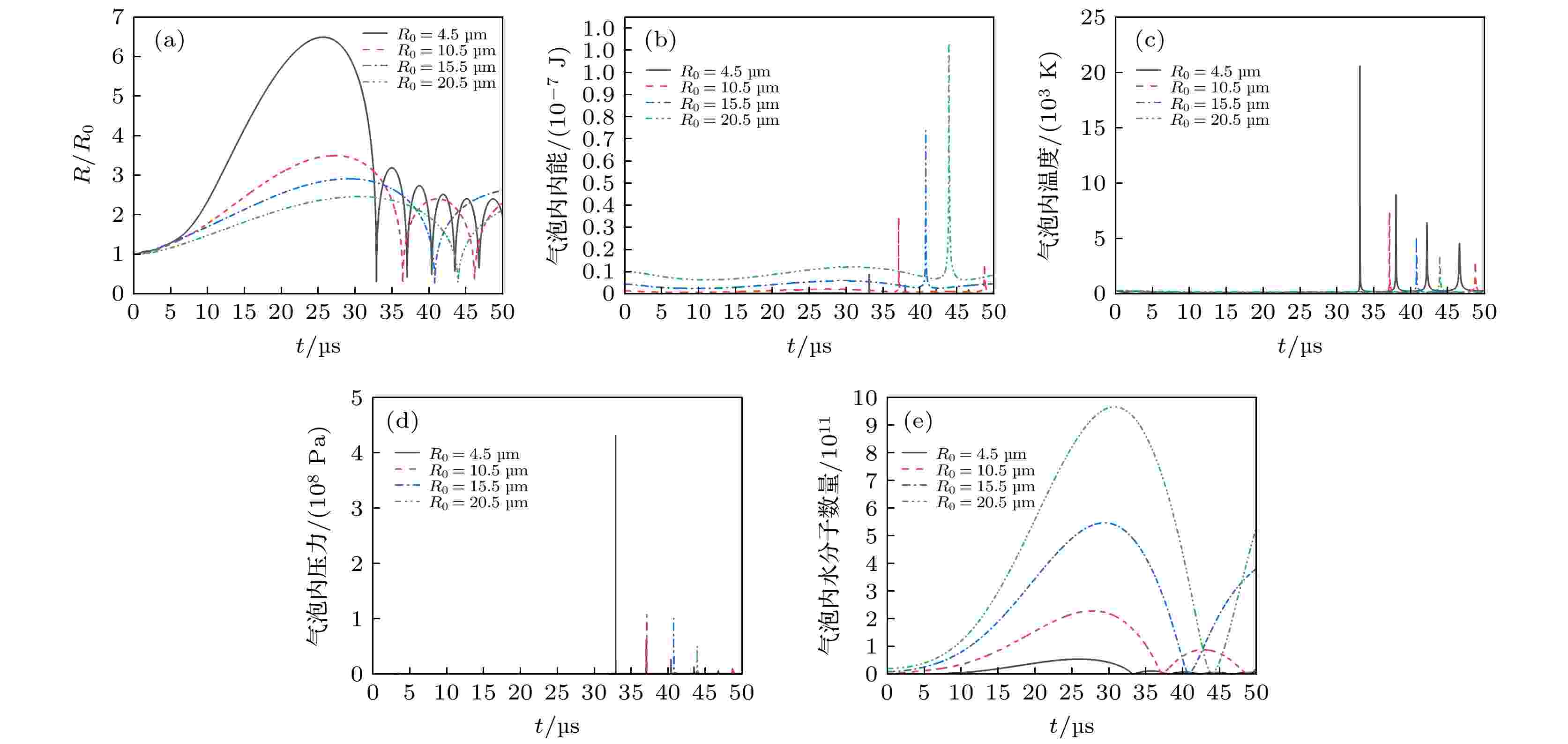
图 2 泡群中不同初始半径的泡的动力学特性　(a) 气泡归一化半径随时间的变化; (b) 气泡内内能随时间的变化曲线; (c) 气泡内温度随时间的变化曲线; (d) 气泡内压力随时间的变化曲线; (e) 气泡内水分子数量随时间的变化曲线
Figure2. Dynamic characteristics of the bubbles with different initial radii in bubble group: (a) Change curve of the normalized radius with the time; (b) change curve of the internal energy in the bubble with the time; (c) change curve of the temperature in the bubble with the time; (d) change curve of the pressure in the bubble with the time; (e) change curve of the number of water molecules in the bubble with the time.

图2(a)为泡中心气泡归一化半径随时间的变化曲线. 可以看出, 在泡群半径相同且泡群内空化泡数目相同的情况下, 初始半径较大的气泡在声场作用下其归一化振幅更小; 初始半径较大的气泡的崩溃时间大于初始半径小的气泡的崩溃时间; 初始半径较大的气泡有较少的振荡. 图2(b)为泡中心气泡内内能随时间的变化曲线. 可以看出, 初始半径较大的气泡其泡内内能更大. 图2(c)和图2(d)分别为泡中心气泡内温度和压力随时间的变化曲线. 观察发现, 初始半径较大的气泡的泡内最高温度和最大压力均小于初始半径较小的气泡的泡内最高温度和最高压力. 图2(e)为泡中心气泡内水分子数量随时间的变化曲线, 可以看出, 初始半径大的气泡内水分子数量更多.
2 -->

3.3.泡群中泡的数量和相对位置对泡群中泡的动力学特性的影响

图3给出了泡群中不同位置的泡的动力学特性. 泡群中泡的初始半径R₀ = 4.5 μm, 根据文献[23-25], 泡群内空化泡个数分别为N = 300, N = 500和N = 1000. 泡群半径r_clust = 1 × 10^–3m, 超声振幅A = 1.5 × P₀, 超声频率f = 20 kHz.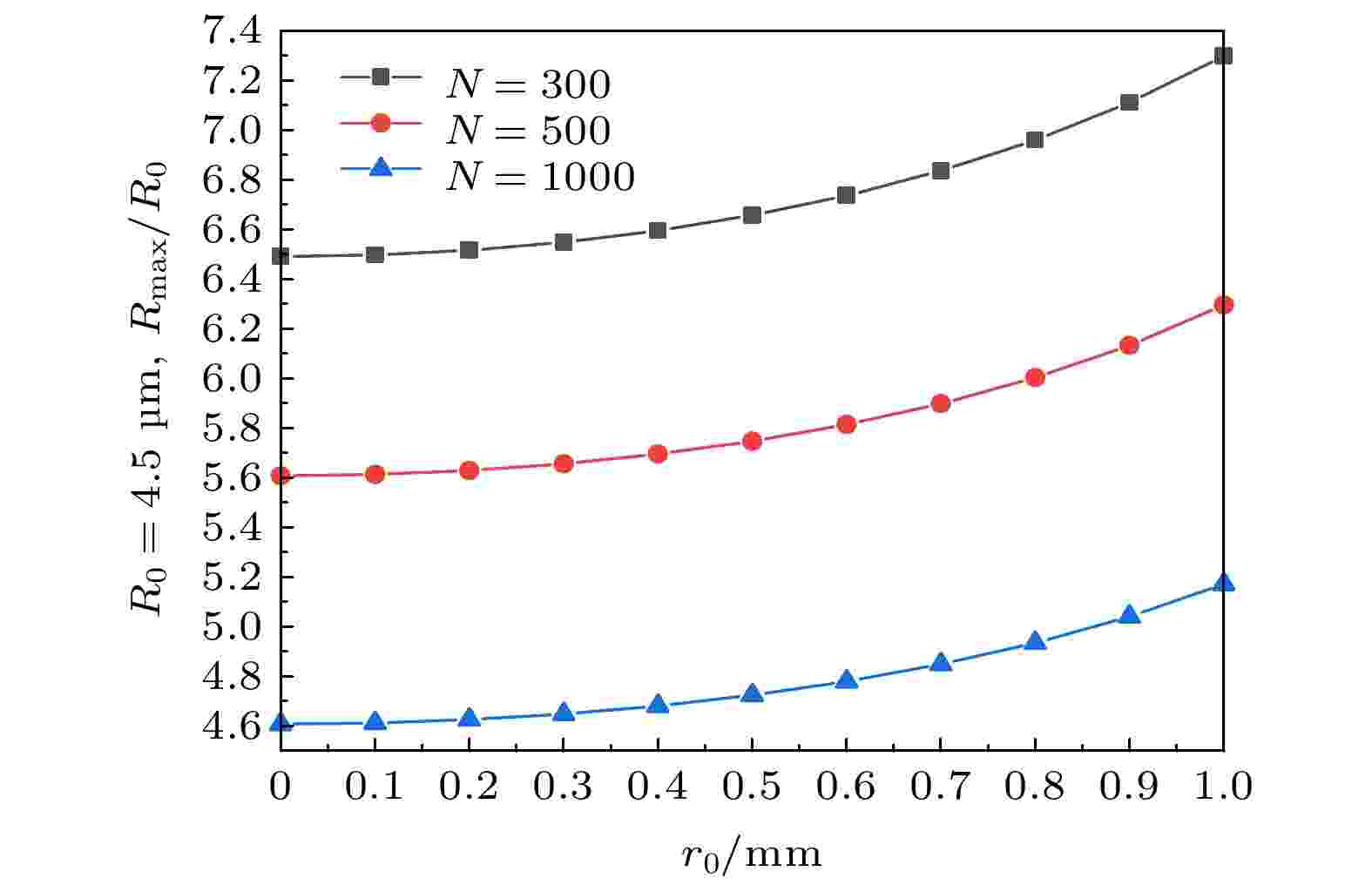
图 3 泡群中不同位置的泡的动力学特性
Figure3. Dynamic characteristics of bubbles at different positions in a bubble group.

图3为含有不同空化泡数量(300, 500和1000个)的泡群中, 初始半径R₀ = 4.5 μm的泡的最大膨胀半径随其距离泡群中心距离的变化关系曲线. 可以发现, 自泡群中心位置到泡群表面的泡, 距离泡群中心越远, 泡的最大膨胀半径R_max越大, R_max/R₀的曲线斜率变大, 说明膨胀半径的增长速率变大. 在泡群半径不变情况下, 随着泡群中空化泡数目的增加(即泡群中空化泡的密度增大), R_max/R₀的值减小, 即泡的振幅减小.
由以上分析可知, 在泡群中, 气泡位置距离泡群中心越远, 它的膨胀半径越大. 随着泡群中泡的数目增加, 泡群中泡的振幅会减小.
2 -->

3.4.声场参数对泡群中泡的动力学特性的影响

3 -->

3.4.1.频率对泡群中泡的动力学特性的影响

图4给出了不同频率下泡群中心泡的动力学特性. 泡群中心泡的初始半径为R₀ = 4.5 μm, 泡群中泡的个数N = 300, 泡群半径r_clust = 1 × 10^–3 m, 超声波的振幅A = 1.5 × P₀, 超声波的频率分别为f = 20 kHz, f = 30 kHz和f = 50 kHz.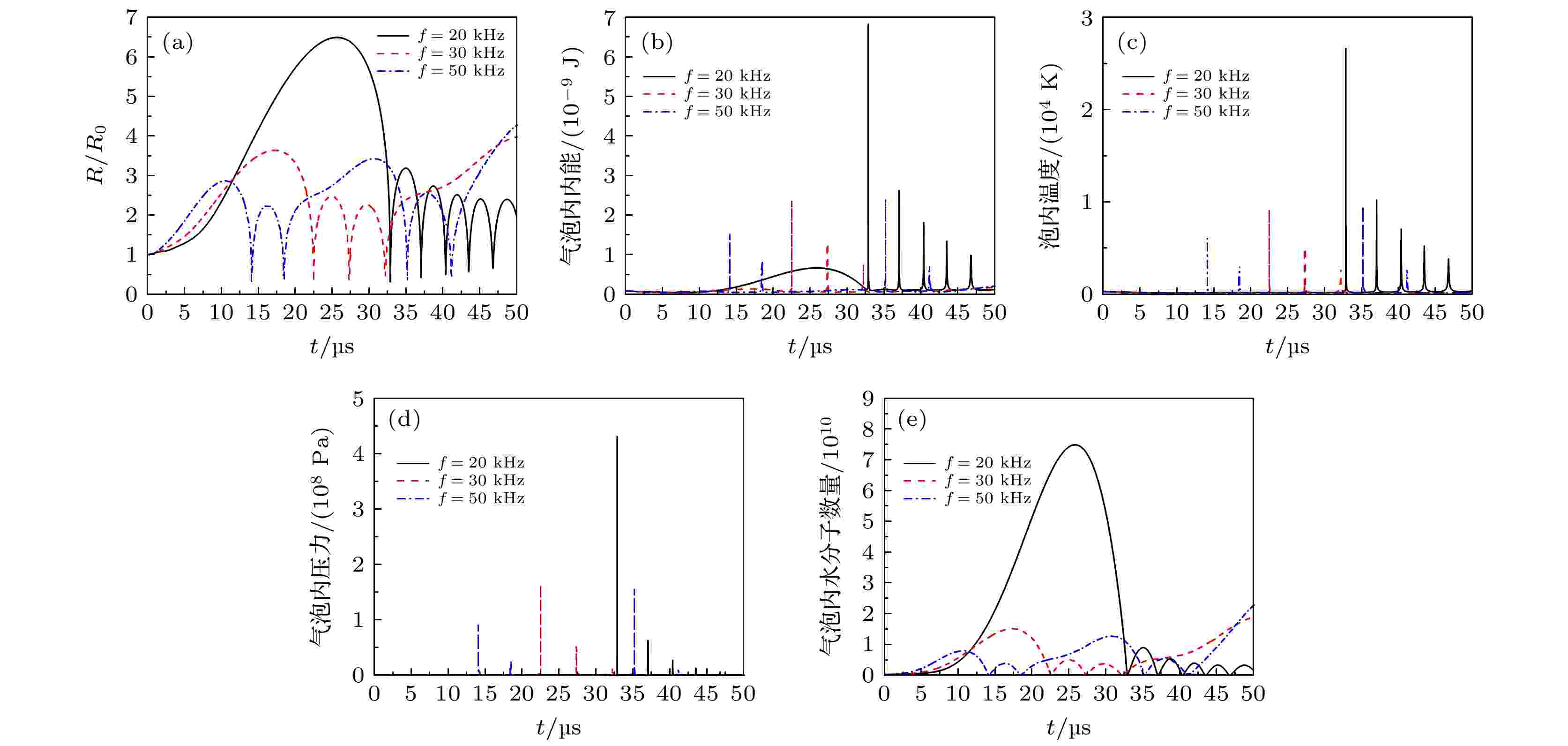
图 4 不同频率下泡群中泡的动力学特性　(a) 气泡归一化半径随时间的变化; (b) 气泡内内能随时间的变化曲线; (e) 气泡内水分子数量随时间的变化曲线
Figure4. Dynamic characteristics of the bubbles in bubble groups at different frequencies: (a) Change curve of the normalized radius with the time for the bubble; (b) change curve of the internal energy in the bubble with the time; (c) change curve of the temperature in the bubble with the time; (d) change curve of the pressure in the bubble with the time; (e) change curve of the number of water molecules in the bubble with the time.

图4(a)为气泡归一化半径随时间的变化曲线. 可以看出, 随着超声频率的增加, 气泡在一个周期内的振荡次数减少, 气泡的振荡幅度减小. 图4(b)—图4(e)分别为气泡内内能、温度、压力和水分子数量随时间的变化关系曲线, 比较可知, 气泡在破裂的瞬间, 泡内内能达到最大值、泡内温度最高、泡内压力最大; 气泡膨胀到最大时泡内水分子数量最多; 随着超声频率的增加, 气泡的泡内最大内能、最高温度、最大压力和水分子数量均减小. 这是因为超声波频率越高, 负压相位的时间缩短, 气泡内部低压持续时间越短, 水蒸气分子蒸发的时间越短, 导致气泡中积累的水蒸气分子越少, 空化效应也会减弱.
3 -->

3.4.2.声压对泡群中泡的动力学特性的影响

图5为泡群中心的泡在不同声压下驱动下的动力学特性. 泡群中泡的初始半径为R₀ = 4.5 μm, 泡群内空化泡个数N = 300, 泡群半径r_clust = 1 × 10^–3 m, 超声波的振幅分别为A = 1.2 × P₀, A = 1.5 × P₀ 和A = 2.0 × P₀, 超声波的频率为f = 20 kHz.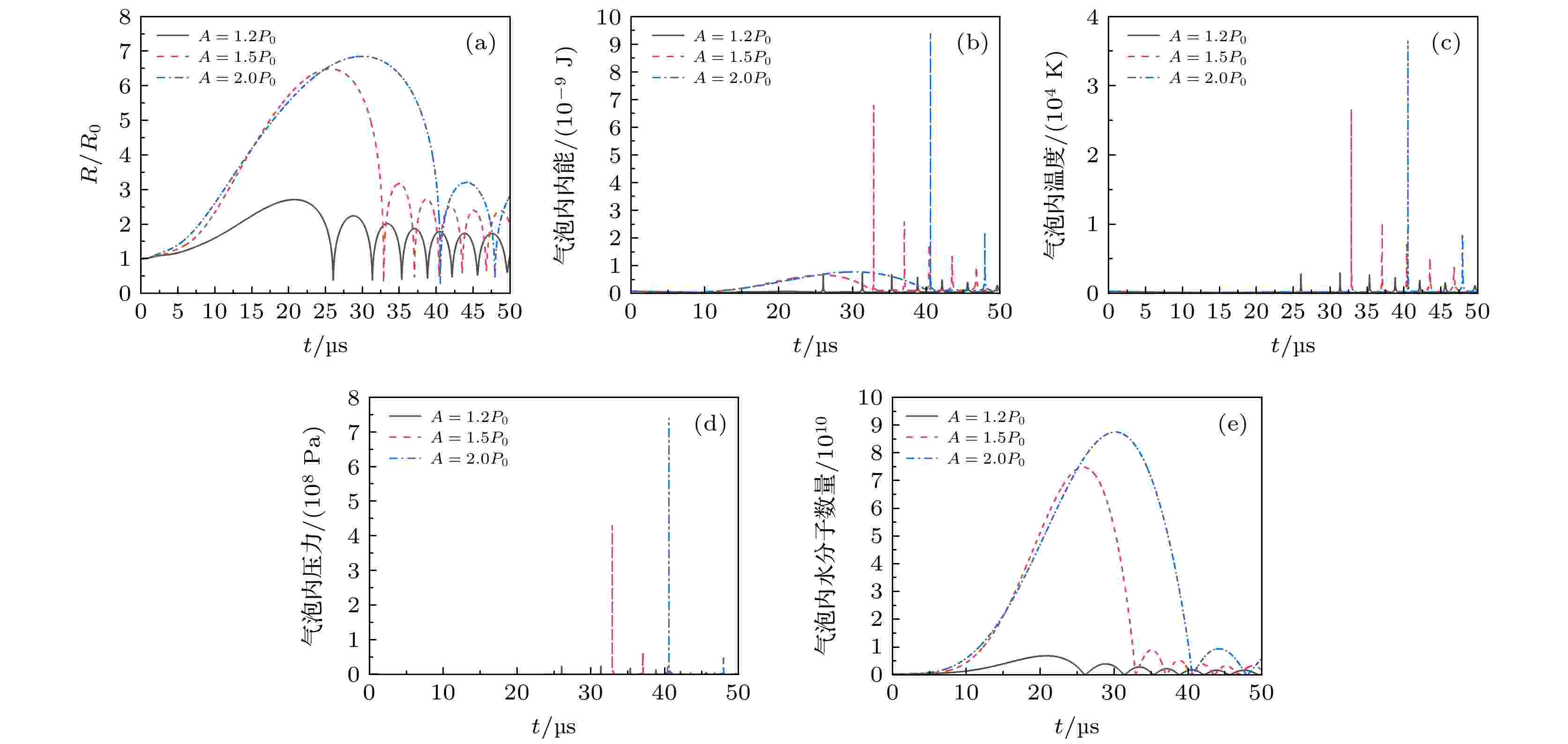
图 5 不同声压下泡群中泡的动力学特性　(a) 气泡归一化半径随时间的变化; (b) 气泡内内能随时间的变化曲线; (c) 气泡内温度随时间的变化曲线; (d) 气泡内压力随时间的变化曲线; (e) 气泡内水分子数量随时间的变化曲线
Figure5. Dynamic characteristics of bubbles in bubble groups under different sound pressures: (a) Change curve of the normalized radius with the time for the bubble; (b) change curve of the internal energy in the bubble with the time; (c) change curve of the temperature in the bubble with the time; (d) change curve of the pressure in the bubble with the time; (e) change curve of the number of water molecules in the bubble with the time.

图5(a)为气泡归一化半径随时间的变化曲线. 随着超声声压的增加, 空化泡振荡幅值增大, 气泡半径最大值增大, 空化泡崩溃时间增加, 空化泡崩溃后振荡减少. 图5(b)—(e)分别为不同声压驱动下泡内内能、温度、压力和水分子数量随时间的变化曲线, 可以看出, 超声声压增大, 气泡内内能、温度和泡内压强的最大值会增大, 气泡内部压强和温度的最小值减小, 气泡泡内水分子数量最大值增大. 这是因为超声振幅越大, 在超声频率不变的情况下, 气泡在相同时间的超声波负压相吸收的能量越多, 同时气泡的膨胀阶段的时间也会延长, 气泡内的压强会越低, 水蒸气分子蒸发速率会增大, 泡内的水蒸气分子数量就増加得越多, 泡内内能也就越高. 由此可知, 当超声声压增加时, 泡群中泡的空化效应也会增加.

考虑空化泡内水蒸气的蒸发和冷凝的前提下, 结合气泡之间的相互作用, 建立了球状泡群中泡的动力学模型, 探讨了泡在泡群中的不同位置以及泡群中泡的数量、初始半径对泡的动力学特性的影响. 进一步研究了不同声场作用下泡群中气泡半径、能量、温度、压力和气泡内水蒸气分子数的变化. 得到以下结论.
1)相比于单泡, 泡群中泡的振动幅度更小, 崩溃时间更长, 泡内的内能、最高温度、最大压力和水分子数量更小. 泡群中泡的位置距离泡群中心越远, 泡的膨胀半径越大.
2)泡群中泡的初始半径大小对泡群中泡的归一化振幅、崩溃时间、泡内内能、温度、压力和水分子数量具有明显影响.
3)随着泡群中泡的数目增加, 泡群中泡的振幅会减小, 会影响泡群的整体空化效果.
4)超声频率越高, 气泡在一个周期内的振荡次数越小, 气泡的振荡幅度越小, 气泡内的最大压力和能量越小, 气泡内部压力和温度的最小值越大, 气泡内水分子数越小. 超声频率增加时, 泡群中泡的空化效应减弱.
5)随着超声声压的增加, 空化泡振荡幅值增大, 气泡半径最大值增大, 空化泡崩溃时间增加, 空化泡崩溃后振荡减少, 气泡内内能、温度和泡内压强的最大值增大, 气泡内部压强和温度的最小值减小, 气泡泡内水分子数量最大值增大. 超声声压增加时, 泡群中泡的空化效应增加.