摘要:惯性约束核聚变成功的关键之一在于靶丸内要形成均匀的燃料冰层, 靶丸外表面温度特性对惯性约束聚变低温靶内形成均匀的燃料冰层有着决定性的影响. 为使得靶丸外表面温度场尽可能均匀, 需采用定向红外的方式对靶丸外表面温度进行局部调控. 采用全三维低温靶物理模型, 建立定向红外光路追踪与温度场计算耦合计算的光热耦合数值模型, 研究了定向红外条件下光纤布置形式及光源参数对低温靶温度场的影响规律. 结果表明: 在光纤总功率不变的前提下, 光纤数量越多, 靶丸外表面温度场均匀性越好. 光纤数量小于等于2时, 靶丸外表面温度场无法得到明显改善; 光纤数量大于2时, 靶丸外表面最大温差和加权温差降低幅值极限为61.94%和76.33%. 光纤投射的光斑向南北两极适量偏移可以改善靶丸外表面温度场均匀性, 其他的偏移方式会恶化温度场均匀性.
关键词: 惯性约束核聚变/
低温靶/
定向红外/
光热耦合/
数值模拟

English Abstract

全文HTML

--> --> -->

近年来, 煤、石油及天然气等化石能源消耗巨大, 能源及环境等问题日渐彰显^[1-4]. 惯性约束核聚变(inertial confinement fusion, ICF)作为一种高效、清洁的能源形式愈发受到世界许多国家的重视^[5,6]. ICF是指依靠烧蚀层残余质量的惯性对高温高密度的热核燃料进行约束, 从而实现可控热核聚变^[7-16]. ICF的核心部件为置于低温靶中心的球形靶丸. 为实现热核聚变要求, 靶丸内D₂或DT燃料冰层厚度均匀性需大于99%, 燃料冰层内表面均方根粗糙度需小于1 μm^[17,18]. 燃料冰层粗糙度主要受靶丸周围的温度场所决定, 因此低温靶温度场控制的重要性尤为突出^[19].
低温靶热核燃料主要有两种选择: D₂或DT^[5,6]. DT作为热核燃料时, 由于氚具有放射性, 固态DT燃料冰层会发生β衰变从而产生体热效应, 靶丸内较厚的DT燃料冰层热效应较强, 局部温度较高, 从而该处的DT燃料冰层会发生升华, 在DT燃料冰层较薄的区域再度凝华, 靶丸内燃料冰层均匀性得到改善, 此过程称为β自均化过程. 由于氘不具备放射性, 因此在D₂作为燃料冰层时, 并无类似于DT燃料的β自均化过程. 为了使靶丸内D₂燃料冰层质量满足热核聚变要求, 需要通过添加外界激励的方式使得D₂产生类似于DT燃料的β自均化过程. 现阶段的主要手段为向低温靶系统内投射定向红外光, 以加热靶丸局部低温区域, 从而使得D₂产生类似于DT燃料的β自均化过程, 改善冰层质量.
目前定向红外辅助均化相关的国外研究主要来自于美国劳伦斯利弗莫尔国家实验室. Kozioziemski等^[20]通过TracePro软件对红外光路进行仿真, 计算出靶丸不同位置对红外的吸收功率, 再将靶丸对红外的吸收功率作为源项输入至COSMOS软件对低温靶温度场进行模拟, 该方式计算可靠性很大程度上依赖于不同软件之间传递的数据精度, 且模拟流程十分繁琐, 但Kozioziemski等^[20]提供了一个较为良好的定向红外辅助均化的研究思路, 为后人的工作奠定了基础. London等^[21]在Kozioziemski等^[20]的工作基础上研究了二维低温靶模型单侧及双侧红外注入形式下靶丸表面温度场的分布规律, 文末简要提及了光纤插入式定向红外辅助的工作展望, 未发表研究成果, 并且由于采用二维低温靶模型, 与实际三维物理模型依旧存在较大的差异. 国内针对定向红外辅助均化方面的研究成果相对较少, 目前仅王凯等^[22]通过TracePro计算了不同定向红外工况下靶丸红外吸收功率的变化情况, 并未进行低温靶温度场的计算模拟.
为了避免软件之间的数据传递的繁琐及可能带来的精度损失, 本文在Fluent软件内同时完成了光路及温度场的模拟, 并且采用全三维低温靶计算模型, 可以有效降低模型维度导致的计算失真. 本文主要研究光纤插入式定向红外注入形式, 分析不同光纤的布置形式、光源参数等因素对低温靶温度场的影响规律.

2

-->

2.1.物理模型

本文的低温靶结构尺寸参考美国国家点火装置(National Ignition Facility, NIF)低温靶^[23], 具体结构尺寸如图1所示. 该模型为柱腔靶模型, 铝套筒上下冷环位置与硅冷却臂接触, 为低温靶系统提供冷量; 铝套筒南北两极各开设有激光入射孔(laser entrance hole, LEH), 为激光打靶提供激光投射路径; 铝套筒上下半腔存在一个夹缝, 夹缝的厚度为0.02 mm; 铝套筒内表面镀金, 金层的厚度为0.02 mm; 铝套筒内表面和靶丸之间的空腔填充氦气作为导热介质, 用来传递冷量; 靶丸置于柱形铝套筒的几何中心, 靶丸具有三层结构, 最外侧为烧蚀层, 中间层为D₂燃料冰层, 最内侧为D₂燃料气体层; 整个低温靶系统置于一个较大的低温屏蔽罩内, 用于隔绝外界的环境辐射. 由于本文重点关注定向红外对靶丸温度场的影响, 充气管及夹持膜等部件暂不考虑.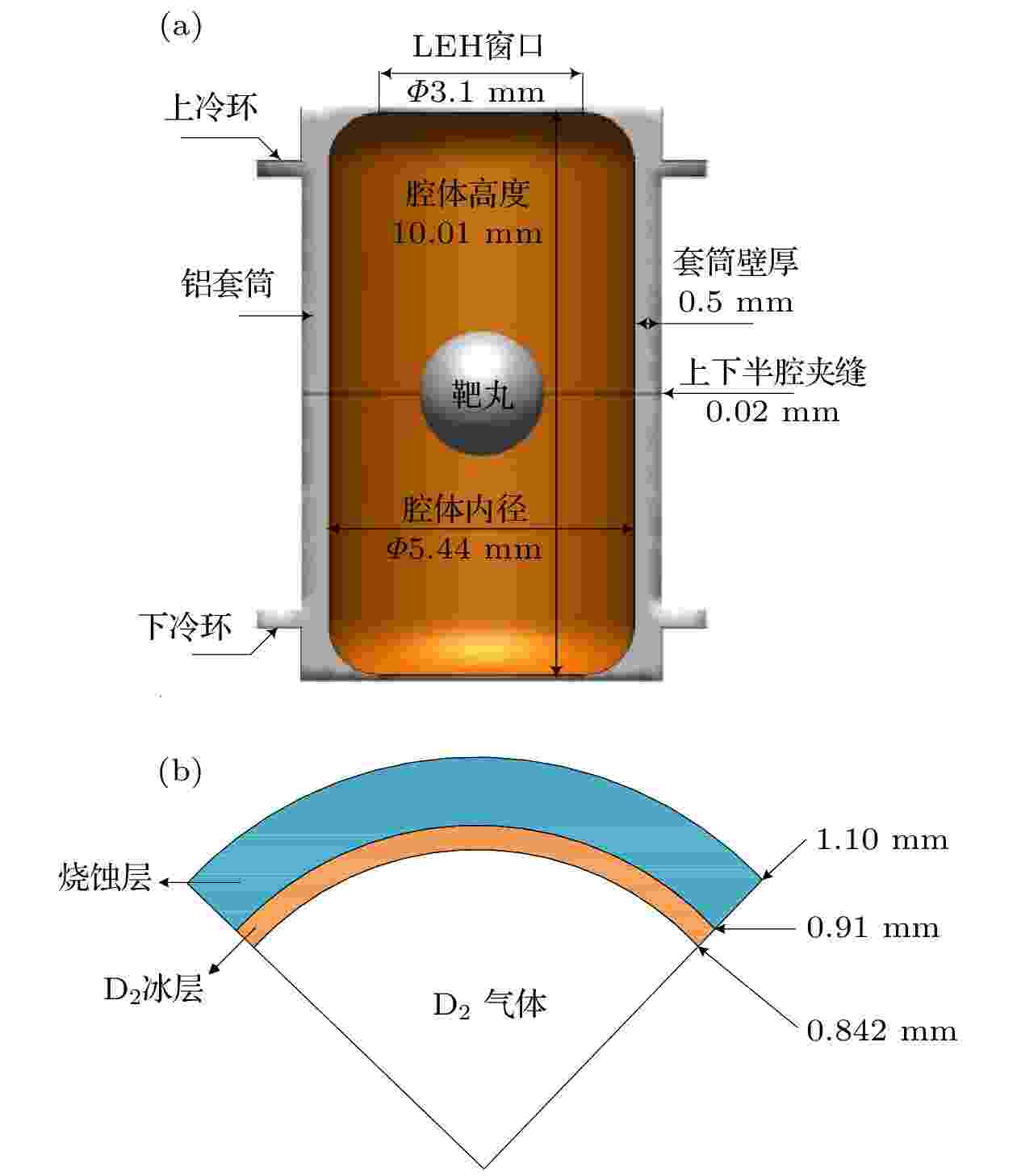
图 1 低温靶系统主要部件结构尺寸　(a)套筒结构尺寸; (b)靶丸结构尺寸
Figure1. Schematic of cryogenic target system: (a) Hohlraum structure; (b) capsule structure

2 -->

2.2.数值方法

为研究定向红外条件下的低温靶温度场特性, 需要同一数值模型中包含定向红外计算模型与低温靶温度场计算模型. 由于光线与辐射线的性质相同, 可以利用辐射传导方程来计算定向红外的传播情形. 同时, 辐射是传热的一种基本方式, 将定向红外作为辐射来考虑, 能够自然地做到光热耦合计算, 避免了光与热计算的割裂, 有效提高了计算可靠性.
鉴于定向红外传播的三维效应较为显著, 对物理模型过度简化会造成计算结果失真, 故对全三维低温靶模型剖分网格. 采用ANSYS Gambit软件对低温靶柱腔模型进行网格划分, 采用ANSYS Fluent 18.0进行模拟计算, 稳态工况下连续性方程、动量方程及能量方程分别为^[24]

$\nabla \left( {\rho {\boldsymbol{u}}} \right) = 0, $

$\begin{split} \nabla \left( {\rho {\boldsymbol{uu}}} \right) =\;& - \nabla p + \nabla \left( {\mu \nabla {\boldsymbol{u}}} \right) \\& + \rho g\left[ {1 - \beta \left( {T - {T_{{\rm{ref}}}}} \right)} \right], \end{split}$

$\rho {c_{\rm{p}}}{\boldsymbol{u}}\nabla T = \lambda {\nabla ^2}T, $

其中ρ, u, p, T分别为密度、速度矢量、压力和温度; λ, μ, β, c_p分别为导热系数、动力粘度、热膨胀系数和定压比热; T_ref为参考温度, g为重力加速度. 在本模型中, 由于自然对流的存在, 气体密度均采用Boussinesq假设.
稳态工况下, 辐射传导方程为^[25]

$\begin{split}\frac{{{\rm{d}}I\left( {{\boldsymbol{r}},{\boldsymbol{s}}} \right)}}{{{\rm{d}}s}} =\;& - \left( {{K_{\rm{a}}} + {K_{\rm{s}}}} \right)I\left( {{\boldsymbol{r}},{\boldsymbol{s}}} \right) + {K_{\rm{a}}}{I_{\rm{b}}}(T) \\&+\frac{{{K_{\rm{s}}}}}{{4{\rm{\pi }}}}\int\nolimits_{4{\rm{\pi }}} {{\rm{d}}I({{\boldsymbol{r}},{\boldsymbol{s}}'})\varPhi ( {{\boldsymbol{s}}\cdot {\boldsymbol{s}}'} ){\rm{d}}\varOmega } \!+\! S, \end{split}$

其中I为辐射强度, 是位置矢量r和方向矢量s的函数; K_a和K_s分别表示吸收系数和散射系数; T为温度, Ω为立体角, S为辐射强度源项, Φ为散射相位函数, 用来表征材料的散射特性. 采用蒙特卡洛光线追踪方法对辐射传导方程进行求解, 为保证蒙特卡洛方法的计算精度, 光线历史记录数需至少达到2000万.
边界条件如下:
1)柱腔外低温屏蔽罩的温度为120 K, 屏蔽罩发射率设为1.0;
2)铝套筒上下冷环温度为18 K, 铝套筒外表面发射率为0.05;
3)铝套管南北两极封口膜透射率为0.05;
4)金腔内表面发射率为0.03, 且金腔内表面认为是朗伯散射体, 即漫反射系数为1.0;
计算中所使用的材料物性参数列于表1.

材料	密度ρ/ kg·m–3	热容cp/ J·kg–1·K–1	导热系数λ/ W·m–1·K–1	动力粘度μ/ kg·m–1·s–1
铝	2710	8.37	27	—
金	19320	14.66	1173.44	—
靶壳	1100	57.49	0.057	—
He@1 kPa	0.3	5292.6	0.021	1.31 × 10–6
气态D2	0.025	5193.7	0.024	3.42 × 10–6
固态D2	260	5000	0.29	—
(注: 本文不考虑气体对定向红外的影响, 因此氦气和氘气的吸收系数和散射系数均为0)

表1不同材料在18 K环境下的物性参数
Table1.Physical properties of different materials at 18 K

以靶丸外表面最大温差作为表征参数, 采用56万、89万、124万、233万和314万网格对无定向红外工况进行计算, 网格无关性验证结果如图2所示, 最终采用124万网格数计算模型进行研究.
图 2 网格无关性验证
Figure2. Gird-independence validation result

靶丸内冰层均匀性表征方式有两种^[26]: 一是冰层随着靶丸温度场的变化而变化, 不均匀的温度场会导致不均匀的冰层, 在进行模拟时需要不断地根据温度场的分布情况手动修改冰层内表面轮廓, 直至冰层内表面温差为0, 此时的冰层轮廓对应于温度场的分布, 但此法较为繁琐, 应用不便; 二是将靶丸内冰层固定为均匀冰层, 研究不同工况条件下靶丸外表面的温度特性, 由于靶丸外表面温度均匀性正比于靶丸内冰层均匀性, 通过研究分析靶丸外表面温度场均匀性的变化规律即可得出靶丸内冰层均匀性的变化规律, 但此法无法精确得出冰层内表面均匀度, 只能反应出其变化趋势. 本文采用第二种表征形式进行研究.
本文主要研究定向红外为光纤插入式下的光纤布置及光源参数对低温靶温度场的影响规律, 分别研究了光纤数量、光源功率密度及光斑位置等影响因素. 结果表明定向红外的添加能够改善靶丸表面温度均匀性, 该结果可以为实验提供理论指导.
2

-->

3.1.无定向红外典型工况

无红外典型工况下红外光纤功率为0，其他边界条件如2.2小节所述, 计算所用材料物性参数同表1. 靶丸外表面温度云图如图3所示, 其中g为重力方向. 靶丸外表面温度呈南北两极高, 赤道温度低的分布规律, 这是由于靶丸赤道平面距离铝套筒内表面最近, 换热效果最好, 导致靶丸外表面赤道区域局部温度较低, 并且由于靶丸南北两极会受到两侧LEH透射来的环境辐射, 使得靶丸外表面南北两极区域局部温度进一步抬升.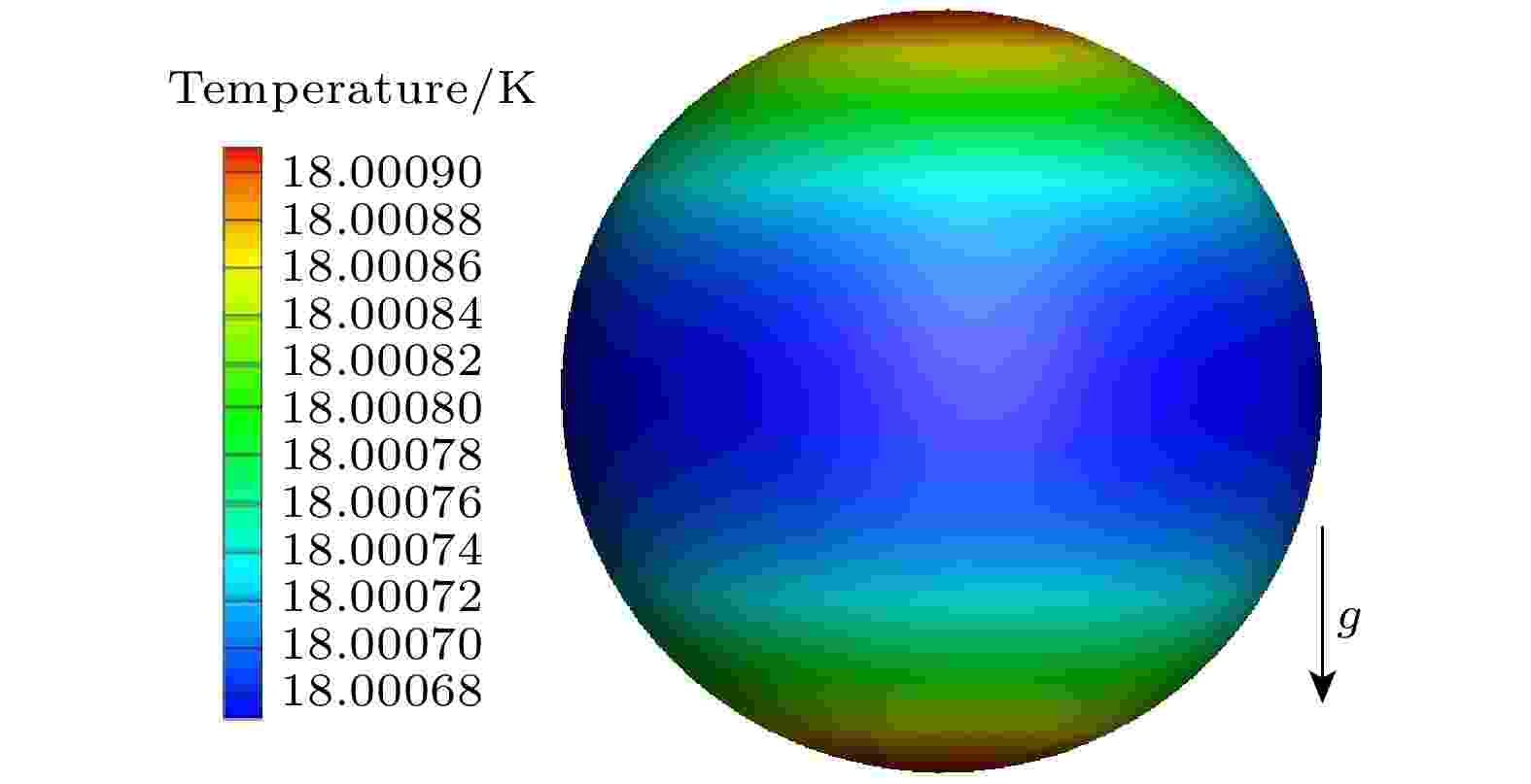
图 3 靶丸外表面温度云图
Figure3. Temperature contour of capsule outside surface

为表征靶丸外表面温度均匀性, 引入最大温差和加权温差两种统计方式, 其表达式为

$\Delta {T_{\max }} = {T_{\max }} - {T_{\min }}, $

$\Delta {T_{\rm{w}}} = \frac{{\displaystyle\sum\limits_{i = 1}^n {\left( {\left| {{T_{\rm{i}}} - \bar T} \right|{A_{\rm{i}}}} \right)} }}{{\displaystyle\sum\limits_{i = 1}^n {{A_{\rm{i}}}} }}, $

其中

$\bar T = \frac{{\displaystyle\sum\limits_{i = 1}^n {{T_{\rm{i}}}{A_{\rm{i}}}} }}{{\displaystyle\sum\limits_{i = 1}^n {{A_{\rm{i}}}} }}, $

式中, ΔT_max, ΔT_w分别表示最大温差和加权温差; T_max, T_min分别表示温度最高值和温度最低值; T_i, A_i分别表示每个网格区域的温度值和网格面积; i, n分别表示网格索引和网格总个数; $\bar T$为平均温度. 通过(5)式、(6)式可以计算得出无红外典型工况下靶丸外表面最大温差为ΔT_max = 0.252 mK, 加权温差为ΔT_w = 0.0608 mK.
2 -->

3.2.光纤数量影响分析

由典型工况结果可知, 为提升靶丸表面温度均匀性, 需要抬升靶丸赤道平面温度. 因此设定定向红外投射的光斑位于铝套筒赤道平面处, 红外光线经过反射后辐照至靶丸赤道区域, 从而加热靶丸赤道区域, 以提高靶丸外表面温度均匀性.
为了将红外光纤引入低温靶系统中, 需要在铝套筒上开设通孔, 红外光纤穿过铝套筒上的通孔固定在系统中, 如图4所示. 光纤出射红外为准直平行光, 为了使光斑能够打在铝套筒赤道区域, 需要对光纤的高度及方位进行限制. 光纤入射口直径为0.3 mm; 光纤入射口距套筒赤道平面2.72 mm; 光纤入射口同重力及径向方向的夹角均为45°, 避免光线直接辐照至靶丸表面.
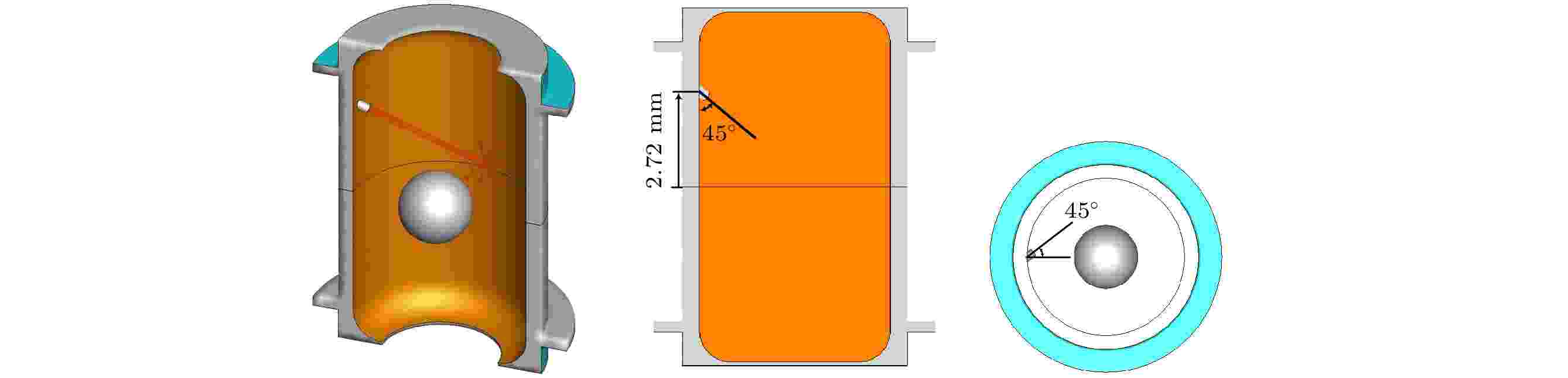图 4 红外光纤布置示意图
Figure4. Schematic of infrared(IR) optical fiber layout

不同光纤数量的配置形式如图5所示, 定义光纤数量为m, 分别研究了m = 1, 2, 4, 6和8的工况. 光纤呈上下对称, 周向均匀布置. 图5中红色光带为上半腔体光纤出射的光线, 黄色光带为下半腔体光纤出射的光线. 为保证定向红外入射的总功率一致, 不同光纤数量下的每根光纤出射功率密度不同, 其他边界条件如2.2小节所述. 不同光纤数量下的每根光纤出射功率密度见表2.
图 5 不同光纤数量下光纤布置形式
Figure5. The layout of optical fiber corresponding to optical fiber numbers

m	1	2	4	6	8
单根功率密度/(W·m–2)	4.00	2.00	1.00	0.67	0.50

表2不同光纤数量下的每根光纤出射功率密度
Table2.The power density of each optical fiber corresponding to optical fiber numbers

图6展示了不同光纤数量下靶丸外表面温度云图. 对比m = 0和1结果可以看出, 增加了定向红外后, 靶丸外表面赤道正对光斑的区域温度会有明显的抬升. 随着光纤数量的增加, 靶丸外表面赤道处的温度逐渐变得均匀.
图 6 不同光纤数量下的靶丸外表面温度云图
Figure6. Temperature contour of capsule outside surface corresponding to optical fiber numbers

为进一步展示靶丸外表面温度分布情况, 定义靶丸外表面水平特征线与靶丸外表面竖直特征线, 如图7所示, 其中蓝线为靶丸外表面水平特征线, 绿线为靶丸外表面竖直特征线. 不同光纤数量下靶丸外表面水平及竖直特征线上的温度分布如图8所示, 对于靶丸外表面水平特征线而言, 由于模型周向均匀性较高, 其极坐标的角度定义不作特殊限制; 对于靶丸外表面竖直特征线而言, 其极坐标角度中90°为靶丸北极点, 270°为靶丸南极点, 0°与180°为靶丸赤道. 从图8可以看出, 在水平方向上, 增加定向红外后靶丸外表面整体温度有一明显上升, 且随着光纤数量的增加, 靶丸外表面水平特征线上的温度越来越均匀; 在竖直方向上, 不同工况下靶丸外表面温度均呈现“南北两极高, 赤道区域低”的分布规律, 增加定向红外后靶丸外表面竖直特征线上温度均匀性有所改善.
图 7 靶丸外表面特征线
Figure7. Characteristic line of capsule outside surface

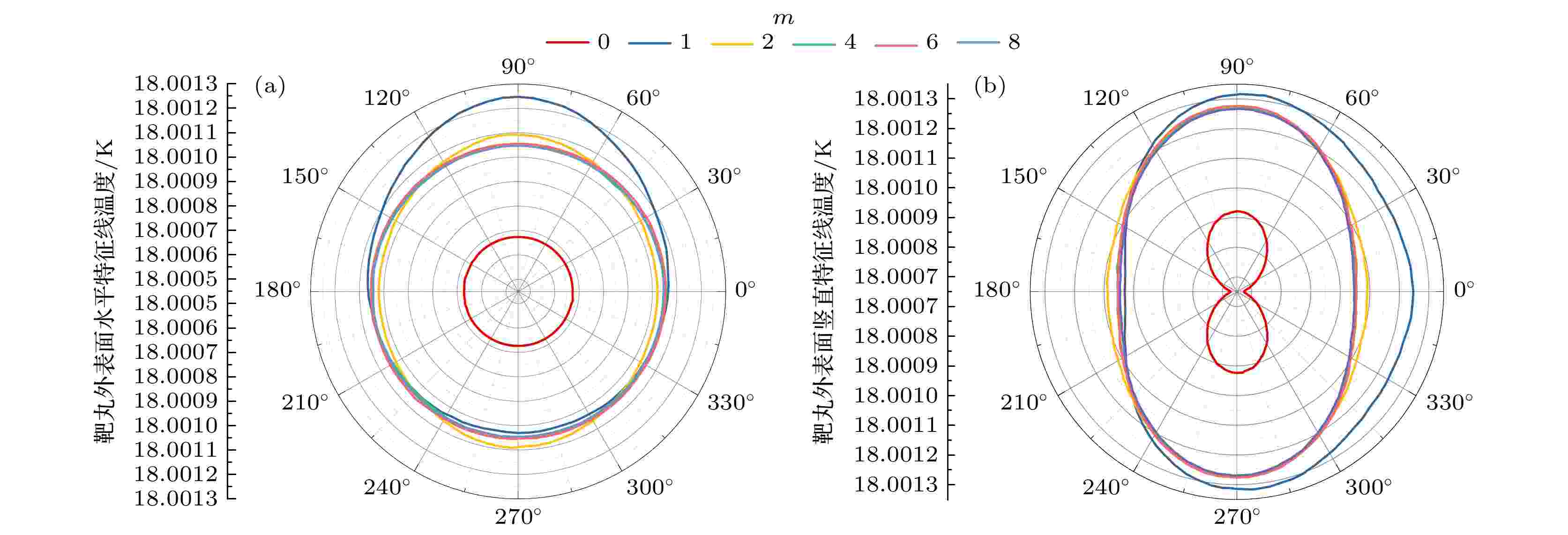图 8 靶丸外表面特征线温度分布　(a)靶丸外表面水平特征线温度分布曲线; (b)靶丸外表面竖直特征线温度分布曲线
Figure8. Temperature distribution of characteristic line of capsule outside surface: (a)Horizontal characteristic line; (b) vertical characteristic line

图9展示了不同光纤数量下, 靶丸外表面最大温差ΔT_max, 加权温差ΔT_w和平均温度$ \bar T$的变化规律. 在入射总功率一定的前提下, 光纤数量较少的时候(m = 1, 2), 由于靶丸周向受到的红外辐照均匀性较差, 靶丸表面的最大温差和加权温差较于无红外工况均有较为明显的增大, 说明靶丸外表面温度均匀性变差; 当m = 4时, 由于靶丸受到的红外辐照周向均匀性得到提升, 与无红外工况相比, 靶丸外表面最大温差和加权温差分别降低了7.66%和11.83%, 温度场均匀性得到改善; 在m ≥ 6时, 靶丸外表面最大温差及加权温差降低率基本维持在12.94%和11.83%, 可认为在总入射功率不变的情况下, m = 6时即可达到较优的靶丸温度场均匀性改善效果, 继续增设光纤性价比较低. 与无红外工况相比, 增设光纤后靶丸外表面平均温度有明显上升, 随着光纤数量的增加, 靶丸外表面平均温度会逐渐降低, 这是由于光纤数量增加会使得靶丸受到的红外辐照的周向均匀性得到改善, 从而改善了靶丸与外界环境的换热.
图 9 不同光纤数量下靶丸外表面最大温差、加权温差及平均温度变化
Figure9. ΔT_max, ΔT_w and $ \bar T$ variations of capsule outside surface responding to optical fiber numbers

2 -->

3.3.光源功率密度影响分析

3.2小节研究的内容以所有光纤入口总功率保持不变为前提, 每种光纤数量下的温度结果不能代表该工况下所能达到的极优值. 本节解除了对光纤入口功率的限制, 研究每种光纤数量下靶丸表面均匀性可达到的极优值, 从而选出最优的光纤配置数量, 为实验提供理论参考.
以m = 1为例, 研究不同光源功率密度下靶丸外表面温度特性. 图10展示了m = 1不同光源功率密度下靶丸外表面温度云图. 可以看出, 随着光源功率不断增大, 靶丸外表面赤道区域温度逐渐抬升, 直至成为全场温度最高点. 在此过程中, 应当存在某一特定功率, 使得靶丸外表面温度均匀性达到极优值.
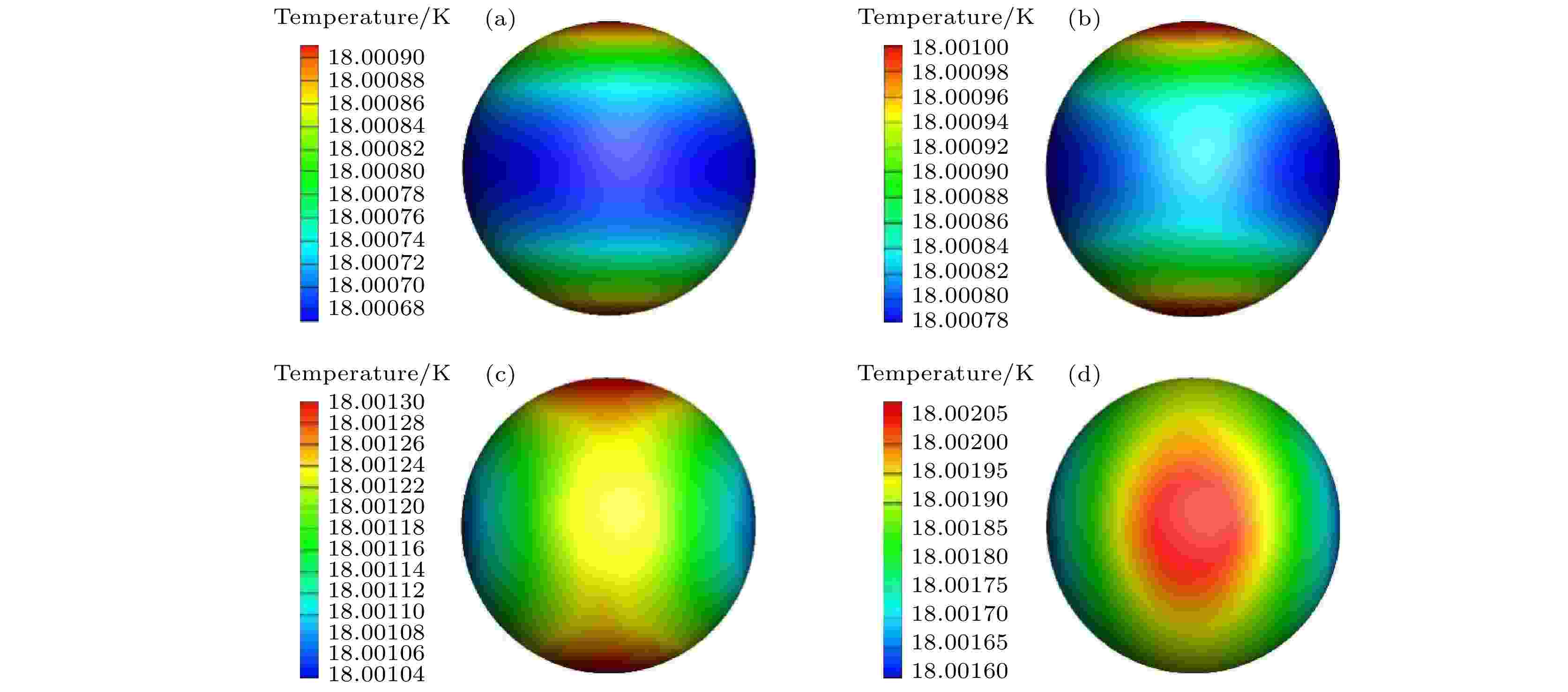图 10 不同光源功率密度下靶丸表面温度云图　(a) 0 W·m^–2; (b) 1 W·m^–2; (c) 4 W·m^–2; (d) 10 W·m^–2
Figure10. Temperature contours of capsule outside surface under different optical fiber power densities: (a) 0 W·m^–2; (b) 1 W·m^–2; (c) 4 W·m^–2; (d) 10 W·m^–2

图11展示了m = 1时不同光源功率密度下靶丸外表面最大温差和加权温差的变化曲线, 可以看出, 随着光源功率密度的增大, 靶丸外表面最大温差持续增大, 并不存在极小值, 这是由于靶丸最高温度点位于南北两极, 最低温度点位于光斑辐照区域的对侧赤道区域, 南北两极点受光斑辐射的影响要比光斑对侧赤道区域更大, 因此随着光源功率密度的增大, 靶丸南北两极升温要比光斑对侧赤道区域处更为剧烈, 靶丸外表面最大温差持续增大; 随着光源功率密度的增大, 靶丸外表面加权温差先减小后增大, 存在极小值, 此时对应的光源功率密度约为1.25 W·m^–2.
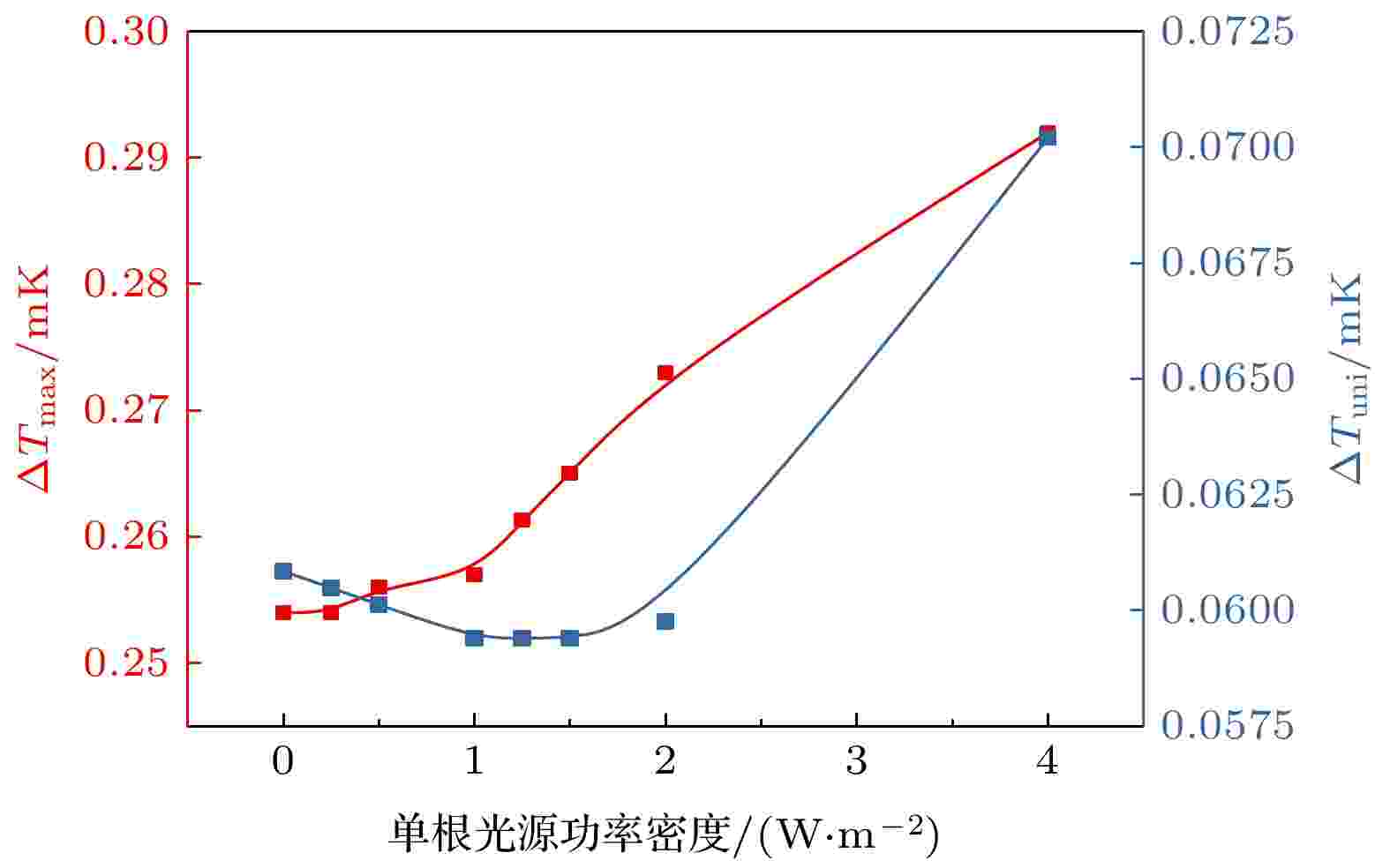图 11 m = 1时靶丸外表面最大温差和加权温差随单根光源功率密度变化曲线
Figure11. ΔT_max and ΔT_w variations of capsule outside surface responding to optical fiber power densities with m = 1

与m = 1研究方法相同, 分别研究了m = 2, 4, 6, 8不同光源功率密度下靶丸外表面温度特性, 结果如图12所示. 对于m = 2 (图12(a)所示), 其计算结果与m = 1基本一致, 随着单根光源功率密度的增大, 靶丸外表面最大温差持续增大, 并不存在极小值, 靶丸外表面加权温差先减小后增大, 在单根光源功率密度为3 W·m^–2取得极小值; 对于m = 4, 6, 8 (如图12(b)—(d)所示), 随着单根光源功率密度的增大, 靶丸外表面最大温差和加权温差都呈先减小后增大的趋势, 分别于单根光源功率密度为8, 5.25 W·m^–2和4.25 W·m^–2时取得极小值.
图 12 靶丸外表面最大温差和加权温差随单根光源功率密度变化曲线　(a) m = 2; (b) m = 4; (c) m = 6; (d) m = 8
Figure12. ΔT_max and ΔT_uni variations of capsule outside surface responding to optical fiber power densities: (a) m = 2; (b) m = 4; (c) m = 6; (d) m = 8

图13展示了不同光纤数量下, 靶丸外表面最大温差的极小值(ΔT_max)_min和加权温差的极小值(ΔT_w)_min及其对应的单根光源功率密度的变化曲线. 从图13(a)可以看出, 在m = 4时, 靶丸外表面最大温差明显降低, 较于无红外工况降幅37.94%; 在m = 6, 8时, 最大温差变化趋平, 此时较于无红外工况降幅61.94%. 随着m的增加, 靶丸外表面最大温差的极小值对应的单根光源功率密度逐渐降低. 由于m = 1, 2时随着单根光源功率密度的增加, 靶丸外表面最大温差无法降低, 因此靶丸外表面最大温差的极小值取为无红外工况下靶丸外表面最大温差, 对应光源功率密度为0.
图 13 不同光纤数量下, 靶丸外表面最大温差极小值和加权温差的极小值及其对应的光源功率密度的变化曲线　(a)最大温差极小值; (b)加权温差的极小值
Figure13. (ΔT_max)_min and (ΔT_w)_min variations of capsule outside surface responding to optical fiber numbers: (a) (ΔT_max)_min; (b) (ΔT_w)_min

图13(b)展示了靶丸外表面加权温差的极小值(ΔT_w)_min及其对应的单根光源功率密度同光纤数量的变化曲线. 同图13(a)的曲线趋势一致, 随着m的增加, 靶丸外表面加权温差的极小值逐渐降低, 靶丸外表面温度所能达到的均匀性越高, 在m = 4时, 靶丸外表面加权温差明显降低, 较于无红外工况降幅62.13%; 在m = 6, 8时, 加权温差变化趋平, 此时较于无红外工况降幅76.33%. 随着m的增加, 靶丸外表面加权温差的极小值对应的单根光源功率密度先增大后减小, 这是由于当m = 1, 2时, 靶丸受到的红外辐照周向均匀性很差, 很小的光纤光源功率密度就会引起很剧烈的温度场变化, 靶丸无法承受较为强烈的红外辐照, 此时靶丸达到的均匀性极小值点无参考价值.
综合靶丸外表面最大温差极小值和加权温差极小值来看, 选取6根光纤布置形式即可有效改善靶丸外表面温度场均匀性, 继续增加光纤数量性价比很低.
2 -->

3.4.光斑位置影响分析

前文中假定红外光纤投射的红外光斑都位于金腔内表面赤道区域, 实际操作中由于加工及装配工艺的限制, 红外光斑无法严格照射在金腔内表面赤道区域. 为研究红外光斑位置对靶丸温度场的影响, 以m = 6为基础, 研究了3种红外光斑偏移方式如图14所示, 其中方式1: 北半腔3根光纤投射光斑固定于金腔内表面赤道处, 南半腔3根光纤投射光斑向北或者向南偏移; 方式2: 6根光纤投射光斑统一向北或者向南偏移; 方式3: 北半腔3根光纤投射光斑向南偏移, 南半腔3根光纤投射光斑向北偏移同样的距离.
图 14 3种红外光斑偏移方式
Figure14. Schematic of 3 kinds of IR spots offsets

由3.3小节中图13的结果可以看出, 在m = 6光源功率密度为5.25 W·m^-2时靶丸外表面最大温差和加权温差都基本达到极小值, 故取5.25 W·m^–2为研究光斑位置影响时的光源功率密度. 图15分别展示了3种红外光斑偏移方式下靶丸表面温度云图. 图中, 正号“+”表示南半腔3根光纤投射光斑向北偏移, 负号“–”表示南半腔3根光纤投射光斑向南偏移, 正负后的数值表示偏移的距离.
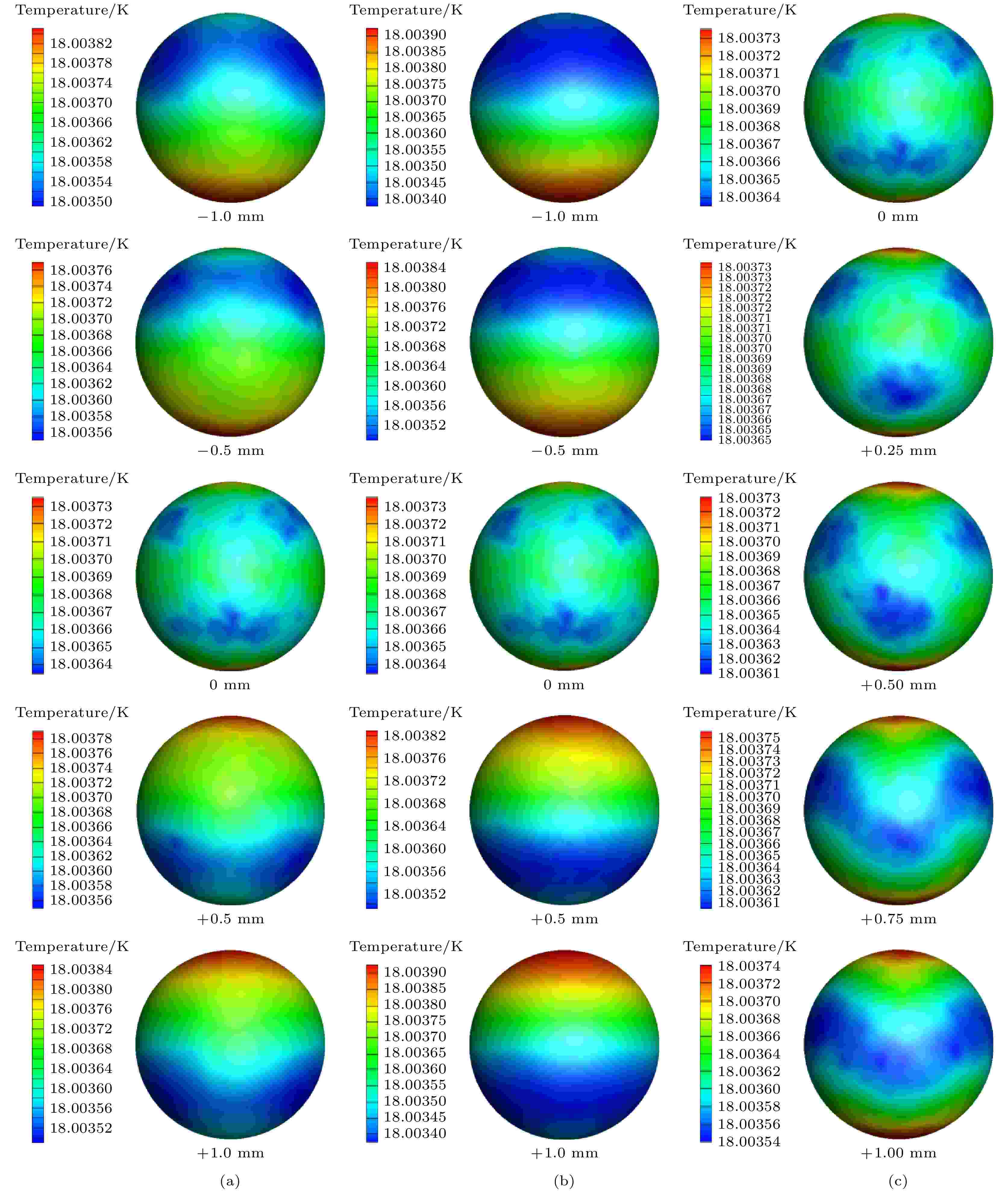图 15 3种光纤光斑偏移方式下的靶丸外表面温度云图　(a)方式1; (b)方式2; (c)方式3
Figure15. Temperature contour of capsule outer surface corresponding to 3 kinds of IR spots offsets: (a) Mode1; (b) mode2; (c) mode3

从图15(a)可以看出, 在方案1下(即北半腔3根光纤投射光斑固定在赤道, 南半腔3根光纤投射光斑位置偏移), 南半腔光纤投射光斑向南偏移, 靶丸南半球温度会明显太高, 向北偏移亦然. 南半球光纤的投射光斑会剧烈影响靶丸外表面温度分布, 造成明显的温度不均匀. 从图15(b)可以看出, 同方案1靶丸外表面温度场展现出来的规律, 方案2下(即6根光纤同时向南或者向北偏移)光斑的位置也会相应影响到靶丸外表面温度场分布, 由于南北两半腔的光纤同时偏移, 因此光斑的对置对靶丸外表面温度场的影响会更加剧烈. 图15(c)展示了方案3(即北半腔光纤光斑向南, 南半腔光纤光斑向北对称偏移)下靶丸表面温度云图, 由于南北两半腔的光纤光斑对称偏移, 因此仅讨论南半腔光纤光斑向北偏移的情况. 可以看出, 随着光纤投射的光斑逐渐向南北两极偏移, 靶丸外表面的低温区域逐渐向赤道处靠拢, 高温区域始终处于南北两极点保持不变.
图16分别展示了3种光纤光斑偏移方式下靶丸外表面最大温差, 加权温差和平均温度的变化规律. 结合图16(a)(b), 可以看出在方式1及方式2的光纤光斑偏移形式下, 靶丸外表面最大温差和加权温差均随着偏移距离的增大而增大, 平均温度$ \bar T$随着偏移距离的增大而降低. 对于方式1而言, ΔT_max, ΔT_w和$ \bar T$随偏移距离的变化率约0.267 mK/mm, 0.075 mK/mm和–0.034 mK/mm. 对于方式2而言, ΔT_max, ΔT_w和$ \bar T$随偏移距离的变化率约0.490 mK/mm, 0.158 mK/mm和–0.096 mK/mm. 由此可以看出, 在相同的南半腔光纤光斑偏移距离下, 方式2对于靶丸外表面温度均匀性的破坏程度要远高于方式1, 在实际操作中应当尽量避免方式2的光纤装配. 从图16(c)可以看出, 在方式3下, 光纤光斑在偏移0.25 mm时可以降低靶丸外表面最大温差及加权温差, 降幅分别为9.17%和4.98%, 靶丸外表面温度均匀性得到改善, 原因在于当所有的光斑均位于赤道区域时, 靶丸外表面的低温区域向南北两极偏移, 此时光纤光斑向两极适量偏移, 会抬升靶丸外表面低温区域的温度, 从而提高温度均匀性; 光纤光斑继续偏移会使得靶丸外表面最大温差及加权温差不断增大, 变化率约0.168 mK/mm和0.055 mK/mm. 方式3下靶丸外表面平均温度随偏移距离的变化率约–0.052 mK/mm, 其值介于方式1与方式3之间.
图 16 3种方案下靶丸外表面最大温差、加权温差和平均温度随南半腔光纤光斑偏移距离变化曲线　(a)方式1; (b)方式2; (c)方式3
Figure16. ΔT_max, ΔT_uni and $ \bar T$ variations with migration distance of southern half hohlraum IR spots corresponding to 3 kinds of IR spots offsets: (a) Mode1; (b) mode2; (c) mode3.

综上所述, 随着光纤光斑位置的偏移, 3种方式下靶丸外表面平均温度均逐渐降低; 在方式3下光纤光斑偏移适当的距离可以降低靶丸外表面最大温差和加权温差, 改善温度场均匀性, 其他2种方式下光纤光斑偏移会恶化靶丸外表面温度场均匀性, 其中方式2的恶化程度最为剧烈.

本文建立了光热耦合的数值模型, 研究了定向红外条件下光纤布置形式及光源参数对低温靶温度场影响规律, 结论如下:
1)在光纤总功率不变的前提下, 对于光纤数量m ≤ 2, 靶丸外表面温度场均匀性较无红外工况没有明显改善; 对于m > 2, 随着m的增加, 靶丸外表面平均温度, 最大温差及加权温差均有所降低, 在m = 4时靶丸温度均匀性得到明显改善, 最大温差及加权温差较无红外工况降幅7.66%和11.83%.
2)对于m > 2, 在同一种光纤布置形式下, 随着光源功率密度的增加, 靶丸外表面最大温差及加权温差先降低后升高, 存在极小值. 随着m的增加, 靶丸外表面最大温差及加权温差取得极小值对应的光源功率密度逐渐降低; 综合靶丸外表面最大温差及加权温差的结果, 靶丸外表面最大温差和加权温差的优化极限降幅为61.94%和76.33%.
3)在本文研究的方式3下光纤投射光斑偏移0.25 mm时靶丸外表面最大温差和加权温差较无偏移工况降幅9.17%和4.98%, 温度场均匀性得到改善, 其他的偏移方式均会恶化靶丸表面温度场均匀性.
定向红外对于低温靶靶丸温度场均匀性调控有着至关重要的作用, 然而相关方面的研究都较为初步, 下一步可继续研究低温靶部件材料物性、表面特性等因素对定向红外的影响, 以为实验提供指导.