全文HTML
--> --> -->作为地球内-外核主要成分和众多工业应用研究的重要材料, 铁在不同压力-温度条件下呈现出一系列复杂的晶体结构. 本文主要研究在高压条件下, α-Fe经历结构转变为另一个物相ε相(六角密排, hcp)[1]的相变, 这一相变行为最初在Minshall等[2,3]的冲击实验中发现, 随后被Barker和Hollenbach[4,5]的速度剖面测量确认, 也在静高压电阻率测量[6]、X射线衍射(XRD)[7-9]中得到证实.
后续的研究工作尤其是动态高压实验表明, 温度、加载路径、减压速率(卸载速率)、剪切应力、样品大小、晶粒尺寸等对α → ε相转变的动力学途径都有很大影响. 例如, 不同加载方式实验表现出与时间依赖的相转变速率明显差异, 其中Barker等[5]冲击实验(应变率~106 /s)给出的相变特征时间从冲击压力17 GPa时的60 ns下降至30 GPa时的12 ns, 且随终态压力呈线性衰减; Jensen等[10]的反向碰撞冲击实验则显示了与先前的理解相反的响应, 相变特征时间随峰值压力呈指数型衰减, 从相变压力处的百纳秒量级到高碰撞压力下的亚纳秒量级; Bastea等[11]的磁驱准等熵加载实验(应变率~105至106/s)给定相变特征时间为12—50 ns左右, 且与准等熵加载上升时间(0.1—1 μs)的对数呈线性关系; 而更高应变率(~107—108/s)的激光斜波实验[12]则表明当应变率大于106 /s时相变起始压力更快速增加, 利用KJMA相变动力学唯象模型拟合的相变特征时间为1—2 ns. 此外, 还报道过卸载过程中ε相→α相的逆相变特性, Barker等[5]给出的逆相变压力阈值为9.8 GPa.
这些关于热物理因素(温度, 卸载速率, 压力)影响相变特性的研究, 使得我们对于复杂工程条件中的单一影响因素有了更为深刻的理解和认识, 然而关于多种因素耦合在一起如何影响动力学路径的基本知识仍十分匮乏. 其中一种典型的工况条件是冲击加载-卸载-再加载的复杂热力学路径. 先前的冲击压缩实验表明α相→ε相有时间依赖的转变速率(几十纳秒内完成)和逆相变迟滞现象, 使得一次冲击加载-卸载作用后可能存在高压ε相残余, 而非全部回到低压α相, 进而改变再加载过程的起始物相状态和动力学路径. 尽管有此假定, 但是基于高速平靶撞击实验的复杂路径加卸载控制技术存在较大的物理设计及可靠实施难度, 至今都缺乏冲击相变实验证据. 鉴于此, 本文利用基于气炮加载的反向碰撞技术, 通过多台阶三层复合飞片的精细设计, 实现典型冲击加载-卸载-再加载路径控制, 结合宏观混合相模型模拟计算对实测波剖面的特征信号进行分析, 揭示了多晶铁α相?ε相动力学特征的路径相关性.
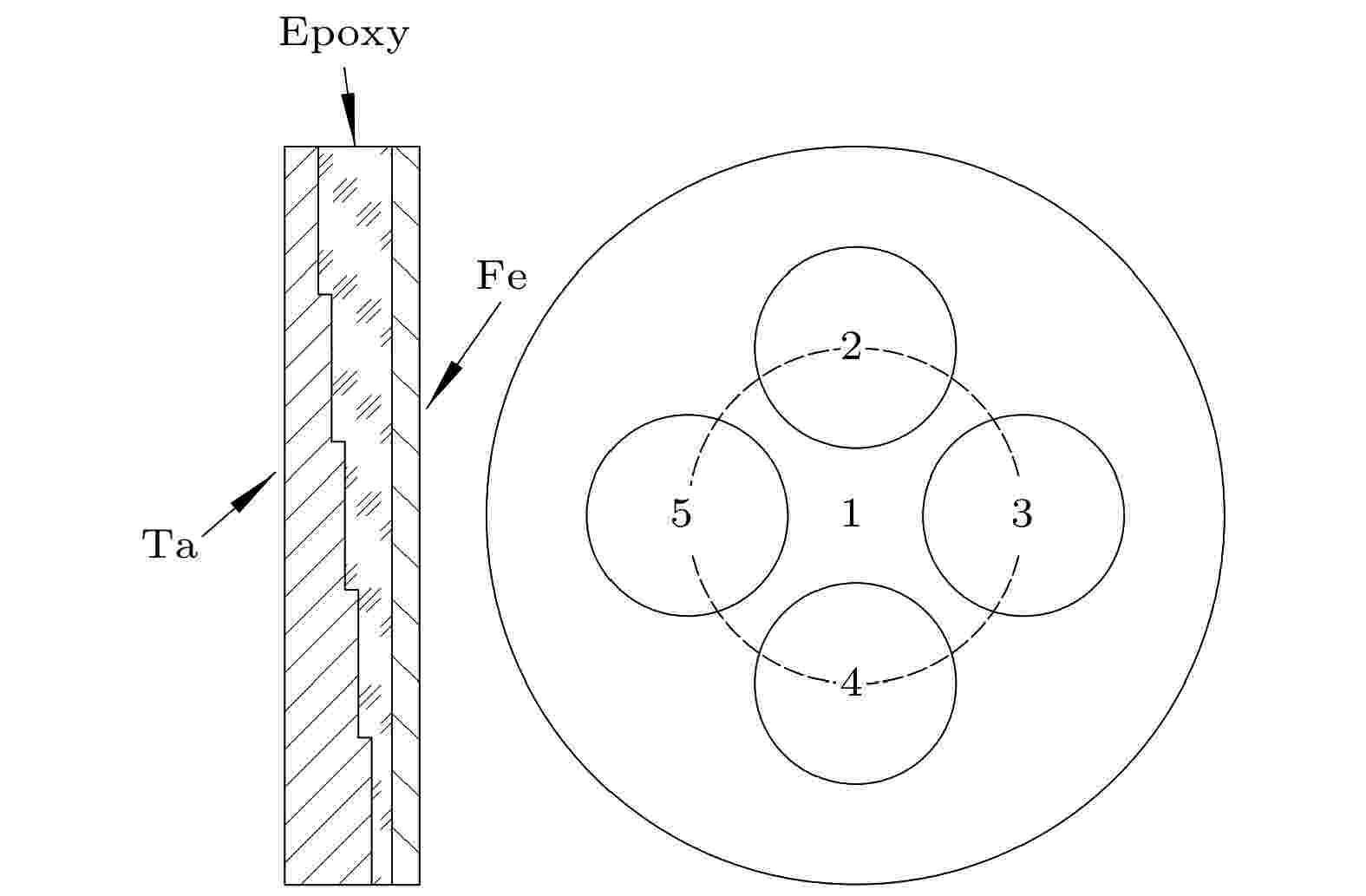图 1 多台阶三层组合飞片结构及台阶分布示意图Figure1. Schematic diagram of multistage triple-layer impactor.
基于上述飞片设计, 选用[100]LiF单晶作为窗口, 在预估弹速1.5 km/s的条件下, 在铁中实现的典型加载-卸载-再加载路径如图2所示. 由阻抗匹配法结合已知材料Hugoniot参数(见表1)预估计算得知, Fe飞片(即样品)一次冲击时最大压力为18 GPa大于文献报道的α→ε相变起始压力13 GPa[5], 卸载后压力降低至2 GPa附近, 发生ε→α逆相变, 再加载时最大压力约为20 GPa, 仍处于α相和ε相混合区域且基本转变为ε相. 与此同时, 复合飞片的多台阶设计使得同一冲击加载后的卸载时间长度可为不同, 有效地调控了再加载的状态起点, 以揭示时间依赖的逆相变及再加载相变特性. 不同台阶(见表2)典型的卸载时间长度设置为355, 483, 630, 750, 940 ns, 5个不同的再加载起始点将使材料处于逆相变的不同演化状态.
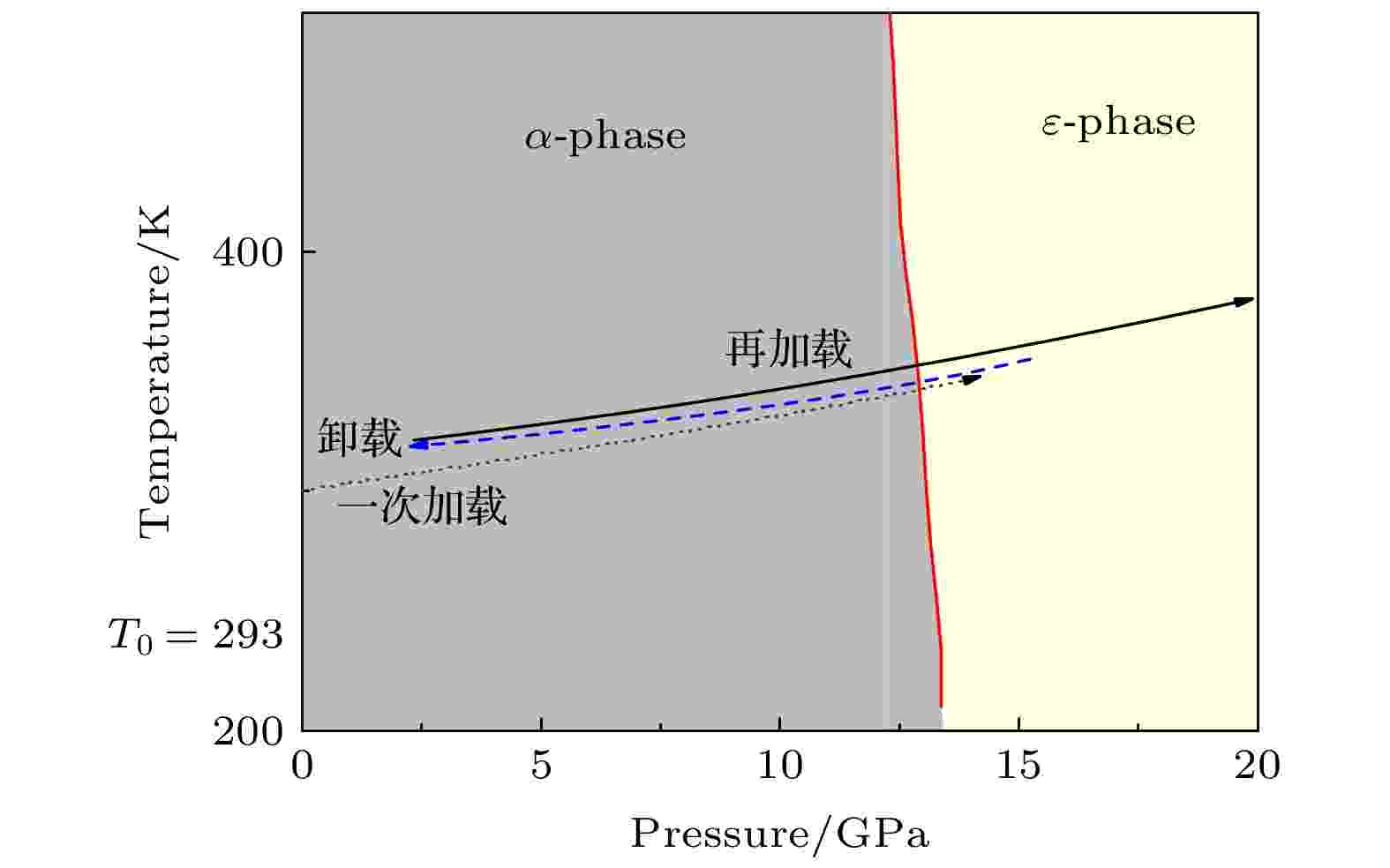图 2 Fe的低压部分相图及热力学加卸载路径设计Figure2. The phase diagram of iron and the thermodynamic loading path.
| 材料 | $ {{\rho }}_{0}/{({\rm{g}} \cdot {\rm{cm}}}^{-3}) $ | $ {{C}}_{0} $/$ ({\rm{km}} \cdot {\rm{s}}^{-1}) $ | λ |
| Ta | 16.65 | 3.43 | 1.19 |
| Epoxy | 1.19 | 2.73 | 1.49 |
| Fe样品 | 7.86 | 3.93 | 1.58 |
| LiF窗口 | 2.64 | 5.21 | 1.34 |
表1实验材料Hugoniot参数
Table1.Hugoniot parameter of materials.
| 部件 | $ {{\rho }}_{0}/\left({{\rm{g}} \cdot {\rm{cm}}}^{-3}\right) $ | 直径 /mm | 厚度 /mm | 对应Epoxy 厚度/mm |
| Ta 1号台阶 | 16.65 | 55 | 2 | 2.2 |
| Ta 2号台阶 | 16.65 | 15 | 2.5 | 1.7 |
| Ta 3号台阶 | 16.65 | 15 | 2.8 | 1.4 |
| Ta 4号台阶 | 16.65 | 15 | 3.2 | 1.0 |
| Ta 5号台阶 | 16.65 | 15 | 3.5 | 0.7 |
| Epoxy | 1.19 | 55 | — | — |
| Fe样品 | 7.86 | 55 | 1.5 | — |
| LiF窗口 | 2.64 | 55 | 20 | — |
表2实验各部件名义尺寸
Table2.Gauges of components.
实验装置及测试系统示意图如图3所示. 其中, 1)飞片速度测量采用安装于发射炮管出口处的磁感应测速系统[13], 即利用飞片穿越磁感应线圈时引起的感应电动势变化确定到达不同位置的时刻, 给定平均速度, 测量误差优于1%; 2)粒子速度测量采用全光纤激光位移干涉测速系统(DPS)[14], 利用单位时间内产生的干涉条纹(即多普勒频移, 反射光频率与入射光频率之差)与界面速度成正比的关系, 获得时间分辨的界面粒子速度历史, 速度测量的不确定度达到了1%以内; 3)为了获得高信噪比的实验数据, DPS探头设计为带有透镜(f = 25 mm)的聚焦探针结构, 其优点是可用于较长工作距离的测量, 同时插入损耗小, 避免样品反射回光信号过低导致干涉信号丢失. 此外测试用的LiF单晶窗口前表面镀有约1 μm铝膜并粘接8 μm铝箔作为测试面, 后表面镀1550 nm增透膜.
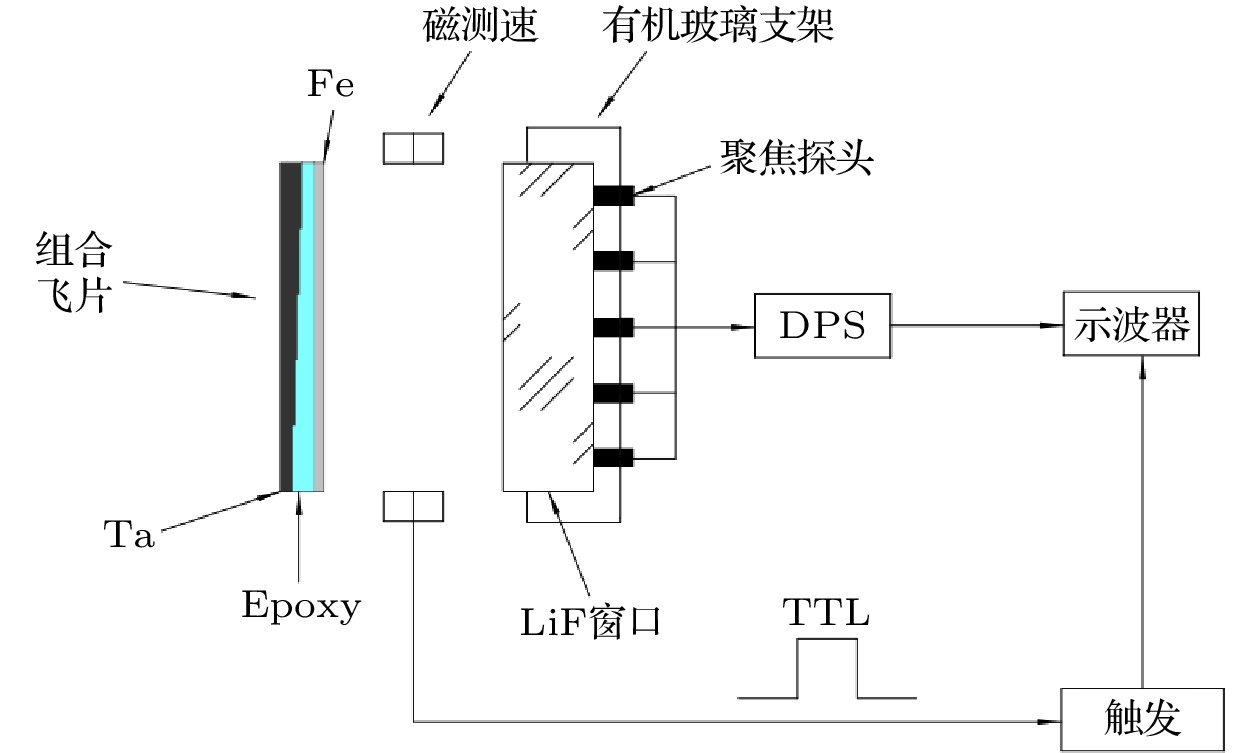图 3 实验装置系统示意图Figure3. Schematic diagram of experimental set up.
对实验中的波系相互作用进行分析:
1)一次冲击过程. 当样品飞片以速度
2)卸载过程. 卸载波为中心稀疏波, 根据特征线理论, 基于卸载过程的速度剖面, 建立声速与粒子速度之间的联系, 进而计算对应的压力[15]. 计算方法如图4所示. 设
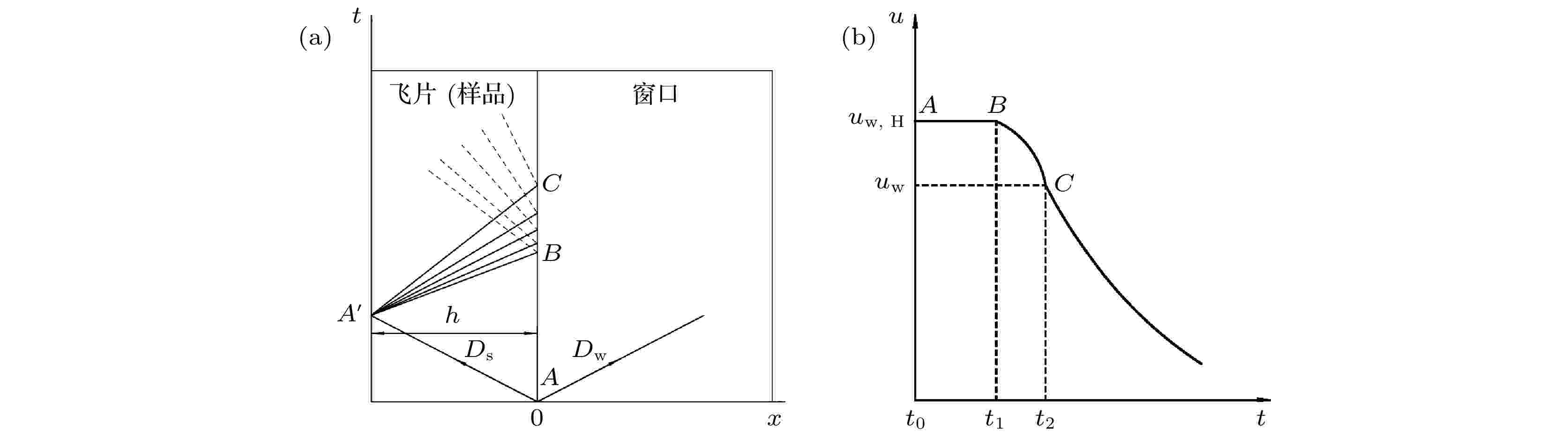图 4 声速计算方法示意图(A点为碰撞时刻, B点为稀疏波到达时刻, C点为卸载过程中任意时刻)Figure4. Schematic diagram of sound velocity calculation(A is the impact moment, B is the rarefaction wave arrival time, C is arbitrary time of unloading process).
3)再加载压缩过程. 由于复杂的波系相互作用影响, 难以直观地利用解析方法求解, 故采用有限元数值模拟计算结果进行分析. 由于冲击相变多为马氏体相变, 相界面迁移依靠位错滑动而达成, 真实材料中存在缺陷阻碍界面迁移, 这是形成亚稳态的微观机制之一. 故本文采用由Hayes混合相模型[16]衍生而出, 引入了亚稳相边界的概念的Boettger-Wallace模型[17]进行计算. 铁的Helmholtz自由能为
3.1.实测典型速度波剖面
在中物院流体物理研究所的
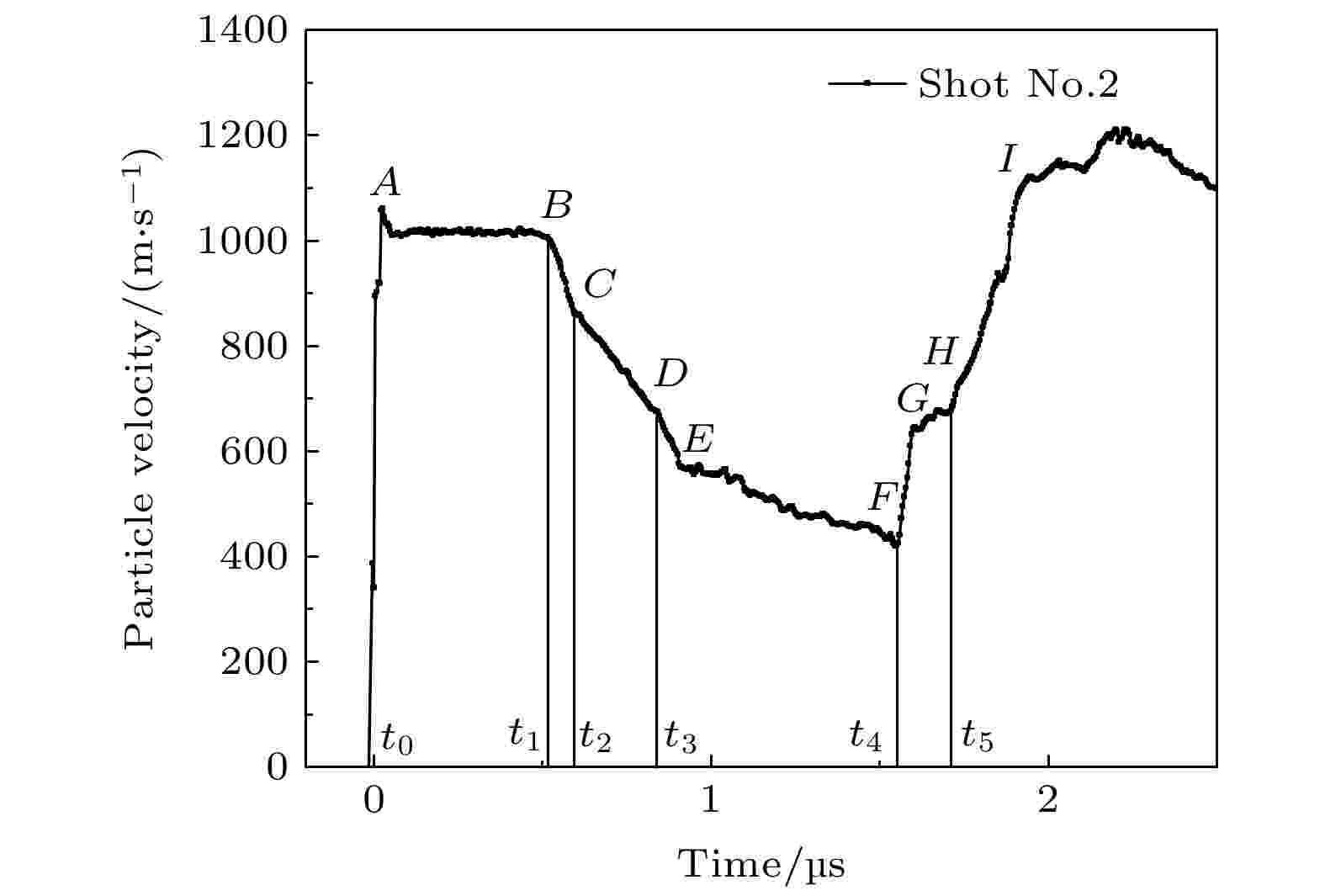图 5 典型飞片/窗口界面粒子速度剖面(A点为碰撞时刻, B点为稀疏波到达窗口界面, C点为弹塑性卸载拐折点, D点为逆相变起始点, E点为卸载过程终点, F点为二次加载起始点, G为相变临界点, H为再加载P2波到达时刻)Figure5. Particle velocity of impactor/window interface (A is the impact moment, B is the rarefaction wave arrival time, C is the elastoplastic unloading crutch point, D is the start point of reverse phase transition, E is the ending of unloading, F is the start point of reloading, G is the phase transition point of the reloading process, H is the reloading P2 wave arrival time).
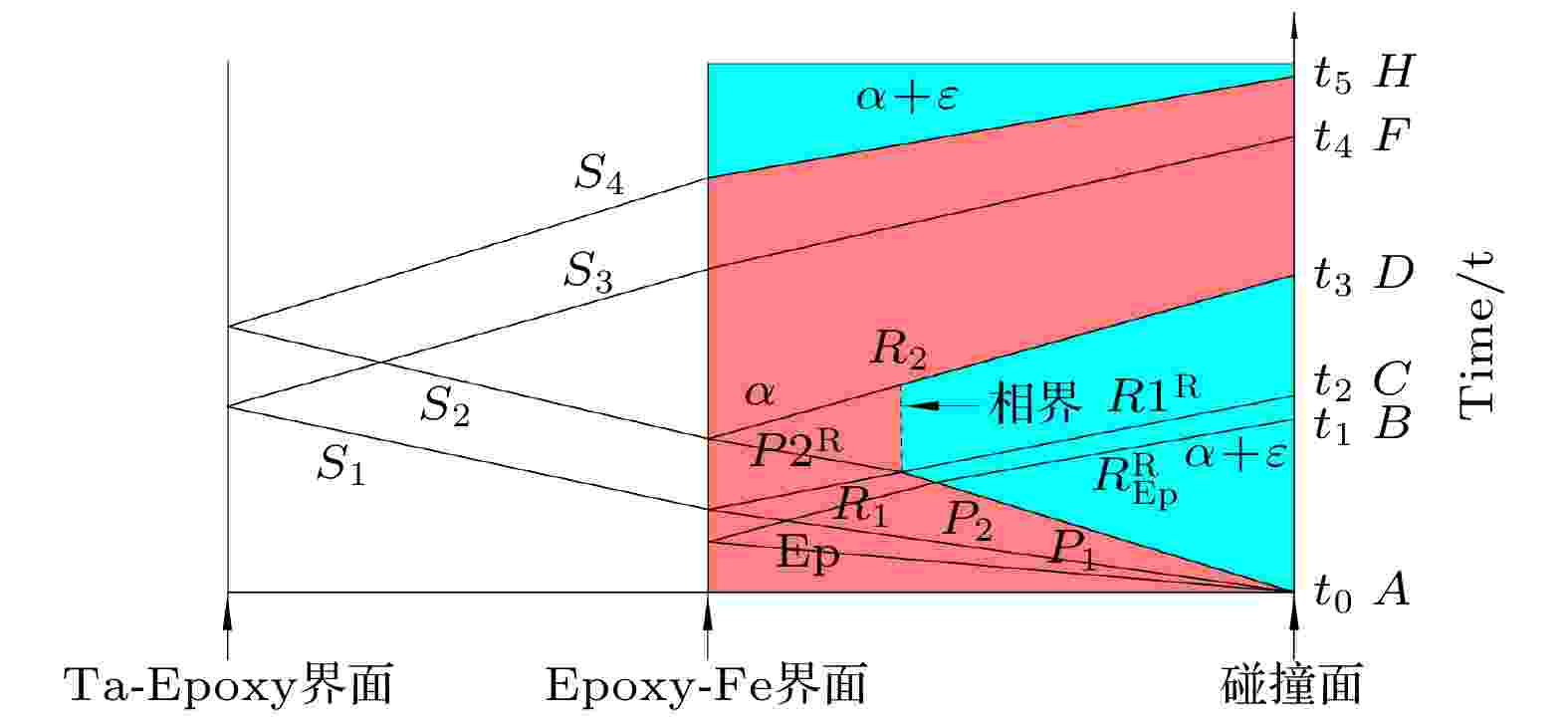图 6 相组织及应力波示意图(字母标识与图5同义)Figure6. Schematic diagram of phase and strain wave(the letters on the time axis have the same meaning with Fig.5).
实验shot No.1及shot No.2中5个不同厚度台阶的粒子速度剖面如图7所示. 不难看出, 两发实验重复性较好, 粒子速度剖面基本展现出相同特征. 在一次冲击及卸载段, 不同厚度台阶粒子速度剖面相同, 再加载起始位置依照实验设计被有效调控, 依次间隔开. 两发实验台阶1的再加载终态压力较其他台阶更低, 因为Ta厚度较薄, Epoxy较厚, 冲击波传播时间较长, 导致来自Ta后界面的稀疏波在尚未达到最高压力即到达飞片/窗口界面, 但这仅影响后续多次冲击过程, 二次加载未受影响, 故表明本实验设计是有效、可靠的.
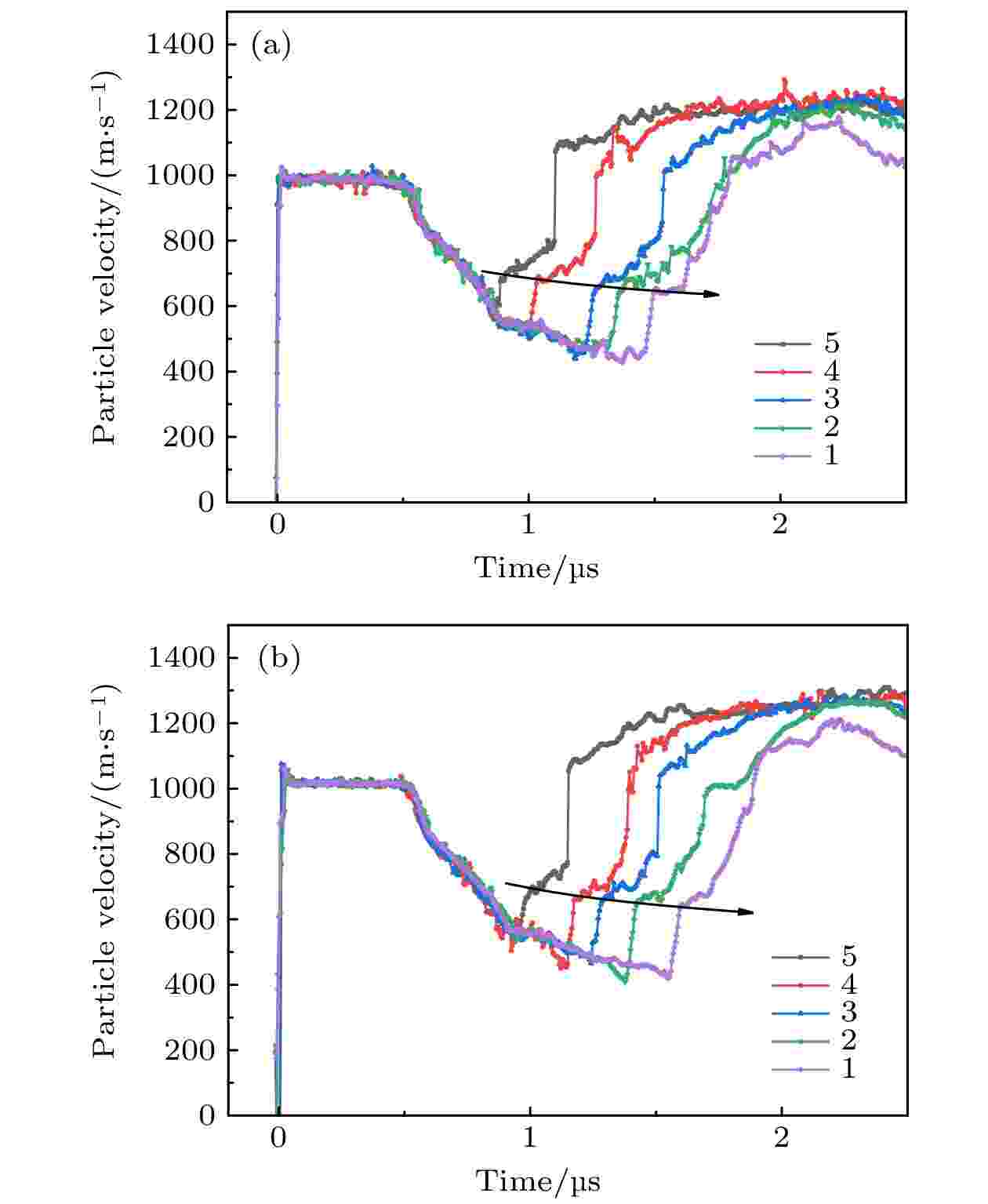图 7 (a) shot No.1和(b)shot No.2各台阶对应界面粒子速度历史(1—5分别表示台阶编号)Figure7. The interface particle velocity history of all stages in (a) shot No.1 and (b)shot No.2 (1–5 is the serial number of each stage).
2
3.2.卸载过程ε→α逆相变特性分析
在首次加–卸载段, 实验中各台阶特征几乎完全相同, 以图5所示典型粒子速度剖面图进行分析. 实验测量值和计算值等列于表3, 其中W为实测飞片速度,
| $ {W}/(\mathrm{m}\cdot {\mathrm{s}}^{-1}) $ | $ {{u}}_{\mathrm{w},\mathrm{H}}/(\mathrm{m}\cdot {\mathrm{s}}^{-1}) $ | $ {{u}}_{\mathrm{m}}/(\mathrm{m}\cdot {\mathrm{s}}^{-1}) $ | $ {{P}}_{\mathrm{m}}/\mathrm{G}\mathrm{P}\mathrm{a} $ | $ {{p}}_{\mathrm{D}}/\mathrm{G}\mathrm{P}\mathrm{a} $ | $ {{p}}_{\mathrm{E}}/\mathrm{G}\mathrm{P}\mathrm{a} $ | $ {\Delta {t}}_{\mathrm{D}\mathrm{E}}/\text{μ}\mathrm{s} $ | |
| Shot No.1 | 1475 ± 15 | 986 ± 10 | 489 ± 10 | 17.0 ± 0.1 | 11.2 ± 0.4 | 10.0 ± 0.2 | 0.08 |
| Shot No.2 | 1521 ± 15 | 1015 ± 10 | 506 ± 10 | 17.6 ± 0.1 | 11.4 ± 0.4 | 10.0 ± 0.2 | 0.07 |
表3实验shot No.2测量及计算结果
Table3.The data of experiment shot No.2.
由于卸载材料的阻抗差异, 本实验中的最低卸载压力为(10.0 ± 0.2) GPa, 远高于文献报道的完全逆相变压力(5.5 GPa), 甚至高于Barker得到的逆相变阈值压力, 可能存在ε相的残余. 对此, 采用唯象的相变动力学模型(Boettger-Wallace模型)[16]对其进行分析. 图8所示为实验shot No.1的4号台阶实测速度剖面与计算结果的比较. 可以看到, 当相变特征时间τ取为30 ns时, 两者符合较好(文献报道中, 相关模型取30 ns与一次冲击实验符合较好[17,18]). 计算结果得到Hugoniot态下ε相质量分数为89%, 处于混合相态, 而卸载最低压力状态下ε相仍残余26%.
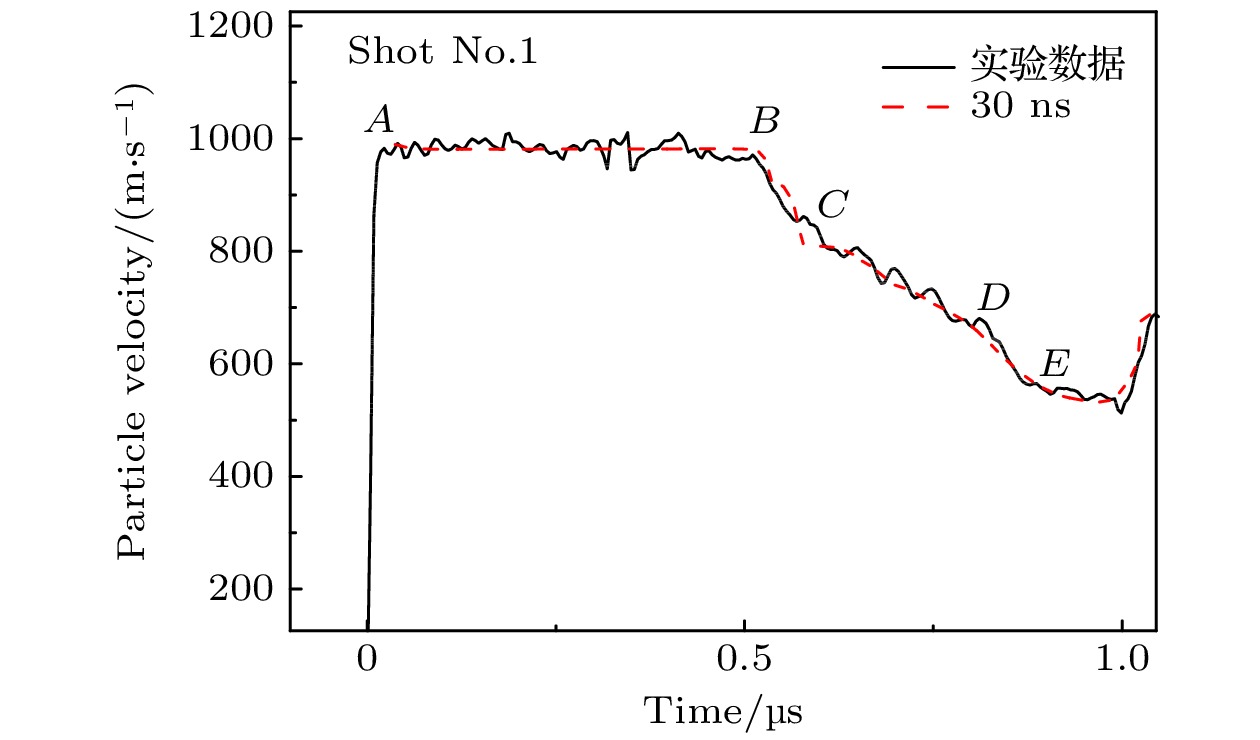图 8 相变特征时间τ取30 ns的模拟结果(字母标识与图5同义)Figure8. Simulation of interface velocity with a characteristic time of 30 ns(the letters have the same meaning with Fig.5).
2
3.3.再加载α→ε相变特性分析
如图9所示为实验shot No.1中4号台阶对应的再加载段速度剖面, 可见, F点处, 再加载塑性冲击波到达界面, 将Fe带到相变临界点G, 再加载相变波将Fe带到二次冲击Hugoniot态I. 由此获得再加载时, α→ε相变的起始压力为10.9 GPa, 较首次加载相转变起始压力(12.8 GPa)低约2 GPa. 其再加载起始点ε相质量分数为27%. 图中同时给出了计算的速度剖面, 可见, τ = 30 ns的结果在受丰富相变动力学因素影响的GH段和HI段与实验结果表现出明显差异, GH段更缓而HI段更陡. 故将相转变特征时间加快到5 ns, 计算得到波剖面与实验结果更为接近. 上述计算结果表明, 相比于首次冲击, 二次再加载段的相转变速率更快. 分析其原因, 涉及的基本物理图像应该为一次加载-卸载后, 由于α→ε相变及其逆相变的发生, 材料内部的孪晶、缺陷、位错等会显著增加[19,20], 导致再加载阶段的二次相变在这些位置更易于成核, 相变成核能降低, 成核密度增加, 从而降低了相变阈值压力, 同时提高了相转变速率[21].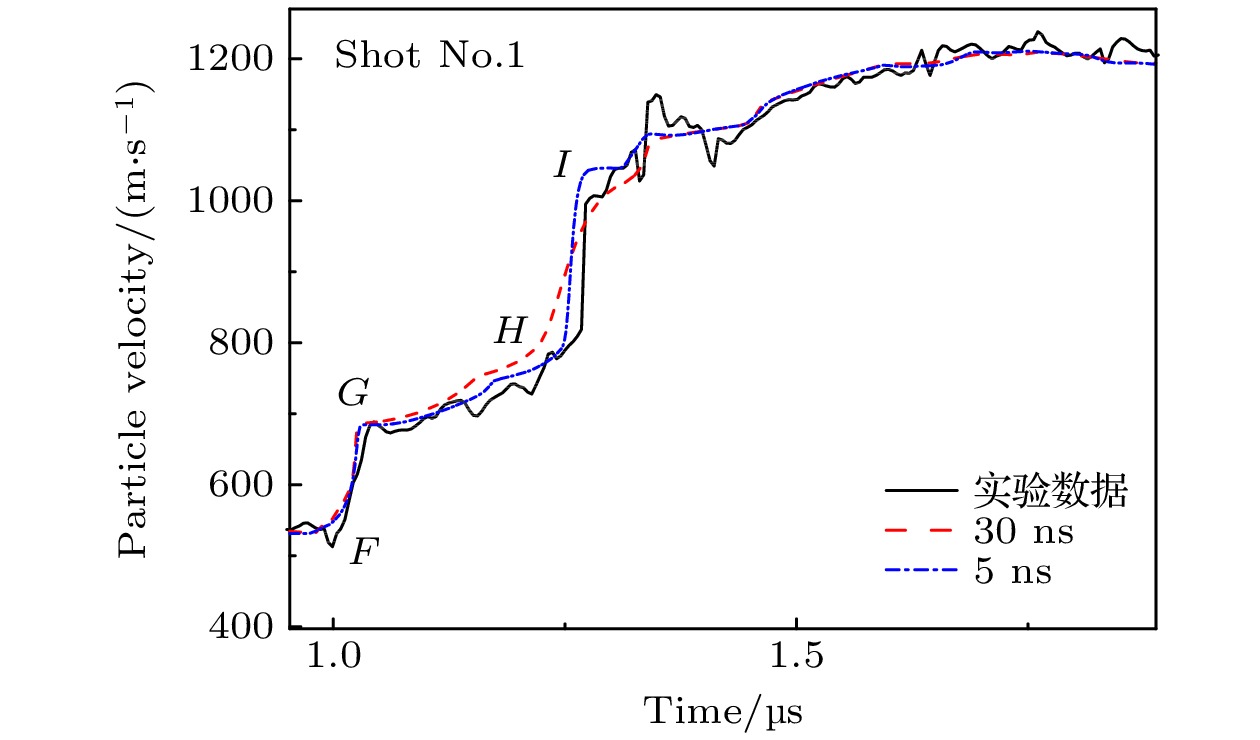
图 9 实测再加载段速度剖面与数值模拟的比较(字母标识与图5同义)Figure9. Comparison of the measured particle velocity and simulation (the letters have the same meaning with Fig.5).
进一步地, 对不同厚度台阶(即不同逆相变时长)的再加载段进行分析, 并于表4中列出了各台阶对应的一次卸载终态残余ε相质量分数及二次相变起始压力. 可发现, 随卸载时间增长, 再加载塑性波顶端粒子速度下降, 且相变波带来的速度跃变逐渐变缓(图7). 卸载时长与ε相质量分数、二次加载相变压力关系如图10所示. 结果表明, 随卸载时长增长, 残余ε相质量分数下降, 二次相变压力降低. 造成此现象的原因可能为: 逆相变完成度越高, ε相残余越少, 材料内部存在的孪晶、缺陷、位错等易于成核位置越多, 从而使相变阈值压力下降.
| Shot No.1 | Shot No.2 | ||||
| 台阶编号 | ε相质量 分数/% | 二次加载相 变压力/GPa | ε相质量 分数/% | 二次加载相 变压力/GPa | |
| 5 | 52 | 11.5 | 77 | 12.0 | |
| 4 | 27 | 10.9 | 36 | 11.1 | |
| 3 | 21 | 10.6 | 26 | 10.8 | |
| 2 | 16 | 10.4 | 20 | 10.5 | |
| 1 | 12 | 10.1 | 15 | 10.2 | |
表4shot No.1和shot No.2各台阶对应卸载尾段残余ε相质量分数及二次加载相变压力
Table4.The mass fraction of ε phase in the end of unloading process and reload phase transition pressure on each stage.
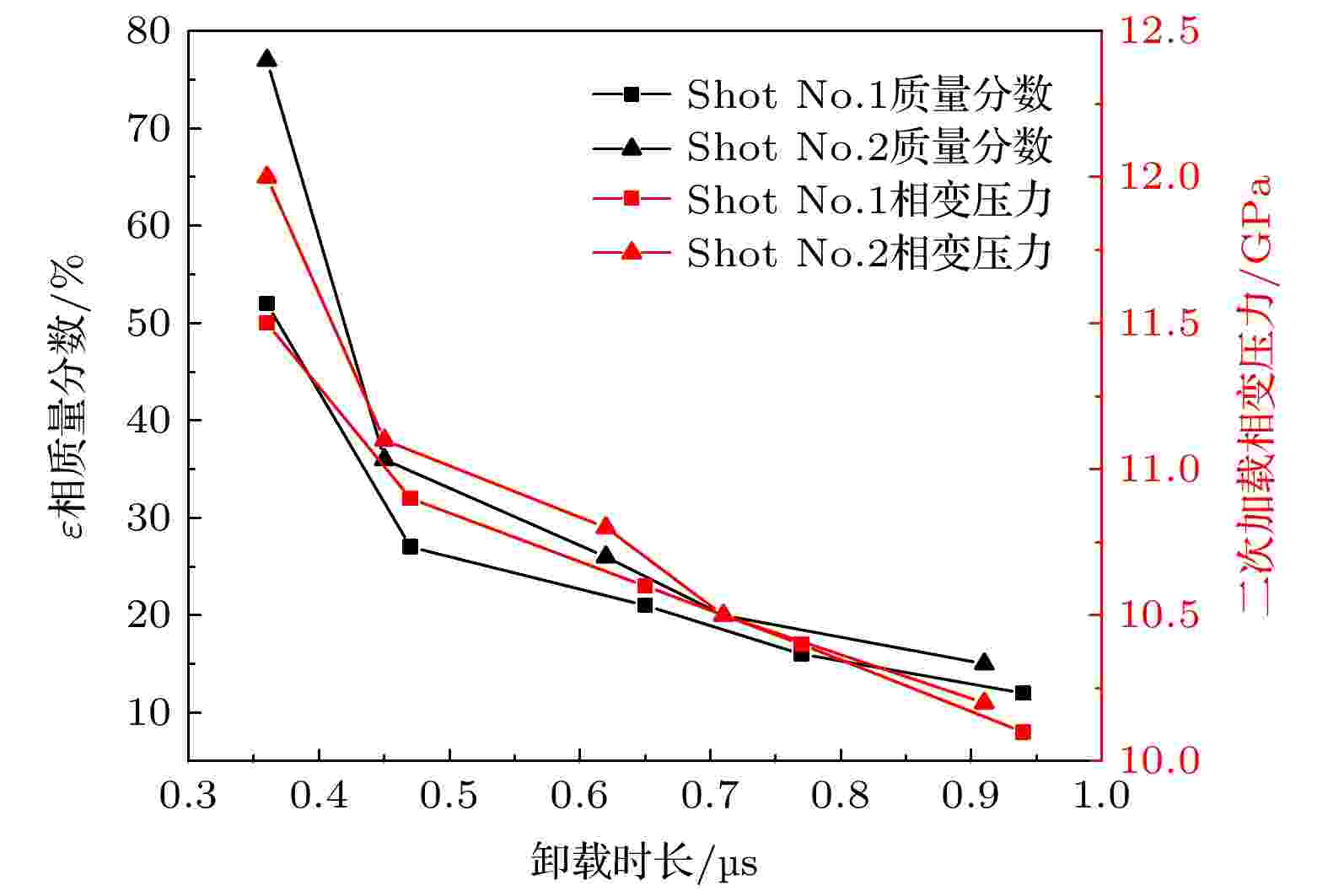图 10 二次相变压力与ε相质量分数关系Figure10. The relation between reloading phase transition pressure and mass fraction of ε phase.
1) 一次冲击加-卸载段, 铁的卸载呈现弹性卸载、塑性卸载、卸载相变三波结构, 逆相变阈值约为(11.3 ± 0.5) GPa, 与Barker文献报道结果不一致, 但仍存在典型相变迟滞特征, 一次卸载压力最低达到10 GPa左右. 确定了相变特征时间τ取30 ns符合一次加-卸载段实验结果.
2)二次加载相变压力为(11 ± 1) GPa附近, 较一次相变压力低约1—2 GPa, 结合不同相转变特征时间τ的计算结果, 指出二次相变过程相转变速率更快. 其根本原因应为一次卸载后材料内孪晶和缺陷的增多, 导致二次相变更易于成核, 相变成核能降低, 成核密度增加, 降低了相变压力阈值, 并加快了相转变速率.
3)不同厚度台阶对应二次相变压力随卸载时长延长而降低, 且均低于一次相变压力. 且随ε相质量分数降低, 相变压力随之降低. 其物理原因或为逆相变完成度越高时, 孪晶、缺陷等易于成核位置越多, 相变成核能越低.
上述结果对理解和探索复杂热力学路径下Fe的相变动力学行为提供了新的角度, 对后续再加载路径实验提出了需待验证的问题, 且为相关数值计算模型提供了重要的实验支撑.
