摘要:螺旋相衬显微术利用螺旋相位滤波器实现了样品振幅和相位的定量测量, 可被广泛应用于生物医学成像、工业检测等领域. 然而, 传统的螺旋相衬显微术需要通过三步相移法进行相位恢复, 图像采集和处理过程相对复杂, 时间分辨率较低. 为了提升其特性, 本文提出了一种基于分数阶螺旋相位片的定量相位成像方法和系统, 通过一幅经分数阶螺旋相位滤波的样品强度图像, 利用改进的Gerchberg-Saxton迭代相位恢复算法实现了样品相位的定量重构, 简化了实验过程和相位重构步骤. 计算机模拟实验研究了基于不同拓扑荷数的螺旋相位片的相位成像和重构过程, 分析了其可行性. 最后, 通过对定制的相位型光栅和生物细胞样品进行了成像和相位重构, 验证了基于分数阶螺旋相位片的相衬显微方法可以有效地提高螺旋相衬显微成像的对比度, 能够定量获其样品的相位信息, 对于螺旋相衬显微术的发展具有重要的研究意义和应用价值.
关键词: 定量相位成像/
螺旋相衬显微术/
螺旋相位片/
相位恢复

English Abstract

全文HTML

--> --> -->

定量相位成像(quantitative phase imaging, QPI)技术将相位成像和光学显微相结合, 为观测透明生物样品提供了一种无标记、快速、无损、高分辨率的成像手段, 广泛应用于生物医学等领域^[1]. 目前, QPI技术主要分为基于干涉法测量和非干涉法测量两大类, 包括离轴法^[2,3]、相移方法^[4,5]、共光路法^[6,7]、 白光法^[8,9]及傅里叶变换光散射法^[10]等多种方法.
径向希尔伯特变换是实现图像边缘增强中最常用的方法之一. 在4f滤波系统的傅里叶谱平面上使用螺旋相位滤波器(spiral phase filter, SPF)能够实现径向希尔伯特变换^[11], 从而使振幅和相位样本产生各向同性的边缘增强, 可用于观察透明生物组织和细胞, 因此, SPF倍受研究人员关注^[12-14]. 在SPF的基础上, Furhapter等^[15]发展了螺旋相衬(spiral phase contrast, SPC)显微成像技术, 通过利用拓扑荷数为1的整数阶螺旋相位片进行相位滤波, 再通过三步相移法进行复杂物体相位的定量重构, 但其图像采集和处理过程相对复杂. 当螺旋相位片的拓扑荷数为分数时, SPF系统点扩散函数的径向对称被打破, 由此产生了可控的边缘位错, 可以通过控制分数阶拓扑荷数的大小和初始相位改变其边缘增强的程度和方向, 实现物体的各向异性边缘增强^[16-18]. 目前, 基于分数阶螺旋相位片的SPF研究主要围绕图像的边缘增强展开, 但在QPI方面研究相对较少.
基于迭代的相位恢复方法, 例如Gerchberg-Saxton (GS)^[19]、输入-输出算法^[20]等, 可以从一幅(或多幅)强度测量中定量恢复物体的相位分布, 实现了非干涉法的QPI, 引起研究人员的广泛关注. 然而, 直接利用样品强度图像恢复相位是一个病态问题, 存在解的唯一性和迭代耗时的问题, 这往往需要通过对强度信息进行过采样来解决这一问题.
基于此, 将相位恢复与螺旋相衬显微相结合, 本文提出了一种基于分数阶螺旋相位片的定量相位成像方法和系统, 通过一幅经分数阶SPF的样品强度图像, 利用基于螺旋相衬的GS相位恢复算法(SPC-based GS phase retrieval algorithm, SGSA)实现了样品相位的定量重构, 简化了螺旋相衬显微的实验过程和相位重构步骤. 计算机模拟实验研究了基于不同拓扑荷数的螺旋相位滤波成像和相位重构过程, 分析了其可行性. 最后, 搭建了基于空间光调制器(spatial light modulator, SLM)的分数阶螺旋相衬显微成像系统, 通过对相位型光栅和生物细胞样品进行了成像和相位重构, 验证了基于分数阶螺旋相位片的相衬显微方法可以有效地提高螺旋相衬显微成像的对比度, 能够定量获其样品的相位信息, 对于定量相衬显微术的发展具有重要的研究意义和应用价值.

2

-->

2.1.成像原理

螺旋相衬显微成像是基于一个4f系统, 其光学系统示意图如图1所示.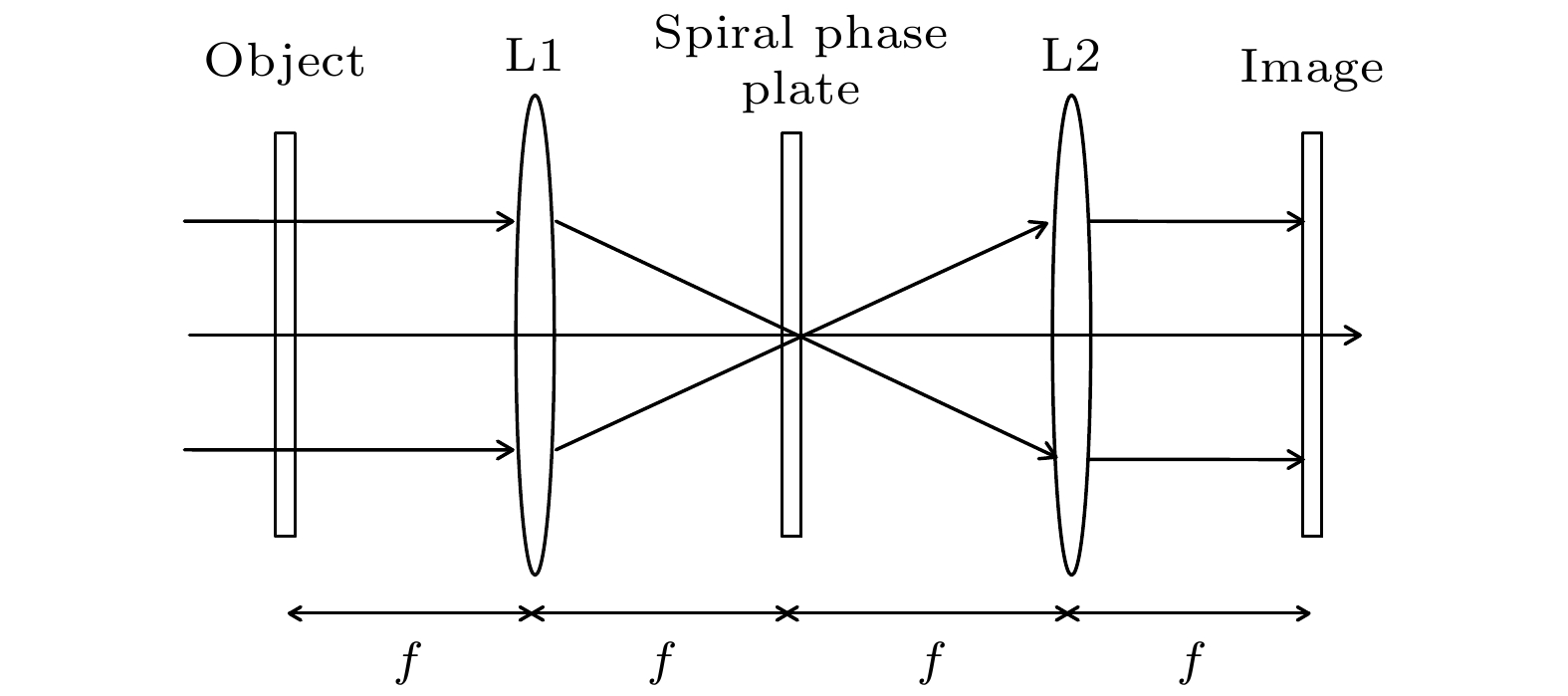
图 1 基于4f系统的螺旋相衬成像系统示意图
Figure1. Schematic diagram of 4f system-based spiral phase contrast imaging system.

平行入射光照射样品后的光场为$g(r, \theta )$, 经过4f系统的第1个透镜L1的傅里叶变换, 在其后焦平面得到物光场的频谱$f(\rho, \phi ) = {\rm{FT}}[g(r, \theta )]$. 然后, 通过螺旋相位片$H(\rho, \phi ) = \exp ({\rm{i}}l\varphi )$对其进行滤波, l为拓扑荷数, φ为绕螺旋相位片中心的方位角. 最后, 螺旋相位片滤波后的光场通过4f系统的第2个透镜的逆傅里叶变换后, 在其后焦平面, 即探测平面, 得到输出光场. 利用探测器记录输出强度图像$\mathop {G = \left| {F(r, \theta )} \right|}\nolimits^2 $, 其成像过程表示如下:

$\begin{split} G(r,\theta ) =\;& \mathop {\left| {F(r,\theta )} \right|}\nolimits^2 = \mathop F\nolimits^{ - 1} \{ F[g(r,\theta )]\exp [{\rm{i}}l\varphi (r,\theta )]\} \\ = \;& f' (r,\theta ) \otimes h(r,\theta ),\\[-10pt] \end{split} $

其中$h(r, \theta )$代表螺旋相位片的傅里叶变换, 相当于4f系统的点扩散函数.
当利用整数阶螺旋相位片进行相位滤波成像时, 由于整数阶螺旋相位片的点扩散函数的中心奇点的振幅为0, 因此, 输入信息的低频部分可以被有效地抑制, 并且主瓣各个方向上的振幅分布比较均匀, 所以, 能够对相位样品产生各向同性边缘增强.
由于分数阶螺旋相位片可以表示为有限个不同整数阶螺旋相位片的线性叠加, 因此, 其透过率函数可以表示为傅里叶级数的形式^[21]:

$H(\rho,\phi ) = \exp ({\rm{i}}l\varphi ){{ = }}\frac{{\exp ({\rm{i}}l{\rm{\pi }})\sin (l\pi )}}{\pi }\sum\limits_{n = - \infty }^\infty {\frac{{\exp ({\rm{i}}n\varphi )}}{{l - n}}} ,$

其中ρ为径向坐标, ?为方位角坐标, n为整数, l取值一般为小于1的分数.
分数阶螺旋相位片作为相位滤波器所对应的点扩散函数可以表示为

$\begin{split}\;& h(r,\theta ) =\frac{k}{{2{\rm{\pi }}f}}\sum\limits_{m = - \infty }^\infty {\mathop {( - {\rm{i}})}\nolimits^{\left| m \right|} } \exp ({\rm{i}}m\theta ) \\&~~~~\times \frac{{\exp [{\rm{i}}2\pi (l - \left| m \right|)] - 1}}{{l - \left| m \right|}}\int_0^R {\mathop {\rm J}\nolimits_{\left| m \right|} } (\tau \rho )\rho {\rm{d}}\rho ,\end{split}$

其中m为最接近l的整数, J_|m| 为第|m|阶贝塞尔函数.
对于拓扑荷数l < 0.5的分数阶螺旋相位片的点扩散函数中并没有涡旋产生, 因此, 并不能对相位物体实现高衬度的边缘增强. 然而, 由于其非对称性, 仍可以获得一定的强度梯度图像^[18]. 利用拓扑荷数l < 0.5分数阶螺旋相位片滤波得到的强度图, 再经过相位恢复算法处理后, 能够得到比整数阶SPF滤波后的强度图经SGSA处理后对比度更高的相位图, 更有利于实现定量相位显微成像.
2 -->

2.2.定量相位重构

将相位恢复算法与SPC相结合, 利用探测到的螺旋相位滤波图像, 实现样品相位的定量重建. 在传统GS算法的基础上, 在迭代过程中, 在频谱面引入螺旋相位片的限制条件, 然后, 进行优化. SGSA的算法框图如图2所示.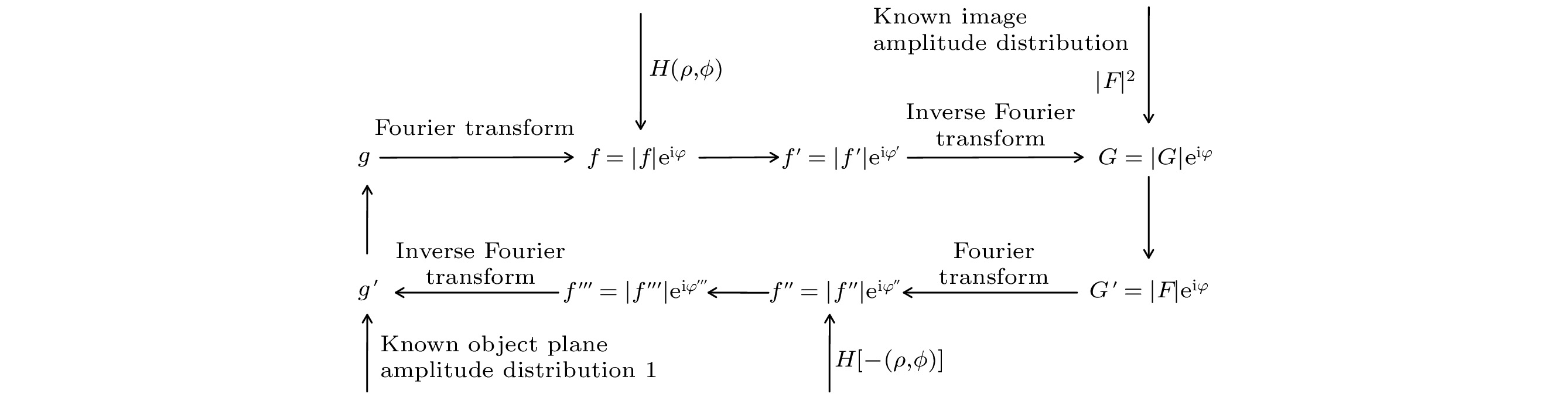
图 2 SGSA框图
Figure2. Block diagram of the SGSA.

以第n阶迭代为例, 具体步骤如下.
1)第n次迭代的目标光场复振幅分布$\mathop g\nolimits_n (r, \theta )$经过傅里叶变换获得其频谱分布$\mathop f\nolimits_n (\rho, \phi )$:

$f_n (\rho,\phi ) \!=\! | { f_n (\rho,\phi )} |\exp [{\rm{i}} \varphi _n (\rho,\phi )] \!=\! {\rm{FT}}[ g_n (r,\theta )].$

2)在频谱面引入SPF对$\mathop f\nolimits_n (\rho, \phi )$进行限制, 获得滤波后的频谱$\mathop f\nolimits_n' (\rho, \phi )$:

$\begin{split}\mathop f\nolimits_n' (\rho,\phi ) =\;& \left| {\mathop f\nolimits_n' (\rho,\phi )} \right|\exp [{\rm{i}}\mathop \varphi \nolimits_n' (\rho,\phi )] \\=\;& \mathop f\nolimits_n (\rho,\phi ) \times H(\rho,\phi ).\end{split}$

3)滤波后的频谱, 经过逆傅里叶变换, 获得像平面的复振幅分布$\mathop G\nolimits_n (r, \theta )$:

$\begin{split}\mathop G\nolimits_n (r,\theta ) =\;& \left| {\mathop G\nolimits_n (r,\theta )} \right|\exp [{\rm{i}}\mathop \varphi \nolimits_n (r,\theta )]\\=\;& {{\rm{FT}}}^{ - 1} [f_n' (\rho,\phi )].\end{split}$

4)引入像面上的限制条件, 即保持相位不变, 但振幅变为预先探测到的像面的振幅分布, 获得新的复振幅分布$G'_n (r, \theta )$:

$G_n' (r,\theta ) = \left| {F(r,\theta )} \right|\exp [{\rm{i}}\mathop \varphi \nolimits_n (r,\theta )].$

5)将新的像的复振幅分布$\mathop G\nolimits_n' (r,\theta )$进行傅里叶变换, 获得频谱面的复振幅分布$\mathop f\nolimits_n'' (r, \theta )$:

$ f_n'' (\rho,\phi ) = |f_n'' (\rho,\phi ) |\exp [{\rm{i}} \varphi _n'' (\rho,\phi )] = {\rm{FT}}\{ G_n' (r,\theta )\} .$

6)在频谱面引入共轭的SPF对其进行滤波, 获得物体的频谱$\mathop f\nolimits_n''' (\rho, \phi )$:

$\begin{split}\mathop f\nolimits_n''' (\rho,\phi ) =\;& \left| {\mathop f\nolimits_n''' \left( {\rho,\phi } \right)} \right|\exp [{\rm{i}}\mathop \varphi \nolimits_n''' (\rho,\phi )]\\=\;& \mathop f\nolimits_n'' (\rho,\phi ) \times H[ - (\rho,\phi )].\end{split}$

7)将获得的物体的频谱, 通过逆傅里叶变换, 获得物体的复振幅分布$\mathop g\nolimits'\left( {r, \theta } \right)$:

$\mathop g\nolimits_n' (r,\theta ) = \left| {\mathop g\nolimits_n' (r,\theta )} \right|\exp ({\rm{i}}\mathop \varphi \nolimits_n' (r,\theta )) = \mathop {{\rm{FT}}}\nolimits^{ - 1} [\mathop f\nolimits_n''' (\rho,\phi )].$

8)再引入物面上的限制条件, 即保持相位不变, 振幅变为已知的物面的振幅分布, 作为下一次迭代的物波函数:

$\begin{split}\mathop g\nolimits_{n + 1} (r,\theta ) =\;& \left| {\mathop g\nolimits_{n + 1} (r,\theta )} \right|\exp [{\rm{i}}\mathop \varphi \nolimits_{n + 1} (r,\theta )] \\=\;& \exp [{\rm{i}}\mathop {\mathop \varphi }\nolimits_{n + 1} (r,\theta )].\end{split}$

9)反复进行1)至8)的迭代运算, 直到定义的误差—均方差之和(sum square error, SSE)到达预先设置的精度或达到设置的最大迭代次数为止. SSE的定义如下:

${\rm{SSE}} = \sum {\mathop {\left[ {{\rho _2} - \rho _2^{(n)}} \right]}\nolimits^2 } \bigg/\sum {\mathop {\rho _2^2} } ,$

其中$\mathop {{\rho _2}} $表示输出平面探测器接收到的像振幅分布, $\mathop \rho \nolimits_{\rm{2}}^{(n)} $表示第n次迭代结束后输出平面像的振幅分布. 下面实验中, 设置迭代终止的${\rm{SSE}} < \mathop {10}\nolimits^{ - 3} $.

基于Matlab, 利用快速傅里叶变换算法, 模拟螺旋相衬成像及相位重构过程. 以图像“LENNA”作为相位物体, 像元数为1024 × 1024, 物理尺寸为332.8 μm × 332.8 μm, 波长$\lambda = 640$ nm, 相位值在[0 1]弧度之间变化^[22], 满足弱相位成像条件, 对于细胞的成像来说, 这是合理的. 对于螺旋相位片, 整数阶的拓扑荷数取$l = 1$, 分数阶拓扑荷数取$l = 0.1$. 利用方程(1)获得了经SPF后的模拟成像图像. 考虑到相机的噪声, 对生成的图像添加了高斯噪声(均值为0, 方差为0.01), 以更符合实际情况. 然后, 再对所得强度图利用SGSA算法重构获得样品的相位信息. 由于SGSA是一个迭代算法, 为了进一步说明迭代次数的选择, 模拟了拓扑荷取0.1时的分数阶螺旋相位滤波成像, 计算了SSE和迭代次数的关系, 如图3所示. 另外, 考虑到数值模拟时相位是已知的, 也计算了恢复相位与真实相位之间的均方误差(mean square error, MSE)与迭代次数的关系, 如图4所示.
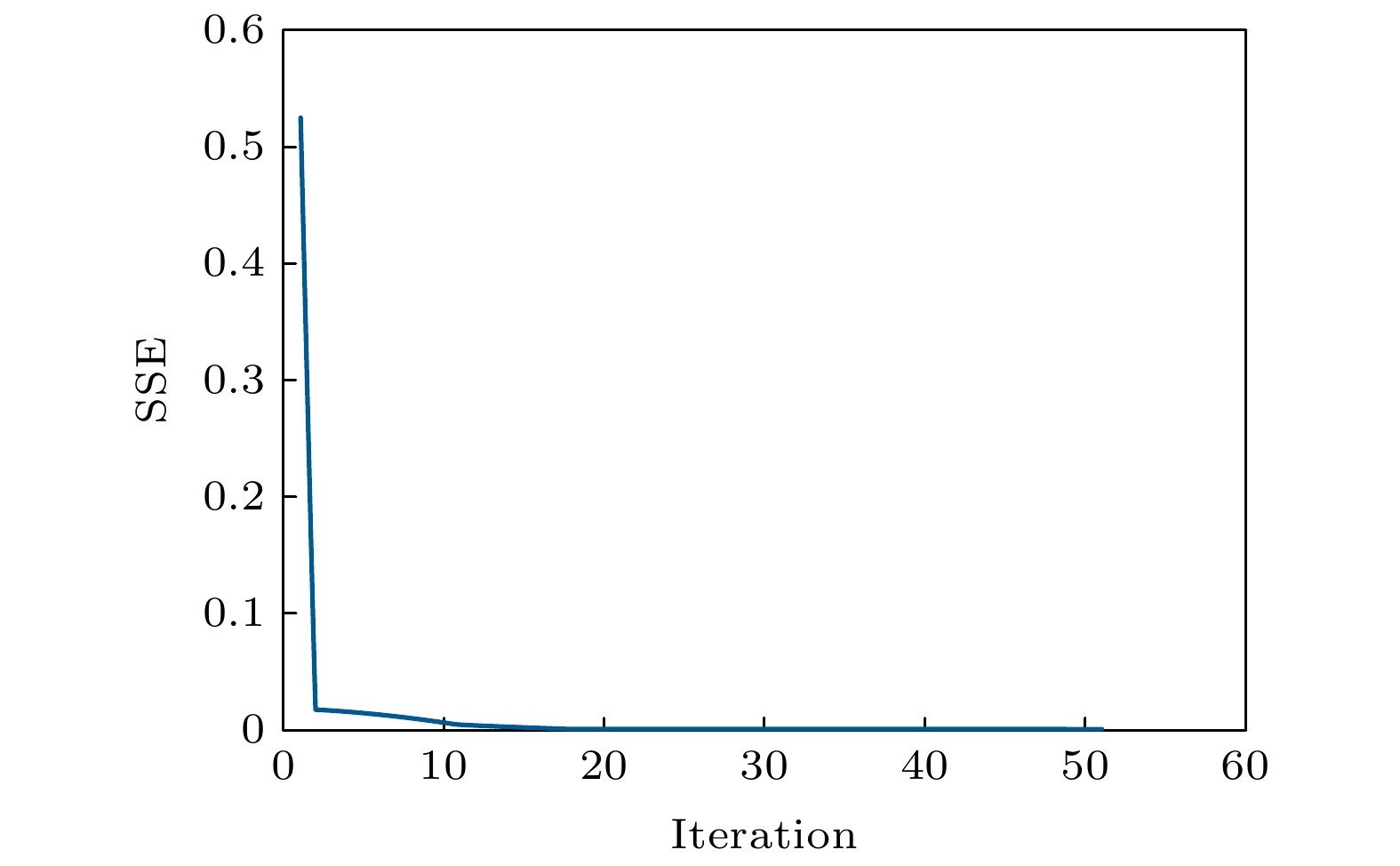图 3 分数阶拓扑荷取0.1时, SSE随迭代次数的变化曲线
Figure3. SSE error vs. the number of iterations when the fractional topological charge is 0.1.

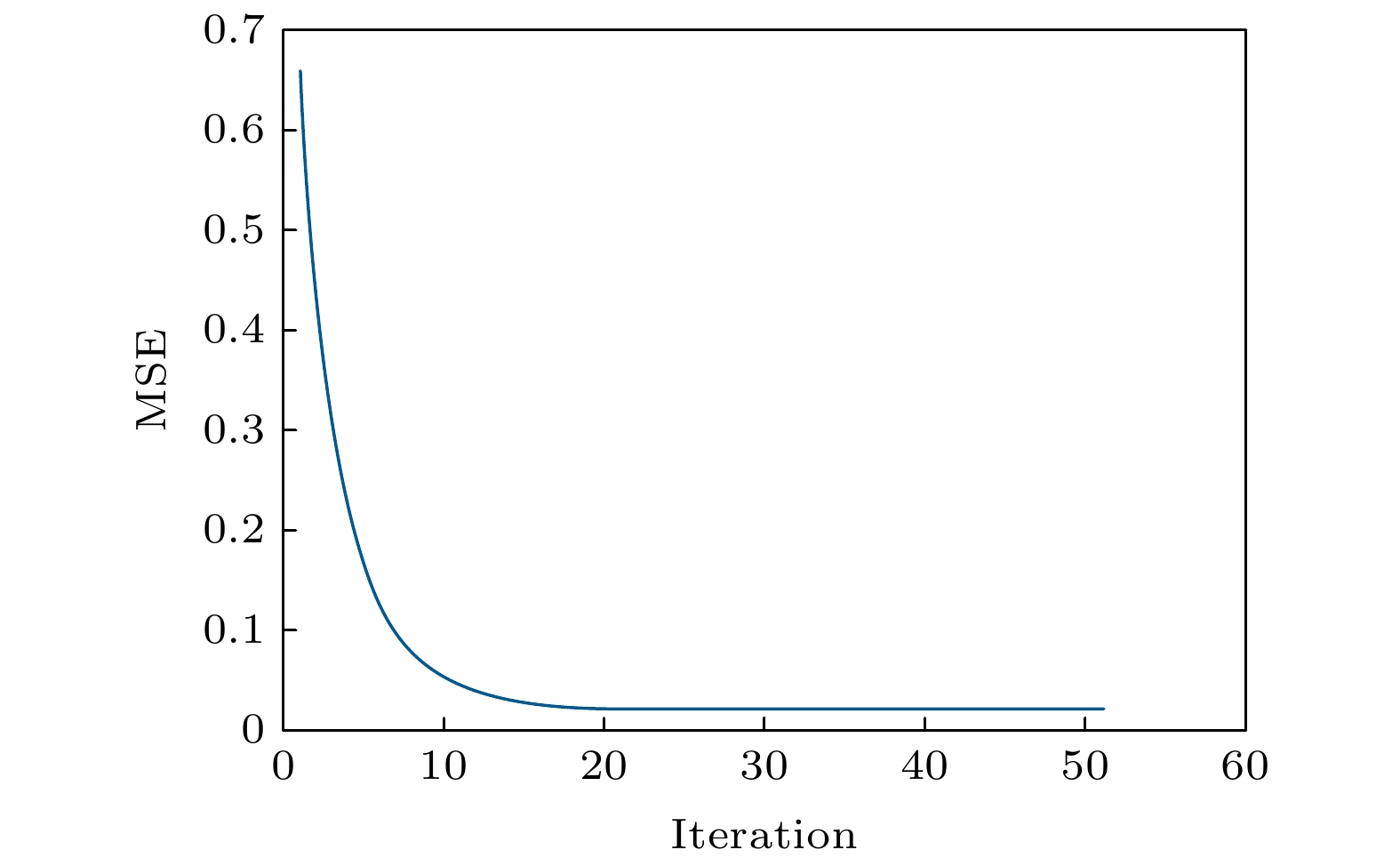图 4 恢复相位与真实相位之间的MSE随迭代次数的变化曲线
Figure4. MSE error between the recovered phase image and ground truth phase image vs. the number of iterations.

MSE定义为

$ {\rm{MSE}} = \frac{1}{{M \times N}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {\mathop {[\varphi_0' (i,j) - \mathop \varphi \nolimits_0 (i,j)]}\nolimits^2 } } , $

其中$\mathop \varphi \nolimits_{\rm{0}}'$表示迭代恢复出的相位值, $\mathop \varphi \nolimits_{\rm{0}} $ 是输入平面样品的相位值.
综合考虑MSE和SSE, 考虑到计算时间, 选择了迭代次数设置为20次. 样品原图像, 整数阶螺旋相位片滤波与分数阶螺旋相位片滤波后的成像强度图对比及重构出的样品相位图对比结果如图5所示.
图 5 螺旋相位滤波成像及恢复结果对比　(a) 相位型样品原图; (b) 传统整数阶螺旋相位片滤波图像; (c) 对图(b)用SGSA恢复的样品相位图; (d) 分数阶螺旋相位片滤波图像; (e) 对图(d)用SGSA恢复的样品相位图
Figure5. Comparisons of the recorded images and the recovered results: (a) The ground truth phase sample image; (b) the recorded image via traditional integer order spiral phase plate filtering; (c) the recovered phase sample image using SGSA for panel (b); (d) the recorded image via fractional spiral phase plate filtering; (e) the recovered phase sample image using SGSA for panel (d).

为了确定分数阶螺旋相位片的拓扑荷数, 模拟分析了拓扑荷数分别取1.0, 0.8, 0.6, 0.5, 0.4, 0.2, 0.1和0.08时的分数阶螺旋相位滤波成像, 成像结果如图6所示. 从图6模拟结果显示, 随着拓扑荷数取值逐渐减小, SPF图像的边缘增强效果逐渐减弱, 但图像中低频信息的对比度逐渐提高, 与文献[16]中的结论一致. 在此基础上, 继续减小l的取值, 使之小于0.1, 成像对比度与l = 0.1时相比, 低频信息对比度提升不大, 主要原因来自于相位片展开式中的高阶项可以忽略不计, 对物的频谱滤波不起作用.
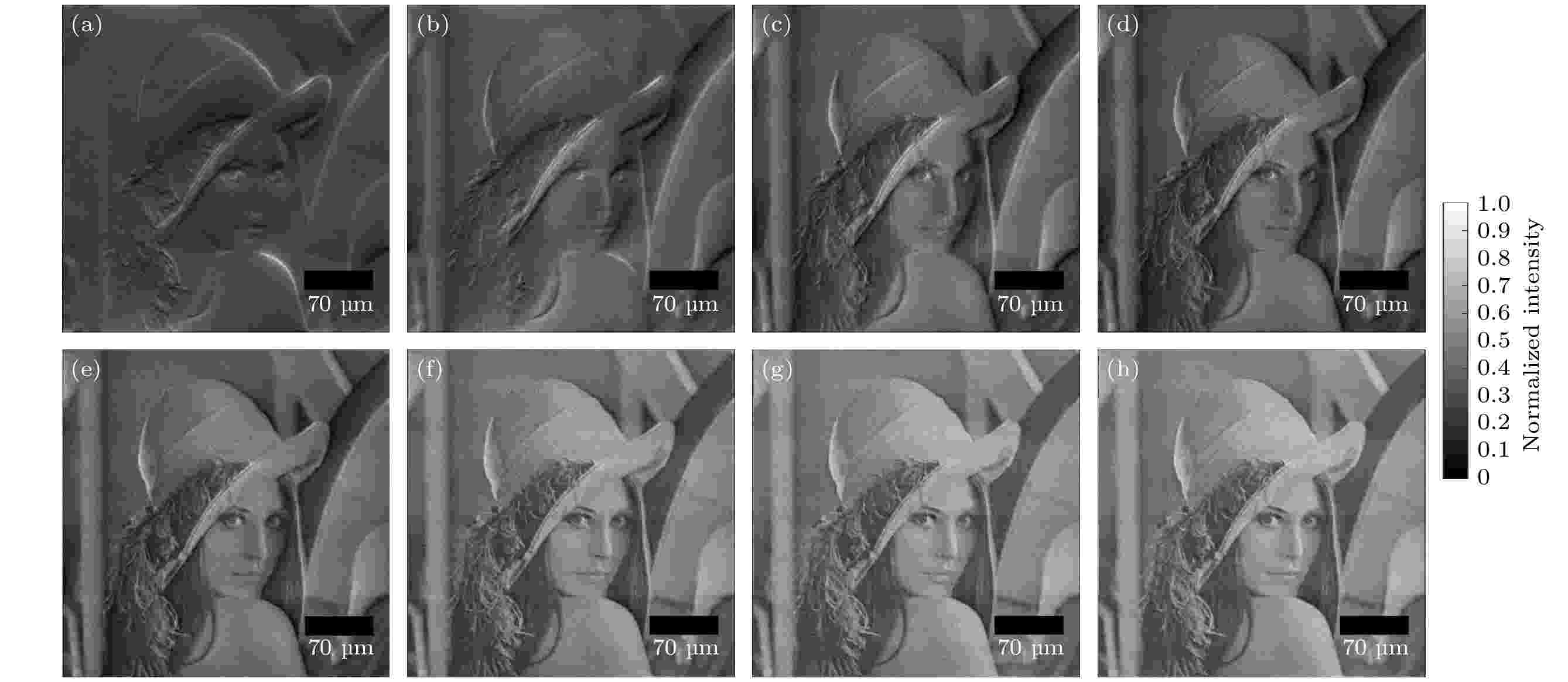图 6 分数拓扑荷l取不同值时的直接相位成像结果　$\left( {\rm{a}} \right)\;l = 1$; $\left( {\rm{b}} \right)\;l = {\rm{0}}.{\rm{8}}$; $\left( {\rm{c}} \right)\;l = {\rm{0}}.{\rm{6}}$; $\left( {\rm{d}} \right)\;l = {\rm{0}}.{\rm{5}}$; $\left( {\rm{e}} \right)\;l = {\rm{0}}.{\rm{4}}$; $\left( {\rm{f}} \right)\;l = {\rm{0}}.{\rm{2}}$; $\left( {\rm{g}} \right)\;l = {\rm{0}}.1$; $\left( {\rm{h}} \right)\;l = {\rm{0}}.{\rm{08}}$
Figure6. Direct phase imaging results for different fractional topological charge l : $\left( {\rm{a}} \right)\;l = 1{{ ;}}$ $\left( {\rm{b}} \right)\;l = {\rm{0}}.{{8 ;}}$ $\left( {\rm{c}} \right)\;l = {\rm{0}}.{{6 ;}}$ $\left( {\rm{d}} \right)\;l = {\rm{0}}.{{5 ;}}$ $\left( {\rm{e}} \right)\;l = {\rm{0}}.{\rm{4}}$; $\left( {\rm{f}} \right)\;l = {\rm{0}}.{\rm{2}}$; $\left( {\rm{g}} \right)\;l = {\rm{0}}.1$; $\left( {\rm{h}} \right)\;l = {\rm{0}}.{\rm{08}}$.

根据图6的模拟成像结果, 选择拓扑荷数较小的分数阶螺旋相位滤波器获得的相位滤波图像, 有利于研究人员直接观察滤波图像, 获取样品的状态, 选择样品感兴趣区域进行成像, 然后再利用相位恢复算法做进一步重构处理.
为了说明分数阶螺旋相位滤波器的特性, 首先, 比较了不同分数阶拓扑荷数下的相位滤波图像; 其次, 在相位滤波强度图对比度接近的情况下, 再继续比较分析了拓扑荷数取0.1与拓扑荷小于0.1的恢复相位, 如图7所示, 并以测量图像质量的结构相似度(structural similarity, SSIM)指数来定量对比:
图 7 不同拓扑荷值恢复结果对比　(a) 拓扑荷取0.1时经SGSA恢复出的相位图; (b) 拓扑荷取0.08时经SGSA恢复出的相位图
Figure7. Comparisons of the recovered results for different topologies: (a) The reovered phase image using SGSA when the topology is 0.1; (b) the revoverd phase image using SGSA when the topology is 0.08.

$ {\rm{SSIM}}(X,Y)=\frac{(2{{\displaystyle \mu }}_{X}{{\displaystyle \mu }}_{Y})(2{{\displaystyle \sigma }}_{XY})}{({{\displaystyle \mu }}_{X}^{2}+{{\displaystyle \mu }}_{Y}^{2})({{\displaystyle \sigma }}_{X}^{2}+{{\displaystyle \sigma }}_{Y}^{2})}, $

其中$\mathop \mu \nolimits_X, \mathop {\;\mu }\nolimits_Y, \mathop {\;\sigma }\nolimits_X, \;\mathop \sigma \nolimits_Y, \mathop {\;\sigma }\nolimits_{XY} $分别表示图像X和Y的局部均值、标准差和互补方差.
由图7可知, 拓扑荷数取值小于0.1时的恢复相位分布图的对比度比拓扑荷等于0.1时恢复相位分布图的对比度差, 且表1中的SSIM值也定量地证明了这一结论. 因此, 综合考虑不同拓扑荷下分数阶螺旋相位滤波直接成像的强度分布图对比度与不同拓扑荷下恢复相位分布图的对比度两个因素, 分数阶螺旋相位片的拓扑荷取0.1较为合适. 因此, 在实际实验中, 选择拓扑荷数为0.1的螺旋相位片来进行实际样品成像.

拓扑荷取值	SSIM
1.0	0.1918
0.1	0.4394
0.08	0.2034

表1三种分数拓扑荷下恢复相位图与原图的SSIM值
Table1.The SSIM between the recovered phase image and the ground truth phase image for three fractional topological values.

2

-->

4.1.螺旋相位片

为了便于实际应用, 在实验中, 利用SLM来产生螺旋相位片, 为了避免零级光的影响, 利用相位型的闪耀光栅与螺旋相位片相结合的方式形成新的螺旋相位图, 如图8所示.
图 8 (a) 相位型闪耀光栅; (b) 螺旋相位片; (c) 复合螺旋相位图
Figure8. (a) Phase-type blazed grating; (b) spiral phase plate; (c) composite spiral phase plate.

2 -->

4.2.实验系统光路

基于SLM的螺旋相衬定量相位成像系统的实验光路如图9所示.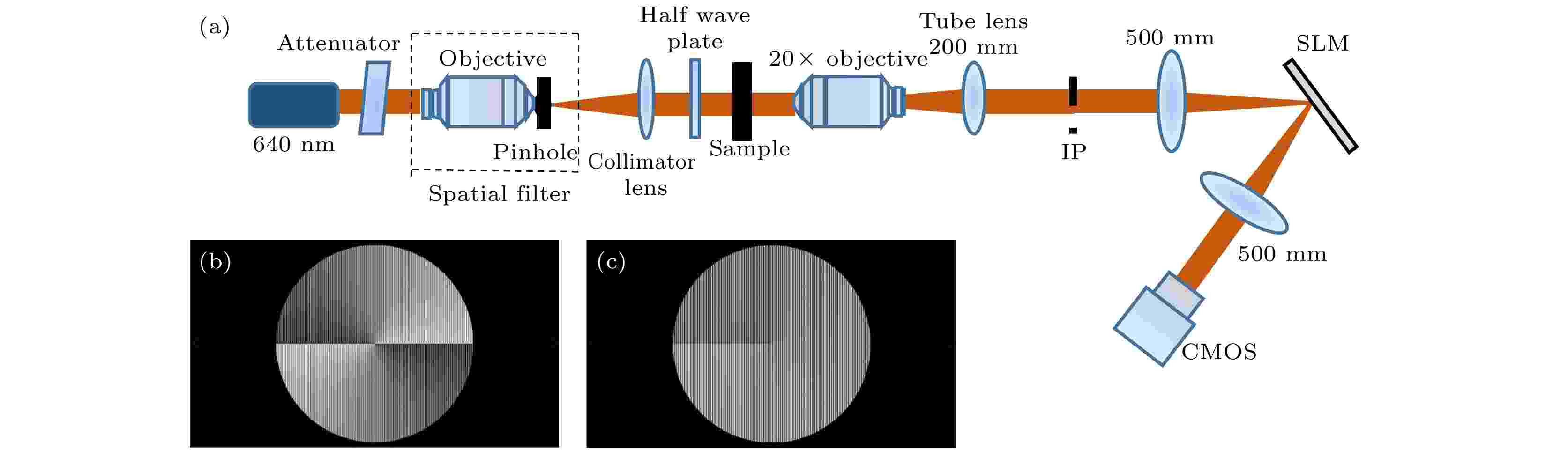
图 9 (a) 基于螺旋相位片滤波的定量相位成像系统光路图; (b) SLM上加载的整数阶叉形光栅; (c) SLM上加载的分数阶叉形光栅
Figure9. (a) Optical setup of quantitative phase imaging system based on a spiral phase filter; (b) the integer order fork grating loaded on SLM; (c) the fractional fork grating loaded on SLM.

波长为640 nm的激光器(Coherent, OBIS)发出的光束经衰减片, 针孔滤波器(物镜, 40/0.65 160/0.17)及准直透镜(焦距100 mm)产生平行光束, 照射透明相位样品. 再经样品调制的光束通过成像物镜(Nikon, Plan Fluor, 20×/0.50), 管镜(焦距为200 mm)成像在一次像面处, 然后经过4f螺旋相位滤波系统成像在探测器CMOS (Hamamatsu, C11440-22 CU, 像元尺寸 6.5 μm × 6.5 μm)上. 其中, 4f透镜焦距是500 mm, 频谱面上放置SLM (Holoeye, NIR, 像元尺寸是8 μm × 8 μm), 用于螺旋相位片的显示.
2 -->

4.3.实验结果

首先, 利用定做的相位光栅($ {\rm{Si}}{{\rm{O}}_2} $玻璃, 折射率1.456, 光栅刻线理论设计深度200 nm, 光栅刻线实际测试深度为150 nm, 光栅周期为6 μm)进行拓扑荷数$l = 1$的螺旋相位片滤波的成像实验, 目的是与分数阶螺旋相位滤波成像结果进行对比, 实验结果如图10所示.
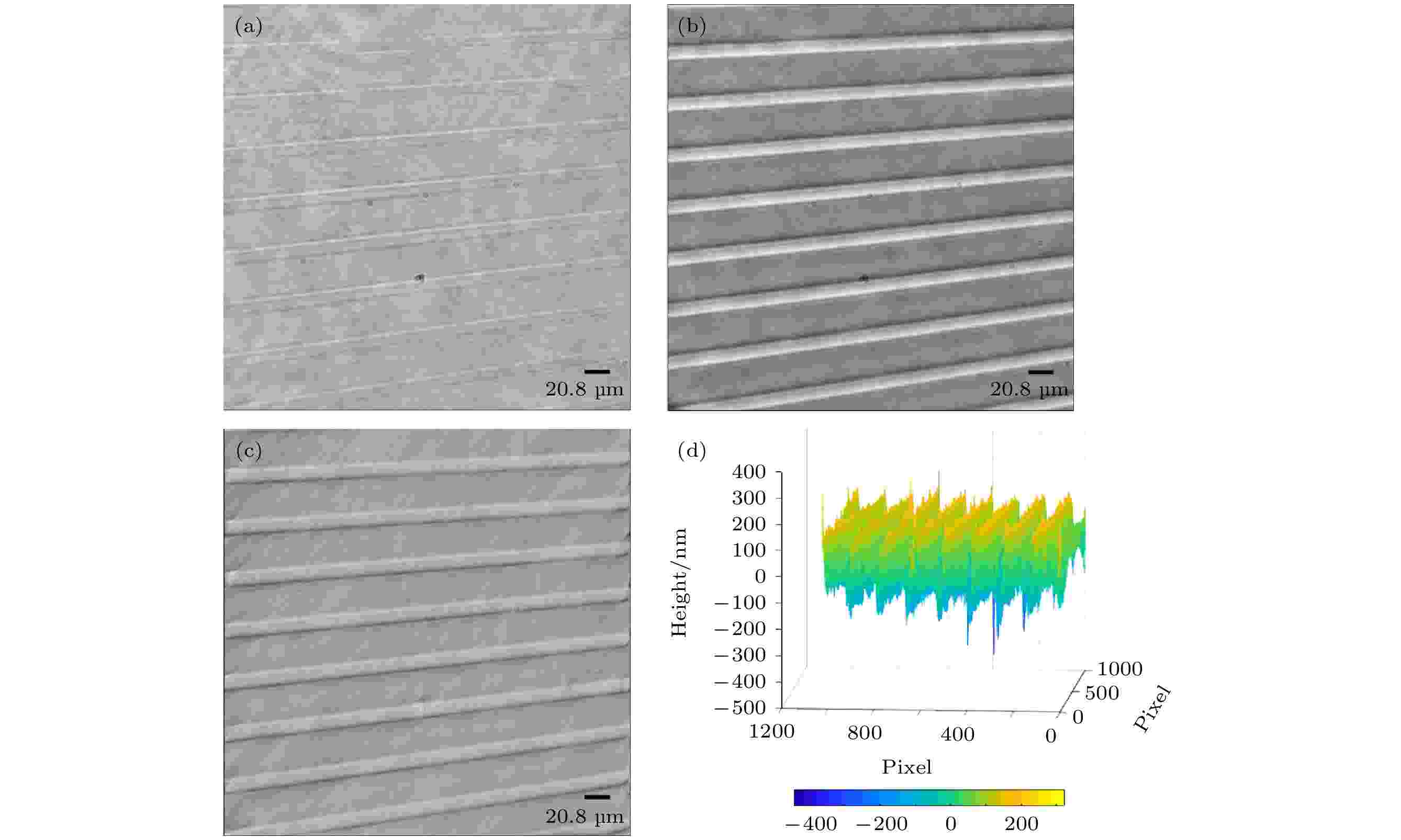图 10 定制相位型光栅的成像　(a) 相位型光栅未滤波明场强度图; (b) 整数阶螺旋相位片滤波成像边缘增强图; (c) 恢复相位图; (d) 恢复深度图, 横纵坐标数值为像素值, 每个像素代表0.325 μm, 总长度为332.8 μm
Figure10. Imaging of a custom phase gratinig: (a) The unfiltered bright field image of the phase grating; (b) the recorded integer-order spiral phase filtered edge enhancement image; (c) the recovered phase image; (d) the recovered depth image, the abscissa and ordinate values are pixel values, each pixel represents 0.325 μm, and the total length is 332.8 μm.

从图10可以看出, 整数阶螺旋相位滤波的图像边缘增强效果显著, 再对采集到的强度图利用SGSA进行相位恢复, 可进一步提高图像的对比度. 由SSE随迭代次数变化曲线图11可知, 只需两次迭代即可使得SGSA趋于收敛, 得到样品相位图, 耗时1.412 s (Windows10, 内存16 GB, CPU: Intel (R) Core(TM) i5-9400F CPU @2.90 GHz; Matlab R2018b).
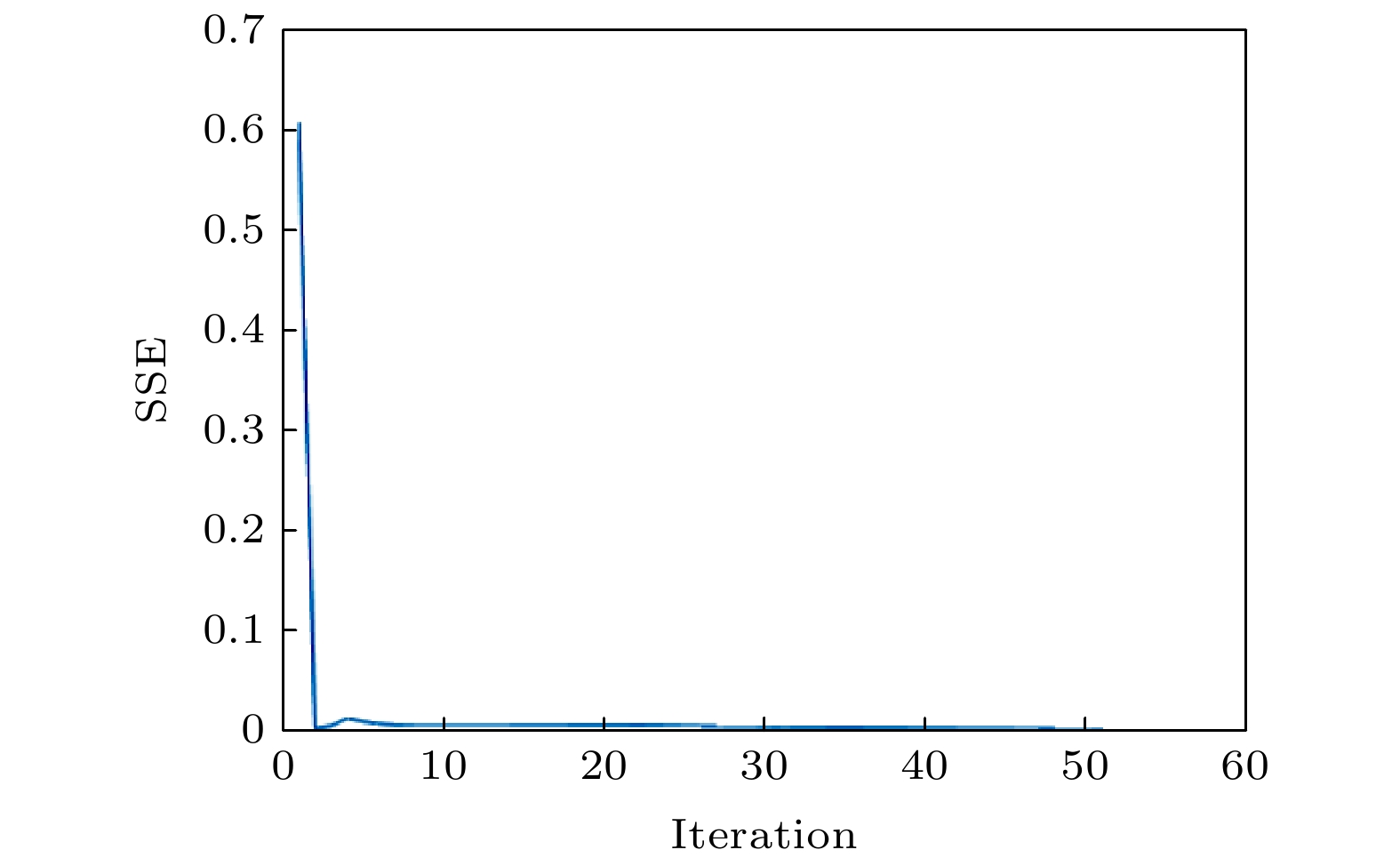图 11 经整数阶螺旋相位片滤波后再由SGSA重构的相位型光栅SSE随迭代次数的变化
Figure11. SSE error vs. the number of iterations for the grating phase reconstruction problem of phase retrieval from a integer-order spiral phase filtering intensity measurement using the SGSA.

再用MATLAB对恢复相位图进一步分析可知, 得到恢复相位光栅顶部相位值为0.24π, 光栅底部相位值为–0.06π, 平均相位差为0.30π, 结合公式$\varphi=\dfrac{{{\rm{2\pi }}}}{\lambda }{{(}}n{{ - }}1{{)}}h$可得, 恢复相位图的定量深度h平均为216 nm, 与已知光栅刻线深度150 nm的高度值误差为66 nm 左右. 分析其误差产生的原因, 主要来自于用SLM的像素化所产生的螺旋相位片精度不高; 另外, 加工的光栅刻线深度也有一定的误差. 为了进一步提高测量精度, 可以加工相关高精度相位片.
其次, 对拓扑荷数$l = 0.1$分数阶螺旋相位滤波进行实验, 结果如图12所示.
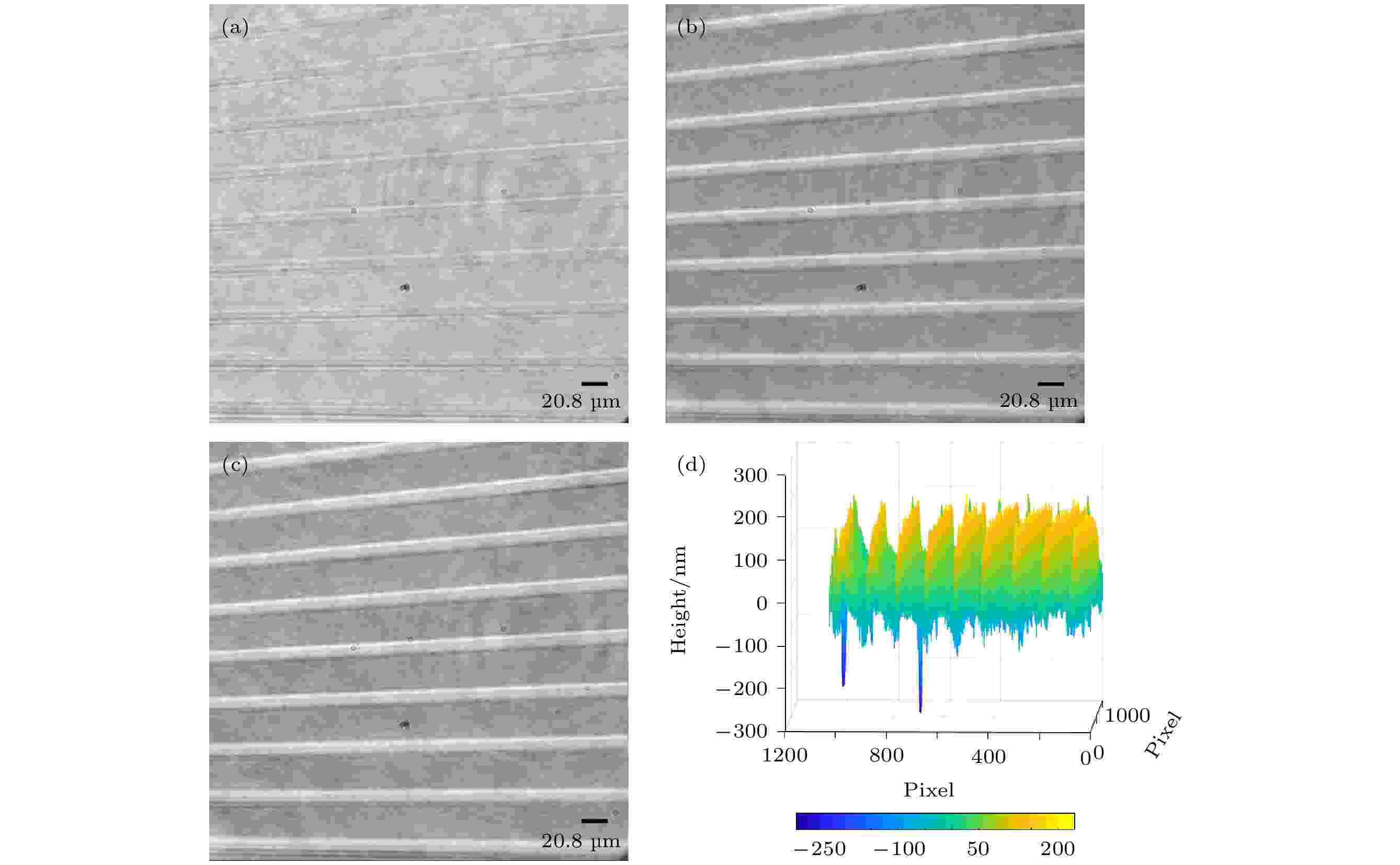图 12 定制相位型光栅的成像　(a) 相位型光栅未滤波明场强度图; (b) 拓扑荷l取0.1时分数阶螺旋相位片滤波成像强度图; (c) 恢复相位图; (d) 恢复深度图(坐标同图10(d))
Figure12. Imaging of a custom phase grating: (a) The unfiltered phase grating bright field image; (b) the fractional spiral phase plate filtered image when the topological charge l is 0.1; (c) the recovered phase image; (d) the recovered depth image (the coordinates are the same as Fig. 10. (d)).

从图13可以看出, 当使用l = 0.1的分数阶螺旋相位片直接对相位型样品进行螺旋相位滤波成像时, 成像图的对比度相对于未经滤波得到的成像图对比度明显得到提升, 效果与模拟结果得出的结论一致. 因此, 为了方便观察样品, 可以直接利用分数阶螺旋相位片进行螺旋相位滤波成像. 然后对单次拍摄采集到的单幅螺旋相位滤波强度图, 利用SGSA进行相位恢复进一步重构样品的相位信息. 实验结果证明, 分数阶螺旋相位滤波可以得到保留更多低频信息的高对比度强度分布图, 有利于对相位物体进行实时显微观测. 从图13的误差曲线可知, 需迭代10次, 耗时2.839 s, 误差几乎减为0. 进一步分析可知, 恢复相位光栅顶部平均相位值为0.25π, 光栅底部平均相位值为–0.03π, 均值相位差为0.28π, 则恢复相位图的定量深度h为198 nm, 与已知光栅实际刻蚀深度150 nm的高度值误差为48 nm. 与整数阶SPC相比, 测量误差减小27%.
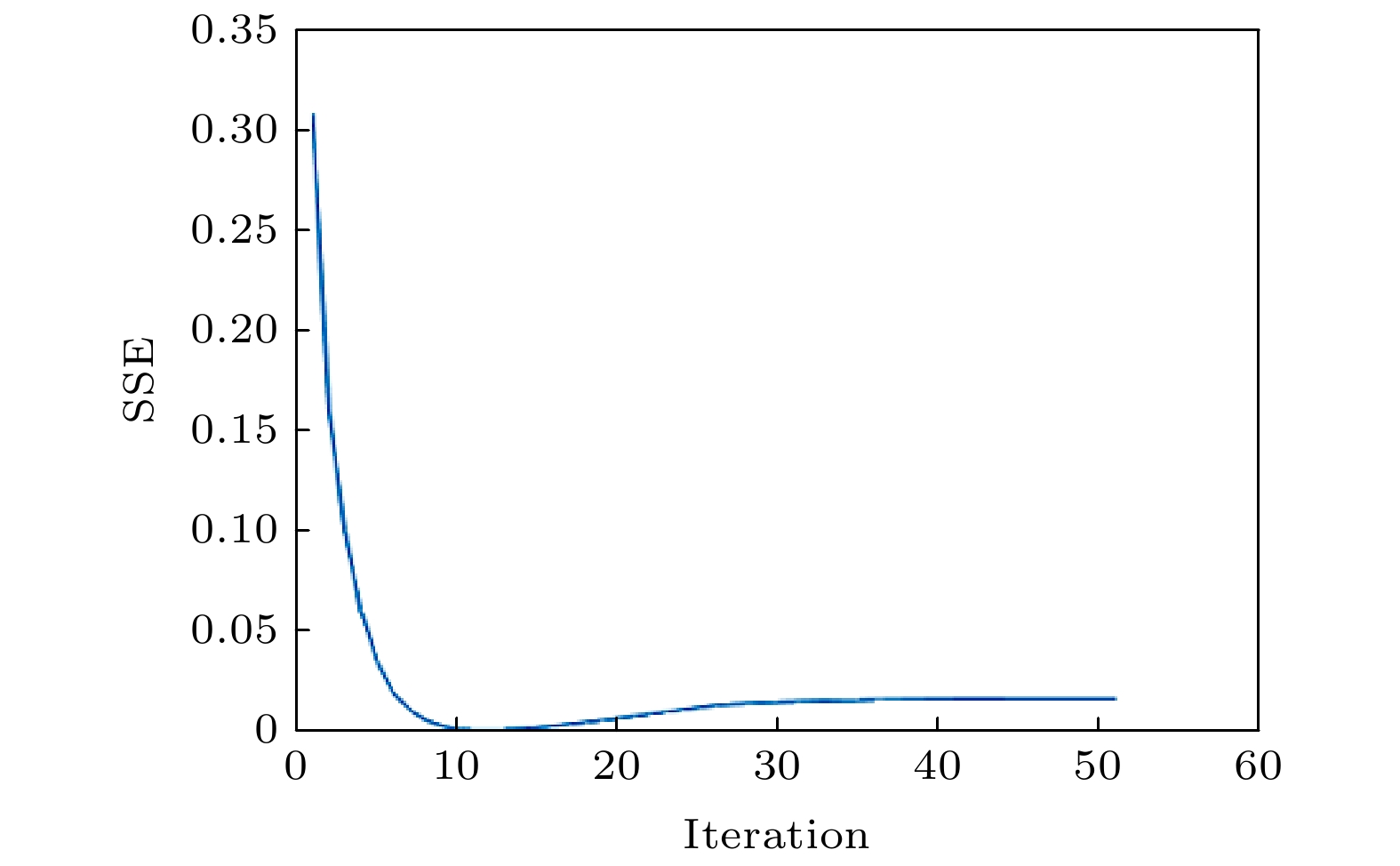图 13 经分数阶螺旋相位片滤波后再由SGSA重构的相位光栅SSE随迭代次数的变化
Figure13. SSE error vs. the number of iterations for the grating phase reconstruction problem of phase retrieval from a fractional spiral phase filtering intensity measurement using the SGSA.

为了进一步验证分数阶SPC成像效果, 对SH-SY5Y人神经母细胞瘤细胞进行成像, 如图14所示.
图 14 SH-SY5Y细胞成像　(a) SH-SY5Y细胞未滤波明场强度图; (b) 拓扑荷l取0.1时分数阶螺旋相位片滤波神经元细胞成像强度图; (c) 恢复相位图; (d) 定量相移图(坐标同图10(d))
Figure14. SH-SY5Y cell imaging: (a) The unfiltered SH-SY5Y cell bright field image; (b) the intensity image of the neuron cell using the fractional spiral phase filter when the topological charge l is 0.1; (c) the recoverd phase image; (d) the quantitative phase image (the coordinates are the same as Fig. 10. (d)).

从图15误差随迭代次数变化曲线可知, 只需迭代5次即可, 耗时1.782 s. 由于并不清楚细胞样品内部的具体折射率分布, 因此, 只给出细胞的定量相移图. 恢复相位图的最大相位值为${\rm{0}}.{\rm{6141\pi }}$, 最小相位值为${{ - 0}}.{\rm{3234\pi }}$. 从图15可以看出, 当使用分数阶螺旋相位片对生物细胞进行成像时, 成像效果明显, 对比度高, 再经过SGSA恢复后得到的样品的相位信息, 与模拟结果相一致.
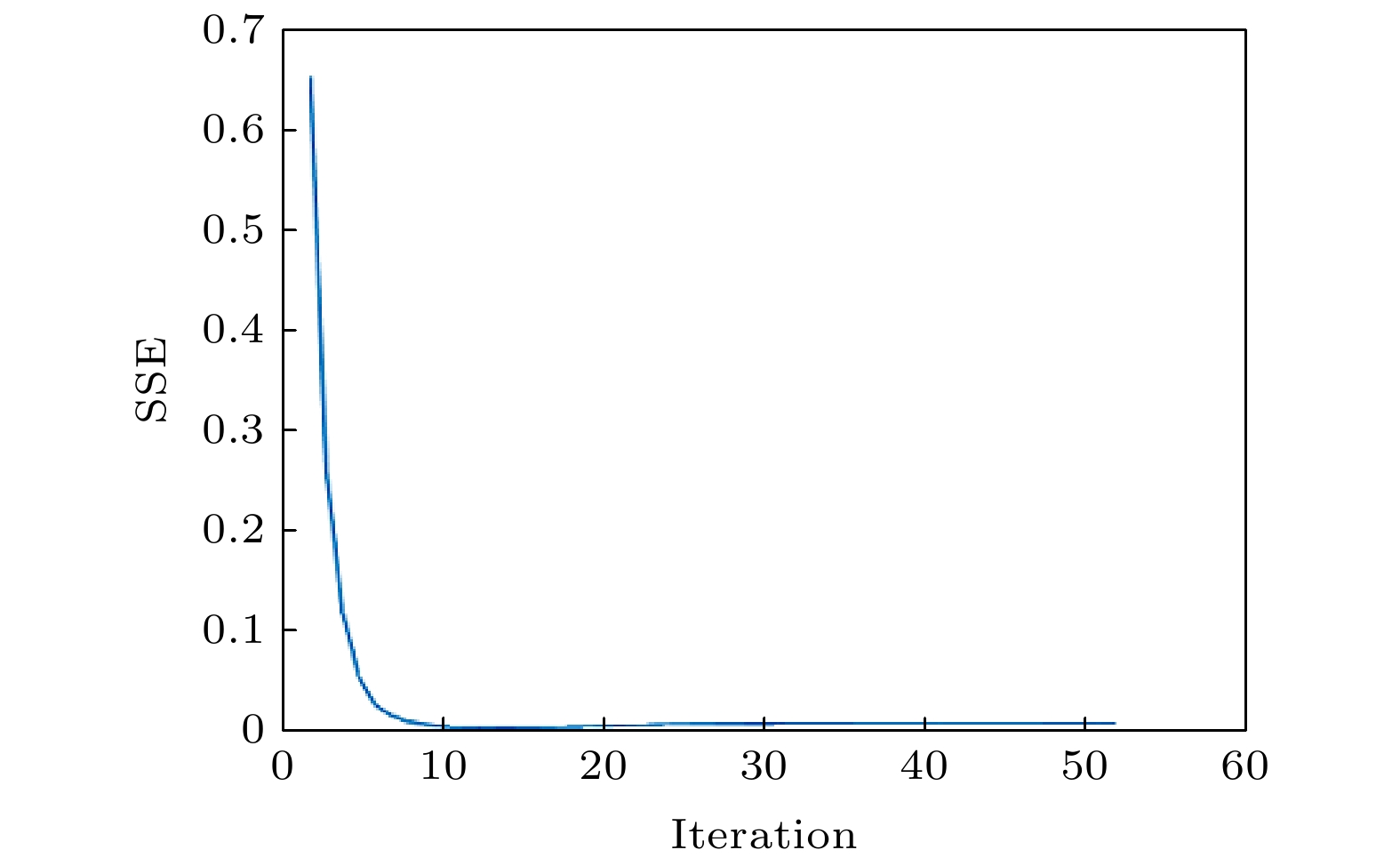图 15 SH-SY5Y细胞经分数阶螺旋相位滤波后再由SGSA重建的SSE随迭代次数的变化
Figure15. SSE error vs. the number of iterations for the SH-SY5Y cells reconstruction problem of phase retrieval from a fractional spiral phase filtering intensity measurement using the SGSA.

本文实现了一种基于空间光调制器的分数阶螺旋相衬显微成像系统, 基于单幅螺旋相位滤波图像, 通过SGSA实现了定量相位显微成像, 简化了螺旋相衬显微的图像采集和相位重构过程. 计算机仿真和实验结果表明, 基于分数阶拓扑荷数的螺旋相位成像, 图像低频信息得到保留, 直接成像对比度高, 更加接近样品真实相位信息, 有利于在实验过程中及时观察样品的形态和选取感兴趣区域进行相位滤波成像, 为进一步开展其在活体细胞快速定量相位成像中的应用奠定了技术基础.