摘要: 近年来, 很多基于生成模型的机器学习算法, 如生成对抗网络、玻尔兹曼机、自编码器等, 在数据生成、概率模拟等方面有广泛的应用. 另一方面, 融合量子计算和经典机器学习的量子机器学习算法也不断被提出. 特别地, 量子生成模型作为量子机器学习的分支, 目前已有很多进展. 量子生成算法是一类量子-经典混合算法, 算法中引入参数量子线路, 通过执行参数线路得到损失函数及其梯度, 然后通过经典的优化算法来优化求解, 从而完成对应的生成任务. 与经典生成模型相比, 量子生成模型通过参数线路将数据流映射到高维希尔伯特空间, 在高维空间中学习数据的特征, 从而在一些特定问题上超越经典生成模型. 在中等规模含噪声的量子体系下, 量子生成模型是一类有潜力实现量子优势的量子机器学习算法.
关键词: 量子机器学习 /
量子生成模型 /
量子优势 English Abstract Quantum generative models for data generation Sun Tai-Ping 1 ,Wu Yu-Chun 1,2 ,Guo Guo-Ping 1,2,3 1.CAS Key Laboratory of Quantum Information, University of Science and Technology of China, Hefei 230026, China Fund Project: Project supported by the National Key Research and Development Program of China (Grant No. 2016YFA0301700), the National Natural Science Foundation of China (Grant No. 11625419), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB24030600), and the Anhui Initiative in Quantum Information Technologies, China (Grant No. AHY080000)Received Date: 17 May 2021Accepted Date: 30 June 2021Available Online: 10 July 2021Published Online: 20 July 2021Abstract: In recent years, many generation-based machine learning algorithms such as generative adversarial networks, Boltzmann machine, auto-encoder, etc. are widely used in data generation and probability distribution simulation. On the other hand, the combined algorithms of quantum computation and classical machine learning algorithms are proposed in various styles. Especially, there exist many relevant researches about quantum generative models, which are regarded as the branch of quantum machine learning. Quantum generative models are hybrid quantum-classical algorithms, in which parameterized quantum circuits are introduced to obtain the cost function of the task as well as its gradient, and then classical optimization algorithms are used to find the optima. Compared with its classical counterpart, quantum generative models map the data stream to high-dimensional Hilbert space with parameterized quantum circuits. In the mapping space, data features are easier to learn, which can surpass classical generative models in some tasks. Besides, quantum generative models are potential to realize the quantum advantage in noisy intermediate-scale quantum devices.Keywords: quantum machine learning /quantum generative models /quantum advantage 全文HTML --> --> --> 1.引 言 在经典计算领域, 生成模型被广泛应用于各个领域, 如图像生成[1 ] 、语音合成[2 ] 、药物设计[3 ] 、图像转换[4 ] 等. 近来已有对经典生成模型的量子版本的研究, 如量子生成对抗网络[5 ,6 ] 、量子玻恩机[7 ,8 ] 、量子玻尔兹曼机[9 -12 ] 、量子自编码器[13 -15 ] 以及量子贝叶斯网络[16 ] 等.[17 ] , 即通过量子计算机和参数化量子门操作集合获得分子的量子态表示, 测量分子模型对应的哈密顿量的期望值, 以此作为目标函数进行变分优化.[18 ] 在大数分解[18 ] 、HHL[19 ] 等被证明有量子优势的算法上具有广泛的应用, 但基于以下原因相位估计算法无法在当前的计算体系下有效实现: 1) 当前硬件体系多集中于单量子门和两比特纠缠门的实现, 相位估计用到的受控幺正门($ c-U^j $ )必须分解为基本门的组合, 此过程会显著降低受控幺正门的保真度; 2) 相位估计用到的量子傅里叶逆变换需要$ O(n^2) $ (n 为量子比特个数)数量级的量子门, 使得深层量子线路的态保真度无法达到量子计算要求. 量子计算体系的噪声不可避免, 当前只有中等规模的量子比特、无法实现有效的量子纠错[20 ] 技术, 这使量子-经典混合算法受到广泛关注.[21 ] , 但对于参数量子线路(Parameterized Quantum Circuit, PQC, 见附录 )的表示能力与经典网络相比是否具有优势还缺少理论的结果. Du等[22 ] 尝试从内在的线路结构出发证明其结论, 而经典深度学习神经网络和量子线路的比较还没有结论. 同样的, 量子生成网络作为量子机器学习的一部分, 如何将经典数据转化为量子态、如何从测量结果获取经典信息仍需要更直观更普适的方法.附录 里会有详细的介绍. 通过对这些模型的比较, 可以从不同角度理解量子生成模型的构建思路, 以此为不同的计算任务构建与之适应的计算模型提供启发.2.量子生成模型 22.1.量子生成对抗网络 2.1.量子生成对抗网络 经典的生成对抗网络[23 ] (generative adversarial Network, GAN)被视为深度学习中的前沿进展. GAN在生成图像[1 ] 、语音[2 ] 、文本[24 ] 等方面具有非常广泛的应用. 经典生成对抗网络是一类有两个玩家的博弈游戏, 一个是生成器(generator), 记为G, 另一个为鉴别器(discriminator), 记为D. 对于已存在的源数据$\vec{x}\sim p_{{\rm{data}}}$ , 生成器G生成新的数据以逼近真实的源数据分布, 使D无法区分数据的来源; 而鉴别器D对每个输入数据给出真或假的决策概率, 以最大程度地区分这两类数据.$ (0, 1) $ 间的概率值, 那么生成对抗网络的损失函数可以被定义为:$\min_{{{{\theta}}}_{\rm{G}}}\max_{{{{\theta}}}_{\rm{D}}}{\cal{L}}(D, G)$ . 采用经典神经网络构建的GAN模型, 可以用反向传播算法来实现梯度计算.[5 ,21 ,25 ,26 ] (quantum GAN, QGAN)基本保留了经典生成对抗模型的特征, 不同之处在于量子生成对抗网络用到的数据集既可以是量子的也可以是经典的, 而且可选择地, 生成器与鉴别器也可以为经典神经网络或参数量子线路.[5 ] 提出了这样的QGAN模型: 源数据的概率分布模型为$ p_R(x) $ , 由某个未知(有可能很复杂)的过程R 生成. 由参数${{{\theta}}}_{\rm{G}}$ 确定的生成器G生成新的数据样本, 由参数${{{\theta}}}_{\rm{D}}$ 确定的鉴别器D识别这两类数据. 用标签λ 指定源数据中的类别, $ R = R({\left| \lambda \right\rangle }) = \rho_\lambda^R $ , 考虑噪声$ {\left| z \right\rangle } $ , 可以按照(1 )式定义与参数有关的损失函数${\cal{L}}({{{\theta}}}_{\rm{D}}, $ $ {{{\theta}}}_{\rm{G}})$ , 这里D的输入是$ R({\left| \lambda \right\rangle }) $ 或$G({{{\theta}}}_{\rm{G}}, {\left| \lambda, z \right\rangle }) )$ :? 的项是调整源数据和生成部分占整体的比例. 一般取$\phi = \dfrac{\pi}{4}$ . Dallaire-Demers等构建的量子生成对抗网络线路图如图1 所示.图 1 量子生成对抗网络结构[5 ] Figure1. The general structure of QGAN[5 ] .$\min_{{{{\theta}}}_{\rm{G}}}\max_{{{{\theta}}}_{\rm{D}}}{\cal{L}}({{{\theta}}}_{\rm{D}}, {{{\theta}}}_{\rm{G}})$ , 从而得到最接近于源数据概率分布的分布模型与鉴别模型. 量子线路的梯度可以用数值差分[27 ] 、参数位移法则[27 ] 、以及Hadamard test线路[5 ] 来求. Dallaire-Demers在数值模拟上实现了源数据为$ {\left| 0 \right\rangle }, {\left| 1 \right\rangle } $ 两个量子态的生成对抗任务.[6 ] 讨论了当数据是量子的, 鉴别器是量子或经典的, 生成器是经典的量子生成对抗模型. Lloyd所述的量子数据是通过对一个量子体系进行固定的测量得到的数据分布. 根据量子优越性[19 ] 的表述, 经典的生成器不能有效地匹配量子数据分布, 或者更准确地, 除非有指数的资源可用, 经典的生成器无法模拟量子数据的分布$p_{\rm{R}}(x)$ . 对于数据是经典的, 生成器和鉴别器都是量子的情况, Lloyd通过对比得出, 经典的生成器和鉴别器在计算梯度时需要$ O(N^2) $ 个比特和$ O(N^2) $ 步时间(N 是经典数据的维度), 而量子的生成器和鉴别器在计算协方差矩阵时, 如果矩阵是低秩和稀疏的, 需要$O({\rm{log}}N)$ 个量子比特和$O({\rm{poly}}({\rm{log}}N))$ 个逻辑门操作.[26 ] 结合量子玻恩机构建了经典数据-量子生成器-经典鉴别器的量子生成对抗模型, 实现条带图(bars and stripes, BAS)[8 ,16 ,26 ,28 ] 的概率生成与识别(见第2 节). 类似的, Situ等[29 ] 将BAS图的每个点都编码至量子比特上, 通过参数量子线路构建的生成器生成量子态, 测量结果输入至经典神经网络构建的鉴别器, 也实现了BAS图的生成. Zouful等[25 ] 通过测量量子态在计算基上的投影, 将其转化为数据对应的概率, 以此为基础构建生成对抗网络, 实现了对数正态分布、双峰高斯分布等概率分布的学习和生成. 值得注意的是, 连续数据被截断并舍入到临近整数值, 所以该模型仍是离散数据的概率学习模型.[30 ] 等利用超导量子体系首次实现了具有量子数据、量子生成器、量子鉴别器的量子生成对抗网络的实验验证, 生成保真度高达98.8%. 在Hu的实验中, 量子数据为单比特量子态, 生成器参数为量子门旋转角度. 在优化D或G时采用梯度下降算法, 量子系统的操控和测量通过FPGA(field programmable gate arrays)实现, 线路梯度通过经典计算机估算得到. 该实验对于NISQ体系下的量子机器学习优势的探索具有重要意义. 此外, Huang等[21 ] 通过将测量量子生成器得到的数据作为经典图像灰度值, 完成了手写数字集0和1的生成对抗任务, 为量子比特资源受限条件下经典数据的生成提供了一个思路.2.2.量子玻恩机 -->2.2.量子玻恩机 量子玻恩机[7 ,8 ] (quantum circuit Born machine, QCBM)是基于波函数的概率解释的一种模型. 量子玻恩机将概率分布编码至初态上, 把量子态在计算基上的投影作为数据的概率. 量子玻恩机是一种隐式的生成模型, 因为我们实际上并不需要知道这个纯态的密度矩阵, 而只需要知道叠加态振幅的模值. 这样的设定对量子线路的结构限制也更少, 所以一般被认为具有更强的表示能力.$ \pi(x) $ 进行采样得到数据集$ {\cal{D}} = \{x\} $ , QCBM通过参数量子线路把初态$ {\left| 0 \right\rangle } $ 演化为$ {\left| \psi_\theta \right\rangle } $ , 并在计算基上的测量得到生成数据$x\sim $ $ p_\theta(x) = |{\left\langle {x|{\psi _\theta }} \right\rangle }|^2$ 的概率分布. 训练目标是让模型的概率分布$ p_{\theta} $ 接近真实数据分布$ \pi(x) $ . QCBM采用所谓的MMD(Maximum Mean Discrepancy)损失函数:? 将x 映射到高维Hilbert空间. 进一步地, 定义核函数$K(x, y) = \phi(x)^{\rm{T}} \phi(y)$ , (3 )式即可避免在高维空间中进行运算, 等价于$K(x, y) = $ $ \exp\left( { - \dfrac{1}{{2\sigma }}|x - y{|^2}} \right)$ . 直接计算上述损失函数的梯度比较困难, 但可以证明, 下式无偏地等价于梯度:$ p_{\theta^+}(x) $ 和$ p_{\theta^-}(x) $ 是在参数$\theta^{\pm} = \theta\pm \dfrac{\pi}{2}{{{e}}}_l^\alpha$ 下的模型输出概率, ${{{e}}}_l^\alpha$ 是参数空间的第$ (l, \alpha) $ 个单位矢量($ \alpha $ 和l 分别表示迭代的步数与当前迭代的第l 个参数的下标).N 个数据的集合, 需要$n\sim $ $ O({\rm{log}}(N))$ 个量子比特. 而生成线路中所用的量子门个数一般为$O({\rm{poly}}(n))$ .[8 ,16 ,26 ,28 ] 任务中取得很好的结果, 对于理想的无误差测量, 量子玻恩机生成真实数据分布的比率为95.7%[8 ] . 此外通过对量子玻恩机的非计算基测量, 可以得到更多的信息, 这种方法可用来生成先验概率分布, 如经典生成对抗网络的先验分布[31 ] . Cheng等[32 ] 还从信息熵的角度比较了量子玻恩机与受限玻尔兹曼机[33 ,34 ] , 为理解基于概率的生成模型和基于能量的生成模型提供了一个新的视角. Coyle等[35 ] 提出一种量子玻恩机的子类—量子伊辛玻恩机—并引入量子核函数[36 ] 来讨论量子学习优势.2.3.量子玻尔兹曼机 -->2.3.量子玻尔兹曼机 与前述模型不同, 量子玻尔兹曼机[9 -12 ] (quantum Boltzmann machine, QBM)需要一种专用的量子计算机—量子退火机.[37 ,38 ] 和深度玻尔兹曼机[37 ,39 ] . 玻尔兹曼机是二进制数节点构成的概率生成网络, 由可见节点和隐藏节点组成, 记为$z_a, a = $ $ 1, 2, \cdots, N$ , 其中N 是总节点数. 这里为了和后面的量子生成模型保持一致, 取$ z_a\in\{+1, -1\} $ 而不是$ z_a\in\{+1, 0\} $ . 为区别可见节点和隐藏节点, 我们分别记为$ z_\nu, z_i $ . 同时用向量符号${{{v}}}, {{{h}}}, {{{z}}} = ({{{v}}}, {{{h}}})$ 表示可见态、隐藏态和组合态. 在物理上其能量可以用伊辛模型表示:$ b_a, w_{ab} $ 是在训练的过程中进行需要优化的参数. 定义负对数相似度损失函数:${{{h}}}$ 的概率为边际分布$P_{{{{v}}}} = $ $ Z^{-1}\sum\nolimits_{{{{h}}}}{\rm{e}}^{-E_{{{{z}}}}}$ , $\quad Z = \sum\nolimits_{{{{z}}}}{\rm{e}}^{-E_{{{{z}}}}}$ . 那么玻尔兹曼机的任务就是优化哈密顿量的参量$ \theta\in\{b_a, w_{ab}\} $ , 使边际分布尽可能接近真实的数据分布$P_{{{{v}}}}^{{\rm{data}}}$ . 这样就可以用梯度的方法来优化玻尔兹曼机:$ {\left\langle \cdots \right\rangle } $ 和${\left\langle \cdots \right\rangle }_{{{{v}}}}$ 分别为对自由变量的玻尔兹曼均值以及对可见变量的玻尔兹曼均值. $\overline{{\left\langle \cdots \right\rangle }_{{{{v}}}}}\equiv $ $ \sum\nolimits_{{{{v}}}}P_{{{{v}}}}^{{\rm{data}}}{\left\langle \cdots \right\rangle }_{{{{v}}}}$ 是双重均值. 这样我们就得到更新法则:[40 ] .$ 2^N \times 2^N $ 维的矩阵. 而且量子力学算符大多是不对易的, 这对于求解梯度十分不便. 横场伊辛模型的哈密顿量形式为:${{I}}, {{\sigma}}^z, {{\sigma}}^x$ 为泡利矩阵, 下标a 表示作用于第a 个量子比特. 与经典玻尔兹曼机类似, 定义配分函数和密度矩阵分别为: $Z ={\rm{ Tr}}[{\rm{e}}^{-H}], \quad \rho = $ $ Z^{-1}{\rm{e}}^{-H}$ . 对于给定的可见态${\left| {{{{v}}}} \right\rangle }$ , 可定义边际分布$P_{{{{v}}}} = {\rm{Tr}}[\varLambda_{{{{v}}}}\rho], \quad \varLambda_{{{{v}}}} = {\left| {{{{v}}}} \right\rangle }\left\langle {{{{v}}}} \right|\otimes {\cal{I}}_{{{{h}}}}$ . 其中${\cal{I}}_{{{{h}}}}$ 为作用在隐藏变量的单位阵.H 和$ \partial_{\theta}H $ 并不对易, 也就是$\partial_{\theta}{\rm{e}}^{-H}\neq $ $ -{\rm{e}}^{-H}\partial_{\theta}H$ . 这样在求解期望值的时候就会十分困难. 尽管Amin[9 ] 通过分析的方法估算除了损失函数的界, 在一些特定的条件下可以估算损失函数的梯度, 但与前述量子生成模型相比, 参数更新的成本已然增加了.[9 ] 用量子玻尔兹曼机实现了伯努利分布的概率生成. Kieferová[12 ] 用量子玻尔兹曼机设计了一种生成模型用以实现部分的量子态层析, 并且除非$ BQP = BPP $ , 经典计算机无法有效地模拟其训练过程. Dorband[41 ] 在D-wave量子退火机上演示了量子玻尔兹曼机的构建过程. 但是, 相较于其他量子生成模型, 量子玻尔兹曼机带来的近似误差是难以避免的, 同时也难以说明相较于经典版本的优势所在.2.4.量子自编码器 -->2.4.量子自编码器 在经典的数据处理中, 通过机器学习中的自编码器可以将数据从一个高维空间缩减到低维空间. 经典的自编码模型可以概括为: 通过参数化的神经网络来训练一个数据集, 其数据维度为$ (n+k) $ , 得到擦除k 个特征或维度的新数据, 如果这些数据可以通过解码器(神经网络)重新生成接近于原数据的一组新数据, 那么留下的n 维数据被称为压缩数据. 这个过程被称为数据压缩. 数据压缩对于处理稀疏特征数据集或高维数据集是十分直观和有效的手段. 受此启发, 量子自编码器[13 -15 ] (quantum autoencoder)被设计为量子态压缩的工具.[13 ] 提出的量子自编码器与经典类似: 记$ \{ p_i, {\left| {\psi_i} \right\rangle }_{AB}\} $ 是$ (n+k) $ 个量子比特上的纯态集合, 子系统A和子系统B分别占有n 和k 个比特. 记$U^{{{{\theta}}}}$ 为作用在$ (n+k) $ 个比特上的幺正算符, 其中${{{\theta}}} = \{ \theta_1, \theta_2, \cdots\}$ 是参数集合, 以及$ {\left| a \right\rangle }_{B'} $ 为k 比特寄存器的参考纯态. 通过经典的优化方式, 我们希望平均保真度函数取得最大值:$F({\left| {\psi_i} \right\rangle }, \rho_{i}^{{\rm{out}}}) = \left\langle {{\psi _i}|\rho _i^{{\rm{out}}}|{\psi _i}} \right\rangle$ , $\rho_{i, {{{\theta}}}}^{{\rm{out}}}$ 是线路经过解码后的密度矩阵:$\psi_{i_{{\rm{AB}}}} = {\left| {\psi_i} \right\rangle }\left\langle {{\psi _i}} \right|_{{\rm{AB}}}$ , 以及$a_{{\rm{B}}'} = {\left| a \right\rangle }\left\langle a \right|_{{\rm{B}}'}$ .${\left| {\psi_i'} \right\rangle } = U^{{{{\theta}}}}{\left| {\psi_i} \right\rangle }_{{\rm{AB}}}$ 是A, B两个子系统的直积态. 即当下式成立时, 才有$ C_1 = 1 $ :${\left| {\psi_i^c} \right\rangle }_{\rm{A}}$ 是$ {\left| {\psi_i} \right\rangle } $ 的压缩后的态.' 寄存器的态保真度等价于AB寄存器初态和末态的保真度(我们称B寄存器输出态为冗态). 这样, 可以定义另一种平均保真度$C_2({{{\theta}}})$ ,[42 ] .$ {\cal{L}} = -\log (1-C_2) $ , 采用经典方式进行优化, 可以得到保真度最高的参数线路, 这样就实现了数据压缩.图2 所示, 量子态压缩模型可以由以下步骤来构建: 第一, 制备初态$ {\left| {\psi_i} \right\rangle } $ 和参考态$ {\left| a \right\rangle } $ , 并假设制备是有效的; 第二, 构建参数线路, 初态在幺正算符U 下演化; 第三, 通过SWAP测试得到冗态和参考态之间的保真度.图 2 量子自编码器的训练示意图, 其中$ {{{p}}}$ 表示变量, 摘自[13 ] Figure2. Schematic representation of the hybrid scheme for training a quantum autoencoder where $ {{{p}}}$ represents variables, image from[13 ] .[13 ] . 其方法是用4 qubits来模拟氢分子, 通过变分量子求解器(VQE)求出对于固定原子间距的量子态, 以此作为量子自编码器的输入态. 氢分子的态并非占满了4 bit的希尔伯特空间, 这就为量子态压缩提供了可能. 直观上看, 量子态压缩的过程就像在整个希尔伯特空间中将若干子空间碎片像拼图一样拼接成紧密的空间. 量子自编码器在量子加法器方面也有一定的应用[14 ] , 这种加法器用以实现将两个相同比特数的量子子系统编码到一个新的子空间. Ding等[43 ] 借助超导量子体系在实验上验证了量子加法器的可行性, 实验保真度与理论值一致.[44 ] 采用了Romero等[13 ] 提出的量子自编码器框架, 不同的是, 其数据压缩任务是将多维量子比特(qutrit, $ {\left| \psi \right\rangle } = \alpha {\left| 0 \right\rangle }+\beta{\left| 1 \right\rangle }+\gamma{\left| 2 \right\rangle } $ (已归一化))压缩为二维量子比特(qubit)态. 通过光量子实验体系, Pepper等在实验上实现了qutrits的压缩, 并且证明了这样的实验优化系统对扰动是鲁棒的. Bondarenko等[45 ] 注意到经典数据通过经典自编码器可以有效地去除噪声, 因此量子自编码器同样有类似的作用. 通过构建以自旋翻转噪声和任意幺正门噪声为主的GHZ含噪声量子态, Bondarenko等验证了量子自编码器在量子数据去噪方面的作用.[46 ] 在理论上论证了实现有效量子自编码态压缩的条件, 并证明了若输入数据的最大线性无关向量的个数不超过隐变量空间(压缩后的低维空间)的维度, 那么量子自编码器就可以无损地将高维数据压缩至低维. Huang等利用量子光学体系在实验上验证了其理论的结果. 此外Cao等[47 ] 提出可在量子退火机上运行、通过噪声辅助的绝热模型, 同样可以完成量子自编码任务. 同时, 对量子态压缩的探索也使得量子梯度消失的现象—也即贫瘠高原的现象—得到进一步的研究[48 ] .2.5.其他生成模型 -->2.5.其他生成模型 从前述量子生成模型可以看出, 经典机器学习给我们带来了很多启发. 类似地, 经典领域中因子图(factor graph)可以作为概率生成模型, Gao等[49 ] 提出了一种量子生成模型(quantum generative model, QGM), 并证明此模型可以高效地表示任意因子图. 并且通过理论证明至少存在一些特定的概率分布, 可以被QGM有效表示, 但不能被任意具有多项式量级变量的因子图有效表示. 如果多项式层次作为P vs . NP问题的泛化是不塌缩的话, QGM相对于经典的因子图具有指数优势.[49 ] 还提出了一种通用的量子学习算法, 该算法利用张量网络、对多体纠缠量子态的父哈密顿量(parent Hamiltonian)构建、以及递归的量子相位估计进行学习. 显然希望这种算法对任意问题都能在多项式时间内解决是不现实的, 但作者证明了至少存在一些问题, QGM相对于任意经典算法均有指数加速的效果, 前提是假设量子计算机不能被经典计算机有效地模拟.[49 ] 提出的QGM模型, 用一个多体纠缠量子态的概率幅对数据的相关性进行参数化. 因为量子概率幅的相干性产生的现象比经典的复杂得多, QGM才有可能在特定情况下实现性能的显著提升. QGM使用图态$ {\left| G \right\rangle } $ 表示, 由m 个量子比特与图G构成. 如图3 所示.图 3 经典和量子生成模型 (a) 因子图表示; (b)张量网络态表示; (c)量子生成模型定义[49 ] Figure3. Classical and quantum generative models: (a) Illustration of a factor graph; (b) illustration of a tensor network state; (c) QGM definition[49 ] [50 ] 有另一篇工作同样旨在发掘量子相关性在生成模型中的作用. 其中比较了经典贝叶斯网络顺序模型与对应的一维张量网络, 展示了矩阵直积态(matrix product states, MPSs)比经典机器学习模型有更强的表示能力. 因为一维模型可以在经典计算机上被有效模拟, Gao等采用数值模拟的方式测试了真实数据集的生成, 发现MPS生成能力比经典模型有提升. 此结果为理解基于MPS的机器学习算法提供了新的视角, 因为有一类张量网络子类不能有效地被经典计算机模拟, 但是可以在量子计算机上构建, 这就使得在机器学习中的生成模型框架下量子优势是可能存在的.[16 ] . 这种量子线路引入辅助比特表示先验概率分布, 通过受控操作传递给数据比特寄存器. 这样可以极大地规避参数量子线路中出现的生成概率不均匀的问题.3.量子生成模型展望 随着量子计算机硬件的不断发展, 量子生成模型也不只在量子虚拟机上得到实现, 基于真实量子芯片的生成模型受到了广泛的关注, 但是量子生成模型存在的问题仍待解决.[49 ,50 ] 从量子相关性出发, 直观上将量子内在相关性的参数化来实现经典生成模型无法模拟的任务, 说明了量子优势在机器学习领域中的存在性.附录A 参数量子线路 量子计算机遵循量子力学定律进行逻辑运算和信息存取. 而量子力学体系区别于经典体系之处在于, 由于叠加态和纠缠态的存在, 相同位数的量子数据比经典数据有着指数强的表示能力. 将量子信息转化为经典信息需要对量子态进行测量.$ {| \psi \rangle } = \alpha {| 0 \rangle }+\beta{| 1\rangle } $ (已归一化). 根据玻恩的几率解释, 对单比特量子态进行测量, 得到0态的概率为$ |\alpha|^2 $ , 得到1态的概率为$ {|1\rangle } $ . 对于多量子比特系统, 根据量子力学体系的完备性, 量子态可在计算基上展开, 由${| \varPhi \rangle } = $ $ \displaystyle\sum\nolimits_i a_i {| i\rangle }$ 测得任意态$ {| i \rangle } $ 的概率为$ |a_i|^2 $ . 对于泡利算符$\sigma_i, $ $ i\in \{0, x, y, z\}$ , 其期望值可以通过算符的谱来计算, 即$\left\langle {\varPhi |{\sigma _i}|\varPhi } \right\rangle = \left\langle {\varPhi|\displaystyle\sum\nolimits_j \lambda_j{\left| {\psi_j} \right\rangle }\left\langle {{\psi _j}} \right||\varPhi} \right\rangle$ , 其中$ \lambda_j $ 为本征值, $ {\left| {\psi_j} \right\rangle } $ 为本征态. 对于一个更复杂的哈密顿量H , 我们总能将其分解为若干泡利算符的直积, 再分别求出各个部分的期望值, 即$H = \displaystyle\sum\limits_{i, j, k,\cdots, m}\alpha_{i, j, k,\cdots, m}\cdot \sigma_i \otimes \sigma_j \otimes \sigma_k\cdots \otimes \sigma_m$ , $i, j, k\cdots $ $ m \in \{0, x, y, z\}$ , $ \alpha_{i, j, k\dots m} $ 为泡利基的实系数.$ U_S(\theta) $ , 常用的有泡利旋转门$R_X(\theta) = {\rm{e}}^{-{\rm{i}}\frac{\theta}{2}\sigma_x}, R_Y(\theta) = {\rm{e}}^{-{\rm{i}}\frac{\theta}{2}\sigma_y}, R_Z(\theta) = $ $ {\rm{e}}^{-{\rm{i}}\frac{\theta}{2}\sigma_z}$ , 多量子门一般采用$U_{{\rm{CZ}}} = {\left| 0 \right\rangle }\left\langle 0 \right|\otimes I+{\left| 1 \right\rangle }\left\langle1 \right|\otimes \sigma_z$ , $U_{{\rm{CNOT}}} = {\left| 0 \right\rangle }\left\langle 0 \right|\otimes I+{\left| 1 \right\rangle }\left\langle1 \right|\otimes \sigma_x$ 等两比特门. 单量子门和多量子门交替的结构极大地提高了态的纠缠能力, 扩展了态的表示空间.${{{\theta}}}$ , 则参数量子线路可以用$U({{{\theta}}})$ 表示. 若要保证参数量子线路是有效的, 其参数总量和线路深度都有相应的限制. 一般设定参数的总量是多项式级的, 即$n\sim O({\rm{poly}}(N))$ , 其中n 为参数个数, N 为量子比特个数. 同时线路的深度也设为多项式级的, 即$L\sim O({\rm{poly}}(N))$ .图A1 中的PQC模块数是常数级的, 不随量子比特数目增长. 而且由于量子噪声的存在, 增加PQC的模块数会极大地影响量子态的保真度, 所以在真实的任务中往往会限制PQC的模块数. 除此之外还可以通过非计算基补充测量的方式, 来获取更多的数据信息, 这种方法在QCAAN线路[31 ] 中被提到.图 A1 参数量子线路示意图FigureA1. Illustration of MPQCs.[22 ] 证明了在多项式层次结构保持的前提下, 具有$O({\rm{poly}}(N))$ 个门的参数量子线路, 其表示能力比具有$O({\rm{poly}}(N))$ 个参数的经典玻尔兹曼机要强. 尽管如此, 参数量子线路和经典神经网络的直接比较还有一些困难, 如何定义对量子和经典体系均适用的表示能力指标, 以及参数量子线路能否体现量子的优越性, 仍是开放性的问题. 














 图 1 量子生成对抗网络结构[5]
图 1 量子生成对抗网络结构[5]















































































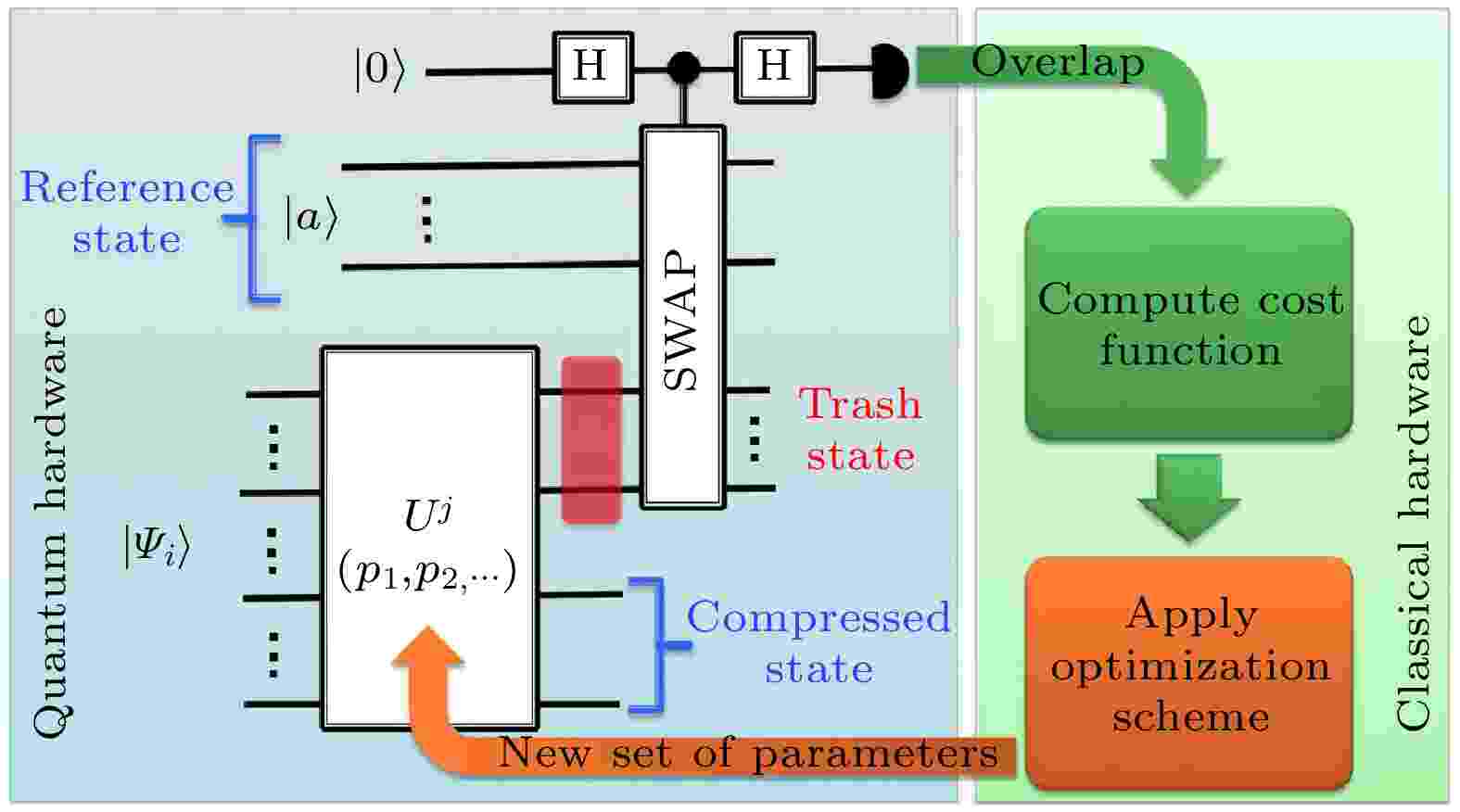 图 2 量子自编码器的训练示意图, 其中
图 2 量子自编码器的训练示意图, 其中



 图 3 经典和量子生成模型 (a) 因子图表示; (b)张量网络态表示; (c)量子生成模型定义[49]
图 3 经典和量子生成模型 (a) 因子图表示; (b)张量网络态表示; (c)量子生成模型定义[49]
























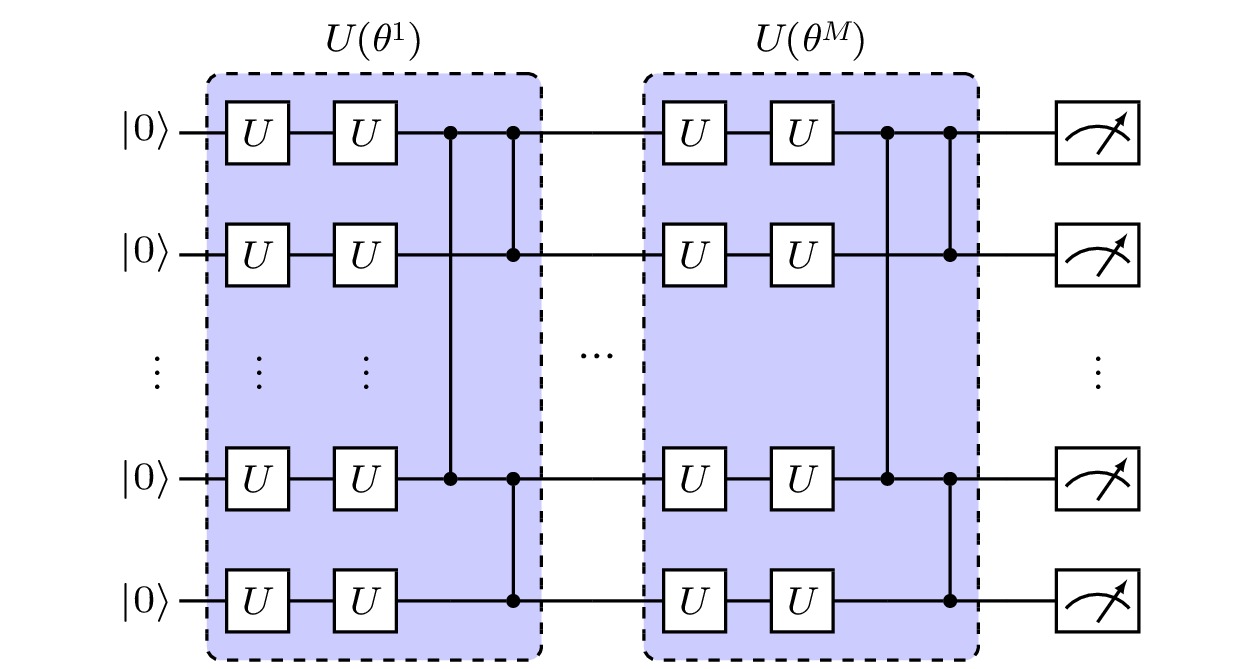 图 A1 参数量子线路示意图
图 A1 参数量子线路示意图



