摘要: 里德伯原子由于具有较长的能级寿命和易于操控的特点已成为卓越的信息载体之一. 近年来, 关于里德伯原子性质的研究得到逐步的发展和完善, 特别是基于里德伯原子间范德瓦耳斯力诱导的单能级里德伯阻塞和反阻塞效应. 然而, 随着原子间距离的改变, 里德伯相互作用将导致更加复杂的动力学行为. 本文主要研究在原子间距小于其特征长度的情况下, 如何根据构建的里德伯反阻塞及双反阻塞机制一步实现两量子比特控制相位门和交换门, 在此范围内的原子间相互作用将涉及多个能级的布居交换. 数值模拟表明: 里德伯阻塞与双反阻塞机制的解析和数值结果能够达到高度一致, 理想情况下控制相位门和交换门的平均保真度分别为99.35%和99.67%, 此结果对于抵抗高激发里德伯态的自发辐射具有一定的鲁棒性. 希望本文的研究能够为里德伯原子系统中实现大规模容错量子计算提供必要的理论支持与实验依据.
关键词: 里德伯原子 /
反阻塞机制 /
量子逻辑门 /
偶极-偶极相互作用 English Abstract Implementation of the Rydberg double anti-blockade regime and the quantum logic gate based on resonant dipole-dipole interactions Jin Zhao 1 ,Li Rui 1 ,Gong Wei-Jiang 1 ,Qi Yang 2 ,Zhang Shou 3 ,Su Shi-Lei 4 1.Department of Physics, College of Sciences, Northeastern University, Shenyang 110819, China Fund Project: Project supported by the Young Scientists Fund of the National Natural Science Foundations of China (Grant No. 11804308), the China Postdoctoral Science Foundation (Grant No. 2018T110735), the Fundamental Research Fund for the Central Universities, China (Grant No. N2005008), and the Postdoctoral Science Foundation of Northeastern University, China (Grant No. 20200322)Received Date: 10 January 2021Accepted Date: 10 February 2021Available Online: 21 June 2021Published Online: 05 July 2021Abstract: Quantum information science is an emerging field that applies the quantum coherence and correlation to cause the revolutionary advances in computation, communication, and fundamental quantum science. As an irreducible ingredient, Rydberg quantum gate is considered to be a powerful resource with great promises to a wide range of quantum information tasks far beyond the original gate proposals, since the remarkable features characterized by Rydberg atom are long lifetime and giant polarizability. In recent years, the research mainly focused on the properties of Rydberg atom, especially for the case where the effects of Rydberg blockade and antiblockade involving single level for each atom are dominated by van der Waals forces. However, with the variation of interatomic distance, Rydberg interactions can induce more complicated dynamical behavior. This paper studies the implementation of controlled-phase gate and swap gate in one step based on the constructed Rydberg antiblockade (RAB) and double antiblockade (RDAB) regimes when the interatomic distance is less than the characteristic length. Different from the conventional RAB regime that requires weak Rydberg-Rydberg interaction (RRI), our attainable strategy is to compensate the RRI-induced energy shift by properly tuning the detuning between the driving field and atomic transition frequencies. In addition, the proposed RDAB mechanism is a new physical insight that can enable two pairs of Rydberg states belonging to different atoms to be excited, simultaneously. In contrast to other blocking schemes or the schemes without requirements for strong interactions, the merits of our proposal lies in the strong dipole-dipole interaction between two atoms, leading to the population exchange of multiple energy levels. Numerical simulations show that the time evolution of the population for collective double-atom basis obtained from the original Hamiltonian agrees well with the analytical results given by the effective Hamiltonian. In the ideal case, the average fidelity of the controlled-phase (swap) gate can reach 99.35% (99.67%) at final time $t=\sqrt{2}\pi\Delta/\Omega^{2}$ ($t=2\pi\Delta/\Omega^{2}$ ), and our protocol is robustness against spontaneous emission of high-lying Rydberg states. We believe our present investigation is feasible in upcoming experimental realization and may offer an new venue with respect to on-demand design of new types of effective Rydberg quantum gate devices.Keywords: Rydberg atom /anti-blockade regime /quantum logic gate /dipole-dipole interaction 全文HTML --> --> --> 1.引 言 量子信息科学是利用量子相干和关联特性进行量子计算和信息处理的一门新兴学科[1 ] , 它推动着量子物理的研究不断革新, 同时也开启了未来全球信息化变革的机遇之门. 量子信息的实现依赖于一个具体的物理系统作为信息载体. 目前, 较理想的量子信息处理平台主要有: 囚禁离子系统[2 ] 、中性原子系统[3 ] 、线性光学系统[4 ] 、超导系统[5 ] 等, 由于它们在量子态操控、存储和传输方面的卓越性质而备受瞩目.$ n $ 的轨道时, 称该类原子为里德伯原子[6 -11 ] . 相比于一般中性原子, 里德伯原子具有轨道半径较大、辐射寿命较长、以及自发辐射几率小等特点. 此外, 里德伯原子的捕获和控制技术比较成熟, 实验上可以通过光镊精准控制里德伯原子的移动[6 ] . 在里德伯原子的众多性质中, 强的长程相互作用一直是研究的热点, 与囚禁离子之间的库仑相互作用不同, 里德伯原子间的相互作用强度变化范围很大[7 ] , 并且可以被耦合光场控制[8 ] . 这些独有的特点使得里德伯原子能够承担更多更复杂的量子信息处理任务. 里德伯原子之间的强相互作用会引起一种抑制激发效应, 称之为里德伯阻塞[12 ] , 由于其特殊的条件激发性质, 已经被普遍应用于制备薛定谔猫态[13 ] 、非破坏性宇称测量[14 ] 、以及非线性光学响应增强[15 ] 等方案.[16 ] 实现的, 其实质是作用在一组基矢上的一种或多种幺正操作. 如果将一系列逻辑门以一定的方式组合起来便可构成需要的量子算法. 与经典计算不同, 量子逻辑门是具有量子态叠加原理和可逆性质的运算机制, 因此, 量子计算机能够以较高的运算速度和较低的能量消耗并行工作. 为了实现大规模量子计算, 量子比特之间的耦合是非常必要的, 里德伯原子长程且可调的相互作用为操控中性量子比特实现可扩展的量子逻辑门提供了强有力的技术手段. 其中有不少的理论方案已经被实验验证[17 ] . 典型的基于里德伯阻塞的受控逻辑门可分为三步[7 ] : (i) 对控制原子执行操作$ |1\rangle\rightarrow|r\rangle $ ; (ii) 对目标原子$ |1\rangle $ 执行$ 2\pi $ 操作; (iii) 对控制原子执行操作$ |r\rangle\rightarrow|1\rangle $ . 如果控制原子初始位于$ |1\rangle $ , 则对目标原子的$ 2\pi $ 操作将会失效; 反之目标原子的$ |1\rangle $ 态将会获得一个相位. 然而, 此类阻塞门存在一个根本的局限, 即由里德伯能级移位$ V $ 引起的固有阻塞错误, 通常正比于$ \varOmega/V^{2} $ ($ \varOmega $ 是有效拉比频率)[18 ] , 这会不可避免地阻止它的拓展和应用.[19 ] ; 也可以通过调制激光驱动的拉比频率, 使其远大于里德伯相互作用强度, 进而打破阻塞机制的限制; 还可以利用激光场失谐补偿里德伯相互作用引起的能级移动来实现反阻塞[20 ,21 ] . 早在2007年, Ates 等[22 ] 在研究制备超冷里德伯原子气的方案中已经预测了反阻塞机制的存在. 而后, Amthor 研究组[23 ] 利用可分辨时间光谱测量技术在实验上观测到了该现象. 相比于里德伯阻塞, 反阻塞是一种新的物理机制[24 ,25 ] , 它允许多个里德伯原子同时被激发. 最近, 包括同时[26 ] 、分步[27 ] 驱动的反阻塞机制、库仑反阻塞机制[28 ] 、以及耗散诱导的反阻塞机制[29 ] 等不同类型的里德伯反阻塞机制被陆续提出, 并作为构建量子逻辑门[30 -32 ] 及制备量子纠缠态[33 ,34 ] 等量子信息处理任务的基本模型被深入研究和细致探讨. 但大部分前期的研究方案[35 -38 ] 均考虑原子距离较远或者共振条件达不到时的情形, 范德瓦耳斯相互作用的效果仅仅是使单里德伯态发生能级移动, 如果缩小原子间距至偶极-偶极相互作用区, 里德伯态间的相互作用将涉及多个能级的布居交换. 正如基于偶极-偶极相互作用的F?rster共振过程[39 ,40 ] , 它是利用里德伯原子中的共振能量转移来增强原子间的相互作用, 该过程可以简单概括为: $|dd\rangle\leftrightarrow $ $|pf\rangle+|fp\rangle$ , 其中, $ |p\rangle = |61 {\rm P}_{1/2},\; m_{j} = 1/2\rangle $ , $|d\rangle = $ $ |59 {\rm D}_{3/2}, \;m_{j} = 3/2\rangle$ , 以及$ |f\rangle = |57 {\rm F}_{5/2},\; m_{j} = 5/2\rangle $ , 为能级间隔相等的三个里德伯态, 即双原子矢量$ |dd\rangle $ , $ |pf\rangle $ , 以及$ |fp\rangle $ 三者能量简并[41 ,42 ] . 然而, 实际操作的非精准性将导致一个相对小的能量移位, 使得原本共振的相互作用存在一个F?rster缺陷. 实验上, 通常利用强度为32 mV·cm–1 的电场消除此类误差[39 ] , 进而构建严格意义上的F?rster共振, 此时原子间的偶极-偶极相互作用强度$V_{\rm dip} = $ $ \sqrt{2}C_{3}/R^{3}$ . 实验测得的弥散系数$C_{3}/2\pi = (2.39 \; \pm \; $ $ 0.03) \;{\rm{GHz}}\! \cdot\!\text{μ} {\rm{m}}^{3}$ , 十分接近于理论值$C_{3}/2\pi = (2.54 \; \pm $ $ 0.03)\; {\rm{GHz}} \!\cdot\! \text{μ} {\rm{m}}^{3}$ . 此外, 另外两种类型的偶极-偶极相互作用为自旋交换型[43 ,44 ] 以及集体交换型[45 ,46 ] , 对应的态矢量转化过程可分别表示为$ |sp\rangle\leftrightarrow|ps\rangle $ 以及$ |ss'\rangle\leftrightarrow|pp'\rangle $ . 正是因为偶极-偶极相互作用的特殊性质, 已经被广泛应用于两比特[47 ] 和三比特[48 ] 逻辑门的构建, 以及最近提出的可选择的里德伯泵浦机制[49 ] .[25 -27 ] , 当前的研究考虑了原子间距小于其特征距离时, 里德伯原子间的强相互作用导致的一系列动力学特征, 提出的双反阻塞动力学允许两个基态矢量$ |01\rangle $ 和$ |10\rangle $ 同时布居在里德伯能级, 如果将提出的双反阻塞动力学应用到耗散制备纠缠等量子信息处理方案中, 这在一定程度上能够提高里德伯泵浦的效率, 从而加快系统演化达到消耗更少资源的目的. 此外, 由于通用量子逻辑门通常需要考虑多个幺正操作的组合, 在数学上的低效率或者在物理实现上存在一定的复杂性. 所以在量子计算中使用直接的多比特门更为方便. 根据两种反阻塞机制的特殊性质, 我们提出了一步实现高保真度的两量子比特控制相位门和交换门的方案. 因此, 本文所讨论的内容对于拓展里德伯反阻塞机制的维度和提升激光泵浦效率等方面的探索具有重要意义.2.里德伯反阻塞效应及控制相位门的实现 两个相距微米量级的里德伯原子能级精细结构如图1 所示, 实验上通常选择Rb87 冷原子气模拟里德伯原子系统的动力学行为, $|0\rangle_{\xi}\equiv |5 {\rm S}_{1/2}, $ $ F \!=\! 1, \; m_{F}\! = \!0\rangle$ 和$|1\rangle_{\xi}\equiv|5 {\rm S}_{1/2}, \;F \!= \!2, \;m_{F}\! = \!2\rangle$ ($\xi \!= $ $ 1, \; 2$ )表示对应原子的基态, $|p\rangle_{\xi}\equiv|63 {\rm P}_{1/2},\; m_{J} = $ $ 1/2\rangle$ 和$ |d\rangle_{\xi}\equiv|62 {\rm D}_{3/2}, \; m_{J} = 3/2\rangle $ 代表高激发里德伯态. 对于第一个原子, 利用一束$ \sigma_{+} $ 极化, 波长为297 nm的单色激光场通过单光子过程实现$ |1\rangle_{1}\leftrightarrow|p\rangle_{1} $ 的跃迁. $ |1\rangle_{2}\leftrightarrow|d\rangle_{2} $ 的泵浦过程则需要利用两束波长分别为 780和479.8 nm的驱动场通过双光子过程来实现[39 ] . 两个跃迁过程对应相同的拉比频率$ \varOmega $ 和失谐量$ \varDelta $ . 当两个原子同时处于里德伯态且样品的空间密度达到约109 cm–3 时, 共振的偶极-偶极相互作用将诱导里德伯能级间的布居交换.图 1 里德伯原子的能级结构. $ |p(0)\rangle_{\xi} $ 和$ |d(1)\rangle_{\xi} $ ($ \xi = 1, 2 $ )代表两个激发(基)态, 具有相同拉比频率的两束非共振的光学激光分别驱动对应原子的跃迁 $ |1\rangle_{1}\leftrightarrow|p\rangle_{1} $ 和$ |1\rangle_{2}\leftrightarrow|d\rangle_{2} $ , 失谐量为$\varDelta$ . $ V_{pd} $ 表示两个里德伯原子间共振的偶极-偶极相互作用强度Figure1. Energy-level configuration of Rydberg atoms. $ |p(0)\rangle_{\xi} $ and $ |d(1)\rangle_{\xi} $ ($ \xi = 1, 2 $ ) represent two Rydberg (ground) states, off-resonance optical lasers drive the transitions $ |1\rangle_{1}\leftrightarrow|p\rangle_{1} $ and $ |1\rangle_{2}\leftrightarrow|d\rangle_{2} $ for the corresponding atom with identical Rabi frequency $\varOmega$ and detuning $\varDelta$ , respectively. $ V_{pd} $ denotes the strength of resonant diploe-diploe interaction between two Rydberg atoms.$ \hbar = 1 $ ):$ |pd\rangle = |p\rangle_{1}\otimes|d\rangle_{2} $ 为双原子基矢, 在接下来的讨论中还将沿用类似的形式; $ V_{pd} $ 为里德伯原子间的偶极-偶极相互作用强度, 由此表征的里德伯相互作用可以进一步表示成对角化的形式$\hat{H}'_{d} = $ $ V_{pd}(|+\rangle\langle+|-|-\rangle \langle-|)$ , 其中$ |\pm\rangle\equiv(|pd\rangle\pm|dp\rangle)/\sqrt{2} $ 是本征值为$ \pm V_{pd} $ 的本征态. 这一部分对角项能够作为自由能哈密顿量, 将系统的相互作用旋转至新的绘景. 在此之前, 需要将外部驱动场的哈密顿量在集体的双原子表象下进行展开, 其表达式为$ |\phi\rangle = (|1 d\rangle+|p1\rangle)/\sqrt{2} $ 为单激发里德伯态. 引入幺正算符$ \hat{h} = \delta(|+\rangle \langle +|-|-\rangle\langle-|) $ , 并以$U = $ $ {\rm{exp}} ({\rm i}\hat{h}t)$ 作为旋转框架, 系统的哈密顿量表示为[50 ] 可以绝热地消除(3 )式中与单激发子空间相关的相互作用项 (高频振荡项), 并结合大失谐条件$ \{\varDelta, \; \varDelta\pm\delta\}\gg\varOmega $ 及反阻塞条件$ \delta = 2\varDelta $ 和$ V_{pd} = 2\varDelta+\varOmega^{2}/(4\varDelta) $ , 最终能够得到一个简洁的相互作用形式, 即系统的有效哈密顿量:4 )式表达了基态$ |11\rangle $ 和双激发里德伯态之间的布居转化将随着时间推移呈现拉比振荡. 当假设系统最初被制备在基态$ |11\rangle $ 上时, 通过解析地求解薛定谔方程${\rm i}\partial t|\psi(t)\rangle/\partial t = H_{\rm eff}|\psi(t)\rangle$ , 任意时刻系统的末态可以表示为$ t = \sqrt{2}(2 n-1)\pi\varDelta/\varOmega^{2} $ ($ n $ 为正整数)出现, 此时, 尽管强的里德伯相互作用存在, 系统的两个基态依然能够同时处于高激发的里德伯态. 然而, 如果系统满足共振条件 $ \varDelta = \delta = 0 $ 和强相互作用条件$ V_{pd}\gg\varOmega $ , 里德伯相互作用将会导致单激发和双激发里德伯态之间的非共振耦合, 这些高频振荡项将会极大地抑制两个原子的同时激发, 此时, 系统表现的则是里德伯阻塞效应.$ V_{pd} = 2\varDelta+\varOmega^{2}/(4\varDelta) $ (解析结果). 为了表明其合理性, 在图2(a) 中, 通过数值求解与原始哈密顿量((1 )式)相关的薛定谔方程, 在时刻$t = \sqrt{2}\pi\varDelta/\varOmega^{2}$ , 从初态$ |11\rangle $ 出发, 画出了双激发里德伯态$ |+\rangle $ 的布居随着$ V_{pd}/\varOmega $ 以及$ \varDelta/\varOmega $ 的变化, 图中的数值结果与解析结果(黑色点线)几乎符合.图 2 (a) 态矢量$ |+\rangle $ 的布居在时刻$ t = \sqrt{2}\pi\varDelta/\varOmega^{2} $ 随着参数$ V_{pd}/\varOmega $ 和$ \varDelta/\varOmega $ 的变化, 系统初态为$ |11\rangle $ , 图中的黑色点线是利用$ V_{pd} = 2\varDelta+\varOmega^{2}/(4\varDelta) $ 得到的解析结果; (b) 由原始哈密顿量(黑色点划线)以及有效哈密顿量(红色实线)支配的布居动力学随时间的演化, 系统的初态和末态分别为$ |11\rangle $ 和$-|11\rangle$ , 相关的系统参数设置为: $ \varOmega/(2\pi) $ = 2 MHz, $\varDelta = 7.5 \; \Omega$ , 以及$ V_{pd} = 2\varDelta+\varOmega^{2}/(4\varDelta) $ Figure2. (a) Population of state $ |+\rangle $ versus $ V_{pd}/\varOmega $ and $ \varDelta/\varOmega $ at the time $ t = \sqrt{2}\pi\varDelta/\varOmega^{2} $ with a fixed initial state $ |11\rangle $ , the solid dots are analytical results based on the equation $ V_{pd} = 2\varDelta+\varOmega^{2}/(4\varDelta) $ ; (b) populations of $-|11\rangle$ versus the evolution time from the initial state $ |11\rangle $ governed by Full Hamiltonian (black dash-dotted line) and effective Hamiltonian (red solid line), the related parameters are chosen as: $\varOmega/(2\pi)$ = 2 MHz, $\varDelta = 7.5\;\Omega$ , and $V_{pd} = $ $ 2\varDelta+\varOmega^{2}/(4\varDelta)$ .4 )式)及任意时刻系统末态的表达式((5 )式)不难计算出当演化时间$ t = $ $ 2\sqrt{2}(2 n-1)\pi\varDelta/\varOmega^{2} $ 时, 态矢量$ |11\rangle $ 的布居能够完全转化为$- |11\rangle $ , 而有效哈密顿量中不包含有关其他三个态矢量($ |00\rangle $ , $ |10\rangle $ , 以及$ |01\rangle $ )的耦合项, 因此它们在整个演化过程中均保持在自身的原始状态. 在不考虑耗散的情况下, 借助于里德伯阻塞机制的控制相位门能够以趋于100%的高保真度成功构建. 在图2(b) 中, 通过数值求解由原始哈密顿量(红色实线)及有效哈密顿量(黑色点划线)分别支配的薛定谔方程, 模拟了当系统初态设置为$ |11\rangle $ 时, 态矢量$ -|11\rangle $ 的布居随时间的演化. 从图2(b) 中可以看出, 两条曲线的演化趋势保持了高度一致, 均在与解析结果相同的时间点$ t = 5.3 \; {\text {μ}}{\rm{s}} $ , 保证了末态$ -|11\rangle $ 的布居分别达到99.72%和99.97%, 这不仅从数值的角度验证了上述理论分析的可行性, 也意味着从原始哈密顿量到有效哈密顿量的推导过程中涉及的一系列假设和近似均是合理且有效的, 更表明了利用当前的有效哈密顿量计算出的解析结果能够准确表征由原始哈密顿量支配系统演化的动力学行为.3.里德伯双反阻塞效应及交换门的实现 作为反阻塞机制的拓展和延续, 这一小节将基于里德伯原子间的偶极-偶极相互作用实现里德伯双反阻塞, 即允许四个双原子基态矢量. $ \{|00\rangle, \; |01\rangle, \; $ $ |10\rangle, \; |11\rangle\} $ 中的两个布居在高激发里德伯态.图3 所示, 假设两束具有相同拉比频率$ \varOmega $ , 相对相位为$ \theta_{\xi} $ ($ \xi = 1, \; 2 $ )的光学激光场分别非共振地驱动原子能级$|0\rangle_{\xi}\leftrightarrow$ $|d\rangle_{\xi} $ 和$ |1\rangle_{\xi}\leftrightarrow|p\rangle_{\xi} $ 之间的跃迁, 失谐量均为$ \varDelta $ , 实验上, 通常利用光镊精确控制和束缚原子在空间中的相对位置, 从而调节两个原子里德伯能级间的作用类型, 这里依然沿用上节中具有“自旋-交换”性质的共振偶极-偶极相互作用. 刻画上述耦合的系统哈密顿量为图 3 里德伯原子的能级结构. $ |p(0)\rangle_{\xi} $ 和$ |d(1)\rangle_{\xi} $ ($ \xi = 1, 2 $ )代表两个激发(基)态, 两束具有相同拉比频率$ \varOmega $ 及相对相位为$ \theta_{\xi} $ 的非共振的光学激光分别驱动对应原子的跃迁 $ |0\rangle_{\xi}\leftrightarrow|d\rangle_{\xi} $ 和$ |1\rangle_{\xi}\leftrightarrow|p\rangle_{\xi} $ , 失谐量为$ \varDelta $ . $ V_{pd} $ 表示两个里德伯原子间共振的偶极-偶极相互作用强度Figure3. Energy-level configuration of Rydberg atoms. $ |p(0)\rangle_{\xi} $ and $ |d(1)\rangle_{\xi} $ ($ \xi = 1, 2 $ ) represent two Rydberg (ground) states, off-resonance optical lasers drive the transitions $ |0\rangle_{\xi}\leftrightarrow|d\rangle_{\xi} $ and $ |1\rangle_{\xi}\leftrightarrow|p\rangle_{\xi} $ for the corresponding atom with identical Rabi frequency $ \varOmega $ , detuning $ \varDelta $ , and different relative phase $ \theta_{\xi} $ , respectively. $ V_{pd} $ denotes the strength of resonant diploe-diploe interaction between two Rydberg atoms.$ \theta_{1} = -\pi $ 和$ \theta_{2} = \pi $ . 同样将(7 )式在双原子基矢下展开, 并以里德伯相互作用哈密顿量的对角形式作为新的旋转框架, 此时激光与原子耦合哈密顿量可以重新表达为$|\varphi\rangle = \!(|p0\rangle\!+\!|1 d\rangle)/\sqrt{2}$ , $|\psi\rangle = \!(|d1\rangle\!+\!|0 p\rangle)/\sqrt{2}$ , $ |\eta\rangle = (|p1\rangle+|1 p\rangle)/\sqrt{2} $ , 和$ |\chi\rangle = (|d0\rangle+|0 d\rangle)/\sqrt{2} $ 分别为不同形式的单激发里德伯态. 在大失谐条件$ \{\varDelta, \; \varDelta\pm V_{pd}\}\gg\varOmega $ 及双反阻塞条件$ V_{pd} = 2\varDelta $ 下, 利用时间平均方法[50 ] , 能够计算出系统的有效哈密顿量9 )式支配的薛定谔方程, 可得到如下演化过程:$\vartheta = \varOmega^{2}t/(4\varDelta)$ . 当操作时间$t = (2 n-1)\pi\varDelta/\varOmega^{2}$ ($ n $ 为正整数), 基态矢量$ |10\rangle $ 和$ |01\rangle $ 的叠加态能够同时布居在双激发里德伯态$ |+\rangle $ , 此时系统呈现里德伯双反阻塞效应. 为了进一步证明上述解析结果以及反阻塞条件的准确性, 在图4(a) 中, 通过数值求解与原始哈密顿量((7 )式)相关的薛定谔方程, 在时刻$ t = \pi\varDelta/\varOmega^{2} $ , 从初态 $|G\rangle = 1/\sqrt{2}(|10\rangle- |01\rangle)$ 出发, 画出了双激发里德伯态$ |+\rangle $ 的布居随着$ V_{pd}/\varOmega $ 及$ \varDelta/\varOmega $ 的变化, 图中的数值结果与双反阻塞条件$ V_{pd} = 2\varDelta $ 的解析结果(黑色点线)能够基本重合.图 4 (a) 态矢量$ |+\rangle $ 的布居在时刻$ t = \pi\varDelta/\varOmega^{2} $ 随着参数$ V_{pd}/\varOmega $ 和$ \varDelta/\varOmega $ 的变化, 系统初态为$|G\rangle = 1/\sqrt{2}(|10\rangle- $ $ |01\rangle)$ , 图中的黑色点线是利用公式$ V_{pd} = 2\varDelta $ 得到的解析结果; (b) 由原始哈密顿量(黑色点划线)以及有效哈密顿量(红色实线)支配的布居动力学随时间的演化, 系统的初态和末态分别为$ |10\rangle $ 和$ |01\rangle $ , 相关的系统参数设置为: $ \varOmega/(2\pi) $ = 2 MHz, $\varDelta = 7.5\;\Omega$ , 以及$ V_{pd} = 2\varDelta $ Figure4. (a) Population of state $ |+\rangle $ versus $ V_{pd}/\varOmega $ and $ \varDelta/\varOmega $ at the time $ t = \pi\varDelta/\varOmega^{2} $ with a fixed initial state $ |10\rangle $ , the solid dots are analytical results based on the equation $ V_{pd} = 2\varDelta $ ; (b) populations of $ |01\rangle $ versus the evolution time from the initial state $ |10\rangle $ governed by Full Hamiltonian (black dash-dotted line) and effective Hamiltonian (red solid line), the related parameters are chosen as: $\varOmega/(2\pi)$ = 2 MHz, $\varDelta = 7.5\;\Omega$ , and $ V_{pd} = 2\varDelta $ .$ t = 2(2 n-1)\pi\varDelta/\varOmega^{2} $ 时, 将出现如下布居转化: $ |10\rangle\rightarrow|01\rangle $ 和$ |01\rangle\rightarrow|10\rangle $ . 在图4(b) 中, 通过数值求解由原始哈密顿量(红色实线)及有效哈密顿量(黑色点划线)分别支配的薛定谔方程, 模拟了当系统初态为$ |10\rangle $ 时, 末态$ |01\rangle $ 的布居随时间的演化. 图4(b) 中的两条曲线的演化趋势依然保持了高度一致, 并且在$t = 2\pi\varDelta/\varOmega^{2} = $ $ 3.7 \;{\text {μ}} {\rm{s}}$ 的时间点初态与末态的布居转化分别达到99.71%和100%, 该结论再一次表明了解析和数值结果的精确对应. 值得注意的是, 另外两个基态矢量$ |00\rangle $ 和$ |11\rangle $ 由于与系统哈密顿量解耦合, 因此布居不发生变化. 以上描述即为标准两量子比特交换门的构建过程, 其算符表示为4.数值分析 量子系统的演化会不可避免地遭受环境的影响进而导致消相干, 对于当前的里德伯原子系统, 唯一的耗散因素即高激发里德伯态的自发辐射. 尽管我们所构建的量子逻辑门均涉及原子基态矢量间的相互转化, 但支配系统动力学演化的有效哈密顿量的导出与基态到激发态的泵浦过程息息相关. 但由于这个过程是非共振激光驱动的, 因此所导致的激发态布居始终保持高频振荡的行为, 从而能够保证构建的量子逻辑门对于抵抗原子自发辐射具有一定的鲁棒性. 为了验证上述理论分析的正确性, 引入量子门操作的平均保真度[51 ,52 ] :12 )式中, $|\varPsi_{i}\rangle = ( \cos\alpha|0\rangle_{1}+ \sin\alpha|1\rangle_{1})\otimes $ $ ( \cos\beta|0\rangle_{2}+ \sin\beta|1\rangle_{2})$ 为初始的直积态; $ U $ 为(6 )式或(11 )式表示的标准门操作算符; $ \alpha $ 和$ \beta $ 为布洛赫球上的极角; $ \hat{\rho}(t) $ 表示任意时刻系统末态的密度算符, 它的演化由如下马尔科夫近似下的主方程决定:$ \hat{H} $ ($ \hat{\cal{H}} $ ) 为(1 )式((7 )式)所表征的原始哈密顿量; $ \hat{L}_{1}^{\xi}\equiv\sqrt{\gamma/2}|0\rangle_{\xi\xi}\langle d| $ , $ \hat{L}_{2}^{\xi}\equiv\sqrt{\gamma/2}|0\rangle_{\xi\xi}\langle p| $ , $\hat{L}_{3}^{\xi}\equiv $ $ \sqrt{\gamma/2}|1\rangle_{\xi\xi}\langle d|$ , 以及$ \hat{L}_{4}^{\xi}\equiv\sqrt{\gamma/2}|1\rangle_{\xi\xi}\langle p| $ ($ \xi = 1, \; 2 $ ) 为描述对应原子四个衰减路径的 Lindblad 算符, $ \gamma $ 为原子自发辐射率.图5(a) (图5(b) )中, 数值模拟了理想情况下, 即$ \gamma = 0 $ 时, 两量子比特控制相位门(交换门)的平均保真度随时间的演化. 可以看出, 原始哈密顿量(红色线)和有效哈密顿量(黑色线)支配的动力学结果和演化趋势基本能够相互重合, 其中, 红色曲线在末态时间点$ t = \sqrt{2}\pi\varDelta/\varOmega^{2} $ ($t = 2\pi\varDelta/\varOmega^{2}$ ), $ \bar{F}(t) = 0.9935\; (0.9967) $ , 而黑色曲线的值则均超过了0.9999, 造成这种轻微差异的原因, 主要是由于原始哈密顿量中存在的高频振荡项所导致的一些微小的误差.图 5 由原始哈密顿量和有效哈密顿量支配的平均保真度随时间的演化 (a)控制相位门; (b)控制交换门. 系统参数为$ \varOmega/(2\pi) $ = 2 MHz, $\varDelta = 7.5\varOmega$ , $V_{pd} = 2\varDelta+ \varOmega^{2}/(4\varDelta)$ ($V_{pd} = $ $ 2\varDelta$ ) 以及$ \gamma $ = 0 kHz. 插图表示不同的原子自发辐射率对平均保真度的影响, 选定的末态时刻为$ t = \sqrt{2}\pi\varDelta/\varOmega^{2} $ ($ t = 2\pi\varDelta/\varOmega^{2} $ ), 其他的系统参数除了$ \gamma $ 以外均与大图相同Figure5. Time-dependence of the average fidelity dominated by full Hamiltonian and effective Hamiltonian: (a) controlled-PHASE gate; (b) controlled-SWAP gate. Values of parameters are: $ \varOmega/(2\pi) $ = 2 MHz, $\varDelta = 7.5\;\Omega$ , $V_{pd} = 2\varDelta+ $ $ \varOmega^{2}/(4\varDelta)$ ($ V_{pd} = 2\varDelta $ ) and $ \gamma $ = 0 kHz. The insets shows the influence of different atomic decay rates $ \gamma $ on the final average fidelity. The chosen final time is $ t = \sqrt{2}\pi\varDelta/\varOmega^{2} $ ($ t = 2\pi\varDelta/\varOmega^{2} $ ) and the other parameters are the same as in panels (a) and (b) except for $ \gamma $ .图5(a) 和5(b) 的插图中利用数值方法进一步研究了原子自发辐射对门操作的平均保真度带来的负面影响. 通过分别求解由原始哈密顿量所支配的主方程并选定对应的末态的时间点, 可以明显观察到, 在$ \gamma $ 从0 kHz增大到2 kHz的范围内, 平均保真度的值呈现出了线性的递减, 减少量仅为0.004. 即使当$\gamma = 2\; {\rm{kHz}}—10^{-3}\varOmega$ 时, 控制相位门和交换门的平均保真度依然可以超过0.99. 这从数值的层面表明了方案所构建的逻辑门对于抵抗原子激发态的衰减具有一定的鲁棒性. 实际上, 高激发的里德伯态具有较长的寿命[8 ] , 对应相对小的自发辐射率, 因此, 在参数条件$\gamma/\varOmega < $ $ 10^{-3}$ 下[53 ] , 保证逻辑门的平均保真度的值大于0.99并非是一个极端挑战, 而是可以轻易达到的要求.5.结 论 本文以四能级里德伯原子为基本模型研究了里德伯反阻塞动力学的性质及应用, 通过调节激光失谐量补偿原子间共振的偶极-偶极相互作用诱导的能级移位实现了双原子基态的同时布居. 在此基础上, 根据反阻塞与双反阻塞各自的泵浦特征, 构建了对应的两量子比特控制相位门及交换门. 数值模拟同时考虑了有效哈密顿量和原始哈密顿量分别支配的动力学演化. 结果表明, 两者表征的解析和数值结果可以达到高度符合, 同时也验证了高保真度量子逻辑门对于抵抗原子自发辐射具有一定的鲁棒性. 希望本文的研究能够积极地推动多维度、高效率的里德伯反阻塞机制的研究走向深入, 并且为中性原子系统中实现大规模量子计算的相关实验提供理论依据. 


















































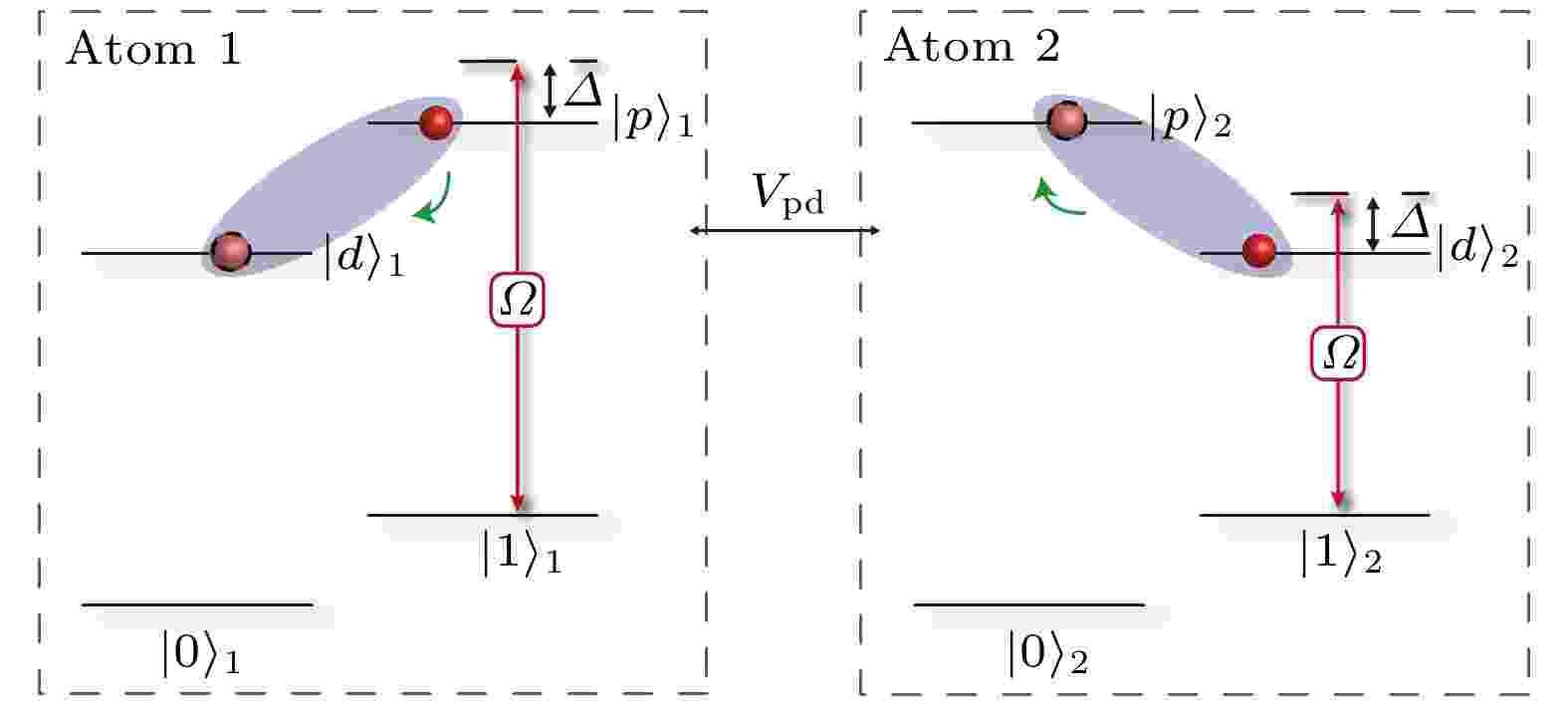 图 1 里德伯原子的能级结构.
图 1 里德伯原子的能级结构. 











































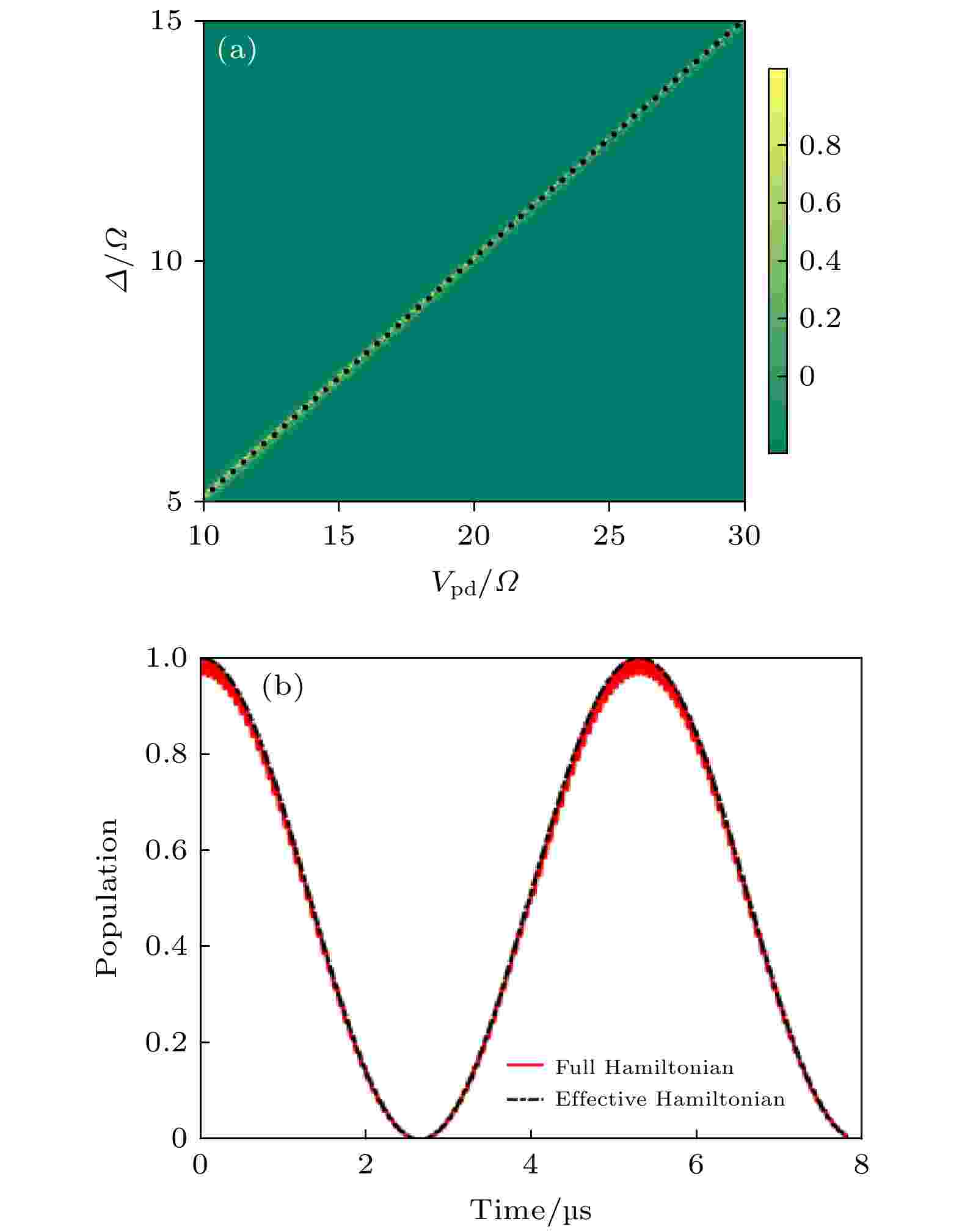 图 2 (a) 态矢量
图 2 (a) 态矢量




















































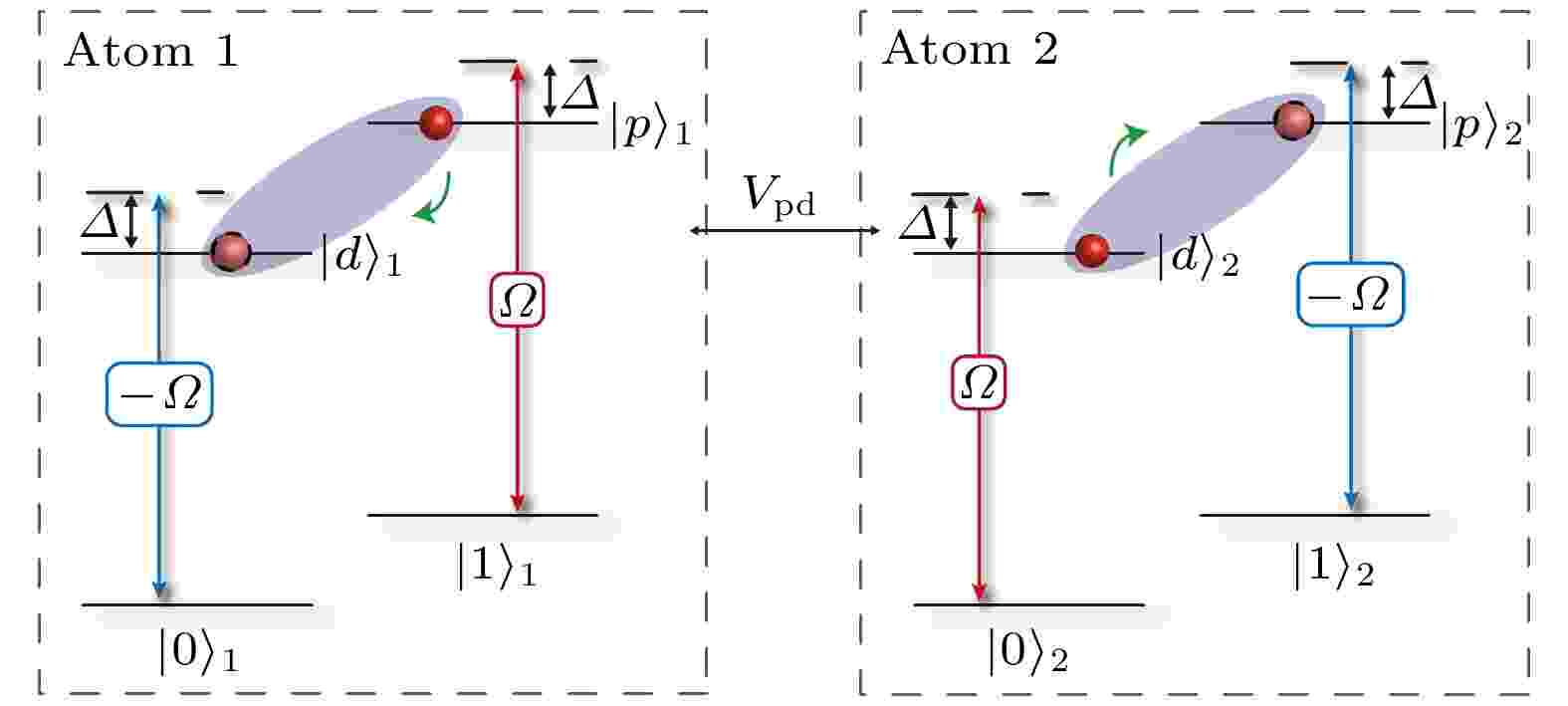 图 3 里德伯原子的能级结构.
图 3 里德伯原子的能级结构. 







































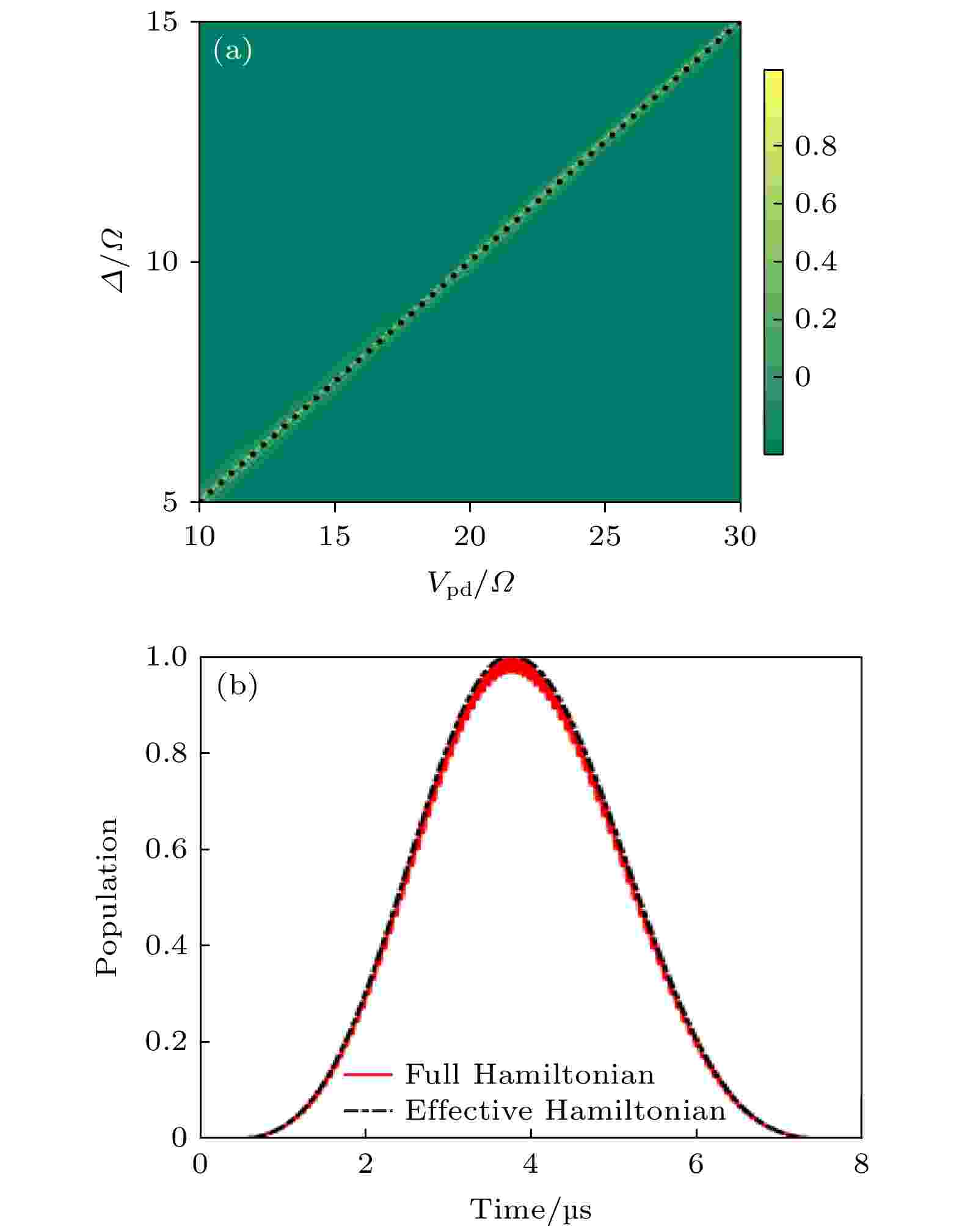 图 4 (a) 态矢量
图 4 (a) 态矢量
























































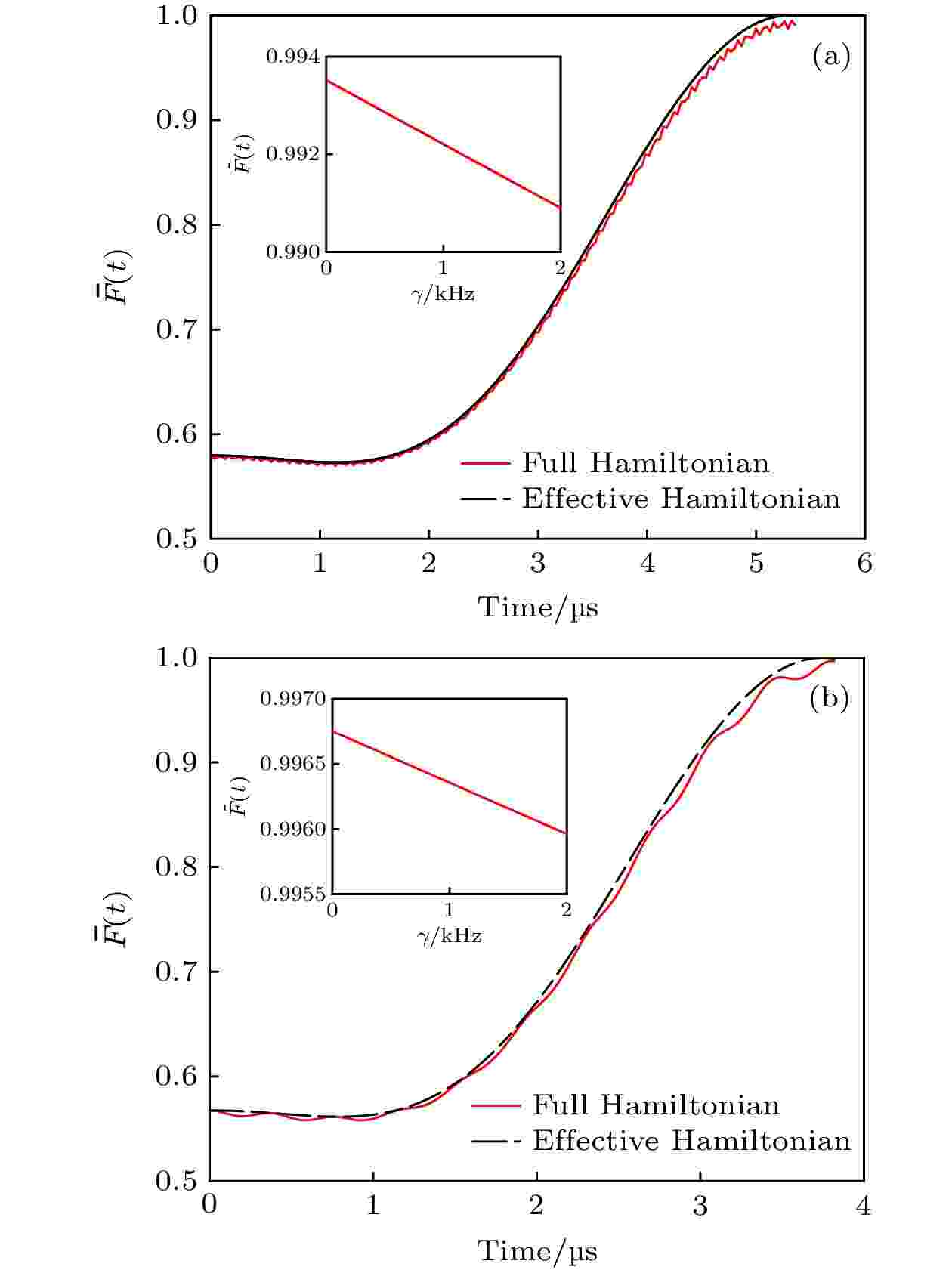 图 5 由原始哈密顿量和有效哈密顿量支配的平均保真度随时间的演化 (a)控制相位门; (b)控制交换门. 系统参数为
图 5 由原始哈密顿量和有效哈密顿量支配的平均保真度随时间的演化 (a)控制相位门; (b)控制交换门. 系统参数为
































