全文HTML
--> --> -->当前, 工业生产金属粉末主要有两种气体雾化方法, 真空感应熔炼气体雾化法(vacuum induction melting gas atomization, VIGA)[4,10,11]和电极感应熔炼气体雾化法(electrode induction melting gas atomization, EIGA)[12,13]. 作为气体雾化的重要组成部分, 雾化喷嘴结构对流场分布、气体加速效果和能量转换效率起着决定性的作用, 进而直接决定粉末的粒径、球形度、表面形貌和晶粒结构等性质. “自由落体式”和“紧密耦合式”是VIGA系统中使用最广泛的两种喷嘴结构. 在“自由落体式”喷嘴结构中, 熔体在遇到雾化气流之前, 会沿重力方向自由飞行一段距离, 这将不可避免地导致热损失. 因此, “自由落体式”喷嘴系统常被用于生产低熔点金属粉末. 此外, 这种结构的喷嘴具有较高的生产效率, 但制备的粉末粒度分布广, 形状不规则[14]. 在“紧密耦合式”喷嘴系统中, 高速雾化气体射流直接冲击自导流管流出的金属熔体[15]. 尽管这种喷嘴可以更好地控制粉末粒径, 但由于导流管会直接受到高速低温气流的冲击, 也更容易在导流管末端出现堵塞问题. 在使用这两种传统雾化喷嘴制备粉末时, 雾化气流在冲击熔体流之前表现为湍流状态, 雾化气体在进入金属熔体流的过程中减速, 同时气体密度降低. 传统的气体雾化方法, 由于对雾化介质能量的利用有限, 且雾化前初始熔体尺寸较大, 雾化粉末粒径较大, 粒径分布较广, 粉末整体质量不高.
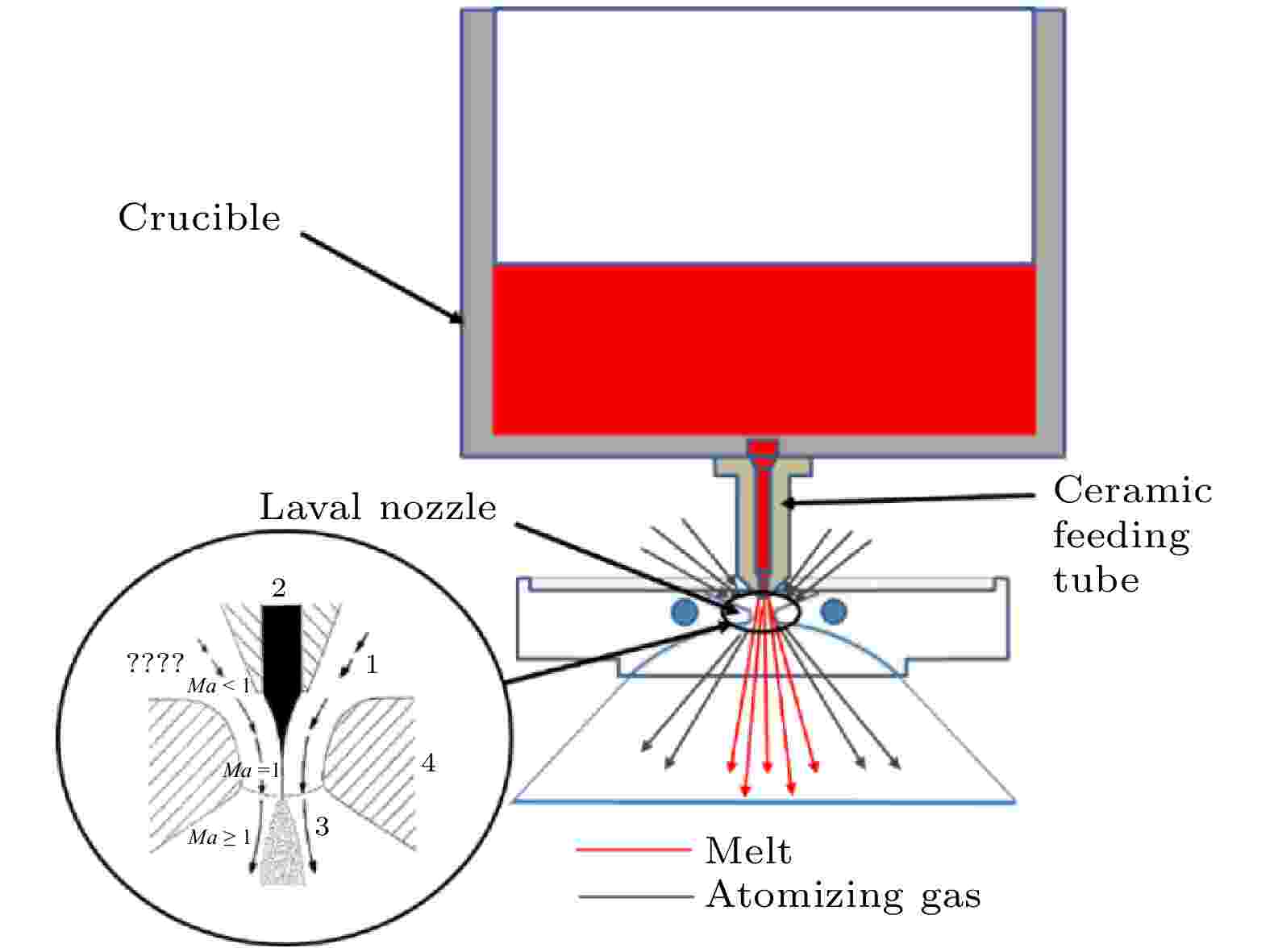图 1 层流气体雾化过程示意图Figure1. Illustration of laminar flow gas atomization process.
迄今为止, 对层流气体雾化的工艺研究还很少, 而且大多关注工艺参数对雾化效果的影响[20]. Planche等[16]和Allimant等[21]研究表明, 层流气雾化工艺可以获得具有较窄粒度分布范围的金属粉末, 同时粉末的平均直径随着雾化压力的增加和导流管中熔体流直径的减小而减小. 由于负超压和熔体流动速率的降低, 气体与金属的流量比(gas to metal ratio, GMR)的增加速度低于雾化压力, 通过改变雾化过程中的气体压力, 可以有效控制并得到更窄的粒度分布. 此外Khatim等[22]通过研究不同雾化阶段收集的粉末特征, 发现在较高的雾化压力下, 层流气体雾化工艺制备的粉末具有相对较窄的粒度分布.
然而, 层流气体雾化的独特雾化机理尚未完全厘清, 其中涉及复杂的物理过程, 包括雾化气体和熔体的流体力学、传热学、凝固过程等[23]. 现有的大多数对基于其他类型喷嘴的非层流气雾化机理和气体流场的研究是通过数值模拟进行的[24-26]. 夏敏等[27]对基于紧耦合式(限制式)喷嘴的EIGA雾化过程进行了数值模拟, 使用流体体积分数法(volume of fluid, VOF)和欧拉-拉格朗日离散相法(discrete phase model, DPM)对一次雾化和二次雾化过程进行了模拟. 戴剑锋等[28]使用耦合水平集-体积分数法(coupled level-set and volume-of-fluid, CLSVOF), 成功模拟了单个液滴撞击液膜时的飞溅现象, 为气雾化中的液滴破碎研究提供了一种很好的方法.
本文使用有限元分析方法对层流气体雾化过程中的雾化原理和液滴破碎机理进行了系统性研究. 采用单相气体流场数值模型对不同进气压力条件下的雾化气体流场进行了数值模拟. 基于雾化气体和熔体两相流模型, 采用耦合水平集-体积分数法(coupled level set-volume of fraction, CLSVOF)研究了一次雾化和二次雾化过程, 并最终将层流气体雾化得到的粉末形貌与数值模拟结果进行了比较, 得到了较高的符合度.
本文基于自制的层流气雾化制粉设备展开了AlSi10Mg粉末的制备研究, 并通过金属粉末实验对数值模拟结果进行比较和验证. 本文的数值模拟与雾化制粉实验均以AlSi10Mg合金铸锭为原料, 并使用高压氩气作为雾化气体. 实验装置示意图如图2所示. 在雾化实验过程中, 采用机械泵和罗茨泵将熔炼室和雾化室的压力抽至50 Pa以下. 在熔炼之后, 向熔炼室中充入高压氩气, 熔炼室中的高压气体作用于熔体上表面并对熔体流动起驱动作用. 雾化室连接风机, 使雾化室内压力低于0.1 MPa, 始终保持熔炼室和雾化室的压力差. 熔体通过陶瓷导流管被细化为直径小于2 mm的液柱, 之后从导流管中流出, 直接通入De Laval喷嘴窄喉部, 利用De Laval喷嘴内部超音速气流直接雾化金属熔体, 如图1所示. 随后熔体在雾化气体流场中经历一次破碎和二次破碎变为小液滴, 并在下落过程中快速冷却, 最终凝固为金属粉末.
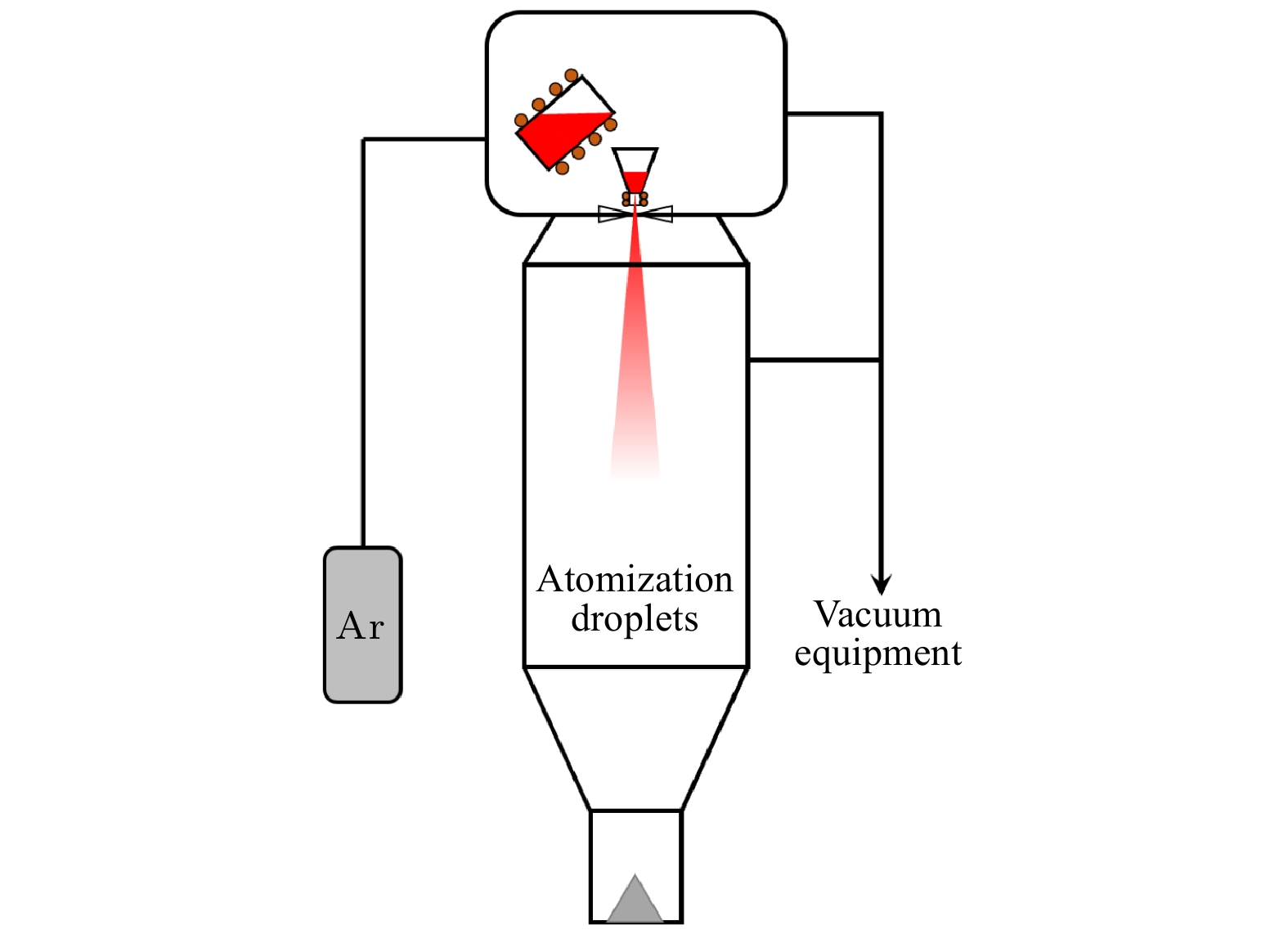图 2 自主设计的气雾化设备示意图Figure2. Schematic diagram of home-made gas atomization equipment.
本文采用Nova Nano 450场发射扫描电子显微镜(field emission scanning electron microscope, FESEM)研究了气雾化AlSi10Mg粉末的表面形貌, 使用LEICA DM 6000M金相显微镜观察了球形粉末横截面的金相组织, 使用激光粒度分布仪Malvern 3000统计气雾化粉末的粒度分布, 使用JHY-1002霍尔流速计测试粉末流动性, 并采用X射线断层扫描计算机重构(X-ray computed tomography, XCT)统计球形度以及空心粉末占比.
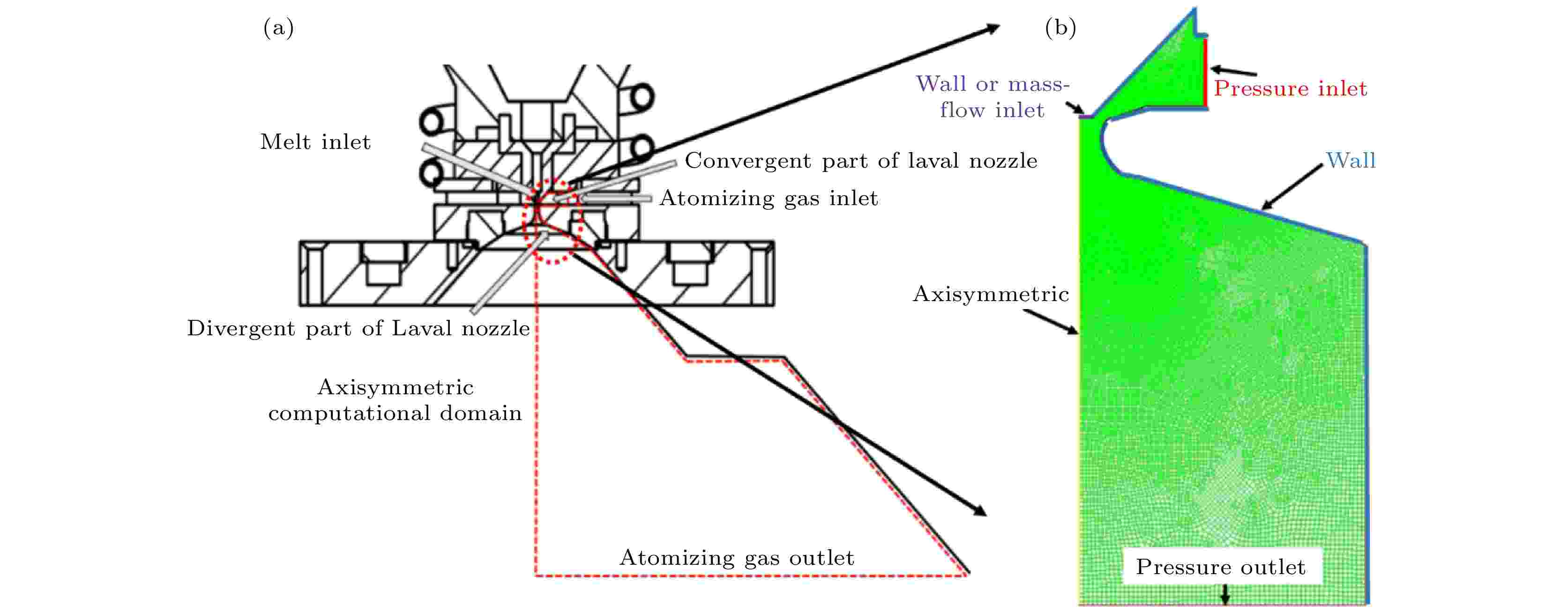图 3 (a)层流气体雾化喷嘴系统及流场结构示意图; (b)气体单相计算域、网格划分及边界条件Figure3. (a) Schematic of the nozzle system and flow field structure in the laminar flow gas atomization; (b) computational domain and mesh grid of single-phase, and primary atomization with boundary conditions.
2
3.1.单相雾化气体流场模拟
如图3(b)所示, 在单相气体流场模型中, 将导流管出口的边界条件设置为壁面, 将雾化室出口的边界条件设置为压力出口. 同时在网格划分时对导流管周围进行网格细化, 以提高模拟精度.单相气体流场模拟的控制方程如下所示. 其中连续性方程为
在单相气体流场的模拟中, 高压雾化气体设定为氩气, 计算了五种不同进气条件下的气体流场, 具体压力条件如表1所列. 迭代时间步长为10–6 s, 为保证流场稳定, 需迭代100000步. 使用隐式二阶迎风离散格式的瞬态求解器求解偏微分方程.
| 参数 | 数值 | ||||
| 入口压力/MPa | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
| 出口压力/MPa | 0.1 | ||||
表1单相流模型的模拟参数
Table1.Simulation parameters of the single-phase flow model.
2
3.2.一次雾化两相流模拟
熔体通过导流管时的流动速度由熔炼室与雾化室之间的压力差和液态金属的流体静压力决定. 为了研究雾化压力对一次雾化过程的影响, 假设雾化过程中熔体流动速率恒定. 根据液态金属和雾化气体的实际流动情况, 在一次雾化两相流模型中, 将收缩部分前端边界条件设置为压力入口, 将导流管出口处边界条件设置为质量流入口. 其余边界条件与单相流模型相同(见第3.1节).对于一次雾化, 采用耦合水平集-体积分数法(CLSVOF)与标准k-ε湍流模型相结合的方法进行研究(见(4)式和(5)式). CLSVOF方法将流体体积法(VOF)与水平集方法(LS)相结合, 克服了VOF法计算界面曲率时精度低及LS法存在的质量泄漏问题[29], 具有较高的界面跟踪精度和较好的质量守恒性, 且计算复杂度低, 分辨率高. 模拟一次雾化两相流使用的控制方程如下:
采用两步法模拟了一次雾化的两相流. 在对单相气流进行计算并使流场稳定后, 将金属熔体引入雾化气流中. 金属材料选用AlSi10Mg合金, 其特性参数如表2所列. 一次雾化两相流模拟的具体边界条件如表3所列.
| 材料 | 参数 | 数值 |
| AlSi10Mg | 比热容/(J·kg–1·K–1) | 871 |
| 密度/(kg·m–3) | 2719 | |
| 黏度/(kg·m–1·s–1) | 0.0135 | |
| 导热系数/(W·m–1·K–1) | 202.4 | |
| 表面张力/(N·m–1) | 0.854 | |
| Ar | 比热容/(J·kg–1·K–1) | 520.64 |
| 导热系数/(W·m–1·K–1) | 0.0158 | |
| 黏度/(kg·m–1·s–1) | 2.125 × 10–5 |
表2数值模拟中使用的AlSi10Mg合金和氩气的特性参数[30]
Table2.Properties of AlSi10Mg alloy and argon used for numerical simulation[30].
| 参数 | 数值 |
| 入口压力/MPa | 2.0 |
| 出口压力/MPa | 0.1 |
| 质量流量/(g·s–1) | 20 |
| 熔体初始温度/K | 1073 |
表3一次雾化模拟参数
Table3.Simulation parameters of primary atomization.
2
3.3.二次雾化的两相流模拟
一次雾化之后, 细丝或液滴状的熔体在雾化气流的作用下继续发生破碎, 即发生二次雾化. 在对二次雾化机理的探索过程中, 首先研究了液滴状熔体的破碎, 其次研究了细丝状熔体的破碎. 为了获得具有普遍代表性的二次雾化机理, 需要根据韦伯数计算不同尺寸液滴的破碎可能性. 经典的二次雾化机理研究是基于雾化气流与一次雾化后不同直径液滴之间的速度差进行的.在二次雾化的两相流模拟之前, 先推导出一次雾化后不同尺寸液滴的飞行速度. 对于雾化气流中的加速液滴, 受力平衡由阻力、重力和浮力组成, 如图4所示. 阻力为
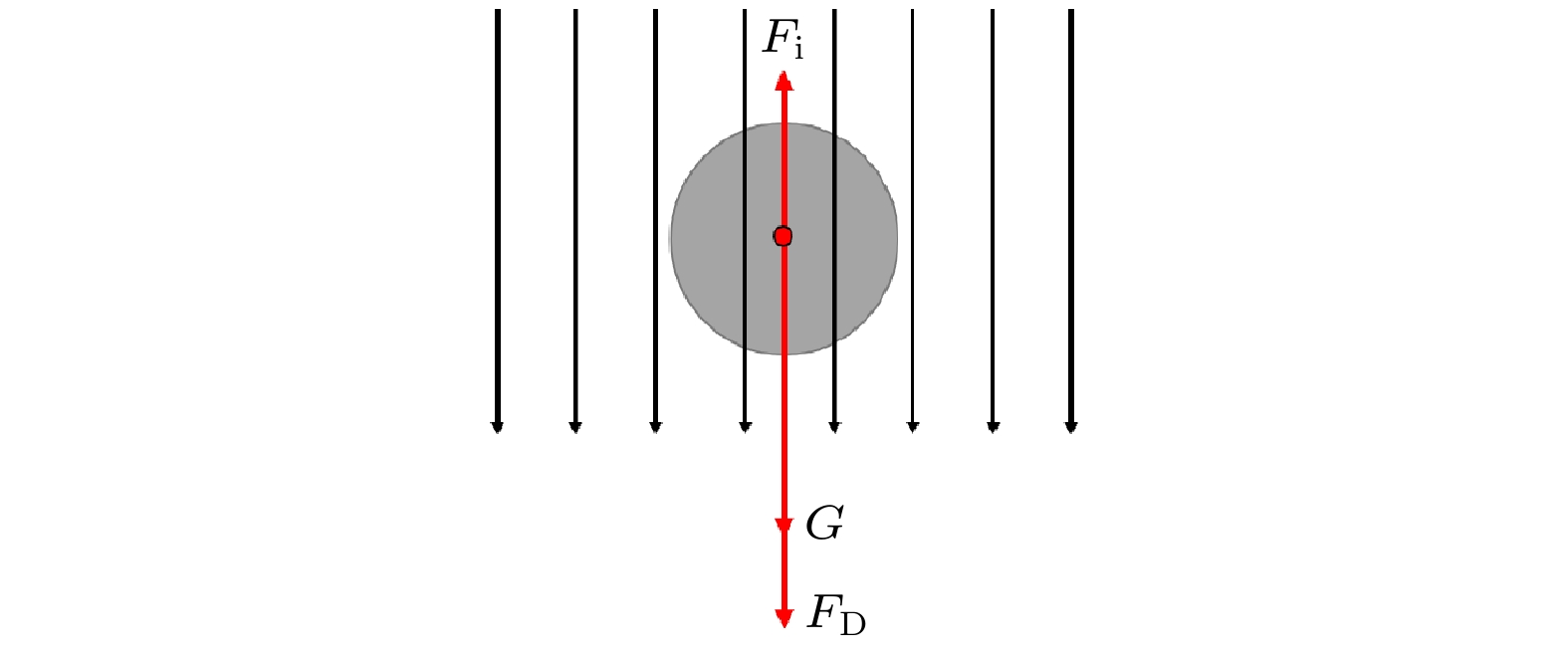图 4 液滴飞行过程中受力平衡示意图Figure4. Schematic diagram of the force balance on the in-flight droplets.
二次雾化的二维模型如图5所示. 模型的左边界设置为速度入口, 其余边界设置为自由边界条件. 将液滴看作牛顿流体, 具有近似线性的应力应变关系. 对二次雾化的整个计算网格也进行了改进, 以捕捉二次雾化产生的子液滴的形貌, 网格尺寸最小约为10 μm. 将CLSVOF模型((6)—(10)式)与标准k-ε湍流模型((4)式, (5)式)相结合, 对二次雾化过程进行数值模拟.
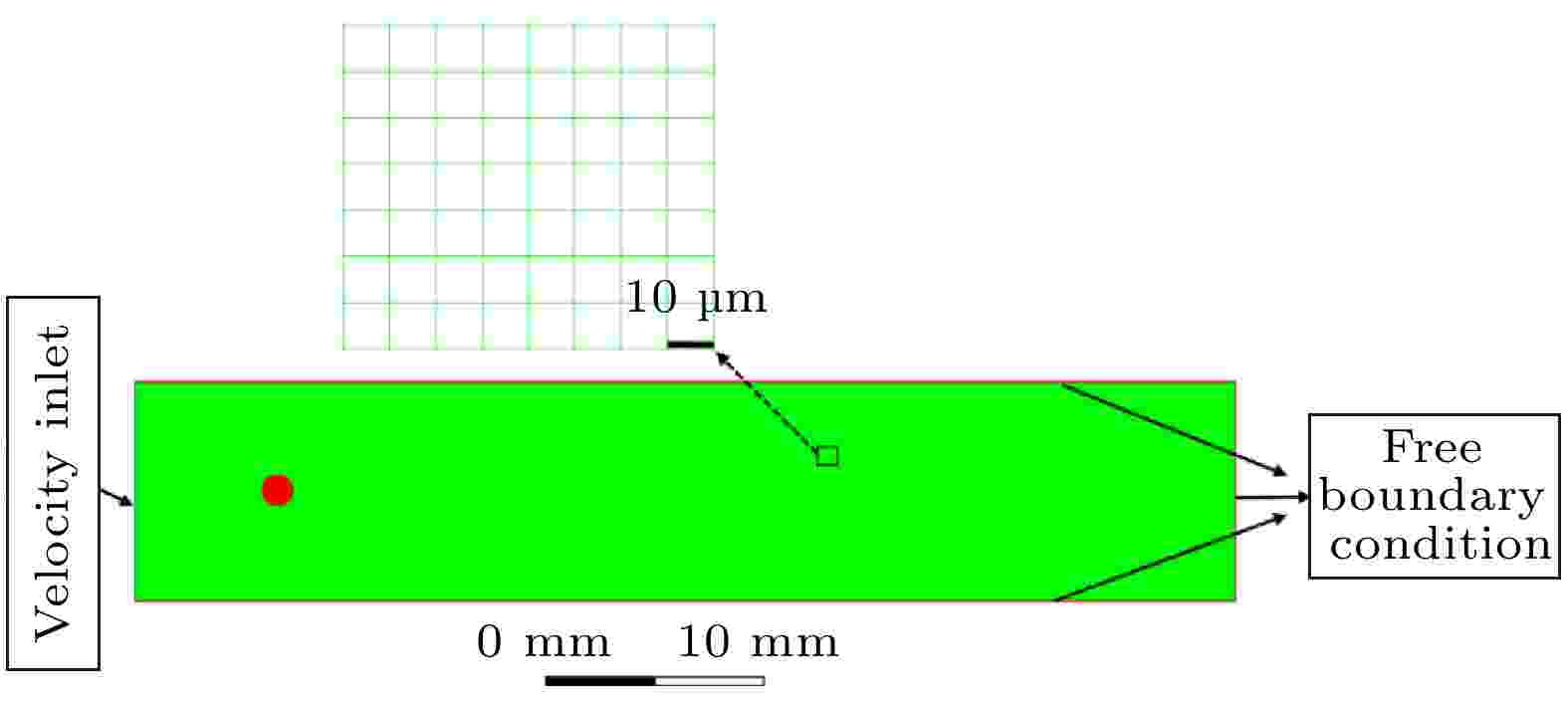图 5 二次雾化数值模拟的计算域、网格和边界条件Figure5. Computational domain, mesh, and boundary conditions for numerical simulation of secondary atomization.
为着重研究破碎过程, 研究中忽略了一次雾化后熔体与雾化气流之间的传热过程. 二次雾化过程数值模拟中所用材料的物理性质与一次雾化相同. 数值模拟参数见表4. 两种不同形状的熔体如球形熔滴和细丝状熔体, 在初始状态之前是分散的. 此外, 在模拟过程中还考虑了不同相之间的相互作用.
| 参数 | 数值 |
| 入口速度/(m·s–1) | 400 |
| 液滴直径/μm | 1000 |
| 丝状熔体尺寸/μm | φ50 × 500 |
表4二次雾化的数值模拟参数
Table4.Parameters for numerical simulation of the secondary breakup.
2
4.1.单相雾化气体流场的特征
对单相气体流场进行模拟, 研究了通过De Laval喷嘴的气流的速度分布和气体压力变化特征, 为熔体的破碎过程提供了重要参照. 如图6(a)所示, 矢量图描绘了2.0 MPa雾化气体压力下的气体流场速度分布. 图6(a)右侧为有效雾化区域的放大图, 加速时雾化气体的速度方向与喷嘴的对称轴成一定角度. 如图6(b)所示, 雾化气体流场呈“项链”状结构, 并带有斜激波的膨胀波团, 氩气气流产生的冲击波沿气流轴线方向逐渐减弱. 在De Laval喷嘴的收缩部分, 氩气气流的速度沿气流方向不断增加, 在De Laval喷嘴的扩张部分, 气体发生膨胀, 氩气气流加速到超音速, 气体速度矢量方向偏离轴向. 在达到最大速度后, 气体速度突然下降到最低值, 并在该位置产生一个驻点.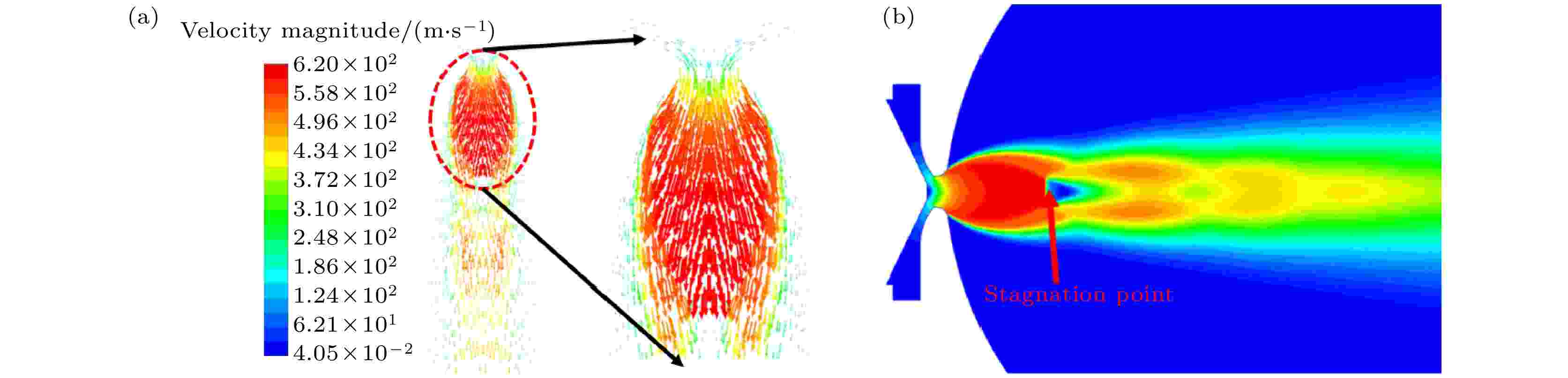
图 6 (a)入口压力为2.0 MPa时流场中的气体速度矢量; (b)入口压力为2.0 MPa时的雾化气体速度等值线Figure6. (a) Gas velocity vector depicting flow characteristics at pressure inlet of 2.0 MPa; (b) atomizing gas velocity contours at an inlet pressure of 2.0 MPa.
图7(a)显示了在不同雾化压力下, 气体速度沿喷嘴中心线的变化. 雾化气流逐渐加速到超音速峰值, 然后突然下降到谷点. 在谷点之后, 气体流速在波动中逐渐减小. 通过观察不同雾化压力下的雾化气流速度变化曲线, 可以发现初次加速阶段几乎重合. 由此可见, 增大雾化压力并不能显著地提高气流的加速度; 然而, 在较高的雾化气体压力下, 气体的加速距离较长, 并由此获得更好的加速效果, 气体速度峰值也相应升高. 气体压力沿喷嘴中心线的变化如图7(b)所示, 随着雾化压力的增大, 驻点下方一次负压区的范围逐渐向下扩展. 而雾化压力的增大对一次负压区的最小压力值影响不大.
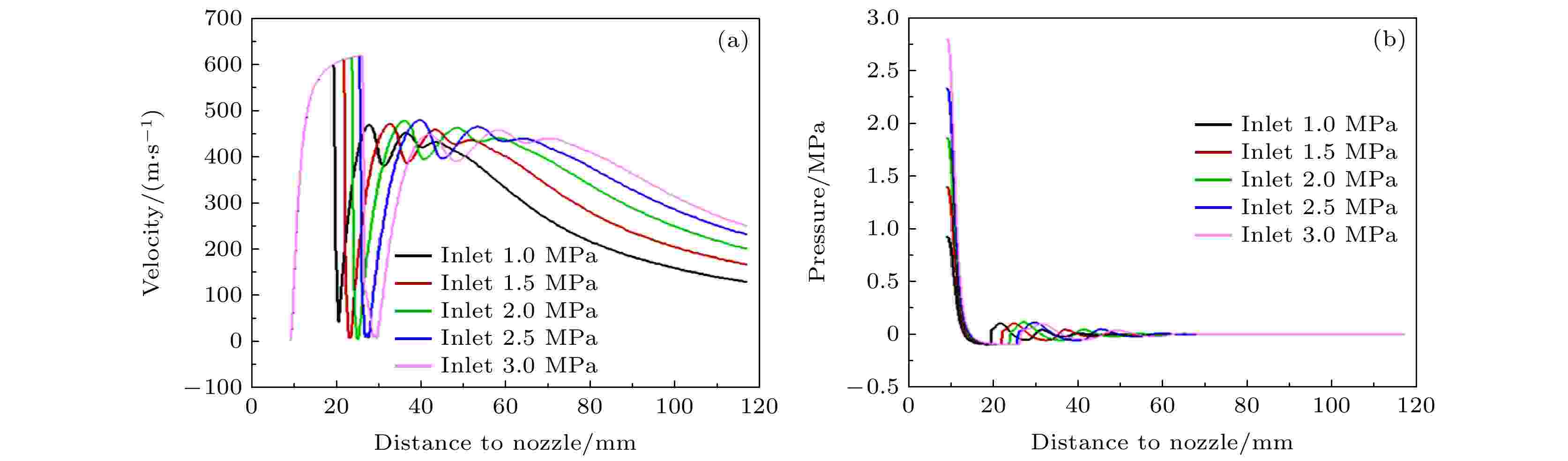图 7 气体流场特性 (a)不同入口压力下沿喷嘴中心线的气体速度曲线; (b)不同入口压力下沿喷嘴中心线的气体压力曲线Figure7. Gas flow field characteristics: (a) Gas velocity curve along nozzle center-line under different inlet pressures; (b) gas pressure curve along nozzle center-line under different inlet pressures.
2
4.2.一次雾化过程及机理
在气体雾化全流程模拟过程中, 一次雾化是连接雾化气体单相流场和二次雾化的中间环节. 研究雾化气流与熔体的相互作用, 特别是熔体通过喷嘴窄喉部分时的速度和形态的变化, 是揭示层流气体雾化机理的关键. 本节对一次雾化气液两相流进行了研究以揭示氩气气流和金属熔体之间的相互作用机制. 如第4.1节所述, 在De Laval喷嘴的扩张部分, 雾化气体迅速减压并加速至超音速状态. 同时, 金属熔体在重力、熔体静压和熔化室内高压气体压力的共同作用下流出导流管, 并与雾化气流发生相互作用.图8显示了金属熔体与氩气气流共同通过De Laval喷嘴时的形态变化. 根据熔体的形态特征, 将一次雾化过程分为初始阶段和稳定阶段. 如图8(a)所示, 熔体受雾化气流的影响, 在初始阶段向喷嘴的轴向收敛, 熔体流尺寸得到细化. 熔体向下输送过程中, 在喷嘴最窄部分, 首先经历一个短暂的稳定期(0.10至0.12 ms), 随后在继续下落过程中, 熔体流受雾化气流干扰, 出现局部紊乱(如图8(a)中“a-1”处所示), 并且在通过最窄喉部位置, 进入De Laval喷嘴扩张部分之后, 在膨胀加速气体的剪切力作用下发生破碎(如图8(a)中“a-2”处所示).
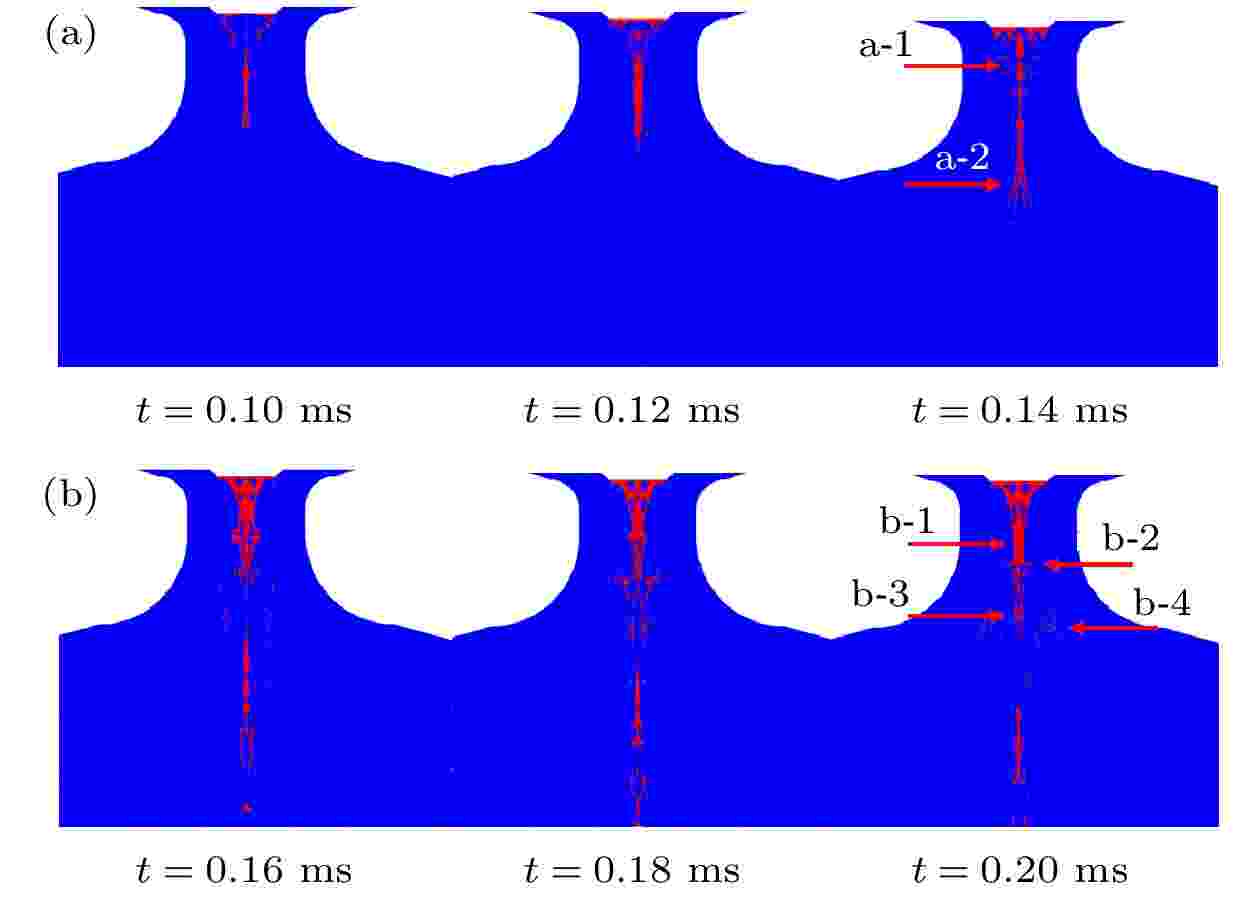图 8 De Laval喷嘴的一次雾化过程 (a)初始阶段; (b)稳定阶段Figure8. Primary atomization process with the De Laval nozzle: (a) Initial period; (b) stable period.
随着熔体的连续流动, 一次雾化进入稳定期, 熔体与气流的相互作用在喷嘴最窄处得到加强. 在轴对称加速气流作用下, 金属熔体快速通过喷嘴最窄部位, 如图8(b)所示, 当金属熔体从导流管流出时, 立即受到高压雾化气体压缩作用而发生变形, 圆柱形熔体的直径逐渐减小. 图9(a)为雾化制粉实验后得到的导流管出口处凝固金属的形态示意图, 可以看到, 金属熔体从内径为2 mm的导流管进入De Laval喷嘴后呈锥形, 且其直径仅有1 mm, 这证实了上述模拟中熔体直径变小的现象, 说明熔体尺寸在雾化前就已得到明显细化, 具有低维度的特征, 有利于熔体在后续过程中破碎成更小尺度的液滴.
图 9 (a) 导流管出口处的凝固熔体; (b) De Laval喷嘴扩张段一次雾化后凝固熔体的形态Figure9. (a) Solidified melts at the outlet of the delivery tube; (b) morphology of solidified melts after primary atomization at the divergent section of De Laval nozzle.
在一次雾化稳定阶段, 金属熔体在De Laval喷嘴喉部出现层流状态, 如图8(b)中“b-1”所示. 为了进一步分析熔体在喷嘴窄喉部呈现层流状态的形成机理, 对De Laval喷嘴窄喉处的雾化气体和金属熔体两相流进行了放大, 如图10(a)所示. 从图10(a)可以看到, 熔体在喷嘴窄喉处的流动方向几乎与雾化气流平行, 金属熔体在被气流加速的同时受到气体的剪切力发生破碎. 离开最窄喉部截面后, 随着雾化气体压力的降低和金属熔体压力的增加, 熔体变得不稳定(如图8(b)中“b-2”所示). 相较于初始阶段, 熔体转变为丝状或片状的趋势更为明显(如图8(b)中“b-4”所示), 在熔体流的中间区域可以观察到不规则的断裂特征(如图8(b)中“b-3”所示). 图9(b)为De Laval喷嘴扩张段凝固熔体的形态, 如图中的红色箭头所示, 喷嘴出口周围的金属呈现细丝状; 如黑色箭头所示, 金属熔体在喷嘴窄喉下方以较大的液滴形式存在. 图11为雾化制粉实验后得到的不规则薄片状和不规则棒状金属碎片, 这些碎片的形成是因为一部分金属熔体在喷嘴扩张段受到气流的膨胀加速作用而脱离了熔体主体(如图8(b)中“b-4”所示), 在随后的下落过程中, 由于偏离了主雾化区, 未发生二次雾化而直接冷却凝固, 形成粗大的不规则金属碎片, 因此保留了一次雾化后的形貌. 这为后续二次雾化的研究提供了重要参考.
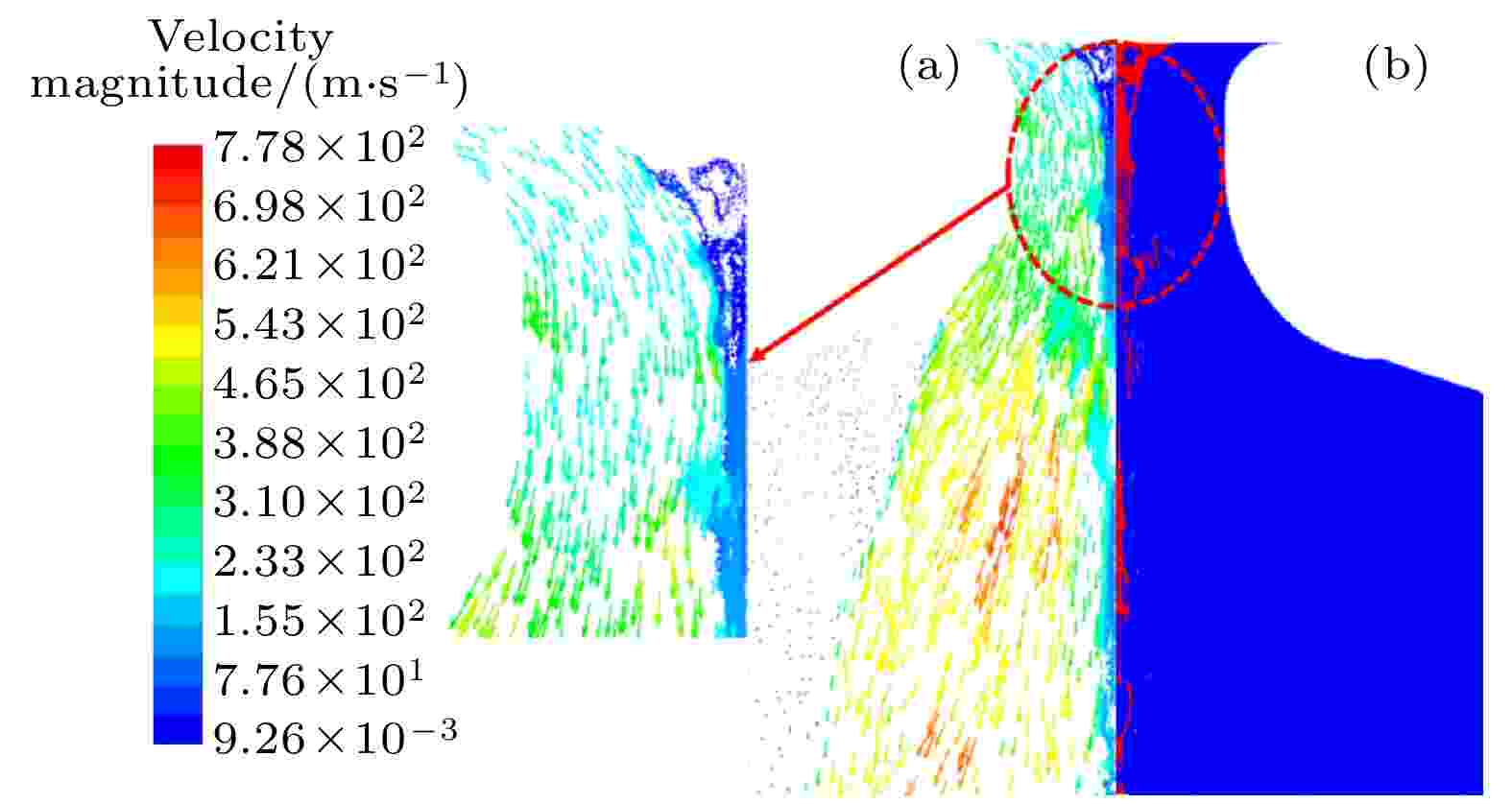图 10 (a) 气液两相速度矢量; (b) 在t = 0.20 ms下一次雾化中熔体形态的比较Figure10. Comparison of (a) two-phase velocity vector; (b) morphology of melt in primary atomization at t = 0.20 ms.
图 11 大液滴形态 (a)不规则薄片; (b)不规则棒状Figure11. Morphology of huge droplet: (a) Irregular flake; (b) irregular bar.
本实验采用的气雾化方法与传统的雾化方法不同, 熔炼室中的高压雾化气体直接作用于熔体的上表面, 推动熔体流过导流管, 从而加大了熔体进入De Laval喷嘴的流速. 此外, De Laval喷嘴收缩段的雾化气流对熔体的细化会减小一次雾化前金属熔体的尺寸. 金属熔体的提前细化有助于减小一次雾化的液滴尺寸. Khatim等[22]通过两相流模拟发现, 在De Laval喷嘴的收缩部分, 熔体在雾化气流的作用下明显得到细化, 这与本文的研究结果一致. 综上所述, 在一次雾化过程中, 熔体中位于液柱外围的部分被剥离, 形成较大的不规则碎片, 而液柱核心部分则破碎成较大的液滴. 一次雾化中的高压驱动与熔体独特的小尺寸特性, 有效地提高了雾化效率和气体利用率.
2
4.3.粒度对一次雾化液滴加速行为和表面张力的影响
金属熔体经历一次雾化破碎后, 液柱核心部分的较大液滴在表面张力的作用下迅速形成球形液滴, 随后发生二次雾化[33,34], 而液柱外围的一些不规则熔体则以细丝的形式从外围脱落. 由于动态不稳定性, 熔融液滴在气流中破碎成更小的液滴, 最后凝固成金属粉末. 根据二次雾化理论, 只有在液滴和雾化气流之间的相对速度足够高时, 才能发生有效破碎[35]. 所以在对二次雾化过程进行数值研究之前, 需要先研究不同尺寸液滴的加速行为. 如图12所示, 雾化气流中的液滴加速行为受液滴尺寸的影响. 不同尺寸的液滴在同一雾化气流中加速时, 小液滴比大液滴具有更好的加速效果. 所以, 大液滴与气流的相对速度高于小液滴与气流的相对速度.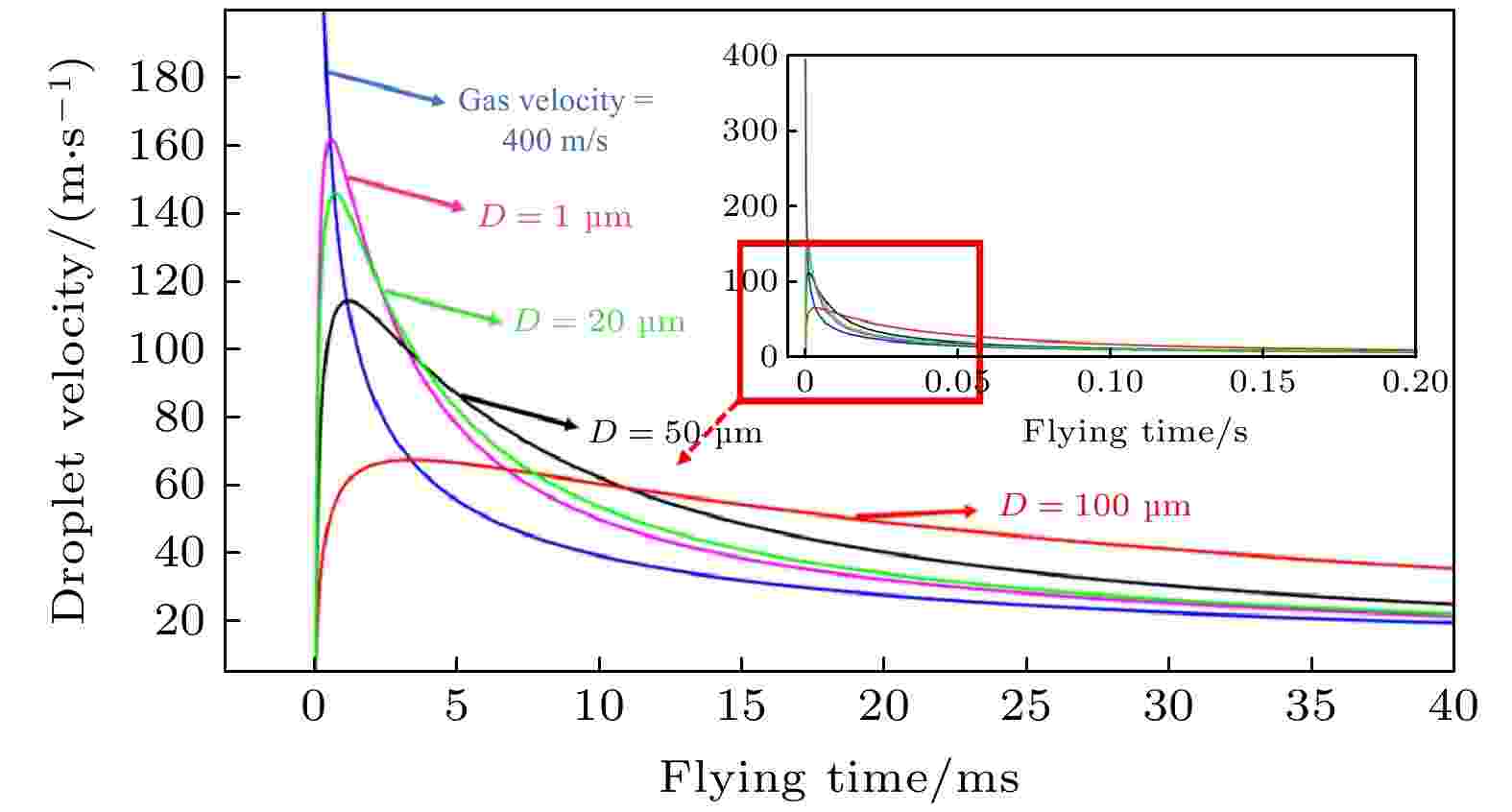
图 12 不同尺寸液滴在气流中的速度随飞行时间的变化Figure12. The velocity of droplets with different sizes in gas flow as a function of flying time.
除相对速度外, 液滴的二次雾化还受液滴表面张力的影响. 同一材料液滴的表面张力直接受到液滴温度的影响. 一次雾化液滴的冷却速度受到液滴尺寸的影响. 液滴尺寸越大, 冷却速度越低[32,36]. 即与小液滴相比, 大液滴具有更低的冷却速率和更高的温度, 也就具有更小的表面张力. 由以上分析可知, 在相同的流场条件下, 大液滴比小液滴具有更高的温度和更大的相对速度. 因此, 大液滴比小液滴更容易发生二次雾化.
2
4.4.二次雾化过程及机理
本文在一次雾化结果的基础上, 对二次雾化过程中的液滴和丝状熔体形貌演化分别进行了研究. 根据经典雾化理论, 一次雾化的熔体在流场中会发生二次雾化[14,37-39]. 在二次雾化数值模拟过程中, 气体流场的初始条件由图12中的液滴相对速度确定.在二次雾化过程中, 流体惯性和表面张力的平衡决定了熔滴的变形和破碎. 通常, 无量纲韦伯数(
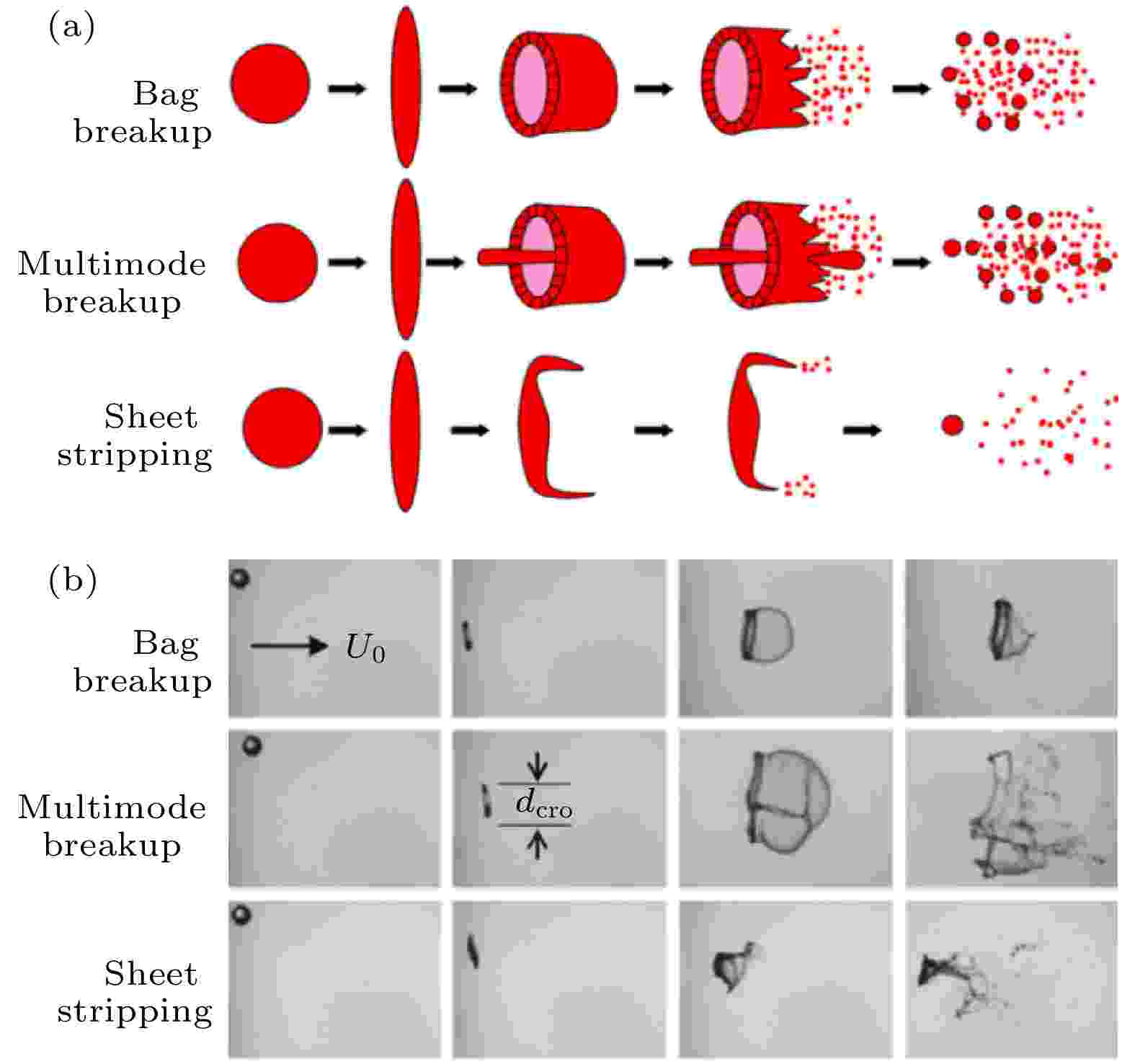图 13 (a)典型的液滴破碎模式[14]; (b)液滴破碎过程的阴影图像[38]Figure13. (a) Schematic diagram of typical droplet breakup modes[14]; (b) shadowgraph of droplet breakup process[38].
对于丝状熔体破碎的研究, 考虑了扩张(对称)扰动和弯曲(非对称)扰动, 如图14所示. 在扩张扰动模式下, 丝状熔体存在一个有对称曲张波的未扰动平面. 而在丝状熔体的弯曲扰动中, 自由表面的运动方向与曲张波相同[40,41].
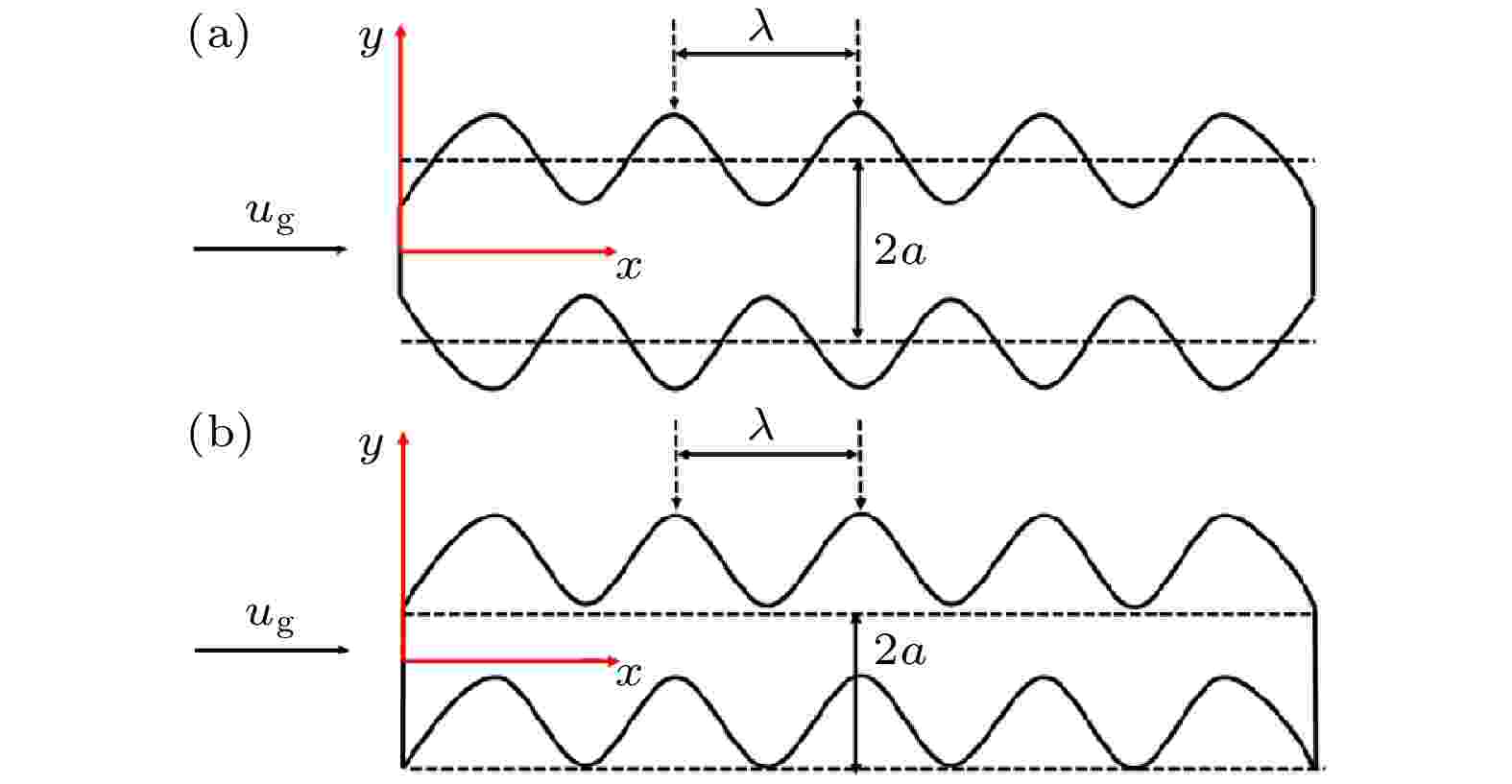图 14 丝状熔体的不同扰动模式 (a) 扩张(对称)扰动; (b)弯曲(不对称)扰动Figure14. (a) Dilatational (symmetric) disturbance; (b) sinuous (asymmetric) disturbance of liquid ligaments.
3
4.4.1.球形熔滴的破碎过程
如图15所示, 由两相流模拟获得了液滴破碎过程的时间序列图像. 从图15可以看到在t = 0至t = 0.15 ms的时间内, 液滴在变形过程中保持对称. 然而, 从t = 0.2 ms到t = 0.4 ms的时间内, 对称的液滴形状被“神经元”形状所取代. 三个“神经末梢”状液滴在气流的作用下继续破碎, 而中央区域没有发生明显破碎. 气流和液滴之间的相互作用决定了液滴的分解方式.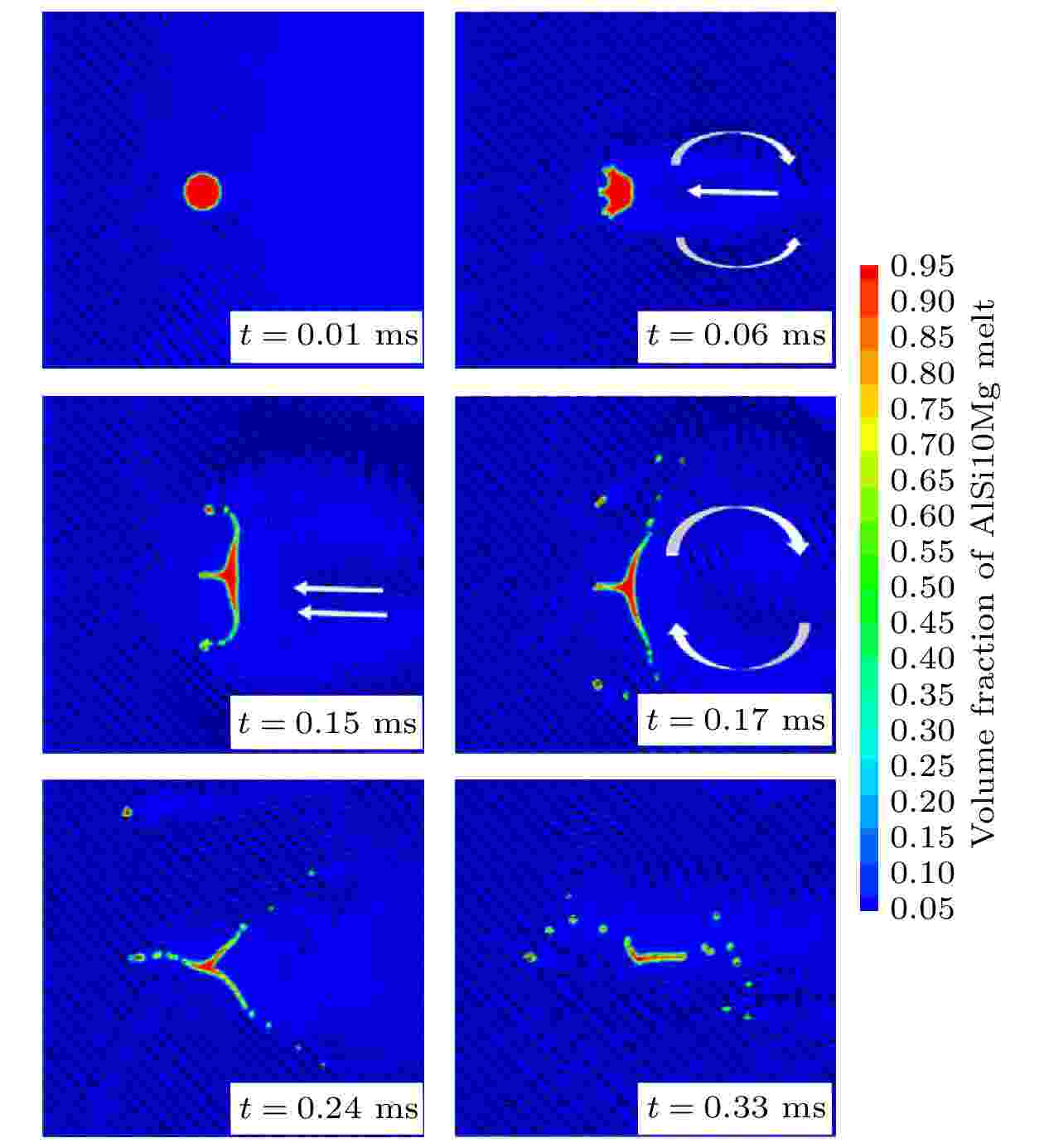
图 15 液滴破碎的不同阶段及雾化气流的运动规律Figure15. Atomizing gas streamline moving with droplet at different breakup stages.
图15显示了在不同破碎阶段围绕液滴移动的气体流线, 白色箭头表示气体流场的大小和方向. 在破碎开始时(t = 0.01 ms), 可以观察到液滴左侧的气流速度远高于液滴右侧的气流速度. 当t = 0.06 ms时, 液滴左侧表面发生明显的Rayleigh-Taylor(R-T)不稳定性变形. Dai和Faeth[42]观察并研究了表面波变形机制, 如图16(a)所示. 在液滴尾部表面后方出现两股对称的旋转回流. 尾部表面回流和“R-T”变形使液滴逐渐变形为不规则的“平顶伞”形状. 从t = 0.06 ms到t = 0.15 ms, 液滴形状沿气流方向变薄, 液滴变成类似数字“3”的形状. Yang等[43]使用VOF模型进行数值模拟, 从阻力系数、
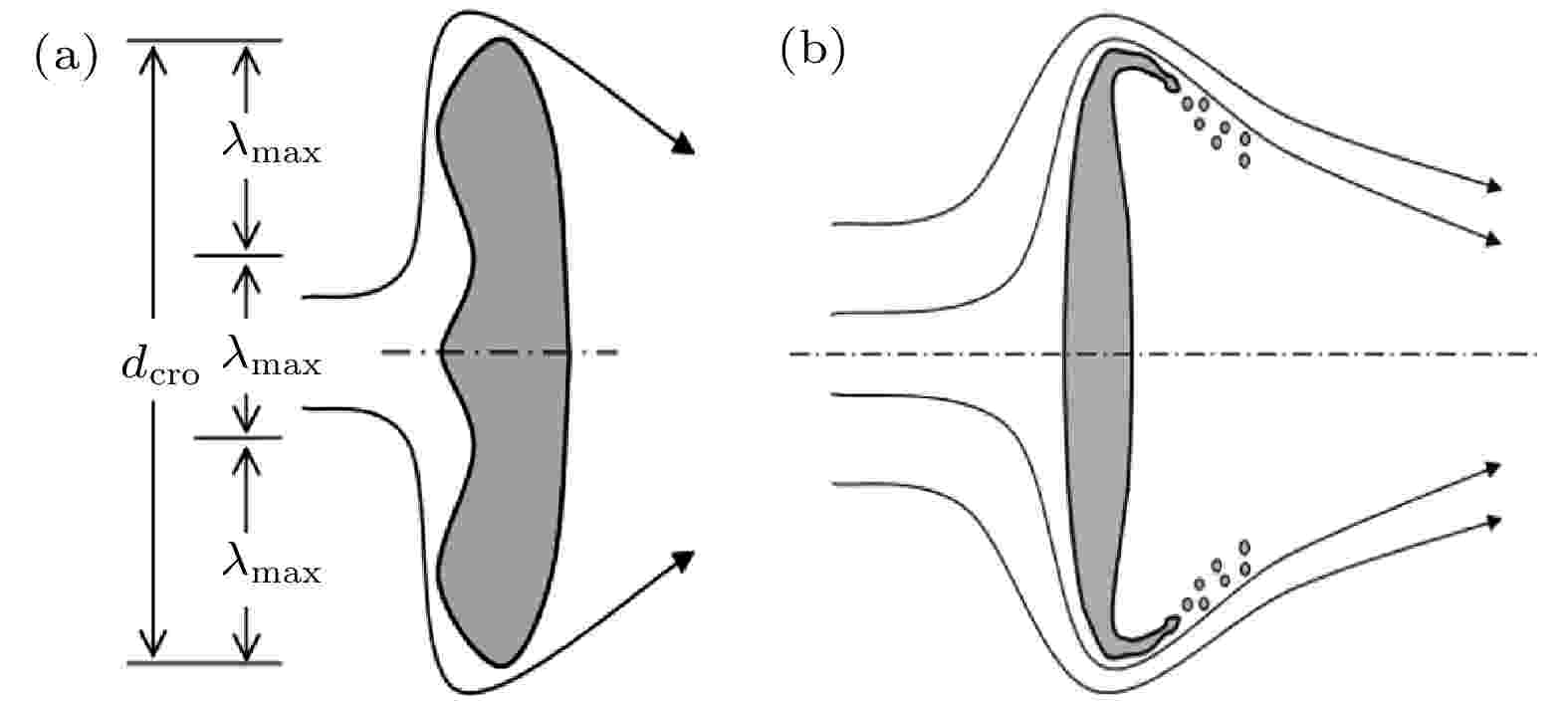图 16 (a) Rayleigh-Taylor不稳定变形; (b) Sheet-Thinning破碎机理[37,43]Figure16. (a) Rayleigh-Taylor instability deformation; (b) Sheet-Thinning breakup mechanism[37,43].
在t = 0.17 ms时, 两股对称的旋转回流汇入一个较大的旋转回流区, 使液滴前后表面产生压力差并导致液滴发生形变. 除了上下部分的弯曲外, 中间部分还出现了类似“3”形状液滴的破碎过程. 随着“S-T”破碎的继续进行, 液滴逐渐变成新月形. 如图17所示, 雾化实验中得到的空心粉末证明了二次雾化的这一过程. 从t = 0.24 ms到t = 0.33 ms的时间内, 在高速氩气气流的加速作用下, “S-T”破碎产生的子液滴逐渐远离主液滴. 在t = 0.24 ms时, 液滴呈三角形, 粉末形貌如图17(b)所示. 随着子液滴从主液滴上剥离, 主液滴的体积逐渐减小, 三个“神经末梢”逐渐消失, 如图15中t = 0.33 ms时的图像所示.
图 17 (a) 层流气流雾化粉末的截面特性; (b) 三角形粉末的扫描电镜图像Figure17. (a) Cross-section characteristics of laminar flow gas atomized powders; (b) SEM images of triangular powder.
3
4.4.2.丝状熔体的破碎过程
如第4.2节中所述, 液柱在一次雾化过程中, 由于平行雾化气流的强大剪切力, 除了破碎成液滴外, 液柱的外围以细丝或液膜的形式剥落. 图18显示了熔融丝状韧带出现扰动和解体的过程. 从图18可以看到在t = 0.08 ms时由于气流的扰动, 丝状熔体出现了曲张波扰动. 这种扰动模式会使熔体韧带变薄, 最终由于气流的作用而破碎成小液滴. 当变形波动增长到一定程度时, 液滴会出现长尾, 由于快速凝固, 液滴在表面张力的作用下不能完全变为球形. 这种情况下, 在二次雾化凝固之后会形成纺锤形粉末. 如图19中红色箭头所示, 气雾化实验得到的粉末中有少部分呈现出带有尾部的不规则形状, 这主要由不稳定的丝状熔体容易在曲张波的波谷处发生破碎而形成的.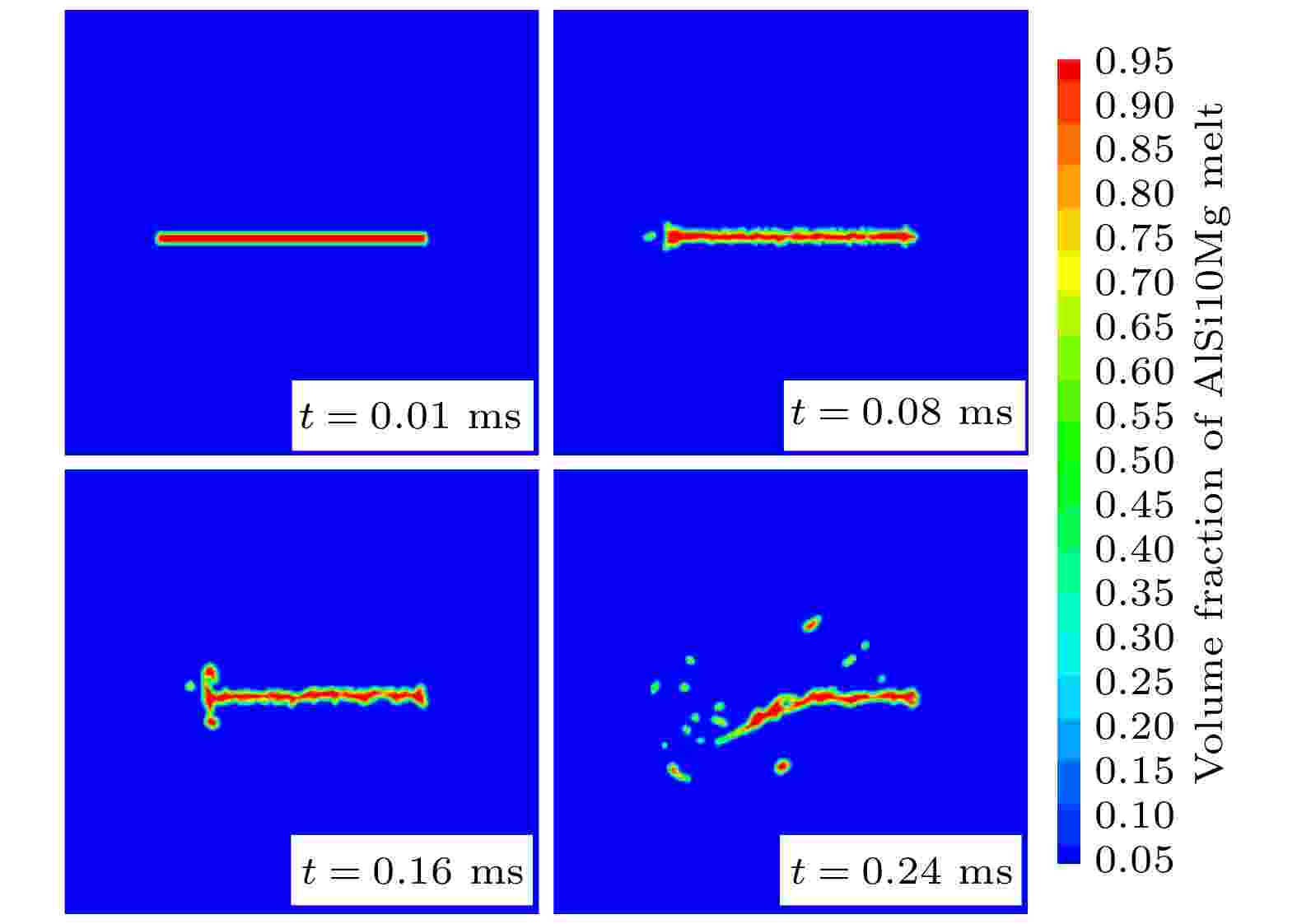
图 18 熔融韧带的二次雾化过程Figure18. Secondary atomization process of melt ligaments.
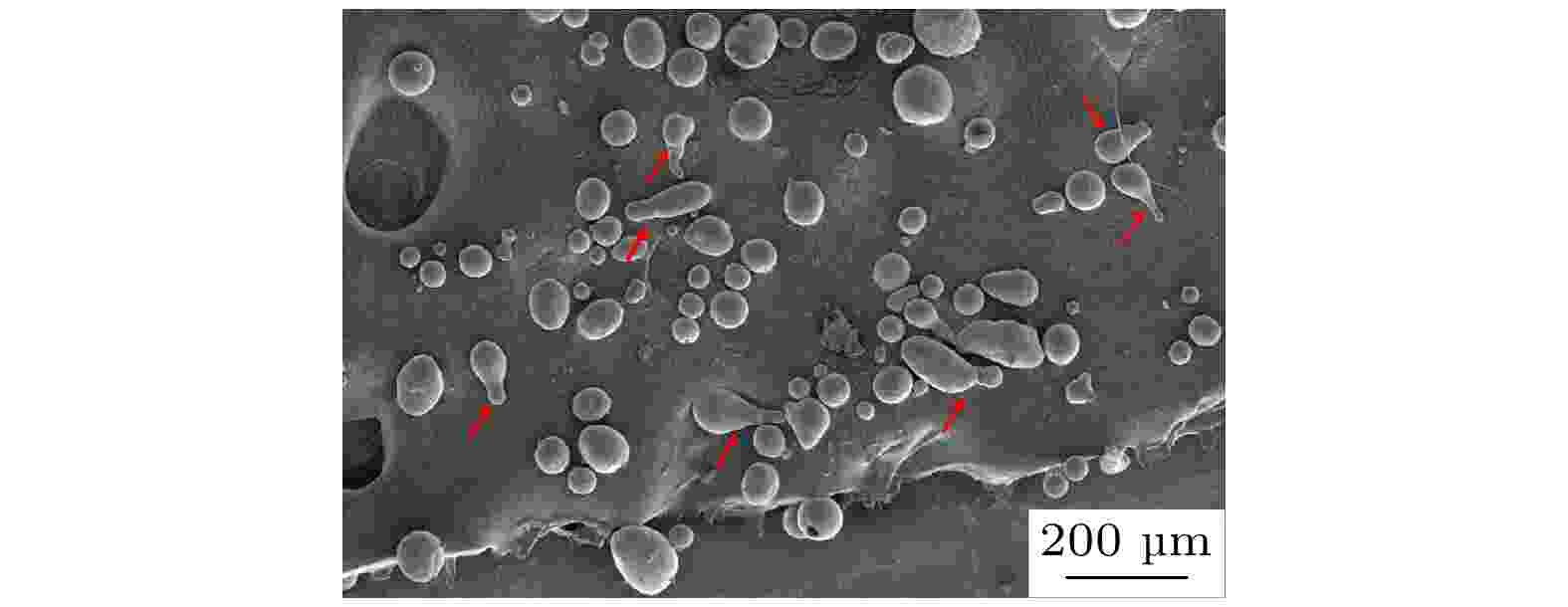图 19 层流气体雾化制备粉末的扫描电镜图像Figure19. SEM image of powders prepared using laminar flow gas atomization.
2
4.5.层流气雾化制粉实验结果
基于上述数值模拟结果, 采用自主设计的层流气雾化制粉设备进行了AlSi10Mg粉末的气雾化制备实验. 基于最高承载条件, 所采用雾化气体压力为2 MPa, AlSi10Mg金属熔体的初始温度为800 ℃, 过热度为150 ℃, 导流管内直径为2 mm, 均与数值模拟对应参数一致. 随后, 对实验制得AlSi10Mg粉末的各项性能进行了表征. 如图20(a)所示, 首先使用激光粒度仪对粉末的粒径分布进行统计, 并得出粉末的粒度分布曲线. 统计结果表明, AlSi10Mg粉末的D50为54.3 μm, 适用于激光选区熔化工艺的细粉(粒径小于53 μm)收得率为48.7%, 而传统的气雾化工艺制备的AlSi10Mg粉末细粉收得率不高于35%, 优化后的耦合压力气体雾化法细粉收得率也仅为40%[44], 可见层流气雾化技术相较于传统气雾化工艺显著提升了粉末的细粉收得率. 此外, 约90%的粉末集中在30—100 μm, 粒度分布范围较窄, 证明了层流气雾化可以有效地控制并得到更窄的粉末粒径分布. 使用霍尔流速计对AlSi10Mg粉末流动性进行了测试, 得到粉末的霍尔流速为56.51 s/50 g, 粉末流动性得到显著提高. 使用XCT技术对上述层流气雾化AlSi10Mg粉末进行检测. 基于XCT技术的计算机图像处理及统计表明, 上述粉末中空心粉数量仅占粉末总数的0.39%, 同时重构图像表明粉末整体球形度较好, 统计显示粉末平均球形度为0.92. 具体的球形度统计分布如图20(b)所示.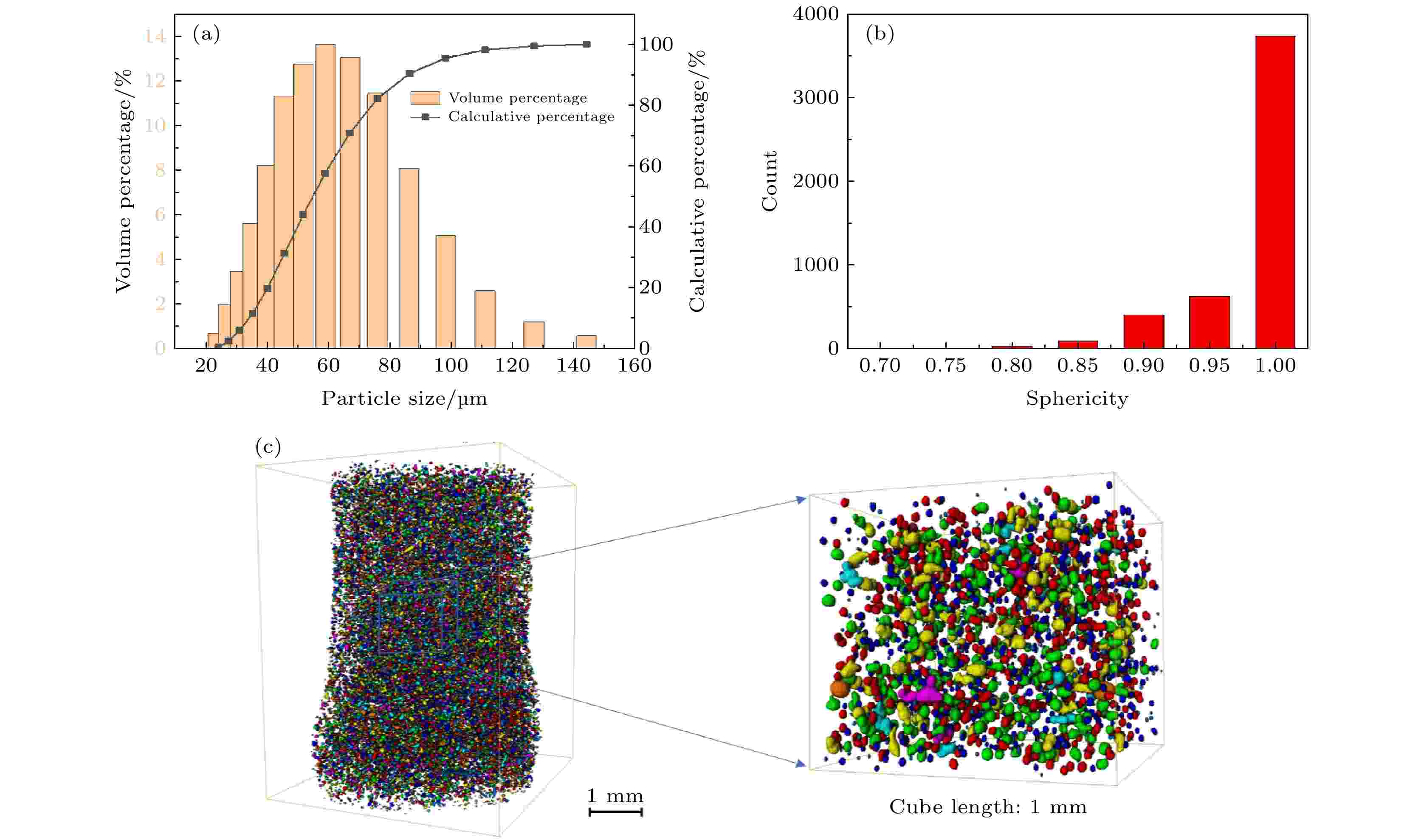
图 20 AlSi10Mg粉末表征 (a) 粒径分布; (b) 球形度; (c) XCT三维重构形貌图Figure20. Characterization of AlSi10Mg powders: (a) Particle size distribution; (b) sphericity; (c) 3D surface view reconstructed by XCT.
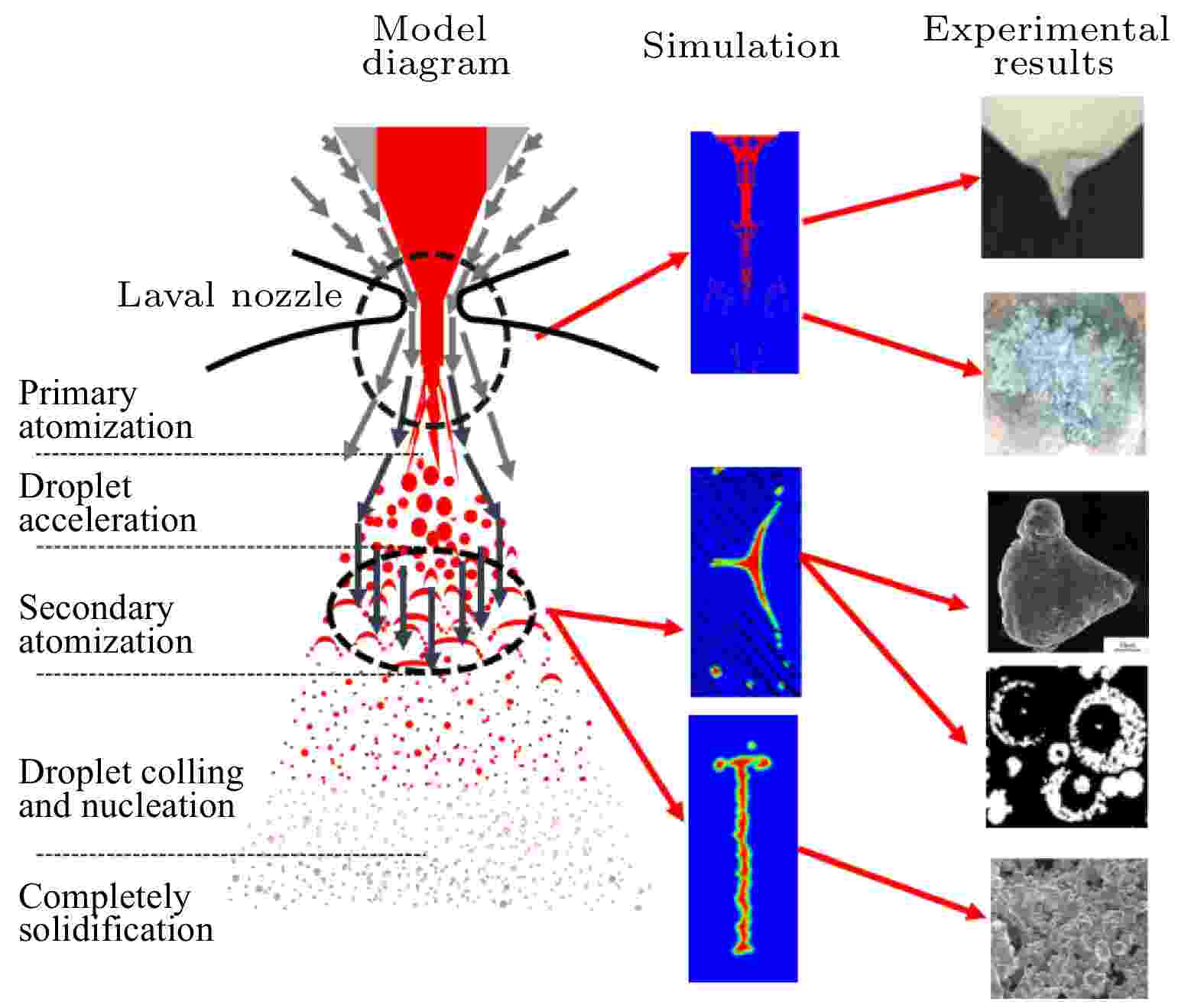图 21 De Laval喷嘴层流雾化过程Figure21. Processes of laminar flow atomization with De Laval nozzle.
需要指出的是, 在本研究中, 氩气气体流场中的温度变化并不是精确耦合的. 但是, 依然能够清楚地揭示金属熔体雾化的全过程及其机理. 本文通过数值模拟和实验分析, 对层流气体雾化过程中的雾化气体流场、一次雾化和二次雾化机理以及最终的粉末颗粒形态进行了系统性研究, 这些结果也为层流气雾化制粉技术的应用和具体工艺提供了重要参考, 具体如下: 1)通过对不同雾化压力下的气体流场模拟结果可知, 增大雾化压力可以延长高速气流加速区的长度, 使气流获得更好的加速效果, 气体动能增加, 可以有效地提高熔体流的破碎率; 2)不规则层片状和不规则棒状粉末产生的主要原因是金属熔体仅发生一次雾化, 之后由于偏离出有效雾化区而未发生二次雾化, 所以增大雾化气体压力, 扩大初次雾化有效区域, 可以在一定程度上减少由于雾化不完全导致的此类不规则粉末数量; 3)在二次雾化阶段, 球形液滴“S-T”破碎形成的三角形粉末以及丝状熔体曲张波扰动形成的纺锤形粉末都是由于未完全球化形成的不规则粉末, 其机理是液滴的球化时间比凝固时间长, 因此提高初始熔体的过热度, 延长液滴的凝固时间使其充分球化是减少此类不规则粉末的有效方法.
1)流场结构呈“项链”状结构, 雾化气体在De Laval喷嘴的特殊结构中被迅速加速至超音速. 增大雾化压力并不能显著提高气流的加速度, 但会延长气流加速区的长度, 增大气流速度峰值, 提高气体动能.
2) De Laval喷嘴收缩段气流对熔体的细化会导致一次雾化前金属熔体的尺寸的减小. 金属熔体的提前细化有助于减小一次雾化的液滴尺寸.
3)当雾化压力为2.0 MPa时, 在一次雾化过程中液柱外围的熔体主要以丝状或韧带状形式剥离, 液柱核心部分以较大的球形液滴的形式继续破碎.
4)二次雾化过程中, 球形液滴主要是以Rayleigh-Taylor不稳定性变形模式和Sheet-Thinning破碎模式发生破碎的. 丝状熔体则主要以曲张波表面发生扰动从而引起波谷处破裂的方式进行破碎.
5)采用自主设计的层流气雾化制粉设备进行制粉实验, 得到的AlSi10Mg粉末流动性较好、球形度高、空心粉少, 且粒度分布较窄, 证明了层流气雾化制粉技术可以有效控制并得到较窄的粉末粒度分布.
6)数值模拟的结果表明, 提高雾化气体压力可以增大气体动能, 提高熔体破碎率, 在一定程度上减少层片状和不规则棒状粉末的数量; 此外, 提高初始熔体的过热度可以延长熔体凝固时间, 使其在凝固前充分球化, 减少三角形和纺锤形粉末等不规则粉末的产生.
| ${{\rho } }_{\rm{g} }$ | 气体密度 |
| t | 时间 |
| ${{u} }_{{i} }$ | $ {x}_{i} $方向上的速度分量 |
| ${{u} }_{{j} }$ | $ {x}_{j} $方向上的速度分量 |
| ${{\mu } }$ | 动力黏度 |
| ${{\tau } }_{{ij} }$ | 雷诺应力张量 |
| ${{S} }_{{i} }$ | 动量守恒方程的广义源项 |
| ${{S} }_{\rm{T} }$ | 粘性耗散函数 |
| T | 温度 |
| K | 热导率 |
| k | 湍流动能 |
| ${{\varepsilon } }$ | 湍流动能耗散率 |
| ${{G} }_{{k} }$ | 平均速度梯度引起的湍流动能k |
| ${{G} }_{\rm{b} }$ | 浮力产生湍流动能k |
| ${{Y} }_{\rm{M} }$ | 可压缩湍流中脉动膨胀 |
| ${\mu }_{{t} }$ | 湍流黏度 |
| ${{S} }_{{k} }$, ${{S} }_{{\varepsilon } }$ | 源项 |
| v | 速度矢量 |
| P | 压力 |
| ${{\tau } }$ | 粘性应力张量 |
| ${{\sigma } }$ | 表面张力 |
| $ \alpha $ | 体积相分数 |
| g | 重力加速度 |
| ${{F} }_{\sigma }$ | 体积表面张力 |
| ${{F} }_{\rm{D} }$ | 阻力 |
| ${{A} }_{\rm{d} }$ | 液滴最大截面积 |
| ${{p} }_{\rm{dg} }$ | 气体作用在液滴上的压力 |
| ${{u} }_{\rm{g} }$ | 气流速度 |
| ${{u} }_{\rm{d} }$ | 液滴速度 |
| ${{\mu } }_{\rm{g} }$ | 气体黏性系数 |
| ${{C} }_{\rm{D} }$ | 阻力系数 |
| d | 特征长度 |
| ${{\rho } }_{\rm{d} }$ | 液滴密度 |
| ${{V} }_{\rm{d} }$ | 液滴体积 |
| ${{Re} }$ | 雷诺数 |
| u | 特征速度 |
| ${{We} }$ | 韦伯数 |
表A1文中所用参数
TableA1.Parameters in the article.
