摘要: 针对软体机器人用水凝胶含摩擦斜向接触问题, 建立了接触力学数值模型, 分析了水凝胶软材料斜向接触时的局部接触大变形及摩擦效应等非线性行为. 基于超弹性材料本构, 推导得到了水凝胶的更新自由能函数. 给出接触计算策略, 数值计算了刚性球状压头正向接触水凝胶和斜向接触水凝胶两个算例, 讨论了经典Hertz接触理论的适用性以及不同摩擦系数对接触区应力分布和接触状态的影响规律. 计算结果表明, 水凝胶的材料非线性以及大变形引起的几何非线性使得经典Hertz接触理论不再适用; 斜向接触时, 摩擦系数的增大会导致水凝胶内部应力的重新分布, 表现为最大应力位置由接触面下方转移到接触表面上, 同时使水凝胶内部和表面出现两个主要高应力区. 此外, 研究还发现当摩擦系数较小时(
μ < 0.05), 水凝胶正向接触事件中所有接触点均处于静摩擦到滑动摩擦的极限状态, 而斜向接触事件中接触面的部分区域始终处于稳定静摩擦状态.
关键词: 水凝胶 /
大变形 /
斜向接触 /
摩擦 English Abstract Nonlinear frictional contact behavior of porous polymer hydrogels for soft robot Chen Kang Shen Yu-Nian Department of Mechanics and Engineering Science, School of Science, Nanjing University of Science and Technology, Nanjing 210094, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 11572157) and the Fundamental Research Fund for the Central Universities, China (Grant No. 30920021149)Received Date: 15 December 2020Accepted Date: 03 February 2021Available Online: 09 June 2021Published Online: 20 June 2021Abstract: Focusing on the oblique frictional contact problem of hydrogel for soft robot, a numerical contact model is developed to analyze the nonlinear behaviors including local contact large deformation and friction effect of hydrogel soft material during oblique contact. Based on the constitutive relation of hyperelastic material, the updated free energy function of hydrogel is derived. The contact algorithm is given to compute the contact responses of both collinear contact example and oblique contact example. The applicability of classical Hertz contact theory is discussed. The influence of coefficient of friction on the stress distribution of contact zone and the contact states of contact surface are also investigated. The numerical results show that the material nonlinearity and the geometric nonlinearity (i.e. large deformation) of hydrogel lead to the invalidation of classical Hertz contact theory. For the oblique contact, the internal stress grads of hydrogel will be redistributed as the coefficient of friction increases. Meanwhile, the maximum stress position moves from underside to the contact surface. Two high stress zones occur inside and on the contact surface at the same time, respectively. Besides, when the coefficient of friction is smaller (i.e. μ < 0.05), for the collinear contact all contact points on the contact surface are in critical state from static friction to dynamic friction. But for the oblique contact, some contact points are always in stable static friction state.Keywords: hydrogel /large deformation /oblique contact /friction 全文HTML --> --> --> 1.引 言 作为一种具有网状结构的高分子聚合物材料[1 ] , 软体机器人用水凝胶在工程领域中存在着大量应用[2 ,3 ] . 软体机器人设计中的一些智能结构常需要利用水凝胶的摩擦接触[4 ] 来实现一定的功能. 例如: 水凝胶手指结构抓取小球[5 ] 、软体机器人行走[6 ] 、水凝胶仿生臂关节的接触[7 ] 等. 然而, 软体机器人用水凝胶材料质地柔软[8 ,9 ] , 富含水分[10 ] , 发生接触行为时, 接触区的变形较大. 同时外部形态的变化会影响内部水溶液的状态, 使水凝胶的力学性能发生显著改变, 进而反作用于接触状态, 导致摩擦接触行为异常复杂[11 ,12 ] . 接触响应不仅会影响软体机器人的操作精度, 而且直接关系到执行任务的成败, 甚至会导致软体结构的失效[13 ,14 ] .[15 ] 使用显微压痕方法测量水凝胶杨氏模量, 用显微镜测量微球体正向压入水凝胶的压痕深度, 并通过经典Hertz接触理论推导杨氏模量. 若将变形量控制在小变形范围内, 忽略表面摩擦, 一定程度上可避免经典Hertz接触理论的局限性. 对于水凝胶接触大变形问题, Long等[16 ] 利用ABAQUS有限元软件结合neo-Hookean模型, 数值模拟了水凝胶正向压痕实验, 并对经典Hertz接触理论进行了修正, 得到了适用于特定条件下的简单经验公式. 但对于复杂情况下水凝胶的含摩擦斜向接触问题未加讨论. Yang和Shen[17 ] 对普通柔性手指敲击过程中的摩擦斜向接触问题提出了新的计算模型, 初步验证了其可行性. 然而, 水凝胶软体机器人含摩擦斜向接触时, 摩擦对水凝胶内部应力分布和接触面摩擦状态的影响目前仍然缺乏深入的研究.[18 ,19 ] , 将接触过程抽象为水凝胶的含摩擦斜向接触力学问题, 并进行了数值计算. 讨论了水凝胶软材料的局部大变形接触行为与小变形线弹性体的Hertz接触行为的不同点, 分析了Hertz接触理论应用于大变形接触行为的局限性. 此外, 比较了水凝胶正向接触与斜向接触时的复杂响应, 研究了摩擦系数对水凝胶内部应力分布和接触面摩擦状态的影响.2.水凝胶斜向接触分析模型 如图1(a) 所示, 外部激励作用下水凝胶软体机器人手对目标体的抓取或软臂对目标体敲击, 是一个典型的硬质物体与软材料的含摩擦接触-碰撞问题. 本文旨在探索水凝胶驱动器与目标体接触过程中局部接触区的摩擦接触行为的特征和机理. 一方面, 实际目标体(钢球、石块等)的弹性模量通常比水凝胶大许多, 在接触过程中变形很小, 可忽略其变形效应; 另一方面, 本文关注的重点是接触过程中水凝胶的变化情况, 其变形效应明显. 因此, 本文将目标体和水凝胶的接触过程抽象为刚性压头与水凝胶的斜向接触模型.图 1 水凝胶软体机器人的接触 (a) 示意图; (b) 力学模型; (c) 离散模型Figure1. Hydrogel soft robot’s contact: (a) Schematic diagram; (b) mechanics model; (c) discrete model.2.1.力学模型 2.1.力学模型 如图1(b) 所示, 本文针对局部接触行为, 将水凝胶手指驱动器与硬质目标体的局部接触简化为球形压头斜向接触半无限大水凝胶的问题. 图1(b) 中, 圆柱形水凝胶的厚度为h , 水凝胶宽度为40h , 球形压头的半径为R , 应足够大以满足半无限大空间的要求. 压头受一个大小为δ 斜向位移载荷的作用, 斜向位移与竖直方向的夹角为φ . 模型中球形压头为刚体, 水凝胶材料变形前的初始弹性模量为E 0 . 当φ = 0°, 斜向接触则转变为经典Hertz理论中的正向接触.图1(c) 为水凝胶斜向接触的离散模型, 模型的压头部分视为刚体, 水凝胶部分进行网格划分. 局部接触区适当加密, 以提高接触力的计算精度. 水凝胶底面节点的位移约束为零, 其他边界自由.2.2.水凝胶材料模型 -->2.2.水凝胶材料模型 水凝胶是典型的软物质, 其力学模型的研究十分复杂. 本文软体机器人用水凝胶材料, 采用超弹性体本构模型[18 ,19 ] . 该模型假设: 1)变形过程中分子体积不可压缩; 2)变形过程中分子数目不发生变化. 将水凝胶整体视为均匀的超弹性体, 运用连续介质力学和分子扩散理论描述水凝胶吸水溶胀和变形过程.图2 为水凝胶在外部溶液或外载荷P 的作用下结构的变形示意图. 溶液和水凝胶之间有时存在水分子等物质交换, 会发生溶胀现象. 假设在初始状态(即t = 0瞬时), 水凝胶的参考构形为水凝胶干网络占据的空间区域. 任意一个质点M 0 的位置矢量和坐标分别记为R RK (K = 1, 2, 3, 分别代表x , y 和z 轴). 在后续任意瞬时t , 水凝胶占据的空间区域为即时构形, 原来的质点从位置点M 0 移动至位置点M , 点M 的位置矢量和坐标分别用r ri (R t ) (i = 1, 2, 3, 分别代表x , y 和z 轴)表示. 根据连续介质力学理论, 水凝胶变形梯度的各个分量GiK 可表示为图 2 水凝胶变形示意图Figure2. Schematic diagram of hydrogel deformation.E (G C ?)描述, 该能量为变形梯度G C 的函数. 由热力学原理, 自由能的变化量应等于外部机械载荷和溶剂所做的功之和, 即:μ 为外部溶液的化学势, Bi (R t )dV 为水凝胶微元的体积力, Ti (R t )dA 为水凝胶微元的表面力, dV 和dA 分别表示微元体积和面积.${\text{δ}} {G_{iK}}$ , 溶剂浓度有一个微小变量${\text{δ}}C$ 时, 微元自由能的变化量可以表示为U 表示微元的内部虚势能, W ext 表示外部虚功. 内部虚势能可进一步表示为${s_{iK}}$ 为名义应力. 由于外力可以分为体积力和表面力, 外部虚功可进一步表示为${\text{δ}}{r_i}$ 为虚位移. 将(5 )式和(6 )式代入(4 )式得3 )式和(7 )式代入(2 )式得${\text{δ}}{G_{iK}}$ 和${\text{δ}}C$ , (8 )式均成立, 故[20 ] , 水凝胶的自由能函数可表示为E s (G E m (C ?)为溶液混入聚合物网络的混合自由能. 两者分别写为如下形式:N 为聚合物分子链数, k 为玻尔兹曼常数, T 为开尔文温度, ${\lambda _i}(i = 1, \;2, \;3)$ 为各向溶胀比, v 为溶剂分子体积, $ \chi $ 为混合焓的无量纲量.13 )式作为约束引入自由能函数, 得到${H_{iK}}$ 表示变形梯度逆的转置, $\prod ({{R}}, t)$ 为拉格朗日乘子.12 )式和(13 )式分别代入(14 )式和(15 )式, 得到水凝胶的状态方程, 即3个名义主应力${s_1}$ , ${s_2}$ 和${s_3}$ 以及化学势μ :C 替换为μ ; 同时为了消除自由能函数中的数值奇异性, 需要将参考构形(水凝胶干网络)替换为具有一定溶胀的水凝胶.E (G C ?)运用勒让德变换(Legendre transformation), 可以得到水凝胶自由能函数的新形式:19 )式代入(2 )式, (9 )式和(10 )式中, 可得11 )—(13 )式代入(18 )式中, 可得$I = {G_{iK}}{G_{iK}}$ 为变形梯度张量的第一不变量, $J = \det ({{G}})$ 为变形梯度张量的第三不变量.22 )式代入(20 )式, 有${\sigma _{ij}} = $ $ {s_{iK}}{G_{jK}}/\det \left( {{G}} \right)$ . 将其代入(23 )式, 可得J = 1时, 自由能函数(22 )式存在数值奇异性, 在数值计算时, 参考构形需要满足J > 1. 选取水凝胶处于各向溶胀比为${\lambda _{\rm{1}}} = {\lambda _{\rm{2}}} = {\lambda _{\rm{3}}} = {\lambda _{\rm{0}}}$ 的自由溶胀状态作为新的参考构形, 水凝胶与化学势为${\mu _0}$ 的外部水溶液浸润并处于平衡态. 将${\lambda _{\rm{0}}}$ 和${\mu _0}$ 代入(23 )式, 并令应力为零, 可得25 )式为新参考构形下水凝胶的溶胀状态平衡关系. 相对于水凝胶干网络状态, 此溶胀状态下水凝胶的变形梯度为G ${{{G}}'}$ 为以溶胀状态为参考构形时水凝胶的变形梯度. 新参考构形下, 水凝胶的自由能函数为${I'} = G_{iK}'G_{iK}'$ , ${J'} = \det ({{{G}}'})$ . (29 )式显示了以溶胀状态为参考构形的水凝胶的超弹性体特性.2.3.有限元程序中材料模型的具体实现 -->2.3.有限元程序中材料模型的具体实现 根据自由能函数((29 )式), 本文利用ABAQUS用户自定义超弹性体的子程序UHYPER, 实现水凝胶有限元程序中的材料定义. 图3(a) 为本文编写的ABAQUS的用户子程序UHYPER的核心部分. 子程序主体以FORTRAN语言编写, 其中的参数$Nv$ , $ \chi $ 和${\lambda _{\rm{0}}}$ 通过有限元主程序中设置的材料参数传递给子程序, 子程序中超弹性体模型的应变能密度U 及其对变形梯度的第一、第三不变量的偏导数等均由水凝胶自由能函数得到.图 3 有限元方法 (a) ABAQUS用户子程序UHYPER; (b) ABAQUS数值计算流程Figure3. Finite element method: (a) ABAQUS user subroutine UHYPER; (b) ABAQUS numerical computation process.图3(b) 为压头与水凝胶斜向接触事件的ABAQUS数值计算流程图. 首先, 通过前处理完成几何模型的建立、材料的设置、约束和外载荷的施加以及网格划分. 其中, 材料的设置包括选择用户自定义超弹性体模型并导入自编的水凝胶材料子程序UHYPER, 并在前处理中输入$Nv$ , $ \chi $ 和${\lambda _{\rm{0}}}$ 的具体数值. 然后, 选择合适的接触算法处理压头和水凝胶之间的接触约束. 同时, 开启几何非线性分析选项以满足水凝胶大变形计算的要求. 此外, 在计算前, 主程序检查用户子程序接口是否打开, 并检验子程序语法的正确性. 最后完成含接触约束条件的静力平衡方程的迭代运算.3.经典Hertz接触理论的适用性分析 Hertz接触理论是解决弹性体小变形接触问题的经典理论方法, 然而运用经典Hertz理论求解水凝胶接触大变形问题值得怀疑, 本节拟通过数值计算, 定量分析水凝胶接触问题中经典Hertz接触理论的适用性.3.1.数值解与经典Hertz接触理论解的比较 3.1.数值解与经典Hertz接触理论解的比较 刚性球状压头正向接触水凝胶的数值实验中, 水凝胶层的横向半径为200 mm, 远大于水凝胶层的厚度h = 10 mm和压头半径R = 3 mm, 水凝胶层可以近似被认为是无限宽. 压头上施加δ = 1 mm的正向位移(φ = 0°), 接触面无摩擦. 因载荷、几何形状以及水凝胶层的接触变形关于y 轴中心对称, 因此采用轴对称的二维几何模型来减少计算量. 本文采用的水凝胶属于一类软体机器人常用的硬质强韧型水凝胶(stiff tough hydrogel)[5 ,19 ] , 不特指某一种化学材料制备的水凝胶. 水凝胶处于室温, 玻尔兹曼常数与温度的乘积$kT = 4 \times {10^{ - 21}}{\rm{ J}}$ , 分子体积$v = {10^{ - 28}}\;{{\rm{m}}^3}$ , 混合焓的无量纲量$ \chi $ = 0—1.2. 为使计算方便, 将等式(5 )两边同除以$kT/v = 4 \times {10^7}\;{\rm{ Pa}}$ 进行无量纲化处理. 没有吸收水分子的干水凝胶在小变形条件下的弹性模量为NkT , 一般为104 —107 N/m2 . 水凝胶的初始溶胀比选择为1.5, 属于典型的硬质强韧型水凝胶(其溶胀比一般在1.2附近). 如无特殊说明, 本文数值算例中水凝胶材料的参数取$Nv = 0.001$ , $\chi$ = 0.2, ${\lambda _0} = 1.5$ . 此类水凝胶属于具有较高弹性模量, 其初始弹性模量E 0 约为80 kPa[5 ] .图3(a) 为刚性球状压头与半无限大空间接触的局部变形示意图. 经典Hertz接触理论中, 假设接触导致的变形很小, 接触体只产生线弹性应变. 因此, 压头与半无限大空间的实际接触半径与图4(a) 中的Hertz接触半径几乎相等, 因此, 经典Hertz接触理论忽略了实际接触半径与Hertz接触半径之间的误差. 同时, 经典Hertz接触理论也忽略了弹性模量会随着压入过程而变化, 将接触力F c 表示为常弹性模量E 和压痕深度δ 的函数:图 4 刚性球状压头-半无限大空间 (a) 接触局部变形示意图; (b) 数值解与经典Hertz理论解的比较Figure4. Rigid spherical indenter-semi-infinite space: (a) Schematic diagram of local contact deformation; (b) comparison between numerical solution and classical Hertz theoretical solution.图4(b) 给出了无量纲量接触力F c /(ER 2 )与无量纲压下量$\delta {{/}}R$ 的关系, 对比了数值解与经典Hertz理论解. 数值解的收敛性已经经过验证, 结果表明, 随着压下量的增大, 经典Hertz理论的解与数值解的误差越来越大, 当$\delta {{/}}R = 0.3$ 时, 二者误差近似达到了100%, 这证明了经典Hertz理论对水凝胶大压下量接触问题不再适用.3.2.经典Hertz接触理论的失效原因 -->3.2.经典Hertz接触理论的失效原因 实际水凝胶具有固液两相性, 接触过程中, 水凝胶内部液体流动, 会导致其材料参数、弹性模量和密度等发生变化, 力学性能表现出明显的材料非线性. 同时, 局部接触区的大变形特征, 需要开启几何非线性数值计算才能得到正确的结果. 经典Hertz接触理论失效的具体原因主要有以下两方面.图5 给出了原长和横截面分别为L 0 和A 0 的水凝胶杆两端受相同大小的力的作用下, 发生纵向拉压时横截面无量纲正应力$\sigma {{/}}{E_0}$ 与拉伸比L /L 0 之间的关系, 其中${E_0}$ 为水凝胶的初始弹性模量, 正应力σ 为本文方法的数值计算结果. 杆变形后的长度为L , 截面面积为A . 图5 中虚线为弹性模量为${E_0}$ 的线弹性材料杆的$\sigma {{/}}{E_0}$ 与L /L 0 之间的关系. 对比水凝胶杆与线弹性材料杆的数值解可以发现, L /L 0 在1附近(即变形量较小)时, 二者几乎重合. 随着L /L 0 远离1(即变形量增大), 二者差距迅速变大, 这说明在大变形条件下, 线弹性本构不再适用于水凝胶材料.图 5 水凝胶材料的非线性Figure5. Nonlinearity of hydrogel material.4.水凝胶的斜向接触机理分析 24.1.离散模型(φ 4.1.离散模型(φ 水凝胶的斜向接触不再呈现中心对称, 需采用三维模型. 这里, 取$\delta = \sqrt 2 \;{\rm{ mm}}$ 和φ = 45°, 以保证压头的竖直方向的压下量和第3 节正向接触时的竖直方向压下量相同. 为尽可能满足减小计算量的要求, 根据结构和载荷的面对称性, 本文取整体模型的一半进行计算(见图6 ).图 6 三维有限元离散模型Figure6. Three-dimensional finite element discrete model.图6 ).4.2.局部接触区应力分布 -->4.2.局部接触区应力分布 图7 给出了两种接触情况下, 摩擦系数分别为μ = 0和μ = 0.3时水凝胶的Von-Mises应力分布情况.图 7 摩擦力导致的应力变化现象 (a) 正向接触; (b) 斜向接触Figure7. Stress changes caused by friction: (a) Collinear contact; (b) oblique contact.图7 可以看出:4.3.接触时摩擦系数对接触力响应的影响 -->4.3.接触时摩擦系数对接触力响应的影响 图8(a) 给出了刚性球状压头接触区与x-o-y 截面交线上受到的接触力情况. 由于结构和荷载的对称性, 对接触弧上的接触力进行分析, 进一步可推出压头整个接触面上的受力情况. 作用于接触弧上任意一点K 的接触力由该点接触面法线方向的接触压力f n 和切线方向的摩擦力f t 组成. f n 和f t 沿坐标轴方向上的投影分别为x 轴分量f nx , f tx 和y 轴分量f ny , f ty . 接触面上各点的接触力向点C 合成得到F c 和力偶矩M F c 在x 和轴y 轴的投影分别为F cx 和F cy . 各接触点上的f t 向点C 合成的结果为F t 和M t ; 各接触点上的f n 向点C 合成的结果为F n 和M n . 根据力的合成原理, 显然有${{{F}}_{\rm{c}}} = {{{F}}_{\rm{t}}} + {{{F}}_{\rm{n}}}$ 和${{M}} = {{{M}}_{\rm{t}}} + {{{M}}_{\rm{n}}}$ .图 8 接触面各点受力分析及接触合力F c 的大小 (a) 接触面各点受力分析图; (b) 不同摩擦系数下接触力F c 的各轴分量Figure8. Force analysis of each point of the contact surface and the magnitude of the contact force F c : (a) Force analysis diagram of each point of the contact surface; (b) axis components of the contact force F c under different friction coefficients.图8(a) 所示, 各力投影分量满足以下关系:图8(b) 给出了不同摩擦系数下接触力F c 沿竖直方向的分量F cy 和水平方向的分量F cx ?. 由于对称性, z 轴方向分量为零. 从图8 可以看出, 当压头正向接触水凝胶时, 接触力的竖直分量始终保持在0.26 N左右, 摩擦系数对其数值变化几乎没有影响; 当压头斜向接触水凝胶时, 由于水凝胶发生了切向变形, 导致其接触力的竖向分量约为0.28 N, 比正向接触时要大, 同时摩擦系数对其的影响也很小. 另外, 在刚性球状压头水平位移不变的情况下, 斜向接触与正向接触相比, 其接触力的水平分量随摩擦系数增大而增大.图9 给出了不同摩擦系数下的各点法向接触压力的合力和各点切向摩擦力的合力. 由于对称性, z 轴方向的分量为零. 分析图9 可以得到以下结论.图 9 不同摩擦系数下的各点的合力 (a) 法向接触压力的合力; (b) 切向摩擦力的合力Figure9. Resultant force of each point under different coefficients of friction: (a) Resultant force of normal contact pressure; (b) resultant force of tangential friction force.y 轴)分量F ny 呈现先逐渐下降后保持不变的特点, 转折点出现在摩擦系数μ = 0.25附近, 但下降幅度很小; 由模型对称性可知, 各点法向接触压力的合力的水平(x 轴)分量F nx 约为0.x 轴)分量F tx 和竖直(y 轴)分量F ty 均呈现先逐渐增大后保持不变的特点, 转折点同样出现在摩擦系数μ = 0.25附近. 由此可见, 较小的摩擦系数(μ < 0.25)会显著影响摩擦力在接触过程中的作用效果, 而较大的摩擦系数(μ > 0.25)对接触力的变化影响很小.F nx 与正向接触的值相差很小, 约0.02 N. 但由于刚性球增大了水平(x 轴)位移, 使得各点切向摩擦力的合力的水平(x 轴)分量F tx 在摩擦系数较大时明显增大. 当μ = 0.5时, 较正向接触增大了约5倍. 此外, 各点切向摩擦力的合力随着μ 的增大而变向.$x\text{-}o\text{-}y$ 一侧(z 轴负方向)的压头接触面上的接触力数据. 图10 给出了接触力在不同方向上投影的比值与摩擦系数之间的关系. 此外已经证明, F t y F n x F t x F n y μ 则表示$ x\text{-}o\text{-}y $ 平面与刚球面交线(弧AB )上各点均处于静摩擦转变为动摩擦的极限状态(证明详见附录A 部分). 观察图10 可以发现: 正向接触时, 摩擦系数较小(μ $ <0.05 $ ), 接触力投影的比值曲线与参考线(比值等于μ )重合, 表明接触弧AB 所有点处于静摩擦到动摩擦的极限状态. 进一步地, 由模型对称性可知, 接触面所有点处于静摩擦到动摩擦的极限状态; 随着摩擦系数的增大, 接触力投影的比值曲线与参考线分离并趋于稳定, 但始终处于参考线下方, 这表明接触面的部分区域处于稳定静摩擦状态. 斜向接触时, 通过与参考线相比, 发现F t y F n x μ , 表明接触弧AB 上的部分区域处于稳定静摩擦状态.图 10 不同摩擦系数下接触力分量的比值F ty /F nx 和F tx /F ny (a) 正向接触情况; (b) 斜向接触情况Figure10. Ratios of contact force components F ty /F nx and F tx /F ny under different friction coefficients: (a) Positive contact situation; (b) oblique contact situation.5.结 论 本文研究了水凝胶的斜向接触大变形行为及其摩擦效应, 数值计算了水凝胶的正向接触和水凝胶的斜向接触两个算例, 研究得到以下主要结论:μ < 0.05)的水凝胶接触面所有点处于静摩擦到动摩擦的极限状态; 而斜向接触中, 任意摩擦系数下均不会出现所有点均处于静摩擦到动摩擦的极限状态.附录A 关于极限状态的证明 命题 : 当接触面满足${F_{{\rm{t}}x}} = \mu {F_{{\rm{n}}y}}$ 和${F_{{\rm{t}}y}} = \mu {F_{{\rm{n}}x}}$ 时, 接触面上任意一点均处于静摩擦转变动摩擦的极限状态.证明 : 利用反证明法, 假设接触面上存在一点P 处于非极限摩擦状态, 即其切向摩擦力$f_{\rm{t}}^P$ 与法向接触压力$f_{\rm{n}}^P$ 的比值为$f_{\rm{t}}^P/f_{\rm{n}}^P \ne \mu $ , 使得${F_{{\rm{t}}x}} = \mu {F_{{\rm{n}}y}}$ 和${F_{{\rm{t}}y}} = \mu {F_{{\rm{n}}x}}$ 同时成立.μ , 故点P 处的接触力应满足条件P 处的接触力的各轴投影分量也满足${F_{{\rm{t}}x}} = \displaystyle\sum {{f_{{\rm{t}}x}} = f_{{\rm{t}}x}^P} + \displaystyle\sum {f_{{\rm{t}}x}^{{\rm{other}}}}$ , 又因为$\displaystyle\sum {f_{{\rm{t}}x}^{{\rm{other}}}} \leqslant $ $ \displaystyle\sum {\mu f_{{\rm{n}}y}^{{\rm{other}}}}$ , 则有${F_{{\rm{t}}x}} < \mu \Big(f_{{\rm{n}}y}^P + \displaystyle\sum {f_{{\rm{n}}y}^{{\rm{other}}}} \Big) = \mu \displaystyle\sum {{f_{{\rm{n}}y}}}$ , 进一步可化简为$f_{{\rm{t}}x}^{{\rm{other}}}$ 表示P 点以外的点的摩擦力的x 轴分量, $f_{{\rm{n}}y}^{{\rm{other}}}$ 表示P 点以外的各点的接触压力的y 轴分量. 同理:A5 )式推论与假设条件矛盾, 故当接触面满足${F_{{\rm{t}}x}} = \mu {F_{{\rm{n}}y}}$ 和${F_{{\rm{t}}y}} = \mu {F_{{\rm{n}}x}}$ 时, 接触面上任意一点均处于静摩擦转变动摩擦的极限状态.  图 1 水凝胶软体机器人的接触 (a) 示意图; (b) 力学模型; (c) 离散模型
图 1 水凝胶软体机器人的接触 (a) 示意图; (b) 力学模型; (c) 离散模型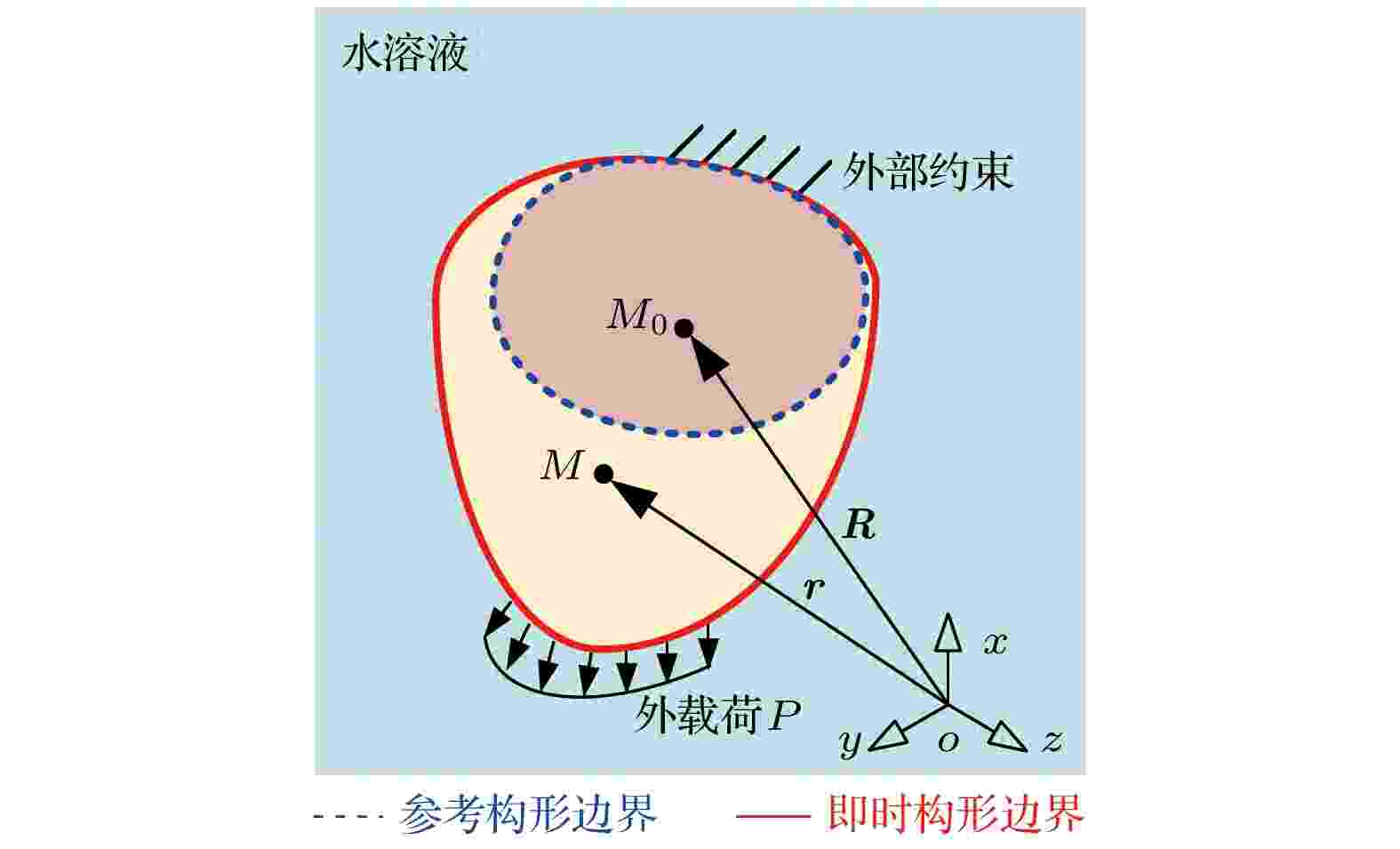 图 2 水凝胶变形示意图
图 2 水凝胶变形示意图




























 图 3 有限元方法 (a) ABAQUS用户子程序UHYPER; (b) ABAQUS数值计算流程
图 3 有限元方法 (a) ABAQUS用户子程序UHYPER; (b) ABAQUS数值计算流程









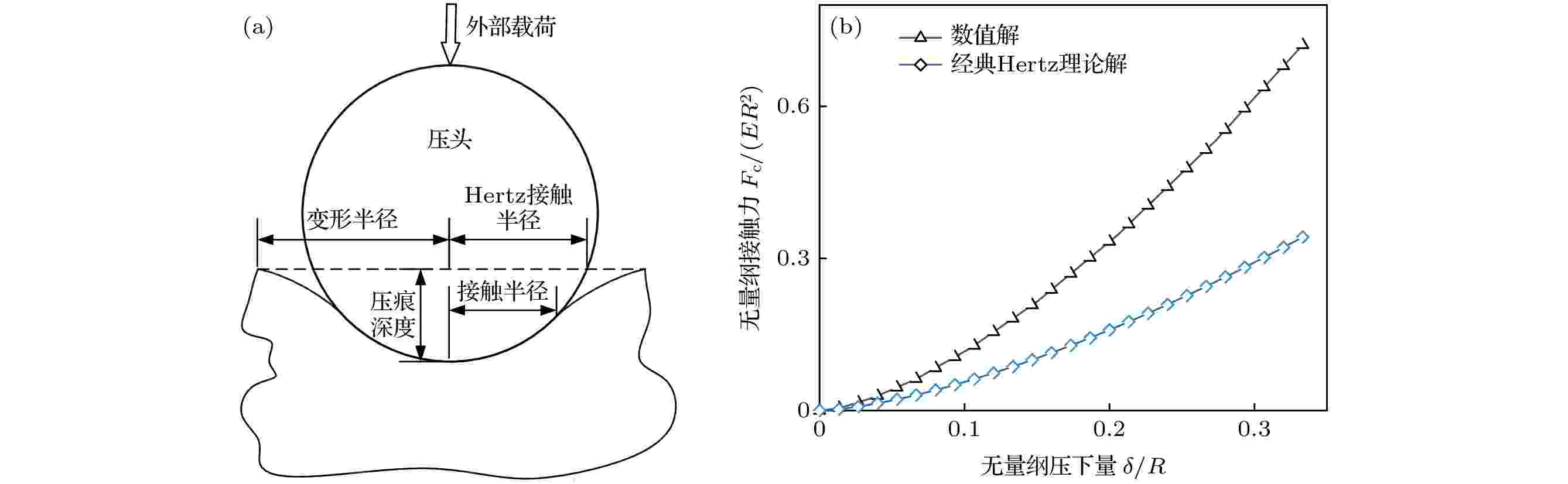 图 4 刚性球状压头-半无限大空间 (a) 接触局部变形示意图; (b) 数值解与经典Hertz理论解的比较
图 4 刚性球状压头-半无限大空间 (a) 接触局部变形示意图; (b) 数值解与经典Hertz理论解的比较









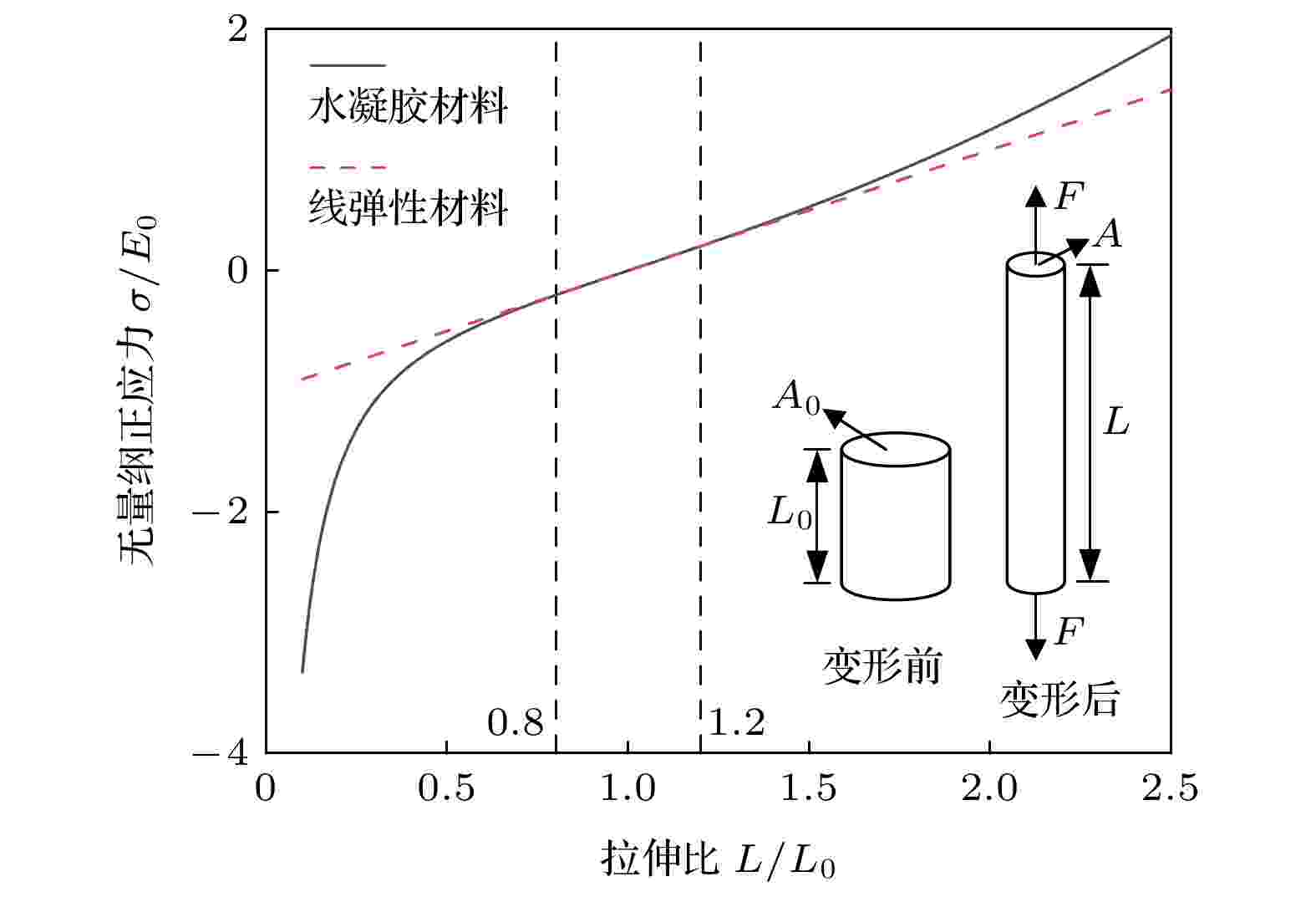 图 5 水凝胶材料的非线性
图 5 水凝胶材料的非线性
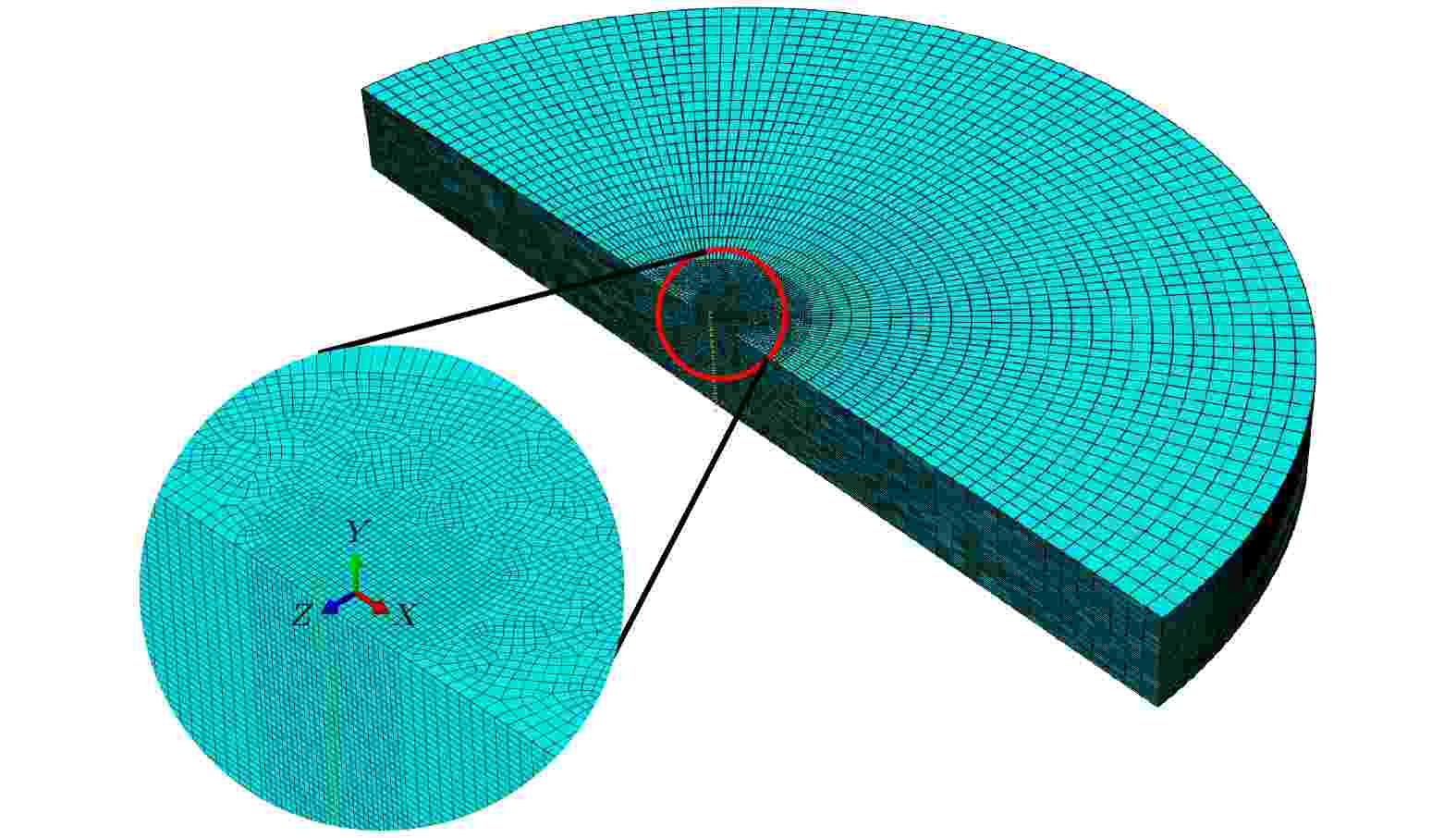 图 6 三维有限元离散模型
图 6 三维有限元离散模型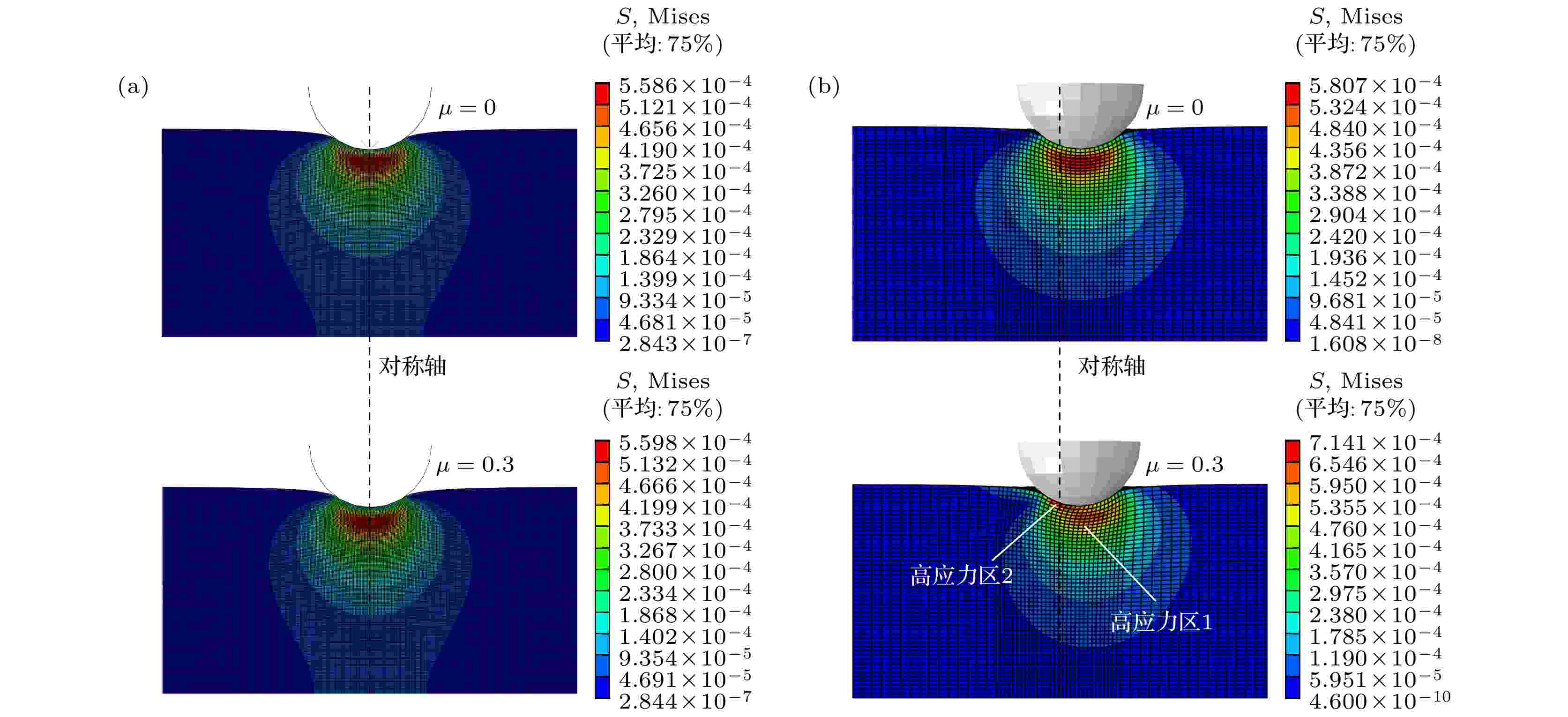 图 7 摩擦力导致的应力变化现象 (a) 正向接触; (b) 斜向接触
图 7 摩擦力导致的应力变化现象 (a) 正向接触; (b) 斜向接触

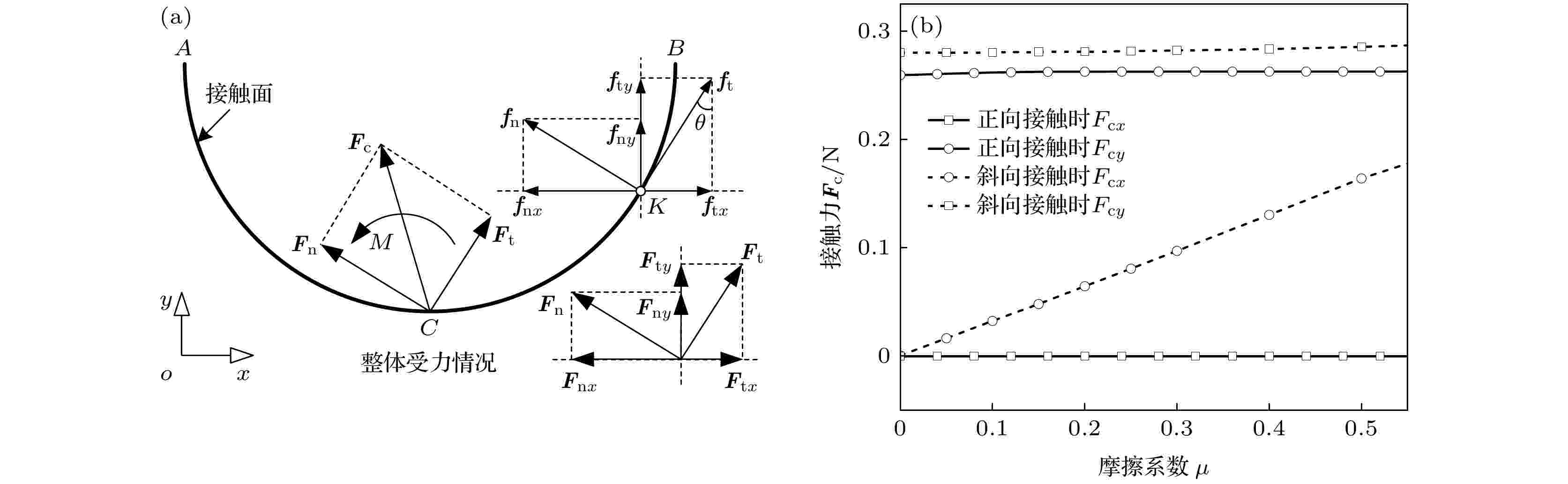 图 8 接触面各点受力分析及接触合力Fc的大小 (a) 接触面各点受力分析图; (b) 不同摩擦系数下接触力Fc的各轴分量
图 8 接触面各点受力分析及接触合力Fc的大小 (a) 接触面各点受力分析图; (b) 不同摩擦系数下接触力Fc的各轴分量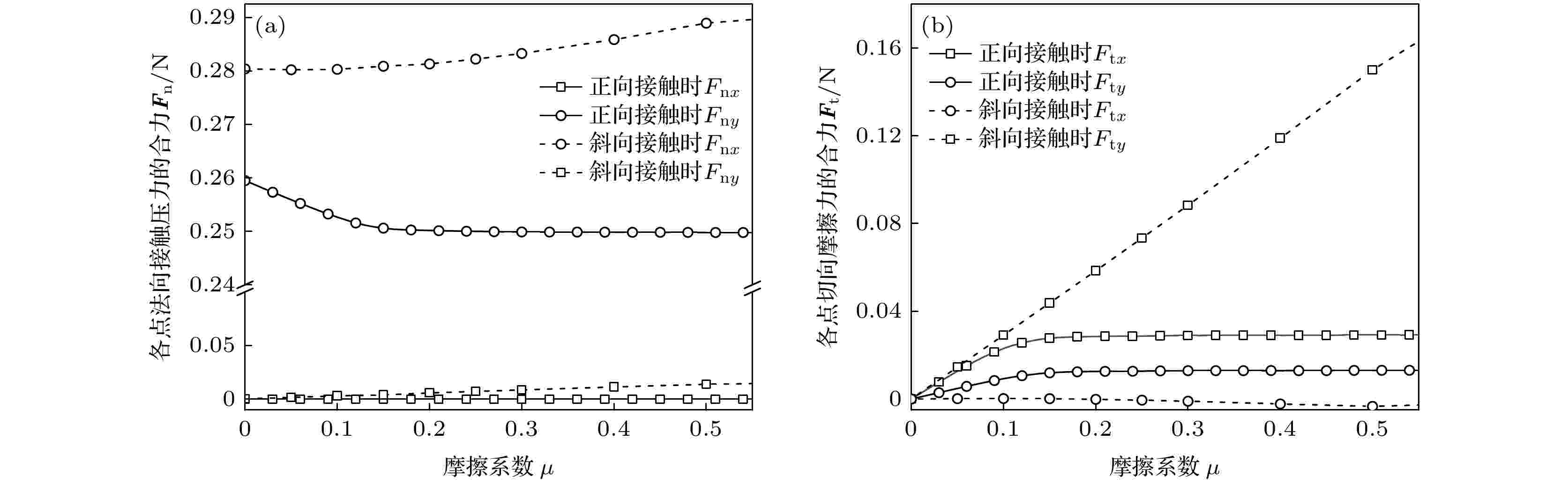 图 9 不同摩擦系数下的各点的合力 (a) 法向接触压力的合力; (b) 切向摩擦力的合力
图 9 不同摩擦系数下的各点的合力 (a) 法向接触压力的合力; (b) 切向摩擦力的合力


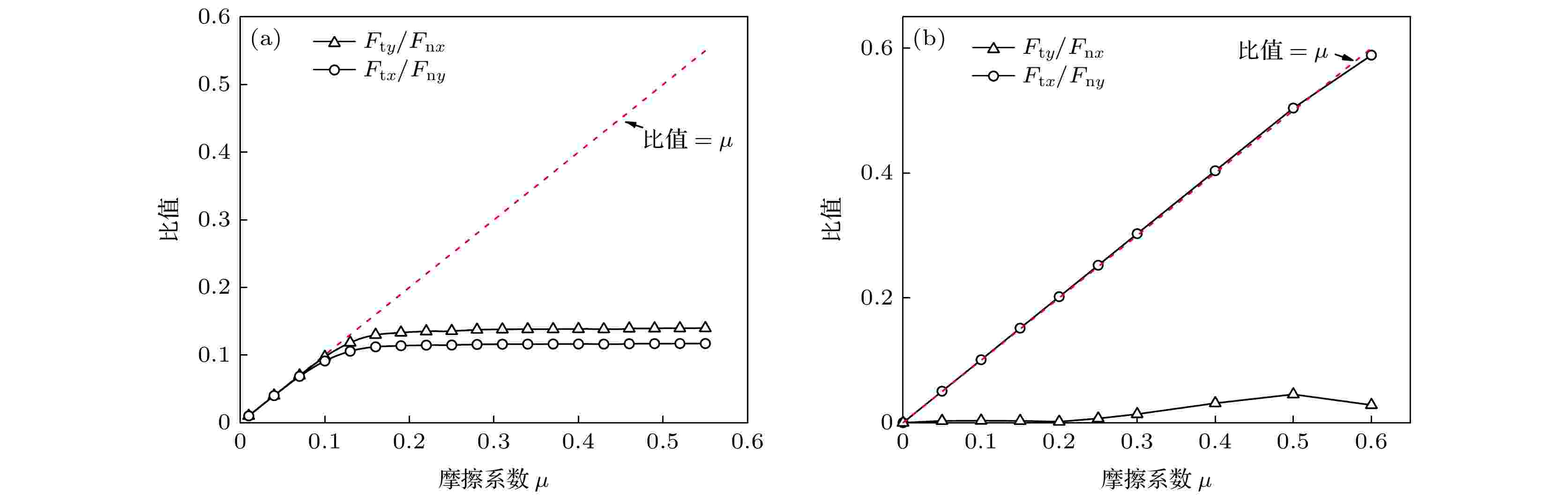 图 10 不同摩擦系数下接触力分量的比值Fty/Fnx和Ftx/Fny (a) 正向接触情况; (b) 斜向接触情况
图 10 不同摩擦系数下接触力分量的比值Fty/Fnx和Ftx/Fny (a) 正向接触情况; (b) 斜向接触情况














